1 Introduction

In recent years, environmentally conscious thinking and efforts to reduce energy use have priority. One feasible form of engineering practice is the appropriate sizing and operation of systems and system components. Furthermore, many critical industrial applications are known, where non-Newtonian fluids are widely delivered by pumping, for instance, wastewater [1], automobile [2], food [3], energy and petroleum industry [4]. Many Bingham plastic fluids are used in these areas, such as toothpaste and mayonnaise [5], activated sludge [1] and ice-slurry [6, 7]. In addition, a study of the Bingham flows appears in recent medical research as well [8].

A large volume of published books and studies is available for hydraulic losses of straight pipes and fittings in the case of Newtonian fluids, e.g., [9,10,11]. Nevertheless, in the design of the piping systems, general rules are often used instead of accurate sizing. However, their influence on the overall pressure drop can be significant for single-phase flow [9]. In addition, the exact estimation of the losses that arise in pipe fittings, such as bends, diffusers, or valves, can also play an essential role in energy efficiency and operation safety, such as on the suction side of a pump.

Several researchers have studied the flow using Newtonian fluid, focusing on one of the most commonly used pipe fittings: pipe bends [9, 12,13,14]. In general, the radius of curvature, the Dean number, and the Reynolds number all play an important role in describing the complex flow pattern. Moreover, Kim et al. [15] found that the swirl intensity of the secondary flow is a strong function of the radius of curvature of the examined bends in turbulent flow. Estimation of the losses and the description of the flow in the bend can also be important for other elements located at the upstream side of the bend. The bends can influence the volumetric flow rate measuring devices [16], erosion effects [17] or particle separation [18].

A considerable amount of literature has been published on straight pipe flow, and friction factors in non-Newtonian, mainly Bingham plastic fluids [19,20,21,22,23,24]. The importance of this research is obvious because the losses due to friction are dominant in hydraulic systems [10]. In addition, the widely published friction factors provide a suitable way to validate our CFD (Computational Fluid Dynamics) models with them.

A growing body of studies investigates the losses of pipe elements and fittings in the case of non-Newtonian fluids. Flow characteristics of power-law fluids were examined with CFD methods in tee junctions [25, 26], and in sudden contraction and expansion [26, 27]. Investigation on the flow field of ice slurry in a horizontal \(90^\circ\) bend by a CFD-PBM (Population Balanced Model) coupled model was presented in Cai et al. [7]. They found that the plug-like velocity profiles indicate the non-Newtonian behavior. As a result of the secondary flow, the ice particles gather on the outer wall of the elbow section. Pressure drops and loss coefficients of a phase change material slurry were also investigated in \(90^\circ\) bend [26]. The extensive experimental results with the applied power-law fluids showed that the loss coefficient mainly decreased with the modified Reynolds number. Similar results were obtained by Liu et al. [27] on coal-water slurry. In addition, an optimum value of the bend diameter ratio was established for the test fluid, to minimize the local pressure loss. Rawat et al. [28] studied the flow field in a \(90^\circ\) elbow-meter with high concentration coal ash slurries. The CFD investigations showed that the effect of yield stress is only marginal for such slurries in the turbulent regime. The velocity profile for the pressure-driven flow of a Bingham fluid was examined in a curved channel by Roberts et al. [8]. The change in velocity profile and the plug were shown at different cross sections in the bend with the analytical and CFD results. Fellouah et al. [29] also provides a detailed analysis of several non-Newtonian models and mentions the importance of the Dean number and the Dean vortices, respectively. Recently, Sutton et al. [30] characterized yield-stress fluids and Li et al. [31] investigated fresh cement mortar like fluids through a pipe bend.

The studies mentioned above indicated that non-Newtonian flows in bends are an actively researched field. However, a wide range of parameters, such as the Hedström number, the Reynolds number, and the Bingham number, needs further analysis. Therefore, the main aim of the present study was to investigate the Bingham plastic flows in pipe bends with a wide range of material properties and geometrical conditions using validated CFD models. The results are significant for guiding the safety and energy-efficient design and operation flow systems with Bingham plastic fluids.

2 Theory and modeling

2.1 Definitions

The pipe friction factor (f) is calculated from the pressure drop in a 1D length straight pipe section before the fitting, on a fully developed flow:

$$\begin{aligned} f =\Delta p_{p} \left( \frac{L}{D} \frac{\rho }{2} \overline{v}^2 \right) ^{-1}, \end{aligned}$$
(1)

in which \(\Delta p_{p}\) is the total pressure drop in the pipe section, \(\rho\) is the fluid density, L is the length of the section, D is the inner diameter of the pipe, and \(\overline{v}\) is the average velocity.

The loss coefficient (\(\zeta\)) of the \(90^\circ\) bend is defined as the non-dimensional difference in total pressure between the two ends of a pipe or fitting (see [27]):

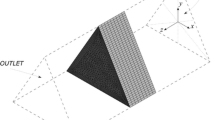
$$\begin{aligned} \zeta =\Delta p_{e} \left( \frac{\rho }{2} \overline{v}^2\right) ^{-1}, \end{aligned}$$
(2)

in which \(\Delta p_{e}\) is the total pressure drop across the element. However, in the case of CFD computations, one usually does not calculate the \(\Delta p_{e}\) pressure loss directly at the upstream and downstream side of the actual element, but straight pipe segments are attached to both sides (see Fig. 1) (similar to [9, 26, 32]). In our research, the pressure drop was calculated between a plane 1D distance before and a plane 9D distance after the bend, which was verified by a preliminary study. Our calculations showed that the pressure loss calculated between these planes has no more than \(2.5\%\) difference, compared to that calculated between the positions 50D before and after the elbow. The loss caused by the wall friction of the added straight sections was subtracted from the calculated total pressure drop. Thus, the \(\Delta p_{e}\) in Eq. (2) included the losses due to the wall friction and the shape inside the bend; furthermore, the forward disturbance caused by the fitting was taken into consideration.

Madlener et al. [21] introduced a generalized Reynolds number (\({\textrm{Re}_\textrm{gen}}\)) for power-law, Bingham, and Herschel–Bulkley type of fluids as well. For Bingham fluids, this is given by

$$\begin{aligned} {\textrm{Re}_\textrm{gen}} = \dfrac{\overline{v} D \rho }{\frac{\tau _{0}}{8}\frac{D}{\overline{v}}+\mu _{B} (\frac{3m+1}{4m})}, \end{aligned}$$
(3)

where \(\mu _{B}\) is the viscosity consistency of the Bingham fluid, \(\tau _{0}\) is the yield stress and m is the local gradient of the shear stress-shear rate in a log-log diagram:

$$\begin{aligned} m = \dfrac{\mu _{B} \frac{8 \overline{v}}{D}}{\tau _{0} + \mu _{B} \frac{8 \overline{v}}{D}}. \end{aligned}$$
(4)

For laminar and fully developed flow, the Darcy friction factor (\(f_{D}=64/\textrm{Re}\)) is defined; for turbulent flow through a hydraulically smooth pipe, the Blasius equation is used (\(f_{B} =0.316/\textrm{Re}^{0.25}\)) to relate the friction factor and the flow conditions in the case of Newtonian fluids (see e.g., [11]). For non-Newtonian flows, using the generalized Reynolds number in the Darcy and the Blasius equations can be considered a good approximation [33,34,35]; although, other calculation methods can be found in [5, 23, 24].

Dean [36] showed that as a result of the curvature, a pair of symmetric, counter-rotating vortices are present in a bend. Due to this fact, the Dean number, defined as \(\textrm{De} = \textrm{Re} \sqrt{\frac{D}{2R}}\), must be considered as a parameter with similar importance as the Re number (e.g., [9]). For non-Newtonian fluids, the generalized De number can be defined with the generalized Reynolds number as [29]

$$\begin{aligned} {\textrm{De}_\textrm{gen}} = {\textrm{Re}_\textrm{gen}} \sqrt{\frac{D}{2R}}, \end{aligned}$$
(5)

where R is the radius of the bend curvature.

If the losses caused by the curvature are negligible compared to the friction losses along the quarter-arc, the pressure loss of the pipe element is purely frictional. From that, in the case of laminar flow purely frictional losses through \(90^\circ\) bend is prescribed

$$\begin{aligned} \zeta \frac{D}{R} \approx \frac{\pi }{2}\frac{64}{{\textrm{Re}_\textrm{gen}}}, \end{aligned}$$
(6)

which means that the \(\zeta \frac{D}{R}\) quantity is inversely proportional to the \({\textrm{Re}_\textrm{gen}}\) when the wall friction is dominant in laminar flow. This happens, when the curvature is small. Similar relationship between \(\zeta \sqrt{\frac{D}{R}}\) and the \({\textrm{De}_\textrm{gen}}\) number under the same circumstances can be derived:

$$\begin{aligned} \zeta \sqrt{\frac{D}{R}} \approx \frac{\pi }{2}\frac{64}{{\textrm{De}_\textrm{gen}}}\frac{1}{\sqrt{2}}. \end{aligned}$$
(7)

In the case of Bingham fluids, another important dimensionless group (highlighting the importance of yield stress) is the Hedström number (He), which is defined [23] as

$$\begin{aligned} He =\frac{D^2 \rho \tau _{0}}{\mu _{B}^2}. \end{aligned}$$
(8)

It is also customary to define the Bingham number (Bi) for fluids with yield stress as

$$\begin{aligned} Bi = \frac{\tau _{0} D}{\mu _{B} \overline{v} }, \end{aligned}$$
(9)

and the Plastic number (Pl) [37]

$$\begin{aligned} Pl = \frac{\tau _{0}}{\tau _{0} + \mu _{B} \overline{v}/D }=\frac{Bi}{1 + Bi}. \end{aligned}$$
(10)

The Plastic number is a normalized quantity \(0 \le Pl \le 1\), when \(Pl=0\) the fluid behaves Newtonian, while \(Pl=1\) means maximum plasticity without viscous properties.

2.2 Rheology

In the case of the Bingham plastic fluids, the rheological behavior is described by

$$\begin{aligned} \tau =\tau _{0} + \mu _{B} \dot{\gamma }, \end{aligned}$$
(11)

with \(\mu _{B}\) viscosity consistency and \(\tau _{0}\) yield stress, see [20].

The friction losses traditionally depend on the Reynolds and Hedström numbers [5, 38]. These dimensionless groups are defined as in Eq. (3) and Eq. (8). In our study, ten different yield stresses were investigated. We note that the Bingham fluid appears only in our CFD computations, where the pipe diameter, the density, and the viscosity consistency were fixed, and the Hedström number was controlled by varying the yield stress. During the research, the He number was used throughout to characterize the fluid. The actual values were \(D = 0.1\) m, \(\rho = 1250\) kg\(/m^3\) and \(\mu _{B} = 0.07\) Pa s, the yield stresses, the Hedström numbers and the investigated mean velocity ranges are given in Table 1 for the ten different viscoplastic materials.

Table 1 Test matrix: yield stresses, Hedström numbers and corresponding mean velocity and generalized Reynolds number ranges of the investigated Bingham plastic flows
Full size table

2.3 Governing equations

The present study used the commercial CFD code ANSYS CFX, and ICEM CFD was applied as a meshing tool. The ANSYS software generally solves the Reynolds-averaged Navier–Stokes equations (RANS), the continuity equation, and the transport equations associated with the actual turbulence model [14, 39, 40]. For non-Newtonian fluids, the software solves RANS-like equations for a Generalized Newtonian Fluid (GNF), in other words, the momentum equations considering a GNF and the Reynolds average approach. The software calculates the specific, local dynamic viscosity value for the Bingham fluids from the apparent viscosity. The material model describing the actual rheology provides the relationship between the stress and strain tensors [28, 33, 40]. Regarding the turbulence modeling, the \(k-\omega\) SST model turned out to be appropriate, which was tested for non-Newtonian flows [28, 41]. The value of the critical modified Reynolds number, indicating the laminar-turbulent transition is unclear. Thus, simulations performed without a turbulence model would have led to significant errors outside the laminar region. In contrast, based on our calculations, using the turbulence model in the laminar region did not cause an error larger than \(5\%\). A high-resolution spatial scheme was used for all equation classes. This scheme is a bounded second-order upwind biased discretization scheme [40].

2.4 Geometry and meshing

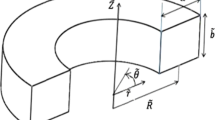
In our study, five different geometries were examined. Beside the fixed D diameter, the curvature was varied by the curvature ratios of \(R/D=1,2,4,6,10\) (see Fig. 1), so the length of the bends differed from each other.

A fully structured 3D mesh was used, which was earlier validated via a grid-independence study [34, 41]. In the boundary layer near the wall, the resolution of the cells was chosen with special care. The \(y^+\) (dimensionless wall distance) values were examined after the calculations and, apart from the narrow (\(\approx 1D\)) environment of the inlet, did not exceed 1 in the vast majority of models, similarly to [42], see [40] for details.

There were 15 cells on the central rectangular lines of the “O-grid” type mesh (see [40]), 60 cells along the circumference, and 20 cells along the connecting lines. More details of the meshes are given in Fig. 2 and in Table 2. Additional straight pipes of 50D length were added to the upstream (similar to [14]) and 10D length [43] to the downstream sides to allow proper boundary conditions (see Fig. 1, which was created in ANSYS CFX). It is important to highlight that our models were also validated by our own laboratory measurements, which the authors described in detail in their previous study [41].

Fig. 1
figure 1

Sketches of the CFD geometries; additional planes for processing the numerical results were defined at \(\phi = 0^\circ ; 45^\circ ; 90^\circ\) angles and in the distance of 1D, 2D, 3D, 4D and 5D after the bend; D: inner diameter of the pipe; R: radius of the curvature

Full size image
Fig. 2
figure 2

The 3D structured numerical mesh

Full size image
Table 2 Number of elements of the CFD model for the bends
Full size table

2.5 Simulation details

Steady-state computations were performed, similar to those in [14, 44]. At the inlet, the fully developed turbulent velocity profile for Newtonian fluids (see e.g., [49]) and at the outlet average static pressure were prescribed as a boundary condition. The 50D long straight pipe was sufficient to let the correct velocity profile develop before the investigated geometry region. The rest of the surfaces were set to no-slip hydraulically smooth walls. The fluids were incompressible, and the flow was isothermal. The built-in material model was employed with the material properties prescribed in Sect. 2.2 and detailed in Table 1.

A complete calculation included 200-25 000 iterations depending on the Reynolds number and material properties and ran for up to 25 h on a standard desktop computer (3.4 GHz CPU, 8 GB RAM). Convergence in the range of the Hedström number of \(He\approx 10^3-10^9\) was only achieved by turning on the Local Timescale Factor option. This factor is a multiplier of the local element-based timescale [40], and in our simulations, we used the value of 5. To stop the calculation, in addition to the \(10^{-6}\) convergence criteria, the total pressure drop change between the inlet and the outlet was also monitored, which had to be less than \(1\%\) in 100 consecutive iteration steps.

3 Results and discussions

3.1 The friction factor of the straight pipe

The survey of the pipe friction factors of the straight sections was mainly used to validate the applied model. The friction factors are presented as the function of the \({\textrm{Re}_\textrm{gen}}\) in Fig. 3a. Based on Madlener et al. [21], \({\textrm{Re}_\textrm{gen}}\) arranged the calculated friction factors to the Darcy curve (\(f_{D}=64/{\textrm{Re}_\textrm{gen}}\)) in the case of laminar flow conditions (red line on the figure). Interestingly, friction factors were arranged quite well to the Blasius form (\(f_{B} =0.316 /{\textrm{Re}_\textrm{gen}}^{0.25}\)) in turbulent conditions (denoted with a black dashed line). Except for the transition range, the difference between the calculated values and the analytical Darcy and experimental Blasius formulas showed a maximum difference of \(12\%\) and an average of \(5\%\).

The mean velocity profiles in the straight pipe section were compared to analytical and experimental results to validate our CFD model further. Li et al. [45] used the analytical solution of the completely developed Herschel–Bulkley flow introduced by Gupta and Zhao [46] as the validation of the laminar mean velocity profile. The comparisons of our velocity profiles to the analytical solution when n=1 are presented at different generalized Reynolds numbers and Hedström numbers in Fig. 3b. There was a good agreement between the CFD simulation and the analytical profiles, except for \({\textrm{Re}_\textrm{gen}}=540\) and \(He=10\); where the velocity profile starts to diverge from the laminar. The literature [47, 48] also contains experimental turbulent velocity profiles for Bingham fluids for Re = 14,500 and He = 125,000. Figure 3c shows the results of our present CFD calculation with the same dimensionless parameters agreeing well with the measured velocity profiles.

Fig. 3
figure 3

Validation of the numerical model: a The calculated friction factor of the straight pipe segment as the function of the generalized Reynolds number; red line: Darcy friction factor; black line: Blasius equation. b Comparison of present calculated and analytical [45, 46] (green solid lines) velocity profiles in the laminar region. c Comparison of present calculated and measured [47, 48] velocity profiles in the turbulent region

Full size image

3.2 Loss coefficients of bends

Figure 4 presents the dimensionless loss coefficient \(\zeta\) of the five different bends calculated with all the investigated Bingham fluids as the function of the generalized Reynolds number (on a) panel) and as the function of the Dean number (on b) panel).

Liu and Duan [27] defined a local resistance coefficient for higher generalized Reynolds numbers, based on their experiments with bends of \(R/D=1.5{-}6\) for power-law fluids. The measured local resistance coefficients were between 1.5 and 0.7 for diameters of \(D = 25,40,50\) mm in the range of the generalized Reynolds number \(1000<{\textrm{Re}_\textrm{gen}}<2000\). Our results also were in this range, as shown in Fig. 4a) panel. Turian [32] had experimental results of \(90^\circ\) bends with \(R/D=4.5\) and \(R/D=8.5\) with non-Newtonian slurries, see also in Fig. 4a and c panel. Spedding et al. [9] stated that the most reliable relationship between the Dean number and the loss coefficient was given by White [50]. Figure 4b panel shows, that our CFD results were in a good agreement with them.

Fig. 4c panel shows that the introduction of the Dean number in itself was not suitable for drawing general conclusions from the results of different curvatures, even if it was calculated from the generalized Reynolds number containing the non-Newtonian material properties, see Eqs. (3) and (5).

Fig. 4
figure 4

The calculated loss coefficients of the five bends a as the function of the generalized Reynolds number; b as the function of the generalized Dean number; c \(\zeta \frac{D}{R}\) as the function of the generalized Reynolds number; d \(\zeta \sqrt{\frac{D}{R}}\)as the function of the generalized Dean number

Full size image

Based on Eqs. (6) and (7) the dimensionless quantities \(\zeta \frac{D}{R}\) and \(\zeta \sqrt{\frac{D}{R}}\) were defined to investigate. The \(\zeta \frac{D}{R}\) is presented as the function of \({\textrm{Re}_\textrm{gen}}\) in Fig. 4c panel. Our calculated losses were close the experimental ones of Turian et al. [32]. Figure 4d panel shows the \(\zeta \sqrt{\frac{D}{R}}\) plotted against the Dean number. The curves of the purely frictional losses in the quarter-arcs can be seen in Fig. 4c and d panels with black dotted lines. In the lower region of \({\textrm{Re}_\textrm{gen}}\) and \({\textrm{De}_\textrm{gen}}\), the calculated loss coefficients fit the lines in the log-log diagram, so in this region, the losses were mainly due to the wall friction.

As it is shown in Fig. 5, the calculated quantities did not differ in this range by more than \(15\%\) from the values resulting from purely frictional ones for any ratio of curvature (\(R/D=1-10\)). This fact proved that in the case of Bingham plastic fluids in such a wide range of Hedström numbers (\(He=10^0-10^9\)), the flow was principally unidirectional for low Dean numbers as well as with Newtonian fluids. Based on our simulations, the limit for the generalized Reynolds and Dean numbers could be set to 20 and 40, respectively. Turian et al. [32], Marn and Ternik [51] and Liu and Duan [27] showed by experiments that the loss coefficient of a bend could be drawn as \(\zeta =K_{1}\cdot {\textrm{Re}_\textrm{gen}}^{{K}_{2}}\), where \(K_{1}\) and \({K}_{2}\) are constants. In this range, the coefficient of determination was \(R^{2}=0.9998\) of our fit as \(\zeta = \sqrt{\frac{R}{D}} {\frac{\pi }{\sqrt{2}}} {\frac{64}{{\textrm{De}_\textrm{gen}}}}= {\frac{R}{D}} {\frac{\pi }{2}}{\frac{64}{{\textrm{Re}_\textrm{gen}}}}\). This showed a good agreement with the previous literature, provided that \(K_{1}\) and \(K_{2}\) were equal to \(K_{1}={\frac{R}{D}} {\frac{64\pi }{2}}\) and \({K}_{2}=-1\).

Fig. 5
figure 5

Comparison of the purely frictional and calculated loss coefficients of the bends; left: the \(\zeta \frac{D}{R}\) in the region of \({\textrm{Re}_\textrm{gen}}<20\); right: the \(\zeta \sqrt{\frac{D}{R}}\) in the region of \({\textrm{De}_\textrm{gen}}<40\). Dotted lines: the range of \(\pm 15 \%\)

Full size image

Although the good fit in the lower region of \({\textrm{Re}_\textrm{gen}}\) and \({\textrm{De}_\textrm{gen}}\) is spectacular, in the higher regions, we found that the loss coefficient takes more values with the same generalized Reynolds number for the same geometry. To take a closer look, we selected the calculations of \({\textrm{Re}_\textrm{gen}}\approx 180\) as a demonstration. This sample is indicated with a dashed vertical line in Fig. 4 c) panel. The generalized Reynolds numbers and Dean numbers of these simulations were within \(5\%\) but they were performed with different material properties via different Hedström numbers, thereby with different mean velocities. Figure 6 presents the velocity magnitude in the symmetry plane in the simulations at \({\textrm{Re}_\textrm{gen}}\approx 180\). Although the \({\textrm{Re}_\textrm{gen}}\) and \({\textrm{De}_\textrm{gen}}\) numbers were almost equal for one geometry in pairs, very different flow patterns are on the left and right panel of Fig. 6. This means that the generalized Reynolds number and Dean number are not sufficient to characterize flow similarity in these bends but the Hedström number is also needed. Thangam and Hur [52] showed that the secondary flow intensity decreases when the curvature ratio increases. Figure 6 illustrates the same at both of the Hedström numbers.

The exact parameters of these analysed cases are summarized in Table 3. The relative differences between the modified loss coefficients in the last row of the table were calculated per bends by taking the \(v=0.1\) m/s as the initial value. The loss coefficient also decreased with the increasing curvature ratio. Our results showed that the lower the R/D ratio, the higher the differences between the losses at the same \({\textrm{Re}_\textrm{gen}}\) (see in the last row in Table 3). Therefore, the next section of the survey is in detail about the bend with \(R/D=1\) ratio.

Table 3 Parameters of the detailed cases at \({\textrm{Re}_\textrm{gen}}\approx 180\) for all the different bends
Full size table
Fig. 6
figure 6

Velocity magnitude in the symmetry plane of the bends at \({\textrm{Re}_\textrm{gen}}\approx 180\); left: \(\overline{v}=0.1\) m/s mean velocity with \(He=10^0\); Right: \(\overline{v}=1\) m/s mean velocity with \(He=10^5\)

Full size image

3.3 Loss coefficients of the bend with R/D=1

Figure 7 shows all the calculated loss coefficients in the bend with \(R/D=1\) as the function of the generalized Reynolds number. The different colored points belong to different He numbers. We remark, that not all \({\textrm{Re}_\textrm{gen} - He}\) pairs exist, we focus only the relevant range in the engineering applications.

The results of the simulations belonging to one given He number are connected to form different curves. In the range of 20 \(<{\textrm{Re}_\textrm{gen}}<\)20 000, these curves are separated from each other. An “eye-shaped” zone of the calculated loss coefficients between \(He=10^0\) and \(He=10^5\) can be recognized. At \({\textrm{Re}_\textrm{gen}}\approx\) 20 000, the loss coefficients values were identical for the investigated fluids. It was generally observed that at larger \({\textrm{Re}_\textrm{gen}}\) numbers, the contours belonging to the higher He numbers converged to the upper curve, to the Newtonian fluid, e.g., the clear water. This observation in agreement with the results of Rawat et al. [28].

The Buckingham’s \(\Pi\)-Theorem offers a framework to determine the quantities assembled to non-dimensional groups relevant to the hydrodynamic problem. Our analysis confirmed the findings that four dimensional groups describe the losses: \(\pi _{1}=R/D\), \(\pi _{2}=\Delta p \rho D^{2}/\mu _{B}^{2}\), \(\pi _{3}=v\rho D/\mu _{B}\) and \(\pi _{4}=\tau _{0} \rho D^{2}/\mu _{B}^{2}\). From these groups, \(Re=\pi _{3}\), \(De=(0.5\pi _{1})^{-0.5}\pi _{3}\), \(He=\pi _{4}\) and \(\zeta =2\pi _{2}/\pi _{3}^{2}\). So, we need the Hedström number beside the Reynolds and the Dean numbers to describe the loss coefficient.

Fig. 7
figure 7

The calculated loss coefficients of the bend with \(R/D=1\) radius of curvature as the function of the generalized Reynolds number; blue dotted line: analytical curve of the purely frictional losses

Full size image

3.4 Laminar flow patterns of the bend with R/D=1

For further analysis, four of the \({\textrm{Re}_\textrm{gen}}\) numbers were selected from the laminar region: \({\textrm{Re}_\textrm{gen}}\approx\) 5, 55, 180, and 540, where we received results in a wide Hedström number range. These \({\textrm{Re}_\textrm{gen}}\) values are marked with dashed black arrows in Fig. 7. The flow patterns in the bend with \(R/D=1\) were investigated at \(He=10^1\), \(He=10^3\) and \(He=10^5\). Table 4 shows the corresponding Dean numbers and calculated loss coefficient values and the relative standard deviation (RSD) in these itemized cases. It is apparent from this table that depending on the Hedström number, the difference could be up to \(60\%\) between the results at the same \({\textrm{Re}_\textrm{gen}}\) and \({\textrm{De}_\textrm{gen}}\) numbers.

To comprehend these results better, the normalized axial velocity profiles along the bend in the symmetry plane were also extracted and presented in Fig. 8. As expected, at \({\textrm{Re}_\textrm{gen}}\approx 5\), there was no significant difference between the loss coefficients (the RSD was \(5.8\%\)), and no secondary vortices appeared. This is in the domain of Stokes or creeping flow, where the flow was unidirectional, although the velocity profiles were not the same. Plug flow characterized only the fluids with the higher yields stresses of \(He=10^3\) and \(He=10^5\). In the case of \({\textrm{Re}_\textrm{gen}}\approx 55\), the loss values differed slightly from each other (no more than 15–25%). The Dean number was \({\textrm{De}_\textrm{gen}}\approx 39\), while De = 40 is considered as the limit for the appearance of secondary vortices in Newtonian flows. In our simulations secondary vortices appeared at \(\textrm{He}=10^1\) and \(\textrm{He}=10^3\), but not at \(\textrm{He}=10^5\).

The largest relative difference between the dimensionless losses of \(-61\%\) was observed at \({\textrm{Re}_\textrm{gen}}\approx 180\) (considering the \(He=10^1\) value as initial one). At \({\textrm{Re}_\textrm{gen}}\approx 180\) and \({\textrm{Re}_\textrm{gen}}\approx 540\) the velocity magnitude showed certain similarity by \(He=10^1\) and \(He=10^3\). The relative difference between the loss coefficients in the latter case was only \(6\%\), as the red and the black curves matched in the last diagram in Fig. 8. In the case of \({\textrm{Re}_\textrm{gen}}\approx 180\) and \({\textrm{Re}_\textrm{gen}}\approx 540\) counter-rotating vortices existed at all the investigated He numbers. As the loss curves opened to widest at \({\textrm{Re}_\textrm{gen}}\approx 180\) (\({\textrm{De}_\textrm{gen}} \approx 126\)), we took a closer look at the secondary vortices formed under these circumstances. The velocity magnitude and the line integral convolution (LIC) of the velocity field on surfaces defined along with the geometry (see Fig. 1) are presented in Fig. 9. Secondary vortices formed with all three different fluids. In the case of \(He=10^1\), the vortices existed even at the distance of 5D after the bend. In the case of \(He=10^3\) and \(He=10^5\), the vortices were less intense and disappeared sooner.

Table 4 Loss coefficients \(\zeta\) of the detailed cases at for the bend with \(R/D=1\) radius of curvature, and the relative standard deviation (RSD) of the cases
Full size table
Fig. 8
figure 8

Normalized axial velocity profiles in the symmetry plane along the bend with \(R/D=1\) radius of curvature at four \({\textrm{Re}_\textrm{gen}}\) and three He number values; the relative radius of 1 belongs to the inner core; the -1 to the outer core; in top-down order: \({\textrm{Re}_\textrm{gen}}\approx 5\), \({\textrm{Re}_\textrm{gen}}\approx 55\), \({\textrm{Re}_\textrm{gen}}\approx 180\), \({\textrm{Re}_\textrm{gen}}\approx 540\) with \(He=10^1\), \(He=10^3\), and \(He=10^5\)

Full size image
Fig. 9
figure 9

Secondary flow contour plots and velocity along the bend with \(R/D=1\) radius of curvature at \({\textrm{Re}_\textrm{gen}}\approx 180\) in the case of \(\textrm{He}=10^1\) (top), \(\textrm{He}=10^3\) (middle), and \(\textrm{He}=10^5\) (bottom)

Full size image

Bingham numbers for all the cases were also calculated. The loss coefficients as the function of the Bingham number are shown in Fig. 10. Supplemented curves for constant Hedström numbers and generalized Reynolds numbers were also provided in the diagram. The curves corresponding to the generalized Reynolds numbers straightened to the Newtonian loss coefficients as the Bingham number, which characterized the yield stress, decreased. This diagram can be useful to read the loss coefficient of the bend with \(R/D=1\) knowing the yield stress, and the consistency index and the mean velocity of the fluid.

Fig. 10
figure 10

Loss coefficients as the function of the Bingham number in the bend with the radius of curvature of \(R/D=1\) for different fluids

Full size image

4 Conclusions

The main goal of the current study was to determine the loss coefficient of five bends of different curvature in a wide range of Reynolds numbers (\(0.1<{\textrm{Re}_\textrm{gen}}<20000\)) with ten different Bingham fluids. The Hedström number set the rheology of the fluids. The detailed simulations were mainly performed in the laminar and the transition domain, considering the relevant engineering range regarding the Bingham plastic rheological properties. It is important to note that such a comprehensive CFD study has not yet been conducted and that we have found a good agreement with the available experimental results.

It was presented that the generalized Reynolds number defined by Madlener et al. [21] for Bingham plastic fluids arranges the wall friction factors over a wide range of Hedström numbers. Apart from the transition zone, the mean deviation from the Darcy formula in the laminar range and the Blasius formula in the turbulent range was below 5\(\%\).

A practical implication of our work that for \({\textrm{De}_\textrm{gen}} <40\) and \({\textrm{Re}_\textrm{gen}}<20\) with Bingham fluids, the loss coefficient of the bend with the curvature of \(R/D=1,2,4,6,10\) can be easily estimated. The estimate in the above mentioned range \(\zeta = \sqrt{\frac{R}{D}} {\frac{\pi }{\sqrt{2}}} {\frac{64}{{\textrm{De}_\textrm{gen}}}}\) yield values within 15\(\%\) of the true value.

In the range \(20<{\textrm{Re}_\textrm{gen}}<20{,}000\), we found that \({\textrm{Re}_\textrm{gen}}\) and \({\textrm{De}_\textrm{gen}}\) numbers by themselves are not sufficient to characterize the flow; equality of the Hedström numbers is also necessary. This is shown by the fact that at equal \({\textrm{Re}_\textrm{gen}}\) and \({\textrm{De}_\textrm{gen}}\) different loss coefficients were obtained, depending on the He, moreover the flow patterns also differed.

At the bend with a radius of curvature of \(R/D = 1\), contour lines corresponding to different Hedström numbers were identified in the region of \(20<{\textrm{Re}_\textrm{gen}}<20{,}000\).

From secondary flow contour plots, it is apparent that the plug-like flow filled a larger part of the cross section in the cases of higher yield stress. Less secondary vortex formation was observed in these cases, which dissipated earlier. It will be worthwhile in future to map the relationship between the secondary vortex intensity and the loss coefficient.

The above conclusions refer to the current study range. The precise mapping of the range, the establishment of the relationship between the dimensionless groups, the secondary vortex intensity and the loss coefficient for all curvatures will also remain for future work.