Flutter characteristics of a rectangular sandwich plate with laminated three-phase polymer/GNP/fiber face sheets and an auxetic honeycomb core in yawed supersonic fluid flow

Abstract

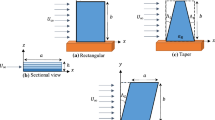
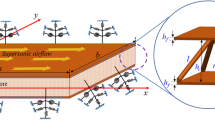
In the presented work, the flutter (aeroelastic stability) behavior of a sandwich plate under yawed supersonic fluid flow is investigated. The plate consists of an auxetic re-entrant honeycomb core and two laminated polymer-based composite face sheets reinforced with graphene nanoplatelets (GNPs) and fibers. The sinusoidal shear deformation theory (SSDT) and linear piston theory are utilized to model the plate and aerodynamic pressure, respectively. The governing equations and associated boundary conditions are derived utilizing Hamilton’s principle, and a numerical solution is performed via the differential quadrature method (DQM). The critical aerodynamic pressure is determined, and the effects of various parameters on the aeroelastic stability characteristics are examined such as the geometric parameters of the auxetic honeycomb core, mass fractions of the GNPs and the fibers, the thickness of the plate, and yaw angle. Numerical results reveal that by considering a specified total thickness for the plate, the critical aerodynamic pressure decreases by increasing the thickness of the auxetic honeycomb core. It is observed that the geometrical characteristics of the cells in the auxetic honeycomb core have no significant effect on the critical aerodynamic pressure.

Appendices

Appendix A

In Eq. (51), $\left\{ s \right\}$, [K], and [M] are defined as follows:

$$ \begin{array}{*{20}c} {\left\{ s \right\}_{{5N_{x} N_{y} \times 1}} = \left\{ {\begin{array}{*{20}c} {\left\{ {U^{*} } \right\}} \\ {\left\{ {V^{*} } \right\}} \\ {\left\{ {W^{*} } \right\}} \\ {\left\{ {X^{*} } \right\}} \\ {\left\{ {Y^{*} } \right\}} \\ \end{array} } \right\},} & {\left[ K \right] = \left[ {\begin{array}{*{20}c} {k_{11} } & {k_{12} } & {k_{13} } & {k_{14} } & {k_{15} } \\ {k_{21} } & {k_{22} } & {k_{23} } & {k_{24} } & {k_{25} } \\ {k_{31} } & {k_{32} } & {k_{33} } & {k_{34} } & {k_{35} } \\ {k_{41} } & {k_{42} } & {k_{43} } & {k_{44} } & {k_{45} } \\ {k_{51} } & {k_{52} } & {k_{53} } & {k_{54} } & {k_{55} } \\ \end{array} } \right],} & {\left[ M \right] = \left[ {\begin{array}{*{20}c} {m_{11} } & {\left[ 0 \right]} & {\left[ 0 \right]} & {\left[ 0 \right]} & {\left[ 0 \right]} \\ {\left[ 0 \right]} & {m_{22} } & {\left[ 0 \right]} & {\left[ 0 \right]} & {\left[ 0 \right]} \\ {\left[ 0 \right]} & {\left[ 0 \right]} & {m_{33} } & {m_{34} } & {m_{35} } \\ {\left[ 0 \right]} & {\left[ 0 \right]} & {m_{43} } & {m_{44} } & {\left[ 0 \right]} \\ {\left[ 0 \right]} & {\left[ 0 \right]} & {m_{53} } & {\left[ 0 \right]} & {m_{55} } \\ \end{array} } \right],} \\ \end{array} $$

(A1)

where [0] is the zero matrix of order N_xN_y and k_ij = k_ji, m_ij = m_ji are presented as follows:

$$ \begin{gathered} k_{11} = A_{11} \left( {I^{y} \otimes B^{x} } \right) + 2A_{16} \left( {A^{y} \otimes A^{x} } \right) + A_{66} \left( {B^{y} \otimes I^{x} } \right), \hfill \\ k_{12} = A_{16} \left( {I^{y} \otimes B^{x} } \right) + \left( {A_{12} + A_{66} } \right)\left( {A^{y} \otimes A^{x} } \right) + A_{26} \left( {B^{y} \otimes I^{x} } \right), \hfill \\ k_{13} = B_{11} \left( {I^{y} \otimes C^{x} } \right) + 3B_{16} \left( {A^{y} \otimes B^{x} } \right) + \left( {B_{12} + 2B_{66} } \right)\left( {B^{y} \otimes A^{x} } \right) + B_{26} \left( {C^{y} \otimes I^{x} } \right), \hfill \\ k_{14} = C_{11} \left( {I^{y} \otimes B^{x} } \right) + 2C_{16} \left( {A^{y} \otimes A^{x} } \right) + C_{66} \left( {B^{y} \otimes I^{x} } \right), \hfill \\ k_{15} = C_{16} \left( {I^{y} \otimes B^{x} } \right) + \left( {C_{12} + C_{66} } \right)\left( {A^{y} \otimes A^{x} } \right) + C_{26} \left( {B^{y} \otimes I^{x} } \right), \hfill \\ m_{11} = I_{0} \left( {I^{y} \otimes I^{x} } \right), \hfill \\ k_{22} = A_{66} \left( {I^{y} \otimes B^{x} } \right) + 2A_{26} \left( {A^{y} \otimes A^{x} } \right) + A_{22} \left( {B^{y} \otimes I^{x} } \right), \hfill \\ k_{23} = B_{16} \left( {I^{y} \otimes C^{x} } \right) + \left( {B_{12} + 2B_{66} } \right)\left( {A^{y} \otimes B^{x} } \right) + 3B_{26} \left( {B^{y} \otimes A^{x} } \right) + B_{22} \left( {C^{y} \otimes I^{x} } \right), \hfill \\ k_{24} = C_{16} \left( {I^{y} \otimes B^{x} } \right) + \left( {C_{12} + C_{66} } \right)\left( {A^{y} \otimes A^{x} } \right) + C_{26} \left( {B^{y} \otimes I^{x} } \right), \hfill \\ k_{25} = C_{66} \left( {I^{y} \otimes B^{x} } \right) + 2C_{26} \left( {A^{y} \otimes A^{x} } \right) + C_{22} \left( {B^{y} \otimes I^{x} } \right), \hfill \\ m_{22} = I_{0} \left( {I^{y} \otimes I^{x} } \right), \hfill \\ k_{33} = D_{11} \left( {I^{y} \otimes D^{x} } \right) + 4D_{16} \left( {A^{y} \otimes C^{x} } \right) + 2\left( {D_{12} + 2D_{66} } \right)\left( {B^{y} \otimes B^{x} } \right) \hfill \\ \quad \quad - R_{55} \left( {I^{y} \otimes B^{x} } \right) + 4D_{26} \left( {C^{y} \otimes A^{x} } \right) - 2R_{45} \left( {A^{y} \otimes A^{x} } \right) + \xi \cos \theta_{\infty } \left( {I^{y} \otimes A^{x} } \right) \hfill \\ \quad \quad + D_{22} \left( {D^{y} \otimes I^{x} } \right) - R_{44} \left( {B^{y} \otimes I^{x} } \right) + \xi \sin \theta_{\infty } \left( {A^{y} \otimes I^{x} } \right), \hfill \\ k_{34} = F_{11} \left( {I^{y} \otimes C^{x} } \right) + 3F_{16} \left( {A^{y} \otimes B^{x} } \right) + \left( {F_{12} + 2F_{66} } \right)\left( {B^{y} \otimes A^{x} } \right) - R_{55} \left( {I^{y} \otimes A^{x} } \right) \hfill \\ \quad \quad + F_{26} \left( {C^{y} \otimes I^{x} } \right) - R_{45} \left( {A^{y} \otimes I^{x} } \right), \hfill \\ k_{35} = F_{16} \left( {I^{y} \otimes C^{x} } \right) + \left( {F_{12} + 2F_{66} } \right)\left( {A^{y} \otimes B^{x} } \right) + 3F_{26} \left( {B^{y} \otimes A^{x} } \right) - R_{45} \left( {I^{y} \otimes A^{x} } \right) \hfill \\ \quad \quad + F_{22} \left( {C^{y} \otimes I^{x} } \right) - R_{44} \left( {A^{y} \otimes I^{x} } \right), \hfill \\ m_{33} = I_{2} \left( {I^{y} \otimes B^{x} } \right) + I_{2} \left( {B^{y} \otimes I^{x} } \right) - I_{0} \left( {I^{y} \otimes I^{x} } \right), \hfill \\ m_{34} = I_{4} \left( {I^{y} \otimes A^{x} } \right), \hfill \\ m_{35} = I_{4} \left( {A^{y} \otimes I^{x} } \right), \hfill \\ k_{44} = H_{11} \left( {I^{y} \otimes B^{x} } \right) + 2H_{16} \left( {A^{y} \otimes A^{x} } \right) + H_{66} \left( {B^{y} \otimes I^{x} } \right) - R_{55} \left( {I^{y} \otimes I^{x} } \right), \hfill \\ k_{45} = H_{16} \left( {I^{y} \otimes B^{x} } \right) + \left( {H_{12} + H_{66} } \right)\left( {A^{y} \otimes A^{x} } \right) + H_{26} \left( {B^{y} \otimes I^{x} } \right) - R_{45} \left( {I^{y} \otimes I^{x} } \right), \hfill \\ m_{44} = I_{5} \left( {I^{y} \otimes I^{x} } \right), \hfill \\ k_{55} = H_{66} \left( {I^{y} \otimes B^{x} } \right) + 2H_{26} \left( {A^{y} \otimes A^{x} } \right) + H_{22} \left( {B^{y} \otimes I^{x} } \right) - R_{44} \left( {I^{y} \otimes I^{x} } \right), \hfill \\ m_{55} = I_{5} \left( {I^{y} \otimes I^{x} } \right), \hfill \\ \end{gathered} $$

(A2)

where I^x and I^y sequentially stand for the identity matrices of orders N_x and N_y.

Appendix B

In Eq. (52), [L] is presented as

$$ \left[ L \right] = \left[ {\begin{array}{*{20}c} {L_{11} } & {L_{12} } & {L_{13} } & {L_{14} } & {L_{15} } \\ {L_{21} } & {L_{22} } & {L_{23} } & {L_{24} } & {L_{25} } \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {L_{241} } & {L_{242} } & {L_{243} } & {L_{244} } & {L_{245} } \\ \end{array} } \right], $$

(B1)

in which, with the following definitions, L₁₁-L₆₅ are related to the boundary conditions at x = 0:

$$ \begin{gathered} {\text{Clamped}}\,\left( {\text{C}} \right){:} \hfill \\ \begin{array}{*{20}c} {L_{11} = L_{22} = L_{33} = L_{54} = L_{65} = I^{y} \otimes I_{1}^{x} ,} & {L_{43} = I^{y} \otimes A_{1}^{x} ,} \\ \end{array} \hfill \\ L_{12} = L_{13} = L_{14} = L_{15} = L_{21} = L_{23} = L_{24} = L_{25} = L_{31} = L_{32} = L_{34} = L_{35} = L_{41} = \hfill \\ L_{42} = L_{44} = L_{45} = L_{51} = L_{52} = L_{53} = L_{55} = L_{61} = L_{62} = L_{63} = L_{64} = \left\{ 0 \right\}_{{N_{y} \times N_{x} N_{y} }} , \hfill \\ {\text{Simply supported }}\left( {\text{S}} \right){:} \hfill \\ L_{22} = L_{33} = L_{65} = I^{y} \otimes I_{1}^{x} , \hfill \\ L_{21} = L_{23} = L_{24} = L_{25} = L_{31} = L_{32} = L_{34} = L_{35} = L_{61} = L_{62} = L_{63} = L_{64} = \left\{ 0 \right\}_{{N_{y} \times N_{x} N_{y} }} , \hfill \\ \begin{array}{*{20}c} {L_{11} = A_{11} \left( {I^{y} \otimes A_{1}^{x} } \right) + A_{16} \left( {A^{y} \otimes I_{1}^{x} } \right),} & {L_{12} = A_{16} \left( {I^{y} \otimes A_{1}^{x} } \right),} & {L_{13} = B_{11} \left( {I^{y} \otimes B_{1}^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{14} = C_{11} \left( {I^{y} \otimes A_{1}^{x} } \right) + C_{16} \left( {A^{y} \otimes I_{1}^{x} } \right),} & {L_{15} = C_{16} \left( {I^{y} \otimes A_{1}^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{41} = B_{11} \left( {I^{y} \otimes A_{1}^{x} } \right) + B_{16} \left( {A^{y} \otimes I_{1}^{x} } \right),} & {L_{42} = B_{16} \left( {I^{y} \otimes A_{1}^{x} } \right),} & {L_{43} = D_{11} \left( {I^{y} \otimes B_{1}^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{44} = F_{11} \left( {I^{y} \otimes A_{1}^{x} } \right) + F_{16} \left( {A^{y} \otimes I_{1}^{x} } \right),} & {L_{45} = F_{16} \left( {I^{y} \otimes A_{1}^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{51} = C_{11} \left( {I^{y} \otimes A_{1}^{x} } \right) + C_{16} \left( {A^{y} \otimes I_{1}^{x} } \right),} & {L_{52} = C_{16} \left( {I^{y} \otimes A_{1}^{x} } \right),} & {L_{53} = F_{11} \left( {I^{y} \otimes B_{1}^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{54} = H_{11} \left( {I^{y} \otimes A_{1}^{x} } \right) + H_{16} \left( {A^{y} \otimes I_{1}^{x} } \right),} & {L_{55} = H_{16} \left( {I^{y} \otimes A_{1}^{x} } \right),} \\ \end{array} \hfill \\ \end{gathered} $$

(B2)

L₇₁-L₁₂₅ are related to the boundary conditions at y = 0:

$$ \begin{gathered} {\text{Clamped}}\,\left( {\text{C}} \right){:} \hfill \\ \begin{array}{*{20}c} {L_{71} = L_{82} = L_{93} = L_{114} = L_{125} = I_{1}^{y} \otimes I^{x} ,} & {L_{103} = A_{1}^{y} \otimes I^{x} ,} \\ \end{array} \hfill \\ L_{72} = L_{73} = L_{74} = L_{75} = L_{81} = L_{83} = L_{84} = L_{85} = L_{91} = L_{92} = L_{94} = L_{95} = L_{101} = \hfill \\ L_{102} = L_{104} = L_{105} = L_{111} = L_{112} = L_{113} = L_{115} = L_{121} = L_{122} = L_{123} = L_{124} = \left\{ 0 \right\}_{{N_{x} \times N_{x} N_{y} }} , \hfill \\ {\text{Simply supported }}\left( {\text{S}} \right){:} \hfill \\ L_{71} = L_{93} = L_{114} = I_{1}^{y} \otimes I^{x} , \hfill \\ L_{72} = L_{73} = L_{74} = L_{75} = L_{91} = L_{92} = L_{94} = L_{95} = L_{111} = L_{112} = L_{113} = L_{115} = \left\{ 0 \right\}_{{N_{x} \times N_{x} N_{y} }} , \hfill \\ \begin{array}{*{20}c} {L_{81} = A_{26} \left( {A_{1}^{y} \otimes I^{x} } \right),} & {L_{82} = A_{26} \left( {I_{1}^{y} \otimes A^{x} } \right) + A_{22} \left( {A_{1}^{y} \otimes I^{x} } \right),} & {L_{83} = B_{22} \left( {B_{1}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{84} = C_{26} \left( {A_{1}^{y} \otimes I^{x} } \right),} & {L_{85} = C_{26} \left( {I_{1}^{y} \otimes A^{x} } \right) + C_{22} \left( {A_{1}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{101} = B_{26} \left( {A_{1}^{y} \otimes I^{x} } \right),} & {L_{102} = B_{26} \left( {I_{1}^{y} \otimes A^{x} } \right) + B_{22} \left( {A_{1}^{y} \otimes I^{x} } \right),} & {L_{103} = D_{22} \left( {B_{1}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{104} = F_{26} \left( {A_{1}^{y} \otimes I^{x} } \right),} & {L_{105} = F_{26} \left( {I_{1}^{y} \otimes A^{x} } \right) + F_{22} \left( {A_{1}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{121} = C_{26} \left( {A_{1}^{y} \otimes I^{x} } \right),} & {L_{122} = C_{26} \left( {I_{1}^{y} \otimes A^{x} } \right) + C_{22} \left( {A_{1}^{y} \otimes I^{x} } \right),} & {L_{123} = F_{22} \left( {B_{1}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{124} = H_{26} \left( {A_{1}^{y} \otimes I^{x} } \right),} & {L_{125} = H_{26} \left( {I_{1}^{y} \otimes A^{x} } \right) + H_{22} \left( {A_{1}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \end{gathered} $$

(B3)

L₁₃₁-L₁₈₅are related to the boundary conditions at x = a:

$$ \begin{gathered} {\text{Clamped}}\,\left( {\text{C}} \right){:} \hfill \\ \begin{array}{*{20}c} {L_{131} = L_{142} = L_{153} = L_{174} = L_{185} = I^{y} \otimes I_{{{\text{end}}}}^{x} ,} & {L_{163} = I^{y} \otimes A_{{{\text{end}}}}^{x} ,} \\ \end{array} \hfill \\ L_{132} = L_{133} = L_{134} = L_{135} = L_{141} = L_{143} = L_{144} = L_{145} = L_{151} = L_{152} = L_{154} = L_{155} = L_{161} = \hfill \\ L_{162} = L_{164} = L_{165} = L_{171} = L_{172} = L_{173} = L_{175} = L_{181} = L_{182} = L_{183} = L_{184} = \left\{ 0 \right\}_{{N_{y} \times N_{x} N_{y} }} , \hfill \\ {\text{Simply supported }}\left( {\text{S}} \right){:} \hfill \\ L_{142} = L_{153} = L_{185} = I^{y} \otimes I_{{{\text{end}}}}^{x} , \hfill \\ L_{141} = L_{143} = L_{144} = L_{145} = L_{151} = L_{152} = L_{154} = L_{155} = L_{181} = L_{182} = L_{183} = L_{184} = \left\{ 0 \right\}_{{N_{y} \times N_{x} N_{y} }} , \hfill \\ \begin{array}{*{20}c} {L_{131} = A_{11} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right) + A_{16} \left( {A^{y} \otimes I_{{{\text{end}}}}^{x} } \right),} & {L_{132} = A_{16} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right),} & {L_{133} = B_{11} \left( {I^{y} \otimes B_{{{\text{end}}}}^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{134} = C_{11} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right) + C_{16} \left( {A^{y} \otimes I_{{{\text{end}}}}^{x} } \right),} & {L_{135} = C_{16} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{161} = B_{11} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right) + B_{16} \left( {A^{y} \otimes I_{{{\text{end}}}}^{x} } \right),} & {L_{162} = B_{16} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right),} & {L_{163} = D_{11} \left( {I^{y} \otimes B_{{{\text{end}}}}^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{164} = F_{11} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right) + F_{16} \left( {A^{y} \otimes I_{{{\text{end}}}}^{x} } \right),} & {L_{165} = F_{16} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{171} = C_{11} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right) + C_{16} \left( {A^{y} \otimes I_{{{\text{end}}}}^{x} } \right),} & {L_{172} = C_{16} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right),} & {L_{173} = F_{11} \left( {I^{y} \otimes B_{{{\text{end}}}}^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{174} = H_{11} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right) + H_{16} \left( {A^{y} \otimes I_{{{\text{end}}}}^{x} } \right),} & {L_{175} = H_{16} \left( {I^{y} \otimes A_{{{\text{end}}}}^{x} } \right),} \\ \end{array} \hfill \\ \end{gathered} $$

(B4)

and L₁₉₁-L₂₄₅ are related to the boundary conditions at y = b:

$$ \begin{gathered} {\text{Clamped}}\,\left( {\text{C}} \right){:} \hfill \\ \begin{array}{*{20}c} {L_{191} = L_{202} = L_{213} = L_{234} = L_{245} = I_{end}^{y} \otimes I^{x} ,} & {L_{223} = A_{end}^{y} \otimes I^{x} ,} \\ \end{array} \hfill \\ L_{192} = L_{193} = L_{194} = L_{195} = L_{201} = L_{203} = L_{204} = L_{205} = L_{211} = L_{212} = L_{214} = L_{215} = L_{221} = \hfill \\ L_{222} = L_{224} = L_{225} = L_{231} = L_{232} = L_{233} = L_{235} = L_{241} = L_{242} = L_{243} = L_{244} = \left\{ 0 \right\}_{{N_{x} \times N_{x} N_{y} }} , \hfill \\ {\text{Simply supported }}\left( {\text{S}} \right){:} \hfill \\ L_{191} = L_{213} = L_{234} = I_{{{\text{end}}}}^{y} \otimes I^{x} , \hfill \\ L_{192} = L_{193} = L_{194} = L_{195} = L_{211} = L_{212} = L_{214} = L_{215} = L_{231} = L_{232} = L_{233} = L_{235} = \left\{ 0 \right\}_{{N_{x} \times N_{x} N_{y} }} , \hfill \\ \begin{array}{*{20}c} {L_{201} = A_{26} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} & {L_{202} = A_{26} \left( {I_{end}^{y} \otimes A^{x} } \right) + A_{22} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} & {L_{203} = B_{22} \left( {B_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{204} = C_{26} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} & {L_{205} = C_{26} \left( {I_{end}^{y} \otimes A^{x} } \right) + C_{22} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{221} = B_{26} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} & {L_{222} = B_{26} \left( {I_{end}^{y} \otimes A^{x} } \right) + B_{22} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} & {L_{223} = D_{22} \left( {B_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{224} = F_{26} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} & {L_{225} = F_{26} \left( {I_{end}^{y} \otimes A^{x} } \right) + F_{22} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{241} = C_{26} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} & {L_{242} = C_{26} \left( {I_{end}^{y} \otimes A^{x} } \right) + C_{22} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} & {L_{243} = F_{22} \left( {B_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {L_{244} = H_{26} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right),} & {L_{245} = H_{26} \left( {I_{end}^{y} \otimes A^{x} } \right) + H_{22} \left( {A_{{{\text{end}}}}^{y} \otimes I^{x} } \right).} \\ \end{array} \hfill \\ \end{gathered} $$

(B5)

In Eqs. (B2)–(B5), the subscripts “1” and “end,” respectively, indicate the first and last row of matrices.