A proposal for the optimization of the geometric configuration of a hollow cylindrical steel damper with slots

Abstract

The energy dissipation capacity (EDC) of most current configurations of yielding steel dampers is susceptible to be improved by applying optimization concepts. Thus, this study proposes a methodology to enhance the EDC of a slotted hollow cylinder steel (HCS) damper under a cyclic displacement protocol while keeping the same quantity of material via shape optimization. The simulated annealing algorithm was selected for solving the optimization problem as it uses only one candidate solution per iteration, reducing the computational cost associated with the EDC computation. In addition, the finite element software ABAQUS is used to model the behavior of the steel damper under cyclic loads. A code is elaborated using the Python programming language for the optimization process, containing the instructions to be executed in ABAQUS. Five slot configurations were proposed for the initial damper to determine the effect of the initial solution on the optimized HCS damper. The results show that the proposed optimization process obtains optimized models with stable hysteretic behavior and a significantly higher energy dissipation capacity than the initial models. The optimal configuration presented an EDC of 5543 J, 16% higher than the HCS damper without slots and with the same material quantity. The material is mainly located parallel to the beam, simulating two 2D shear steel plates. The difference in EDC with other optimized configurations reaches 955 J, indicating the dependence of the solution on the initial damper configuration. In addition, the difference in the optimized damper topologies proves the multi-modality characteristic of the problem. The proposed algorithm is easy to implement in a computer and reaches the optimal solution with less than 50 iterations.

1 Introduction

The possibility of using the yield of metallic material through hysteresis cycles to dissipate seismic energy has gained attention over the last decades in developing seismic protection systems. The mechanical principle of metallic hysteretic dampers is to dissipate energy through the inelastic strains induced in the device during the seismic movement. Thus, the material used in damper manufacturing should present a low cycle yield point to initiate the yield process with a low level of stress and large ductility to guarantee important energy dissipation. So, many energy dissipation devices have been manufactured from metallic materials such as steel, aluminum, lead, copper, and some memory-shape alloys, with each material presenting its own characteristics. Low-yield point steel is preferred because it allows several inelastic cycles before total failure [1]. Copper is suitable for protection against impulsive-type earthquakes but presents a high cost [2]. Aluminum has lower yield points and more significant ductility than steel [3]. Lead has recrystallization properties that help it recover its original internal structure after an earthquake, preventing the device from being replaced [4]. Shape-memory alloys allow recovering the device form after using it during a seismic event and have excellent behavior to environmental factors [5], with Tabrizikahou et al. [6] presenting a complete review on the subject. Most metallic hysteretic (MH) dampers show the following characteristics: (i) displacement-depending behavior with stable hysteretic cycles, (ii) a low-cost associated with their manufacturing, and (iii) strength to the environment [7]. However, it is worth considering that the final behavior of the devices can be influenced by factors such as the Bauschinger effects [8], the possibility of buckling [9], and low cycle fatigue [10].

The MH dampers are typically located on braces connected to the main structure so that the relative movement between two stories induces inelastic strains in the device. Depending on the geometric configuration, these strains could be raised by axial, flexure, or shear effects. For example, the yield of the steel core in buckling restrained braces is induced through the axial forces generated in their extremes [11]. The geometrical shape of a TADAS device and the hinges in the lower part cause inelastic displacements by flexure [12]. Nonetheless, it is possible to induce shear stress in perforated steel plates by locating the thickness perpendicular to the beam [13]. Other modifications of the devices allow combining the shear and flexure effects to obtain a higher energy dissipation capacity (EDC), such as in reference [14]. Therefore, it is possible to guide a search process for the best metallic damper shape by understanding the stress trajectories on the device in the presence of several load reverse cycles. To the authors’ best knowledge, a unique criterion for determining which geometrical configuration is the most outstanding, under the material or cost-based constraints, is unavailable. A simple criterion would correspond to the ratio between the EDC and the material quantity used in the device. A more complex criterion would be the device’s cost (including the manufacturing process). On the other hand, no study generates a framework to compare the different available damper’s geometrical configurations fairly.

Optimization is one strategy for determining the damper geometrical configuration that produces the highest EDC. There are different strategies to apply optimization to the mentioned problem: (i) to compute the dimensions of the device if the geometric configuration is known, (ii) to obtain the topology of the device from a user-defined initial configuration while keeping the material quantity constant, and (iii) to define the minimum quantity and distribution of materials to achieve a specific EDC. Most research follows the second strategy with application to slotted plate steel (SPS) dampers and considering maximizing the EDC. Ghabraie et al. [15] presented in 2010 one of the first papers to optimize an SPS damper from the gradient-based method, obtaining an increment in the EDC of 1124–2203 J for an initial configuration with horizontal slots. Park et al. [16] use the sequential quadratic programming method to derive an optimal shape for a metallic damper with application to bridges. In addition, the problem definition could include a smoother function for the boundaries that generate better computational modeling of the devices and a reduction in the number of variables [17]. The possibility of using a computer-aided design to create shapes and isogeometric analysis has increased the feasibility of obtaining better devices [18]. In brief, a correct definition of the stress state plays a critical role in the optimization process. Farzampour [19] shows the optimal solution could be affected by the presence of a combination of flexural and shear stresses in a butterfly-shaped damper by considering a Von Mises criterion.

On the other hand, it is possible to use nature-based optimization algorithms in the shape optimization of yielding steel dampers as an alternative to ease the mathematical representation of the problem. Khatibinia et al. [20] used the particle swarm optimization algorithm to obtain the optimal shape of a U-shaped steel damper, using a support vector machine model to reduce the computational cost related to the finite element analysis. Kiani et al. [21] configured a Tabu search algorithm to solve a multiobjective approach where the low-cycle fatigue and the EDC are considered simultaneously. Kim et al. [22] employed the whale optimization algorithm to determine the best shape of a curved steel damper, supported by a B-splines-based strategy for defining the damper boundaries. Ferrer and Villalba [23] used a binary model to indicate the presence or not of material, which allowed the generation of heuristics to improve the convergence process. Independent of the type of algorithm, the optimization process will need to interact with a finite element software, such as ANSYS [24] or ABAQUS [25], to determine the behavior of the devices under the cyclic load.

This paper generates the numerical shape optimization of an HCS damper with slots from a nature-based metaheuristic. The HCS damper was selected in this research as it proved to have a good capacity for energy dissipation [26]. The optimization process was based on that proposed in [23] but used a conventional simulated annealing (SA) algorithm, which had an excellent convergence behavior. The SA algorithm is chosen as it has proved its value in other problems of the structural engineering field and uses only one solution per iteration, reducing the computational cost. The initial slots’ shapes were selected from simple geometrical forms; vertical slots are commonly used in the literature, as in reference [15]. The main contributions of the current research are related to the following issues:

• The obtained results represent the first attempt to optimize the HCS damper;

• A specific representation scheme was proposed to computationally represent a damper configuration, which allows analyzing the tridimensional plate through a bidimensional binary array;

• The use of the SA algorithm proved to reach feasible solutions with few iterations;

• Including problem-knowledge-based heuristics in the computational strategy accelerated the convergence process;

• Several initial configurations for slots were tested to determine their influence on the optimized solution;

• The procedure could be easily adapted to other metallic hysteretic dampers working by shear.

Even though this research is numerically developed, results in [21] were used to calibrate the finite element simulation. Finally, the study is limited to determining the structural behavior of the HCS damper working separately under one cyclic displacement-based protocol. Therefore, the computation of the seismic response of a primary structural system equipped with the device under seismic loads will be carried out in future research.

2 The hollow cylinder steel (HCS) damper

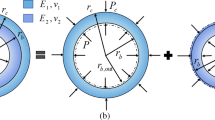
The HCS damper is a seismic protection device introduced by Abebe et al. [26], which dissipates energy through the yielding of the material induced by the displacement relative between the upper and bottom parts during an earthquake movement. Therefore, the device should be made from steel with low yield points and good ductility, such as A-36. Figure 1 presents the material distribution for the device, whose radial symmetry allows better behavior in two orthogonal directions. Its standard installation on braces in Chevron configuration is illustrated in Fig. 2 for a one-story steel frame. Typical values for H are between 2.5 and 4.5 m, while L is between 6 to 10 m. It is worth mentioning that the main application of MH dampers is in buildings, but they have also been applied in bridges [27]. For example, Javanmardi et al. [28] present the simultaneous application of a hexagonal honeycomb steel damper with a lead-rubber-bearing isolator to control vibrations in a cable-stayed bridge.

Fig. 1

HCS damper

Fig. 2

HCS damper in a one-story steel frame

From a theoretical point of view, the device could be structurally analyzed as fixed at the bottom part and loaded with a displacement protocol in its upper side (free extreme), introducing stresses in the device due to a combination of flexure and shear. Abebe et al. [26] determined that the effective aspect ratio (height/diameter) to produce the best performance is $\sqrt{3}$. Higher ratios result in a predominant flexure failure, while lower ratios induce shear failure. Utomo [29] added metallic reinforcement in the device outward to avoid strain concentrations in the support element, increasing the number of supported load cycles. Kim et al. [30] experimentally observed that the cylinder damper could adequately support bidirectional loads, with a failure initiated in the weld toe. Such results prove the value of cylinder dampers to dissipate the energy induced by an earthquake in a structure but raise the question if the device could be improved.

One possibility to increase the device’s performance is by introducing slots because they modify the stress trajectories inside. Figure 3 presents the original HCS damper in the middle and two configurations with slots, while Fig. 4 shows the stress distribution for induced cyclic displacement energy. The differences in such distributions imply that the dissipated energy was different for the event, raising the question: Which is the best shape configuration for the slotted HCS damper that produces the highest EDC? The methodology presented in Sect. 3 tries to answer the above question. It is noteworthy that the results shown in Fig. 4 are only illustrative of the mentioned problem.

Fig. 3

Different configurations of the HCS damper with slots

Fig. 4

Illustrative stress distribution: a front view and b lateral view

3 Simulated annealing algorithm

Simulated annealing (SA) is a heuristic optimization technique that follows an analogy with the annealing process in metals, developed in 1983 by Kirkpatrick et al. [31]. Manufacturing an imperfect-free solid implies slow cooling after the material is heated to a high temperature. The SA algorithm randomly generates a new solution from a current iteration and iteratively searches for the optimal solution. In that sense, using random numbers generated from a uniform probability distribution is necessary. The algorithm allows the selection of the current trial solution in a given iteration, even when this solution is worst, mainly at the beginning of the process. This characteristic enables the algorithm to escape local optimums. The acceptance probability ($p$) of a worst current solution is computed in terms of the objective function for the current and previous iteration ($\Delta f)$ and the parameter control ($T$), as given by:

$$p={e}^{-\frac{\Delta f}{T}}$$

(1)

Suppose the generated solution is better than the previous solution; the current solution is kept. But if the current solution is worst, Eq. (1) is assessed, and the $p$-value is compared against a uniform random number, nr, between 0 and 1. If nr is higher than $p$ the generated solution continues the process. Otherwise, the previous solution is kept. Then, the temperature value is updated, considering a controlled decrement.

The user must define a criterion that stops the search process. Possible criteria are related to a maximum number of iterations or a pre-specified number of them without a significant improvement in the quality of the solution. The number of iterations has to be defined previously by the user, and it depends on the characteristics of the analyzed problem. Due to the stochastic nature of the algorithm, it is necessary to execute the algorithm several times and then provide the solution to the problem. In addition, the algorithm’s success in solving a specific problem depends on the use of heuristics based on the knowledge of the problem, as the SA was derived as a general optimization algorithm. Figure 5 presents the SA pseudocode for its computational implementation, which shows the iterative process in the search for the optimal solution.

Fig. 5

Conventional simulated annealing algorithm

The possibility of proposing solution representations according to the problem domain, incorporating problem knowledge-based heuristics, and the ease of its computational implementation turns the SA suitable to be applied to different real problems. For example, SA has proven its value in solving solid mechanics problems. Some applications include structural optimization [32], machines [33], composite materials [34], vibration control [35], bio-engineering [36], structural damage detection [37], mechanical systems [38], sensor placement for dynamic tests [39], model identification parameters [40], among others. Most of the mentioned problems require the evaluation of an objective function based on results from a finite element model, which increments the computation cost. SA presents the advantage of being a single-solution metaheuristic, an essential characteristic for solving problems with an objective function whose computational cost is high.

4 Methodology for the shape optimization of slotted HCS dampers

The definition of the proposed methodology for the optimization of slotted HCS dampers follows that presented in Ferrer-Fuenmayor and Villalba-Morales [23] for the case of SSP dampers. It is worth mentioning that the optimization process aims to obtain the cylinder shape with the maximum EDC when the user pre-defined material volume. The method introduces four key steps to form the proposed methodology: (1) input data, (2) finite element modeling, (3) application of the simulated annealing, and (4) heuristics. Figure 6 visually describes the interaction between the previous steps, executed from a main computational routine. In this case, the Python language was selected for the computational implementation due to its practical applicability to scientific computing [41]. Furthermore, as proved in this research, the strategy by Ferrer-Fuenmayor and Villalba-Morales [23] can easily be modified to be applied explicitly to different configurations of MH dampers. The main changes carried out in this research are related to the optimization algorithm, the representation scheme for the variables, and the determination of the best solution.

Fig. 6

Flowchart for the optimization process of the HCS damper

The beginning section refers to the user-provided input data for executing the algorithm. First, it is necessary to define the geometry of the damper’s initial configuration, which includes the diameter, height, and thickness of the cylinder and the number, shape, position, and dimensions of the slots. Next, the material description defines the stress–strain relationship and the failure criterion, while the displacement protocol is given in function of the maximum values expected for the devices. Such protocol can be obtained from design codes such as ASCE 7–16 [42]. Then, the parameters that detail the finite element modeling (element type, mesh, analysis type, numerical method) are provided. With that information, it is possible to build a base-finite element model to initiate the optimization process. Then, the SA parameters (number of runs, maximum number of iterations, and cooling temperature) and the variable domain must be given. Finally, the python code implements the solution representation for the optimization algorithm, as shown in Sect. 4.2. It is worth mentioning that the general cylinder dimensions, the material properties, the finite element modeling, and the SA parameters will not change during the optimization process.

The proposed method implies using finite element software that determines the structural response of a specific slotted HCS damper under a cyclic displacement protocol. This research used ABAQUS because it has high numerical capabilities, directly computes EDC, and can be handled from python. It is worth mentioning that the quality of a damper configuration is measured as the energy dissipated under the displacement protocol. The damper finite element model is created from the previous data and numerically solved under the consideration of large deformations. Then, the geometrical configuration of the HCS damper, stress distribution, and energy dissipation are saved. Previous papers on steel damper optimization have used ABAQUS as a finite element tool [17, 26, 43,44,45].

The SA application implies generating a new solution (new damper configuration) from the neighborhood of the current solution. First, the process creates another solution by applying problem knowledge-based heuristics in Sect. 4.3. Then, the finite element analysis section is carried out to determine the EDC for the new geometrical configuration of the damper.

The last section corresponds to the SA routine’s implementation to determine which solution will be kept in the iterative process. The algorithm finishes when it achieves the maximum iteration, reporting the best configuration computed. After that, the process is repeated for the number of runs the user previously defined, obtaining one damper configuration per run. Among all the devices generated, the one with the highest energy dissipation is chosen as the optimized solution for the initial configuration. In addition, several initial HCS damper configurations require optimization due to the dependence of the SA algorithm on the initial solution. When all the initial geometrical arrangements are tested, the optimized solution with the highest EDC will correspond to the best shape for a cylinder steel damper with slots.

4.1 Description of the finite element model for the no slotted hollow cylinder

The HCS damper optimized in this study is based on that reported in [26], which presents a material volume of 2.337 × 10^–4 m³, see Fig. 7, with a thickness of 5 mm. The ratio height/width of $\sqrt{3}$ is kept to obtain the best aspect ratio in the case of the complete hollow cylinder. Slots were introduced in the solid cylinder, corresponding to a material reduction of 23%. The user gives the initial configuration for the slots before the optimization process begins. It is worth mentioning that the optimal solution found works for the damper dimensions defined in this research, but the methodology could be applied to cylinders of different sizes.

Fig. 7

Dimensions in mm of the HCS damper without slots

Figure 8 presents the plastic stress–strain relationship for the steel material used in the damper [26], as introduced in the process of structural modeling in ABAQUS for nonlinear analysis. The steel properties are: a yielding point of 321 MPa, an ultimate strength of 511 MPa, and a unit strain of 22.38%. It is worth noting that for steel devices, other low-point yield steels could begin the yield process with lower values of displacements and support more prolonged strains. Therefore, this paper does not assess the steel-type effect on the damper’s optimal shape. In addition, a second material was used to represent voids in the damper slots to ease the computational representation for the optimization strategy, as it is not necessary to reformulate de mesh configuration. This material is elastic, presenting Young’s modulus of 0.01E3 MPa and Poisson’s ratio of 0.3, as suggested by Zou and Xie [41]. The low value for young’s modulus allows simulating of a highly fragile element, representing the contribution of a void. In this way, the damper with slots is computationally considered without slots and composed of two materials, which contributes to decreasing convergence problems during the finite element analysis of each solution.

Fig. 8

The stress–strain curve in ABAQUS

The finite element model presents 25,080 elements, from which 5664 correspond to void areas (22.58%). The element S4R in ABAQUS was used to model the behavior of the plate because it offers the properties to model the behavior of the problem. Based on the literature and available computational resources, the element size was 1.4 mm. This value allowed a correct assessment of the EDC of the studied device. It should be noted that each geometrical configuration of the device can require its mesh definition. Figure 9 presents the boundary conditions of the problem that simulate the operation condition of the apparatus, with a movement mainly oriented in the direction of the beam due to the installation scheme. Thus, the bottom extreme is wholly fixed (all the degrees of freedom are constrained), while the upper part is released to allow displacement in the longitudinal beam axis (x-axis in Fig. 9). Such conditions have been previously applied in other papers, such as [26].

Fig. 9

Boundary conditions for the device

The loading protocol consists of the imposed displacements at the device’s top, as shown in Fig. 10. Only one displacement cycle is considered with an amplitude of 10 mm. It is essential to mention that for real applications, it would be necessary to apply load protocols like that established in the FEMA-461. Such protocol presents more than one load and discharge situation, but it is considered in this research that the failure does not occur for the one-cycle protocol. The non-linear analysis in ABAQUS includes large deformations due to the levels of displacements induced in the damper. As mentioned before, ABAQUS allows the computing of the EDC from the results by an internal procedure. That functionality eases the interaction with the optimization program.

Fig. 10

Displacement protocol

4.2 Optimization problem formulation

In other words, the optimization problem deals with determining the shape of an HCS damper that presents the maximum EDC given a material volume constant, a standard cyclic displacement protocol, and performance constraints. The following paragraphs describe the mathematical model for the optimization problem, including the objective function, the constraints, and the design variable and parameters.

The general process for generating a possible configuration for the Slotted HCS damper is explained using circular slots for convenience (Fig. 11left). First, the representation considers the device’s general conditions by examining three symmetry axes. The first one is a vertical plane crossing the beam’s middle line that makes possible to use a half cylinder in the optimization process. Then, the remaining half can be divided into four areas around two symmetric axes: one horizontal plane and the other with a vertical location perpendicular to the beam. Thus, only one quarter must be defined, producing optimal symmetrical solutions as shown in Fig. 11 right side. Therefore, only one would be used during the optimization process, reducing the search space’s complexity and computational cost. Furthermore, forcing symmetry in the damper configuration makes it possible to increase the device performance for loading conditions that will suffer during an earthquake. For the best understanding, Fig. 12 shows a two-dimensional representation of the cylinder with eight areas that subdivide it. Such conceptual representation eases the implementation of the optimization algorithm and the computational handling of different damper configurations.

Fig. 11

Symmetry for the device

Fig. 12

Representation of the cylinder as a plane

This research proposes to take advantage of the mesh to create a natural representation for possible solutions. Optimizing the material distribution involves determining each material point’s position in the cylinder domain, considering that the material mass is constant. A material point can correspond to one of the finite element domain types: steel material or void. A binary representation implies using a value of one to represent a material point and a value of zero to define a void point, as shown in Fig. 13. In this case, the void is not a void point but a material point with mechanical properties, such as Young’s modulus, with low values. This technique, known as soft kill [41], has the advantage that only one connectivity process is required to identify each element in the cylinder; otherwise, it is necessary to mesh each time the configuration changes, as in [23]. A strategy to ease the computational representation of each material point is used, in which the tridimensional cylinder can be seen as an unwrapped sheet, as shown in Fig. 13. Also, the eight quarters that divided the sheet due to symmetry can be appreciated. Then each finite element in the cylinder can be represented by either one (material point) or zero (void point); see Fig. 13. The number of variables corresponds to the number of finite elements, easing the handle of the variables. Notwithstanding, at this point, refining the mesh in zones with high-stress gradients is impossible. In addition, the element size is precise to correctly describe the geometry for contours such as circles. The algorithm in each iteration will generate a new solution by intelligently interchanging some positions of ones or zeros under some constraints.

Fig. 13

Numerical representation of the cylinder with material and void points

The main problem of this representation would be the considerable quantity of variables to be determined. As mentioned before, the problem size was reduced by forcing the device’s symmetry so that only a quarter of the device needs to be defined, as shown in Fig. 14. In addition, it is necessary to specify that the rectangle board always has a point material to guarantee the correct connection between the parts and the beam and braces. Then, the procedure forces the algorithm to maintain a value equal to 1 in the contour (design parameters). Finally, keeping the material volume constant during the optimization process must be addressed; that is, the volume of material and void between two consecutive iterations is the same. Therefore, the algorithm does not produce unfeasible solutions from the above considerations and focuses on obtaining the best shape to maximize the EDC given a mass quantity.

Fig. 14

Quarter selected for optimization

Finally, the optimization problem can be defined as:

Find ${\varvec{X}}=\left[{x}_{1},{x}_{2},{x}_{3},\dots , {x}_{n}\right]$

To maximize

$${E}_{p}= \oint F*du$$

(2)

where ${E}_{p}$ is the plastic energy. More complex objective functions could be used considering other physical parameters, but satisfactory results have been obtained with Eq. (2), such as in [15].

4.3 Configuration of the SA algorithm and heuristics

The SA algorithm used in this research corresponds to that reported in Sect. 3, considering a decrement of the simulated annealing varying linearly from 1 to 0.01. The cooling rate was defined to be 0.75. However, to improve the algorithm’s convergence, it is necessary to propose heuristics based on the knowledge of the problem.

The first heuristic implies that generating a table with the values of the stresses in each element and sorting from the minimum value to the maximum is necessary. The idea is to identify which point materials present the least contribution to the EDC, then modify the probability of a material to be chosen to change the position with a void. The changing possibility for a domain point, ${Ps}_{ij}$, is given by:

$${Ps}_{ij}= \frac{{S}_{ij}}{{S}_{max}}$$

(3)

where ${S}_{ij}$ is the stress of the element $ij$ and ${S}_{max}$ is the maximum stress in the damper. Then, a random number is generated and compared with the probability computed in Eq. (3). If the random number is higher than the probability, the material point is changed to a void point in the next iteration. This operation has to be carried out for all material points, and the number of point changes has to be saved to ensure that the amount of material is maintained in the next iteration.

A similar process is carried out for the void-type elements to define the probability of being modified to a material-type element. In this case, the probability, ${P01}_{ij}$, is computed from the probability stress level from the bottom, upper, left, and right elements to the element $ij$, as given by:

$${P01}_{ij}= \frac{{S}_{\left(i-,j\right)}}{{S}_{max}}+\frac{{S}_{\left(i+1-j\right)}}{{S}_{max}}+\frac{{S}_{\left(i,j+1\right)}}{{S}_{max}}+\frac{{S}_{\left(i,j-1\right)}}{{S}_{max}}$$

(4)

A list of the void-type elements is generated and sorted from the highest. Then, the number of material-type elements that changed to zero is selected from the first position in the list and modified to 1.

In addition, the relocation process of materials could generate unfeasible solutions that may affect the optimization process. The first condition is caused when a material-type element is connected only by one node to another, as shown in Fig. 15. The second condition refers to the possibility of having disconnected material regions in the device, as shown in Fig. 16. Thus, a heuristic rule is used based on a connectivity index to avoid such situations given by:

Fig. 15

Possible solution with elements connected only in one node

Fig. 16

Possible solution with disconnected material regions

$$\left({M}_{\left(i-1,j\right)}+{M}_{\left(i+1,j\right)}+{M}_{\left(i,j+1\right)}+{M}_{\left(i,j-1\right)}\right)>2$$

(5)

This equation assesses the number of connections of the element, which must be at least 2. When it does not satisfy this equation, the element is changed to void, turning the next element in the list to 1. There is the possibility of generating new wrong configurations, which implies that the process must be repeated.

5 Numerical results

5.1 Initial configurations for the slotted HCS damper

The optimization process requires that the user defines the initial configuration of the slotted HCS damper to run, however with multiple configurations. The selected geometrical design influences the optimization process and drives the algorithm to specific regions in the search space, finishing locally. In this paper, the five initial shape configurations presented in Fig. 17 are analyzed and selected by corresponding to basic geometric slot shapes. The devices’ width, height, and thickness are given in Sect. 4.1, while the distribution of slots and sizes are defined to guarantee that all devices present the same mass. A mass of 1.5 kg for all devices was defined, corresponding to void elements in 22.2% of the complete cylinder model. The proposed optimization methodology was applied to optimize the HCS damper in three independent runs, with 50 iterations for initial configuration in each run. This number was defined after a process of trial and error. The computational cost for each example run is about 1.5 h in a PC with an Intel(R) Xeon(R) CPU E5-2650 v4 @ 2.20 GHz, 64 Gb RAM. It is necessary to execute the algorithm three times due to the stochastic nature of the algorithm. A higher number of executions can be used, but this increments the computational cost, and it was observed that three runs were enough.

Fig. 17

Initial configurations

The results are presented visually considering two views, one parallel to the load’s axis (frontal view) and the other transversal (lateral view), as shown in Fig. 18. In addition, the different results were identified as follows: the first letter corresponds to the initial configuration (C—circular, S—Square, T—Triangular, H—Horizontal, and V—Vertical slots); the second letter “O” refers to the optimized condition and the number refers to the number of the run (1, 2 or 3). For example, the model CO1 corresponds to the optimized shape obtained in the first run for the initial damper configuration with circular slots.

Fig. 18

Visual representation of the optimized devices

5.2 Energy dissipation capacity for the initial configurations of the damper

Figure 19 presents the stress distribution for the five initial configurations of the slotted HCS damper when submitted to the displacement protocol defined in Fig. 10. As observed, all the configurations present stress distribution, with most zones keeping an elastic behavior. The presence of the slots induces stress concentrations that made yield the material in the nearest region since the energy dissipation capacity (EDC) ranges from 540 to 2527 J. The configuration with circular slots induces an outstanding amount of material yield. On the other hand, rectangular slots with either vertical or horizontal orientations do not produce optimal stress trajectories during the cyclic load, inducing a few areas with yielding of the material. The difference in the computed EDC shows the importance of determining the optimal shape for the slots. It is worth mentioning that the finite element modeling strategy used in this research was first validated by using results from other MH dampers in the literature.

Fig. 19

Stress distribution and EDC for the five initial configurations

5.3 Optimized slotted HCS damper shape

Table 1 reports the EDC obtained for the best shape found when each initial configuration was used to start the optimization process. It is observed that there is a difference of almost 1000 J between the best (VO1) and the worst (SO₂) solutions, which shows how the initial solution affects the optimization process by achieving local optimums. Thus, this opens the possibility of generating new strategies to define the initial configuration to find the global optimum. Results from the original cylinder are included to account for the case where a slotted configuration does not correspond to the best solution. Comparison concerning the cylinder without slots shows that the configuration VO1 produces an EDC/mass ratio 16% higher than the original cylinder. Most of the optimized devices presented an EDC/mass ratio more elevated than the original cylinder. It is worth noting that this comparison criterion does not consider the cost associated with perforating the cylinder to generate the slots. Further investigations are necessary to use a more complex objective function based on the device’s total cost.

Table 1 EDC for the optimized configurations

Figure 20 presents the optimized shapes obtained from each initial configuration, which offer different degrees of complexity for possible manufacturing. Such complexity could be associated with the number and shape of holes to punch out in the solid cylinder. Results show no apparent relation between the original and optimized shapes for the slots. In addition, the number of slots can vary for the optimized solutions, with the best shape presenting only one slot. The stress distribution differs from one configuration to another due to the slot shapes, showing the necessity of understanding how the presence of a slot guides the stress trajectory. However, different slot topologies produce a similar value for the EDC, indicating multiple local optima in the objective function. This issue is essential to define as there is a possibility that the SA could get stuck in a local optimum. The increment in the EDC after applying the proposed methodology to the original configuration is also reported, showing a high variation depending on the initial damper configuration. Such a difference is generated as some slot shapes produce very low EDC, but the iterative process for transforming the shape found better ways to take advantage of the material. The results show the solution’s dependence on the initial configuration and raise the following questions: if other initial configurations were tested, would it be possible to obtain better arrangements? It is worth mentioning that “manual” refinement could be carried out to get a more regular shape that does not present so many irregular contours.

Fig. 20

Optimized shapes for the HCS damper

Figure 21 presents the Von Mises stress state for the different configurations of the slotted HCS damper. The results show that the frontal regions in the device are highly used for energy dissipation, obtaining more uniform distributions for all the optimized devices. Furthermore, the lateral views show that most material quantity in the device was removed and that there are zones with stress concentrations and low stresses. Therefore, it could be concluded that the optimization process keeps the material elements found along the movement in most areas and removes that material perpendicular to the beam axis. Regions that present nearby slots can introduce stress concentrations in the material between them. Also, in the front views, the highest stress values are induced in the proximity of the boundary conditions. It is worth mentioning that the brace supporting the device has to provide full restriction for the horizontal displacement in the bottom part of the device.

Fig. 21

Von Mises stress states for the optimized configurations

The computed solution for the three runs in each case allowed for verifying the multi-modality nature of the search space. In addition, using random operators in the SA algorithm produces possibly different configurations for each run. For example, Fig. 22 shows that the difference in the EDC (objective function) for the various solutions was less than 200 J (corresponding to 3% of the optimal EDC), which means that different topologies could produce similar values for the EDC. Furthermore, it can be seen that in all the configurations, the algorithms try to generate more areas with high stresses that induce yielding in the material. These results indicate that improving the SA is essential to obtaining the global optimum.

Fig. 22

Optimal shapes for the three different runs

5.4 The optimal slotted HCS damper configuration

So far, the best configuration is the simplest to be fabricated, as shown in Fig. 23, which takes advantage of most materials in the device. The stress trajectory from the extreme is guided to a section reduction in the device’s middle for the part perpendicular to the longitudinal axis. This device configuration resulted in considering that the beam movement is along its longitudinal axis. As a result, most device areas present high values of stresses that induce material yielding, compared with the other configurations shown in Fig. 19. The obtained solution is approximately equal to two parallel plates of the solution obtained in Ferrer and Villalba [16], a result that is similar to the initial slot configuration in [19] or [21]. This way, the device works as a fusible because it presents a weak section where failure can be induced.

Fig. 23

3D optimal shape

One modeling issue that must be considered in the optimization process is the mesh size, as small sizes increase the computational cost considerably. Figure 24 shows the dependence of the EDC for the optimal solution in Fig. 23 on the element size, considering a range from 0.8 to 1.8 mm for the element side. It is observed that the value of 1.4 mm was adequate for the optimization process as the difference in the EDC with the solution of 0.8 mm is less than 20 J. It is worth mentioning that in this study, the effect of the element type was not considered.

Fig. 24

Influence of the mesh size in the computed energy dissipation capacity

The strain distribution in the optimal device was obtained (see Fig. 25) using a 1.4 mm mesh size for the finite element model. Results indicate high values in the middle zone of the damper, as expected. In addition, a diagonal plane of symmetry is observed for the strain distribution in the front view. In contrast, the lateral view indicates a different strain distribution between the bottom and upper parts. Therefore, it is worth controlling the strains generated in the device during the displacement cycles in shape optimization of MH dampers.

Fig. 25

Strain distribution for the optimal shape

5.5 On the hysteresis cycles

A hysteresis cycle diagram is an obligatory figure to show the performance of an MH damper under cycling displacement protocol. Also, it allows for visually determining the improvement in the EDC between the original and the optimized configuration. Figure 26 presents the original and optimized model’s hysteresis cycle cases, obtained from the displacements at the top of the device and reactions at the bottom.

Fig. 26

Hysteresis cycle. a Circular model, b horizontal model, c vertical model

Only three cases are presented related to the worst, middle, and best device optimization. The area increment level can be appreciated for all cases under the load–displacement curve. The elastic stiffness for all instances is increased in the optimal solution, which indicates that this parameter could be considered in the definition of the objective function. It is essential to mention that the protocol could affect the optimal shape. By only including one load cycle is not possible to consider the effects when the material starts to be degraded. Thus, further research has to include several cyclic displacement loops.

5.6 Evolution of the optimization process

Figure 27 presents the convergence process for the different examples, showing the proposed method’s ability to improve the EDC for the initial damper configuration. In general, the solution from the three runs for a device produces a similar EDC (even with the stochastic nature of the algorithm), but it is suggested to increment the number of executions to guarantee a better exploration of the search space. Nevertheless, the number of runs was enough to ensure that the algorithm had converged. Most cases present fast improvement on the EDC until iteration 20, with shallow changes in the following iterations. Only for the initial damper configuration with horizontal slots seems that the convergence was not achieved, as the variation in the EDC keeps increasing for the last iterations. Furthermore, it was observed that it is possible to achieve different local optimums from a particular shape configuration.

Fig. 27

Convergence process

One strategy that could help to understand the optimal topology for the slotted HCS damper consists of analyzing the initial configuration’s evolution. Figures 28, 29, 30 present the evolution of three initial configurations, in which two produce the worst and better EDC. Results allow concluding that the algorithm can change the topology of the cylinder (defined in terms of the number of slots) while keeping some similarities to the original device. In iteration 10, the topology of the optimized device is practically obtained. All examples try to eliminate material in the center of the lateral view and keep material in the center of the front view. Figure 30 shows that vertical slots’ evolution consists of jointing these vertical strips until getting the optimal shape.

Fig. 28

Evolution of the optimal configuration for the circular slot initial configuration

Fig. 29

Evolution of the optimal configuration for the initial damper with horizontal slots

Fig. 30

Evolution of the optimal configuration for the initial damper with vertical slots

In addition, Fig. 31 presents the evolution in the stress of the optimal slotted HCS configuration. This figure illustrates that the algorithm learns to redistribute the material as the new configuration offers a better distribution of the stresses in the cylinder. It is observed that the algorithm has achieved a similar response from iteration five.

Fig. 31

Stress evolution of the optimized shape

6 Conclusions

This paper proposed a methodology to find the optimal shape of an HCS damper with slots to produce the maximum energy dissipation capacity under material constraints using a heuristic optimization algorithm. The main findings are summarized in the following:

• The optimal device was obtained from an initial configuration with vertical slots, resulting in a geometrical configuration with only one big rhombic slot, making it suitable for manufacturing. Such configurations could indicate that a solution with two optimized parallel plates would be more efficient

• The optimal device presented an EDC/mass ratio of 16% higher than the original HCS damper, which can be proved from the hysteresis cycle computed. Such improvements show the importance of applying optimization for energy dissipation devices

• The optimal shapes obtained from other geometrical initial configurations also presented high EDC values, demonstrating the objective function’s multi-modality nature. Such characteristic is vital in understanding the search process

• The convergence figures show that the optimization algorithm achieves a good solution with few iterations and that the three runs achieve a similar value for the EDC. This finding is an essential advantage of the proposed algorithm because assessing the objective function requires a high computational cost

• The methodology proposed could be easily adapted to other configurations of MH dampers, while being defined solution representations for each case in particular.

Future research can raise based on the following issues:

• Considering a significant quantity of initial damper configurations to explore the search space further

• Using a complete cycling displacement protocol to assess the effects for more cycles

• Adding new characteristics in SA to face the multi-modality of the objective function

• Implementing a set of a few solutions simultaneously takes advantage of high-performance computing.