1 Introduction

Passive isolators effectively mitigate the vibrations in the isolation region, but these isolators do not function satisfactorily as the excitation frequency is varied. On the contrary, the semi-active isolators are adaptable and can be effective in stiffness and mass-controlled region vibrations. The ability of a semi-active isolator to mitigate vibration primarily depends on the functional element, which can change properties in response to external stimuli. Various semi-active isolator devices have been developed over the last decade using smart materials or mechanical means. Recent research has concentrated on the use of smart materials. A review of the literature revealed that semi-active isolator devices are typically made of shape memory alloys (SMAs), piezoelectric and magnetorheological elastomers. Among the list, MRE is the promising resilient element to realize the intelligent material-based semi-active vibration isolator. MRE is comprised of elastomer that contains matrix and micron-sized ferromagnetic filler particles. The stiffness and damping properties of the MRE are altered by the magnetic field [1], and it reverted to its initial state when the magnetic field is removed. This phenomenon is associated with the attempt by the ferromagnetic fillers to achieve the minimum energy state [2].

The performance of isolators is measured with respect to the ability to mitigate the vibration. Often transmissibility measurements are employed to assess the isolation effect induced by an isolator. The previous works carried out by our group [3] was reported that the transmissibility response was sensitive to the variation in the magnetic field. Additionally, the viscoelastic response of MRE resilient element was a function of frequency and amplitude of excitation. The change of natural frequency is associated with the change of dynamic properties of the material itself. In addition to the external magnetic field, the dynamic properties of MRE is strongly influenced by strain amplitude and excitation frequency [4,5,6,7].

Apart from material characterization, number of researchers focused on the development of isolators. Depending on the direction of the excitation force and magnetic field, these isolators operate in shear or squeeze mode. Weihua Li et al. [8] developed a magnetorheological elastomer isolator to isolate seat vibration. To reduce the vibration in the seat suspension system for frequency range of 1–20 Hz, the stiffness of the MRE isolator system was varied from 3000 N/m to 9000 N/m by varying current from 0 to 3 A. Fu et al. [9] used shear compression mode MRE isolator that suppresses the high-frequency and micro-amplitude vibration of a precision-fabrication platform. To reduce vibration, the natural frequency of the isolator was shifted from 45.82 to 82.55 Hz as the applied current was varied from 0 to 1.5 A. Tao et al. [10] developed a squeeze/elongation–shear mode isolator. To control the vibrations, input current to the isolator was varied from 0 to 2.5 A, resulting in an increase in stiffness and damping of approximately 66.57% and 45.55%, respectively. Yang et al. [11] developed a novel multi-layer MRE isolator with negative changing stiffness characteristics to reduce the horizontal vibration of the seat. The stiffness of the MRE isolator was reduced from 23,903 N/m at 0A to 11,442 N/m at 4A current input, correspondingly the natural frequency of the MRE isolator was decreases from 32 to 21 Hz. Opie and Yim [12] investigated a tunable stiffness MRE vibration isolator, and the experimental results showed that when compared to passive systems, the MRE isolator with SA controller system reduced the resonances and payload velocities by 16–30%. In a scaled building system, Behrooz et al. [13] designed and tested a new magnetorheological elastomer-based semi-active/passive variable stiffness and damping isolator (VSDI). The top floor vibration amplitudes in acceleration and displacement were effectively reduced by varying the current from 0 to 3 A which changes the natural frequency of the isolator from 41 to 51 Hz.

Following the design phase of the MRE isolator, a mathematical representation is created to aid in the implementation of control strategies. Developing a mathematical model for transmissibility of the MRE isolator is complex as its response varies with the magnetic field, the preload, strain amplitude, and the frequency of excitation [14]. There are few attempts made to develop a mathematical model for transmissibility of the MRE isolator for wide frequency range. Faramarz Gordaninejad et al. developed a viscoelastic model for variable stiffness and damping of isolator based on the Bouc–Wen hysteresis (VSDI). The model parameters are estimated from the force vs displacement curve for 2, 4, and 10% strain at 0.1 Hz excitation frequency in passive and active states (4 A). The model was used to estimate the transmissibility of the VSDI isolator for different currents, but it failed to estimate the transmissibility of the MRE isolator for different excitation amplitudes [15]. Other authors developed viscoelastic models such as hysteresis model [16], a standard linear solid model with Coulomb friction [17], Kelvin–Voigt Bouc–Wen model [18], strain-stiffening model [19], fractional viscoelastic models [20, 21] and LuGre friction model [22] for various MRE isolators. However, these models are based on the estimation of parameters of the model with respect to the steady-state force vs displacement responses at different amplitude of excitation and the current. These models fail to reproduce the dynamic response of the MRE isolator over wide frequency range [16, 17, 23,24,25,26,27,28]. Moreover, these models necessitating extensive experimentation to develop a mathematical model for predicting MRE isolator transmissibility. Also, this approach demands a greater amount of experimental data which is time-consuming. A mathematical model that responds to the change in amplitude of excitation at a different frequency, as well as the input current supplied, simplifies the process of effective implementation of control strategies for MRE isolator. This method is advantageous as it simplifies the process of identifying parameters for a given set of input operating conditions.

Success of MRE isolator necessitates an effective control strategy. The controller should activate the isolator for a specific frequency range of interest. When the frequency excitation reaches the isolation region, the controller should turn off and should function as a passive device. Furthermore, the controller should be adaptable to changes in amplitude and frequency of excitation. On–off or bang-bang controllers are the most commonly used controllers [29,30,31,32]. The on–off controller generates pulse-like control output based on the oscillating member position, causing jerks in the member. Another difference is that the on–off controller generates controller output for the entire frequency range, which is not an essential requirement in the case of an MRE isolator. The fuzzy controller is a popular alternative for the on–off controller [33,34,35,36,37]. In contrast to on–off controllers, which generate pulse signals, fuzzy controllers generate a continuous control signal for a given input, which eliminates jerks. However, the limitations of developed fuzzy controller are associated with the rules that were created in the data base. Because these rules are based on an on–off control, the control output is generated for full frequencies, which is not necessary in the case of an MRE isolator [17, 38]. Therefore, the present work focussed to identify the controller turn off frequency for the fuzzy controller through developing modal-based fuzzy controller.

To achieve the required goal, the current work is devoted to developing a mathematical model for the system via a simplified approach based on the state space approach and the controller stopping frequency. Transmissibility tests were conducted using a sine sweep input with a range of excitation amplitudes and frequencies, as well as a current input supply to the isolator. The state-space approach was used to develop the viscoelastic model for the MRE isolator when the input current was varied. The amplitude dependent properties of the viscoelastic modelling were estimated by relating the current input to the MRE isolator model to the excitation amplitude based on the controller stopping frequency. After developing the viscoelastic model, a model-based fuzzy controller was developed and its performance was evaluated both in simulation and in real time.

2 Semi-active MRE isolator construction detail and its performance analysis through transmissibility tests

2.1 MRE isolator design

The proposed MRE isolator is operating in shear mode, as it offers a larger enhancement due to lower values of initial stiffness. A schematic representation of the MRE isolator is presented in Fig. 1a. The details about the list of components, weight of each component, and their permeability is listed in Table 1. The isolator comprises main isolator body and the casing. The isolator body has the stationary electromagnet, a movable central core, two ring-shaped MRE elements and an aluminium piston attached to the movable central core. The electromagnet consists of a copper coil (20 AWG gauge wire with 980 number turns (Resistance is 6.02 Ω and inductance is 51.7 mH)) wound around the bobbin (inner diameter 20 mm, Outer diameter 100 mm and height 40 mm) [39]. The core material (fixed and moving steel core) is manufactured from low-carbon steel. For the proposed design, two ring-shaped MRE resilient elements are attached between the fixed and the moving core at the top and bottom of the isolator. A non-magnetic piston is attached to the moving steel core to accommodate the motion transmission from the shaker to the receiving end. To accommodate the vertical motion of the moving cylindrical core a gap of 10 mm is maintained between the MRE resilient element and the coil. The constituents and the synthesis process of the MRE are discussed in the Sect. 2.2. A stationary steel plate core and the central moving cylindrical steel core are employed to concentrate the flux lines through the MRE. The electromagnetic coil is designed such that the flux lines that pass through the core are perpendicular to the loading direction of MRE resilient element. Magnetic field simulations were performed in ANSYS Maxwell to analyse the field distribution in the MRE region (Fig. 1b). The effective magnetic permeability of MRE is calculated according to the Maxwell Garnett mixing rule [40], and it is expressed as,

$$\mu_{{{\text{ef}}f}} = \mu_{m} + 2\phi \mu_{m} \frac{{\mu_{p} - \mu_{m} }}{{\mu_{p} + \mu_{m} - \phi \left( {\mu_{p} - \mu_{m} } \right)}}$$
(1)

where \({\mu }_{m}\) and \({\mu }_{p}\) are permeability of the matrix and particle and \(\phi\) is the volume fraction of the particle. The proposed design of electromagnet could generate a maximum magnetic flux density of around 0.37 T through the MRE resilient element corresponding to 3 A input current. The corresponding magnetic flux density values for 1 A and 2 A input current are 0.123 T and 0.246 T.

Fig. 1
figure 1

a Schematic representation of MRE isolator. b Magnetic field simulation of a cross section of the isolator using ANSYS Maxwell 15

Full size image
Table 1 Weight and permeability of the different Parts of the MRE isolator
Full size table

The casing of the isolator is a cylindrical aluminium housing of dimension (inner diameter 120 mm and outer diameter 150 mm and height 170 mm). Two aluminium support rings (inner diameter 100 mm and outer diameter 120 mm and height 25 mm) are provided at the top and bottom to facilitate the movement of the central core. Two mounting plates one at the bottom and other at the top (plate diameter 180 mm and thickness of 10 mm) are provided to firmly position the MRE isolator body in the casing. The isolator assembly is rigidly fixed to the electrodynamic shaker using the bottom mounting plate.

2.2 MRE sample preparation

The field-induced enhancements are critical for MRE isolators to achieve isolation over a wide frequency range. Past studies have revealed that silicone rubber as a matrix for MRE isolator could achieve a high relative MR effect [41]. For the proposed design, two-ring shaped MRE resilient elements are prepared (inner diameter 40 mm, outer diameter 50 mm and thickness 5 mm). The MRE is synthesized with the silicone matrix and CIP fillers. The silicone matrix is procured from Aditya Silicone Rubber (MurtiSil, Rtv 1010), and the CIP fillers from BASF (CC grade, size 3–5 µm). As reported by the past studies, an optimum content of 72% by weight of CIP is chosen for the synthesis process [41]. Additionally, silicone oil is added as an additive for the ease of the synthesis process. These materials are mixed thoroughly with a weight ratio of 72% carbonyl iron, 16% silicone rubber, and 12% silicone oil, and the mixture is poured into the mould. The mould was kept in the vacuum chamber for about 20 min to remove the trapped air bubbles. After the vacuuming process, the MRE samples are cured for about 24 h at room temperature under constant pressure.

2.3 Experimental set-up for transmissibility test

A displacement transmissibility test was used to determine the isolation performance of the MRE isolator. To determine the effect on isolation, natural frequency and controller stopping frequency, tests at various excitation amplitudes and input currents were conducted. The experimental set-up is depicted schematically in Fig. 2. The MRE isolator was attached to an inertial mass of 0.583 g, and the isolator was mounted on the electrodynamic shaker (APS 420 ELECTRO-SEIS). Two accelerometers (KISTLER type 8774A50) were used to measure the input and output accelerations; one was placed on the base plate and the other on top of the inertial mass. The MRE isolator was connected to a programmable power source, which supplies an input current up to 3 A to the coil. The initial testing of the MRE isolator in passive mode revealed that the natural frequency was around 30 Hz, and the corresponding value at 3 A input current is 50 Hz. Consequently, to assess the performance of the MRE isolator, a region close to the resonance region is considered. Thus, performance assessment of the MRE isolator is focused on the frequency region of 15–80 Hz. To study the effect of excitation amplitude the performance of the MRE isolator, the tests were conducted at different amplitude of excitation between 0.00125 and 0.00225 m. To have a better conrol over excitation amplitude, initial tests were conducted to calibrate the voltage output of the function generator in terms of amplitude of excitation, where 2 V represents 0.00125 m amplitude excitation and 4 V represents 0.00225 m amplitude excitation. A sine sweep frequency of 15–80 Hz was generated from the function generator to shaker, and the disturbances were transferred to the inertial mass via the MRE isolator. Following that, a series of tests were performed at an interval of 8 s. The current to the coil varied from 0 to 3 A with a 0.5 A step increment for each test. The accelerometer sensor responses at the base and inertial mass were collected (25,000 samples in 8 s) using a data acquisition device (NI 9234) and analysed with LabVIEW software.

Fig. 2
figure 2

Schematic representation of the test set-up for measuring the displacement transmissibility response of the isolator

Full size image

2.4 Results and discussion

2.4.1 Magnetic field dependency of transmissibility

Figure 3 depicts the displacement transmissibility responses of the MRE isolator at different input currents under 0.0015 m amplitude of excitation. As evident from the graph, the natural frequency of the system increases with an increase in input current. At 0 A input current, the natural frequency of the system is 28 Hz, and it increased to 47.2 Hz for the input current of 3 A with a frequency shift of 19.2 Hz. The amount of shift in the natural frequency at different input currents is listed in Table 2. Among the tested conditions, the frequency shift is lower for the input current is 0.5 A, and it is maximum for 3 A current input. The shift in natural frequency of the system with the input current is associated with the enhancement in the stiffness under the influence of magnetic field. Additionally, the damping characteristics of the system also vary in response to the magnetic field. Using the following relations, the stiffness and damping characteristics of MRE resilient element are extracted from the transmissivity plots.

Fig. 3
figure 3

Displacement transmissibility of MRE isolator at different current inputs

Full size image
Table 2 Stiffness and damping ratio of the MRE under various current Inputs
Full size table

The effective stiffness keff of the isolator expressed as

$$k_{{{\text{eff}}}} = m\left( {2\pi f_{n} } \right)^{2}$$
(2)

where m is inertial mass and fn is the natural frequency of the isolator.

The transmissibility \({T}_{r}\) of the isolator is

$$T_{r} = \sqrt {\frac{{1 + \left( {2\frac{\omega }{{\omega_{n} }}\xi } \right)^{2} }}{{\left( {1 - \frac{\omega }{{\omega_{n} }}} \right)^{2} + \left( {2\frac{\omega }{{\omega_{n} }}\xi } \right)^{2} }}}$$
(3)

where \(\omega\) excitation frequency in rad/sec and \({\omega }_{n}\) natural frequency in rad/sec.

At natural frequency, where \(\frac{\omega }{{\omega }_{n}}=1\), then the damping ratio \(\xi\) of the isolator expressed as

$$\xi = \sqrt {\frac{1}{{4\left( {T_{rn}^{2} - 1} \right)}}} = \frac{c}{{2\sqrt {km} }}$$
(4)

where \({T}_{rn}\) represents transmissibility at the natural frequency and \(c\) is the damping coefficent.

The stiffness and the damping ratio values listed in Table 2 confirm that with the increase in input current the stiffness and the damping increase. At 3A input current, the enhancement in the stiffness is 184.76%. Compared to stiffness variation, the enhancement in the damping is not significant. A maximum enhancement of 19.96% in damping is noticed as the input current is increased to 3A.

2.4.2 Amplitude dependency of transmissibility

The property of MRE isolator is sensitive to the input amplitude of excitation. This typical behaviour is associated with Payne effect [42] exhibited by MRE under the dynamic loading, which is characterized by the decrease in stiffness with an increase in input strain under dynamic loading. Figure 4 shows a comparison between the displacement transmissibility response of MRE isolator registered at different amplitude of excitation corresponding to 0 A and 3 A input current. As evident from the graph, the natural frequency decreases with an increase in the amplitude of excitation. This response is consistent under both passive (0A) and active (3A) state. From the response plots, natural frequency, frequency shift, stiffness and damping values are extracted at different amplitude of excitation and input current and the corresponding values are listed in Table 3.

Fig. 4
figure 4

Transmissibility of the MRE with different excitation inputs without magnetic field 0 A and with magnetic field 3 A

Full size image
Table 3 Properties of MRE isolator under different amplitude of the excitation
Full size table

As shown in Table 3, the natural frequency of the isolator system decreases with an increase in amplitude of excitation. Under passive state, for an input amplitude of 0.00125 m, the natural frequency of the system is 31 Hz, and with increasing the input current to 3A, the natural frequency is increased to 52.70 Hz, with a total frequency shift of 21.07 Hz. For the amplitude of excitation of 0.00225 m, the natural frequency of the system registered at 0 A is 27 Hz, and it increases to 43.09 Hz for an input current of 3 A. It is also observed that the frequency shift is a function of input amplitude. At larger excitation amplitude, the frequency shift with respect to the active state of MRE decreases.

With an increase in amplitude of excitation, the stiffness and the damping ratio of the isolator system are decreased. Among the tested input excitation amplitude levels, the stiffness and the damping ratio values are maximum for an input amplitude of 0.00125 m. At 0 A input current, the stiffness of the isolator is reduced from 22,039.5 N/m to 16,721.04 N/m for varying the amplitude of excitation from 0.00125 m to 0.00225 m. Corresponding values for the input current of 3 A current decreases from 63,936.1 N/m to 42,602.12 N/m. This implies that the stiffness reduction with increasing strain is more pronounced in the presence of a magnetic field [43]. With increased excitation amplitude, the overall relative change in stiffness of the MRE isolator decreases from 190.08 to 154.78%. The damping ratio of MRE isolator is decreased with an increase in amplitude of excitation. At 0 A input current, the damping ratio is decreased from 0.2886 to 0.0999 as the input amplitude of excitation is varied from 0.00125 to 0.00165 m [44]. At 3 A input current, the corresponding changes in damping ratio is from 0.2224 to 0.1668 [44]. The damping in the MRE isolator is due to frictional sliding at the interfaces between the free rubber and the particles [45]. At low strain levels, the particle can easily slide over the rubber, causing friction and thus resulting in higher damping ratio. At higher strain levels, the rubber locks the particle and partially allows the particle to slide over the rubber, resulting in relatively lower damping [46]. The relative increase in damping ratio with increasing excitation amplitude is from -22.91% to 67%, which indicates that at lower strain, dipole interaction between the particles is stronger, reducing the friction between the particle and rubber [46]. However, at higher strain levels, dipole interactions between the particles are not pronounced, which increases the friction between the rubber and particle [46].

3 Viscoelastic modelling of the MRE isolator

3.1 State-space equation of MRE isolator

The performance analysis of MRE isolator confirms that its repose varies with the frequency, magnetic field and the input amplitude. To implement semi-active control strategies, these responses need to be represented mathematically. The material behaviour of MRE is viscoelastic in nature [47], and it can be mathematically represented by the viscoelastic constitutive relations. In addition, MRE also exhibits hysteretic behaviour as the input strain is increased. Thus, the modelling process of MRE is complex as its it should portray the response at different loading conditions [15].

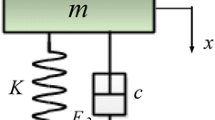
A single-degree-of-freedom system (SDOF) representation of the MRE isolator model is shown in Fig. 5. The model comprises Zener [48] and Bouc–Wen [49] combined together, representing the viscoelastic and hysteresis behaviour of the MRE isolator. The governing equation of the MRE isolator model with the Zener and Bouc–Wen elements is,

$$m\ddot{x}\left( t \right) + (k_{1} + \Delta k_{1} )\left( {x\left( t \right) - w\left( t \right)} \right) + \left( {c + \Delta c} \right)\left( {\dot{x}\left( t \right) - \dot{y}\left( t \right)} \right) + z = 0$$
(5)
$$(k_{2} + \Delta k_{2} )\left( {y\left( t \right) - w\left( t \right)} \right) = \left( {c + \Delta c} \right)\left( {\dot{x}\left( t \right) - \dot{y}\left( t \right)} \right)$$
(6)

where \(z\) is hysteretic force.\(\Delta {k}_{1}\),\(\Delta {k}_{2}\) and \(\Delta c\) parameters are the change of properties under the influence of the magnetic field.

$$\dot{z} = \alpha \left( {\dot{x}\left( t \right) - \dot{w}\left( t \right)} \right) - \beta \left| {\dot{x}\left( t \right) - \dot{w}\left( t \right)} \right|z - \gamma \left| z \right|\left( {\dot{x}\left( t \right) - \dot{w}\left( t \right)} \right)$$
(7)

where \(\alpha\), \(\beta\) and \(\gamma\) are non-dimensional parameters responsible for the shape and size of the hysteretic loops.

Fig. 5
figure 5

Viscoelastic model of the MRE isolator

Full size image

The state-space equation for the system is given as

$$\left[\begin{array}{c}\dot{x}(t)\\ \ddot{x}(t)\\ \begin{array}{c}\dot{y}(t)\\ \begin{array}{c}\ddot{y}(t)\\ \dot{z}(t)\end{array}\end{array}\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{ccc}\begin{array}{c}0\\ -{(k}_{1}+\Delta {k}_{1})/m\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}& \begin{array}{c}1\\ -(c+\Delta c)/m\\ \begin{array}{c}1\\ \begin{array}{c}0\\ \alpha \end{array}\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}-{(k}_{2}+\Delta {k}_{2})/(c+\Delta c)\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0\\ (c+\Delta c)/m\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}& \begin{array}{c}0\\ -1/m\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}x(t)\\ \dot{x}(t)\\ \begin{array}{c}y(t)\\ \begin{array}{c}\dot{y}(t)\\ z(t)\end{array}\end{array}\end{array}\right]+\left[\begin{array}{cc}\begin{array}{c}0\\ {(k}_{1}+\Delta {k}_{1})/m\\ \begin{array}{c}{(k}_{2}+\Delta {k}_{2})/(c+\Delta c)\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ \begin{array}{c}0\\ -\alpha \end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}w(t)\\ \dot{w}(t)\end{array}\right]+\left[\begin{array}{cc}\begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ \begin{array}{c}0\\ -\beta \end{array}\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ \begin{array}{c}0\\ -\gamma \end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}\left|\dot{x}\left(t\right)-\dot{w}\left(t\right)\right|z(t)\\ (\dot{x}\left(t\right)-\dot{w}(t)\left|z(t)\right|\end{array}\right]$$
(8)

where \(x\left(t\right)\),\(y\left(t\right)\) and \(w(t)\) are the response, intermitted, and input excitation in time-domain signals. The MRE isolator viscoelastic model parameters are sensitive to the magnetic field, excitation amplitude and frequency. To incorporate the control strategies, identification of these parameters is crucial. A procedure to identify the parameters are discussed in the following section.

3.2 Viscoelastic model parameter identification procedure

MRE isolator properties are strongly nonlinear functions of magnetic flux density, excitation frequency, and displacement amplitude [45]. Considering all the parameters and developing a mathematical model for MRE isolator is a quite difficult task, since it involves the nonlinearity. To simplify this process, in the current work the nonlinear responses of the MRE isolator is converted to linear response using the system identification toolkit in the MATLAB, and then the MRE isolator is represented as a second order linear state-space (LSS) equation [50]. The linear state-space matrix identified from system identification process is nonparametric in nature and its parametric form of viscoelastic model are obtained by using optimization toolkit in the MATLAB [51]. Figure 6 depicts the process of determining the parameters of the viscoelastic state-space model. The following paragraph provides a detailed description of each individual process.

Fig. 6
figure 6

Steps for identifying viscoelastic model parameters

Full size image

Step 1: In this stage, a linear second-order state-space equation is extracted using the MATLAB system identification toolkit for the measured input and output sine sweep signal. Continuous time-domain second-representation of the order state-space model is,

$$\frac{ds}{{dy}} = A\; s\left( t \right) + B\; u\left( t \right)$$
(9)
$$x_{{{\text{NPSS}}}} \left( t \right) = C s\left( t \right) + D u\left( t \right)$$
(10)

where s(t) is the state vector, u(t) is the input vector, \({x}_{NPSS}(t)\) is displacement response of the nonparametric the state-space equation. Matrix A is the state matrix, B is the input matrix, C is the output matrix, and D is the feedthrough matrix.

Step 2: The state-space equation obtained in step 1 is in nonparametric form, and it does not have any physical meaning. The model is represented in parametric form by incorporating in Zener-based state-space equation. The parameters of this model are identified using the Simulink parameter optimization toolkit by minimizing the sum squared error between Zener parametric state-space response (\({x}_{ZPSS}\left(t\right)\)) and NPSS (nonparametric state-space model) response (\({x}_{NPSS}\)). The parametric form of the model with Zener-based viscoelastic state-space model response is expressed as,

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {\dot{x}\left( t \right)_{{{\text{PSS}}}} } \\ {\ddot{x}\left( t \right)_{{{\text{PSS}}}} } \\ {\begin{array}{*{20}c} {\dot{y}\left( t \right)} \\ {\ddot{y}\left( t \right)} \\ \end{array} } \\ \end{array} } \right] = & \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - k_{1} /m} \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 1 \\ { - c/m} \\ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} { - k_{2} /c} \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {c/m} \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\;\left[ {\begin{array}{*{20}c} {x\left( t \right)_{{{\text{PSS}}}} } \\ {\begin{array}{*{20}c} {\dot{x}\left( t \right)_{{{\text{PSS}}}} } \\ {\begin{array}{*{20}c} {y\left( t \right)} \\ {\dot{y}\left( t \right)} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \\ & + \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {k_{1} /m} \\ {\begin{array}{*{20}c} {k_{2} /c} \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\;\left[ {\begin{array}{*{20}c} {w\left( t \right)} \\ {\dot{w}\left( t \right)} \\ \end{array} } \right] \\ \end{aligned}$$
(11)
$$x_{{{\text{ZPSS}}}} \left( t \right) = \frac{dx}{{dt}}\left( {\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } & 0 & 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {w\left( t \right)} \\ {\dot{w}\left( t \right)} \\ \end{array} } \right]} \right)$$
(12)

The objective function to find the parameters of the Zener-based viscoelastic model is [52]

$$J = \mathop \sum \limits_{i = 1}^{N} \left( {x_{{{\text{ZPSS}}}} \left( i \right) - x_{{{\text{NPSS}}}} \left( i \right)} \right)^{2}$$
(13)

Step 3: The Bouc–Wen is a hysteresis element considered for modelling the hysteresis behaviour. Its parameters are identified using the Simulink parameter optimization toolkit by minimizing the sum squared error between NPSS response (\({x}_{NPSS}(t)\)) and the viscoelastic state-space model (VSS) response (\({x}_{VSS}(t)\)). The response of the viscoelastic state-space model is expressed as

$$x_{{{\text{VSS}}}} \left( t \right) = \frac{{dx}}{{dt}}\left( {\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x\left( t \right)} \\ {\dot{x}\left( t \right)} \\ {\begin{array}{*{20}c} {y\left( t \right)} \\ {\begin{array}{*{20}c} {\dot{y}\left( t \right)} \\ {z\left( t \right)} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {w\left( t \right)} \\ {\dot{w}\left( t \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left| {\dot{x}\left( t \right) - \dot{w}\left( t \right)} \right|z\left( t \right)} \\ {(\dot{x}\left( t \right) - \dot{w}\left( t \right)\left| {z\left( t \right)} \right|} \\ \end{array} } \right]} \right)$$
(14)

The objective function to find the Bouc–Wen parameter is

$$J = \mathop \sum \limits_{i = 1}^{N} \left( {x_{{{\text{VSS}}}} \left( i \right) - x_{{{\text{NPSS}}}} \left( i \right)} \right)^{2}$$
(15)

3.3 Parameter estimation and generalizing the variation with respect to the input current

Table 4 shows the nonparametric linear second order state-space matrix estimated using the system identification toolkit (MATLAB) for various input currents. The state-space matrix is linear, and its linearity component is assessed in terms of best fit (Estimated from system identification toolkit from MATLAB), which represents the percentage of fit with respect to experimental data. For an input current of 0 A, the linear state-space matrix provides the best fit of about 81.84%. This indicates that the MRE isolator has a nonlinearity of approximately around 18.16%. The nonlinearity in the MRE isolator decreases from 18.16 to 6.8% as the current to the isolator increases from 0 to 3 A.

Table 4 Linear state-space matrix identified from MATLAB system identification toolkit
Full size table

The parameters of the Zener viscoelastic model for different current input to MRE isolator estimated from optimization process are listed in Table 5. The hysteresis behaviour accounts for the nonlinearity present in the transmissibility response. The source of nonlinearity is either the magnetic field or the input strain [53]. In the present study, the hysteresis element Bouc–Wen parameters were estimated only for the response corresponding to 0 A input current and 0.0015 m amplitude of excitation. The corresponding Bouc–Wen parameters α, β, γ and n estimated from optimization process are − 2172, 30, 30 and 1, respectively. The Bouc–Wen parameters for other input current are considered to be the same as that of 0 A input current. By considering that the maximum error achieved by the viscoelastic model for other current input in estimating the experimental natural frequency and transmissibility at natural frequency is about 1.6 and 3.8%, hence, Bouc–Wen parameters for other current input considering 0 A current input are justified.

Table 5 Identified optimized Zener model parameter
Full size table

A comparison between the experimental and the predicted transmissibility response from the viscoelastic model with optimized parameters at different current inputs is presented in Fig. 7. It can be visualized that the viscoelastic model accurately predicts the natural frequency of the MRE isolator with the least error of 1.6% registered at 2 A input current. However, the magnitude of transmissibility predicted by the model at the natural frequency deviates with respect to the experimental data, with a maximum error of 3.8% corresponding to the 2 A input current. The corresponding error for an input current of 1A is 1.53%, and it is negligible for 0 A and 3 A input currents. At 0A input current, the predicted response by the optimized parameters of the viscoelastic model perfectly simulates transmissibility response, but for other current inputs, the model estimates natural frequency for transmissibility rather than amplitude, especially for 1 and 2 A current input. This disparity is primarily due to the hysteresis behaviour accounted for in the model.

Fig. 7
figure 7

Comparison between experimental transmissibility and the viscoelastic model optimized parameter transmissibility for current input 0, 1 and 3 A

Full size image

To implementing the control strategies in the MRE isolator, the viscoelastic model parameter under variation of current input must be generalized. A polynomial function is chosen to generalize the variation of the parameters with respect to the input current i. The mathematical expression for generalizing variation in the Zener model parameters is

$$k_{1} {\text{f}}\left( {\text{I}} \right) = 1112{\text{i}}^{5} - 8628{\text{i}}^{4} + 21400{\text{i}}^{3} - 14860{\text{i}}^{2} + 9201{\text{i}} + 30540$$
(16)
$$\begin{aligned} c{\text{f}}\left( {\text{I}} \right) = & - 0.010667{\text{i}}^{5} + 0.62364{\text{i}}^{4} - 1.9485{\text{i}}^{3} \\ & - 0.083182{\text{i}}^{2} + 13.415{\text{i}} + 63.888 \\ \end{aligned}$$
(17)
$$k_{2} {\text{f}}\left( {\text{I}} \right) = 331.3{\text{i}}^{5} - 4394{\text{i}}^{4} + 10840{\text{i}}^{3} + 10840{\text{i}}^{2} + 49240{\text{i}} + 557900$$
(18)

The mathematical expression to generalize the variation in parameters of the Zener model parameters with the applied current was obtained with respect to the input currents of 0, 1, 2 and 3 A. However, for developing model-based control, it is important to assess the ability of the generalized expression in predicting the transmissibility response of MRE isolator. The ability of the proposed model in predicting the transmissibility response is assessed in terms of the responses estimated at 0.5, 1.5 and 2.5 A. The parameters values corresponding to this input current are estimated using the expressions 16, 17 and 18 and substituted in Eq. 8 to get the model-predicted transmissibility response.

A comparison between the experimentally determined transmissibility response and the model-predicted response at 0.5 A, 1.5 A and 2.5 is presented in Fig. 8.

Fig. 8
figure 8

A comparison between the experimental and generalized mathematical expression predicted transmissibility response for current input 0.5, 1.5 and 2.5 A

Full size image

As visualized in Fig. 8, the transmissibility responses predicted by the model effectively portray the experimentally determined responses at 0.5, 1 and 2.5 A. The model predicts the natural frequency of isolator with an error of less than 1%. The model, however, indicates that the error in estimating the amplitude of the transmissibility is approximately 4.6% for 2.5 A, 3.2% for 1.5 A and 1.7% for 0.5 A. It is concluded that the developed viscoelastic model efficiently estimates the natural frequency of the MRE isolator, but less efficiently estimates the amplitude of transmissible few currents.

The ability of the model in portraying the experimentally determined is expressed in terms of fitness value. The fitness values are estimated from Eq. 19 which is given below.

$${\text{Fitness value}} \left( \% \right) = \left[ {\frac{{{\text{norm}}\left( {T_{P} - T_{E} } \right)}}{{{\text{norm}}\left( {T_{P} - {\text{mean}}\left( {T_{E} } \right)} \right)}}} \right] \times 100$$
(19)

where \({T}_{P}\) is predicted transmissibility and \({T}_{E}\) experimental transmissibility of the MRE isolator.

Fitness value of the viscoelastic model for different current is listed in Table 6. The fitness value of the model-predicted response is least about 89.47 for 2.5 A and highest about 96.66 for 1A and 0.5 A, implying that model that moderately fits the experiment transmissibility can be used for control implementation.

Table 6 Fitness value of the viscoelastic model for different current
Full size table

3.4 The relationship between the excitation amplitude and current supplied to the isolator

The transmissibility response differs with the change in input amplitude of excitation under passive as well as active states. To develop an effective control strategy, these responses need to be represented in the form of mathematical expressions where the parameters of the viscoelastic models are identified for each amplitude of excitation under passive and active states. This approach is time-consuming and requires a huge amount of experimental data. To simplify this process, a novel method based on the controller stopping frequency is developed to incorporate the amplitude-dependent attributes to the MRE isolator model. The controller stopping frequency concept is formulated based on the operation of an efficient controller. This concept is illustrated by the frequency response curves shown in Fig. 9. The response of MRE isolator under passive state (0A) is represented by a frequency response curve with lower natural frequency, and the active state (3A) is characterized by a response curve with higher natural frequency. To restrict the isolator system from reaching the resonance region corresponding to the passive state, the controller should be operated under active state so that it traces the response curve corresponding to the 3A input current. The controller should turn off the supply to the isolator when it reaches the frequency corresponding to the intersection of the active and passive state, representing the controller stopping frequency. (Table 5) In addition, it is very important that the control signal should be off at the stopping frequency so that the isolator traces the response curve corresponding to the passive state; otherwise, the isolator system passes through the resonance region of the active state and violates the law of the efficient controller.

Fig. 9
figure 9

Controller stopping frequency

Full size image

For developing a controller based on the controller stopping frequency, it is important to identify different amplitudes of excitation. The controller stopping frequencies estimated from the displacement transmissibility test corresponding to different amplitudes of excitation (Fig. 4) are listed in Table 7. As evident from the experimental response (Fig. 4) and model-predicted response (Fig. 7) plots, the difference exists with respect to the controller stopping frequency. For example, the controller stopping frequency for the transmissibility response of MRE isolator model corresponding to 0.00150 m amplitude of excitation is 34.8 Hz and the corresponding value estimated from experimental is 35.16 Hz. This difference needs to be accounted; otherwise, it deteriorates the performance of the controller. To match the experimentally determined stopping frequency, the current input I to the model needs to be estimated. For the 0.00150 m excitation amplitude and 3A input current, the model-predicted controller stopping frequency is lower than the experimentally determined value. This implies that the input current needs to be increased from 3 A since the controller stopping frequency is less than the experimental value. However, for 0.00225 m amplitude of excitation, the current need to be decreased from 3 A as the controller stopping frequency of the model is more than the experimental value. To accurately predict the controller stopping frequency, the response of MRE isolator model for a specific amplitude of excitation under passive state is considered as a reference. For the developed isolator, the response curve corresponding to the amplitude of 0.0015 m under passive state is chosen as the references curve. With respect to this curve, the current input to the isolator is either decreased or increased from 3 A to obtain the accurate controller stopping frequency for the required input current and the excitation amplitude.

Table 7 Required current input for the model-based controller for the change of excitation input
Full size table

To incorporate semi-active control strategies, the values of viscoelastic model parameters must be estimated with respect to the amplitude of excitation as well. A polynomial function is chosen for this purpose in order to establish a generalized equation that describes the relationship between the current input to the MRE isolator model and the amplitude of excitation. The polynomial equation current I expressed as a function of excitation amplitude A is written as

$$I = 45.67 - 66866.66A + 3.5E7 A^{2} - 6.13E9 A^{3}$$
(20)

where A denotes the amplitude of excitation.

For a given amplitude of excitation, the current input I to the MRE isolator model is estimated using Eq. 20. The parameters of the model (Eqs. 16–18) are estimated for this current, and the corresponding values are listed in Table 8. Using these parameters, the transmissibility response is estimated according to Eq. 8, and the corresponding plots for amplitudes of excitation ranging from 0.00125 to 0.00225 m are shown in Fig. 10. As discussed above, the controller stopping frequency is the intersection of the passive response of the MRE isolator model with its active response. This is the key parameter for developing the isolator model and model-based control technique. The experimental transmissibility test confirms that the control stopping frequency was decreased with the amplitude of excitation. The similar behaviour is predicted by the isolator model. At 0.0125 m amplitude, the stopping frequency of isolator corresponding to the input current of 3 A is 39.51 Hz. The same value is estimated from using the equation. This confirms that controller stopping frequency predicted by the isolator model gives a similar feature corresponding to the experimental transmissibility under different amplitudes of excitation. The developed model could effectively portray the amplitude and the field sensitive responses, and based on this model, a model-based fuzzy controller algorithm is developed.

Table 8 Estimated parameter values of the viscoelastic model for the different amplitude of excitation
Full size table
Fig. 10
figure 10

Simulated amplitude dependency of the MRE isolator

Full size image

4 Control algorithm

Developing an appropriate control strategy is very critical for using MRE isolator real-life applications. Past researchers have reported on the MRE isolator based on on–off [54] and fuzzy controller [33]. These controllers are modal free and easy to control. However, the above stated controller has inherent drawback in that they produce control output for all frequencies, which is not essential. To address these shortcomings, the current research is focused on the development of a model-based fuzzy controller for vibration isolation. The developed viscoelastic state-space model was used to control the fuzzy controller output so that its controller stopping frequency is not exceeding. This is accomplished by comparing the passive viscoelastic state-space model response of the MRE isolator \({\ddot{x}}_{{I}_{0}}\), with the response from active viscoelastic state-space model \({\ddot{x}}_{I}\). The condition for enabling or disabling the fuzzy controller is listed below.

$${\text{Fuzzy}} = \left\{ {\begin{array}{*{20}c} {\ddot{x}_{{I_{0} }} \le \ddot{x}_{I} } & 0 \\ {\ddot{x}_{{I_{0} }} > \ddot{x}_{I} } & 1 \\ \end{array} } \right.$$
(21)

where \(0\) and \(1\) denote the fuzzy controller, which receives the off and on command, respectively.

Figure 11 depicts the block diagram for representing the fuzzy controller implementation process. A fuzzy controller generates the required output in three steps: fuzzification, fuzzy inference and defuzzification. The following section illustrates a detailed description of each process.

Fig. 11
figure 11

Block diagram of the fuzzy controller

Full size image

4.1 Fuzzification

In this phase, the displacement response (x(t)), relative displacement response (x(t)-w(t)) and controller output u(t) signals scaled for unity for better differentiation. The fuzzy controller initially converts both the continuous numerical signal into linguistic variables. The linguistic variables named as positive big (PB), positive medium (PM), positive small (PS), zero (ZO), negative small (NS), negative medium (NM) and negative big (NB). This process of conversion is called fuzzification. The range of each linguistic variable for input and output variables is depicted in Fig. 12, and for each linguistic variable, a specific membership function (triangular membership or sigmoidal membership function) is assigned. The detailed mathematical information about triangular and sigmoidal membership functions is provided in the subsection of this section. The designation of membership functions of displacement and relative displacement is \(\mu_{x\left( t \right)} \left( d \right)\) and \(\mu_{{\left( {x\left( t \right) - w\left( t \right)} \right)}} \left( r \right)\) for the fuzzy set of \(x\left( t \right)\) and (x(t)-w(t)), and the output membership is \(\mu_{u\left( t \right)} \left( i \right)\) for the fuzzy set u(t).

Fig. 12
figure 12

Triangular and sigmoidal membership function of x(t), (x(t)-w(t)) and u(t)

Full size image

4.1.1 Triangular membership

The triangular membership is defined for NM, NS, ZO, PS and PM of the input and output signals. If a, b and c represent the lower, centre, upper boundary of the input and output signal and the membership function [55]

$$\mu _{{x\left( t \right)}} \left( d \right) = \left\{ {\begin{array}{*{20}c} 0 & {if\;d \le a} \\ {\frac{{d - a}}{{b - a}}} & {if\;a \le d \le b} \\ {\frac{{c - d}}{{c - b}}} & {if\;b \le d \le c} \\ 0 & {if\;d \ge c} \\ \end{array} } \right\}$$
(22)
$$\mu _{{\left( {x\left( t \right) - w\left( t \right)} \right)}} \left( r \right) = \left\{ {\begin{array}{*{20}c} 0 & {if\;r \le a} \\ {\frac{{r - a}}{{b - a}}} & {if\;a \le r \le b} \\ {\frac{{c - r}}{{c - b}}} & {if\;b \le r \le c} \\ 0 & {if\;r \ge c} \\ \end{array} } \right\}$$
(23)
$$\mu _{{u\left( t \right)}} \left( i \right) = \left\{ {\begin{array}{*{20}c} 0 & {if\;i \le a} \\ {\frac{{i - a}}{{b - a}}} & {if\;a \le i \le b} \\ {\frac{{c - i}}{{c - b}}} & {if\;b \le i \le c} \\ 0 & {if\;i \ge c} \\ \end{array} } \right\}$$
(24)

where \(d\), \(r\) and \(i\) are the universe of discourse of the triangular membership function for the \(x\left( t \right), \left( {x\left( t \right) - w\left( t \right)} \right) and u\left( t \right)\) fuzzy set.

4.1.2 Sigmoidal membership function

The sigmoidal membership function is defined for input and output signal linguistic variables NB and PB. The selected sigmoidal membership will improve the control processing and stability of the controller. This member function has an exponential function that depends on two parameters. The sigmoidal membership function mathematically is defined as [55]

$$\mu_{{{\text{x}}\left( {\text{t}} \right)}} \left( d \right) = \frac{1}{{1 + e^{{ - a\left( {d - c} \right)}} }}$$
(25)
$$\mu_{{\left( {{\text{x}}\left( {\text{t}} \right) - {\text{w}}\left( {\text{t}} \right)} \right)}} \left( r \right) = \frac{1}{{1 + e^{{ - a\left( {r - c} \right)}} }}$$
(26)
$$\mu_{{{\text{u}}\left( {\text{t}} \right)}} \left( i \right) = \frac{1}{{1 + e^{{ - a\left( {i - c} \right)}} }}$$
(27)

where \(d\), \(r\) and \(i\) are the universe of discourse of the sigmoidal membership function for the \(x\left( t \right), \left( {x\left( t \right) - w\left( t \right)} \right) and u\left( t \right)\) fuzzy set.

4.1.3 The fuzzy inference

After fuzzification, the next phase is the fuzzy inference, where in the present study Mamdani fuzzy inference [56] method is considered. This inference contains 49 rules (Table 9) on linguistic variables based on the on–off control algorithm. Based on Mamdani fuzzy inference, fuzzy operation OR (OR = max) in implemented on two fuzzy input membership functions. Then, the maximum value of the membership function \(\mu_{u\left( t \right)} \left( d \right)\) and \(\mu_{{\left( {x\left( t \right) - w\left( t \right)} \right)}} \left( r \right)\)

$$\mu_{D \cup R} \left( {dr} \right) = \max \left( {\mu_{u\left( t \right)} \left( d \right),\mu_{{\left( {x\left( t \right) - w\left( t \right)} \right)}} \left( r \right)} \right)$$
(28)
Table 9 List of rules used in the fuzzy controller
Full size table

Apply implication method (min)

$${\text{sat}}\left( {\mu_{u\left( t \right)} \left( i \right)} \right) = \left\{ {\begin{array}{*{20}c} 0 & {if} & {\mu_{u\left( t \right)} \left( i \right) = 0} \\ {\mu_{u\left( t \right)} \left( i \right)} & {if} & {0 < \mu_{u\left( t \right)} \left( i \right) < \mu_{D \cup R} \left( {dr} \right)} \\ {\mu_{D \cup R} \left( {dr} \right)} & {if} & {\mu_{u\left( t \right)} \left( i \right) \ge \mu_{D \cup R} \left( {dr} \right)} \\ \end{array} } \right.$$
(29)

Apply aggregation method for 49 rules (max)

$$\mu_{{u\left( t \right){\text{sum}}}} \left( i \right) = \mathop \sum \limits_{j = 1}^{49} {\text{sat}}\left( {\mu_{u\left( t \right)} \left( i \right)} \right)_{j}$$
(30)

4.1.4 Defuzzification

The last phase of the operation is performed to produce the required current for controlling the system stiffness. This process is called defuzzification. In this process, the centre-of-gravity method is adapted to compute the output driving current I. The calculated output of the fuzzy is scaled to the required value and supplied to the MRE isolator.

The mathematical expression to represent the fuzzy output calculated from the centre of gravity (COG) / centroid of area (COA) method is [57],

$$I = \frac{{\mathop \sum \nolimits_{j = 1}^{n} i_{j} .\mu_{{u\left( t \right){\text{sum}}}} \left( i \right)_{j} }}{{\mathop \sum \nolimits_{j = 1}^{n} \mu_{{u\left( t \right){\text{sum}}}} \left( i \right)_{j} }}$$
(31)

where n represents the number of elements of membership function \(\mu_{{u\left( t \right){\text{sum}}}}\).

4.2 Block diagram representation of the model-based fuzzy controller

The block diagram depicts the process of generating the required current input to the MRE isolator (Fig. 13). The actual MRE isolator and two state-space models 0 A & I A are fed with the excitation signal input w(t). The state-space model response corresponding to 0 A current input is\({\ddot{x}}_{{I}_{0}}\). The current I in the state-space model is estimated using Eq. 20 based on the given excitation signal and generate the response signal \({\ddot{x}}_{I}\). The MRE isolator generates displacement response and relative response signals ((x(t) & (x(t)-w(t)) from the excitation input. The fuzzy controller receives the x(t) and x(t)-w(t) responses and generates a unit control output signal u(t). This signal is multiplied by current input I to obtain the required value for scaling the control output. Based on the condition block (Eq. 21), the fuzzy controller output is sent to the MRE isolator.

Fig. 13
figure 13

Block diagram of the control scheme

Full size image

4.3 Simulations of control performance under multi-frequency excitation

A multi-frequency of excitation is used to evaluate the performance of the MRE isolator with modal-based fuzzy controller. The MRE isolator system was excited at frequencies ranging from 15 to 80 Hz (Fig. 14a). Based on the excitation amplitude, the controller generates an output, and it is fed into the MRE isolator. In response to input signal from the controller, MRE isolator generates an output. The output response of the isolator with and without control is shown in Fig. 14b. The isolator is active for 1.8 s (Fig. 14c), and after that, it is turned off. Without control signal, the isolator function as a passive device, which implies that after 1.8 s there is no difference between the response signal obtained from the MRE isolator with and without control. However, as evident from Fig. 14b, the passive response of the MRE isolator merges with the active response of MRE isolator after 1.8 s which confirms that MRE isolator system reaches the isolation region. This aspect can be visualized from the transmissibility plot of the controller shown in Fig. 14(d). According to this plot, MRE isolator with control stops at 35 Hz and works as the passive MRE isolator beyond 35 Hz frequency. Overall, when compared to the passive state of the MRE isolator, the model-based fuzzy controller effectively isolates vibrations by 52.94% and generates control output up to the required frequency before stopping automatically.

Fig. 14
figure 14

a Excitation input; b isolator response signal with and without control; c controllers output signal; d transmissibility plots

Full size image

5 Real-time implementation of the controller

5.1 Experimental set-up for real-time implementation

The performance of the MRE isolator was examined in real time by implementing modal-based controller. The experimental set-up for measuring the performance of the MRE isolator is shown in Fig. 15. The MRE isolator was mounted on the shaker table (Model: APS 420, APS DYNAMICS, INC). The real-time implementation control algorithm was incorporated using an NI cRIO (CompactRIO Controller)-9024 embedded real-time controller. The function generator generates a sine sweep excitation signal with 2.5 V excitation amplitude for frequencies ranging from 15 to 50 Hz. These signals were generated for a duration of 10 s, and its execution was controlled by using NI 9264 voltage output module. The generated sine sweep signal was fed into the amplifier and the amplified signal is received by the shaker. Two accelerometers (Model: 8774A50, Kistler) were used, one mounted on the table and the other on the inertial mass to measure the input and output response, respectively. The data from the sensors were collected using the NI 9234 DAQ module acquired through LabVIEW.

Fig. 15
figure 15

Experimental set-up for controlling vibration in the MRE isolator

Full size image

5.2 Real-time assessment of the performance of MRE isolator with modal-based fuzzy controller under multi-frequency excitation

The response of MRE isolator without a controller for a given amplitude of excitation input is shown in Fig. 16(a). Under passive state, the response of the MRE isolator generates a maximum acceleration of around 27.39 m/s2. The controller calculates and produces controller output based on the given excitation amplitude, which is shown in Fig. 16(b). The MRE isolator receives the generated controller signal and isolates the vibrations at the inertial mass about 55.55% at natural frequency. By analysing the response of the MRE isolator, one can conclude that the controller effectively reduces vibration in the inertial mass up to 35 Hz, as evidenced by the control output signal, which stops at 5.5 s. This confirms that the model-based fuzzy controller is an effective control strategy and can be easily incorporated into MRE devices. This controller is adaptable and can be used to achieve wide frequency range isolation. However, it is also required to assess the influence larger strain on the controller stopping frequency needed to be estimated for developing the viscoelastic model. The major drawback of the MRE isolator is the time delay, which needs to be addressed by considering the design modification of the coil without compromising the magnetic field.

Fig. 16
figure 16

a Controlled and uncontrolled acceleration response; b controller output

Full size image

6 Conclusions

This study focuses on developing a mathematical model for MRE isolator by incorporating current input and amplitude of excitation-dependant properties to attain wide frequency range isolation. Based on this model, a model-based fuzzy controller was developed for the MRE isolator and its performance was evaluated from control simulation and real time tests. The MRE isolator is sensitive to input current and variations in excitation amplitude. The isolator can effectively mitigate the vibrations by 58% with respect to the passive state, when it is supplied by an input current of 3 A. The natural frequency of the isolator system decreases with an increase in amplitude of excitation. In addition, this overall decrease is a function of the initial excitation amplitude. The dynamic range of isolator depends on the input amplitude. At an excitation amplitude of 0.00125 m amplitude, the maximum change in the natural frequency of the system is 21.07 Hz and at 0.0025 m amplitude, the shift in natural frequency of the dynamic isolator system is lesser than 16.09 Hz.

For implementing the control, it is very important that the response should be represented by a mathematical expression. A viscoelastic modelling approach is very effective in portraying the response of the isolator system. The isolator models based on the viscoelastic models often fail to predict the nonlinearity due to the amplitude of excitation and the magnetic fields which are contributing to the overall response. A Bouc–Wen element coupled with the viscoelastic model is more effective as the model can portray the amplitude dependent viscoelastic responses. This modelling technique is an equivalent parametric approach, which requires finding the parameters with respect to the experimental data. The parameter estimation with respect to the steady state is a proven method, but it requires a larger amount of experimental data. A method based on identifying the parameters with respect to the sweep test is more advantageous. This approach is beneficial as it avoids the process of finding the parameters corresponding to the specific set with respect to the steady-state excitation frequencies.

The Bouc–Wen element can predict the hysteresis behaviour in the model, but identifying the unique parameters corresponding to the specific set of input conditions requires a larger amount of data, which is time-consuming. This process can be simplified with respect to the viscoelastic models developed based on the controller stopping frequency. The concept of controller stopping frequency simplifies the overall development phase of the isolator models. This approach demands an accurate prediction of the stopping frequency by the model with respect to the experimentally determined values. Moreover, it is very important to choose the reference curve, and it should be the exact representation of the experimental response. The critical phase of this process is a generalization of the input current to accurately predict the stopping frequency, which needs to be accurately modelled, or else the system may reach resonance, and the control law will be violated. In the case of the MRE isolator, the previously developed modal free fuzzy controller generates the control output for all frequencies, which is not required. So, in simulation, the proposed model fuzzy based controller knows when to stop the controller output and is effective, reducing vibration by 52.9%. Under real time tests it could effectively mitigate the vibration by 55.5%. For implementing in real time, the performance of the isolator needs to be evaluated at larger strain, and the corresponding correction factor needs to be accommodated in the developed isolator model.

7 Future research and scope

  • The effect of larger amplitude of excitation on the controller stopping frequency needs to be estimated for developing the viscoelastic model.

  • Considering time delay in the system and developing the model-based controller.

  • Model-based control development for other excitation like bump and random needs to tested.

  • Creating a design that includes permanent magnets in the coil circuit to reduce the amount of current supplied and, as a result, the temperature generation in the coil.