1 Introduction

Four-Footed Heavy Duty (FFHD) robots have enhanced abilities and heavy object carrying stability compared to their unipedal and bipedal counterparts. Their structural design redundancy is also lower than hexapods and robots with more legs. As a result, extensive research and development have been devoted to FFHD robots. The development of multi-feet robots has significantly informed the evolution of FFHD robots, including their structure and motion. An FFHD drive unit has the characteristics of a larger initial starting force and accurate positioning, higher power density, and compact high-strength structure. Electro-Hydraulic Servo (EHS) actuators have already been adopted in some special engineering industries. The outstanding dynamic response characteristics of FFHD robots have attracted widespread attention in the field of electromechanical engineering. Boston Power Corporation (BPC) recently announced their research and pre-development of lightweight hydraulic four-footed robots, such as Wildcat, BigDog, Spot, LS3, and others [1, 2].

Numerous countries have launched research projects exploring FFHD robots. Several types of FFHD robots have been designed and developed by the Advanced Robotics Division of Italian Industrial Robotics (IIT) [3], where multifunctional robot systems with hydraulic control, including the HyQ, MiniHyQ, and HyQ2Max, were designed (shown in Fig. 1). Electric and hydraulic hybrid control was employed in the HyQ system, in which the hip and yaw joints were driven by an electric motor, and the hip and knee joints were driven by hydraulic pressure. The Wandfluh proportional valve and moog E024LA servo valve were employed as the control valves. A four-footed robot named JINPOONG was also successfully developed and launched by the Korea Institute of Science and Technology [4,5,6,7,8].

Fig. 1
figure 1

Physical images of a hydraulic four-footed robot. Left: Robot images with stereo cameras were not installed (2012). Right: Robot images with stereo cameras were installed (2012)

Full size image

To the author’s knowledge, apart from the LS3 robot, the connection positions of the hip joints of four-footed robots are typically controlled and driven by a single hydraulic actuator. While a single electric motor was used in the HyQ robot, single EHS actuators have been widely adopted by other robots. We propose a two-cylinder EHS actuator cylindrical transmission solution in this work. The unique background of the LS3's dynamic characteristics, including its payload that reached 181 kg, are considered in this work; however, BPC’s report provides minimal technical reference data [9]. FFHD motion has remained a critical focus of discussion in current heavy load robot research. A four-feet platform parallel EHS cylinder transmission system with force/position control hydraulic integrated technology has not been explored in the research so far [10].

Walking (or feet) robots have emerged over the past few decades as an exciting area of research [11,12,13]. Studies into EHS-type four-footed robots have demonstrated that real-time control of the hip motion process is extremely complex and involves four rotating joints, hydraulic actuators for its four symmetrical legs, and a single leg to a hinged trunk with controllers and sensors [14]. Kinematics and dynamics simulations, as well as the optimal design of the mechanical structure for a hydraulic actuated four-footed robot require further research attention. So far, a four-footed robot with four DOFs per supporting leg has achieved motion redundancy to better adapt to rugged terrain [15].

Like the research on related topics, scholars have largely assumed that the distance between the foot and the rolling axis of a hydraulic actuated four-footed robot is larger and that the required driving torque is increased under the same foot end force [16]. Gehring et al. [17] also analyzed the impact of supporting leg impedance on leg gait stability and efficiency. While few researchers have actively contributed to the dynamic motion posture of four-footed robots, it is well known that tetrapod in nature usually twist, dive, or bend their trunks to walk, run, or crawl [18,19,20]. The turning strategy of a four-footed robot based on leg gait was first mentioned by Liu et al. [21], and Zhang et al. studied the transition between a single supporting leg of the four-footed robot and walking posture [22]. These research results on the leg gait of a twisted torso have been widely popularized and provide significant advances in the movement of inherent tripod structures, especially during rapid hydraulic robot movements with heavy loads. Similarly, a twisted torso will also contribute to the leg gaits of a hydraulic four-footed robot. Therefore, the study of the torsional trunk gait of FFHD robots has significant practical guiding significance. Based on increasing the output pressure and effective equivalent area of an EHS execution cylinder, the required driving torque is achieved using methods such as multi-cylinder parallel schemes. The fuel supply pressure of a hydraulic system is restricted by the amplitude of the hydraulic components, which makes it difficult to increase further indefinitely beyond a certain point. Since the increase in the equivalent area of the EHS execution cylinder will inevitably add the additional torque it bears, it is difficult to increase the design size due to structural limitations. This is illustrated in the green and red circles in Fig. 4, where the green parallel hydraulic larger cylinder has a small running space margin, which in turn limits the interchange cycle of the actuators. Manufacturing costs will also increase with expanded EHS control functions.

In view of the hybrid control performance of the roller joint position and the output force used for driving, a numerical analysis model of a parallel servo-executed hydraulic cylinder system is proposed in this work. A mathematical theory model solution is then explored, and a decoupling algorithm of the parallel EHS-executed cylinder force/position hybrid control is constructed. Considering the force control model characteristics of an EHS parallel actuator, a minimally integrated controller is developed to optimize the design of driving force control. The semi-physical system with parallel cylinders is then used to verify the hybrid force/position control strategy, and the feasibility of the proposed control scheme is analyzed according to actual operating experiments.

2 Modeling and adjustable parameter analysis of an FFHD robot mechanical system

2.1 Research on cylinder arrangement with an EHS actuator

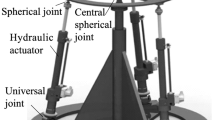
Most researchers have focused solely on the periodic and time-varying amplitude characteristics of joint angles, neglecting the force/position stability of continuous motion trajectories. The stable force/position hybrid control of FFHD robot plays a vital role in the motion of parallel servo execution cylinder transmission systems, which are affected by the constraints of the EHS actuator. It is worth mentioning that the motion form of a four-footed robot is derived from the imitation of an animal's walking posture in nature. The motion form of an EHS cylinder is a representation of the gait of the FFHD robot. A joint illustration of an FFHD robot driven by a cylinder with an EHS actuator is shown in Fig. 2.

Fig. 2
figure 2

Structure diagram of a joint illustration of FFHD robot driven by a cylinder with an EHS actuator

Full size image

The movement trajectory of the parallel actuator of the EHS cylinder is numerically simulated in the figure. The three connection points of the bottom of the cylinder with an EHS actuator, its associated axis, and the end of the piston rod are expressed as A, B, and C, respectively. The position at point is described when the hydraulic cylinder is fully extended to ensure that the FFHD robot always moves in a preset direction. Figure 2 shows that the torsional trajectory of the hydraulic cylinder of a four-footed robot is a prerequisite for the normal operation of the parallel actuator. When switching the driving mode to a dual EHS cylinder, the active bottom range of the other EHS cylinders must be located outside the sector area composed of DBE. Currently, a fixed center exists in the transmission joint of the EHS cylinder, and it is difficult to achieve its expected form of motion. (Table 1).

Table 1 Main parameter symbols and specification values of the four-footed robot
Full size table

As shown in Fig. 3a and b, the form of motion of the EHS cylinder has nothing to do with the twist of the FFHD manipulator body, and the body translation of the FFHD robot has no effect on its horizontal coordinates. It can also be observed that another EHS actuating cylinder and its bottom end movement range should not exceed the sector area enclosed by \(C^{^{\prime}} BE\) and CBD. If the layout design form in Fig. 3d is adopted in this work, where point \(A^{^{\prime}}\) is precisely controlled in the area \(C^{^{\prime}} BE\). These methods can easily cause motion disturbance to the FFHD robot's leg support structure in the internal and external pendulums. In Fig. 3a and b, the overall width limit of the FFHD robot is extended. Thus, it can be concluded that the torso torsion behavior is independent of the robot’s body motion on the horizontal coordinate. In the design shown in Fig. 3d, the two EHS cylinders are located on both sides of the joint axis. Assuming that the layout design form in Fig. 3d is adopted in this work, two EHS actuator cylinders mounted on both sides of the joint axis. However, as illustrated in Fig. 3c, the two EHS actuators are arranged in the same orientation as the articulated joint, thereby eliminating the existence of similar factors in Fig. 3d. In view of these issues, the structure form in Fig. 3c is selected and employed. In Fig. 3d, the parallel arrangement form of a double EHS cylinder is pre-developed. Based on the above analysis, the force vector of the EHS actuator at the hinge joint is different in the positive/negative directions, the connection form in Fig. 3e is the best choice for this project. As the rotation angle of the rotary joint is set to exceed 45°, the EHS actuating cylinder must be connected to a fixed position at the hinge joint. By increasing the length of the supporting leg, the angle-constraining effect of the articulated joint will promote the joint rotation angle, which fulfills the original design requirements of an FFHD robot compact structure. The positive/negative directions shown in Fig. 3f can ensure that the EHS cylinder has an equivalent applied force at the hinge joint, which is an ideal layout design form. The comprehensive influencing factors consider the dynamic changes in the form of the link mechanism, which makes it difficult to perform real-time replacement of EHS actuators.

Fig. 3
figure 3

Layout diagrams of a parallel EHS cylinder for the study

Full size image

2.2 Modeling of an actuator with EHS

The configuration relationship between an EHS actuator and the robot joint rotation angle is shown in Fig. 4, where a is the distance from the bottom of the EHS actuator to the joint, b is the arm of the EHS actuator, and c is the distance between the two ends of the EHS actuator. The relationship between the output force of the EHS actuator and the joint torque, and the displacement of the actuator and the joint rotation angle shown in Fig. 4 are expressed by the following formulas, respectively. The 3D model of the proposed four-footed robot driven by a parallel execution cylinder with an EHS system is shown in Fig. 6. To achieve a reasonable configuration of the actuator, within the range of motion of the joint angle, according to the mathematical mapping relationship between the joint torque and the joint rotation angle and the mathematical mapping relationship between the actuator driving torque and the actuator stroke, the optimal solution for the optimal arrangement of the EHS actuator should be determined. Based on the motion range of the joint angle, determine the actuator arm and the effective stroke of the actuator, and then determine the actuator configuration parameters a, b, and c.

Fig. 4
figure 4

Arrangement diagram of EHS actuator and joint angle

Full size image

In view of the similarities and differences between the joint positions of the actuator and the robot, three configuration methods are presented as follows. The transmission angles of the limit position of the actuator are \(\gamma_{11}\),\(\gamma_{12}\),\(\gamma_{21}\),\(\gamma_{22}\),\(\gamma_{31}\), and \(\gamma_{32}\), respectively. The distribution diagram of EHS actuators is shown in Fig. 5.

$$ F = \frac{\tau }{{a\sin (\arccos \frac{{a^{2} - b^{2} + c^{2} }}{{2{\text{ac}}}})}} $$
(1)
$$ c = \sqrt {a^{2} + b^{2} - 2{\text{ab}}\cos \theta } $$
(2)
Fig. 5
figure 5

Distribution diagram of EHS actuators

Full size image

For the three operating conditions illustrated in the figure, when the actuator arm b is the same, the following characteristics are required to achieve the desired joint rotation angle:

  1. 1.

    For the EHS actuator in Fig. 5b, the required actuator stroke is the largest, but the transmission angle of the mechanism is the same under the two extreme conditions (actuator fully extended or fully retracted), \(\gamma_{21} { = }\gamma_{22}\);

  2. 2.

    For the EHS actuator in Fig. 5a and c, the required actuator stroke is relatively small, but in extreme conditions, the transmission angles of the two mechanisms are different. In Fig. 5a, the transmission angle is \( \gamma_{11} \gamma_{12}\), and in Fig. 5c, the transmission angle \( \gamma_{31} \gamma_{32}\).

In this work, the posture stability of the force/position of the FFHD robot during motion is further determined and checked. The strategy of EHS actuator control is launched and the PID control method is selected to track the joint angles in real-time operating conditions. The feasibility of the technical solution is then analyzed in detail, and the results are finally verified by kinetic analysis simulations. The various forms of motion posture trajectories in FFHD robot movement are planned by tracking the real-time changes in the joint angles to ensure smoothness, which in turn reduces the trajectory deviation of the torsional driving torque and the robot's movement posture. In Fig. 6, the FFHD robot with an EHS cylinder has active and passive degrees of freedom of 12° and 4°, respectively. The robot system studied in this subject consists of 16 actuators of the same model with EHS functions.

Fig. 6
figure 6

An EHS four-footed robot model a 3D configuration of a four-footed robot with electro-hydraulic system b Single-leg 3D configuration of a four-footed robot c Enlarged rendering

Full size image

The following assumptions are proposed: (1) The moment of inertia of a four-footed robot single-leg mechanism with an electro-hydraulic servo cylinder (EAC) around its rolling axis is identified as \(J_{L}\);(2) The torsional moment of the rolling axis is represented as \(T_{L}\);(3) For the damping spring and joint axis, the equivalent characterization of its stiffness is noted as \(K_{L1}\). Figure 7 provides an equivalent model of the actuator with an established EHS function using the modular planning method and a controllable framework, which complies with the equivalent principle of load balancing of a parallel servo cylinder with an electro-hydraulic system.

Fig. 7
figure 7

System diagram of parallel form of EHS cylinders

Full size image

A parallel EHS actuator for the scroll axis is provided in the figure, which is a representative redundant driving system. The asynchronous operation of the two actuators will generate an increased internal force, which may also significantly weaken the necessary driving torques of the actuators. Herein,\(m = J_{{L_{0} }} /L_{0}^{2}\),\(K_{{L_{0} }} = K_{L1} /L_{0}^{2}\),\( {\text{F}}_{{{\text{L}}_{{\text{0}}} }} {\text{ = T}}_{{{\text{L}}_{{\text{0}}} }} {\text{ /L}}_{{\text{0}}} \), and \(L_{0}\) is defined as a distance parameter between the scroll axis and joint loading of a parallel actuator with an EHS piston rod. To avoid the interference of asynchronous motion, we focus on the position of a servo actuator with an electro-hydraulic system in its control mode. Where, ESC is expressed as the abbreviation of Electro-Servo Cylinder. According to the related research [23,24,25,26], the transfer function expression of the single-cylinder servo system with an electro-hydraulic position is derived according to Eq. (3).

$$ y = \frac{{\frac{{K_{{\text{a}}} K_{{{\text{sv}}}} }}{{A_{{\text{P}}} }}u - \frac{{K_{{{\text{ce}}}} }}{{A_{{\text{p}}}^{2} }}(1 + \frac{{V_{{\text{t}}} }}{{4\beta_{{\text{e}}} K_{{{\text{ce}}}} }}s)f}}{{\left( {\frac{{s^{2} }}{{\omega_{0}^{2} }} + \frac{{2\zeta_{0} }}{{\omega_{0} }}s + 1} \right)(\frac{{K_{{{\text{ce}}}} K}}{{A_{{\text{p}}}^{2} }} + (1 + \frac{K}{{K_{{\text{h}}} }})s)}}\omega_{0} $$
(3)

where \(A_{{\text{P}}}\) represents the effective regions of the EHS cylinder piston, \(K_{{\text{a}}}\) indicates the gain features for an amplifier with an EHS function, \(K_{{{\text{sv}}}}\) indicates the parameter of flow gain for an EHS controllable regulating valve, \(\omega_{0}\) represents the integrated natural frequency of the system, \(\zeta_{0}\) indicates the comprehensive damping ratio of the system, and \(K_{{\text{h}}}\) represents the stiffness parameter of the equivalent hydraulic spring. Additionally, \(K\) represents the load equivalent spring stiffness variable of the aforementioned spring, \(K_{{{\text{ce}}}}\) expresses the total flux pressure coefficient of the cylinder, \(f\) represents an external comprehensive interference force of the system, which indicates both the externally applied loading force \( {\text{F}}_{{{\text{L}}_{{\text{0}}} }} \) and the internal inherent force based on the asynchronous movement of the EHS cylinder, Finally,\(\beta_{e}\) represents the volume parameter (elastic modulus) of a particular hydraulic oil, and \(y\) is the displacement parameter output by the EHS cylinder.

2.3 Motion analysis of a double linear EHS cylinder

Since the servo actuators and joints are in rigid contact, as the displacement amplitude deviation value of the EHS actuator is low, the internal force generated by the servo actuator bearing load is larger, thereby resisting the actual output force of the electro-hydraulic actuator with servo characteristics. Real-time controllable position and instantaneous drive force control are performed on two actuators. That is to say, the hybrid form of the force/position control mode of the roll joint is directly completed. Thus, the pre-set torque index required in the design of the driving link is verified, and the posture and position of the articulated joint space movement of the four-footed robot in this article are also ensured. The motion strategy of a bilinear EHS cylinder should traverse along a specific gait trajectory to accommodate the dynamic requirements of an FFHD robot, and the linear EHS cylinder must alternately follow the specific rule during a position posture cycle. As illustrated in Eq. 3, focusing on models with motion posture/position control, for the EHS cylinder, the external excitation factor interference force is used as the output parameter of the EHS force control mode. It can be determined that there is an interconnected coupling relationship between the force/position control motion posture outputs of the EHS cylinder. Considering the mutual influence of the FFHD robot system output, the accuracy of the position/driving force servo will be reduced. The force/position control accuracy required by the FFHD robot system can be obtained once the decoupling requirements are achieved. The curve of knee joint torque over time at a certain gait is shown in Fig. 8. The torque is negative, which means it is opposite to the prescribed positive direction. Figure 9 shows the joint torque-joint angle curve. It can be seen from both figures that in this gait, the joint torque increases with the increase in the joint rotation angle. When the joint rotation angle is the smallest, the joint torque is also the lowest. Figures 10 and 11 show the driving force–displacement curve and the driving force speed of the EHS actuator determined according to the configuration relationship shown in the curve of Fig. 5a.

Fig. 8
figure 8

Knee joint torque versus time curve

Full size image
Fig. 9
figure 9

Knee joint rotation angle versus torque curve

Full size image
Fig. 10
figure 10

EHS actuator displacement versus driving force curve

Full size image
Fig. 11
figure 11

EHS actuator speed versus driving force curve

Full size image

It is assumed that the EHS actuator output characteristic curve can envelop the actuator load curve proposed in this work, which the auxiliary operating condition is shown in Fig. 12. The mathematical expression for the trajectory of the load centerline can be expressed as:

$$ F_{{{\text{sdf}}}} { = }\frac{{p_{{\text{s}}} A_{{\text{s}}} (1{ - }n)}}{2} $$
(4)

where \(F_{{{\text{sdf}}}}\) represents the output force of a single-leg EHS actuator,\(p_{s}\) expresses the oil supply pressure of the hydraulic cylinder, \(A_{s}\) denotes the cavity area of the hydraulic cylinder (without piston rod), \(n\) is the ratio of the cavity area of the hydraulic cylinder with a piston rod to the cavity area of that without a piston rod. Simcenter Amesim software is then employed to simulate and analyze the EHS actuator step response in order to test its performance.

Fig. 12
figure 12

Load trajectory envelope trajectory curves of EHS actuator

Full size image

In the simulation, the hydraulic cylinder oil supply pressure is set to 16 Mpa. Figure 13a provides the actuator step response curve, where Fig. 13b shows a partial enlargement of the curve. Curve 1 is the command signal, curve 2 is the actuator area increased by nearly 21.3%, curve 3 is the optimized actuator structure, and curve 4 is the actuator area reduced by nearly 21.27%.

Fig. 13
figure 13

EHS actuator step response curves

Full size image

It can be seen from the above diagram that when the area of EHS actuator increases by 21.3%, the rise time of the system step response curve is extremely small, and when the area of EHS actuator decreases by 21.27%, the rise time of step response curve becomes a maximum value. The optimized EHS actuator response curve rise time is in the middle value, and its value is about 0.07 s. Under the cases, the steady-state error of EHS actuator is close to zero, which means that the EHS actuator has a large force area and good dynamic characteristics, but the area of that can reach the extreme value at this time.

3 Decoupling analysis of the hybrid mode of force/position control

In this section, the coupling interconnection relationship of the EHS cylinder with force/position control hybrid mode is considered, the servo precision of the cylinder is restricted by each direct input signal command, and each direct input signal is accurately selected to achieve decoupling analysis of the two EHS cylinders. The coupling interconnection effects of the alternating movement of the two EHS cylinders are largely eliminated in this process to improve the control accuracy and quality of the FFHD robot system.

If

$$ V(s) = \frac{{K_{a} K_{sv} }}{{A_{P} \left( {\frac{{s^{2} }}{{\omega_{0}^{2} }} + \frac{{2\zeta_{0} }}{{\omega_{0} }}s + 1} \right)((1 + \frac{K}{{K_{h} }})s + \frac{{K_{ce} K}}{{A_{p}^{2} }})}} $$
$$ \frac{1}{{C_{a} (s)}} = \frac{{K_{ce} + \frac{{V_{t} }}{4\beta e}s}}{{A_{p}^{2} \left( {\frac{{s^{2} }}{{\omega_{0}^{2} }} + \frac{{2\zeta_{0} }}{{\omega_{0} }}s + 1} \right)((1 + \frac{K}{{K_{h} }})s + \frac{{K_{ce} K}}{{A_{p}^{2} }})}} $$

Hence, Eq. 3 is expressed as:

$$ {\text{y}} = \frac{{\text{u}}}{{\text{s}}}{\text{V}}({\text{s}}) - \frac{{{\text{f}}_{{0}} }}{{{\text{sC}}_{{\text{a}}} (s)}} $$
(5)

For EHS cylinders 1 and 2, Eq. 5 is described as Eq. 6:

$$ \begin{gathered} f_{1} = C_{a1} (V(s)u_{1} - y_{1} {)} \hfill \\ y_{2} = - \frac{1}{{C_{a2} }}f_{2} + V(s)u_{2} \hfill \\ \end{gathered} $$
(6)

For a four-footed robot with a large self-weight load, the correlation between the vectors of the displacement/force of parallel execution cylinder EHS system is expressed as:

$$ y_{2} = y_{1} $$
(7)
$$ f_{2} = - f_{1} $$
(8)

The matrix expression of Eq. 6 is derived as:

$$ \left[ {\begin{array}{*{20}c} {f_{1} } \\ {y_{2} } \\ \end{array} } \right] = V(s)\left[ {\begin{array}{*{20}c} {C_{a1} } & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {C_{a1} } & 0 \\ 0 & { - 1/C_{a2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {f_{1} } \\ {y_{2} } \\ \end{array} } \right] $$
(9)

Equation 9 can then be expressed as follows:

$$ \left[ {\begin{array}{*{20}c} 1 & {C_{a1} } \\ { - 1/C_{a2} } & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {f_{1} } \\ {y_{2} } \\ \end{array} } \right] = V(s)\left[ {\begin{array}{*{20}c} {C_{a1} } & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] $$
(10)

where Eq. 10 is rephrased as:

$$ \left[ {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {C_{a1} } & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\mu_{1} } \\ {\mu_{2} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} 1 & { - 1/C_{a1} } \\ {(1 + {{C_{a1} } \mathord{\left/ {\vphantom {{C_{a1} } {C_{a2} }}} \right. \kern-\nulldelimiterspace} {C_{a2} }})/C_{a2} } & {1 + {{C_{a1} } \mathord{\left/ {\vphantom {{C_{a1} } {C_{a2} }}} \right. \kern-\nulldelimiterspace} {C_{a2} }}} \\ \end{array} } \right] \times \frac{V(s)}{{1 + {{C_{a1} } \mathord{\left/ {\vphantom {{C_{a1} } {C_{a2} }}} \right. \kern-\nulldelimiterspace} {C_{a2} }}}} $$
(11)

and Eq. 11 is written as:

$$ \left[ {\begin{array}{*{20}c} {f_{1} } \\ {y_{2} } \\ \end{array} } \right] = \frac{V(s)}{{1 + C_{a1} /C_{a2} }} \times \left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {C_{a1} } & { - 1/C_{a1} } \\ {C_{a1} (1 + C_{a1} /C_{a2} )/C_{a2} } & {1 + C_{a1} /C_{a2} } \\ \end{array} } \right] $$
(12)

If

$$ \left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 1 \\ { - C_{a1} /C_{a2} } & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ \end{array} } \right] $$
(13)

Thus:

$$ \left[ {\begin{array}{*{20}c} {f_{1} } \\ {y_{2} } \\ \end{array} } \right] = V(s)\left[ {\begin{array}{*{20}c} {C_{a1} } & 0 \\ 0 & {1 + C_{a1} /C_{a2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] $$
(14)

The input signal decoupling process is achieved by Eq. 14, and the input signal is described as:

$$ \left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 1 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ \end{array} } \right] $$
(15)

Then, Eq. 15 is characterized as:

$$ \begin{gathered} \left[ {\begin{array}{*{20}c} {f_{1} } \\ {y_{2} } \\ \end{array} } \right] = V(s) \times \left[ {\begin{array}{*{20}c} {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {C_{a1} /(1 + C_{a1} /C_{a2} )} & 0 \\ {C_{a1} /C_{a2} } & {1 + C_{a1} /C_{a2} } \\ \end{array} } \right] \hfill \\ \hfill \\ \end{gathered} $$
(16)

Usually, the required driving force is obtained with a smaller control signal. Herein the parameter \(u^{\prime}_{2}\) is much larger than \(u^{\prime}_{1}\), and Eq. 16 is approximately described as:

$$ \left[ {\begin{array}{*{20}c} {f_{1} } \\ {y_{2} } \\ \end{array} } \right] \approx V(s) \times \left[ {\begin{array}{*{20}c} {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{{C_{a1} }}{{(1 + r^{2} C_{a1} /C_{a2} )}}} & 0 \\ 0 & {1 + \frac{{r^{2} C_{a1} }}{{C_{a2} }}} \\ \end{array} } \right] $$
(17)

According to Eq. 17, the decoupling process analysis of the input signal is confirmed and completed by the parallel servo system with a dual-electro-hydraulic execution cylinder. Thus, the force/position control modes of the EHS cylinders will not affect each other. The principle diagram of the proposed position/force control mode of a parallel system with double EHS cylinders is shown in Fig. 14..

Fig. 14
figure 14

Force/position control parallel cylinders

Full size image

Considering the importance of position constraints to the operational stability of FFHD robots, we propose a hybrid control strategy based on dynamics mode, which is illustrated in Fig. 15. The inner loop adopts force control, and the outer loop adopts position and speed control. In the figure \(q_{a}\), \(\dot{q}_{a}\), and \(\ddot{q}_{a}\) are the actuator position, velocity, and acceleration commands, respectively, and \(q\), \(\dot{q}\) and \(\ddot{q}\) are the corresponding feedback signals; \(F_{f}\),\(F_{v}\) and \(F_{p}\) the force commands generated by the dynamic equations, velocity signals, and position signals, respectively; \(K_{f}\) is the actuator force controller; \(K_{v}\) and \(K_{p}\) are the speed controller and force controller respectively; \(F\) is the actuator force feedback signal.

Fig. 15
figure 15

FFHD robot joint force/position hybrid control

Full size image

The dynamic equation calculates the joint torque through the FFHD robot joint acceleration command and joint position and speed feedback information, and the speed command is obtained through the acceleration command integration. The dynamic equations of the swing phase and the support phase can directly calculate the commands of each joint. The existence of a position loop in the system can ensure the accurate planning of the foot end of the swing leg and avoid the EHS actuator force/position switch.

To realize the driving force control of the EHS actuator, the joint position is constrained, and the position, speed, and force of the EHS actuator are controlled by a hybrid method. The servo valve input signal can be expressed as:

$$ i = K_{pp} (q_{a} - q) + K_{vv} (\dot{q}_{a} - \dot{q}) + K_{ff} (F_{a} - F) + c $$
(18)

where \(i\) is the input signal of the servo valve, \(K_{pp}\) is the EHS actuator position controller, \(K_{vv}\) is the EHS actuator speed controller, \(K_{ff}\) is the EHS actuator driving force controller, and \(c\) is the actuator feed-forward or constant bias (constant term). Figure 16 presents the response curves of the EHS actuator driving force under the force-position hybrid control.

Fig. 16
figure 16

Force/position hybrid control driving force response curves

Full size image

The direct drive force control of the EHS actuator has the best compliance effect, while the force position hybrid control has the worst compliance but the highest drive force control accuracy. The controller selection should comprehensively consider both compliance and control accuracy. A hybrid driving force control method is adopted for the EHS actuator in this article.

4 Comprehensive analysis of the designed FFHD robot kinematics/dynamics

Based on the command signal of a certain frequency applied by each joint, the joint driving force information collected by the EHS actuator driving force sensor is compared with the information given by the dynamic model. The influence of the elastic support stiffness on the synchronization performance of the EHS controller is then analyzed, and the elastic support phase dynamics model is explained. The walking frequency of a four-footed robot decreases with the increase in body length and improves with the increase in walking speed. When the gait frequency is higher, the walking efficiency is lower. The target mass of the four-footed robot developed in this study is no more than 125 kg (total weight), and the theoretical target speed is no less than 1.80 m/s. The optimal gait frequency of the four-footed robot is in the range of 1.0 to 2.0 Hz, and the dynamic response frequency of the EHS cylinder should meet and adapt to these requirements.

It is emphasized here that the abduction/hip joints intersect at a certain point on each supporting leg, and each liner hydraulic cylinder contains a single rod cylinder block, an EHS control valve, a linear displacement sensor, two pressure sensors, and other components. The robot support leg uses a spring to absorb the energy of the ground and to release energy during the lifting cycle. Herein, \(l_{0} ,l_{1} ,l_{2}\), and \(l_{3}\) are expressed as length variables related to the hinge joint coupling links; \(q_{0} ,q_{1}\), and \(q_{2}\) describe the related hinge joint angles; \(l_{m0} ,l_{m1}\), and \(l_{m2}\) represent the centroid displacement variables of interconnected links; \(m_{0} ,m_{1}\), and \(m_{2}\) represent the quality variables of correlation links; \(\varepsilon_{0} ,\varepsilon_{1}\), and \(\varepsilon_{2}\) are the connection angles between the quality center and related links; \(\tau_{0} ,\tau_{1}\), and \(\tau_{2}\) are the torques of the corresponding joints.

4.1 Solving the kinematics equations of an FFHD robot

The dynamic stability of the FFHD robot is characterized by its kinematics, and its coordinate systems and kinematic vectors are defined in Fig. 17. Figure 17 shows the geometric dimensions of an FFHD robot. As the mechanical structure design of the spring-support legs is almost identical, the four-leg coordinate system and the transformation matrix are also similar. The posture of the rear legs and forelegs is the only difference. Referring to the walking posture of four-feet animals, the displacement of the four-footed robot is achieved by the force control unit of the support legs.

$$ \left\{ {\begin{array}{*{20}l} {x_{f} = - (l_{1} \sin q_{1} + l_{2} \sin (q_{1} + q_{2} ))} \\ {y_{f} = - (l_{0} + l_{1} \cos q_{1} + l_{2} \cos (q_{1} + q_{2} )){ + }l_{3} \cos q_{0} } \\ {z_{f} = - (l_{0} + l_{1} \cos q_{1} + l_{2} \cos (q_{1} + q_{2} ) + l_{3} )sinq_{0} } \\ \end{array} } \right. $$
(19)
Fig. 17
figure 17

Geometric dimensions of mechanical structure of FFHD robot support leg

Full size image

According to Eq. 19, the correlation between the displacement of the roller hinge joint actuator and the full-space rotation angle of the hip joints can be expressed as:

$$ \tan\,\,q_{0} = \frac{{z_{f} }}{{y_{f} }} \Leftrightarrow q_{0} = {\text{arc}}\tan \frac{{z_{f} }}{{y_{f} }} $$
(20)

Due to the limitations of the structure, the coordinate value of the end of the support leg is \(y_{f} \ne 0\), and the coordinate values \(x_{f}\) and \(y_{f}\) from Eq. 19 are identified as:

$$ \left\{ \begin{gathered} l_{1} \sin q_{1} + l_{2} \sin (q_{1} + q_{2} ) - x_{f} = 1 \hfill \\ l_{1} \cos q_{1} + l_{2} \cos (q_{1} + q_{2} ) - \frac{{y_{f} }}{{\cos q_{0} }} = - (l_{0} + l_{3} ) \hfill \\ \end{gathered} \right. $$
(21)

where the calculation values of \(\cos q_{2}\) and \(q_{2}\) are defined as:

$$ \cos q_{2} = \frac{{x_{f}^{2} - l_{1}^{2} - l_{2}^{2} + (\frac{{y_{f} }}{{\cos q_{0} }} + l_{0} + l_{3} )^{2} }}{{2l_{1} l_{2} }} $$
(22)
$$ q_{2} = \arccos \frac{{x_{f}^{2} - l_{1}^{2} - l_{2}^{2} + (\frac{{y_{f} }}{{\cos q_{0} }} + l_{0} + l_{3} )^{2} }}{{2l_{1} l_{2} }} $$
(23)

Equation 20 can then be rewritten as:

$$ \left\{ {\begin{array}{*{20}l} {(l_{1} + l_{2} \cos q_{2} )\cos q_{1} - l_{2} sinq_{2} sinq_{1} - (\frac{{y_{f} }}{{\cos q_{0} }} + l_{0} + l_{3} ) = 0} \hfill \\ {(l_{1} + l_{2} \cos q_{2} )\sin q_{1} + l_{2} sinq_{2} cosq_{1} - x_{f} = 0} \hfill \\ \end{array} } \right. $$
(24)

Herein, the calculation values of \(\sin q_{1}\) and \(q_{1}\) are expressed as:

$$ sinq_{1} = \frac{{(\frac{{y_{f} }}{{\cos q_{0} }} + l_{0} + l_{3} )l_{2} sinq_{2} - x_{f} (l_{1} + l_{2} \cos q_{2} )}}{{l_{1}^{2} + 2l_{1} l_{2} \cos q_{2} + l_{2}^{2} }} $$
(25)
$$ q_{1} = {\text{arcsin}}\frac{{(\frac{{y_{f} }}{{\cos q_{0} }} + l_{0} + l_{3} )l_{2} sinq_{2} - x_{f} (l_{1} + l_{2} \cos q_{2} )}}{{(\frac{{y_{f} }}{{\cos q_{0} }} + l_{0} + l_{3} )^{2} + x_{f}^{2} }} $$
(26)

Considering the comprehensive structural limitations of the FFHD robot studied in this paper, the expressions \( q_{2} \pi\) and \(l_{1}^{2} + 2l_{1} l_{2} \cos q_{2} + l_{2}^{2} \ne 0\) are justified. That is, Eq. 25 is considered valid. The angle of the joint is solved by Eq. 19, and the mathematical correlation between the EHS actuator displacement vector and the full-space angle of the joint is described above. Therefore, the specific requirement instruction signal of an EHS actuator is solved according to Eq. 19. As the dynamic gait of a spring-supported leg is symmetrical in form, the mass properties or inertial indicators of the support legs have little effect on the dynamics of the heavy load robot because the proportions of the two diagonal legs swinging together are arbitrary, and their dynamic effects almost counteract each other. Hence, only the quality of the torso walking posture design is considered in the study.

4.2 Solving dynamics equations of an FFHD robot

The time-domain curves of required position and physical position are drawn using Amesim software, and the decoupling characteristics of force/position hybrid control model are realized. The system dynamics are obtained using the Lagrangian equation, as shown in Eq. 27.

$$ \left[ {\begin{array}{*{20}c} {\tau_{0} } \\ {\tau_{1} } \\ {\tau_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & {A_{13} } \\ {A_{21} } & {A_{22} } & {A_{23} } \\ {A_{31} } & {A_{32} } & {A_{33} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{q}_{0} } \\ {\ddot{q}_{1} } \\ {\ddot{q}_{2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & {B_{13} } \\ {B_{21} } & {B_{22} } & {B_{23} } \\ {B_{31} } & {B_{32} } & {B_{33} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{q}_{0} } \\ {\dot{q}_{1} } \\ {\dot{q}_{2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {g_{11} } \\ {g_{21} } \\ {g_{31} } \\ \end{array} } \right] $$
(27)

where

$$ \begin{gathered} A_{12} = A_{13} = A_{21} = A_{31} = 0 \hfill \\ A_{11} = m_{0} l_{m0}^{2} cos^{2} \varepsilon_{0} + m_{1} [l_{0} + l_{m1} \cos (q_{1} + \varepsilon_{1} )]^{2} + m_{2} [l_{0} + l_{1} \cos q_{1} + l_{m2} \cos (q_{1} + q_{2} + \varepsilon_{2} )]^{2} \hfill \\ A_{22} = m_{1} l_{m1}^{2} + m_{2} l_{1}^{2} + m_{2} l_{m2}^{2} + 2m_{2} l_{1} l_{m2} \cos (q_{2} + \varepsilon_{2} ) \hfill \\ A_{23} = A_{32} = m_{2} l_{m2}^{2} + m_{2} l_{1} l_{m2} \cos (q_{2} + \varepsilon_{2} ) \hfill \\ A_{33} = m_{2} l_{m2}^{2} \hfill \\ \end{gathered} $$
$$ \begin{aligned} B_{{13}} & = B_{{22}} = B_{{33}} = 0B_{{11}} = - 2m_{2} [l_{0} + l_{1} \cos q_{1} + l_{{m2}} \cos (q_{1} + q_{2} + \varepsilon _{2} )] \\ &\quad \times \,[l_{1} \dot{q}_{1} \sin q_{1} + l_{{m2}} (\dot{q}_{1} + \dot{q}_{2} )\sin (q_{1} + q_{2} + \varepsilon _{2} )] \\ B_{{21}} & = m_{1} l_{{m1}} [l_{0} + l_{{m1}} \cos (q_{1} + \varepsilon _{1} )]sin(q_{1} + \varepsilon _{1} )\dot{q}_{0} \\ &\quad + \,m_{2} [l_{0} + l_{1} \cos q_{1} + l_{{m2}} \cos (q_{1} + q_{2} + \varepsilon _{2} )] \\ &\quad \times \,[l_{1} \sin q_{1} + l_{{m2}} sin(q_{1} + q_{2} + \varepsilon _{2} )]\dot{q}_{0} \\ B_{{31}} & = m_{2} l_{{m2}} [l_{0} + l_{1} \cos q_{1} + l_{{m2}} \cos (q_{1} + q_{2} + \varepsilon _{2} )] \times sin(q_{1} + q_{2} + \varepsilon _{2} )\dot{q}_{0} \\ B_{{12}} & = - 2m_{1} l_{{m1}} [l_{0} + l_{{m1}} \cos (q_{1} + \varepsilon _{1} )]sin(q_{1} + \varepsilon _{1} )\dot{q}_{0} \\ B_{{23}} & = - m_{2} l_{1} l_{{m2}} \sin (q_{2} + \varepsilon _{2} )(2\dot{q}_{1} + \dot{q}_{2} )B_{{32}} = m_{2} l_{1} l_{{m2}} sin(q_{2} + \varepsilon _{2} )\dot{q}_{1} \\ \end{aligned} $$
$$ \begin{aligned} g_{{11}} & = m_{0} l_{{m0}} cos\varepsilon _{0} gsinq_{0} + m_{1} [l_{0} + l_{{m1}} \cos (q_{1} + \varepsilon _{1} )]gsinq_{0} \\ & + \,m_{2} [l_{0} + l_{1} \cos q_{1} + l_{{m2}} \cos (q_{1} + q_{2} + \varepsilon _{2} )]gsinq_{0} \\ \end{aligned} $$
$$ \begin{aligned} g_{{21}} & = m_{1} l_{{m1}} sin(q_{1} + \varepsilon _{1} )gcosq_{0} + m_{2} l_{{m2}} sin(q_{1} + q_{2} + \varepsilon _{2} )gcosq_{0} \\ & + \,m_{2} l_{1} sin(q_{1} )gcosq_{0} \\ \end{aligned} $$
$$ g_{31} = m_{2} gl_{m2} sin(q_{1} + q_{2} + \varepsilon_{2} )cosq_{0} $$

The desired planned trajectory is determined according to the kinematics equations, which also provide the required multiple joint torques. The designed FFHD robot joint is actuated by an EHS execution cylinder placed at the end of the spring-supported legs. The output decoupling of the FFHD robot force/position hybrid controllable model is described, and the output variable decoupling process of the force/position control hybrid model is implemented in Amesim.

Precise position control of the swing phase must be obtained to achieve accurate planning of the foot end of the swing leg, and the support phase achieves torque control through actuator force control. The adjustment of the robot body posture is realized in the swing phase, and support phase actuators carry out position control and driving force control switching. Considering the control method of the robot leg mechanism during robot operation, a force position switching control strategy is constructed to realize control of the robot joints. The step response curve of an EHS actuator excited by a square wave signal is shown in Fig. 18, where number 1 represents the command signal curve, and number 2 describes the system response curve. The displacement response curve of the EHS actuator under the excitation of a sinusoidal signal is as described in Fig. 19. The positive and negative directions of the EHS actuator have different system characteristics under the excitation of the square wave signal. The maximum amplitude overshoot is 30.2% and 25.3%, respectively, and the rise time is 0.063 and 0.06 s, respectively, which indicates that the EHS actuator has different characteristics in the positive and negative direction strokes. The system without flow compensator compensation also has different system characteristics in the positive and negative directions. After flow compensation, the phase lag of the system is the same during positive and negative strokes.

Fig. 18
figure 18

EHS actuator excited by square wave signal

Full size image
Fig. 19
figure 19

EHS actuator excited by sinusoidal signal

Full size image

4.3 Influence of elastic support stiffness variable on the synchronization performance of an EHS controller

In this section, the effects of joint stiffness and system stiffness on the dynamic synchronization characteristics of the EHS controller are discussed under three typical loads, the step load, alternating load, and impact load.

Among them, the system stiffness \(K_{1} = 1.80 \times 10^{5} N \cdot m/rad\), and the joint connection stiffness \(K_{2} = 2.32 \times 10^{7} N \cdot m/rad\). Figure 20 shows the influence curves of system stiffness on EHS controller synchronization. Additionally, the influence curves of joint connection stiffness on EHS controller synchronization are shown in Fig. 21, where number 1 represents the command signal curve, and number 2 describes the response curve of the FFHD robot system. The reduction in the objective system stiffness effectively increases the elastic buffer of the FFHD robot and is beneficial to its protection; however, the change in joint stiffness also has a significant influence.

Fig. 20
figure 20

Influence curves of system stiffness on EHS controller synchronization a Variation curves under alternating load b Variation curves under step load c Variation curves under impact load

Full size image
Fig. 21
figure 21

Curves of joint connection stiffness on synchronization of EHS controller a Variation curves under alternating load b Variation curves under step load c Variation curves under impact load

Full size image

4.4 Optimal design of the controller

The model of the PID controller with position control is confirmed in this section. A compound strategy with minimum flow/speed compensation and EHS control is employed in the force control mode, and Reference [27] provides further details. The robotic planning path trajectory generator provides a reference joint angle through the EHS controller with a PID strategy. Based on the research, a force control loop is added to deal with the joint force error, and the joint displacement value of the corresponding part is solved. Namely, considering the time-varying disturbance of the joint angle reference value, the system provides joint force feedback to realize position tracking of the PID controller. The force vector control and position vector control modes are always in an interconnected configuration operation. The connection joint must become compliant if a force error occurs, and force/position control joint tracking is preferred when there is no force error. The joints of the key components must guarantee their predetermined rigidity/softness for a long time, no matter how the force error changes. The connection modulation strategy between force feedback and active obedience is established friendly. Considering the structure of the EHS actuator driving force control model and the time-varying characteristics of the model parameters, the EHS actuator servo valve in this paper is assumed to be a two-stage flow servo valve with a large pressure gain, which creates certain challenges in the control of actuator driving force. To this end, the mathematical model of the driving force of the EHS actuator is established, its structure is determined, and the design of the controller is refined. This study is based on flow and speed compensators, which compensate the force closed-loop control process. The force controller adopts the PID controller, and the driving force response curve is shown in Fig. 22.

Fig. 22
figure 22

Driving force control curves

Full size image

It can be seen from the above figure that after compensation by the compensator, the EHS actuator has an improved driving force tracking effect under different frequency excitation signals. The driving force response curve amplitude attenuation is less than 5.2%, and the maximum phase lag is 20°. The lag adopts feed-forward compensation and square compensation and does not affect the stability of the system. It also guarantees high driving force control accuracy and has the characteristic of fast response, which is suitable for the FFHD robot's requirements for driving force control performance of the EHS actuator. The flow compensator and speed compensator can improve the EHS actuator force control accuracy. Its position determines the joint angle of the FFHD robot and the relative position of the foot end and the body. Foot end trajectory planning of the FFHD robot is vital to avoid robot working conditions like foot movement interference.

4.5 Calculation model of supporting leg variable damping force

Based on the hybrid mode, the variable damper is the core component of the supporting leg. The damping force is regarded as the sum of multiple driving forces in the supporting leg controls. Herein, assuming that the effective leg diameter of the supporting leg control mode is equal to the diameter of its control valve, the tolerance area \(D_{e} \pi L_{d}\) is displayed during a specific calculation control process and is set as equal to the resistance area during the actual operation variable \(Lb\). The parameter \(D_{e} \pi L_{d}\) is used instead of \(Lb\), and a mathematical calculation model for damping force control by the supporting leg is performed. Its expression is:

$$ F_{d} = \frac{{\pi \lambda D_{e} L_{d} }}{{h_{d} }}v_{s} + \pi D_{s} L_{d} \gamma_{y} {\text{sgn}} (v_{s} ) $$
(28)

According to the above discussion, the damping force in the outrigger control is composed of two parts. The first part is related to the dynamic viscosity of lubricating oil, which generally indicates the viscous damping characteristics of the legs in the intelligent control technology. The second part illustrates that the force is related to yield strength, revealing that yield strength is a quantitative parameter of Coulomb damping characteristics. The above damping force demonstrates an exponential change trend with the control process. The expression of its change multiplier \(\beta_{d}\) can be written as:

$$ \beta_{d} = \frac{{\gamma_{y} h_{d} }}{{\lambda \left| {v_{s} } \right|}} $$
(29)

The correlation time-varying curves between two parameters are shown in Fig. 23.

Fig. 23
figure 23

Correlation time-varying curve between two parameters \(P_{0}\) and \(T_{0}\)

Full size image

The analytical formula used to solve the flow pressure difference in the outrigger control mode is an algebraic equation, which reflects the valve unit force in the damping force control mode and presents the relationship between the external pressure difference and the yield strength. The simplified expression is described as:

$$ P_{0} = \frac{b}{12L}\frac{{\Delta ph_{d}^{3} }}{Q\lambda } $$
(30)
$$ T_{0} = \frac{b}{12}\frac{{h_{d}^{2} \gamma_{y} }}{Q\lambda } $$
(31)

where \(P_{0}\) represents the external excitation load pressure of the control valve, \(T_{0}\) is the transient time-varying stress on the supporting leg joint bearings, and \(\Delta p\) is the differential pressure of the control valve. Then, the correlation between the two parameters is:

$$ P_{0}^{3} - (1 + 3T_{0} )P_{0}^{2} + 4T_{0}^{3} = 0 $$
(32)

With reference to the typical actual environment, the outrigger is in a normal progress state when the value \(T_{0}\) should not be greater than 1.0 (that is, \( T_{0} 1.0\)). If the mode control speed of the outrigger is lower, the value \(T_{0}\) may not be less than 1.0 (that is, if \(T_{0} \ge 1.0\), then \(P_{0} { = }2T_{0} { + }{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}\)).

5 Experimental research and results

The compound strategy presented in this work can effectively reduce the internal force and enhance the actual driving force. The experimental prototype is validated on a test platform of a parallel EHS execution cylinder system. Figure 24 shows the prototype of the servo actuator with an electro-hydraulic system of a four-footed robot.

Fig. 24
figure 24

source for FFHD

FFHD force/position balance control experiment. Left: EHS system assembly for FFHD. Right: EHS oil

Full size image

As illustrated in Fig. 24, the experimental verification process employs a preset low-pass filter with a lower cut-off frequency of 250 rad/s to further improve and enhance the sensor signal quality, and its power supply pressure is 7.0 MPa.

5.1 Response experiment of the position vector unit control mode

Considering the diagonally extended spatial state of the FFHD robot in this test, the movement form of the two legs on the diagonal are exactly the same, and the walking posture transition phase or the support dynamics phase are also in a time-varying period. The controllable method of spatial gait position has the advantages of reduced energy loss, quick response, and relatively stable and constant stride in all directions. The proposed gait position control mode has the advantages of reduced energy loss, fast travel speed, and relatively stable walking posture. The dynamic response curves of hip joint positioning are shown in Fig. 25.

Fig. 25
figure 25

Comparison of dynamic response curves of actual position and expected position of hip joint

Full size image

Where, the ordinate Null expresses the value reserved in the calculation, and is used to indicate that no valid object is referenced. Programs usually use Null to represent conditions and compare them with the "Nothing" value in nullable types and option types. The parallel EHS system has zero-bound damping characteristics, and its steady-state error and speed asymmetry are revealed in the amplitude of attenuation and asymmetric phase lag. Figure 26 shows the displacement response curves of 1.0, 1.5, and 2.0 Hz simulation systems. As the dynamic response characteristics of curves 2 and 3 have too many similarities, the dynamic response curve 1 is employed in the predetermined input command signal, and curves 2 and 3 are one-to-one designated corresponding positions of the dynamic real-time response of EHS cylinders 1 and 2, respectively. Figure 27 provides the force response curves of the 1.0, 1.5, and 2.0 Hz systems. Response curves 1 and 2 are the corresponding forces of EHS cylinders 1 and 2, respectively. Curves 1 and 2 have different functions under the dynamic real-time response characteristics of the same position.

Fig. 26
figure 26

Position response curves at different frequencies a Response curves of 1.0 Hz b Response curves of 1.5 Hz c Response curves of 2.0 Hz

Full size image
Fig. 27
figure 27

Force curves a Response curves of 1.0 Hz b Response curves of 1.5 Hz c Response curves of 2.0 Hz

Full size image

The dynamic response curve 2 always shows a negative trend, and curve 1 shows a positive and negative equilibrium state. Therefore, if the force value is shown as positive, the output forces of the actuator decrease.

5.2 Experiments for internal force inhibition

The dynamic response curves of displacement and force variables for 1.0, 1.5, and 2.0 Hz systems are shown in Figs. 28, 29 and 30. Graph (a) describes the change trend of the dynamic response curve of the EHS actuating cylinder driving force, where the signal amplitude is set to 2.0kN. Graph (b) represents the time-varying law of the dynamic response curve of the displacement of the EHS cylinder, in which the signal amplitude is set to 20.0 mm. Curve 1 is the design request command signal, and Curve 2 represents the corresponding dynamic real-time response process. Based on the above relevant research preconditions, the results show that the parallel double-cylinder hydraulic actuator system designed in this paper has excellent EHS tracking capabilities under the given demand signal. Thus, the amplitude reduction and phase lag of the trajectory tracking signal in the dual vector (force/position) hybrid control modes are similar. When the specific command signal frequencies are 1.0, 1.5, and 2.0 Hz, the amplitude attenuation values are 5.53%, 7.56%, and 8.54%, and the phase lag values are 9.0°, 13.0°, and 18.0°, respectively.

Fig. 28
figure 28

Real-time response curves of 1.0 Hz a curves of driving force b curves of position

Full size image
Fig. 29
figure 29

Real-time response curves of 1.5 Hz a curves of driving force b curves of position

Full size image
Fig. 30
figure 30

Real-time response curves of 2.0 Hz a curves of driving force b curves of position

Full size image

In actual application engineering, the adverse effect of the phase lag can be compensated by the front-feedback EHS controller. As the frequency of the external excitation signal increases, the amplitude attenuation and phase lag of parallel EHS system are both increased. The conclusion of this research has proved the effectiveness of a parallel EHS cylinder with force/position hybrid control mode.

6 Conclusions

A scheme to obtain the motion and dual vector (force/position) hybrid control modes of a parallel-executed cylinder mechanical integration system for an FFHD robot was proposed in this work. The preliminary results validated a proof-of-concept FFHD robot prototype. The simulated kinematics and dynamics results of the relative force/position controller were then analyzed. The obtained results are detailed as follows.

  1. (1)

    In view of the larger deadweight load and torsional moment of the supporting and hip joints of a non-lightweight FFHD robot, a parallel cylinder actuation scheme was designed to improve the initial active torsional moment.

  2. (2)

    A hybrid control mode servo actuator was designed in this paper based on the performances of the parallel-executed cylinder mechanical integration system with dual vectors (force/position). The decoupling analysis of the force/position control mode was realized by optimizing the dual vectors of force and position signals.

  3. (3)

    The compound optimization strategy was reasonably verified on the simulation platform of the parallel-executed cylinder mechanical integration system. The experimental results showed that the dual vector (force/position) hybrid control modes had excellent dynamic response characteristics, and the effectiveness of the proposed design scheme and control strategy was verified using the original sample model.

  4. (4)

    The scientific research results obtained in this paper provide relevant data for many specific fields of industrial robot system hybrid control, including military and aerospace, flexible manufacturing, improved operation, and remote control.