1 Introduction

Arc welding is a typical manufacturing means (amongst others) in which power calculations are used to control the process quality/performance. The energy that is produced by an electric welding arc is transferred onto/into a plate as heat input. Consequently, the heat input is proportional to the arc energy, which governs weld bead geometric formation and metallurgical transformations, influencing the mechanical properties of the joint. Arc energy (En), in turn, is expressed in welding as the ratio of arc power (P) and arc travel speed (TS), as in Eq. 1. This equation represents the expected value of energy [J] per unit of length [m or mm] of the weld. Heat input would be the product of arc energy and heat transfer efficiency, which are always present in welding documentation, as written documents that define welding procedures according to the related standard/codes, prepared instructions for the welder/operators/inspectors towards sound and quality assured welds, etc. Also, arc energy and corresponding heat input and heat transfer efficiency are important issues at the research level in welding process/metallurgy/modelling studies.

$${\text{En}} = \frac{P}{{{\text{TS}}}}.$$
(1)

Notwithstanding, current literature shows a difference of opinion amongst authors regarding the methods used to calculate arc power. Jorge et al. [1] cite that there are three different methods still currently being used to quantify arc power (P) in welding technology, as presented by Eqs. 2, 3 and 4 (where \(\overline{U}\) and \(\overline{I}\) are the average of voltage and current measured values, URMS and IRMS are the voltage and current RMS calculated values, U(i) and I(i) are the instantaneous voltage and current measured values and n is the number of samples used for the measurement).

$$P_{{{\text{effective}}}} = U_{{{\text{RMS}}}} \cdot I_{{{\text{RMS}}}}$$
(2)
$$P_{{{\text{arithmetical}}}} = \overline{U} \cdot \overline{I}$$
(3)
$$P_{{{\text{inst}}}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} U\left( {ki} \right) \cdot I\left( i \right)$$
(4)

For many years, P has been defined in welding as the product of the U and I averages (Eq. 2 or Eq. 3). The main reason is likely the limitation on measurement systems for P in the past, in contrast to for U and I measurands. It is important to mention that most commercial voltmeters and amperemeters are calibrated to RMS values, the reason for Eq. 2, and some difference in P when using Eqs. 2 and 3 is noticeable (although not always recognised by users, because this comparison is not usually performed), depending on the waveform of U and I. In the 1990s, with the advent of waveform-controlled power sources, some papers appeared and showed that P calculated as a product of the averages U and I (Eqs. 2 and 3) differs in value from P calculated as the average of instantaneous power (Eq. 4). Bosworth [2], for instance, has found that the results of each method can be up to 30% different from each other. Joseph et al. [3], using calorimetry, stated that the only measure of welding energy, which is reasonably well correlated to current variations, is the instantaneous power measurement. Nascimento et al. [4] analysed all the aforementioned methods and the respective consequences on the heat input and thermal efficiency calculations. They claimed that the method of arithmetic mean power can be applied in few cases, in which there is no oscillation in current and voltage (like in spray transfer gas metal arc welding).

In the second decade of the 2000s, when the microprocessor became more accessible at the shop floor level, making data acquisition and instantaneous power calculations more affordable, some standards started proposing that the power calculation should follow the instantaneous power concept in both waveform-controlled operations and short-circuit metal transfers. Melfi [5] showed that the method to calculate the arc energy based on the average instantaneous power was added in the 2010 edition of the ASME Boiler and Pressure Vessel Code: Section IX, item QW409.1, for waveform-controlled welding, and this amendment has been used in the lasted versions since then. The ISO/TR 18491–2015 standard [6], in its Section 7.4, uses this method in the guidelines for the welding energies measurement. It is important to mention that the concept of Eq. 4 is the integration of power (different from Eqs. 2 and 3), thus applicable to any current (DC and AC) and welding conditions (from steady constant current to unsteady pulsed current). Therefore, Eq. 4 does not apply only to waveform controllable power source signals, as the code/standard may imply. Norrish [7] presented a comprehensive analysis of heat input determination and the implications for international fabrication standards. He concluded that inappropriate use of mean power and energy calculations for waveform-controlled processes would lead to significant inaccuracies in true arc energy calculations. Thus, average instantaneous power seems to be gaining acceptance in the welding community. Indeed, they are reasonably easy to be calculated from digitalised voltage and current monitoring, using commercial computer spreadsheets, if it is still not available in the welding machine microprocessor.

However, even today most papers and even commercial simulation packages still use power calculated as the product of the averages of U and I (usually not mentioned if they refer to mean or RMS values) to define arc energy and heat input. Arc power and arc energy are very much correlated to each other, since arc energy is calculated by the ratio of the calculated arc power and set travel speed (Eq. 1). Heat input, in turn, would be the product of arc energy and heat transfer efficiency, mostly referred to as a factor determinable by experimentation. This factor has its precise experimental determination questioned in recent literature, such as in Hurtig et al. [8] and Liskévych et al. [9]. Examples of papers that use the product of the averages of U and I as arc power calculation method would be Li et al. [10], Cambon et al. [11], Perić et al. [12] and Unnikrishnakurup et al. [13]. The likely reason for this is related to tradition and well-recognised previous publications. Therefore, the objective of this work was to give subsidies, via a statistically based demonstration, to welding personnel at different levels (engineers, researchers, modelling experts) to understand this dilemma (inaccuracies) of power (P) calculation from continuous voltage and current data monitoring. A secondary objective is to investigate the effect of measurement errors on these calculations.

2 Work development

2.1 The dependences of two variables

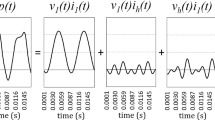
Figure 1 presents several combinations of hypothetical data arrays of voltage (U) and current (I), aiming at mimicking several situations usually met during arc welding processes. It is important to note that the averages of voltage (\(\overline{U}\)) and current (\(\overline{I}\)) were purposively kept the same for all combinations. Using simulated data instead of actual data makes it easier to have comparative conditions, using the same average values of variables. This approach would prevent interferences from external error sources in the signal if actual signals were used. Units were not stated because they are not important for this demonstration, as well as suggesting that variables could be of any kind (not only U and I). Last, but not least, it is important to state for clarification that Fig. 1 refers to continuous signals, yet usually discretised during A/D data acquisition. The standard deviations are due to waveforms, not to measurement errors (for simplification, let us consider here that the signals are clean of measurement error, a topic that will be treated in Sect. 3). As a whole, Fig. 1 depicts several waveforms that could generate different levels of power by the arcs, waveform in which power is represented by a same arithmetical value (Eq. 3), yet also by different effective (Eq. 2) and instantaneous (Eq. 4) values.

Fig. 1
figure 1

Hypothetical data arrays of variables U and I and their respective statistics

Full size image

It is initially important to remark that the topic under discussion is calculating Arc Power and not on how to measure arc power (or arc energy or heat input). In the authors' opinion, there is a subtle difference between "to calculate" and "to measure”. To calculate would be to find a representation for the product of the digitally monitored U and I signals, while to measure would mean to quantify the resultant quantity physically. Power is power; it does not change whatever the way of representing it (either by Eq. 2 or Eq. 3 or Eq. 4). Neither will the effect of the power on the material be changed according to the form of representation. This statement is similar to that of the current signal can be represented by either the mean value or the RMS value (but the current signal is the same). These statements emphasise that the variable signals of each frame in Fig. 1 are the same and the referred equations are just different means of representing the same signals.

As seen in the introductory section, arc power calculation is basically the product of U(i−n) and I(i−n), where the subscript (i−n) stands for the range from an initial (i) to a final (n) data in the arrays of voltage and current (the measurands). However, this product can be quantified by different means, expressed by Eqs. 2 to 4. Therefore, the average values of voltage (\(\overline{U}\)) and current (\(\overline{I}\)), the root-mean-squares (RMS) of voltage (URMS) and current (IRMS), the average arithmetical power (Parit), calculated from the mean values of U and I, the effective power (Peff), obtained from the RMS values, and the instantaneous power (Pinst) are presented in Fig. 1. In addition, Fig. 1 denotes the standard deviations related to \(\overline{U}\) and \(\overline{I}\) and the corresponding power calculations, the subtraction of the arithmetical or effective powers from the instantaneous power, as well as covariances (Cov) and correlations (Cor).

The frame (a) of Fig. 1 mimics a condition of the welding process Pulsed Gas Metal Arc Welding (P-GMAW). One can see that U and I are very much correlated to each other (Cor = 1) and the difference Parit − Pinst = 57.6 is significant. By chance, Peff = Pinst in Fig. 1a, which should be seen as a coincidence and not as a rule, unless in the cases that the average value is equal to the RMS value of a same variable, as in frame (c). Figure 1b does not mimic an arc welding process, but shows an inverse correlation, still very much correlated (Cor = − 1). Even though, Cov increased in value, suggesting that the covariance alone does not control the correlation between the variables. Figure 1c, d, in turn, simulates a process in which the power source has almost constant current delivery or is an ideally constant current, respectively. In these cases, U and I hardly oscillate (very low standard deviations). These are cases of welding processes, such as the Shielded Metal Arc Welding (SMAW) or the Gas Tungsten Arc Welding (GTAW) processes, for which Cor and Cov are low or do not exist and, henceforth, Parit = Pinst. Finally, Fig. 1e, f illustrates the simulation of variables that the signals have an intermediate value of correlation. The frame (e) chart mimics the short-circuit period of a conventional GMAW, while the frame (f) would mimic an erratic arc. As seen, the decrease in correlation from (e) to (f) does not correspond to a reduction in the covariance.

Covariance and correlation are similar concepts, although they are not synonymous. When these concepts are applied to continuous, yet random, variables, they describe how two arrays of variables are inclined to diverge from their average values (the force of interaction between the variables). Covariance (Cov) and correlation (Cor) are mathematically represented by Eqs. 5 and 6, adapted from Pitman [14], p. 465], if one considers that the first and second variables are continuous, like voltage (Ui−n) and current (Ii−n). A continuous probability distribution is defined as when the data array can take on any value within a specified range (which may be infinite). In addition, they must represent the event (event, in this case, means the welding condition) and have a specific range (the acquisition time) representing the phenomenon. In the continuous domain, the covariance between two continues stochastic variables U and I is defined by:

$${\text{Cov}}_{UI} = \sigma_{UI} = \, E\left[ {\left( {U_{(i - n)} - \overline{U}} \right)\left( {I_{(i - n)} - \overline{I}} \right)} \right]$$
(5)
$${\text{Cor}}_{UI} = \rho_{UI} = \, E\left[ {\left( {U_{(i - n)} - \overline{U}} \right)\left( {I_{(i - n)} - \overline{I}} \right)} \right](\sigma_{U} \sigma_{I} )$$
(6)

where E[ ] stands for the statistical expectation operator, which is actually an averaging operator in the continuous domain. \(\overline{U}\) and \(\overline{I}\), in turn, are the average values and σU and σI the standard deviations, respectively, of the samples U and I in the array from j to i. Therefore, the terms (U − \(\overline{U}\)) and (I − \(\overline{I}\)), where \(\overline{U}\) and \(\overline{I}\) can be the average or the RMS values of the variables, are the variability, i.e. the deviations of each value of the variables in relation to the variable mean. Then, Cov is the expected value of the variability of each value within the array of variables. By this definition, it is straightforward to understand that covariance is the average of the products of residuals of two samples, where residuals mean the differences between the elements of each sample and the sample mean.

Correlation is dimensionless, while covariance is in units of the product of the two samples. Therefore, correlation is a more practical measure than covariance, the latter being more conceptual. In this context, correlation can be understood simply as a normalised version of covariance (varying from − 1 to 1), as deducible from Eq. 6. A Cor = 1 or − 1 means that the two variables are highly correlated (see Fig. 1a, b). It means that one can expect that voltage, for instance, would increase or decrease according to the variation of current. If Cor is positive, it means that this dependence is direct, i.e. while one variable changes in one direction (up or down), the other variable also varies in the same direction (see Fig. 1a). A negative Cor does not mean non-dependence. On the contrary, it just means that the dependence is inverse, i.e. while one variable changes into one direction (up or down), the other variable also varies in the opposite direction (see Fig. 1b). A Cor = 0, in turn, indicates that the variables are not correlated or are independent (see Fig. 1d).

From the above, one could say that the closer Cor is to 1 means the higher correlation between the variables. The sign of this statistical parameter shows the tendency of dependence. However, when the product of the variances of each variable (σ1 or σ2) is zero, Cor is undermined (see Fig. 1c), since Cor computation (Eq. 6) would involve division by 0. The fact that Cov is still determinable helps the reader understand the importance of analysing together correlation and covariance.

2.2 Proofs and mathematical reasoning

The main point is: can one calculate arc power using any of Eqs. 2, 3 or Eq. 4? The axiom for a negative answer would be that a product of two variable averages (Eq. 2 or Eq. 3) is not the same as the average of the product of each element pair of the variables (Eq. 4), i.e. E(UI) ≠ E(U) × E(I), where E(UI) is the expected (average) value of the products of I and U from i to n, E(U) = \(\overline{U }\) and E(I) = \(\overline{I}\), unless the variables are fully independent (Cov and Cor = 0). To demonstrate this axiom, let us rearrange Eq. 5 as Eq. 7:

$${\text{Cov}}_{UI} = \, E\left[ {\left( {U_{(i - n)} - \overline{U}} \right)\left( {I_{{\left( {i - n} \right)}} - \overline{I}} \right)} \right] = E\left( {U_{{\left( {i - n} \right)}} I_{{\left( {i - n} \right)}} } \right) \, {-}\overline{U } \times \overline{I}$$
(7)

or

$$E\left( {U_{{\left( {i - n} \right)}} I_{{\left( {i - n} \right)}} } \right) \, = {\text{Cov}}_{UI} + \left( {\overline{U } \times \overline{I}} \right)$$
(8)

Equation 6, in turn, can be rewritten as:

$${\text{Cor}}_{UI} = \, E\left[ {\left( {U_{(i - n)} - \overline{U}} \right)\left( {I_{(i - n)} - \overline{I}} \right)} \right]/(\sigma_{U} \sigma_{I} ) \, = {\text{Cov}}_{UI} /(\sigma_{U} \sigma_{I} )$$
(9)

or

$${\text{Cov}}_{UI} = {\text{Cor}}_{UI} \times (\sigma_{U} \sigma_{I} )$$
(10)

If Eq. 10 is inserted into Eq. 8, hence:

$$E\left( {U_{{\left( {i - n} \right)}} I_{{\left( {i - n} \right)}} } \right) \, = Cor_{UI} \times \left( {\sigma_{U} \sigma_{I} } \right) + \left( {\overline{U } \times \overline{I}} \right)$$
(11)

If U(i−n) and I(i−n) are dependent on each other, then CorUI ≠ 0. In addition, the standard deviations of \(\overline{U }\) and \(\overline{I}\) are always positive (and so is the product σUσI). Therefore, Eq. 11 can be notated as Eq. 12:

$$E\left( {U_{{\left( {i - n} \right)}} I_{{\left( {i - n} \right)}} } \right) \, < \left( {\overline{U } \times \overline{I}} \right)$$
(12)

when 0 < CorUI ≤ 1 (direct dependence, as illustrated in Fig. 1a, e), or as Eq. 13:

$$E\left( {U_{{\left( {i - n} \right)}} I_{{\left( {i - n} \right)}} } \right) \, > \left( {\overline{U } \times \overline{I}} \right)$$
(13)

when − 1 ≤ CorUI < 0 (inverse dependence, as illustrated in Fig. 1b, f.

Equations 12 and 13 are true if, and only if, CorUI ≠ 0. Otherwise (if they are fully independent, i.e. CorUI = 0), hence:

$$E\left( {U_{{\left( {i - n} \right)}} I_{{\left( {i - n} \right)}} } \right) = \overline{U } \times \overline{I}$$
(14)

as quantified in Fig. 1c, d (Q.E.D.)

Reminding ourselves that arc power (P), by definition, is equal to a product of voltage (U) and current (I), yet not necessarily the product of the mean or RMS values of voltage and current. Based on the above reasoning, one can summarise by saying that the expected value (or mean value) of the products of U(i−n) and I(i−n) (represented by E(U(i−n)I(i−n)), in other words, the instantaneous power (Eq. 4), is not the same as the product of the mean values of average voltage and average current (\(\overline{U }\) × \(\overline{I}\)), represented by the effective (Eq. 2) or arithmetic powers (Eq. 3), unless voltage and current traces are entirely independent of each other (CorUI ≠ 0). However, to be fully independent of each other is an exception, not a rule in electrical arc signals. Henceforth, the calculated true value of arc power is that from the average products of U(i−n) and I(i−n) and not from the products of the mean values of \(\overline{U }\) and \(\overline{I}\). And, the arc power calculation inaccuracy would be the difference between (\(\overline{U }\) × \(\overline{I}\)) and E(U(i−n)I(i−n)), not considering the RMS values instead of the average values (\(\overline{U } \, {\text{and}}\) \(\overline{I}\)) for simplification.

2.3 Covariance as a means of quantifying the inaccuracy between power calculation methods

At first view, one could assume that the calculation inaccuracy between E(U(i−n)I(i−n)) and \(\overline{U }\) × \(\overline{I}\) quantities would be wider when CorUI is closer to 1 or − 1, considering a potential degree of correlation (or dependence) between U and I. Figure 1a, b shows a great difference between these two methods of calculating arc power (> 10%), in which case CorUI = 1. However, observing Fig. 1e, f, in which there are lower nominal correlations (CorUI < 0.76), the calculation inaccuracy was even higher (> 11%). This shows that the correlation factor alone is not able to indicate the dimension of the inaccuracy between the two calculation methods. The lack of relationship between Cor and inaccuracy also justifies the reason for Hosseini et al. [15] having found similar values when Eqs. 3 and 4 were employed over their continuous U and I measurements, although there was a reasonably high correlation (CorUI = − 0.63276) between the data arrays.

In reality, standard deviations of U(i−n) and I(i−n) play an essential role in the power value differences. For instance, when a constant current power source is used (as in the case of SMAW or GTAW), the standard deviation of I(i−n) (represented by σI) is null or very small, regardless of the standard deviation of U(i−n) (σU). Observing Eq. 10, one can see that, irrespectively the sizes of CorUI and σU, a very small value of σI will end up in a very small value of CovUI. If the first operator of the second term of Eq. 11 is replaced by Eq. 10 and the equation is rearranged, hence Eq. 15 is a demonstration that the covariance quantifies the difference between the two methods (the greater the CovUI, the larger the difference). The determination of covariance in this study is shown again as imperative for the reader to understand the importance of analysing correlation and covariance together. In addition, it is implicit from Eq. 15 that covariance (which unit in this case would be Volts × Amperes) is the magnitude of the calculation inaccuracy. This inaccuracy should be seen as absolute [VA] or relative [%] to the true value.

$$E\left( {U_{(i - n)} I_{(i - n)} } \right) \, - \, \left( {\overline{U } \times \overline{I}} \right) = {\text{Cov}}_{UI}$$
(15)

3 The measurement error in the context of the arc power calculation

It was highlighted in Sect. 2.1 that the main objective of the work was to calculate Arc Power and not how to measure arc power. Nevertheless, one could argue that Arc Power is also measured, yet indirectly by making direct measurements of other quantities (U and I) that are functionally related to the desired unknown quantities. This argument does not interfere with the above analysis, since, as mentioned, the analysis was made considering signals without errors of any sort (systematic or random). In fact, this definition supports the use of the metrological term inaccuracy for the calculations. According to Ghilani [16], since all directly observed quantities contain errors, any values computed from them will also contain errors. Keeping this in mind, in order to have a more accurate value of Arc Power, regardless of the calculation method, the quality of the data that compose U and I must also be observed. Although out of this work main scope, it is important to mention the quality governing factors that assure higher certainty from the measured values of U and I, and consequently, the calculated value of P. Below are presented (order not related to importance) the main quality factors and their measurement error sources:

  1. (a)

    Sampling: It is compulsory that the sample timespan (time of measurement) be representative of the event and that the taken event represents the quantity target. For instance, to sample just the period in which the pulse current occurs in a pulsed GTAW process will not represent the whole event (pulsing cycle). Likewise, monitoring just one weld pass (event) may not represent the arc power of the total weld. To reduce uncertainties, longer data acquisition times may be needed. It will all depend on the variabilities of the signal itself, according to changes in the boundary conditions. Error due to sampling has a systematic character if it is too short in relation to the event timespan, but it may also become random if the measurement, with short or long sampling, is replicated to different welds or welding passes;

  2. (b)

    Accuracy of the instrument for electrical value measurements: although not easily determined, yet possible, the manufacturer generally supplies this information. The devices used to measure U and I can reach significant error from the true measurands. Standard analogue multimeters have accuracy typically from ± 3 to 1%. When A/D data acquisition systems are used, more refined accuracy can be reached, depending on the resolution of the converter (8, 12, 24 bits). Instrument accuracy presents random behaviour. The systematic character of this measurement error is minimised with calibrations using reliable references;

  3. (c)

    Data acquisition rate: one needs to specify carefully the sample rate of a data acquisition system to reach the actual waveform. As a rule of thumb, one could say that to detect a change as small as 1% of the signal, it is necessary to sample 100 times per second. The Nyquist sampling theorem, according to Weik [17], states that an analogue signal waveform may be uniquely and precisely reconstructed from samples taken from the waveform at equal time intervals, provided the sampling rate is equal to, or greater than, twice the highest significant frequency in the analogue signal. In short-circuit GMAW, for instance, the considered frequency to determine the sampling rate is not the short-circuit frequency (which is very low), but the inverse of the peak of current duration. Fast Fourier Transform (FFT) is a technique that helps in finding the fastest transient frequencies. Similar to sampling, data acquisition rate assumes a systematic character if the rate is too low in relation to the transient frequencies, but this error source is also random when replicated to different welds or welding passes. According to Kumar et al. [18], interference signals often occur with high frequency, leading to the dominance of noise on the signal. On the other hand, some interference signals may be lost under low sampling frequency;

  4. (d)

    Noise (aliased signal): aliasing causes distortion of signals when sampled, i.e. the signal becomes different from the original continuous signal. The sources of noises are diverse and sometimes not identified. Filtering (analogic or digital) may minimise the problem, but it can also change the signal waveform. Therefore, noise is classically a measurement error of random character, but waveform deformation can lend to the measurement a systematic character as well;

  5. (e)

    Position of measurement: voltage, for instance, can be measured either at the power source connectors or between the contact tube and the workpiece. As there may be impedance (combined effects of ohmic resistance and reactance) along with the cables, the signal can be different depending on the position of the U probe. Even a mispositioning of an effect-hall sensor for current measurement can induce inaccuracy in the current values. This source of measurement error is characteristically of systematic character.

Therefore, a second point could arise: would measurement error increase the uncertainties of arc power calculation? In order to answer this question, let one assume that the clean signal is the most meaningful and desirable information. Accidental error sources would be random variation superimposed to the signal (in this case, overlapped individually to the U and I signals), excluding, therefore, systematic sources of error. In addition to being unwanted, random interferences (generically named noise) out of the desired signal are classified as error, difficult to be eliminated (on the contrary of systematic errors, that are usually compensated by calibrations). However, to some extent, one can separate the noise from each signal for analysis purposes. Therefore, let us take the noises (errors) over the U and I signals as separate signals (εU and εI) and calculate the similar equality from Eq. 11, as seen in Eq. 16.

$$E(\varepsilon_{U} \varepsilon_{I} ) = {\text{Cor}}\varepsilon_{UI} \times_{ } \left( {\sigma \varepsilon_{U} \sigma \varepsilon_{I} } \right) + \left( {\overline{{\varepsilon_{U} }} \times \overline{{\varepsilon_{I} }} } \right)$$
(16)

Using equivalent reasoning as for Eqs. 12 to 14, as the standard deviation product (σεUσεI) is positive, if εU and εI are dependent on each other (CorεUI ≠ 0), Eq. 16 can be notated as Eq. 17:

$$E(\varepsilon_{U} \varepsilon_{I} ) < \left( {\overline{{\varepsilon_{U} }} \times \overline{{\varepsilon_{I} }} } \right)$$
(17)

when 0 < CorεUI ≤ 1 (direct dependence), or as Eq. 18:

$$E(\varepsilon_{U} \varepsilon_{I} ) < \left( {\overline{{\varepsilon_{U} }} \times \overline{{\varepsilon_{I} }} } \right)$$
(18)

when − 1 ≤ CorUI < 0 (inverse dependence). In the case that εU and εI are fully dependent (CorεUI = 0), Eq. 16 can be notated as Eq. 19:

$$E(\varepsilon_{U} \varepsilon_{I} ) = \left( {\overline{{\varepsilon_{U} }} \times \overline{{\varepsilon_{I} }} } \right)$$
(19)

(Q.E.D.)

The above consideration means that the contribution of the random measurement error to the calculation inaccuracy of arc power will depend on the measuring error standard deviation amplitudes and as well as on the correlation between the noises. One must remember that arc power involves a mathematical operation between two signals (the main signal embedded by noises). Therefore, the random errors of each signal are statistically propagated [16], becoming larger than that of the individual signal error (and quantitatively different for each calculation method, since each method has a particular mathematical operator). Regardless of the amplitude of the errors, in the case that εU and εI are fully dependent (CorεUI = 0), the measurement errors will not change the difference E(U(i−n)I(i−n)) − (\(\overline{U }\) × \(\overline{I}\)), that is, the calculation inaccuracy will not be altered (see frame (c) of Fig. 1, which waveform mimics a constant signal with noises). On the other hand, when εU and εI are dependent (CorεUI ≠ 0), the measurement error will change the difference E(U(i−n)I(i−n)) − (\(\overline{U }\) × \(\overline{I}\)), becoming lower when 0 < CorUI ≤ 1 (direct dependence) or higher when -1 ≤ CorUI < 0 (inverse dependence). It is important to state that this does not mean that measurement errors, independent or not of each other, will not change the values of the calculated arc power by any method (the mentioned effect is on the difference of values between the equations, not taking into account systematic errors). There is even a possibility, according to the error amplitude, that the value resultant from Eq. 2 or Eq. 3 has the difference inversed (becoming positive rather than negative, for instance), turning higher than that from Eq. 4 (measurement error disguises calculation error).

In summary, distortions of the actual U and I waveforms are prone to occur, affecting the correlation and covariance of the signals. Moreover, the above-listed sources of measurement inaccuracies and uncertainties have systematic and random characters, i.e. they may be accumulative or not. Consequently, in the end, since most of these error sources cannot be totally eliminated (or, sometimes, even mitigated), in order to reduce the uncertainty of the calculated P, one should at least avoid the inaccuracy from the correlation between the signals by using Eq. 4 in the Power calculation.

4 Remarks on other ways to determine arc power

It is important to state that electrical power (in this case, arc power) cannot be measured directly. Power is always measured indirectly through other quantities. As mentioned before, the calculation of arc power from a product of U and I values would be an indirect way of measuring power, based on the electrical definition of power. As exampled by Eqs. 2 to 4, the different ways of calculating arc power are only distinct ways to represent this indirect measurement of power. In addition, U and I are continuous signals varying over time. As already reinforced, the U and I signals do not change, regardless of the quantity indirectly measured by the different calculation methods (equations). As non-constant values and statistical approaches were used, the expected value of power was indeed calculated as a function of the expectation of U and I values (remembering, the expectation was beforehand translated as statistical average value).

So far, we have demonstrated that if calculation is chosen as a means of measuring arc power, the expectation of the power is more adequate if calculated from the average (expected value) of the product of Ui−n and Ii−n. However, other ways of measuring indirectly electrical power could be employed, rather than the statistically based calculation above described. For example, one could create a composed signal derived from a multiplication of U and I signals, theoretically a power signal. Then, several ways could be applied to quantify this new quantity, such as the average value or RMS value. The outcomes from these characterisations could agree or not in value with those found by the statistically based calculation approach. Anyway, this would be only another way to represent the combination of U and I signals (electrical power, by definition).

One must remember that there would exist other ways for measuring indirectly electrical power. For instance, by transforming electrical energy into thermal energy (or heat) and measuring heat with calorimetry (yet not using welding calorimetry, with which absorbed heat by the plate is measured, not arc energy). Alternatively, by transforming electrical energy into mechanical energy and measuring torque with dynamometers. Regardless of the intrinsic measurement errors of these techniques, one could plot the calculated expectations of power as a function of the power derived from energy measurements. One way or the other, uncertainties will persist. The above reasoning only emphasises that the mathematical demonstration shown in Sect. 2.2 does not mean to certify a method for determining power. This earlier statistical approach was just to propose that if calculation is going to be used, the average of the product of U and I (P = (\(\overline{UxI}\)) is preferable than the product of the averages of U and I (P = \(\overline{U}{ }x{ }\overline{I}\)).

5 Conclusion

As implicit along with the text, Power is indirectly measured by directly measuring the U and I signals, followed by multiplication of these quantities. As above exposed, the subside taken from this work would be that the use of the product between the averages of U (voltage array) and I (current array) as a means of calculating P (the arc power, for instance) is accurate only when the two variable arrays are uncorrelated (independent) or when the product standard deviations of the voltage and current array and the correlation (i.e. the covariance) is quantitatively insignificant. Therefore, before using the effective (RMS) or the arithmetic methods of calculating P, one should test the two data sets to determine the correlation between the two samples and their respective standard deviations. However, before applying these statistical tests to the variables, the reader could ask if it would not be easier to calculate the instantaneous power instead. Therefore, the main conclusion of this work is that the safer way to calculate arc power in welding is through the instantaneous power equation (Eq. 4). A subordinate conclusion is that correlation (Cor) is a straightforward way to visualise the dependence between two arrays of variables. Covariance (Cov) represents the calculation inaccuracy obtainable by using power computation as the product of the means (P = \(\overline{U }\) × \(\overline{I}\)) or the RMS (P = URMS × IRMS) values. Finally, the measurement errors should be minimised as much as possible because the contribution of the random measurement errors to the calculation inaccuracy of power will depend on the measuring error standard deviation amplitudes and the correlation between both error signals.