Abstract
We evaluate the aerodynamic performance of several passive vortex generators (VGs) placed on a standard Ahmed body, with a slant angle (α = 35º), subjected to different yawing angles (β) using RANS-based models. Rigorous validation of the numerical results is performed with previously published experimental data for (β ≤ 8º) for the Ahmed body. Our model results depict a good overall agreement with several experimental data sets. An array of different vortex generators such as the delta-winglet (DVGs), the cylindrical (CVGs) and trapezoidal (TVGs) types are introduced on to the validated model. The introduction of CVGs and DVGs tends to have a beneficial aerodynamic performance for (β = 0º). In contrast, the TVGs tend to impair the performance by producing massive flow separation over the slant for (β = 0º). Conversely, for (β > 0º), a swift transition happens with TVGs wherein the high-energy streamwise vortices that are produced tend to improve the pressure footprint, thereby reducing the overall drag. A deterioration in the performance of DVGs is predicted during (β > 4º), wherein the ‘c’-pillar vortex on the leeward side interferes with the streamwise vortical structure, which adversely influences the flow over the roof-slant edge. Overall, a maximum of ~ 8.5% and ~ 7.7% drag reduction appears to be possible with the designed CVGs and TVGs at smaller vehicle yawing conditions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Drag reduction techniques on standard aerodynamic vehicles are of significant interest to automobile manufacturers owing to higher repeatability and additionally provide an enhanced understanding of the fuel consumption to protect the global environment. Typically, a reduction in aerodynamic drag of ground vehicles by 10% can potentially reduce fuel consumption by 5% Bellman et al. [6]. Since most fast-back, square-back, and notch-back vehicles inherit the bluff-body shapes with blunt trailing edges, the reduction in base drag therefore becomes one of the key goals [16].
To date, several experimental methods have focused on techniques such as (1) active, (2) passive or (3) a combination of ((1) & (2)) control strategies for achieving drag reduction on generic vehicle geometries such as an Ahmed body [1] to gain key understanding on the relation between the pressure drag generation and the complex wake structure [24, 57]. Active drag reduction techniques such as steady blowing [58], through synthetic jet actuation [34], using pulsed jets [28], using pulsed jets and Coanda effect [5] and by a combination of blowing and suction [9] to influence the wake behind the Ahmed body have shown a remarkable performance in reducing drag. Passive methods that are relatively more straightforward to both implement and manufacture such as the use of deflector plates [22], geometric modifications such as rounding the edge between the roof and slant [53], through afterbody rounding [48], by producing body cavity at the base [17] and through the use of vortex generators (VGs) [2, 46] have been successful in achieving drag reduction between 10 and 20%. Some stand-alone experimental studies on VGs have shown to exhibit greater efficiency in both delaying and at times inhibiting boundary layer separation, together, they have shown to be preferred devices for transition-to-turbulence delay [50]. More recently, through the use of stereo-particle image velocimetry, [54] assessed the performance of various vortex generators and showed that sweep angles in (DVGs) should carefully be selected to maintain the effectiveness in momentum transport while producing minimum drag.
Simulation methodologies on flow control strategies on standard bodies have prominently complemented the experimental findings mentioned above by resolving the formation of streamwise streaks that can lead to delayed separation with the presence of VGs, establishing optimization actuation strategies for imitating the Coanda blowing leading to fluidic boat-tailing, resolving the intricate flow structures of the vortex loops, identifying the sources that lead to symmetrization of low-pressure toroidal structures in the near-wake region [19, 21, 35, 39, 41].
Of particular interest to realistic passenger vehicles are the VGs which have not only demonstrated high effectiveness as a part of passive drag reduction technique but have proven to be viable for commercialization in vehicles. The classical work of Koike et al. [33] used a Reynolds-averaged Navier–Stokes (RANS)-based approach. It explored the effects of two different types of vortex generators, namely the ‘bump’ shape and the delta-winglet type on a realistic sedan vehicle, the Mitsubishi LANCER EVOLUTION VIII. Their findings provided significant insight into the optimum height of the VGs being equal to the thickness of the boundary layer and a meaningful reduction in both the drag and lift coefficients through the application of VGs. Also, the surface pressures on the rear of the vehicle appeared to enhance with the presence of VGs indicating a delay in flow separation compared to a standard car. Besides, Koike et al. [33], reported that the delta-winglet-type vortex generators (DVGs) were superior to the ‘bump’-shaped VGs. Since then, not much attention seems to be evident with investigating the effect of VGs on realistic passenger vehicles until recently. [18] experimentally tested both the cylindrical vortex generators (CVGs) and DVGs on a real car model, viz. the Peugeot 208, and a standard square-back Ahmed body on a full-scale wind tunnel at 120 km h−1 with ground effect and rotating wheels. Their findings suggest that for the square-back Ahmed body, the base suction appeared to decrease with similar magnitudes for both CVGs and DVGs, showing a favourable effect of the vortex generator on the Ahmed body. However, with a realistic vehicle, contrary results were evidenced wherein the base suction is enhanced with both the DVGs and CVGs in comparison with the standard vehicle used. Nevertheless, [18] further reported that, contrary to previous findings, the overall drag increased with both types of VGs regardless of the nature of vehicles used. [31] presented experimental results by testing Indy-type race cars using four different kinds of VGs, namely the long and short rectangular types and long and short DVG types. Their results indicated that the simple DVG types were the most efficient in terms of the incremental lift to drag ratio compared to the rectangular-type VGs. Furthermore, experimental investigations have demonstrated that the counter-rotating vortex generator configurations such as the DVGs can suppress flow separation [30, 37]. Therefore, the use of VGs has adequately evidenced to provide beneficial aspects by enhancing the flow features over standard test bodies, passenger vehicles and race car variants.
Despite many probing experimental and numerical investigations conducted over two decades by several researchers mentioned above, many aspects of the flow physics generated by VGs, such as the vortex roll-up or breakdown behind the VGs, remain unclear for both realistic and standard vehicles. Of critical importance is the performance of different types of VGs under yawing (or) during conditions when a standard test body is being subjected to cross-winds, which has never received any attention to date both numerically and from the experimental standpoint to the best of authors' knowledge. The objective behind this work is motivated by the reasons mentioned above, which is to elucidate the aerodynamic performance of several commonly employed vortex generators such as (1) the delta-winglet vortex generators (DVGs), (2) the cylindrical vortex generators (CVGs) and (3) the trapezoidal vortex generators (TVGs) when placed on a standard Ahmed Body (with a slant angle (α = 35º)) subjected to yawing conditions.
The rest of the paper is organized as follows: Section “2. Baseline Model and VG Design Configurations” describes the selection and choice of VGs on the Ahmed body employed in this study. In Section “3. Numerical method and computational details”, the computational domain, the boundary conditions and a comparison of various RANS-based turbulence closures are presented and investigated alongside by assessing different solver performance. In Section “4. Comparison with experimental data sets”, an inclusive 'two-part' validation of the numerical model(s) is presented within the same section, wherein (I) the standard Ahmed body model is compared against several available experimental results for comparable Reynolds numbers (ReL) based on the length of the model geometry and (II) during yawing conditions. The “5. Effect of VGs on Ahmed Body” section details the numerical simulations of several vortex generators such as the DVGs, CVGs and TVGs on the baseline Ahmed body when subjected to several yaw angles (β); conditions that lead to both their performance enhancement and deterioration are critically examined. “6. Conclusions” section summarizes the critical contributions and findings from this study.
2 Baseline model and VG design configurations
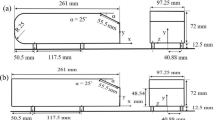
A recent study by Cheng et al. [13] investigated the effect of (β) on a 75% scale Ahmed body with a slant angle (α = 35º). Their study was extended to cases where the Ahmed body was fitted with a spoiler and splitter to examine the bi-stable wake behaviour. The conclusions reached from the study suggest that yawing the Ahmed body adversely affects its performance and the presence of wing and spoilers on the Ahmed body can help prevent bi-stability that occurred for (β > 8º). The experimental conditions and the Ahmed body model of [13] are used in this work as a baseline configuration, as shown in Fig. 1a, which facilitates us to systematically compare our numerical findings described in Sect. (3. Numerical method and computational details).
(i) The geometry of the Ahmed body, along with the coordinate systems. (ii), (iii) and (iv) Detailed dimensions of DVGs, CVGs and TVGs examined in the present study. A superimposed view of the arrangement of the three vortex generators attached on to the Ahmed body is shown in (v). All dimensions are in (mm)
As far as the choice of VGs is concerned, we investigate three different types of VGs on the baseline model that were previously employed on ground vehicles and square-back Ahmed bodies such as the DVGs [18, 33] and that have been previously tested on Ahmed body models but with different slant angles such as CVGs [46] and TVGs [2] as shown in Fig. 1ii-iv.
The height \(\left(h\right)\) of all VGs employed is within the boundary layer thickness \(\delta = 0.37L\left( {Re_{L} } \right)^{{ - \frac{1}{5}}}\);\(\left( {h < \delta } \right)\) as per recommendations by Koike et al. [33]. Besides the height, we have preserved the original shape specifications of the designs by [46] and [2] so that a balanced representation shall be presented across all VGs investigated in this study. Under the conditions mentioned above, the maximum area (Aref) increase between the baseline and any VG configuration is found to be < 6%, and the maximum differences in the area amongst the VGs are found to be < 1.7% as shown in Table 1.
The definition of yawing angle (β) for the direction of airflow (U) and the representation of the leeward and windward sides w.r.t. to the coordinate systems are presented in Fig. 2. Considering that for (β > 8º), the high level of flow unsteadiness creates bi-stability that switches the flow between high and low aerodynamic forces as determined by [13]; the present analysis is therefore restricted to values of (β ≤ 8º).
3 Numerical method and computational details
The Ahmed body baseline case and cases with VGs present on the baseline model, as shown in Fig. 1, were included in a computational wind tunnel configuration Ω = (Linlet, Lx, Ly, Lz) = (2L, 8L, 4L, 2L) scaled based on the length (L) of Ahmed body, as shown in Fig. 1a. The computational domain shown in Fig. 3 is chosen to be consistent with the ERCOFTAC guidelines [19, 20, 25, 47] to capture the flow with minimal blockage effects adequately. The flow at the inlet is set to Reynolds number of ReL = 2.7 × 106 based on the length of the body and the incoming velocity of U = 53 ms−1 with a turbulence intensity of 0.06% as per the experimental conditions of [13]. The other boundary conditions correspond to a: no slip on all the body surfaces and the ground, free slip at the sides and top of the domain, and a null pressure at the outlet [15].
A schematic of the computational domain with dimensions normalized by the length of the Ahmed body defined in Fig. 1(i) along with the specified boundary conditions
The high-fidelity modelling approaches such as the large eddy simulations (LES) and hybrid versions of RANS-LES have shown to resolve the near-wake structure and flow intricacies in the shear layer over Ahmed bodies sufficiently. The computational resource requirements for such simulations along with the higher-order discretization schemes that need to complement the high level of grid refinements pose challenges, especially when a systematic study with several test cases is involved like ours. Previous investigations have shown that the slant angle (α) of the Ahmed body influences the choice of the turbulence modelling strategies for an Ahmed body [25, 36]. RANS models have been recently employed on Ahmed bodies for both α = 25º and 35º slant angles when investigating flap mechanisms with orientation during cornering [49] and were successfully demonstrated with different turbulence model calibrations [7]. Specifically for α = 35º, most RANS-based approaches, as simple as a linear k-ε to more advanced Reynolds stress models (RSM), have shown to be quite successful [4, 25] in predicting the flow reattachment and separation points over the slant. Therefore, we adopt the realizable k-ε model (R-k-ε) of Shih et al. [51] as a starting point for grid independence check considering that all topologies such as the baseline and VGs embedded on the baseline have α = 35º as slant angle. Besides, two additional RANS-based turbulence closures, namely the SST-k-ω of Menter [44] and the (RNG-k-ε) from Yakhot et al. [56] models, are examined as a rationality check on the free-stream grid resolution and to assess the discretization schemes used in this study. The numerical analysis in the present study was carried out using ANSYS Fluent (Ver. 19.1). The transport equations for the three turbulence models as mentioned above are comprehensively documented in the references [3, 15]; therefore, the readers are directed to these references for more details.
3.1 Grid resolution study
Before describing the grid resolution checks, we define the aerodynamic force coefficients used in the present study, namely the drag force coefficient (\({\text{C}}_{d}\)), the lift force coefficient (\({\text{C}}_{l}\)) for usefulness:
where \(\rho\), \({\mathrm{F}}_{\mathrm{d}}\) and \({\mathrm{F}}_{\mathrm{l}}\) correspond to the density of air, aerodynamic drag and lift forces, respectively.
The grid consisted of tetrahedral elements on the free-stream (the departure region (DR)) and with prism layers on the body surfaces and the ground. An additional refinement region, the focus region (FR) with a volume (3.5L × 2L × 1L), was considered around to the body [52]. By proportionally refining the surface elements over the Ahmed body and the free-stream meshes on both the (FR) and the (DR), a grid resolution study was performed on the baseline model for (β = 0º) with seven grids as shown in Fig. 4. The difference in the coefficient of drag (\({\mathrm{C}}_{\rm d}\)) (Eq. 1) between the 6th grid distribution consisting of ~ 2.62 × 106 cells (marked by a green circle) against the 7th grid distribution (~ 3.08 × 106 cells) was found to be < 1%. Furthermore, the predicted value of (\({\mathrm{C}}_{\mathrm{d}}\)) is found to be in reasonable agreement with the data of Cheng et al. (2019) as shown in Fig. 4. Therefore, the grid distribution with ~ 2.62 × 106 cells was deemed to be sufficient for further investigations carried out in this study.
Grid independence test demonstrated for the variation of coefficient of drag (\({\text{C}}_{d}\)) w.r.t. the cell count examined in the present study for (β = 0º) compared against the experimental results of Cheng et al. [13]
However, with the inclusion of vortex generators and yaw angle effects in the system, this size varied between 2.62 × 106 and 4.76 × 106 cells. The maximum surface size on the baseline Ahmed body was 3 mm, whereas on the VGs a maximum surface size of 0.5 mm was chosen with a local minimum surface mesh size of 1 × 10−4 mm. A detailed view of the cross section of the final grid in different planes along with the surface refinements over the Ahmed body and VGs is presented in Fig. 5. Typically the grid consists of 24 prism layers on the body and on the ground with the stretching ratio of 1.2. A prism layer thickness of 40 mm was applied on the ground to ensure a velocity profile that satisfies a fully developed turbulent boundary layer before the flow impinges the vehicle, as given by
Grid used in the current study showing (i) regions of the domain refinement (FR) and (DR) in the x–y plane, (i') a close-up view is shown illustrating the prism-layer mesh, (i'') shows the grid distribution in the y–z plane at the centre of the body. The figures (ii), (iii) and (iv) illustrate the surface refinements on DVGs, CVGs and TVGs, respectively, and the surface refinement on the Ahmed body
Considering that the wall-bounded turbulence effects are predominantly crucial in this study, the treatment of the wall and the near-wall modelling effects have been carefully evaluated as follows.
3.2 Near-wall modelling strategy
For (R-k-ε) and (RNG-k-ε) models, the dimensionless wall distance value of \(y^{ + } = 8\) was fixed, and an enhanced wall treatment (EWT) was adopted ((ANSYS Fluent Theory Guide, v.14.5 (2011 [3]). The (EWT) is a near-wall modelling approach that combines a (a) two-layer model with (b) enhanced wall function. With a fine near-wall mesh (\({y}^{+}\approx 1)\) which ensures that the viscous sublayer is resolved closest to the wall, the (EWT) would revert to the traditional two-layer zonal model, but this imposes significant computational resource requirement. Conversely, a hybrid treatment is adopted to combine the applicability of coarse (wall-function meshes) and fine (low-Re) meshes by blending the two-layer model with the enhanced wall function in which the demarcation between the viscosity-affected region and a fully-turbulent region is determined based on wall-distance-based, turbulent Reynolds number (\({Re}_{y})\) given as follows:
where \(k\), \(\mu\) and \(\rho\) represent the turbulence kinetic energy, the viscosity and density, respectively. The term \(y\) denotes the distance to the nearest wall given by:
where \(\overrightarrow{r}\) and \(\overrightarrow{{r}_{w}}\) represent the position vectors at the field point and wall boundary, respectively. \(\Gamma \omega\) is the union of all the wall boundaries that are involved. This representation is robust and defines \(y\) to not only accommodate complex shapes involving multiple walls but makes it independent of mesh topology.
In the fully-turbulent region \(\left( {Re_{y} > Re_{y}^{*} } \right)\), the R-k-ε or the RNG-k-ε turbulence model is solved. In the viscosity-affected region \(\left( {Re_{y} < Re_{y}^{*} } \right)\), the one-equation model of Wolfshtein [55] is solved instead, in which the equations for momentum and \(k\) are retained, and the turbulent viscosity is computed as follows:
where \({C}_{\mu }=0.220\) is the turbulence viscosity constant proposed by Wolfshtein (1969) and \({l}_{\mu }\) is the length scale given by
where \(C_{l}^{*} = kC_{\mu }^{ - 3/4}\) and \(A_{\mu } = 70\) given by Chen and Patel (1988).
The two-layer formulation for turbulent viscosity used as a part of EWT is derived by blending the high Re \(\left( {\mu_{t} } \right)\) (i.e. either obtained from the R-k-ε or the RNG-k-ε turbulence model, in this case) and the low Re \(\left( {\mu_{t, 2layer} } \right)\) [27] using a blending function \(\lambda_{\varepsilon }\). The advantage of this system is that divergence in the solution can be suppressed if \(\left( {\mu_{t} } \right)\) predicted in the outer layer does not match with that predicted by Wolfshtein [55] at the edge of the viscosity-affected region.
The width of the blending function is determined by the constant \((A)\) so that \({\lambda }_{\varepsilon }\) is within 1% of its far-field value given by the variation of \(\Delta {Re}_{y}\), given by
In the viscosity-affected areas, the rate of dissipation of turbulence kinetic energy (\(\varepsilon\)) is given by
The length scale term \(\left({l}_{\mu }\right)\) given by Chen and Patel (1988) is as follows.
Until now, we have described the treatments for turbulent viscosity, turbulence kinetic energy and rate of dissipation. However, the momentum needs blending as well, which is described as follows:
The momentum condition is based by blending the linear (laminar) and logarithmic (turbulent) laws of the wall using a function proposed by Kader [29]:
where the blending function is given by:
where \(a = 0.01\) and \(b = 5\).
Similarly, the general equation for the derivative \(\frac{{du^{ + } }}{{dy^{ + } }}\) is given by:
The formula mentioned above has several advantages: (a) effects such as pressure gradients or variable properties can be accounted for in the formulation; furthermore, (b) it guarantees the correct asymptotic behaviour for large and small values of \({y}^{+}\) and reasonable representation of velocity profiles in the cases where \(y^{ + }\) falls inside the wall buffer region (3 < \(y^{ + }\) < 10). As mentioned previously, \(y^{ + } = 8\) was fixed as the desired value in the current study for both (R-k-ε) and (RNG-k-ε) models. However for the (SST-k-ω) model, a value of \(y^{ + } = 0.98\) was specified so that the viscosity-affected near-wall region fully resolves the viscous sublayer and that we utilize the capability of this low-Re model at its best.
3.3 Solver evaluation and computing time
An evaluation of three turbulence closures, viz. the (R-k-ε), the (RNG-k-ε) and the (SST-k-ω), for the baseline model with (β = 0º) against SIMPLEC and pressure-based coupled (PBC)-pseudo-transient pressure–velocity coupling schemes were carried out. For anisotropic meshes such as ours, some degree of skewness always persists, and therefore, solver robustness is critical for convergence. With SIMPLEC, a skewness correction of 1 was employed, in which the pressure-correction gradient is recalculated and used to update the mass flux corrections, to enhance the rate of convergence. At this juncture, it is essential to highlight that the maximum skewness for all simulated cases in this work was below 0.86 as per best practice guidelines for tetrahedral volume meshes [38]. The (PBC) pseudo-transient solver, which is a form of implicit under-relaxation for steady-state cases, has shown significant potential to speed up the solution [32]. For both the solvers, the spatial discretization was based on second-order upwind for all equations except for pressure where 'PRESTO!' was used. At this stage, we compare the numerical predictions of different solvers and model combinations investigated in this study against experimental values and discuss our findings against the numerical results presented by other researchers under comparable conditions in terms of α, β and ReL as shown in Table 2 and Table 3. This exercise is key to identifying the right combination for modelling the rest of the cases with VGs and under yawing conditions. The starting point of such comparisons can be explained using the Reynolds number dependency test shown in Fig. 6 that illustrates the scaling of (\({\mathrm{C}}_{d}\)) against ReL obtained from several experimental results for models of different scales and variations in ReL [13], Meile et al. [42], Meile et al. [43], Ahmed et al. [1] as previously demonstrated in the work of Cheng et al. [13]. These results indicate that the aerodynamic forces settle down at a value of ReL = 2.7 × 106 used in this present study that is identical with the experiments of Cheng et al. [13].
Experimental values of (\({\text{C}}_{d}\)) obtained by several researchers [1, 13, 42, 43] versus Reynolds number (ReL) scaled based on the length of the Ahmed body for slant angle (α = 35º) and yaw angle (β = 0º) demonstrated by Cheng et al. [13]. The (\({\text{C}}_{d}\)) prediction from the current numerical result using (R-k-ε,) is included in the plot for comparison
Compared to the predictions of (RNG-k-ε), the predictions for (\({\text{C}}_{d} )\) by (R-k-ε) is marginally closer to the experimentally determined values of Cheng et al. [13] (75% scale geometry) and Ahmed et al. [1] (full-scale geometry) and provides an excellent match by showing ~ 1.5% difference between the experimental values of Meile et al. [42] (full-scale geometry) and Meile et al. [43] (full-scale geometry). However, by maintaining the stringent \(y^{ + } = 1\) requirement near the wall for (SST-k-ω), the cell count proportionally increases compared to the (R-k-ε) and (RNG-k-ε) models. As shown in Table 2, the values predicted by (SST-k-ω) for (\({\text{C}}_{d}\)), (\({\text{C}}_{l}\)) in the current effort aligns well with a) the (SST-k-ω) predictions of Guilmineau et al. [25] that resulted in (\({\text{C}}_{d} = 0.2999; {\text{C}}_{l} = 0.0052)\) and b) the for a full-scale baseline experimental results of Meile et al. [42]. All turbulence models investigated in this study predict positive values for (\({\text{C}}_{l}\)) in agreement with the (SST-k-ω) models of Guilmineau et al. [25] and Meile et al. [42].
Regarding the convergence criteria, the residual convergence for continuity was found to be < 1 × 10 − 5; however, for the rest of the equations for all turbulence models, the residual convergence was < 1 × 10 − 7. For any given turbulence model, the maximum difference between the predicted (\({\text{C}}_{d}\)), (\({\text{C}}_{l}\)) between the SIMPLEC and the (PBC) solver was < 0.05% and < 0.2%, respectively, and therefore deemed to be negligible. We notice a twofold increase in the time taken per iteration for SST-k-ω when compared with (R-k-ε) and (RNG-k-ε) models, as shown in Table 3. We observe that for each of the turbulence models, the time elapsed per iteration for (PBC) is always higher compared to SIMPLEC, as shown in column 5. Nevertheless, the 'rate of convergence' indicated in column 6, which shows the overall computing time for convergence for (PBC), was always smaller than compared to SIMPLEC. Therefore, significant speed-up on the overall computing time was achieved with the (PBC)-pseudo-transient solver. Specifically, the (R-k-ε) tends to show the lowest total computing time with (PBC) solver that results in a reasonable agreement with experimental data sets. Therefore, considering that a large number of simulations are to be undertaken in this investigation, the (R-k-ε) together with the (PBC)-pseudo-transient solver was examined further for its reliability in resolving the wake structure, TKE, and surface pressure distributions over the base and the slant of the baseline model.
4 Comparison with experimental data sets
In this section, we present a comprehensive two-part comparison against field variables predicted by the (R-k-ε) model for the baseline case against the full scale, and baseline body with 75% scale experimental data sets for all values of (β ≥ 0º) examined in this study.
4.1 Part I: Baseline model (75% scale) vs experiments (full scale) (β = 0º)
The rationale behind comparing the baseline numerical results against experiments with a full-scale Ahmed body Lienhart and Becker [40] is substantiated by the experimental results of Reynolds scaling dependency test by Cheng et al. [13] together with the close match between model and experimental results presented in Fig. 6 and Table 2.
The dimensionless quantities for the model are represented as (x* = x/Lref; y* = y/Lref; z* = z/ Lref;; Ux* = Ux/Uref); for the model, the reference values correspond to Lref = 0.783 m and Uref = 53 ms−1, whereas for experiments Lref = 1.044 m and Uref = 40 ms−1. A comparison of the streamlines of the flow in the symmetry plane between the current model results and the experimental data of Lienhart and Becker [40] is shown in Fig. 7a. Although the location of the upper recirculation bubble (N1) predicted by the numerical result is reassuring, some degree of discrepancy with the upper recirculation bubble (N'1) from the experiments in terms of its overall toroidal shape is evident. The numerical result does not predict a lower recirculation bubble and may be attributed as a RANS model limitation, but with the experimental data, the lower separation bubble (N'2) is although weak but apparent. The RANS models such as the Explicit Algebraic Stress Model (EARSM) and (SST-k-ω) that were published in the previous work of Guilmineau et al. [25] do not predict the lower separation bubble, whereas the RANS-LES variants, viz. the detached eddy simulation (DES) and the improved delay detached eddy simulation (IDDES) models, tend to resolve the lower separation bubble. The TKE distribution of the model shown at the symmetry plane in Fig. 7b shows good qualitative agreement with the experimental results by predicting higher TKE spectrum closer to the (N'2) region and by capturing adequate levels of TKE in the shear layer. Nevertheless, the TKE predicted by the model in the upper shear layer over the slant is significantly higher than compared to the experimental result. Quantitatively, the TKE values predicted by the model overall appear to be higher, and this may be attributed to the higher inflow velocity present in the model compared to the experiments.
The numerical predictions of the streamlines (a) and turbulent kinetic energy (TKE) (b) is shown in y* = 0 plane, whereas the figures (a') and (b') show the experimental results of Lienhart and Becker [40] for (β = 0º). The experimental data of Lienhart and Becker [40] are presented in the work of Guilmineau et al. [25] and are reproduced here with permissions from Elsevier, Copyright (2018)
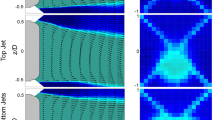
Figure 8 shows the normalized streamwise velocity vectors Ux* at several y–z planes compared against the experimental data to comprehensively represent the wake structure. At x* = 0 and 0.0766, a reasonably qualitative and a good quantitative agreement is shown by the model by accurately capturing the negative-to-positive transition region. With x* = 0.1915, the negative region appears to be marginally shorter in the spanwise direction unlike the experimental data but with weaker vortical structures on the edges of the baseline model similar to that seen in the experiments. Although no negative values of Ux* are present at x* = 0.4789, its magnitude is smaller compared to that seen in the experiments.
(a-d) correspond to the numerical predictions of the dimensionless streamwise velocity in the y*-z* plane in the wake compared against the experimental results of Lienhart and Becker [40] shown by the figures (a'-d'). From top to bottom, the images correspond to x* = x/Lref = 0, 0.0766, 0.1915, 0.4789, respectively, for (β = 0º). The experimental data of Lienhart and Becker [40] are demonstrated in the work of Guilmineau et al. [25] and are reproduced here with permissions from Elsevier, Copyright (2018)
Despite such differences, the numerical model in the present study accurately captures the length, the overall height of the near-wake structure and flow feature at the end of the roof-slant characterized by massive separation with a reasonable overall agreement with the TKE as seen in the experimental data.
4.2 Part II: Baseline model (75% scale) vs experiments (75% scale) (β ≥ 0º)
The experimental data from Cheng et al. [13] provide us with a whole-field description of the surface pressure coefficient (\({\mathrm{C}}_{\mathrm{p}}\)) for the same geometry scale (75%) as a direct comparison to further assess the validity of the numerical result.
The pressure coefficient (\({\mathrm{C}}_{\mathrm{p}}\)) is defined as follows:
where \(P\) and \(P_{ref}\) correspond to the calculated mean pressure and reference (ambient) pressure, respectively.
A comparison of the centreline (\({\text{C}}_{{\text{p}}}\)) for various values of (β) between the numerical predictions and experimental data of Cheng et al. [13] is shown in Fig. 9(a–e). The locations (22–30) correspond to metering points (MPs) where pressure tappings were located in the experiments; at identical locations, we compare the result from our numerical model. These locations are critical in our study because the influence of VGs shall have a direct consequence on these locations, which is presented in the next section. The agreement between the model and experimental data for MPs (22–24) located on the roof-slant edge is reasonable and consistent for all values of (β). On the MPs (25–27) located on the slant, the model provides an excellent match with experiments. For all cases, the largest deviations between the model and experiment tend to be on the base shown by MPs (28–30), suggesting that the numerical results overpredict the flow separation on the base. Despite this discrepancy, the overall trend shown by the experimental MPs (28–30) depicting an increase in (\({\text{C}}_{{\text{p}}}\)) and a dip in the value at the end of the base is very well captured by the model.
A comparison of the numerical predictions of the surface Cp along the centreline of the roof end, slant, and base against the previously published experimental results of Cheng et al. [13]. a corresponds to (β = 0º) shown with the location of metering points (MPs) 22–30 identical to locations of the pressure taps in the experiments of Cheng et al. [13]. b–e correspond to the numerical predictions for (β = 2º, 4º, 6º and 8º) compared against the experimental results at the same metered locations
A summary of the results comparing the overall drag and lift coefficients, namely the (\({\text{C}}_{{\text{d}}}\)) and (\({\text{C}}_{l}\)), between the model and the experiment Cheng et al. [13] is presented in Fig. 10a and b for all (β) values investigated in this study. The most significant difference in (\({\text{C}}_{d}\)) between the model and experiment is observed for (β = 8º); however, with (β ≤ 4º), a consistently good agreement is seen with the experiments. The (\({\text{C}}_{l}\)) values predicted by the model are always positive for all values of (β) unlike the experiment, and we indicate that such has been the case with previous predictions obtained from RANS evaluations for the baseline Ahmed body with α = 35º by Cheng and Mansor [12], Cheng and Mansor, [11], Guilmineau et al. [25], and Meile et al. [42]. This deviation may be attributed to the model over-predicting the flow separation on the base as seen in Fig. 9. Despite such differences, we identify that (a) the differences in (\({\mathrm{C}}_{l}\)) and (b) its trend showing an increase in values with increasing (β) appear to manifest consistently between the model and experiment, which appears to be encouraging. Overall, the numerical model is able to replicate the tendency that yawing the vehicle adversely affects the aerodynamic performance as shown by the experiments of Cheng et al. [13] and Meile et al. [42]. With these correlations in place, the forthcoming section is focused on the numerical simulation results on baseline Ahmed body by embedded different types of VGs and critically examines their aerodynamic performance by subjecting the baseline Ahmed body to different (β) values.
A comparison of (a) drag and (b) lift coefficients between the current numerical predictions and experimental results of Cheng et al. [13] for various values of (β)
5 Effect of VGs on Ahmed Body
5.1 Near-wake and vortex structures for (β = 0º)
Figure 11 shows the streamlines of the wake of the Ahmed body and VGs embedded on to it in a) y-x plane (z* = 0.1285) and b) x–z plane (y* = 0) for (β = 0º). In comparison with the baseline case as shown in Fig. 11 a(i) and b(i)), with the presence of CVGs Fig. 11 a(iii) and b(iii)), the wake elongation is prominent in both the streamwise and spanwise directions, and with DVGs Fig. 11 a(i) and b(ii), this is less noticeable in streamwise but quite evident in the spanwise direction.
Numerical predictions of the velocity streamlines in the near wake of the Ahmed body in a y-x plane (z* = 0.1285) and b x–z plane (y* = 0) and a schematic representing the length of the separation bubble and centre of the recirculation zone in x–z plane. The part figures (i–iv) correspond to the baseline, DVG, CVGs and TVG models, respectively, for (β = 0º). The box in (iv, b) indicates the flow separation region
The wake elongation observed with employing the DVGs and especially the CVGs must be pronounced as a favourable outcome since the elongation of the wake is a good indicator of drag reduction, as given by Han et al. [26], Lucas et al. [41], Li et al. [39], Pastoor et al. [45]. With the presence of TVGs, the recirculation bubble is shorter, and the centre of the upper recirculation bubble appears closer to the base compared to the other cases. Also, there is a prominent recirculation bubble closer to the base. For each case, the location of the centres of the upper recirculation zone and the length of the separation bubble (Lxz*) as illustrated in Fig. 11c are summarized in Table 4. Flow separation at the roof (marked by an orange square) indicates the presence of TVG interfering with the oncoming flow that eventually unfavourably alters the wake dynamics downstream.
To resolve the critical vortices that dominate the flow structure, we plot the vortex-core region resolved using absolute helicity, \(H=\overrightarrow{U}\bullet \overrightarrow{\omega }\), where \(\overrightarrow{U}\) is the velocity vector and \(\overrightarrow{\omega }\) is the vorticity vector. Figure 12 shows the iso-surface surface at \(H=7500{\text {ms}^{-2}}\) coloured by mean velocity for (β = 0º). Vortices with high velocities appear at the roof-slant edge where the VGs are positioned compared to the baseline, especially with CVGs and DVGs they appear pronounced. The C-pillar vortices for the TVG case (d and d') appear to be thicker and longer compared to the rest of the other cases, as shown in Fig. 12 (iv).
Numerical result for (β = 0º) depicting the iso-surface of absolute helicity (H = 7500 ms−2) coloured by mean velocity (U) in each of figures (i-v) that represent the cases for baseline, DVG, CVG and TVG cases. In each case, the counter-rotating streamwise vortices are represented by (a-d) and (a'-d'). The vortices (a''-d'') represent the co-rotating vortex on the leeward side with its counterpart (not shown) that emanates from the corners of the leading edge
5.2 Vortex structures, near-wake and roof pressure foot prints for (β ≥ 0º)
The vortical structures that emanate from the body are more complex with nonzero and increasing values of (β). Figure 13 shows the leeward side (a–d) and windward side (a'-d') roof vortices for all cases for (β = 6º) of which the windward side appears to be dominant in structure. A unique feature is evident wherein the vortices from DVG appear to interfere with the leeward side c-pillar vortex (b''') shown by a dotted circle in Fig. 13b. The attachment and separation characteristics of the flow over the body are noticeable by plotting the \({(\mathrm{C}}_{\mathrm{p}}\)) over the surface as shown in Fig. 14 for the same case (β = 6º). In all the four cases, the windward side exhibits an apparent region where the vortical structure (a'-d') is present.
Numerical result for (β = 6º) depicting the iso-surface of absolute helicity (H = 7500 ms−2) coloured by mean velocity (U) in each of figures (i-v) that represent the cases for baseline, DVG, CVG and TVG models. In each case, the leeward and windward roof vortex are represented by (a-d) and (a'-d'), respectively. The vortices (a''-d'') represent the co-rotating vortex on the leeward side with its counterpart (not shown) that emanates from the corners of the leading edge. The vortices (a'''-d''') correspond to the leeward side c-pillar vortex. The dashed circle in figure (ii) identifies the interference of the vortices from DVG on the leeward side with vortices b'' and b'''
On the leeward side, the significant low-pressure footprint evident behind the DVG and closer to the roof-slant edge as shown in Fig. 14(ii) suggests massive flow separation, indicating that the performance of the DVG at this stage is fading. However, some reattachment is evidenced closer to the edge of the slant. In Fig. 14(iii), just behind (downstream) of the CVGs, hotspots that are relatively uniform in the magnitude in \({(\mathrm{C}}_{\mathrm{p}}\)) are seen, suggesting that the CVGs attempt to inhibit the flow separation, and therefore, the \(({\text{C}}_{{\text{p}}}\)) values over the slant for this case appear relatively more uniformly distributed and higher. With the TVGs shown in Fig. 14(iv), although the hot spots in \(({\text{C}}_{{\text{p}}}\)) are evident, this feature does not appear to be as promising as compared to the CVGs. In some regions within the edge of the roof-slant, the flow appears to be separated with the presence of TVGs. One may observe an additional interesting feature that the presence of VGs has a direct effect of the upstream flow, i.e. over the roof. Most certainly, compared to the distribution of \(({\text{C}}_{{\text{p}}}\)) over the roof for the baseline Ahmed body case as given in Fig. 14(i), the flow is less separated over the roof for the case with the CVGs given in Fig. 14(iii) but more separated with DVGs as shown in Fig. 14(ii). However, with the TVGs given in Fig. 14(iv), the flow separation over the roof does not appear to be as curtailed as seen with the DVG case and is only marginally better over the roof compared to the baseline case as shown in Fig. 14(i).
The near-wake structure for (β = 6º) is shown for all cases in Fig. 15 at sections closer to the leeward edge (y* = -0.115), the model symmetry (y* = 0) and closer to the windward edge (y* = 0.115). Sectionwise, the wake structure exhibited by the baseline in Fig. 15(i), the CVG in Fig. 15(iii), and the TVG in Fig. 15(iv) are different but such differences appear to be minimal. With the DVGs, the flow is initially attached closer to the roof-slant edge for (y* = 0.115) but significantly detaches further downstream, and as a consequence a distinctively deformed wake structure is seen with the DVG in Fig. 15(ii), wherein closer to the leeward side it is characterized by massive separation over the slant, and near the model symmetry (y* = 0), two distinct non-symmetric (upper and lower) recirculation zones are evidenced, unlike just the one recirculation zone that is exhibited by other the models.
5.3 Slant, base pressure and aerodynamic coefficients (β ≥ 0º)
Figure 16 presents the \({(\mathrm{C}}_{\mathrm{p}}\)) distributions on the slant and the base (seen from View1) for all (β) values and for all cases investigated in this study. We shall examine these in conjunction with the overall (\({\text{C}}_{d}\)), (\({\text{C}}_{l}\)) values presented for all cases shown in Fig. 17.
For (β = 0º), the distribution presented by the CVG given in Fig. 16(iii) is more uniform and higher over the slant than compared to the baseline case as shown in Fig. 16(i), and marginally than the DVG case given in Fig. 16(ii). The pressure footprint on the edges of the base is higher for the DVG case compared to the rest of the cases. With the TVGs, the \({(\mathrm{C}}_{\mathrm{p}}\)) not only appears non-uniform but shows significantly lower values over the slant with less pressure recovery over the base. This appears to be in consensus with Fig. 17 where a reduction in both the (\({\text{C}}_{d}\)) and (\({\text{C}}_{l}\)) are seen for the CVG and DVG cases compared to the baseline case, whereas, with the TVGs, a significant increase in aerodynamic coefficients is seen.
As soon as some yawing is introduced (β = 2º), a favourable transition appears with the TVGs, wherein some regions over the slant experience higher values of \(({\text{C}}_{{\text{p}}}\)) suggesting a delay in separation than compared to (β = 0º). In comparison with the baseline and the DVG cases for (β = 2º and 4º), the \(({\text{C}}_{{\text{p}}}\)) distribution over the slant with the TVGs is better although with the CVGs the distribution is more reassuring. Therefore, a reduction in (\({\mathrm{C}}_{d}\)) is seen for (β = 2º and 4º) for all VGs compared to the baseline case as seen in Fig. 17a. There appears to be a transition point at (β = 4º) beyond which (β > 4º) the downforce for all the VGs is increasingly penalized as given in Fig. 17b but less so with the CVGs until (β = 6º). For (β = 8º), the base pressure is higher and more uniform with CVGs and especially with the TVGs than compared to the baseline case, perhaps, a reduction in (\({\text{C}}_{d}\)) is expected to be a direct consequence of this as seen in Fig. 17a. However, the pressure on the slant is significantly lower and non-uniform for all VGs and especially with CVGs, suggesting that a disadvantage in downforce is expected owing to the increase in (\({\text{C}}_{l}\)) as shown in Fig. 17b.
5.4 Streamwise trailing vortices behind VGs
The VGs installed on the baseline model are expected to generate streamwise vortices, which in turn generate high-amplitude streaks in the flow given by Fransson et al. [23], Pujals et al. [46]. These structures, viz. the streaks and streamwise vortices, relate to each other by the lift-up effect as given by Brandt [8]. To visualize the streamwise vortical structures produced by the VGs, we adopt the swirling strength (S) to examine the local behaviour as shown in Fig. 18. Proposed by Zhou et al. [59], this method is frame independent and eliminates the difficulty of choosing a frame of reference. To visualize the vortices, we have used the iso-surfaces of the swirling strength (S) using the imaginary part of the complex eigenvalue of the velocity gradient tensor given by Zhou et al. [59] given as follows:
The numerical result of the swirling strength (S = 1160 s−1) coloured by TKE; the surface \({(\mathrm{C}}_{\mathrm{p}}\)) distribution is superimposed on all the figures seen from View 2 for cases with vortex generators. Cases (a'-c') represent the cases with DVGs, CVGs and TVGs for (β = 2º), whereas the cases (a''–c'') represent cases with DVG, CVG and TVG for (β = 6º)
where \(\lambda_{r}\) is the real eigenvalue with a real eigenvector \(\vec{v}_{r}\), and \(\lambda_{cr} \pm \lambda_{ci}\) are the conjugate pair of the complex eigenvectors \(\vec{v}_{cr} \pm \vec{v}_{ci}\). By expressing the local streamlines in a coordinate system spanned by the three vectors \(\left( {\vec{v}_{r} , \vec{v}_{cr} , \vec{v}_{ci} } \right),\) depending on the nature of the flow, one may see that the local flow is either stretched or compressed along the axis \(\vec{v}_{r}\) while on the plane spanned by the vectors \(\vec{v}_{cr}\) and \(\vec{v}_{ci}\) the flow is swirling. The \(\lambda_{ci}\) value is positive only if the discriminant is positive and its value represents the strength of swirling motion around local centres. For all cases in this study, the threshold of \(\lambda_{ci}\) was chosen to be 0.0015 for a smoother visualization of the near-wall vortical structures.
The iso-surface of \({\mathbf{S}}\) (coloured by TKE, together with the surface \(({\text{C}}_{{\text{p}}}\)) (shown in grey scale)) is extracted to represent the streamwise vortices generated by all VGs to investigate their performance at low and high values of (β). The streamwise counter-rotating vortices generated by the DVGs are elongated in comparison with that produced by TVGs and CVGs. In the case of CVGs, these streamwise trailing vortices appear to be shorter but ‘coherent’ even during higher yaw angles, which in turn influences the shear layer by delaying the separation on the slant. The same effect is also the case with the TVGs when (β = 6º). The overall effect of such consistency in the structure of streamwise vortices from CVGs, and TVGs demonstrate a decrease in (\({\mathrm{C}}_{d}\)) and at smaller yawing angles, some downforce advantage is also predicted as shown in Fig. 17b. Specifically, the maximum overall drag reduction achieved with the CVGs and TVGs for (β = 2º) is 8.43% and 7.69%, respectively, in reference to the baseline case. However, with the DVGs, with an increase in (β) Fig. 18a''), the high TKE closer to the leeward side appears to create higher-pressure footprint on the slant but is only adversely influenced by an initial massive separation at the roof owing to streamwise vortices interfering with the c-pillar vortex; this effect is undesirable, and therefore, the overall aerodynamic performance tends to decline.
6 Conclusions
The performance of several vortex generators placed on a 35º slant Ahmed body model subjected to yawing angles (β) has been numerically investigated. As a starting point, several RANS-based turbulence closures are examined as a rationality check, which shows good qualitative and reasonable quantitative comparisons for the baseline configuration against previously published experimental results for various (β). The validation of the numerical results is then followed by embedding the commonly employed, small vortex generators (VG) structures such as the delta-winglet (DVG), cylindrical (CVG) and trapezoidal (TVG) types on the baseline configuration subjected to different values of (β); the outcomes are as follows:
(1) The DVGs show beneficial trend in terms of drag reduction for (β ≤ 4º), beyond which the streamwise vortices produced by the DVGs tend to interfere with c-pillar vortex on the leeward side adversely. Besides, for (β = 0º), excellent downforce enhancement is predicted compared to the other VGs, an undesirable enhancement in (\({\mathrm{C}}_{l}\)) is predicted for (β ≥ 2º). The results suggest that the choice of DVGs could be a function of sweep angle as well as vehicle yaw (β) to be able to obtain an optimum overall aerodynamic performance.
(2) With the CVGs, high energy, streamwise trailing vortices appear to be more consistent in terms of their structure and tend to enhance the aerodynamic performance by potentially energizing the boundary layer, and therefore, the flow separation appears to be dampened. A net reduction in the overall (\({\mathrm{C}}_{d}\)) is predicted for all values of (β) compared to the baseline model with the maximum reduction of ~ 8.5% for (β = 2º). The overall (\({\mathrm{C}}_{l}\)) is reduced for (β ≤ 2º), but for values of (β > 4º), the downforce is penalized.
(3) Originally designed as a device for active drag reduction, the TVGs tend to underperform when (β = 0º) with the flow over the slant characterized by massive separation and with lower-pressure footprint over the base eventually enhancing both drag and lift. For the range of (β) values examined, besides for (β = 2º), they continue to enhance (\({\text{C}}_{l}\)) for the rest of the values. For (β > 0º), the TVGs exhibit a rapid transformation by producing highly consistent vortical structures similar to that predicted by the CVGs for incremental values of (β). Especially when (β ≥ 2º), the TVGs tend to either match or exhibit superior performance in reducing drag compared to the CVGs, DVGs and the baseline for incremental (β) values.
The outcomes presented in this work can potentially be extended to (a) examining the actuation characteristics of the VGs mentioned above during vehicle yawing conditions, (b) the effect of VGs and their interplay with other add-on devices such as spoilers and wings, and (c) possibly with high-fidelity simulations such as LES or hybrid LES-RANS methods [14, 15] to resolve the flow physics better.
Abbreviations
- A:
-
Constant that determines the width of the blending function
- A ref :
-
Reference area
- Cd, Cl :
-
Drag and lift coefficients
- Cp :
-
Surface pressure coefficient
- \(C_{\mu }\) :
-
Turbulence viscosity constant
- h:
-
Height of vortex generator
- k:
-
Turbulence kinetic energy
- \(l_{\varepsilon }\), \(l_{\mu }\) :
-
Definition of length scale(s)
- H:
-
Absolute helicity
- \({\mathbf{S}}\) :
-
Swirling strength
- L ref :
-
Reference length
- L :
-
Length of the baseline model
- P:
-
Calculated mean pressure
- \(P_{{ref}}\) :
-
Reference pressure
- U :
-
Inflow velocity
- U x*, U y, U z*:
-
Dimensionless velocity components
- U ref :
-
Free-stream (Reference) velocity
- Re L :
-
Reynolds number based on length
- N' 1 , N' 2 :
-
Centre(s) of the recirculation zone
- \(\vec{r}\) \(\overrightarrow {{r_{w} }}\) :
-
Position vectors at field points
- \(y^{ + }\) :
-
Dimensionless wall distance
- x, y, z :
-
Coordinate systems
- x*, y*, z*:
-
Coordinate systems non-dimensionalized by reference length
- α:
-
Slant angle
- β:
-
Yawing angle
- \(\delta\) :
-
Boundary layer thickness
- ε:
-
Turbulence dissipation rate
- \(\rho\) :
-
Density of air
- \(\mu\) :
-
Dynamic viscosity of air
- ω:
-
Specific turbulence dissipation rate
- \(\lambda _{\varepsilon }\) :
-
Blending function
- \(\mu _{t}\) :
-
Turbulence eddy viscosity
- \(\vec{\omega }\) :
-
Vorticity vector
- Ω:
-
Computational domain dimension
- VG:
-
Vortex generator
- CVG:
-
Cylindrical vortex generator
- DVG:
-
Delta-winglet vortex generator
- TVG:
-
Trapezoidal vortex generator
- TKE:
-
Turbulence kinetic energy
- RANS:
-
Reynolds-averaged Navier–Stokes
- RNG:
-
Re-normalization group
- SST:
-
Shear stress transport
- LES:
-
Large eddy simulations
- EWT:
-
Enhanced wall treatment
- FR:
-
Focus region
- DR:
-
Departure region
- MPs:
-
Metering points
- PBC:
-
Pressure-based coupled (Solver)
- SIMPLEC:
-
Semi-Implicit Method for Pressure Linked Equations-Consistent
References
Ahmed SR, Ramm G, Faltin G (1984) Some salient features of the time-averaged ground vehicle wake. SAE technical paper series. Presented at the SAE international congress and exposition.10.4271/840300
Aider J-L, Beaudoin J-F, Wesfreid JE (2009) Drag and lift reduction of a 3D bluff-body using active vortex generators. Exp Fluids 48(5):771–789. https://doi.org/10.1007/s00348-009-0770-y
ANSYS Fluent (2011) ANSYS fluent theory guide. ANSYS, USA
Ashton N, West A, Lardeau S, Revell A (2016) Assessment of RANS and DES methods for realistic automotive models. Comput Fluids 128:1–15. https://doi.org/10.1016/j.compfluid.2016.01.008
Barros D, Borée J, Noack BR, Spohn A, Ruiz T (2016) Bluff body drag manipulation using pulsed jets and coanda effect. J Fluid Mech 805:422–459. https://doi.org/10.1017/jfm.2016.508
Bellman M, Agarwal R, Naber J, Chusak, L (2010, January 1). Reducing energy consumption of ground vehicles by active flow control. ASME 2010 4th International conference on energy sustainability, Volume 1 ASME 2010 4th International Conference on Energy Sustainability. https://doi.org/10.1115/es2010-90363
Bounds CP, Zhang C, Uddin M (2020) Improved CFD prediction of flows past simplified and real-life automotive bodies using modified turbulence model closure coefficients. Proc Inst Mech Eng Part D: J Automob Eng 234(10–11):2522–2545. https://doi.org/10.1177/0954407020916671
Brandt L (2014) The lift-up effect: the linear mechanism behind transition and turbulence in shear flows. Eur J Mech B Fluids 47:80–96. https://doi.org/10.1016/j.euromechflu.2014.03.005
Brunn A, Nitsche W (2006) Active control of turbulent separated flows over slanted surfaces. Int J Heat Fluid Flow 27(5):748–755. https://doi.org/10.1016/j.ijheatfluidflow.2006.03.006
Chen HC, Patel VC (1988) Near-wall turbulence models for complex flows including separation. AIAA Journal 26(6):641–648. https://doi.org/10.2514/3.9948
Cheng SY, Mansor S (2017) Rear-roof spoiler effect on the aerodynamic drag performance of a simplified hatchback model. J Phys: Conf Ser 822:12008. https://doi.org/10.1088/1742-6596/822/1/012008
Cheng S-Y, Mansor S (2016) Influence of rear-roof spoiler on the aerodynamic performance of hatchback vehicle. MATEC Web of Conf 90:1027. https://doi.org/10.1051/matecconf/20179001027
Cheng S-Y, Chin K-Y, Mansor S, Abd Rahman AB (2019) Experimental study of yaw angle effect on the aerodynamic characteristics of a road vehicle fitted with a rear spoiler. J Wind Eng Ind Aerodyn 184:305–312. https://doi.org/10.1016/j.jweia.2018.11.033
Chode KK, Viswanathan H, Chow K (2020a). Computational aeroacoustics of a generic side view mirror using stress blended eddy simulation. preprint: arXiv:2007.12783
Chode KK, Viswanathan H, Chow K (2020) Numerical investigation on the salient features of flow over standard notchback configurations using scale resolving simulations. Comput Fluids 210:104666. https://doi.org/10.1016/j.compfluid.2020.104666
Choi H, Lee J, Park H (2014) Aerodynamics of Heavy Vehicles. Annu Rev Fluid Mech 46(1):441–468. https://doi.org/10.1146/annurev-fluid-011212-140616
Evrard A, Cadot O, Herbert V, Ricot D, Vigneron R, Délery J (2016) Fluid force and symmetry breaking modes of a 3D bluff body with a base cavity. J Fluids Struct 61:99–114. https://doi.org/10.1016/j.jfluidstructs.2015.12.001
Evrard A, Cadot O, Sicot C, Herbert V, Ricot D, Vigneron R (2017) Comparative effects of vortex generators on Ahmed’s squareback and minivan car models. Proc Inst Mech Eng Part D: J Automob Eng 231(9):1287–1293. https://doi.org/10.1177/0954407016681696
Evstafyeva O, Morgans AS, Dalla Longa L (2017) Simulation and feedback control of the Ahmed body flow exhibiting symmetry breaking behaviour. J Fluid Mech. https://doi.org/10.1017/jfm.2017.118
Fares E (2006) Unsteady flow simulation of the ahmed reference body using a lattice boltzmann approach. Comput Fluids 35(8–9):940–950. https://doi.org/10.1016/j.compfluid.2005.04.011
Filip G, Maki K, Bachant P, Lietz R (2018, April 3). Simulation of flow control devices in support of vehicle drag reduction. SAE technical paper series. WCX World Congress Experience. https://doi.org/10.4271/2018-01-0713
Fourrié G, Keirsbulck L, Labraga L, Gilliéron P (2010) Bluff-body drag reduction using a deflector. Exp Fluids 50(2):385–395. https://doi.org/10.1007/s00348-010-0937-6
Fransson JHM, Talamelli A, Brandt L, Cossu C (2006) Delaying transition to turbulence by a passive mechanism. Phys Rev Lett. https://doi.org/10.1103/physrevlett.96.064501
Grandemange M, Gohlke M, Cadot O (2013) Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability. J Fluid Mech 722:51–84. https://doi.org/10.1017/jfm.2013.83
Guilmineau E, Deng GB, Leroyer A, Queutey P, Visonneau M, Wackers J (2018) Assessment of hybrid RANS-LES formulations for flow simulation around the Ahmed body. Comput Fluids 176:302–319. https://doi.org/10.1016/j.compfluid.2017.01.005
Han X, Krajnović S, Basara B (2013) Study of active flow control for a simplified vehicle model using the PANS method. Int J Heat Fluid Flow 42:139–150. https://doi.org/10.1016/j.ijheatfluidflow.2013.02.001
Jongen T (1992). Simulation and modeling of turbulent incompressible flows. PhD thesis, EPF Lausanne, Lausanne, Switzerland
Joseph P, Amandolese X, Edouard C, Aider J-L (2013) Flow control using MEMS pulsed micro-jets on the Ahmed body. Exp Fluids. https://doi.org/10.1007/s00348-012-1442-x
Kader BA (1981) Temperature and concentration profiles in fully turbulent boundary layers. Int J Heat Mass Transf 24(9):1541–1544. https://doi.org/10.1016/0017-9310(81)90220-9
Katz J (2006) Aerodynamics of race cars. Annu Rev Fluid Mech 38(1):27–63. https://doi.org/10.1146/annurev.fluid.38.050304.092016
Katz J, Morey F (2008) Aerodynamics of large-scale vortex generator in ground effect. J Fluids Eng 10(1115/1):2948361
Keating M (2011) Accelerating CFD solutions. ANSYS Advant. 5(1):48–49
Koike M, Nagayoshi T, Hamamoto N (2004) Research on aerodynamic drag reduction by vortex generators. Mitsubishi Motors Tech Rev 16:11–16
Kourta A, Leclerc C (2013) Characterization of synthetic jet actuation with application to ahmed body wake. Sens Actuators A 192:13–26. https://doi.org/10.1016/j.sna.2012.12.008
Krajnović S (2014) Large eddy simulation exploration of passive flow control around an ahmed body. J Fluids Eng 10(1115/1):4027221
Krajnović S, Davidson L (2004). Large-eddy simulation of the flow around simplified car model. SAE Technical Paper Series. SAE 2004 World Congress and Exhibition. https://doi.org/10.4271/2004-01-0227
Kuya Y, Takeda K, Zhang X, Beeton S, Pandaleon T (2009) Flow separation control on a race car wing with vortex generators in ground effect. J Fluids Eng. https://doi.org/10.1115/1.4000420
Lanfrit M (2005). Best practice guideline for handling automotive external aerodynamics with FLUENT. Technical report. ANSYS, Inc
Li Y, Cui W, Jia Q, Li Q, Yang Z, Noack BR (2019). Optimization of active drag reduction for a slanted Ahmed body in a high-dimensional parameter space. preprint arXiv:1905.12036
Lienhart H, Becker S (2003). Flow and turbulence structure in the wake of a simplified car model. SAE technical paper series. Presented at the SAE 2003 World Congress and Exhibition. https://doi.org/10.4271/2003-01-0656
Lucas J-M, Cadot O, Herbert V, Parpais S, Délery J (2017) A numerical investigation of the asymmetric wake mode of a squareback Ahmed body–effect of a base cavity. J Fluid Mech 831:675–697. https://doi.org/10.1017/jfm.2017.654
Meile W, Brenn G, Reppenhagen A, Lechner B, Fuchs A (2011) Experiments and numerical simulations on the aerodynamics of the ahmed body. CFD Lett. 3(1):32–39
Meile W, Ladinek T, Brenn G, Reppenhagen A, Fuchs A (2016) Non-symmetric bi-stable flow around the Ahmed body. Int J Heat Fluid Flow 57:34–47. https://doi.org/10.1016/j.ijheatfluidflow.2015.11.002
Menter FR (1994) Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J 32(8):1598–1605. https://doi.org/10.2514/3.12149
Pastoor M, Henning L, Noack BR, King R, Tadmor G (2008) Feedback shear layer control for bluff body drag reduction. J Fluid Mech 608:161–196. https://doi.org/10.1017/s0022112008002073
Pujals G, Depardon S, Cossu C (2010) Drag reduction of a 3D bluff body using coherent streamwise streaks. Exp Fluids 49(5):1085–1094. https://doi.org/10.1007/s00348-010-0857-5
Read C, Viswanathan H (2020) An aerodynamic assessment of vehicle side wall interaction using numerical simulations. Int J Automot Mech Eng 17(1):7587–7598
Rossitto G, Sicot C, Ferrand V, Borée J, Harambat F (2016) Influence of afterbody rounding on the pressure distribution over a fastback vehicle. Exp Fluids. https://doi.org/10.1007/s00348-016-2120-1
Roy A, Dasgupta D (2020) Towards a novel strategy for safety stability and driving dynamics enhancement during cornering manoeuvres in motorsports applications. Sci Rep. https://doi.org/10.1038/s41598-020-63243-w
Shahinfar S, Sattarzadeh SS, Fransson JHM, Talamelli A (2012) Revival of Classical Vortex Generators Now for Transition Delay. Phys Rev Lett. https://doi.org/10.1103/physrevlett.109.074501
Shih T-H, Liou WW, Shabbir A, Yang Z, Zhu J (1995) A new k-ϵ eddy viscosity model for high Reynolds number turbulent flows. Comput Fluids 24(3):227–238. https://doi.org/10.1016/0045-7930(94)00032-t
Spalart, P. R. (2001). Young person’s guide to detached-eddy simulation grids. Tech. Rep NASA CR-2001–211032.Langley Res. Center, Hampton, Va. http://techreports.larc.nasa.gov/ltrs/PDF/2001/cr/NASA-2001-cr211032.pdf
Thacker A, Aubrun S, Leroy A, Devinant P (2012) Effects of suppressing the 3D separation on the rear slant on the flow structures around an Ahmed body. J Wind Eng Ind Aerodyn 107–108:237–243. https://doi.org/10.1016/j.jweia.2012.04.022
Wang S, Ghaemi S (2019) Effect of vane sweep angle on vortex generator wake. Exp Fluids. https://doi.org/10.1007/s00348-018-2666-1
Wolfshtein M (1969) The velocity and temperature distribution in one-dimensional flow with turbulence augmentation and pressure gradient. Int J Heat Mass Transf 12(3):301–318. https://doi.org/10.1016/0017-9310(69)90012-x
Yakhot V, Orszag SA, Thangam S, Gatski TB, Speziale CG (1992) Development of turbulence models for shear flows by a double expansion technique. Phys Fluids A 4(7):1510–1520. https://doi.org/10.1063/1.858424
Zhang BF, Zhou Y, To S (2015) Unsteady flow structures around a high-drag ahmed body. J Fluid Mech 777:291–326. https://doi.org/10.1017/jfm.2015.332
Zhang B, Liu K, Zhou Y, To S, Tu J (2018) Active drag reduction of a high-drag ahmed body based on steady blowing. J Fluid Mech 856:351–396. https://doi.org/10.1017/jfm.2018.703
Zhou J, Adrian RJ, Balachandar S, Kendall TM (1999) Mechanisms for generating coherent packets of hairpin vortices in channel flow. J Fluid Mech 387:353–396. https://doi.org/10.1017/s002211209900467x
Acknowledgements
The author thanks Dr Cheng See-Yuan of the Universiti Teknikal Malaysia, Melaka, for sharing the experimental data for comparison purposes. The author wishes to thank Mr Steven Brandon for the CAD support and Mr Anthony Owers for helping with the initial design of the Delta Vortex Generators. This work was supported by ANSYS Academic Research Partnership Grant.
Author information
Authors and Affiliations
Corresponding author
Additional information
Technical Editor: André Cavalieri.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Viswanathan, H. Aerodynamic performance of several passive vortex generator configurations on an Ahmed body subjected to yaw angles. J Braz. Soc. Mech. Sci. Eng. 43, 131 (2021). https://doi.org/10.1007/s40430-021-02850-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40430-021-02850-8