Finite element and numerical vibration analysis of a Timoshenko and Euler–Bernoulli beams traversed by a moving high-speed train

Abstract

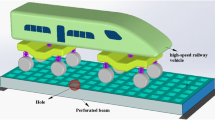
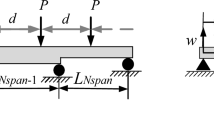
In this paper, two different numerical methods are presented for the dynamic response of Euler–Bernoulli and Timoshenko beam under the impact of 10-DOF high-speed train (HST). Bridge beam is modeled in simply supported and uniform structure. The train traveling at high and constant speed on the bridge is modeled by taking into consideration primary and secondary suspension systems. The motion equation of the system was obtained using the Hamilton principle. These differential equations have been solved in the time domain using the fourth-order Runge–Kutta algorithm. The motion equations of the system have been converted to finite element format using Galerkin’s weak-form formulation. The finite element solution of the system was solved using the Newmark-β algorithm, and both algorithms were compared. In addition, Timoshenko beam theory and Euler–Bernoulli beam theory presented in the study were compared in terms of both bridge dynamics and train dynamics. As a result, although the speed difference between the two theories is significant at the critical speed values of HST, this difference in certain speed values decreases considerably.

Appendices

Appendix A.

These ten two-degree equations which represent HST dynamic are reduced to twenty first-degree equations by using the variables given with Eq. (A.1).

$$\begin{array}{*{20}c} {x_{1} = r_{1} \Rightarrow \dot{x}_{1} = \dot{r}_{1} = x_{2} } & {x_{8} = \dot{r}_{4} \Rightarrow \dot{x}_{8} = \ddot{r}_{4} } & { \, x_{15} = r_{8} \Rightarrow \dot{x}_{15} = \dot{r}_{8} = x_{16} } \\ {x_{2} = \dot{r}_{1} \Rightarrow \dot{x}_{2} = \ddot{r}_{1} } & {x_{9} = r_{5} \Rightarrow \dot{x}_{9} = \dot{r}_{5} = x_{10} } & { \, x_{16} = \dot{r}_{8} \Rightarrow \dot{x}_{16} = \ddot{r}_{8} } \\ {x_{3} = r_{2} \Rightarrow \dot{x}_{3} = \dot{r}_{2} = x_{4} } & {x_{10} = \dot{r}_{5} \Rightarrow \dot{x}_{10} = \ddot{r}_{5} } & { \, x_{17} = r_{9} \Rightarrow \dot{x}_{17} = \dot{r}_{9} = x_{18} } \\ {x_{4} = \dot{r}_{2} \Rightarrow \dot{x}_{4} = \ddot{r}_{2} } & {x_{11} = r_{6} \Rightarrow \dot{x}_{11} = \dot{r}_{6} = x_{12} } & { \, x_{18} = \dot{r}_{9} \Rightarrow \dot{x}_{18} = \ddot{r}_{9} } \\ {x_{5} = r_{3} \Rightarrow \dot{x}_{5} = \dot{r}_{3} = x_{6} } & {x_{12} = \dot{r}_{6} \Rightarrow \dot{x}_{12} = \ddot{r}_{6} } & { \, x_{19} = r_{10} \Rightarrow \dot{x}_{19} = \dot{r}_{10} = x_{20} } \\ {x_{6} = \dot{r}_{3} \Rightarrow \dot{x}_{6} = \ddot{r}_{3} } & { \, x_{13} = r_{7} \Rightarrow \dot{x}_{13} = \dot{r}_{7} = x_{14} } & { \, x_{20} = \dot{r}_{10} \Rightarrow \dot{x}_{20} = \ddot{r}_{10} } \\ {x_{7} = r_{4} \Rightarrow \dot{x}_{7} = \dot{r}_{4} = x_{8} } & {x_{14} = \dot{r}_{7} \Rightarrow \dot{x}_{14} = \ddot{r}_{7} } & {} \\ \end{array}$$

(A.1)

The state variables for the Euler–Bernoulli bridge beam are written as follows:

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{21} = q_{1} \Rightarrow \dot{x}_{21} = \dot{q}_{1} = x_{22} } & {x_{25} = q_{3} \Rightarrow \dot{x}_{25} = \dot{q}_{3} = x_{26} } \\ {x_{22} = \dot{q}_{1} \Rightarrow \dot{x}_{22} = \ddot{q}_{1} } & {x_{26} = \dot{q}_{3} \Rightarrow \dot{x}_{26} = \ddot{q}_{3} } \\ {x_{23} = q_{2} \Rightarrow \dot{x}_{23} = \dot{q}_{2} = x_{24} } & {x_{27} = q_{4} \Rightarrow \dot{x}_{27} = \dot{q}_{3} = x_{28} } \\ {x_{24} = \dot{q}_{2} \Rightarrow \dot{x}_{24} = \ddot{q}_{2} } & {x_{28} = \dot{q}_{4} \Rightarrow \dot{x}_{28} = \ddot{q}_{4} } \\ \end{array} } \\ {} \\ \end{array} \,$$

(A.2)

The state variables for the Timoshenko bridge beam are written as follows:

$$\begin{aligned} \begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{21} = q_{1} \Rightarrow \dot{x}_{21} = \dot{q}_{1} = x_{22} } & {x_{25} = q_{3} \Rightarrow \dot{x}_{25} = \dot{q}_{3} = x_{26} } \\ {x_{22} = \dot{q}_{1} \Rightarrow \dot{x}_{22} = \ddot{q}_{1} } & {x_{26} = \dot{q}_{3} \Rightarrow \dot{x}_{26} = \ddot{q}_{3} } \\ {x_{23} = q_{2} \Rightarrow \dot{x}_{23} = \dot{q}_{2} = x_{24} } & {x_{27} = q_{4} \Rightarrow \dot{x}_{27} = \dot{q}_{3} = x_{28} } \\ {x_{24} = \dot{q}_{2} \Rightarrow \dot{x}_{24} = \ddot{q}_{2} } & {x_{28} = \dot{q}_{4} \Rightarrow \dot{x}_{28} = \ddot{q}_{4} } \\ \end{array} } \\ {} \\ \end{array} \, \hfill \\ \begin{array}{*{20}c} {x_{29} = \theta_{1} \Rightarrow \dot{x}_{29} = \dot{\theta }_{1} = x_{30} } & {x_{33} = \theta_{3} \Rightarrow \dot{x}_{33} = \dot{\theta }_{3} = x_{34} } \\ {x_{30} = \dot{\theta }_{1} \Rightarrow \dot{x}_{30} = \ddot{\theta }_{1} } & {x_{34} = \dot{\theta }_{3} \Rightarrow \dot{x}_{34} = \ddot{\theta }_{3} } \\ {x_{31} = \theta_{2} \Rightarrow \dot{x}_{31} = \dot{\theta }_{2} = x_{32} } & {x_{35} = \theta_{4} \Rightarrow \dot{x}_{35} = \dot{\theta }_{43} = x_{36} } \\ {x_{32} = \dot{\theta }_{2} \Rightarrow \dot{x}_{32} = \ddot{\theta }_{2} } & {x_{36} = \dot{\theta }_{4} \Rightarrow \dot{x}_{36} = \ddot{\theta }_{4} } \\ \end{array} \, \hfill \\ \end{aligned}$$

(A.3)

When Eqs. (11a-j) are written in state space form with state variables given by Eqs. (A.1–3), together with the motions of equation belonging to other coordinates, the following is obtained:

$${\dot{\mathbf{X}}}(t) = {\mathbf{A}}(t){\mathbf{X}}(t) + {\mathbf{f}}(t),$$

(A.4)

$${\mathbf{X}}(t) = \left\{ \begin{aligned} x_{1} \, x_{2} \, x_{3} \, x_{4} \, x_{5} \, x_{6} \, x_{7} \, x_{8} \, x_{9} \, x_{10} \, x_{11} \, \ldots \hfill \\ \, x_{12} \, x_{13} \, x_{14} \, x_{15} \, x_{16} \, x_{17} \, x_{18} \, x_{19} \, x_{20} \, x_{20 + (2n - 1)} \, x_{20 + 2n} \hfill \\ \end{aligned} \right\}^{T} ,$$

(A.5)

Four repetitive coefficients of Runge–Kutta method are written as follows for the differential equation system, comprising of a total of twenty first-degree differential equations:

$$\begin{aligned} k_{1(1)}^{i} = f\left( {t_{i} ,x_{1(i)} , \, x_{2(i)} , \, x_{3(i)} ,\ldots,x_{20 + 2n(i)} } \right), \hfill \\ \vdots \hfill \\ k_{1(20 + 2n)}^{i} = f\left( {t_{i} ,x_{1(i)} , \, x_{2(i)} , \, x_{3(i)} ,\ldots,x_{20 + 2n(i)} } \right), \hfill \\ \end{aligned}$$

(A.6)

$$\begin{aligned} k_{2(1)}^{i} = f\left( {t_{i} + \frac{1}{2}\Delta t,x_{1(i)} + \frac{1}{2}k_{1(1)}^{i} \Delta t, \, x_{2(i)} + \frac{1}{2}k_{1(2)}^{i} \Delta t, \, x_{3(i)} + \frac{1}{2}k_{1(3)}^{i} \Delta t,\ldots,x_{20 + 2n(i)} + \frac{1}{2}k_{1(20 + 2n)}^{i} \Delta t} \right), \hfill \\ \vdots \hfill \\ k_{2(20 + 2n)}^{i} = f\left( {t_{i} + \frac{1}{2}\Delta t,x_{1(i)} + \frac{1}{2}k_{1(1)}^{i} \Delta t, \, x_{2(i)} + \frac{1}{2}k_{1(2)}^{i} \Delta t, \, x_{3(i)} + \frac{1}{2}k_{1(3)}^{i} \Delta t,\ldots,x_{20 + 2n(i)} + \frac{1}{2}k_{1(20 + 2n)}^{i} \Delta t} \right), \hfill \\ \end{aligned}$$

(A.7)

$$\begin{aligned} k_{3(1)}^{i} = f\left( {t_{i} + \frac{1}{2}\Delta t,x_{1(i)} + \frac{1}{2}k_{2(1)}^{i} \Delta t, \, x_{2(i)} + \frac{1}{2}k_{2(2)}^{i} \Delta t, \, x_{3(i)} + \frac{1}{2}k_{2(3)}^{i} \Delta t,\ldots,x_{20 + 2n(i)} + \frac{1}{2}k_{2(20 + 2n)}^{i} \Delta t} \right), \hfill \\ \vdots \hfill \\ k_{3(20 + 2n)}^{i} = f\left( {t_{i} + \frac{1}{2}\Delta t,x_{1(i)} + \frac{1}{2}k_{2(1)}^{i} \Delta t, \, x_{2(i)} + \frac{1}{2}k_{2(2)}^{i} \Delta t, \, x_{3(i)} + \frac{1}{2}k_{2(3)}^{i} \Delta t,\ldots,x_{12 + 2n(i)} + \frac{1}{2}k_{2(20 + 2n)}^{i} \Delta t} \right), \hfill \\ \end{aligned}$$

(A.8)

$$\begin{aligned} k_{4(1)}^{i} = f\left( {t_{i} + \Delta t,x_{1(i)} + k_{3(1)}^{i} \Delta t, \, x_{2(i)} + k_{3(2)}^{i} \Delta t, \, x_{3(i)} + k_{3(3)}^{i} \Delta t,\ldots,x_{20 + 2n(i)} + k_{3(20 + 2n)}^{i} \Delta t} \right), \hfill \\ \vdots \hfill \\ k_{4(20 + 2n)}^{i} = f\left( {t_{i} + \Delta t,x_{1(i)} + k_{3(1)}^{i} \Delta t, \, x_{2(i)} + k_{3(2)}^{i} \Delta t, \, x_{3(i)} + k_{3(3)}^{i} \Delta t,\ldots,x_{20 + 2n(i)} + k_{3(20 + 2n)}^{i} \Delta t} \right), \hfill \\ \end{aligned}$$

(A.9)

Numerical analysis is realized as follows: At t = 0, i.e., the i th iteration, the train’s first wheel is not yet entered the bridge and stands on the left edge of the bridge. At that time, all initial conditions are considered as zero, with X = {0, 0, 0, …, 0}_36x1, and the coefficients given in Eq. (A.1–3) Δt time passes and the new values at (i + 1).iteration as a result of the entrance of the front axle to the bridge, are calculated by using Eq. (A.10). These values calculated for (i + 1).iteration will be considered as the initial condition for (i + 2) and the same is repeated until the last wheel of the vehicle leaves the bridge.

$$\begin{aligned} x_{1(i + 1)} =& x_{1(i)} + \frac{\Delta t}{6}\left( {k_{1(1)}^{i} + 2k_{2(1)}^{i} + 2k_{3(1)}^{i} + k_{4(1)}^{i} } \right) \hfill \\ x_{2(i + 1)} = &x_{2(i)} + \frac{\Delta t}{6}\left( {k_{1(2)}^{i} + 2k_{2(2)}^{i} + 2k_{3(2)}^{i} + k_{4(2)}^{i} } \right) \hfill \\ \vdots \hfill \\ x_{(20 + 2n)(i + 1)} =& x_{(20 + 2n)(i)} + \frac{\Delta t}{6}\left( k_{1(20 + 2n)}^{i} + 2k_{2(20 + 2n)}^{i} \right. \\ & \left.+ 2k_{3(20 + 2n)}^{i} + k_{4(20 + 2n)}^{i} \right) \hfill \\ \end{aligned}$$

(A.10)

Appendix B.

The finite element formulation representing the train bridge interaction is given by Eq. (21). In Eq. (21), the M_v is the mass matrix of the equation representing the train bridge integrated system. The mass matrix of TBI system is given by Eq. (B.1).

$${\mathbf{M}}_{{\mathbf{v}}} = \left[ {\begin{array}{*{20}c} {\frac{{\rho Al_{e} }}{3}} & 0 & {\frac{{\rho Al_{e} }}{6}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {\frac{{\rho Il_{e} }}{3}} & 0 & {\frac{{\rho Il_{e} }}{6}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {\frac{{\rho Al_{e} }}{6}} & 0 & {\frac{{\rho Al_{e} }}{3}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {\frac{{\rho Il_{e} }}{6}} & 0 & {\frac{{\rho Il_{e} }}{3}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {m_{c} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {I_{c} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {m_{b1} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {I_{b1} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {m_{b2} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {I_{b2} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {m_{w1} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {m_{w2} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {m_{w3} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {m_{w4} } \\ \end{array} } \right]$$

(B.1)

In Eq. (21), the parameters K_v and C_v represent the stiffness and damping matrices of the equation representing the train bridge integrated system. The stiffness and damping matrices of TBI system are given by Eqs. (B.2–3).

$${\mathbf{K}}_{v} = \left[ {\begin{array}{*{20}c} {\frac{{K_{s} AG}}{{l_{e} }} + \left\{ \begin{aligned} \alpha_{1} + \alpha \alpha_{1} \hfill \\ \beta_{1} + \beta \beta_{1} \hfill \\ \end{aligned} \right\}} & {\frac{ - 1}{2}K_{s} AG} & {\frac{{ - K_{s} AG}}{{l_{e} }} + \left\{ \begin{aligned} \alpha_{2} + \alpha \alpha_{2} \hfill \\ \beta_{2} + \beta \beta_{2} \hfill \\ \end{aligned} \right\}} & {\frac{ - 1}{2}K_{s} AG} & 0 & 0 & 0 & 0 & 0 & 0 & { - \alpha_{4} } & { - \alpha \alpha_{4} } & { - \beta_{4} } & { - \beta \beta_{4} } \\ {\frac{ - 1}{2}K_{s} AG} & {\frac{1}{4}K_{s} AGl_{e} + \frac{EI}{{l_{e} }}} & {\frac{1}{2}K_{s} AG} & {\frac{1}{4}K_{s} AGl_{e} - \frac{EI}{{l_{e} }}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {\frac{{ - K_{s} AG}}{{l_{e} }} + \left\{ \begin{aligned} \alpha_{2} + \alpha \alpha_{2} \hfill \\ \beta_{2} + \beta \beta_{2} \hfill \\ \end{aligned} \right\}} & {\frac{1}{2}K_{s} AG} & {\frac{{K_{s} AG}}{{l_{e} }} + \left\{ \begin{aligned} \alpha_{3} + \alpha \alpha_{3} \hfill \\ \beta_{3} + \beta \beta_{3} \hfill \\ \end{aligned} \right\}} & {\frac{1}{2}K_{s} AG} & 0 & 0 & 0 & 0 & 0 & 0 & { - \alpha_{5} } & { - \alpha \alpha_{5} } & { - \beta_{5} } & { - \beta \beta_{5} } \\ {\frac{ - 1}{2}K_{s} AG} & {\frac{1}{4}K_{s} AGl_{e} - \frac{EI}{{l_{e} }}} & {\frac{1}{2}K_{s} AG} & {\frac{1}{4}K_{s} AGl_{e} + \frac{EI}{{l_{e} }}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {k_{v1} + k_{v2} } & {k_{v1} l_{1} - k_{v2} l_{2} } & { - k_{v1} } & 0 & { - k_{v2} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {k_{v1} l_{1} - k_{v2} l_{2} } & {k_{v1} l_{1}^{2} + k_{v2} l_{2}^{2} } & { - k_{v1} l_{1} } & 0 & {k_{v2} l_{2} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & { - k_{v1} } & { - k_{v1} l_{1} } & {k_{v1} + k_{w1} + k_{w2} } & {k_{w1} d_{1} - k_{w2} d_{1} } & 0 & 0 & { - k_{w1} } & { - k_{w2} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {k_{w1} d_{1} - k_{w2} d_{1} } & {k_{w1} d_{1}^{2} + k_{w2} d_{1}^{2} } & 0 & 0 & { - k_{w1} d_{1} } & {k_{w2} d_{1} } & 0 & 0 \\ 0 & 0 & 0 & 0 & { - k_{v2} } & {k_{v2} l_{2} } & 0 & 0 & {k_{w3} + k_{w4} + k_{v2} } & {k_{w3} d_{3} - k_{w4} d_{3} } & 0 & 0 & { - k_{w3} } & { - k_{w4} } \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {k_{w3} d_{3} - k_{w4} d_{3} } & {k_{w3} d_{3}^{2} + k_{w4} d_{3}^{2} } & 0 & 0 & { - k_{w3} d_{3} } & {k_{w4} d_{3} } \\ { - \alpha_{4} } & 0 & { - \alpha_{5} } & 0 & 0 & 0 & { - k_{w1} } & { - k_{w1} d_{1} } & 0 & 0 & {k_{w1} + k_{r1} } & 0 & 0 & 0 \\ { - \alpha \alpha_{4} } & 0 & { - \alpha \alpha_{5} } & 0 & 0 & 0 & { - k_{w2} } & {k_{w2} d_{1} } & 0 & 0 & 0 & {k_{w2} + k_{r2} } & 0 & 0 \\ { - \beta_{4} } & 0 & { - \beta_{5} } & 0 & 0 & 0 & 0 & 0 & { - k_{w3} } & { - k_{w3} d_{3} } & 0 & 0 & {k_{w3} + k_{r3} } & 0 \\ { - \beta \beta_{4} } & 0 & { - \beta \beta_{5} } & 0 & 0 & 0 & 0 & 0 & { - k_{w4} } & {k_{w4} d_{3} } & 0 & 0 & 0 & {k_{w4} + k_{r4} } \\ \end{array} } \right]$$

(B.2)

$${\mathbf{C}}_{{\mathbf{v}}} = \left[ {\begin{array}{*{20}c} {\frac{{cl_{e} }}{3} + \left\{ \begin{aligned} \varepsilon_{1} + \varepsilon \varepsilon_{1} \hfill \\ \gamma_{1} + \gamma \gamma_{1} \hfill \\ \end{aligned} \right\}} & 0 & {\frac{{cl_{e} }}{6} + \left\{ \begin{aligned} \varepsilon_{2} + \varepsilon \varepsilon_{2} \hfill \\ \gamma_{2} + \gamma \gamma_{2} \hfill \\ \end{aligned} \right\}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & { - \varepsilon_{4} } & { - \varepsilon \varepsilon_{4} } & { - \gamma_{4} } & { - \gamma \gamma_{4} } \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {\frac{{cl_{e} }}{6} + \left\{ \begin{aligned} \varepsilon_{2} + \varepsilon \varepsilon_{2} \hfill \\ \gamma_{2} + \gamma \gamma_{2} \hfill \\ \end{aligned} \right\}} & 0 & {\frac{{cl_{e} }}{3} + \left\{ \begin{aligned} \varepsilon_{3} + \varepsilon \varepsilon_{3} \hfill \\ \gamma_{3} + \gamma \gamma_{3} \hfill \\ \end{aligned} \right\}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & { - \varepsilon_{5} } & { - \varepsilon \varepsilon_{5} } & { - \gamma_{5} } & { - \gamma \gamma_{5} } \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {c_{v1} + c_{v2} } & {c_{v1} l_{1} - c_{v2} l_{2} } & { - c_{v1} } & 0 & { - c_{v2} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {c_{v1} l_{1} - c_{v2} l_{2} } & {c_{v1} l_{1}^{2} + c_{v2} l_{2}^{2} } & { - c_{v1} l_{1} } & 0 & {c_{v2} l_{2} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & { - c_{v1} } & { - c_{v1} l_{1} } & {c_{v1} + c_{w1} + c_{w2} } & {c_{w1} d_{1} - c_{w2} d_{1} } & 0 & 0 & { - c_{w1} } & { - c_{w2} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {c_{w1} d_{1} - c_{w2} d_{1} } & {c_{w1} d_{1}^{2} + c_{w2} d_{1}^{2} } & 0 & 0 & { - c_{w1} d_{1} } & {c_{w2} d_{1} } & 0 & 0 \\ 0 & 0 & 0 & 0 & { - c_{v2} } & {c_{v2} l_{3} } & 0 & 0 & {c_{w3} + c_{w4} + c_{v2} } & {c_{w3} d_{3} - c_{w4} d_{3} } & 0 & 0 & { - c_{w3} } & { - c_{w4} } \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {c_{w3} d_{3} - c_{w4} d_{3} } & {c_{w3} d_{3}^{2} + c_{w4} d_{3}^{2} } & 0 & 0 & { - c_{w3} d_{3} } & {c_{w4} d_{3} } \\ { - \varepsilon_{4} } & 0 & { - \varepsilon_{5} } & 0 & 0 & 0 & { - c_{w1} } & { - c_{w1} d_{1} } & 0 & 0 & {c_{w1} + c_{r1} } & 0 & 0 & 0 \\ { - \varepsilon \varepsilon_{4} } & 0 & { - \varepsilon \varepsilon_{5} } & 0 & 0 & 0 & { - c_{w2} } & {c_{w2} d_{1} } & 0 & 0 & 0 & {c_{w2} + c_{r2} } & 0 & 0 \\ { - \gamma_{4} } & 0 & { - \gamma_{5} } & 0 & 0 & 0 & 0 & 0 & { - c_{w3} } & { - c_{w3} d_{3} } & 0 & 0 & {c_{w3} + c_{r3} } & 0 \\ { - \gamma \gamma_{4} } & 0 & { - \gamma \gamma_{5} } & 0 & 0 & 0 & 0 & 0 & { - c_{w4} } & {c{}_{w4}d_{3} } & 0 & 0 & 0 & {c_{w4} + c_{r4} } \\ \end{array} } \right]$$

(B.3)

In Eq. (B.2), the constant parameters related to the front bogie front wheel are given by:

$$\begin{array}{*{20}c} \begin{aligned} \alpha_{1} = \int_{0}^{l} {D_{1} } K_{r1} \varphi_{1}^{2} \delta^{*} \left( {x - \overline{\xi }_{1} } \right){\rm d}x \hfill \\ \alpha_{2} = \int_{0}^{l} {D_{1} } K_{r1} \varphi_{1} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{1} } \right){\rm d}x \hfill \\ \alpha_{3} = \int_{0}^{l} {D_{1} } K_{r1} \varphi_{2}^{2} \delta^{*} \left( {x - \overline{\xi }_{1} } \right){\rm d}x \hfill \\ \alpha_{4} = \int_{0}^{l} {D_{1} } K_{r1} \varphi_{1} \delta^{*} \left( {x - \overline{\xi }_{1} } \right){\rm d}x \hfill \\ \alpha_{5} = \int_{0}^{l} {D_{1} } K_{r1} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{1} } \right){\rm d}x \hfill \\ \end{aligned} & \begin{aligned} \varepsilon_{1} = \int_{0}^{l} {D_{1} } c_{r1} \varphi_{1}^{2} \delta^{*} \left( {x - \overline{\xi }_{1} } \right){\rm d}x \hfill \\ \varepsilon_{2} = \int_{0}^{l} {D_{1} } c_{r1} \varphi_{1} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{1} } \right){\rm d}x \hfill \\ \varepsilon_{3} = \int_{0}^{l} {D_{1} } c_{r1} \varphi_{2}^{2} \delta^{*} \left( {x - \overline{\xi }_{1} } \right){\rm d}x \hfill \\ \varepsilon_{4} = \int_{0}^{l} {D_{1} } c_{r1} \varphi_{1} \delta^{*} \left( {x - \overline{\xi }_{1} } \right){\rm d}x \hfill \\ \varepsilon_{5} = \int_{0}^{l} {D_{1} } c_{r1} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{1} } \right){\rm d}x \hfill \\ \end{aligned} \\ \end{array}$$

(B.4)

In Eq. (B.2), the constant parameters related to the front bogie rear wheel are given by:

$$\begin{array}{*{20}c} \begin{aligned} \alpha \alpha_{1} = \int_{0}^{l} {D_{2} } K_{r2} \varphi_{1}^{2} \delta^{*} \left( {x - \overline{\xi }_{2} } \right){\rm d}x \hfill \\ \alpha \alpha_{2} = \int_{0}^{l} {D_{2} } K_{r2} \varphi_{1} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{2} } \right){\rm d}x \hfill \\ \alpha \alpha_{3} = \int_{0}^{l} {D_{2} } K_{r2} \varphi_{2}^{2} \delta^{*} \left( {x - \overline{\xi }_{2} } \right){\rm d}x \hfill \\ \alpha \alpha_{4} = \int_{0}^{l} {D_{2} } K_{r2} \varphi_{1} \delta^{*} \left( {x - \overline{\xi }_{2} } \right){\rm d}x \hfill \\ \alpha \alpha_{5} = \int_{0}^{l} {D_{2} } K_{r2} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{2} } \right){\rm d}x \hfill \\ \end{aligned} & \begin{aligned} \varepsilon \varepsilon_{1} = \int_{0}^{l} {D_{2} } c_{r2} \varphi_{1}^{2} \delta^{*} \left( {x - \overline{\xi }_{2} } \right){\rm d}x \hfill \\ \varepsilon \varepsilon_{2} = \int_{0}^{l} {D_{2} } c_{r2} \varphi_{1} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{2} } \right){\rm d}x \hfill \\ \varepsilon \varepsilon_{3} = \int_{0}^{l} {D_{2} } c_{r2} \varphi_{2}^{2} \delta^{*} \left( {x - \overline{\xi }_{2} } \right){\rm d}x \hfill \\ \varepsilon \varepsilon_{4} = \int_{0}^{l} {D_{2} } c_{r2} \varphi_{1} \delta^{*} \left( {x - \overline{\xi }_{2} } \right){\rm d}x \hfill \\ \varepsilon \varepsilon_{5} = \int_{0}^{l} {D_{2} } c_{r2} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{2} } \right){\rm d}x \hfill \\ \end{aligned} \\ \end{array}$$

(B.5)

In Eq. (B.2), the constant parameters related to the rear bogie front wheel are given by:

$$\begin{array}{*{20}c} \begin{aligned} \beta_{1} = \int_{0}^{l} {D_{3} } K_{r3} \varphi_{1}^{2} \delta^{*} \left( {x - \overline{\xi }_{3} } \right){\rm d}x \hfill \\ \beta_{2} = \int_{0}^{l} {D_{3} } K_{r3} \varphi_{1} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{3} } \right){\rm d}x \hfill \\ \beta_{3} = \int_{0}^{l} {D_{3} } K_{r3} \varphi_{2}^{2} \delta^{*} \left( {x - \overline{\xi }_{3} } \right){\rm d}x \hfill \\ \beta_{4} = \int_{0}^{l} {D_{3} } K_{r3} \varphi_{1} \delta^{*} \left( {x - \overline{\xi }_{3} } \right){\rm d}x \hfill \\ \beta_{5} = \int_{0}^{l} {D_{3} } K_{r3} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{3} } \right){\rm d}x \hfill \\ \end{aligned} & \begin{aligned} \gamma_{1} = \int_{0}^{l} {D_{3} } c_{r3} \varphi_{1}^{2} \delta^{*} \left( {x - \overline{\xi }_{3} } \right){\rm d}x \hfill \\ \gamma_{2} = \int_{0}^{l} {D_{3} } c_{r3} \varphi_{1} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{3} } \right){\rm d}x \hfill \\ \gamma_{3} = \int_{0}^{l} {D_{3} } c_{r3} \varphi_{2}^{2} \delta^{*} \left( {x - \overline{\xi }_{3} } \right){\rm d}x \hfill \\ \gamma_{4} = \int_{0}^{l} {D_{3} } c_{r3} \varphi_{1} \delta^{*} \left( {x - \overline{\xi }_{3} } \right){\rm d}x \hfill \\ \gamma_{5} = \int_{0}^{l} {D_{3} } c_{r3} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{3} } \right){\rm d}x \hfill \\ \end{aligned} \\ \end{array}$$

(B.6)

In Eq. (B.2), the constant parameters related to the rear bogie rear wheel are given by:

$$\begin{array}{*{20}c} \begin{aligned} \beta \beta_{1} = \int_{0}^{l} {D_{4} } K_{r4} \varphi_{1}^{2} \delta^{*} \left( {x - \overline{\xi }_{4} } \right){\rm d}x \hfill \\ \beta \beta_{2} = \int_{0}^{l} {D_{4} } K_{r4} \varphi_{1} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{4} } \right){\rm d}x \hfill \\ \beta \beta_{3} = \int_{0}^{l} {D_{4} } K_{r4} \varphi_{2}^{2} \delta^{*} \left( {x - \overline{\xi }_{4} } \right){\rm d}x \hfill \\ \beta \beta_{4} = \int_{0}^{l} {D_{4} } K_{r4} \varphi_{1} \delta^{*} \left( {x - \overline{\xi }_{4} } \right){\rm d}x \hfill \\ \beta \beta_{5} = \int_{0}^{l} {D_{4} } K_{r4} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{4} } \right){\rm d}x \hfill \\ \end{aligned} & \begin{aligned} \gamma \gamma_{1} = \int_{0}^{l} {D_{4} } c_{r4} \varphi_{1}^{2} \delta^{*} \left( {x - \overline{\xi }_{4} } \right){\rm d}x \hfill \\ \gamma \gamma_{2} = \int_{0}^{l} {D_{4} } c_{r4} \varphi_{1} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{4} } \right){\rm d}x \hfill \\ \gamma \gamma_{3} = \int_{0}^{l} {D_{4} } c_{r4} \varphi_{2}^{2} \delta^{*} \left( {x - \overline{\xi }_{4} } \right){\rm d}x \hfill \\ \gamma \gamma_{4} = \int_{0}^{l} {D_{4} } c_{r4} \varphi_{1} \delta^{*} \left( {x - \overline{\xi }_{4} } \right){\rm d}x \hfill \\ \gamma \gamma_{5} = \int_{0}^{l} {D_{4} } c_{r4} \varphi_{2} \delta^{*} \left( {x - \overline{\xi }_{4} } \right){\rm d}x \hfill \\ \end{aligned} \\ \end{array}$$

(B.7)

Appendix C.

Using Newmark’s integration method [41], the solution of Eq. (21) can be obtained according to the following steps:

• 1. Determine the integration parameters β and γ and magnitude of the time interval Δt. Calculate integration constants:

  $$\begin{aligned} a_{0} = \frac{1}{{\beta \Delta t^{2} }}, \, a_{1} = \frac{\gamma }{\beta \Delta t}, \, a_{2} = \frac{1}{\beta \Delta t}, \, a_{3} = \frac{1}{2\beta } - 1, \hfill \\ a_{4} = \frac{\gamma }{\beta } - 1, \, a_{5} = \frac{\Delta t}{2}(\frac{\gamma }{\beta } - 2), \, a_{6} = \Delta t(1 - \gamma ), \, a_{7} = \gamma \Delta t. \hfill \\ \end{aligned}$$

  (C.1)

• 2. Using Eqs. (B1-3), define the mass, stiffness, and damping, $\left[\mathbf{M}\right],\left[\mathbf{C}\right]$, and $\left[\mathbf{K}\right]$ matrices at t_n = (t_n-1 + Δt) time.

• 3. Calculate effective stiffness matrix at (= t_n-1 + Δt) time:

  $$[{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K} }}] = [{\mathbf{K}}] + a_{0} [{\mathbf{M}}] + a_{1} [{\mathbf{C}}].$$

  (C.2)

• 4. Calculate effective force $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (t)\}$ at time t_n (= t_n-1 + Δt):

  $$\begin{aligned} \{ {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }}(t_{n} )\}& = \{ {\mathbf{F}}(t_{n} )\} + [{\mathbf{M}}](a_{0} \{ {\mathbf{U}}(t_{n - 1} )\} \\ &\quad+ a_{2} \{ {\dot{\mathbf{U}}}(t_{n - 1} )\} + a_{3} \{ {\mathbf{\ddot{U}}}(t_{n - 1} )\} ) \hfill \\ &\quad+ [{\mathbf{C}}](a_{1} \{ {\mathbf{U}}(t_{n - 1} )\} + a_{4} \{ {\dot{\mathbf{U}}}(t_{n - 1} )\} \\ &\quad+ a_{5} \{ {\mathbf{\ddot{U}}}(t_{n - 1} )\} ). \hfill \\ \end{aligned}$$

  (C.3)

  where $\left\{\ddot{\mathbf{U}}\left({t}_{n-1}\right)\right\}$,$\left\{\dot{\mathbf{U}}\left({t}_{n-1}\right)\right\}$ and $\left\{\mathbf{U}\left({t}_{n-1}\right)\right\}$ are, respectively, the initial conditions for the accelerations, velocities, and displacements of the structural system at time t = t₀ = 0.

• 5. Calculate deflections at t_n time:

  $$\{ {\mathbf{U}}(t_{n} )\} = [{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K} }}]^{ - 1} \{ {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }}(t_{n} )\} .$$

  (C.4)

• 6. Calculate accelerations and velocities at t_n time:

  $$\begin{aligned} \{ {\mathbf{\ddot{U}}}(t_{n} )\} =& a_{0} (\{ {\mathbf{U}}(t_{n} )\} - \{ {\mathbf{U}}(t_{n - 1} )\} ) \\ &- a_{2} \{ {\dot{\mathbf{U}}}(t_{n - 1} )\} - a_{3} \{ {\mathbf{\ddot{U}}}(t_{n - 1} )\} , \end{aligned}$$

  (C.5)
  $$\{ {\dot{\mathbf{U}}}(t_{n} )\} = \{ {\dot{\mathbf{U}}}(t_{n - 1} )\} + a_{6} \{ {\mathbf{\ddot{U}}}(t_{n - 1} )\} + a_{7} \{ {\mathbf{\ddot{U}}}(t_{n} )\} .$$

  (C.6)

Steps 3–7, t = t_n = t_n-1 + Δt (n = 1, 2, 3, and t₀ = 0) are repeated for all time steps, for deflections $\left\{\ddot{\mathbf{U}}\left({t}_{n}\right)\right\}$, velocities $\left\{\dot{\mathbf{U}}\left({t}_{n}\right)\right\}$, and accelerations $\left\{\mathbf{U}\left({t}_{n}\right)\right\}$ of the entire system.