Skip to main content
SpringerLink
Log in

Equivalent mechanical model of rectangular container attached to a pendulum compared to experimental data and analytical solution

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

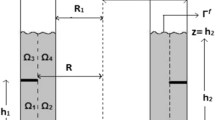
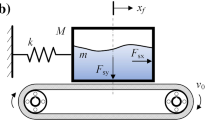
A tuned liquid damper (TLD) is a passive control device that transfers kinetic energy from the main structure to a liquid sloshing in a tank. The mechanical description of a sloshing liquid contained in a tank requires an intricate mathematical formulation. An alternative technique describes the TLD dynamic behavior as an equivalent mechanical model comprising a series of pendulums or mass–spring systems attached to the tank walls. To validate this approach, this paper compares the discrete model to experimental results and an analytical solution for a rectangular container attached to a pendulum (pendulum-slosh problem). At first, the fundamental oscillation period of the discrete model, representing a rectangular tank, is compared to experimental data and a classic analytical solution. Finally, we compare the pendulum-slosh problem modeled as a discrete model with the analytical solution and experimental results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Novo T, Varum H, Teixeira-Dias F, Rodrigues H, Silva MF, Costa AC et al (2014) Tuned liquid dampers simulation for earthquake response control of buildings. Bull Earthq Eng 12:1007–1024. https://doi.org/10.1007/s10518-013-9528-2

    Article  Google Scholar 

  2. Espinoza G, Carrilloa C, Suazoa A (2018) Analysis of a tuned liquid column damper in non-linear structures subjected to seismic excitations. Lat Am J Solids Struct. https://doi.org/10.1590/1679-78254845

    Article  Google Scholar 

  3. Battaglia L, Cruchaga M, Storti M, D’Elía J, Núñez Aedo J, Reinoso R (2018) Numerical modelling of 3D sloshing experiments in rectangular tanks. Appl Math Model 59:357–378

    Article  MathSciNet  Google Scholar 

  4. Castillo EF, Cruchaga MA (2012) Experimental vibration analysis for a 3D scaled model of a three-floor steel structure. Lat Am J Solids Struct Associação Brasileira de Ciências Mecânicas. 9:597–613

    Article  Google Scholar 

  5. Zhang Z, Staino A, Basu B, Nielsen SRK (2016) Performance evaluation of full-scale tuned liquid dampers (TLDs) for vibration control of large wind turbines using real-time hybrid testing. Eng Struct 126:417–431

    Article  Google Scholar 

  6. Zhang Z, Nielsen SRK, Basu B, Li J (2015) Nonlinear modeling of tuned liquid dampers (TLDs) in rotating wind turbine blades for damping edgewise vibrations. J Fluids Struct 59:252–269

    Article  Google Scholar 

  7. Xue SD, Ko JM, Xu YL (1999) Experimental study on performance of tuned liquid column damper in suppressing pitching vibration of structures. J Intell Mater Syst Struct 10:386–396. https://doi.org/10.1177/1045389x9901000504

    Article  Google Scholar 

  8. Shum KM, Xu YL, Guo WH (2008) Wind-induced vibration control of long span cable-stayed bridges using multiple pressurized tuned liquid column dampers. J Wind Eng Ind Aerodyn 96:166–192

    Article  Google Scholar 

  9. Lackner MA, Rotea MA (2011) Passive structural control of offshore wind turbines. Wind Energy 14:373–388

    Article  Google Scholar 

  10. Noji T, Yoshida H, Tatsumi E, Kosaka H, Hagiuda H (1988) Study on vibration control damper utilizing sloshing of water. J Wind Eng. 37:557–566

    Google Scholar 

  11. Fujino Y, Pacheco BM, Chaiseri P, Sun LM (1988) Parametric studies on tuned liquid damper (TLD) using circular containers by free-oscillation experiments. Doboku Gakkai Ronbunshu. 1988:177–187

    Article  Google Scholar 

  12. Abramson HN (1966) The dynamic behavior of liquids in moving containers with applications to space vehicle technology. Technical Report NASA SP-106, p 467

  13. Dodge FT (2000) The new “dynamic behaviour of liquids in moving containers”. Technical Report, Southwest Research Institute, San Antonio, TX

  14. Ibrahim RA (2014) Recent advances in vibro-impact dynamics and collision of ocean vessels. J Sound Vib 333:5900–5916

    Article  Google Scholar 

  15. Li Y, Di Q, Gong Y (2012) Equivalent mechanical models of sloshing fluid in arbitrary-section aqueducts. Earthq Eng Struct Dyn. 41:1069–1087

    Article  Google Scholar 

  16. Li Y, Wang J (2012) A supplementary, exact solution of an equivalent mechanical model for a sloshing fluid in a rectangular tank. J Fluids Struct 31:147–151

    Article  Google Scholar 

  17. Tait MJ, El Damatty AA, Isyumov N (2002) The dynamic properties of a tuned liquid damper using an equivalent amplitude dependent tuned mass damper. In: 4th Structure Specification Conference on Canadian Society Civil Engineering, p 1–10

  18. Tait MJ, Isyumov N, El Damatty AA (2008) Performance of tuned liquid dampers. J Eng Mech Am Soc Civ Eng 134:417–427

    Article  Google Scholar 

  19. Kareem A, Sun WJ (1987) Stochastic response of structures with fluid-containing appendages. J Sound Vib 119:389–408

    Article  Google Scholar 

  20. Ashasi-Sorkhabi A, Malekghasemi H, Ghaemmaghami A, Mercan O (2017) Experimental investigations of tuned liquid damper-structure interactions in resonance considering multiple parameters. J Sound Vib 388:141–153

    Article  Google Scholar 

  21. Yu J, Wakahara T, Reed DA (1999) A non-linear numerical model of the tuned liquid damper. Earthq Eng Struct Dyn 28:671–686

    Article  Google Scholar 

  22. Sun LM, Fujino Y, Chaiseri P, Pacheco BM (1995) The properties of tuned liquid dampers using a TMD analogy. Earthq Eng Struct Dyn. 24:967–976. https://doi.org/10.1002/eqe.4290240704

    Article  Google Scholar 

  23. Nichkawde C, Harish PM, Ananthkrishnan N (2004) Stability analysis of a multibody system model for coupled slosh-vehicle dynamics. J Sound Vib 275:1069–1083

    Article  Google Scholar 

  24. Yue B-Z (2011) Study on the chaotic dynamics in attitude maneuver of liquid-filled flexible spacecraft. AIAA J 49:2090–2099. https://doi.org/10.2514/1.j050144

    Article  MATH  Google Scholar 

  25. Cooker MJ (1994) Water waves in a suspended container. Wave Motion 20:385–395

    Article  Google Scholar 

  26. De Langre E (2001) Fluides et solides. Editions Ecole Polytechnique

  27. Park J, Im S, Sung HJ, Park JS (2015) PIV measurements of flow around an arbitrarily moving free surface. Exp Fluids 56(3):56

    Article  Google Scholar 

  28. Di Matteo A, Lo Iacono F, Navarra G, Pirrotta A (2015) Innovative modeling of Tuned Liquid Column Damper motion. Commun Nonlinear Sci Numer Simul 23:229–244

    Article  Google Scholar 

  29. Di Matteo A, Lo Iacono F, Navarra G, Pirrotta A (2014) Direct evaluation of the equivalent linear damping for TLCD systems in random vibration for pre-design purposes. Int J Non Linear Mech 63:19–30

    Article  Google Scholar 

  30. Di Matteo A, Lo Iacono F, Navarra G, Pirrotta A (2014) Experimental validation of a direct pre-design formula for TLCD. Eng Struct 75:528–538

    Article  Google Scholar 

  31. Furtmüller T, Di Matteo A, Adam C, Pirrotta A (2019) Base-isolated structure equipped with tuned liquid column damper: an experimental study. Mech Syst Signal Process 116:816–831

    Article  Google Scholar 

  32. Di Matteo A, Di Paola M, Pirrotta A (2016) Innovative modeling of tuned liquid column damper controlled structures. Smart Struct Syst. 18:117–138

    Article  Google Scholar 

  33. Love J, Tait M (2015) The response of structures equipped with tuned liquid dampers of complex geometry. J Vib Control 21:1171–1187. https://doi.org/10.1177/1077546313495074

    Article  Google Scholar 

  34. Love JS, Tait MJ (2013) Equivalent mechanical model for tuned liquid damper of complex tank geometry coupled to a 2D structure. Struct Control Heal Monit 21:43–60

    Article  Google Scholar 

  35. Love JS, Tait MJ (2011) Equivalent linearized mechanical model for tuned liquid dampers of arbitrary tank shape. J Fluids Eng 133:61105–61109. https://doi.org/10.1115/1.4004080

    Article  Google Scholar 

  36. Le Mehaute B (2013) An introduction to hydrodynamics and water waves. Springer, Berlinm

    MATH  Google Scholar 

  37. Peña N, Credidio BC, Corrêa LPNRM, França LGS, Cunha M, de Sousa MC et al (2013) Free instrument for measurements of motion. Rev Bras Ensino Física 35:1–5

    Google Scholar 

  38. Alemi Ardakani H, Bridges TJ, Turner MR (2012) Resonance in a model for Cooker’s sloshing experiment. Eur J Mech B/Fluids. 36:25–38

    Article  MathSciNet  Google Scholar 

  39. JCGM (2008) Evaluation of measurement data: guide to the expression of uncertainty in measurement. Int Organ Stand 100(1):134

    Google Scholar 

  40. Alkmim MH, Fabro AT, de Morais MVG (2018) Optimization of a tuned liquid column damper subject to an arbitrary stochastic wind. J Braz Soc Mech Sci Eng 40:1–11. https://doi.org/10.1007/s40430-018-1471-3

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported by the Brazilian Coordination for the Improvement of Higher Education Personnel (CAPES) – Finance Code 001, Brazilian Council for Scientific and Technological Development (CNPq) and Research Support Foundation of the Federal District (FAPDF). The second author acknowledges the Group of Dynamics of Systems (UnB-FT/EnM/GDS) for its support to make possible the present experiments.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Brasília, Darcy Ribeiro Campus, Asa Norte, Brasília, DF, 70910-900, Brazil

    Marcus V. G. de Morais

  2. Department of Civil Engineering, University of Brasília, Darcy Ribeiro Campus, Asa Norte, Brasília, DF, 70910-900, Brazil

    Alejandro A. O. Lopez & Lineu J. Pedroso

  3. PPG, Graduate Program in Engineering Material Integrity, University of Brasilia (UnB), Campus of Gama (FGA), Gama (Brasília), 72444-240, Brazil

    Marcus V. G. de Morais & Juliano F. Martins

Authors
  1. Marcus V. G. de Morais
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alejandro A. O. Lopez
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Juliano F. Martins
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lineu J. Pedroso
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marcus V. G. de Morais.

Additional information

Technical Editor: Thiago Ritto.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A: Curve Fitting Toolbox

Appendix A: Curve Fitting Toolbox

Figure 11 shows an example of dynamic parameter identification performed by the Curve Fitting Toolbox (CFTOOL/MATLAB). This illustration presents the liquid’s dynamic level motion in a rectangular container observed by motion capture, as shown in Fig. 5.

Fig. 11
figure 11

Example of identification of modal parameters by the Curve Fitting Toolbox (MATLAB)

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

de Morais, M.V.G., Lopez, A.A.O., Martins, J.F. et al. Equivalent mechanical model of rectangular container attached to a pendulum compared to experimental data and analytical solution. J Braz. Soc. Mech. Sci. Eng. 42, 143 (2020). https://doi.org/10.1007/s40430-020-2232-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-020-2232-7

Keywords

Search

Navigation