Nonlinear vibration analysis of an elastically connected double-non-classical Timoshenko microbeam subject to moving particle based on the modified couple stress theory

Abstract

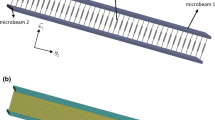
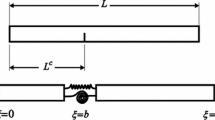
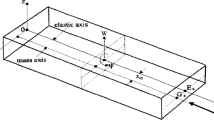
In this article, the nonlinear transverse vibration of an elastically connected double microbeam system carrying a moving particle is assessed based on the modified couple stress and non-classical Timoshenko beam theories. Hamilton’s principle is applied to develop the motion equations and corresponding boundary conditions, and the Galerkin method is used to solve these equations. The numerical study reveals that the nonlinear and modified couple stress theories predict a stiffer system than the linear and classical theories do. A parametric study is run to determine the different parameters’ influence like the aspect ratio, the stiffness modulus of the elastic layer and the velocity of the moving particle, on the dynamic response of the system. The results show that the aspect ratio has a significant effect on the dynamic response of the system, indicating that the classical theory cannot predict the dynamic behavior of micro-size beam systems. The elastic layer stiffness modulus and the velocity of the moving particle have considerable effects on the dynamic deflections of the double-microbeam system.

Appendix

The components of Eq. (29) are as follows:

$$\begin{aligned} {\mathbf{M}} = \left[ {\begin{array}{llll} {M_{1} } &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad {M_{2} } &\quad 0 &\quad 0 \\ 0 &\quad 0 & \quad {M_{3} } &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad {M_{4} } \\ \end{array} } \right], \hfill \\ {\mathbf{K}} = \left[ {\begin{array}{llll} {K_{11} } &\quad {K_{12} } &\quad {K_{13} } &\quad 0 \\ {K_{21} } &\quad {K_{22} } &\quad 0 &\quad 0 \\ {K_{31} } &\quad 0 &\quad {K_{33} } &\quad {K_{34} } \\ 0 &\quad 0 &\quad {K_{43} } &\quad {K_{44} } \\ \end{array} } \right] \hfill \\ \end{aligned}$$

(33)

and

$$K_{\text{nonlinear}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - \epsilon_{1} \varLambda_{1} p_{1}^{3} \mathop \int \limits_{0}^{1} \left( {\mathop \int \limits_{0}^{1} \frac{1}{2}\left( {\bar{W}_{1}^{\prime } } \right)^{2} {\text{d}}\xi } \right)\bar{W}_{1}^{\prime \prime } \bar{W}_{1} \left( \xi \right){\text{d}}\xi } \\ 0 \\ \end{array} } \\ { - \epsilon_{2} \varLambda_{2} p_{2}^{3} \mathop \int \limits_{0}^{1} \left( {\mathop \int \limits_{0}^{1} \frac{1}{2}\left( {\bar{W}_{2}^{\prime } } \right)^{2} {\text{d}}\xi } \right)\bar{W}_{2}^{\prime \prime } \bar{W}_{2} \left( \xi \right){\text{d}}\xi } \\ 0 \\ \end{array} } \right], F = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\mathop \int \limits_{0}^{1} \kappa \bar{W}_{1} \delta \left( {\xi - \tau } \right){\text{d}}\xi } \\ 0 \\ \end{array} } \\ 0 \\ 0 \\ \end{array} } \right]$$

(34)

where

$$\begin{aligned} {\text{M}}_{1} & = \beta_{1} \mathop \int \limits_{0}^{1} \bar{W}_{1} \left( \xi \right)\bar{W}_{1} \left( \xi \right){\text{d}}\xi , \quad {\text{M}}_{2} = \beta_{1} \mathop \int \limits_{0}^{1} {\bar{{\varPsi }}}_{1} \left( \xi \right){\bar{{\varPsi }}}_{1} \left( \xi \right){\text{d}}\xi \\ {\text{M}}_{3} & = \beta_{2} \mathop \int \limits_{0}^{1} \bar{W}_{2} \left( \xi \right)\bar{W}_{2} \left( \xi \right){\text{d}}\xi , \quad {\text{M}}_{4} = \beta_{2} \mathop \int \limits_{0}^{1} {\bar{{\varPsi }}}_{2} \left( \xi \right){\bar{{\varPsi }}}_{2} \left( \xi \right){\text{d}}\xi \\ K_{11} & = - \gamma_{1} {{\varLambda }}_{1} \mathop \int \limits_{0}^{1} \bar{W}_{1}^{\prime \prime } \left( \xi \right)\bar{W}_{1} \left( \xi \right){\text{d}}\xi + \eta_{1} \mathop \int \limits_{0}^{1} \bar{W}_{1}^{\prime \prime \prime \prime } \left( \xi \right)\bar{W}_{1} \left( \xi \right){\text{d}}\xi \\ &\quad+ {{\varGamma }}_{1} \mathop \int \limits_{0}^{1} \bar{W}_{1} \left( \xi \right)\bar{W}_{1} \left( \xi \right){\text{d}}\xi \\ K_{12} & = \gamma_{1} {{\varLambda }}_{1} \mathop \int \limits_{0}^{1} \bar{W}_{1} \left( \xi \right){\bar{{\varPsi }}}_{1}^{\prime } \left( \xi \right){\text{d}}\xi + \eta_{1} \mathop \int \limits_{0}^{1} \bar{W}_{1} \left( \xi \right){\bar{{\varPsi }}}_{1}^{\prime \prime \prime } {\text{d}}\xi ,\quad \\ K_{13} &= - {{\varGamma }}_{1} \mathop \int \limits_{0}^{1} \bar{W}_{2} \left( \xi \right)\bar{W}_{1} \left( \xi \right){\text{d}}\xi \\ K_{21} & = - \gamma_{1} {{\varLambda }}_{1}^{2} \mathop \int \limits_{0}^{1} \bar{W}_{1}^{\prime } \left( \xi \right){\bar{{\varPsi }}}_{1} \left( \xi \right){\text{d}}\xi - \eta_{1} {{\varLambda }}_{1} \mathop \int \limits_{0}^{1} \bar{W}_{1}^{\prime \prime \prime } \left( \xi \right){\bar{{\varPsi }}}_{1} \left( \xi \right){\text{d}}\xi \\ K_{22} & = - \epsilon_{1} {{\varLambda }}_{1} \mathop \int \limits_{0}^{1} {\bar{{\varPsi }}}_{1}^{\prime \prime } \left( \xi \right){\bar{{\varPsi }}}_{1} \left( \xi \right){\text{d}}\xi + \gamma_{1} {{\varLambda }}_{1}^{2} \mathop \int \limits_{0}^{1} {\bar{{\varPsi }}}_{1} \left( \xi \right){\bar{{\varPsi }}}_{1} \left( \xi \right){\text{d}}\xi \\ &\quad- \eta_{1} {{\varLambda }}_{1} \mathop \int \limits_{0}^{1} {\bar{{\varPsi }}}_{1}^{\prime \prime } \left( \xi \right){\bar{{\varPsi }}}_{1} \left( \xi \right){\text{d}}\xi \\ K_{31} &= - {{\varGamma }}_{2} \mathop \int \limits_{0}^{1} \bar{W}_{1} \left( \xi \right)\bar{W}_{2} \left( \xi \right){\text{d}}\xi \\ K_{33} & = - \gamma_{2} {{\varLambda }}_{2} \mathop \int \limits_{0}^{1} \bar{W}_{2}^{\prime \prime } \left( \xi \right)\bar{W}_{2} \left( \xi \right){\text{d}}\xi + \eta_{2} \mathop \int \limits_{0}^{1} \bar{W}_{2}^{\prime \prime \prime \prime } \left( \xi \right)\bar{W}_{2} \left( \xi \right){\text{d}}\xi \\ & \quad + {{\varGamma }}_{2} \mathop \int \limits_{0}^{1} \bar{W}_{2} \left( \xi \right)\bar{W}_{2} \left( \xi \right){\text{d}}\xi \\ K_{34} & = \gamma_{2} {{\varLambda }}_{2} \mathop \int \limits_{0}^{1} {\bar{{\varPsi }}}_{2}^{\prime } \left( \xi \right)\bar{W}_{2} \left( \xi \right){\text{d}}\xi + \eta_{2} \mathop \int \limits_{0}^{1} {\bar{{\varPsi }}}_{2}^{\prime \prime \prime } \left( \xi \right)\bar{W}_{2} \left( \xi \right){\text{d}}\xi \\ K_{43} & = - \gamma_{2} {{\varLambda }}_{2}^{2} \mathop \int \limits_{0}^{1} \bar{W}_{2}^{\prime } \left( \xi \right){\bar{{\varPsi }}}_{2} \left( \xi \right){\text{d}}\xi - \eta_{2} {{\varLambda }}_{2} \mathop \int \limits_{0}^{1} \bar{W}_{2}^{\prime \prime \prime } \left( \xi \right){\bar{{\varPsi }}}_{2} \left( \xi \right){\text{d}}\xi \\ K_{44} & = - \epsilon_{2} {{\varLambda }}_{2} \mathop \int \limits_{0}^{1} {\bar{{\varPsi }}}_{2}^{\prime \prime } \left( \xi \right){\bar{{\varPsi }}}_{2} \left( \xi \right){\text{d}}\xi + \gamma_{2} {{\varLambda }}_{2}^{2} \mathop \int \limits_{0}^{1} {\bar{{\varPsi }}}_{2} \left( \xi \right){\bar{{\varPsi }}}_{2} \left( \xi \right)d\xi \\ &\quad- \eta_{2} {{\varLambda }}_{2} \mathop \int \limits_{0}^{1} {\bar{{\varPsi }}}_{2}^{\prime \prime } \left( \xi \right){\bar{{\varPsi }}}_{2} \left( \xi \right){\text{d}}\xi \\ \end{aligned}$$

(35)