Analysis of processing methods for combustion pressure measurement in a diesel engine

Abstract

This paper analyzes combustion chamber pressure data processing methods related to the number of cycles averaged, top dead center referencing and pressure referencing (pegging). A total of 1000 consecutive engine cycles were measured in a four-cylinder diesel engine. The number of cycles that minimizes the influence of cycle-to-cycle oscillations depends on engine operating conditions and the parameters under analysis. The top dead center (TDC) referencing, using the motored curve, revealed that the thermodynamic loss shifts the peak pressure − 0.4 °CA from TDC. Four pegging methods were compared—least-squares, fixed-point, three-point and two-point—introducing as main novelty the fact they have not been previously investigated on the same baseline conditions. The least-squares based method showed the lowest sensitivity to random noise, but with longer processing time, and the fixed-point method presented higher dispersion in the heat release analysis. The three-point referencing method considers a variable polytropic coefficient, but suffers from noise sensitivity, and the two-point referencing method presented close values and higher dispersion in comparison with the least-squares method. The choice of which method to use depends on the type of analysis, signal quality and processing time available.

Introduction

The treatment of combustion pressure data consists of pressure referencing, crank angle phasing, cycle averaging and experimental signal filtering [1]. The accuracy of combustion and performance parameters obtained from pressure data are also affected by the number of cycles used for the calculations. There are several sources of error that affect the signal quality and cycle-to-cycle variations [2], motivating the proposition of data metrics for the quality of combustion pressure measurement [3]. Several works used different numbers of cycles to obtain the average cycle and remove the effects of cyclic variations. The optimal number of cycles to be averaged depends on several factors such as engine type, engine operating condition and data acquisition system [1]. Cyclic variations are caused by chemical and physical phenomena, as they are related to mixture composition, cycle cylinder charging and in-cylinder mixture motion [4].

The minimum number of cycles for an accurate calculation of the average pressure varies from 25 to 2800 [4]. From tests in a spark ignition engine operating at different conditions, 50 cycles were reported to be sufficient to provide accurate averaged values [4]. Elsewhere, the optimum number of cycles for tests in a homogeneous charge compression ignition (HCCI) engine was taken as 500, and increasing the number of cycles for averaging from this value did not improve the precision of the results [1].

There are various methods of pressure pegging, but no single method is an ideal solution for every situation. The main methods can be grouped in two strategies [5, 6]. The first one references the pressure signal to a known point, measured by a fast-response piezoresistive pressure transducer capable of measuring the absolute pressure in the intake manifold [7]. Alternatively, it can be assumed that the pressure at bottom dead center (BDC) after the intake stroke is equal to the mean intake manifold pressure [4, 8, 9], based on the assumption that with piston velocity variation near zero, while the valve is still significantly open, the pressure drop across the intake port and valve will be near zero [10]. In the other strategy, the compression stroke is modeled assuming a fixed polytropic coefficient, using the least-squares [11, 12] or the two-point [13] referencing methods, or assuming a variable polytropic coefficient [14]. Each method presents advantages, limitations and accuracy levels [15]. The inlet manifold is the region with the lowest pressure in the engine cycle, being this the major problem with pressure referencing in this location as linearity errors and signal noise can be very large in comparison with other regions [15]. The inlet manifold and polytropic index pressure referencing methods produced similar performance when applied to a gasoline engine operating under different conditions.

There is also the so-called real pegging strategy, where a piezoresistive transducer is installed in the lower barrel of the cylinder liner to measure the pressure at bottom dead center (BDC) [16]. The main limitation of this method is the requirement to create a passage for the transducer in the engine block, which is an additional installation difficulty. Also, the piezoresistive transducer at this condition highly suffers from temperature-dependent characteristics, such as zero-line shift, change of linearity and varying sensitivity [17]. This will need extra signal treatment and conditioning to obtain accurate results.

The two-point referencing (2ptR), three-point referencing (3ptR) and least-squares method (LSM) were compared with a modified LSM with a variable polytropic coefficient as pegging methods to a diesel engine [14]. The 2ptR and LSM methods assume a fixed polytropic coefficient for all engine cycles, while the 3ptR and modified LSM methods assume a variable polytropic coefficient. The modified LSM method presented the lowest standard deviation for the polytropic coefficient. The LSM and the modified LSM methods produced the lowest peg drift, which is determined by the changes in the sensor offset from one cycle to the next. The least-squares-based methods produced the lowest variation in the center of gravity (COG) of pressure difference and reduced sensitivity to random noise. It was concluded that the assumption of a fixed polytropic coefficient for all engine cycles could result in an erroneous calculation of the sensor offset and that the modified least-squares method has the least sensitivity to random measurement noise [14].

This work aims to analyze pressure referencing, cycle averaging and TDC referencing as combustion pressure data processing methods. Experiments were carried out in a four-cylinder engine with different engine loads to evaluate the influence of the number of cycles averaged on combustion pressure and indicated mean effective pressure (IMEP) standard deviation. Referencing to TDC was done using the engine motored curve from a thermodynamic method. A comparative study on four different pegging methods was done, analyzing the polytropic coefficient, pressure shift value and influence on heat release rate. The main novelties of this work are the evaluation of four different pegging methods from the same baseline experiments, and the presentation of updated recommended values for the optimized number of averaged cycles and the thermodynamic loss angle of TDC.

The group of pegging methods here analyzed are different from the ones investigated in previous works [18, 19]. A comparison has previously been made between the three-point referencing method, its variant with five-point averaging, a linear and a nonlinear least-squares method [18]. Elsewhere, a comparison between least-squares methods with a fixed polytropic coefficient, variable polytropic coefficient and polytropic coefficient with cyclic learning has been reported [19]. Here, a comparison is made between the fixed-point referencing (1ptR), 2ptR, 3ptR and LSM methods.

Methodology

Experiments

The experiments were carried out in a four-cylinder, naturally aspirated, 44 kW stationary diesel engine, which main characteristics are shown in Table 1. As indicated by the valve timings in Table 1, there was no valve overlap. The engine was fueled by diesel oil containing 7% of biodiesel (B7) injected by a mechanical system, keeping a constant crankshaft speed of 1800 rpm.

Table 1 Diesel engine and generator details

The experiments were performed with load power of 10.0 kW, 20.0 kW, 27.5 kW and 35.0 kW. These points were chosen to cover most of the engine operational range, from about 20% to 80% of the rated power. The measurements were performed at steady state condition, after stabilization of the inlet and outlet coolant water temperatures and exhaust gas temperature at a set load condition. The results shown in the forthcoming sections are the average of three sets of experiments performed at each load condition. At motored engine conditions, the cylinder with the pressure sensor installed was operated without fuel injection, while the other three cylinders were fired. The experimental procedure to make the measurements was the same as adopted when load was applied.

The combustion pressure was measured by a Kistler model 6061B water-cooled piezoelectric transducer installed in the first engine cylinder. The cooling system conferred stability to the sensor and reduced the thermal drift [17]. The transducer was connected to a Kistler 5037B3 charge amplifier, to convert the electric charge into analog voltage signal. The pressure transducer operation was in the range from 0 to 250 bar with a sensitivity of − 25.6 pC/bar, linearity ≤ ± 0.5% of full-scale output, natural frequency ≈ 90 kHz and sensitivity shift ≤ ± 0.5%.

A 60-2 crank trigger wheel and a magnetic sensor were used to synchronize the pressure data with the first cylinder at TDC. The time-based technique was used for the in-cylinder pressure phasing with crank angle, resulting in an angular resolution of 0.1 °CA with an acquisition rate of 100 kHz. As the engine had four cylinders and was operated at constant speed (1800 RPM), the crank angle phasing errors due to instantaneous crankshaft speed fluctuations were reduced [20]. The analog signal from the magnetic sensor was conditioned by a LM1815 adaptive variable reluctance amplifier to turn it into a digital signal and eliminate noise. The pressure and magnetic data were simultaneously acquired using a National Instruments Data Acquisition system (NI USB-6211) with an acquisition rate of 100 kHz. A fourth-order low-pass Butterworth filter with a frequency of 1 kHz was used to remove high-frequency noise. The delay between the filter output and input signals was determined by plotting the unfiltered and filtered signals against the crankshaft position. The filtered pressure signal was then advanced by the delay time of 25 μs to be consistent with the unfiltered pressure signal.

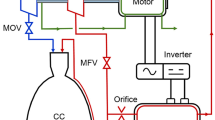
In addition to the in-cylinder pressure data, several other parameters were monitored during the experiments, including temperature at different locations, air and fuel mass flow rates, atmospheric conditions and electrical characteristics of the generated energy. The intake air flow conditions were 200 ± 8 kg/h, 0.92 ± 0.01 bar, 30 ± 1 °C, measured by an orifice plate, a Torricelli barometer and a K-type thermocouple, respectively. The air pressure in the intake manifold was measured by a piezoresistive pressure transducer with uncertainty of ± 0.05 bar. A schematic drawing of the experimental apparatus is shown in Fig. 1.

Fig. 1

Schematics of the experimental apparatus

Combustion pressure processing

The thermodynamic TDC position was determined using the FEV method [21], which is an algorithm executed on an averaged motored pressure curve. Initially the mechanical TDC was assumed at the peak pressure position of the curve obtained from the motored engine and is determined from the maximum point of a second degree polynomial equation fitted around the peak pressure, eliminating the points that produce an error higher than 5% of the fitted curve. Then, the loss angle (θ_loss) that shifts the peak pressure due to thermodynamically non-ideal compression and expansion processes resulting from heat transfer, crevice and blow-by effects [22] was calculated. To calculate θ_loss, which is the angular difference of the mechanical TDC position and thermodynamic TDC position, the motored curve was bisected at equidistant points of − 14 to − 4 °CA and 4 °CA to 14 °C. From each symmetrical point, a straight line was connected and the center position was derived from that line. Using linear regression, a straight line was calculated through the central points and the intersection of this line with the crank angle axis determined θ_loss and, therefore, the thermodynamic TDC [20]. The absolute pressure at a crank angle position p(θ) was obtained from the shift of the measured pressure p_meas(θ) by the zero-line shift ∆p [17]:

$$p\left( \theta \right) = p_{\text{meas}} \left( \theta \right) + \Delta p$$

(1)

In this study, four different pegging methods were compared: fixed-point referencing (1ptR), two-point referencing (2ptR), three-point referencing (3ptR) and least-squares method (LSM).

In the 1ptR method [23], the in-cylinder pressure at BDC, at the end of the intake process, was considered equal to the intake manifold absolute pressure. The whole in-cylinder pressure curve was shifted until, at the fixed-point, the reference pressure was achieved. This method is not suitable for tuned intake system or high engine speed [14]. It is considered very accurate procedure in naturally aspirated engines, but is limited by signal noise that can lead to inaccurate referencing for the total cycle [14, 23, 24]. In this work, the average pressure of 78 kPa in the inlet manifold was used as pressure referencing, as adopted by other authors [23].

The 2ptR method assumed pressure evolution as a polytropic process during the compression stroke, before the combustion process, which is not true when mass loss or excessive heat loss occurs [14, 22, 24]. The method considered a fixed polytropic coefficient κ and used the pressure at two points, θ₁ and θ₂, related to the cylinder volume by:

$$p_{\text{meas}} \left( {\theta_{1} } \right)V\left( {\theta_{1} } \right)^{{}} = p_{\text{meas}} \left( {\theta_{2} } \right)V\left( {\theta_{2} } \right)$$

(2)

The ∆p shift can be written as:

$$\Delta p = \frac{{\left[ {\frac{{V_{1} \left( {\theta_{1} } \right)}}{{V_{2} \left( {\theta_{2} } \right)}}} \right]^{{}} \Delta p\left( {\theta_{1} } \right) - p\left( {\theta_{2} } \right)}}{{1 - \left[ {\frac{{V_{1} \left( {\theta_{1} } \right)}}{{V_{2} \left( {\theta_{2} } \right)}}} \right]^{{}} }}$$

(3)

The recommended crank angle values for diesel engines are 100 °CA BTDC ≤ θ₁ ≤ 80 °CA BTDC and 40 °CA BTDC ≤ θ₂ ≤ 30 °CA BTDC [18], or θ₁ = 100 °CA BTDC and θ₂ = 65 °CA BTDC [21]. The main uncertainty of this method is based on the use of a constant polytropic exponent. To minimize this influence, the crank angle interval must be as large as possible. This method is frequently used due to its simplicity and good level of accuracy [17].

The 3ptR method also assumed that the pressure evolution behaves as a polytropic process during the compression stroke, but with a variable polytropic coefficient. The use of three points resulted in:

$$\frac{{p\left( {\theta_{2} } \right) - p\left( {\theta_{1} } \right)}}{{p\left( {\theta_{3} } \right) - p\left( {\theta_{1} } \right)}} = \frac{{\left[ {\frac{{V\left( {\theta_{1} } \right)}}{{V\left( {\theta_{2} } \right)}}} \right]^{ } - 1}}{{\left[ {\frac{{V\left( {\theta_{1} } \right)}}{{V\left( {\theta_{3} } \right)}}} \right]^{ } - 1}}$$

(4)

Equation (4) was expanded in a first-order Taylor series to calculate the polytropic coefficient. The value of ∆p was calculated from Eq. (3):

Pressure shift in the LSM method was determined by evaluating several measurement samples and applying regression calculations [14]. Due to the polytropic process assumption, the pressure samples must be made between the inlet valve close and the start of injection. Using this method, fifteen pressure samples at equidistant crank angles between 49 and 91 °CA BTDC have been recommended [12]. The polytropic exponent was also fixed and became a source of error, as it could vary from cycle to cycle due to heat transfer and mass loss (blow-by). The measured pressure and shift were related by:

$$p_{\text{meas}} = \Delta p + \left( {p_{0} V_{0}^{k} } \right)V^{ - k}$$

(5)

The heat release rate is an important parameter for the study of the combustion process characteristics. The apparent net heat release rate, ${\text{d}}Q_{n} /{\text{d}}\theta$ (J/ °CA), was calculated from application of the first law of thermodynamics to the cylinder content [24]:

$$\frac{{{\text{d}}Q_{n} }}{{{\text{d}}\theta }} = \left( {\frac{\gamma }{\gamma - 1}} \right).p.\frac{{{\text{d}}V}}{{{\text{d}}\theta }} + \left( {\frac{1}{\gamma - 1}} \right).V. \frac{{{\text{d}}P}}{{{\text{d}}\theta }}$$

(6)

where $\gamma$ is the ratio of specific heats, c_p/c_v, p is the cylinder pressure (Pa), V is the cylinder volume (m³) and $\theta$ is the crank angle ( °CA).

Results and discussion

In-cylinder pressure of 1000 consecutive cycles was measured with resolution of 0.1 °CA to study the effects of the number of cycles on the standard deviation of the mean values. For this analysis, the absolute in-cylinder pressure data was determined using the LSM method. Figure 2 shows the variation of the standard deviation of in-cylinder pressure with crank angle. It is noticed that the maximum pressure variation occurred during the combustion process, near TDC. Cylinder pressure variation is caused by different physical–chemical parameters, such as fuel–air ratio, residual gas fraction, ignition timing and heat losses [4].

Fig. 2

Standard deviation of in-cylinder pressure of 1000 consecutive cycles at the load of 35 kW

Figure 3 shows the behavior of the coefficient of variation (COV) of IMEP as a function of the number of cycles. The COV (%) is given by the ratio of the standard deviation of IMEP, σ_IMEP (kPa) and its mean value [25], and it was here used to evaluate the influence of the number of cycles on the cyclic variability. It can be observed that the optimum number of cycles for this parameter depends on the engine operating condition. The COV of IMEP was stabilized after a certain number of cycles at a given load and did not significantly change with additional cycles. There was an increase in COV of IMEP with the decrease in engine load, indicating a higher engine instability at low loads. The cyclic variability increases with increasing relative air–fuel ratio [4], explaining the need for less cycles to be acquired at high engine loads when increased fuel amounts are utilized. At a given load and increasing the number of cycles, stabilization was considered to occur when the ratio of the COV of IMEP to the COV of IMEP of 1000 cycles reached a value lower than 3%. The stabilization of COV of IMEP was achieved at the number of cycles of 500, 700, 250 and 250, for the loads of 10.0 kW, 20.0 kW, 27.5 kW and 35.0 kW, respectively.

Fig. 3

Variation of the coefficient of variation (COV) of the indicated mean effective pressure with the number of averaged cycles

Figure 4 shows the coefficient of variation (COV) of the in-cylinder maximum pressure as a function of the number of the cycles, given by the ratio of the in-cylinder maximum pressure standard deviation and its mean value. A ratio between the standard deviation of the average maximum pressure of each cycle and the standard deviation of 1000 cycles lower than 3% was achieved after around 350 cycles for all loads. Thus, the indicated number of cycles to calculate mean pressure values was decreased at low loads and increased at high loads when taking the COV of maximum cylinder pressure as a reference instead of the COV of IMEP.

Fig. 4

Variation of the coefficient of variation (COV) of maximum in-cylinder pressure with the number of averaged cycles

The dynamic determination of the angular position of the thermodynamic TDC was carried from the measurement of the motored pressure diagram and the determination of the thermodynamic loss angle (θ_loss). This angle was determined applying the FEV method to the in-cylinder pressure of the motored engine, averaged from 1000 cycles. The calculations resulted in a θ_loss of − 0.4 °CA, which is near the reported values of − 1.0 °CA [26], 0.35 °CA [27] and 0.7 °CA [28]. The small differences may be accounted to some dependence of θ_loss on engine configuration, which ranged from 4-cylinder spark ignition [27] to 6-cylinder supercharged diesel engine [28]. Figure 5 shows the in-cylinder pressure and volume of the motored engine, and θ_loss.

Fig. 5

Thermodynamic loss angle, in-cylinder pressure and volume of motored engine

The pegging methods were evaluated analyzing the effects on the polytropic coefficient, shift value, heat release rate and CA50, which represents the crank angle at which 50% of the cumulative heat release occurred [29, 30]. The calculations of each pegging method were done cycle-by-cycle for 1000 cycles, and then the in-cylinder pressure mean and standard deviations were calculated using a program developed in MATLAB^® software. Comparing the processing time of each method, the calculation using the LSM method took the longer processing time, followed by the 3ptR, 2ptR and 1ptR methods. For all methods, the processing time was of the order of milliseconds.

The polytropic coefficients of the 1ptR, 2ptR and LSM methods were considered fixed and obtained from the estimation given by the 3ptR method. For the 3ptR method, four different estimations of the initial guess of the polytropic coefficient were used [14], ranging from 1.25 to 1.30. The polytropic coefficient always converged to values between 1.31 and 1.33, varying for each operating condition. Table 2 shows the mean and the standard deviation of the polytropic coefficient for each engine load. The polytropic coefficient decreased with the increase of engine load, because engine operating temperature is increased, thus increasing heat loss [14, 22, 24]. The standard deviation of the polytropic coefficient increased with engine load, due to larger variability of the heat transfer process. With the justification that a wrong polytropic coefficient choice would result in a wrong $\overline{\Delta p}$, the use of a variable polytropic coefficient has been recommend [14].

Table 2 Polytropic coefficients (κ) and standard deviations (σ) of 3ptR method

Figure 6 shows the sensor original curve and the absolute in-cylinder pressure determined from the four pegging methods. It can be noticed that the 1ptR method presented the highest difference among all methods, with a lower $\overline{\Delta p}$, justified by this method not being suitable for high engine speed operation [14]. Table 3 shows the $\overline{\Delta p}$ value calculated from 1000 cycles for each pegging method and engine load. In general, comparing the methods with variable pressure referencing value, the 3ptR method produced the highest $\overline{\Delta p}$ and standard deviation, while the LSM produced the lowest $\overline{\Delta p}$ [14] and the second lowest standard deviation, just behind the 1ptR method. The use of all points between 49 and 91 °CA to determine $\overline{\Delta p}$ in the LSM method could reduce the influence of signal noise and the standard deviation.

Fig. 6

Transducer measured and absolute in-cylinder pressure calculated by the pegging methods at 35 kW

Table 3 Pressure shift and standard deviation of the different pegging methods with varying engine load

Table 4 shows the mean and standard deviation values of CA50, and Table 5 shows total heat released (total HR) for 1000 cycles for each method and engine load. The CA50 and total HR values obtained from the curves determined by the 1ptR method were always lower than the other methods, due to shorter combustion duration. In general, the 1ptR method caused higher standard deviations, justified by the use of fixed pressure referencing value, which ignores the variation of the condition inside the cylinder. The 2ptR and LSM methods presented close results to each other, probably due to the use of fixed polytropic coefficient. Figure 7 shows the values of CA50 for 1000 cycles for each method at the load of 35 kW, highlighting the dispersion. For this load, the LSM method presented the lowest dispersion, in comparison with the other three methods. This is explained by the reduced sensibility of the LSM method to random noise [14].

Table 4 CA50 and deviations for the different pegging methods and engine loads

Table 5 Total HR and deviations for the different pegging methods and engine loads

Fig. 7

Crank angle of 50% total heat released (CA50) calculated by the different pegging methods for 1000 cycles at 35 kW

Conclusions

The optimum number of cycles to minimize cycle-to-cycle variation effects on calculated parameters from cylinder pressure measurement was shown to be dependent on engine operating conditions and the analyzed parameter. For the engine tested, higher engine loads reduced the number of cycles required for the standard deviation of in-cylinder pressure and heat release analysis, ranging from 250 to 800 cycles. The TDC position was adequately determined from a thermodynamic method using the motored curve method, and a shift of − 0.4 °CA of the peak pressure in relation to TDC was calculated. From the pegging methods compared, the least-squares-based method showed the lowest standard deviation in relation to the shift value and the CA50 parameter and less sensitivity to random noise, but with longer processing time, which is critical for online analysis. The fixed-point method presented higher dispersion for CA50 determination and differences in the heat release analysis, in comparison with the other methods, being the least recommended, as it does not consider in-cylinder variations. The 3ptR method considered a variable polytropic coefficient, but suffered from noise sensitivity, and the 2ptR method presented values close to those presented by the LSM, but with higher dispersion. The LSM was proved to be the most recommended pegging method for the tested engine and operating conditions, showing the lowest sensitivity to noise and lowest dispersion.