1 Introduction

Nanotechnology has important interest in manufacturing, aerospace, and medical industries. The term nanofluid was generated by Choi [1] in 1995, designated as fluids that contain solid nanoparticles having 1–100 nm size dispersed in the base fluids, namely ethylene, water, toluene, oil, etc. Nanoparticles such as coppers, silicone, aluminum, and titanium tend to improve the thermal conductivity and convective heat assignment rate of liquids. Impact of variable viscosity on flow of non-Newtonian material with convective conditions over a porous medium is investigated by Rundora et al. [2]. Babu and Sandeep [3] discussed the numerical solution on MHD nanomaterials over a variable thickness of the surface along with thermophoresis and Brownian motion effects. Haiao [4] presented the numerical solution of magnetohydrodynamic micropolar fluid flow with the addition of nanomaterials toward a stretching sheet with viscous dissipation. Mahdavi et al. [5] illustrated the slip velocity along with multiphase approach of nanofluids. Xun et al. [6] obtained the numerical solution of bioconvection heat flow nanofluid flow over a rotating plate with temperature-based viscosity. Khan et al. [7] numerically analyzed heat and mass diffusion in Jeffery nanofluid passed by inclined stretching surface. Lebon and Machrafi [8] analyzed the two-phase change in Maxwell nanofluid flow along with thermodynamic description. Ansari et al. [9] investigated the comprehensive analysis in order to calculate the relative viscosity of nanofluids. Khan et al. [10] considered the chemical reaction on Carreau–Yasuda nanomaterials over a nonlinear stretching surface.

Magnetohydrodynamic (MHD) flow of heat and mass transfer Maxwell fluid flow over a continuous stretching surface has great significance in several applications in engineering such as melts, aerodynamics extrusion of plastic sheet, geothermal extractions, and purification of molten metals. Numerous researchers have made great interest and evaluated the transport phenomena for magnetohydrodynamic. Zhao et al. [11] solve the differential equations labeling MHD Maxwell fluid in permeable sheet by considering Dufour and Soret impact. Hsiao [12] investigated the combined effects of thermal extraction on MHD Maxwell fluid over stretching surface with viscous dissipation and energy conversion. Ghasemi and Siavashi [13] demonstrated the Cu–water MHD nanofluid in square permeable surface with entropy generation. Nourazar et al. [14] illustrated the heat transfer in flow of single-phase nanofluid toward a stretching cylinder with magnetic field effect. Dogonchi and Ganji [15] addressed the unsteady squeezed MHD nanofluid flow over two parallel plates with solar radiation. Hayat et al. [16] investigated the heat and mass diffusion for stagnation point flow toward a linear stretching surface along with magnetic field. Sayyed et al. [17] investigated the analytical solution of MHD Newtonian fluid flow over a wedge occupied in a permeable sheet. Representative analyses on MHD flow can be seen in Refs. [18,19,20].

The Maxwell model is a subclass of rate-type fluids, which calculates stress relaxation so it has become popular. This model also eliminates the complicating behavior of shear-dependent viscosity and is thus useful for focusing exclusively on the impact of a fluid’s elasticity on the characteristics of its boundary layer. Nadeem et al. [21] deliberated the numerical study on heat transfer of Maxwell nanofluid flow over a linear stretching sheet. Reddy et al. [22] studied the approximate solution of magnetohydrodynamic Maxwell nanofluid flow over exponentially stretching surface. Liu [23] indicated the 2D flow of frictional Maxwell fluid over a variable thickness. Solution of the differential equations was obtained numerically here by \(L_{1}\) technique. Yang et al. [24] considered the fractional Maxwell fluid through a rectangular microchannel.

Inspired by the above studies, the current study illustrates the MHD Maxwell nanofluid flow over a linearly stretched sheet near the stagnation point and slip boundary conditions. Fourier’s and Fick’s laws are presented in the constitutive relations. The nonlinear ODEs are deduced from the nonlinear PDEs by similarity transaction. The solutions are obtained via shooting method (Cash and Karp). The different involved physical parameters are examined for velocity, concentration, and temperature fields.

2 Mathematical formulation

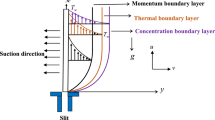
Let us consider two-dimensional laminar steady heat and mass transfer flow of an electrically conducting Maxwell nanofluid flow passed by a linear stretched surface placed along x-axis and y-axis vertical to the sheet with stagnation point at the origin (as illustrated in Fig. 1). The free stream velocity \({\mathbf{u = u}}_{e} ({\mathbf{x}}) = {\mathbf{cx}}\) and the velocity via which sheet is stretched are \({\mathbf{u}} = {\mathbf{U}}_{w} ({\mathbf{x}}) = {\mathbf{ax}}\), where \(a\) and \(c\) are positive constants. The temperature at the surface is conserved at \(T_{w}\) and \(T_{\infty }\) far away from the plate; in similar a manner, the nanoparticle volume fractions are \(C_{w}\) and \(C_{\infty }\). An external magnetic field \(H_{0}\) is applied normal to the sheet.

Fig. 1
figure 1

Geometry of the problem

Full size image

Under the above assumptions, the required equations are as follows:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(1)
$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + \lambda \left[ {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right] = - \frac{1}{\rho }\frac{\partial P}{\partial x} + \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\sigma \mu_{e}^{2} H_{0}^{2} }}{\rho }\left( {u + \lambda v\frac{\partial u}{\partial y}} \right),$$
(2)

where \(\rho\) is the density, \(\mu_{e}\) is the magnetic permeability velocity, \(\sigma\) is the electrical conductivity, \(\lambda\) is the Maxwell fluid parameter, and \(\nu\) is the kinematic viscosity. Due to hydrostatic and magnetic pressure gradient, the force will be in equilibrium as given by

$$- \frac{1}{\rho }\frac{\partial P}{\partial x} = u_{e} \frac{{du_{e} }}{dx} + \frac{{\sigma \mu_{e}^{2} H_{0}^{2} }}{\rho }u_{e}$$
(3)

Hence, Eq. (2) becomes

$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + \lambda \left[ {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right] = u_{e} \frac{{{\text{d}}u_{e} }}{{{\text{d}}x}} + \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\sigma \mu_{e}^{2} H_{0}^{2} }}{\rho }\left( {u - u_{e} + \lambda v\frac{\partial u}{\partial y}} \right).$$
(4)

The classical form of Fourier’s and Fick’s laws with the ray of Cattaneo–Christov equations takes the following form:

$$q + \lambda_{T} \left[ {\frac{\partial q}{\partial t} + V.\left( {\nabla q} \right) - q.\left( {\nabla V} \right) + (\nabla .V)q} \right] = - k_{f} \nabla T,$$
(5)
$$J + \lambda_{c} \left[ {\frac{\partial J}{\partial t} + V.\left( {\nabla J} \right) - J.\left( {\nabla V} \right) + (\nabla .V)J} \right] = - D_{B} \nabla C.$$
(6)

Assume that \(\nabla .q = 0,\,\;\nabla .J = 0,\) and for steady state \(\tfrac{\partial q}{\partial t} = 0,\,\;\tfrac{\partial J}{\partial t} = 0,\) the new equations become:

$$q + \lambda_{T} \left[ {V.\nabla q - q.\nabla V} \right] = - k_{f} \nabla T,$$
(7)
$$J + \lambda_{C} \left[ {V.\nabla J - q.\nabla J} \right] = - D_{B} \nabla C.$$
(8)

Now in component form, energy and concentration Eqs. (7) and (8) take the following form:

$$\begin{aligned} & u\partial_{x} T + v\partial_{y} T + \lambda_{T} \left[ {\partial_{x} Tu\left( {\partial_{x} u} \right) + \partial_{x} Tv\left( {\partial_{y} u} \right) + u\left( {\partial_{x} v} \right)\partial_{y} T + v\left( {\partial_{y} v} \right)\partial_{y} T} \right] \\ & \quad + \lambda_{T} \left[ {2uv\partial_{xy} T + v^{2} \partial_{yy} T + u^{2} \partial_{xx} T} \right] = \alpha \partial_{yy} T + \tau \left\{ {D_{B} \left( {\partial_{y} T\partial_{y} C} \right) + \frac{{D_{T} }}{T\infty }\left( {\partial_{y} T} \right)^{2} } \right\}, \\ \end{aligned}$$
(9)
$$\begin{aligned} & u\left( {\partial_{x} C} \right) + v\left( {\partial_{y} C} \right) + \lambda_{c} \left[ {u\partial_{x} u\left( {\partial_{x} C} \right) + v\partial_{y} u\left( {\partial_{x} C} \right) + u\left( {\partial_{x} v} \right)\partial_{y} C + v\left( {\partial_{y} v} \right)\partial_{y} C} \right] \\ & \quad \lambda_{c} \left[ { + 2uv\partial_{xy} C + v^{2} \partial_{yy} C + u^{2} \partial_{xx} C} \right] = D_{B} \partial_{yy} C + \frac{{D_{T} }}{T\infty }\partial_{yy} T - K_{1} (C - C_{\infty } ), \\ \end{aligned}$$
(10)

where \(\partial_{x} = \tfrac{\partial }{\partial x}\) and \(\partial_{y} = \tfrac{\partial }{\partial y}.\)

The specified boundary conditions of the current problem take the form

$$\begin{aligned} {\mathbf{u}}({\mathbf{x}},{\mathbf{y}}) & = {\mathbf{U}}_{w} ({\mathbf{x}}){\mathbf{ \,= ax}} + g\frac{\partial u}{\partial y},\, \, v(x,\,y) = 0, \\ T(x,\,y) & = T_{w} (x)\, = T_{\infty } + bx,\,\;C(x,\,y) = C_{w} = C_{\infty } + bx,\,{\text{at }}y = 0, \\ {\mathbf{u}}({\mathbf{x}},\,{\mathbf{y}}) & {\mathbf{ \,= u}}_{e} ({\mathbf{x}}){\mathbf{ \,= cx}} , { }T(x,\,y) = T_{\infty } , { }C(x,\,y) = C_{\infty } \;{\text{as }}y \to \infty . \\ \end{aligned}$$
(11)

Here (\(u,\,\;v\)) are the velocity components along the (\(x,\,\;y\)) directions, \(q\), \(J\) are the normal heat and mass flux, respectively, \(\;k_{f}\) represents the thermal conductivity, \(D_{B} \;\) is the Brownian motion, \(\lambda_{T}\), \(\lambda_{C}\) are the relaxation parameters for thermal and concentration, \(\alpha_{f} = \tfrac{{(\rho c)_{s} }}{{(\rho c)_{f} }}\) is the ratio of nanoparticle heat capacity to base fluid thermal capacity, \(\alpha_{f} = \tfrac{{k_{f} }}{{(\rho C_{p} )_{f} }}\) represents thermal diffusion, \(T_{w} (x,\,y)\) is known as temperature at the wall, \(C_{w} (x,\,y)\) is known as concentration at the wall, \(T\;\) and \(C\) are the temperature and concentration of the fluid, respectively, \(C_{p} \;\) is the specific heat, and \(C_{\infty }\) and \(T_{\infty }\) are the concentration and temperature free streams. Temperature of the sheet is \(T_{w} = T_{\infty } + bx,\) for heated surface \(b > 0\) so \(T_{w} > T_{\infty }\) and for cooled surface \(b < 0\) and \(T_{w} < T,\) where \(b\) is a constant and \(D_{T}\) is known as thermophoresis diffusivity.

Considering the similarity transformations, we have

$$\eta = y\sqrt {\frac{a}{\nu }} ,\, \, {\varvec{\uptheta}}\left( \eta \right) = \frac{{{\mathbf{T - T}}_{\infty } }}{{{\mathbf{T}}_{w} {\mathbf{ - T}}_{\infty } }},\,\;\phi \left( \eta \right) = \frac{{{\mathbf{C - C}}_{\infty } }}{{{\mathbf{C}}_{w} {\mathbf{ - C}}_{\infty } }},\,u = \frac{\partial \psi }{\partial y},\,\;v = - \frac{\partial \psi }{\partial x}.$$
(12)

Substituting Eq. (12) into Eqs. (1), (4), (9), (10), the present problem boundary conditions (11) are as follows:

$$\frac{{{\text{d}}^{3} f}}{{{\text{d}}\eta^{3} }} + \frac{{{\text{d}}f}}{{{\text{d}}\eta }}\frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }} - \left( {\frac{{{\text{d}}f}}{{{\text{d}}\eta }}} \right)^{2} + \lambda_{m} \left( {2f(\eta )\frac{{{\text{d}}f}}{{{\text{d}}\eta }}\frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }} - \left( {f(\eta )} \right)^{2} \frac{{{\text{d}}^{3} f}}{{{\text{d}}\eta^{3} }}} \right) + Ha^{2} \left( {1 - \frac{{{\text{d}}f}}{{{\text{d}}\eta }} + \lambda_{m} \frac{{{\text{d}}f}}{{{\text{d}}\eta }}\frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }}} \right) + 1 = 0,$$
(13)
$$\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }} + Pr\left[ {f(\eta )\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }} + N_{b} \frac{{{\text{d}}\varphi }}{{{\text{d}}\eta }}\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }} + N_{t} \left( {\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }}} \right)^{2} + \delta_{t} \left( {f(\eta )\frac{{{\text{d}}f}}{{{\text{d}}\eta }}\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }} - \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }}\left( {f(\eta )} \right)^{2} } \right)} \right] = 0,$$
(14)
$$\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}\eta^{2} }} + \frac{{N_{t} }}{{N_{b} }}\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }} + PrLe\left[ {f(\eta )\frac{{{\text{d}}\phi }}{{{\text{d}}\eta }} - K\phi (\eta ) + \delta_{c} \left( {f(\eta )\frac{{{\text{d}}f}}{{{\text{d}}\eta }}\frac{{{\text{d}}\phi }}{{{\text{d}}\eta }} - \frac{{{\text{d}}^{2} \phi }}{{{\text{d}}\eta^{2} }}\left({f(\eta } \right)^{2}) } \right)} \right] = 0.$$
(15)

Using (11), the associated boundary conditions become

$$\begin{aligned} \frac{{{\text{d}}f}}{{{\text{d}}\eta }} & = 1 + k\frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }},\,\;f(\eta ) = 0 , { }\theta (\eta ) = 1,\,\;\phi (\eta ) = 1,\,\;{\text{at}}\;\eta = 0, \\ \frac{{{\text{d}}f}}{{{\text{d}}\eta }} & \to A,\, \, \theta \to 0,\,\;\phi \to 0,\,\;{\text{as}}\;\eta \to \infty . \\ \end{aligned}$$
(16)

where the fluid relaxation parameter is \(\lambda_{m} = \lambda a\), Hartmann number is \(Ha^{2} = \mu_{e} H_{0} \sqrt {\tfrac{\sigma }{\rho a}}\), concentration relaxation parameter is \(\delta_{c} = a\lambda_{C}\), ratio parameter is \(A = \frac{c}{a}\), Lewis number is \(Le = \tfrac{\alpha }{{D_{B} }}\), thermal relaxation parameter is \(\delta_{t} = a\lambda_{T}\), thermophoresis parameter is \(N_{t} = \tfrac{{\tau D_{t} (T_{w} - T_{0} )}}{{T_{\infty } \nu }}\), Prandtl number is \(Pr = \tfrac{{\mu c_{p} }}{k}\), Brownian motion parameter is \(N_{b} = \tfrac{{\tau D_{B} (C_{w} - C_{0} )}}{\nu }\), slip parameter is \({\mathbf{k = g}}\sqrt {\tfrac{a}{v}}\), and chemical reactive species is \(K = \tfrac{{K_{1} }}{a}\).

Friction factor coefficient (\(C_{f}\)) is defined as:

$$C_{f} = \frac{{\tau_{w} }}{{\rho u_{e}^{2} }} = Re_{x}^{{\tfrac{ - 1}{2}}} (f^{{\prime \prime }} (0) + \lambda_m(f^{{\prime \prime }} (0)f^{\prime } (0)+f(0) f^{{{\prime \prime \prime }}} (0)).$$
(17)

Here \(\tau_{w}\) denotes the wall shear stress and is given by

$$\tau_{w} = \mu \frac{\partial }{\partial y}(u + \lambda v\frac{\partial u}{\partial y})_{y = 0} .$$
(18)

where \(Re_{x} = u_{e} x\tfrac{x}{\nu }\) is local Reynolds number.

3 Numerical procedure

Numerical solution of the nonlinear differential Eqs. (13)–(15) along with Neumann boundary conditions (16) is achieved by applying the shooting method with RK-4 integration technique for various values of parameters. Let \(y_{1} = f,\,\;y_{2} = f^{{\prime }} ,\,\;y_{3} = f^{{\prime \prime }} ,\,\;y_{4} = \theta ,\,\;y_{5} = \theta^{{\prime }} ,\,\;y_{6} = \phi\) and \(y_{7} = \phi^{{\prime }} .\)

Hence, the leading equations become

$$y_{1} = y_{2}^{{\prime }} ,$$
(19)
$$y_{2}^{{\prime }} = y_{3} ,$$
(20)
$$y_{3}^{{\prime }} = \frac{{y_{2}^{2} - y_{2} y_{3} - \lambda_{m} \left( {y_{1} y_{2} y_{3} } \right) - Ha^{2} \left( {1 - y_{2} + \lambda_{m} y_{2} y_{3} } \right) - 1}}{{\left( {1 - \lambda_{m} y_{1} } \right)}},$$
(21)
$$y_{4}^{{\prime }} = y_{5} ,$$
(22)
$$y_{5}^{{\prime }} = \frac{{ - Pr\left( {y_{1} y_{5} + N_{b} y_{7} y_{5} + N_{t} \left( {y_{5} } \right)^{2} + \delta_{t} \left( {y_{2} y_{1} y_{5} } \right)} \right)}}{{\left( {1 - \delta_{t} \left( {y_{1} } \right)^{2} } \right)}},$$
(23)
$$y_{6}^{{\prime }} = y_{7} ,$$
(24)
$$y_{7}^{{\prime }} = \frac{{ - PrLe\left( {y_{1} y_{6} - Ky_{6} + \delta_{c} \left( {y_{2} y_{1} y_{6} } \right)} \right) - \tfrac{{N_{t} }}{{N_{b} }}y_{5}^{{\prime }} }}{{\left( {1 - \delta_{c} \left( {y_{1} } \right)^{2} } \right)}},$$
(25)

and subsequent initial conditions are:

$$\begin{aligned} y_{1} \left( 0 \right) & = 0,\,\;y_{2} \left( 0 \right) = 1 + ky_{2} ,\,\;y_{4} \left( 0 \right) = 1,\,\;y_{6} \left( 0 \right) = 1,\, \\ y_{2} \left( \eta \right) & \to A,\,\;\;y_{4} \left( \eta \right) \to 0,\,\;y_{6} \left( \eta \right) \to 0\;{\text{when}}\,\,\eta \to \infty . \\ \end{aligned}$$
(26)

This technique is successfully used to solve the different problems related to boundary layer flows. The boundary conditions \(f^{{\prime }} (0),\,\;\theta (0)\) and \(\phi(0)\) for \(\eta \to \infty\) are converted into finite interval length (here it is \(\eta = 5\)). Insert three initial guesses to \(f^{{\prime \prime }} (0)\), \(\theta^{{\prime }} (0)\) and \(\phi^{{\prime }} (0)\) for approximate solution. Here the step size and convergence criteria are chosen to be \(0.001\) and \(10^{ - 6}\) (in all cases).

4 Results and discussion

The main effort of this work is to examine the influence of magnetic field and stagnation point Maxwell nanofluid flow due to a linear stretching surface with slip conditions. The governing differential Eqs. (12)–(15) along with corresponding boundary conditions (16) are solved numerically by implying shooting procedure (Cash and Karp). Figure 2 represents the change in velocity profile for distinct values of Hartmann number \(Ha\). From this figure, the enhancement in \(Ha\) results in decrease in velocity profile. Since the Hartmann number \(Ha\) represents the ratio of MHD force to viscous force, the enhancement in \(Ha\) leads to stronger the MHD force, which declares the velocity motion. Figure 3 depicts the variation of slip parameter \(k\) on velocity profile. The influence of slip parameter \(k\) significantly enhances the velocity profile. Figure 4 illustrates the variation of fluid relaxation parameter \(\lambda_{m}\) on velocity profile. It can be analyzed that the velocity of the fluid reduces by enhancing the fluid relaxation parameter \(\lambda_{m}\). Figure 5 represents the change in temperature distribution for distinct values of \(N_{t}\). It is found that by enhancing \(N_{t}\), the temperature distribution also increases. Figure 6 depicts the variation of Brownian motion \(N_{b}\) on temperature distribution. It can be analyzed that by increasing \(N_{b}\), the mass diffusivity trekked up which leads to enhancement in the temperature and the boundary layer thickness. Figure 7 shows the behavior of Prandtl number \(Pr\) on temperature profile. It is found that the temperature profile reduces with rising values of Prandtl \(Pr\). Figure 8 presents the deviation of temperature profile for distinct values of \(\delta_{t}\). It is seen that by enhancing thermal relaxation parameter \(\delta_{t}\), fluid particles require more time to heat the boundary layer region, and as a result temperature profile reduces. Figure 9 displays the effect of relaxation parameter \(\delta_{c}\) on concentration distribution. From this figure, it is observed that by increasing the relaxation parameter \(\delta_{t}\), the concentration profile reduces. Figure 10 represents the variation on concentration profile for different values of chemical reaction \(K\). It is found that for large values of chemical reaction \(K\) reduces the concentration profile. Figure 11 represents the influence of Lewis number \(Le\) on nanoconcentration profile. It is found that the higher values of Lewis number \(Le\) lead to reduction in the mass diffusivity, so the concentration profile reduces. Figures 12 and 13 validate the distribution of skin friction coefficient \(C_{f} \;Re_{x}^{{\tfrac{1}{2}}}\) with respect to Hartmann number \(Ha\) and for several values of slip parameter \(k\) and fluid relaxation parameter \(\lambda_{m}\). It is very important to see that the skin friction coefficient \(C_{f} \;Re_{x}^{{\tfrac{1}{2}}}\) enhances by enhancing slip parameter \(k\) but decreases by increasing the fluid relaxation parameter \(\lambda_{m}\). Table 1 shows that the fraction factor rises due to an increase in Hartmann number \(Ha\) and fluid relaxation parameter \(\lambda_{m}\) and opposite behavior is noticed for slip parameter \(k\). The achieved results are in good agreement with Afify and Elgazery [25] for different values \(Ha\) and \(\lambda_{m}\) as shown in Table 2. Table 3 is sketched for the comparative investigation between Hsiao [26] and present results. \(N_{t}\) \(N_{b} = 0.1,\,\;Le = Pr = 10\) and \(\lambda_{m} = Ha = k = St = \delta t = \delta c = K = A = 0.0\).

Fig. 2
figure 2

Outcome of Ha on \(f^{{\prime }} (\eta )\)

Full size image
Fig. 3
figure 3

Outcome of k on \(f^{{\prime }} (\eta )\)

Full size image
Fig. 4
figure 4

Outcome of \(\lambda_{m}\) on \(f^{{\prime }} (\eta )\)

Full size image
Fig. 5
figure 5

Outcome of \(Pr\) on \(\theta \left( \eta \right)\)

Full size image
Fig. 6
figure 6

Outcome of \(N_{b}\) on \(\theta \left( \eta \right)\)

Full size image
Fig. 7
figure 7

Outcome of \(N_{t}\) on \(\theta \left( \eta \right)\)

Full size image
Fig. 8
figure 8

Outcome of \(\delta_{t}\) on \(\theta \left( \eta \right)\)

Full size image
Fig. 9
figure 9

Outcome of \(\delta_{t}\) on \(\phi \left( \eta \right)\)

Full size image
Fig. 10
figure 10

Outcome of K on \(\phi \left( \eta \right)\)

Full size image
Fig. 11
figure 11

Outcome of \(Le\) on \(\phi\left( \eta \right)\)

Full size image
Fig. 12
figure 12

\(C_{f} Re_{x}^{{\frac{1}{2}}}\) for various values of Ha and \(\lambda_{m}\)

Full size image
Fig. 13
figure 13

\(C_{f} Re_{x}^{{\frac{1}{2}}}\) for various values of Ha and k

Full size image
Table 1 Computational results of \(C_{f} Re_{x}^{{\frac{1}{2}}}\) for different values of \(Ha,\,\;k\;\) and \(\lambda_{m}\) when \(K = A = N_{b} = 0.1,\,\;Le = 1.0,\,\;\delta_{c} = \delta_{t} = 0.0,\,\;N_{t} = 0.5,\) and \(Pr = 1.1\)
Full size table
Table 2 Comparison of \((f^{{\prime \prime }} (0) + \lambda_{m} (f^{ \prime } (0)f^{{\prime \prime }} (0)+f(0)f^{{{\prime \prime \prime }}} (0)))\) with the previous literature when \(N_{b} = k = St = 0.1,\,\;\delta t = \delta c = K = A = 0.0,\,\;N_{t} = 0.5\) and \(Le = Pr = 1.0\)
Full size table
Table 3 Comparison of \(- \theta^{{\prime }} (0)\) and \(- \phi^{{\prime }} \left( 0 \right)\) with the previous literature when \(\lambda_{m} = Ha = k = St = \delta t = \delta c = K = A = 0.0,\,\;N_{t} = 0.1\) and \(Le = Pr = 10\)
Full size table

5 Conclusions

The main results for heat and mass exchanger in MHD stagnation point Maxwell nanofluid flow past a linear stretching surface in the presence of slip effects are summarized below:

  • Rising the Hartmann number \(\;Ha\) and slip parameter \(k\) leads to decline in velocity profile.

  • Larger values of fluid relaxation parameter \(\lambda_{m}\), increase the velocity profile.

  • For increasing values of chemical reaction, \(K,\) Prandtl number \(Pr\), thermal relaxation parameter \(\delta_{t}\), concentration relaxation parameter \(\delta_{c}\) and Lewis number \(Le\) reduce the concentration and temperature profiles.

  • Temperature profile increases for increasing values of thermophoresis parameter \(N_{t}\) and Brownian motion \(N_{b}\).

  • Skin friction coefficient reduces \(C_{f} \;Re_{x}^{{\tfrac{1}{2}}}\) for large values of slip parameter \(k\) but opposing behavior is noticed for fluid relaxation parameter \(\lambda_{m}\).