High-order triangular finite elements applied to visco-hyperelastic materials under plane stress

Abstract

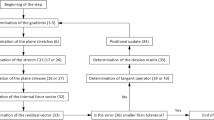
A finite element formulation for analysis of highly deformable viscoelastic materials under plane stresses is presented. The element is the isoparametric plane triangle of any-order. The constitutive modeling is based on a Lagrangian visco-hyperelastic framework, in which the multiplicative split of the deformation gradient is used. The internal variable employed is the viscous right Cauchy–Green stretch tensor. The work is restricted to the compressible neo-Hookean hyperelastic law, the Zener rheological model and an isochoric nonlinear evolution equation, although other models can be further implemented. The plane stress condensation and the compact 2D constitutive relation are described. Three large deformation problems are numerically analyzed to validate the methodology: a membrane with high compressive strain levels and mesh distortion; a perforated plate with stress concentration; and a circular ring under nonlinear bending. Meshes with different element orders (from linear to sixth) are employed. Results confirm that, except for the linear degree, mesh refinement completely remove locking problems, providing an accurate and, thus, a reliable prediction of the mechanical behavior. It is also demonstrated that the creep phenomenon can be reproduced in finite strain regime. The novelty of the paper is the convergence analysis regarding displacements, strains and stresses in the context of plane stress visco-hyperelasticity.

Appendices

Appendix 1: Viscous incompressibility

The viscous incompressibility can be shown by determining the rate of the squared viscous Jacobian from expression (24):

$$\begin{aligned} \mathop {\overline{{\left( {J^{v} } \right)^{2} }} }\limits^{ \cdot } & = \frac{{\partial \left( {J^{v} } \right)^{2} }}{{\partial {\mathbf{C}}^{v} }} :\mathop {{\mathbf{C}}^{v} }\limits^{ \cdot } = \left[ {\left( {J^{v} } \right)^{2} \left( {{\mathbf{C}}^{v} } \right)^{ - 1} } \right] :\left[ {\frac{2}{\eta }{\text{dev}}\left( {{\mathbf{CS}}_{q} } \right){\mathbf{C}}^{v} } \right] = \left( {J^{v} } \right)^{2} \frac{2}{\eta }{\mathbf{I}} :\left[ {{\text{dev}}\left( {{\mathbf{CS}}_{q} } \right)} \right] \\ & = \left( {J^{v} } \right)^{2} \frac{2}{\eta }{\text{tr}}\left[ {{\text{dev}}\left( {{\mathbf{CS}}_{q} } \right)} \right] = 0 \\ \end{aligned}$$

(42)

Moreover, since the initial value of the viscous Jacobian is always unitary, then:

$$\left( {J^{v} } \right)^{2} = J^{v} = 1$$

(43)

In other words, the viscous strain is incompressible, as assumed in finite elastoplasticity.

Appendix 2: Derivatives of stress tensor S

From the last result of expression (27), one can obtain the following consistent tangent operator:

$$\frac{{\partial {\mathbf{S}}}}{{\partial {\mathbf{C}}}} = \frac{\partial }{{\partial {\mathbf{C}}}}\left[ { - C_{33} \left( {\mu_{\infty } + \frac{{\mu_{e} }}{{C_{33}^{v} }}} \right)\left( {{\mathbf{C}}^{ - 1} } \right)} \right] = - \left( {\mu_{\infty } + \frac{{\mu_{e} }}{{C_{33}^{v} }}} \right)\left( {{\mathbf{C}}^{ - 1} } \right) \otimes \frac{{\partial C_{33} }}{{\partial {\mathbf{C}}}} - C_{33} \left( {\mu_{\infty } + \frac{{\mu_{e} }}{{C_{33}^{v} }}} \right)\frac{{\partial \left( {{\mathbf{C}}^{ - 1} } \right)}}{{\partial {\mathbf{C}}}}$$

(44)

where symbol $\otimes$ represents the tensor product. The derivatives of stress tensor S regarding the viscous stretch tensor C^v has been neglected in (44), since the consistent tangent operator above is used along the elastic prediction phase. The derivative $\partial C_{33} /\partial {\mathbf{C}}$ can be found using a scalar auxiliary variable defined from the last result of (26):

$$f = C_{11} C_{22} - C_{12}^{2} = \frac{1}{{C_{33} }}\left\{ {\exp \left[ {\frac{{\mu_{\infty } \left( {1 - C_{33} } \right) + \mu_{e} - \mu_{e} \frac{{C_{33} }}{{C_{v33} }}}}{{K_{\infty } + K_{e} }}} \right]} \right\}^{2}$$

(45)

This scalar can be understood as the determinant of the plane tensor C (with dimensions 2 × 2). Applying the definition (45), one can obtain the following result:

$$\frac{{\partial C_{33} }}{{\partial {\mathbf{C}}}} = \frac{{\partial C_{33} }}{\partial f}\frac{\partial f}{{\partial {\mathbf{C}}}} = \left( {\frac{\partial f}{{\partial C_{33} }}} \right)^{ - 1} \frac{\partial f}{{\partial {\mathbf{C}}}}$$

(46)

$$\frac{\partial f}{{\partial {\mathbf{C}}}} = {\text{adj}}\left( {\mathbf{C}} \right) = \left[ {\begin{array}{*{20}c} {C_{22} } & { - C_{12} } \\ { - C_{12} } & {C_{11} } \\ \end{array} } \right]$$

(47)

$$\frac{\partial f}{{\partial C_{33} }} = - \frac{f}{{C_{33} }} + \frac{2}{{C_{33} }}\left\{ {\exp \left[ {\frac{{\mu_{\infty } \left( {1 - C_{33} } \right) + \mu_{e} - \mu_{e} \frac{{C_{33} }}{{C_{v33} }}}}{{K_{\infty } + K_{e} }}} \right]} \right\}^{2} \left( {\frac{{ - \mu_{\infty } - \frac{{\mu_{e} }}{{C_{v33} }}}}{{K_{\infty } + K_{e} }}} \right)$$

(48)

where ${\text{adj}}\left( {} \right)$ denotes the adjugate matrix.

The remaining derivate in (44) is determined from the inverse of tensor C:

$${\mathbf{C}}^{ - 1} = \frac{1}{{C_{11} C_{22} - C_{12}^{2} }}\left[ {\begin{array}{*{20}c} {C_{22} } & { - C_{12} } \\ { - C_{12} } & {C_{11} } \\ \end{array} } \right] = \frac{1}{f}{\text{adj}}\left( {\mathbf{C}} \right)$$

(49)

$$\frac{{\partial {\mathbf{C}}^{ - 1} }}{{\partial {\mathbf{C}}}} = {\text{adj}}\left( {\mathbf{C}} \right) \otimes \frac{\partial }{{\partial {\mathbf{C}}}}\left( {\frac{1}{f}} \right) + \frac{1}{f}\frac{{\partial {\text{adj}}\left( {\mathbf{C}} \right)}}{{\partial {\mathbf{C}}}}$$

(50)

Using expressions (45) and (47), one can find the following derivatives:

$$\frac{\partial }{{\partial {\mathbf{C}}}}\left( {\frac{1}{f}} \right) = - \frac{1}{{f^{2} }}\frac{\partial f}{{\partial {\mathbf{C}}}} = - \frac{1}{{f^{2} }}\left[ {\begin{array}{*{20}c} {C_{22} } & { - 2C_{12} } \\ { - 2C_{12} } & {C_{11} } \\ \end{array} } \right]$$

(51)

$$\frac{{\partial {\text{adj}}\left( {\mathbf{C}} \right)_{11} }}{{\partial C_{22} }} = \frac{{\partial {\text{adj}}\left( {\mathbf{C}} \right)_{22} }}{{\partial C_{11} }} = - \frac{{\partial {\text{adj}}\left( {\mathbf{C}} \right)_{12} }}{{\partial C_{12} }} = - \frac{{\partial {\text{adj}}\left( {\mathbf{C}} \right)_{21} }}{{\partial C_{12} }} = 1$$

(52)

where the remaining terms of $\partial {\text{adj}}\left( {\mathbf{C}} \right)/\partial {\mathbf{C}}$ are null.

Along the viscous update, the derivative of stress tensor S regarding viscous tensor C^v is needed. From the compact form (27):

$$\frac{{\partial {\mathbf{S}}}}{{\partial {\mathbf{C}}^{v} }} = - \left( {\mu_{\infty } + \frac{{\mu_{e} }}{{C_{33}^{v} }}} \right){\mathbf{C}}^{ - 1} \otimes \frac{{\partial C_{33} }}{{\partial {\mathbf{C}}^{v} }} - C_{33} \mu_{e} {\mathbf{C}}^{ - 1} \otimes \frac{\partial }{{\partial {\mathbf{C}}^{v} }}\left( {\frac{1}{{C_{33}^{v} }}} \right) + \mu_{e} \frac{{\partial \left( {{\mathbf{C}}^{v} } \right)^{ - 1} }}{{\partial {\mathbf{C}}^{v} }}$$

(53)

The derivative of C₃₃ is obtained from (45):

$$\frac{{\partial C_{33} }}{{\partial {\mathbf{C}}_{v} }} = \frac{{\partial C_{33} }}{\partial f}\frac{\partial f}{{\partial {\mathbf{C}}_{v} }} = \left( {\frac{\partial f}{{\partial C_{33} }}} \right)^{ - 1} \frac{\partial f}{{\partial {\mathbf{C}}_{v} }}$$

(54)

$$\frac{\partial f}{{\partial {\mathbf{C}}_{v} }} = - 2\left\{ {{ \exp }\left[ {\frac{{\mu_{\infty } \left( {1 - C_{33} } \right) + \mu_{e} - \mu_{e} \frac{{C_{33} }}{{C_{v33} }}}}{{K_{\infty } + K_{e} }}} \right]} \right\}^{2} \frac{{\mu_{e} }}{{K_{\infty } + K_{e} }}\frac{\partial }{{\partial {\mathbf{C}}_{v} }}\left( {\frac{1}{{C_{v33} }}} \right)$$

(55)

To determine the derivative of the inverse of the component $C_{33}^{v}$, one can use the viscous incompressibility Eq. (25):

$$\frac{\partial }{{\partial {\mathbf{C}}_{v} }}\left( {\frac{1}{{C_{v33} }}} \right) = \left[ {\begin{array}{*{20}c} {C_{v22} } & { - C_{v21} } \\ { - C_{v12} } & {C_{v11} } \\ \end{array} } \right] = {\text{adj}}\left( {{\mathbf{C}}^{v} } \right)$$

(56)

Finally, the derivative $\partial \left( {{\mathbf{C}}^{v} } \right)^{ - 1} /\partial {\mathbf{C}}^{v}$ can be obtained in the same way as performed in (49) and (50).