1 Introduction

The traditional gear cutting method for spiral bevel gears has been unable to meet the high precision, flexibility and efficiency requirements of modern machining. The development of a multi-axis numerical control (NC) machine tool and optimization of the interpolation algorithm have greatly improved the machining quality and efficiency of complex curved surfaces. At the same time, this has made the processing of spiral bevel gears using general multi-axis NC machine tools an important developing direction and research hotspot [1,2,3,4,5]. For example, a study conducted by Alvarez et al. [6] revealed that air turbine technology and special finishing tools can be used in the finish machining of the spiral bevel gear tooth surface to improve machining accuracy. Furthermore, in studies conducted by Adayi et al. [7, 8], electrochemical finishing was applied to optimize the tooth surface. This method improved the processing quality and realized the modification of the tooth surface micro-profile. In order to reduce the influence of tool and transmission error on the quality of the tooth surface, Tang Jinyuan improved the machining quality of the gear with a feedback correction method and machine settings [9,10,11,12,13]. These studies provided ways and means from different aspects to improve the machining quality of spiral bevel gears and ameliorate tooth surface quality. Nonetheless, although a great number of published studies have focused on the machining process and tooth surface treatment after machining, hardly any of these methodologies considered the establishment of a digital model before machining. A related research [14] revealed that the surface smoothness and complexity of the digital model are key factors that influence machining quality.

According to the wavelet theory, any curved surface can be decomposed into low frequency curved surfaces, which represent the principal features and high frequency curved surfaces, which represent the detailed features. The detail features exhibited by the high frequency curved surfaces are important factors that influence the smoothness and complexity of the curved surfaces. Based on the enormous advantages of the non-uniform rational basis spline (NURBS) curve, the surface and its interpolation algorithm [15,16,17] had a high precision NC machining process. The present study used the cubic B-spline wavelet to decompose and reconstruct discrete points of the tooth surface to reduce the influence of high frequency curvature on surface smoothness. On the premise of ensuring design accuracy, the complexity of the tooth surface was reduced; and the smoothness of the tooth surface was improved, realizing the accurate fitting of the tooth surface. This provides a theoretical basis for machining spherical involute spiral bevel gears with general multi-axis NC machine tools.

2 Obtaining the discrete points of tooth surfaces

2.1 Spherical involute theory

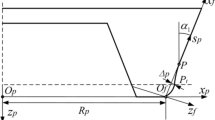
In the actual transfer motion of the spiral bevel gears, the distance between the fixed point on the tooth surface and vertex of the pitch cone remained unchanged. Hence, the curves that consisted of the tooth surface were spherical involutes [18]. As shown in Fig. 1, when the rolling section Q was tangent to the base cone K and these had pure rolling, and the motion track (AB) of the fixed point B on plane Q became the spherical involute.

Fig. 1
figure 1

Formation of the spherical involute

Full size image

In the moving coordinate system OX′Y′Z′, the equation of line OB is

$$\left\{ {\begin{array}{*{20}l} {x^{{\prime }} = l\sin (\psi )} \hfill \\ {y^{{\prime }} = 0} \hfill \\ {z^{{\prime }} = l\cos (\psi )} \hfill \\ {\psi = \beta \sin (\delta_{b} )} \hfill \\ \end{array} } \right.$$
(1)

where l is the length of OB and the other parameters are as described in Fig. 1. According to the coordinate transformation principle, and the relationship between coordinate system OX′Y′Z and coordinate system OXYZ, this can be described as follows:

$$\left[ {\begin{array}{*{20}c} {x^{{\prime }} } \\ {y^{{\prime }} } \\ {z^{{\prime }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\sin (\beta )} \hfill & { - \cos (\beta )} \hfill & 0 \hfill \\ {\cos (\delta_{b} )\cos (\beta )} \hfill & {\cos (\delta_{b} )\sin (\beta )} \hfill & { - \sin (\delta_{b} )} \hfill \\ {\sin (\delta_{b} )\cos (\beta )} \hfill & {\sin (\delta_{b} )\sin (\beta )} \hfill & {\cos (\delta_{b} )} \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right]$$
(2)

The coordinates of different points on the tooth surface can be obtained by changing the value of ω and l [19]. The distribution situation of the initial points of the spherical involute on the base cone surface determines the shape of the bevel gears. If a set of initial points on the base cone surface is a straight line along the generatrix, a straight bevel gear is generated. If a set of initial points on the base cone surface is an oblique line, a skew bevel gear is generated. Furthermore, if a set of initial points on the base cone surface is a spiral line, a spiral bevel gear is generated.

2.2 Spiral line

The spiral line is solved based on the principle of the gear cutting theory, as depicted in Fig. 2. The circle O1 represents the position of the cutter head. The cutter head rotates at an angular speed ω1. At the same time, it rotates around axis Z at an angular speed ω, and ω1 = 2ω. Furthermore, the base cone rotates at angular speed ω2 and ω/ω2 = sin (b). According to the geometric relation, the track of point A that belongs to the head cutter is a line along axis X and the equation of the track can be represented as follows:

$$\left\{ {\begin{array}{*{20}l} {x = - 2r\sin (\omega t)} \hfill \\ {y = 0 \, } \hfill \\ {z = 0 \, } \hfill \\ \end{array} } \right.$$
(3)

where r is radius of the cutter head, and t is the time variable. Since the motion between the base cone and surface O is pure rolling, the track of A on the base cone surface is a spiral line [20].

Fig. 2
figure 2

Principle of gear cutting

Full size image

In the present study, the surface width factor was 1/3, while r = 5/6La. La is the outer cone distance.

2.3 Example

The main parameters of a pair of meshing spiral bevel gears which were zero modified gears are shown in Table 1. According to the data in Table 1, the value of β, \(\psi\), l, r and ω can be confirmed according to a Ref. [21]. As shown in Fig. 3, 55 discrete points of each tooth surface were obtained by programming in MATLAB. The coordinate values of these points can also be obtained from MATLAB.

Table 1 Main parameters of a pair of meshing gears
Full size table
Fig. 3
figure 3

Distribution situation of discrete points of the tooth surface gear (left) and pinion (right)

Full size image

3 Wavelet representation of the NURBS tooth surface

3.1 Representation of cubic NURBS surfaces

The equation for the cubic NURBS curved surface is

$$\varvec{S}(\varvec{u},\varvec{v}) = \frac{{\sum\limits_{i = 0}^{n} {\sum\limits_{j = 0}^{m} {\varvec{N}_{i,3} \text{(}\varvec{u}\text{)}\varvec{N}_{j,3} (\varvec{v})W_{i.j} V_{i,j} } } }}{{\sum\limits_{i = 0}^{n} {\sum\limits_{j = 0}^{m} {\varvec{N}_{i,3} \text{(}\varvec{u}\text{)}\varvec{N}_{j,3} (\varvec{v})W_{i.j} } } }} \, \varvec{u},\varvec{v} \in [\text{0,1}]$$
(4)

where Ni,3(u) and Ni,3 (v) represent the cubic B-spline base function at the u-direction and v-direction, respectively, which can be confirmed using the de Boor-Cox recursion formula. Wi,j are weighting factors, while Vi,j are control vertices. The value of Wi,j and Vi,j can be inversely calculated using the NURBS curve interpolation method, and the calculation procedure was according to a Ref. [22], p 159. Furthermore, u and v are node vectors. In the present study, a modified radial accumulated chord length parameter method was applied to solve these node vectors.

3.2 Decomposition and reconstruction of NURBS surfaces by cubic B-spline wavelet

The essence of wavelet processing toward the curves and surfaces is the wavelet processing of the control points of the curve and surface. According to the wavelet decomposition principle, NURBS surfaces can be decomposed into low frequency curved surfaces with high smoothness and high frequency curved surfaces with low smoothness.

SL (u, v) represents the tooth surface to be processed, Niu and Niv are the function spaces at the u-direction and v-direction on the tooth surface, respectively. Niu and Njv are the 2i + 3 cubic B-spline base functions defined by node vector \(\left[ {0,0,0,0,\frac{1}{{2^{i} }},\frac{2}{{2^{i} }}, \ldots ,1 - \frac{1}{{2^{i} }},1,1,1,1} \right]\) and \(\left[ {0,0,0,0,\frac{1}{{2^{j} }},\frac{2}{{2^{j} }}, \ldots ,1 - \frac{1}{{2^{j} }},1,1,1,1} \right]\), respectively. Therefore:

$$\varvec{N}_{u}^{i} = \left( {\varvec{N}_{u0}^{i} ,\varvec{N}_{u1}^{i} , \ldots ,\varvec{N}_{{u2^{i} + 2}}^{i} } \right)$$
(5)
$$\varvec{N}_{v}^{j} = \left( {\varvec{N}_{v0}^{j} ,\varvec{N}_{v1}^{j} , \ldots ,\varvec{N}_{{v2^{i} + 2}}^{j} } \right)$$
(6)

Since the principle of the u-direction and v-direction is the same, the u-direction was taken as an example to make the explanation.

\(\varvec{N}_{u}^{i - 1} = \left( {\varvec{N}_{u0}^{i - 1} ,\varvec{N}_{u1}^{i - 1} , \cdots \varvec{N}_{{u2^{i - 1} + 2}}^{i - 1} } \right)\) are the 2i−1 + 3 cubic B-spline base functions defined by node vectors \(\left[ {0,0,0,0,\frac{1}{{2^{i - 1} }},\frac{2}{{2^{i - 1} }}, \ldots ,1 - \frac{1}{{2^{i - 1} }},1,1,1,1} \right]\). Hence, Ni−1u is the base function of Niu. According to the nodes inserting algorithm, there is a matrix Ai ((2i + 3) rows and (2i−1 + 3) columns) to make Ni−1u = Niu Ai, and \(\varvec{N}_{u}^{i - 1} \in \varvec{N}_{u}^{i}\). However, Ni−1u can not represent the whole message that Niu contained. Therefore, \(\varvec{M}_{u}^{i - 1} = \left( {\varvec{M}_{u0}^{i - 1} ,\varvec{M}_{u1}^{i - 1} , \ldots ,\varvec{M}_{{u2^{i - 1} + 2}}^{i - 1} } \right)\) was introduced constituted by wavelet basic functions. Mi−1u is the orthogonal complement space of Ni−1u in Niu, that is

$$\varvec{N}_{u}^{i} = \varvec{M}_{u}^{i - 1} \oplus \varvec{N}_{u}^{i - 1}$$
(7)

Mi−1u is the subspace of Niu, and it can be linearly represented by Niu. Hence, there is a matrix Bi ([2i + 1] rows and 2i−1 columns) to make Mi−1u = Niu Bi. Ai and Bi are decomposition matrices, and the value of which can be referred to a Ref. [23]. Correspondingly, there are reconstruction matrices Pi and Qi to arrive at the following:

$$\left[ {\varvec{N}_{u}^{i - 1} |\varvec{M}_{u}^{i - 1} } \right]\left[ {\begin{array}{*{20}c} {\varvec{P}_{i} } \\ {\varvec{Q}_{i} } \\ \end{array} } \right] = \varvec{N}_{u}^{i}$$
(8)

According to the relationship between decomposition and reconstruction, there is

$$\left[ {\varvec{A}{}_{i}|\varvec{B}_{i} } \right]\left[ {\begin{array}{*{20}c} {\varvec{P}_{i} } \\ {\varvec{Q}_{i} } \\ \end{array} } \right] = \varvec{E}$$
(9)

where Ni−1u is the scaling function represented by the low frequency curved surface with high smoothness and Mi−1u is the wavelet function represented by the high frequency curved surface with low smoothness.

The vector form of the NURBS surface is

$$\varvec{S}^{L} (\varvec{u},\varvec{v}) =\varvec{N}_{u}^{i} \varvec{V}_{i.j}^{L} \left[ {\varvec{N}_{v}^{j} } \right]^{\rm T}$$
(10)

VLi,j is the coordinates of the control points. SL(u,v) can be decomposed into low frequency surface SL−1(u,v) and high frequency surface GL−1(u,v), that is

$$\varvec{S}^{L} (\varvec{u},\varvec{v}) = \varvec{S}^{{L{ - }1}} (\varvec{u},\varvec{v}){ + }\varvec{G}^{L - 1} (\varvec{u},\varvec{v})$$
(11)

where \(\varvec{S}^{{L{ - }1}} (\varvec{u},\varvec{v}) = \varvec{N}_{u}^{{i{ - }1}} \varvec{V}_{i - 1.j - 1}^{{L{ - }1}} \left[ {\varvec{N}_{v}^{{j{ - }1}} } \right]^{\rm T}\), \(\varvec{G}^{L - 1} (\varvec{u},\varvec{v}) = \varvec{M}_{u}^{{i{ - }1}} \varvec{D}_{1}^{L - 1} \left[ {\varvec{M}_{v}^{j - 1} } \right]^{\rm T} + \varvec{M}_{u}^{{i{ - }1}} \varvec{D}_{2}^{L - 1} \left[ {\varvec{M}_{v}^{j - 1} } \right]^{\rm T}\)\(\varvec{ + M}_{u}^{{i{ - }1}} \varvec{D}_{3}^{L - 1} \left[ {\varvec{M}_{v}^{j - 1} } \right]^{\rm T}\), and DL−1i(1 = 1, 2, 3) are the detailed data of the control points [24]. Combining with Eqs. (10) and (11), VLi,j can be expressed as follows:

$$\varvec{V}_{i.j}^{L} { = }\left[ {\begin{array}{*{20}c} {\varvec{P}_{i} } & {\varvec{Q}_{i} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{V}_{i - 1.j - 1}^{{L{ - }1}} } & {\varvec{D}_{1}^{L - 1} } \\ {\varvec{D}_{2}^{L - 1} } & {\varvec{D}_{3}^{L - 1} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{P}_{j} } \\ {\varvec{Q}_{j} } \\ \end{array} } \right]$$
(12)

Since the value of \(\varvec{V}_{i.j}^{L} ,\varvec{A}_{i} ,\varvec{B}_{i} ,\varvec{A}_{j} ,\varvec{B}_{j}\) has been confirmed, the value of \(\varvec{V}_{i - 1.j - 1}^{{L{ - }1}}\) and \(\varvec{D}_{i}^{L - 1} (i = 1,2,3)\) can be determined. Keeping \(\varvec{V}_{i - 1.j - 1}^{{L{ - }1}}\) as is and making \(\varvec{D}_{i}^{L - 1} (i = 1,2,3)\) equal to zero, \(\varvec{V}_{i - 1.j - 1}^{{L{ - }1}}\) and \(\varvec{D}_{i}^{L - 1} (i = 1,2,3)\) are introduced in Eq. (12) to calculate the value of \(\varvec{V}_{i.j}^{L}\), which marked \(\varvec{V}_{i.j}^{{L_{1} }}\). \(\varvec{V}_{i.j}^{{L_{1} }}\) is the coordinate of a set of new control points that eliminated the high frequency message. A NURBS tooth surface with higher smoothness was generated while \(\varvec{V}_{i.j}^{{L_{1} }}\) was introduced in Eq. (4).

The mesh surface generated by Eq. (4) was imported into the UG9.0 software. With some basic operations, the digital models of a pair of meshing gears shown in Fig. 4 were generated. The average fitting error of 50 points is described in Fig. 5.

Fig. 4
figure 4

Assembly drawing of spiral bevel gears

Full size image
Fig. 5
figure 5

Fitting error

Full size image

The gauss curvature of tooth surfaces is shown in Table 2. According to the data in Table 2, the range and maximum absolute value of the gauss curvature became smaller after being processed by the wavelet. Consequently, the tooth surface processed by the wavelet had lower complexity and higher smoothness when compared to the original one. According to a Ref. [20], the lower the complexity of the surface, the smaller the residual height of the milling process, the higher the machining accuracy. Therefore, the wavelet can be helpful to improve the machining accuracy of the tooth surface.

Table 2 Gauss curvature of the tooth surface
Full size table

In order to ensure the accuracy of NC machining and avoid excessive contour error during machining, the requirements that feed speed needs to meet are as follows:

$$\varvec{v}_{i} \le \frac{2}{{T_{S} }}\sqrt {\delta_{\hbox{max} } (2\varvec{\rho}_{i} - \delta_{\hbox{max} } )}$$
(13)
$$\varvec{v}_{i}^{2} \le\varvec{\rho}{}_{i}\varvec{a}_{{\text{max}}}$$
(14)

where ρi is the radius of the curvature, δmax is maximum contour error, TS is the interpolation cycle, vi is the feed speed and \(\varvec{a}_{{\text{max}}}\) is the maximum permissible acceleration of the CNC system [16].

Since the maximum absolute value of the gauss curvature is smaller than the original surface, it had a bigger curvature radius than the original surface. That is, the value of \(\varvec{v}_{i}\) can be set bigger, allowing the wavelet to be helpful in improving machining efficiency.

4 Experimental verification

4.1 Simulating manufacturing

Taking a gear, for example, the verifying test was carried out in three-axis CNC machine tool. A single-tooth model is shown in Fig. 6. A base was added under the tooth to avoid machining interference and ensure the machining quality of the root when machining the underneath of the concave and convex. The material of the blank is 45 steel, and the size is 65 * 55 * 30 (mm).

Fig. 6
figure 6

Single-tooth model

Full size image

The process of the simulation was carried out using UG9.0, and the result is shown in Fig. 7. The blue area is with finishing allowance but was no more than 15 μm, and the red area is with overcut phenomenon but was no more than 20 μm. From the algorithms inside the software, and in comparing with the images in Table 2, it can be observed that the overcut phenomenon shows at the tooth surface with a large gauss curvature or abrupt change in curvature. However, the main function of the wavelet was to reduce the curvature and curvature change rate. That is, the phenomenon of over-cutting would be improved.

Fig. 7
figure 7

Finishing allowance of the simulated manufacturing

Full size image

4.2 Experimental condition

The processing equipment and processing settings are presented in Table 3. The processing flow is shown in Fig. 8. The processing flow consists of rough machining and finishing machining, and the final product is shown in Fig. 8c.

Table 3 Equipment and processing parameters
Full size table
Fig. 8
figure 8

Processing flow

Full size image

The measurement process is shown in Fig. 9, and the origin of the coordinate system is at the center of the base plane.

Fig. 9
figure 9

Measurement process

Full size image

4.3 Experimental results

The points measured by the three-coordinate measuring machine and theoretical tooth surface were compared, and the deviation was calculated. The machining error of the concave of the gear processed by wavelet is shown in Fig. 10. The convex of the gear and tooth surface without being processed have the same error distribution with the concave of the gear which shows the machining allowances at the top and over-cutting at the root. Due to the influence of all kinds of factors, such as machine tool vibration, and measurement error in actual manufacturing, the error distribution is incompatible with simulating manufacturing which just takes algorithms into account. The value of the maximum machining allowance, average machining error and maximum over-cutting is shown in Fig. 11.

Fig. 10
figure 10

Machining error (concave of the gear process processed by wavelet)

Full size image
Fig. 11
figure 11

Deviation value of the tooth surface

Full size image

4.4 Analysis and comparison of experimental results

  1. 1.

    Table 4 is established based on Figs. 5 and 11. According to Table 4, the fitting error of the tooth surface processed by wavelet was approximately 1/3 of the machining error, while the fitting error of the tooth surface without being processed was approximately 1/5 of the machining error. Hence, machining error was the main factor that influenced the final error of the tooth surface. Although the fitting error as bigger than the tooth surface without being processed, the smaller machining error shows the advantage of the wavelet theory in tooth surface optimization. At the same time, this also points out that it is not conducive to improve machining precision by simply improving the fitting accuracy of the digital model in the machining process of general precision CNC machine tools.

    Table 4 Fitting error and machining error
    Full size table
  2. 2.

    According to Fig. 11, the average machining error of the tooth surface without being processed was bigger than the value of the maximum machining allowance. That is, over-cutting was the main reason for machining error. After being processed by the wavelet, the average machining error of the tooth surface was smaller than the value of the maximum machining allowance and the maximum value of over-cutting of the concave and convex was reduced by 11.3 μm and 20.7 μm, respectively. This shows that the phenomenon of over-cutting was effectively improved.

  3. 3.

    According to the data in Table 2, after being processed by the wavelet, the maximum and minimum difference of the gauss curvature for the concave and convex was reduced by 0.84E−3 and 1.06E−3, respectively. Hence, the complexity of the tooth surface became lower, and the smoothness of the tooth surface improved. Based on Fig. 11, the average machining error of the concave and convex was reduced by 16.4 μm and 11.2 μm, respectively, after being processed by the wavelet. In combining Table 2 with Fig. 11, it can be concluded that the lower the complexity of the tooth surface, the smaller the machining error, and the higher the machining precision. The average machining error became smaller after being processed by the wavelet, which shows that wavelet processing of the discrete points of the original tooth surface can reduce the complexity of the tooth surface and improve the smoothness of the tooth surface thereby improving machining precision.

5 Conclusions

Based on the performed research, the following conclusion could be drawn:

  1. 1.

    The relationship between the fitting error of the model and machining error was analyzed. This shows that it is not conducive to improve machining precision by simply improving the fitting accuracy of the digital model in the machining process of general precision CNC machine tools.

  2. 2.

    By using the multi-resolution representation of the wavelet theory to eliminate the high frequency information of the tooth surface, the Gauss curvature of the tooth surface and the difference between the maximum and minimum of the Gauss curvature of the tooth surface are reduced. Therefore, the complexity of the surface became lower, and the smoothness of the tooth surface improved. This effectively improved the phenomenon of over-cutting and helped to improve the machining precision of the tooth surface. A new method for improving the machining precision of spiral bevel gears has been put forward from the establishment of the digital model.

  3. 3.

    Starting from discrete points of the tooth surface, the tooth surface of the spiral bevel gears was reconstructed by combining the NURBS theory and multi-resolution representation principle of the cubic B-spline wavelet, realizing the accurate tooth surface design of spiral bevel gears. Moreover, this would provide a better numerical model for the application of NURBS interpolation algorithm in the NC machining of spiral bevel gears. At the same time, this would also provide a new modeling method for complex surface construction and reverse engineering.