Skip to main content
SpringerLink
Log in

Analysis of Eyring–Powell liquid flow in curved channel with Cattaneo–Christov heat flux model

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

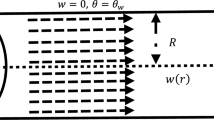
The article concentrates on the analysis of heat transfer phenomena incorporated with Cattaneo–Christov model of heat flux in magnetohydrodynamic Eyring–Powell fluid flow in a semipermeable curved channel. The flow equations are modeled by introducing the curvilinear coordinates system. The governing mathematical equations are reformed into ordinary differential equations by utilizing nonlinear type of similarity variables. The obtained mathematical model is solved numerically by utilizing shooting method. The obtained results are also validated with the well-known finite difference algorithm known as Keller-box method. The impact of diverse parameters on the flow and physical quantities like rate of heat transport and shear stress is investigated and discussed in detail via graphs and table. It is noticed that an increase in the fluid parameter increases the velocity of the fluid, whilst an increase in the thermal relaxation parameter decreases the temperature of the fluid.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Abbreviations

B 0 :

Constant magnetic field

R 1 :

Radius of the curved channel

b :

Eyring–Powell constant

A 1 :

First Rivlin–Ericksen tensor

f :

Dimensionless fluid velocity in r-direction

\(f^{{\prime }}\) :

Dimensionless fluid velocity in s-direction

k 1 :

Thermal conductivity of the fluid

H :

Distance between the walls of the curved channel

M :

Dimensionless magnetic parameter

p :

Pressure of the fluid

P :

Dimensionless pressure

Pr:

Prandtl number

r :

Distance normal to surface of the curved channel

q w :

Heat flux at the wall

\(\bar{L}\) :

Horizontal length scale

\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K}\) :

Dimensionless radius of curvature

s :

Flow directional coordinate along the curved wall of the channel

\(\bar{u}\) :

Velocity component in the s-direction

\(\bar{v}\) :

Velocity component in the r-direction

\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T}\) :

Temperature

\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T}_{\text{w}}\) :

Surface temperature

\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T}_{0}\) :

Ambient fluid temperature

U :

Fluid velocity

α :

Thermal relaxation parameter

β :

Eyring–Powell constant

η :

Dimensionless variable

μ :

Dynamic viscosity of the fluid

ν :

Kinematics viscosity of the fluid

ρ :

Density of fluid

\(\bar{\delta }\) :

Boundary layer thickness

λ E :

Relaxation time of heat flux

λ 1, λ 2 :

Fluid parameters

λ :

Reynolds number

\(\bar{\tau }\) :

Stress tensor

\(\bar{\tau }_{\text{rs}}\) :

Wall shear stress

c p :

Specific heat at constant pressure

σ :

Electrical conductivity

\(\bar{\gamma }\) :

Constant

θ :

Dimensionless fluid temperature

References

  1. Berman AS (1953) Laminar flow in channel with porous walls. J Appl Phys 24:1232–1235

    Article  MathSciNet  MATH  Google Scholar 

  2. Hayat T, Abbas Z (2008) Heat transfer analysis on the MHD flow of a second grade fluid in a channel with porous medium. Chaos Solitons Fractals 38:556–567

    Article  MathSciNet  MATH  Google Scholar 

  3. Kumar JP, Umavathi JC, Chamkha Ali J, Pop I (2010) Fully developed force-convective flow of micropolar and viscous fluids in vertical channel. Appl Math Modell 34:1175–1186

    Article  MATH  Google Scholar 

  4. Sajid M, Abbas Z, Hayat T (2009) Homotopy analysis for boundary layer flow of a micropolar fluid through a porous channel. Appl Math Modell 33:4120–4125

    Article  MathSciNet  MATH  Google Scholar 

  5. Rassoulinejad-Mousavi SM, Seyf HR, Abbasbandy S (2013) Heat transfer through a porous saturated channel with permeable walls using two-equations energy model. J Porous Med 16:241–254

    Article  Google Scholar 

  6. Sheikholeslami M, Hatami M, Ganji DD (2013) Analytical investigation of MHD nanofluid flow in a semi-porous channel. Powder Technol 246:327–336

    Article  Google Scholar 

  7. Hatami M, Sheikholeslami M, Ganji DD (2014) Nanofluid flow and heat transfer in an asymmetric porous channel with expanding or contracting wall. J Mol Liq 195:230–239

    Article  Google Scholar 

  8. Hatami M, Sheikholeslami M, Domairry G (2014) High accuracy analysis for motion of a spherical particle in plane Couette fluid flow by multi-step differential transformation method. Powder Technol 260:59–67

    Article  Google Scholar 

  9. Dogonchi AS, Hatami M, Domairry G (2015) Motion analysis of a spherical solid particle in plane Couette Newtonian fluid flow. Powder Technol 274:186–192

    Article  Google Scholar 

  10. Abbas Z, Naveed M, Sajid M (2013) Heat transfer analysis for stretching flow over a curved surface with magnetic field. J Eng Thermophys 22(4):337–345

    Article  Google Scholar 

  11. Chakrabarti A, Gupta A (1979) Hydromagnetic flow and heat transfer over a stretching sheet. Q Appl Math 33:73–78

    Article  MATH  Google Scholar 

  12. Chandran P, Sacheti NC, Singh A (1996) Hydromagnetic flow and heat transfer past a continuously moving porous boundary. Int Commun Heat Mass Transf 23(6):889–898

    Article  Google Scholar 

  13. Desseaux A (1999) Influence of a magnetic field over a laminar viscous flow in a semi-porous channel. Int Eng Sci 37(14):1781–1794

    Article  MATH  Google Scholar 

  14. Fang T, Zhang J (2009) Closed form exact solutions of MHD viscous flow over a shrinking sheet. Commun Nonlinear Sci Numer Simul 14(7):2853–2857

    Article  MATH  Google Scholar 

  15. Hamad MAA (2011) Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field. Int Commun Heat Mass Transf 38:487–492

    Article  Google Scholar 

  16. Hayat T, Qasim M (2010) Effects of thermal radiation on unsteady magnetohydrodynamic flow of a micropolar fluid with heat and mass transfer. Zeitschrift fur Naturforschung A (ZNA) 65(11):950–960

    Google Scholar 

  17. Hatami M, Songand D, Jing D (2016) Optimization of a circular-wavy cavity filled by nanofluid under the natural convection heat transfer condition. Int J Heat Mass Transf 98:758–767

    Article  Google Scholar 

  18. Sheikholeslami M, Hatamiand M, Ganji DD (2015) Numerical investigation of nanofluid spraying on an inclined rotating disk for cooling process. J Mol Liq 211:577–583

    Article  Google Scholar 

  19. Hatami M, Zhou J, Geng J, Song D, Jing D (2017) Optimization of a lid-driven T-shaped porous cavity to improve the nanofluids mixed convection heat transfer. J Mol Liq 231:620–631

    Article  Google Scholar 

  20. Hatami M (2017) Nanoparticles migration around the heated cylinder during the RSM optimization of a wavy-wall enclosure. Adv Powder Technol 28(3):890–899

    Article  Google Scholar 

  21. Hatami M, Jing D (2017) Optimization of wavy direct absorber solar collector (WDASC) using Al2O3-water nanofluid and RSM analysis. Appl Therm Eng 121:1040–1050

    Article  Google Scholar 

  22. Pourmehran O, Rahimi-Gorji M, Hatami M, Sahebi SAR, Domairry G (2015) Numerical optimization of microchannel heat sink (MCHS) performance cooled by KKL based nanofluids in saturated porous medium. J Taiwan Inst Chem Eng 55:49–68

    Article  Google Scholar 

  23. Abbas Z, Naveed M, Naeem M, Zia QMZ (2018) Analytical investigation of Maxwell fluid flow with radiation in an axisymmetric semi-porous channel by parameterized perturbation method. J Braz Soc Mech Sci Eng 40:65

    Article  Google Scholar 

  24. Abbas Z, Imran M, Naveed M (2018) Hydromagnetic flow of a Carreau fluid in a curved channel with nonlinear thermal radiation. Therm Sci. https://doi.org/10.2298/TSCI171011077A

    Google Scholar 

  25. Carreau PJ (1972) Rheological equations from molecular network theories. Trans Soc Rheol 16:99–127

    Article  Google Scholar 

  26. Capobianchi M, Aziz A (2012) Laminar natural convection from an isothermal vertical surface to pseudoplastic and dilatant fluid. ASME J Heat Transf 134:122502

    Article  Google Scholar 

  27. Misra J, Shit G, Rath HJ (2008) Flow and heat transfer of a MHD viscoelastic fluid in a channel with stretching walls: some applications to hemodynamics. Comput Fluids 37(1):1–11

    Article  MATH  Google Scholar 

  28. Hsiao KL (2017) Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int J Heat Mass Transf 112:983–990

    Article  Google Scholar 

  29. Hayat T, Sajjad R, Abbas Z, Sajid M, Hendi AA (2011) Radiation effects on MHD flow of Maxwell fluid in a channel with porous medium. Int J Heat Transf 54(4):854–862

    Article  MATH  Google Scholar 

  30. Raftrari B, Vajravelu K (2012) Homotopy analysis method for MHD viscoelastic fluid flow and heat transfer in a channel with a stretching wall. Commun Nonlinear Sci Numer Simul 17(11):4149–4162

    Article  MathSciNet  MATH  Google Scholar 

  31. Abbas Z, Ahmad B, Ali S (2015) Chemically reactive hydromagnetic flow of a second grade fluid in a semi-porous channel. J Appl Mech Tech Phys 56:878–888

    Article  MathSciNet  MATH  Google Scholar 

  32. Khan M, Hashim MH, Azam M (2016) Magnetohydrodynamic flow of Carreau fluid over a convectively heated surface in the presence of non-linear radiation. J Magn Magn Mater 412:63–68

    Article  Google Scholar 

  33. Qayyum S, Hayat T, Shehzad S, Alsaedi A (2017) Nonlinear convective flow of Powell–Erying magneto nanofluid with Newtonian heating. Res Phys 7:2933–2940

    Google Scholar 

  34. Akinshilo AT, Olaye O (2017) On the analysis of the Erying Powell model based fluid flow in a pipe with temperature dependent viscosity and internal heat generation. J (K.S) Univ Eng Sci. https://doi.org/10.1016/j.jksues.2017.09.001

    Google Scholar 

  35. Hayat T, Hussain S, Muhammad T, Alsaedi A, Ayub M (2017) Radiative flow of Powell–Eyring nanofluid with convective boundary conditions. Chin J Phys 55(4):1523–1538

    Article  Google Scholar 

  36. Malik MY, Bilal S, Bibi M (2017) Numerical analysis for MHD thermal and solutal stratified stagnation point flow of Powell–Eyring fluid induced by cylindrical surface with dual convection and heat generation effects. Res Phys 7:482–492

    Google Scholar 

  37. Khan M, Irfan M, Khan WA, Ahmad L (2017) Modeling and simulation for 3D magneto Eyring–Powell nanomaterial subject to nonlinear thermal radiation and convective heating. Res Phys 7:1899–1906

    Google Scholar 

  38. Ibrahim W (2018) Three dimensional rotating flow of Powell–Eyring nanofluid with non-Fourier’s heat flux and non-Fick’s mass flux theory. Res Phys 8:569–577

    Google Scholar 

  39. Cattaneo C (1948) Sulla conduzione del calore. Atti Sem Mat Fis Univ Modena 3:83–101

    MathSciNet  MATH  Google Scholar 

  40. Christov CI (2009) On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech Res Commun 36(4):481–486

    Article  MathSciNet  MATH  Google Scholar 

  41. Farooq M, Ahmad S, Javed M, Anjum A (2017) Analysis of Cattaneo–Christov heat and mass fluxes in the squeezed flow embedded in porous medium with variable mass diffusivity. Res Phys 7:3788–3796

    Google Scholar 

  42. Liu L, Zheng L, Liu F, Zhang X (2017) Heat conduction with fractional Cattaneo–Christov upper-convective derivative flux model. Int J Eng Sci 112:421–426

    Google Scholar 

  43. Hayat T, Qayyum S, Shehzad SA, Alsaedi A (2018) Cattaneo–Christov double-diffusion theory for three-dimensional flow of viscoelastic nanofluid with the effect of heat generation/absorption. Res Phys 8:489–495

    Google Scholar 

  44. Awais M, Awan SE, Iqbal K, Khan ZA, Raja MAZ (2018) Hydromagnetic mixed convective flow over a wall with variable thickness and Cattaneo–Christov heat flux model: OHAM analysis. Res Phys 8:621–627

    Google Scholar 

  45. Khuri A (2006) Stokes flow in curved channel. J Comput Appl Math 187(2):171–191

    Article  MathSciNet  MATH  Google Scholar 

  46. Fu WS, Chen CJ, Lai YC, Huang SH (2014) Effects of a porous medium on forced convection of a reciprocating curved channel. Int Commun Heat Mass Transf 58:63–70

    Article  Google Scholar 

  47. Naveed M, Abbas Z, Sajid M (2016) Flow and heat transfer in a semi porous curved channel with radiation and porosity effects. J Porous Med 19(5):1–11

    Article  Google Scholar 

  48. Abbas Z, Naveed M, Sajid M (2015) Nonlinear radiative heat transfer and Hall effects on a viscous fluid in a semi-porous curved channel. AIP Adv 5:107124

    Article  Google Scholar 

  49. Sajid M, Iqbal SA, Naveed M, Abbas Z (2016) Joule heating and magnetohydrodynamics effects on ferrofluid flow in a semi-porous curved channel. J Mol Liq 222:1115–1120

    Article  Google Scholar 

  50. Hina S, Mustafa M, Hayat T, Alsaedi A (2016) Peristaltic transport of Powell–Erying fluid in a curved channel with heat/mass transfer and wall properties. Int J Heat Mass Transf 101:156–165

    Article  Google Scholar 

Download references

Acknowledgements

We are thankful to the reviewers for their encouraging comments and constructive suggestions to improve the quality of the manuscript.

Author information

Authors and Affiliations

  1. Department of Mathematics, The Islamia University of Bahawalpur, Bahawalpur, 63100, Pakistan

    Z. Abbas & M. Rafiq

  2. Department of Mathematics, Khwaja Fareed University of Engineering and Information Technology, Rahim Yar Khan, 64200, Pakistan

    M. Naveed

Authors
  1. Z. Abbas
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Rafiq
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Naveed
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Naveed.

Additional information

Technical Editor: Cezar Negrao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abbas, Z., Rafiq, M. & Naveed, M. Analysis of Eyring–Powell liquid flow in curved channel with Cattaneo–Christov heat flux model. J Braz. Soc. Mech. Sci. Eng. 40, 390 (2018). https://doi.org/10.1007/s40430-018-1312-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1312-4

Keywords

Search

Navigation