1 Introduction

It is a well-established fact that Navier–Stokes equations do not characterize the flow pattern of non-Newtonian fluids, most of the times. Such fluids involve a highly nonlinear relation between stress and strain as compared to viscous fluid. To capture the behaviour of non-Newtonian fluids, various theoretical models are proposed such as Micropolar fluid, Power law fluids, Giesekus fluid, Williamson fluid, Jeffery fluid and Maxwell fluid etc. In addition to, these Eyring-Powell fluid model is also one of such fluid models that exhibits the non-Newtonian behaviour. Eyring-Powell fluid model preference over other non-Newtonian fluid models for mainly two reasons: (i) the kinetic theory of liquids is used to develop the concept instead of empirical relation as observed in power-law fluids model. (ii) This also characterizes the behaviour of Newtonian fluid and non-Newtonian fluid for high and intermediate shear rate. This model has various applications in science and technology such as, chemical and polymer engineering processes etc. A brief discussion on this fluid model relevant to the different geometries is highlighted in the next paragraph.

Finite element method (FDM) is used in [1] to obtain the numerical solution of an Eyring-Powell fluid. Numerical simulation of the nanofluid is performed in a Riga surface intact with porous medium. The magnetized flow of heat and mass transfer in affected by thermal radiation. They concluded that the velocity profile decreases by increasing the modified magnetic number. Similar type of investigation of Eyring-Powell fluid by Nazeer et al. [2]. The nano flow is examined numerically by FEM. It is observed that the wall shear rate decreases by increasing the values of an Eyring-Powell fluid parameter. Javed et al. [3] apply Keller Box method to get an approximate solution for an unsteady flow of Eyring-Powell fluid under the influence of magnetic effects. They infer that thermophoresis constrain declines the mass transfer profile.

A theoretical study of magnetohydrodynamics (MHD) Ering-Powell fluid saturated with porous medium under the effects of variable thermal conductivity was reported by Salawu et al. [4]. They also discussed the entropy generation phenomenon and noted that the entropy generation can be minimized by radiation. Rahimi et al. [5] have developed a numerical algorithm of collocation method to solve the nonlinear flow problem over a stretching sheet. They noted that Eyring-Powell inertial parameter accelerates the velocity distribution. Khan et al. [6] present the idea of cross flow of Eyring -Powell fluid with entropy generation. The homotopy analysis method (HAM) and Runge Kutta methods were used to obtain the solution. Ahmad et al. [7] used the perturbation theory to discuss the flow of an Eyring-Powell fluid through a circular pipe. They also used the finite difference method to validate their perturbation results and noted a good agreement within both solutions.

Motivated the above important studies, in this paper we have presented two types of mathematical models of cross flow of Eyring Powell fluid with the heat and mass transfer analysis. The dimensional form of the partial differential equations is transformed into ordinary differential equations by using the suitable non-dimensional quantities. The perturbation theory is used to find the solution of velocity, temperature and concentration.

This paper is organized in a manner such that, a concise and compact studies relevant to Eyring-Powell are cited in the section of introduction. The mathematical modeling and formulation of Eyring Powell fluid is developed in section two. The solutions of two type of flows namely, Plane Couette and Generalized Couette Flow of nano fluids are reported with the help of the perturbation theory in sections three and four respectively. Such types of flows are commonly using in the lubrication technology and tribiological problems et. [8]. The physical interpretation of the numerical results is explained in section five. The conclusions section is added before the references and the important references are added at the end of the paper.

2 Problem formulation of cross flow

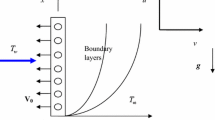
A steady state cross flow of Eyring-Powell fluid is described in Fig. 1. A Cartesian coordinate system is used for two-dimensional non-Newtonian fluid through parallel plates placed at \(Z=2l.\)

Fig. 1
figure 1

Cross flow of Eyring-Powell fluid

Full size image

The incompressible flow is “Suction flow” [9] as Eyring-Powell fluid seeps out of the channel with uniform velocity such that \({w}_{0}<0\) (positive).

To develop the mathematical model of cross flow of an Eyring-Powell fluid, we define the extra stress tensor [10] given below

$$S_{xz} = \overline{\mu }\frac{\partial w}{{\partial z}} + \frac{1}{\sigma }\sinh^{ - 1} \left( {\frac{1}{\delta }\frac{\partial w}{{\partial z}}} \right)$$
(1)

Employing Taylor’s series expansion, one can define as

$$\sinh^{ - 1} \left( {\frac{1}{\delta }\frac{\partial w}{{\partial z}}} \right) = \frac{1}{\delta }\frac{\partial w}{{\partial z}} - \frac{1}{6}\left( {\frac{1}{\delta }\frac{\partial w}{{\partial z}}} \right)^{3} ,\left| {\frac{1}{\delta }\frac{\partial w}{{\partial z}}} \right| \ll 1.$$
(2)

Invoking Eq. (2) in mass conservation and momentum conservation equations one gets

$$\frac{\partial w}{{\partial z}} = 0,$$
(3)
$$\frac{\partial }{\partial z}\left( {\overline{\mu }\frac{\partial w}{{\partial z}} + \frac{1}{\sigma }\left( {\frac{1}{\delta }\frac{\partial u}{{\partial y}} - \frac{1}{6}\left( {\frac{1}{\delta }\frac{\partial w}{{\partial z}}} \right)^{3} } \right)} \right) + \rho w_{0} \frac{\partial w}{{\partial z}} - \frac{\partial p}{{\partial x}} = 0.$$
(4)

Similarly, energy equation along with concentration of particles are given as:

$$k\frac{{\partial^{2} \vartheta }}{{\partial w^{2} }} + \rho C_{P} w_{0} \frac{\partial \vartheta }{{\partial z}} + \frac{\partial w}{{\partial z}}\left( {\overline{\mu }\frac{\partial w}{{\partial z}} + \frac{1}{\sigma }\left( {\frac{1}{\delta }\frac{\partial w}{{\partial z}} - \frac{1}{6}\left( {\frac{1}{\delta }\frac{\partial w}{{\partial z}}} \right)^{3} } \right)} \right) = 0,$$
(5)
$$D_{1} \frac{{\partial^{2} C}}{{\partial z^{2} }} + \frac{{D_{2} }}{{\vartheta_{0} }}\frac{{\partial^{2} \vartheta }}{{\partial z^{2} }} + w_{0} \frac{\partial C}{{\partial z}} = 0.$$
(6)

The following boundary constraints are imposed for heat and mass transfer of Eyring-Powell fluid

$$\left. {\begin{array}{*{20}c} {w = 0, \vartheta = \vartheta_{1} , C = C_{0} , \hbox{at}\,\, z = - l ,} \\ {w = w_{0} , \vartheta = \vartheta_{2} , D_{1} \frac{\partial C}{{\partial z}} + \frac{{D_{2} }}{{\vartheta_{0} }}\frac{\partial \vartheta }{{\partial z}} = 0; at z = l} \\ \end{array} } \right\}$$
(7)

Assuming that the nanofluid flow is caused merely, due to the motion of top plate while keep the lower wall of the channel as rigid. Besides, contribution of pressure gradient is neglected. In view of these constraints and further considering the following quantities

$$\left. \begin{gathered} Z = \frac{z}{l},X = \frac{x}{l}, W = \frac{W}{{W_{0} }}, \varphi = \frac{{\vartheta - \vartheta_{1} }}{{\vartheta_{2} - \vartheta_{1} }}, \Phi = \frac{{C - C_{0} }}{{C_{0} }}, K_{1} = \frac{1}{{\overline{\mu }\gamma \delta }}, \Gamma = \frac{{ - l^{2} }}{{W_{0} \rho \upsilon }}\frac{\partial P}{{\partial x}} \hfill \\ K_{2} = \frac{{W_{0} l}}{\upsilon }, K_{3} = \frac{{\eta_{1} W_{0}^{2} }}{{2H^{2} C^{2} }}, K_{4} = \frac{{\overline{\rho }W_{0} C_{P} }}{k}, K_{5} = \frac{{\overline{\mu }W_{0}^{2} }}{{k\left( {\theta_{2} - \theta_{1} } \right)H^{2} }}, K_{6} = \frac{{W_{0}^{2} }}{{\overline{\mu }\gamma C^{3} H^{2} }} \hfill \\ K_{t} = \frac{{\tau D_{2} \left( {\vartheta_{2} - \vartheta_{1} } \right)}}{{\vartheta_{0} \alpha }} , K_{b} = \frac{\alpha }{{\tau D_{1} C_{0} }}. \hfill \\ \end{gathered} \right\}$$
(8)

Equations (3–7) take the following dimensionless form

$$\frac{dW}{{dX}} = 0,$$
(9)
$$\left( {1 + K_{1} } \right)\frac{{d^{2} W}}{{dZ^{2} }} + K_{2} \frac{dW}{{dZ}} - K_{3} \frac{{d^{2} W}}{{dZ^{2} }}\left( {\frac{dW}{{dZ}}} \right)^{2} = 0,$$
(10)
$$\frac{{d^{2} \theta }}{{dZ^{2} }} + K_{4} \frac{d\theta }{{dZ}} + K_{5} \left( {\left( {1 + K_{1} } \right)\left( {\frac{dW}{{dZ}}} \right)^{2} - \frac{{K_{6} }}{6}\left( {\frac{dW}{{dZ}}} \right)^{4} } \right) = 0,$$
(11)
$$\frac{{d^{2} \Phi }}{{dZ^{2} }} + K_{2} Sc\frac{d\Phi }{{dZ}} + \frac{{K_{t} }}{{K_{b} }}\frac{{d^{2} \varphi }}{{dZ^{2} }} = 0.$$
(12)

The boundary conditions in dimensionless form are given as

$$\left. {\begin{array}{*{20}c} {\left( i \right)\, W\left( { - 1} \right) = 0} \\ {\left( {ii} \right)\, \varphi \left( { - 1} \right) = 0} \\ {\left( {iii} \right)\, \Phi \left( { - 1} \right) = n} \\ {\left( {iv} \right)\, W\left( 1 \right) = 1} \\ {\left( v \right)\, \varphi \left( 1 \right) = 1} \\ {\left( {vi} \right)\, \frac{d\Phi \left( 1 \right)}{{dZ}} + \frac{{K_{t} }}{{K_{b} }}\frac{d\varphi \left( 1 \right)}{{dZ}} = 0} \\ \end{array} } \right\}.$$
(13)

On the other hand, taking the role of constant pressure gradient into account and following the above procedure. Then the momentum equation takes the form as given below.

$$\left( {1 + K_{1} } \right)\frac{{d^{2} W}}{{dZ^{2} }} + K_{2} \frac{dW}{{dZ}} - K_{3} \frac{{d^{2} W}}{{dZ^{2} }}\left( {\frac{dW}{{dZ}}} \right)^{2} + \Gamma = 0$$
(14)

3 Solution of the problem

Since, two different sources of heat and mass transfer of nano flows are developed. Therefore, separate solution for each case is sought out, which are given as:

3.1 Plane Couette flow

To achieve an exact form of solution for Eqs. (10)–(12) corresponding to boundary conditions (13) is not easy, due to highly nonlinearity. Therefore, for a reliable solution for system of coupled differential equations, perturbation technique is taken into account. We seek a series solution of the following form:

$$\left. {\begin{array}{*{20}c} {W\left( {z,\varepsilon } \right) = W_{0} \left( {z,\varepsilon } \right) + \varepsilon W_{1} \left( {z,\varepsilon } \right) + O\left( {\varepsilon^{2} } \right)} \\ {\varphi \left( {z,\varepsilon } \right) = \varphi_{0} \left( {z,\varepsilon } \right) + \varepsilon \varphi_{1} \left( {z,\varepsilon } \right) + O\left( {\varepsilon^{2} } \right)} \\ {\Phi \left( {z,\varepsilon } \right) = \Phi_{0} \left( {z,\varepsilon } \right) + \varepsilon \Phi_{1} \left( {z,\varepsilon } \right) + O\left( {\varepsilon^{2} } \right)} \\ \end{array} } \right\}.$$
(15)

where \(\epsilon\) is known as perturbation parameter and to meet convergence \(0<\varepsilon \ll 1\). In order to tackle with the nonlinear terms, it is most suitable to choose

$$K_{3} = \varepsilon \alpha ,\;{\text{and}}\; K_{5} = \varepsilon \beta$$
(16)

Invoking Eqs. (15–16) into Eqs. (10–13) and further Using the assumption to express velocity of nano fluid, transport of temperature and concentration of the nano species in terms of power series of \({\varepsilon }^{m}\), such that (\(m=\mathrm{0,1},2\dots )\). Then, one can easily identify the zeroth problem subject to boundary conditions as:

$$\left( {1 + K_{1} } \right)\frac{{d^{2} W_{0} }}{{dZ^{2} }} + K_{2} \frac{{dW_{0} }}{dZ} = 0,$$
(17)
$$\frac{{d^{2} \varphi_{0} }}{{dZ^{2} }} + K_{4} \frac{{d\varphi_{0} }}{dZ} = 0,$$
(18)
$$\frac{{d^{2} \Phi_{0} }}{{dZ^{2} }} + K_{2} Sc\frac{{d\Phi_{0} }}{dZ} + \frac{{K_{t} }}{{K_{b} }}\frac{{d^{2} \varphi_{0} }}{{dZ^{2} }} = 0.$$
(19)

The boundary conditions are:

$$\left. {\begin{array}{*{20}c} {W_{0} \left( { - 1} \right) = 0} \\ {W_{0} \left( 1 \right) = 1} \\ {\varphi_{0} \left( { - 1} \right) = 0} \\ {\varphi_{0} \left( 1 \right) = 1} \\ {\Phi_{0} \left( { - 1} \right) = n} \\ {\frac{{d\Phi_{0} \left( 1 \right)}}{dZ} + \frac{{K_{t} }}{{K_{b} }}\frac{{d\varphi_{0} \left( 1 \right)}}{dZ} = 0} \\ \end{array} } \right\}$$
(20)

In the same way one can easily identify the first order problems corresponding to the boundary conditions are:

$$\left( {1 + K_{1} } \right)\frac{{d^{2} W_{1} }}{{dZ^{2} }} + K_{2} \frac{{dW_{1} }}{dZ} - \alpha \left( {\frac{{dW_{0} }}{dZ}} \right)^{2} \left( {\frac{{d^{2} W_{0} }}{{dZ^{2} }}} \right) = 0,$$
(21)
$$\frac{{d^{2} \varphi_{1} }}{{dZ^{2} }} + K_{4} \frac{{d\varphi_{1} }}{dZ} + \beta \left( {\left( {1 + K_{1} } \right)\left( {\frac{{dW_{0} }}{dZ}} \right)^{2} - \frac{{K_{6} }}{3}\left( {\frac{{dW_{0} }}{dZ}} \right)^{4} } \right) = 0,$$
(22)
$$\frac{{d^{2} \Phi_{1} }}{{dZ^{2} }} + K_{2} Sc\frac{{d\Phi_{1} }}{dZ} + \frac{{K_{t} }}{{K_{b} }}\frac{{d^{2} \varphi_{1} }}{{dZ^{2} }} = 0.$$
(23)
$$\left. {\begin{array}{*{20}c} {W_{1} \left( { - 1} \right) = W_{1} \left( 1 \right) = 0} \\ { \varphi_{1} \left( { - 1} \right) = 0, \varphi_{1} \left( 1 \right) = 0} \\ {\Phi_{1} \left( { - 1} \right) = 0} \\ {\frac{{d\Phi_{1} \left( 1 \right)}}{dZ} + \frac{{K_{t} }}{{K_{b} }}\frac{{d\varphi_{1} \left( 1 \right)}}{dZ} = 0} \\ \end{array} } \right\}$$
(24)

The zeroth order solution of Eqs. (17–19) subject to boundary conditions given in (20) are obtained as

$$W_{0} = \Omega_{0} + \Omega_{1} e^{{\frac{{K_{2} - K_{2} Z}}{{\left( {1 + K_{1} } \right)}}}} ,$$
(25)
$$\varphi_{0} = \Psi_{0} + \Psi_{1} e^{{ - K_{4} Z}} ,$$
(26)
$$\Phi_{0} = \Lambda_{0} + \Lambda_{1} e^{{ - K_{4} Z}} + \Lambda_{2} e^{{ - K_{4} + K_{2} Sc - K_{2} ScZ}} ,$$
(27)

now, the first order solutions of velocity of nanofluid, heat transport and convection of nano particles are obtained below

$$W_{1} = \Omega_{2} + \Omega_{3} e^{{ - \frac{{K_{2} Z}}{{\left( {1 + K_{1} } \right)}}}} + \Omega_{4} e^{{ - \frac{{3K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}}$$
(28)
$$\varphi_{1} = \beta \left( {\Psi_{2} + \Psi_{3} e^{{ - K_{4} Z}} + \Psi_{4} e^{{ - \frac{{2K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} + \Psi_{5} e^{{ - \frac{{4K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} } \right),$$
(29)
$$\Phi_{1} = \Lambda_{3} - e^{{ - K_{2} ScZ}} \Lambda_{4} + \beta \left( {\Lambda_{5} e^{{ - K_{4} Z}} + \Lambda_{6} e^{{ - \frac{{2K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} + \Lambda_{7} e^{{ - \frac{{4K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} } \right).$$
(30)

Replacing Eqs. (25–30) in Eq. (15), the final form of the perturbed solutions of nano flow of Eyring-Powell fluid transporting heat and mass, up-to first order are given as

$$W = \Omega_{0} + \Omega_{1} e^{{\frac{{K_{2} - K_{2} Z}}{{\left( {1 + K_{1} } \right)}}}} + K_{3} \left( {\Omega_{2} + \Omega_{3} e^{{ - \frac{{K_{2} Z}}{{\left( {1 + K_{1} } \right)}}}} + \lambda_{4} e^{{ - \frac{{3K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} } \right),$$
(31)
$$\varphi = \Psi_{0} + \Psi_{1} e^{{ - K_{4} Z}} + K_{5} \left( {\Psi_{2} + \Psi_{3} e^{{ - K_{4} Z}} + \Psi_{4} e^{{ - \frac{{2K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} + \Psi_{5} e^{{ - \frac{{4K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} } \right),$$
(32)
$$\Phi = \Lambda_{0} + \Lambda_{1} e^{{ - K_{4} Z}} + \Lambda_{2} e^{{ - K_{4} + K_{2} Sc - K_{2} ScZ}} + K_{5} \left( \begin{gathered} \Lambda_{3} - e^{{ - K_{2} ScZ}} \Lambda_{4} + \Lambda_{5} e^{{ - K_{4} Z}} \hfill \\ + \Lambda_{6} e^{{ - \frac{{2K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} + \Lambda_{7} e^{{ - \frac{{4K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} \hfill \\ \end{gathered} \right).$$
(33)

3.2 Generalized Couette flow

Now, use Eq. (14) instead of Eq. (10), to solve Eqs. (11–12) subject to the boundary conditions (13) and adopting the same procedure. Then final form of perturbed solution of generalized Couette flow is presented as

$$W = \Omega_{5} + \Omega_{6} e^{{\frac{{K_{2} - K_{2} Z}}{{\left( {1 + K_{1} } \right)}}}} + K_{3} \left( {\Omega_{7} + \Omega_{8} e^{{ - \frac{{K_{2} Z}}{{\left( {1 + K_{1} } \right)}}}} + \Omega_{10} e^{{ - \frac{{3K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} } \right),$$
(34)
$$\varphi = \Psi_{6} + \Psi_{7} e^{{ - K_{4} Z}} + K_{5} \left( {\Psi_{8} + \Psi_{9} e^{{ - K_{4} Z}} + \Psi_{10} e^{{ - \frac{{2K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} + \Psi_{11} e^{{ - \frac{{4K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} } \right),$$
(35)
$$\Phi = \Lambda_{8} + \Lambda_{9} e^{{ - K_{4} Z}} + \Lambda_{10} e^{{ - K_{4} + K_{2} Sc - K_{2} ScZ}} + K_{5} \left( \begin{gathered} \Lambda_{11} - e^{{ - K_{2} ScZ}} \Lambda_{12} + \Lambda_{13} e^{{ - K_{4} Z}} \hfill \\ + \Lambda_{14} e^{{ - \frac{{2K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} + \Lambda_{15} e^{{ - \frac{{4K_{2} \left( { - 1 + Z} \right)}}{{\left( {1 + K_{1} } \right)}}}} \hfill \\ \end{gathered} \right).$$
(36)

The expression of Nusselt number and Sherwood is defined by.

Nuseelt Number = \(-{\varphi }^{^{\prime}}\left(1\right),\)

$${\text{Sherwood Number }} = \Phi^{\prime}\left( 1 \right).$$
(37)

4 Results

Since, the study deals with two kinds of mechanical cross flows, namely; plane Couette flow and generalized Couette flow. Therefore, this portion also further subdivided into two sections which relate to the contribution of emerging parameters on nano flows of Eyring-Powell fluid such as \({K}_{1}\) first order Eyring-Powell parameter, \({K}_{2}\) Reynolds number, \({K}_{3}\) second order Eyring-Powell parameter, Peclet number \({K}_{4}\), Brinkman number \({K}_{5}\), third order Eyring-Powell parameter \({K}_{6}\), Brownian motion parameter \({K}_{b}\), thermophoresis parameter \({K}_{t}\), concentration scale parameter \(n\), Schmidt number \(Sc\) and dimensionless pressure gradient \(\Gamma\).

4.1 Plane Couette flow

Nano flow of Eyring-Powell fluid through horizontal channel due to constant motion of the upper plate subject to variation in different parameters, is shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Figure 2, shows the impact of first order Eyring Powell parameter on momentum of nano flow. One can witness that momentum of nanofluid gradually, declines with the respect to \({K}_{1}\). On the contrary, effect of the suction Reynolds number enhances momentum of nano flow as shown in Fig. 3. Similarly, nano flow of Eyring-Powell fluid is supported by varying second order Eyring-Powell parameter in Fig. 4.

Fig. 2
figure 2

Velocity profile for different values of first order Eyring-Powell parameter

Full size image
Fig. 3
figure 3

Velocity profile for different values of Reynolds number

Full size image
Fig. 4
figure 4

Velocity profile for different values of second order Eyring Powell parameter

Full size image
Fig. 5
figure 5

Temperature profile for different values of Peclet

Full size image
Fig. 6
figure 6

Temperature profile for different values of Brinkman numbers

Full size image
Fig. 7
figure 7

Temperature profile for different values of first-order Eyring Powell parameter

Full size image
Fig. 8
figure 8

Temperature profile for different values of third order Eyring Powell parameter

Full size image
Fig. 9
figure 9

Concentration profile for different values of concentration scale parameter

Full size image
Fig. 10
figure 10

Concentration profile for different values of Brownian motion parameter

Full size image
Fig. 11
figure 11

Concentration profile for different values of thermophoresis parameter

Full size image
Fig. 12
figure 12

Concentration profile for different values of Schmidt number

Full size image

Temperature profile of nanoflow against different parameter is exhibited in Figs. 5, 6, 7, 8. Variation of Peclet number on temperature of nanofluid is given in Fig. 5. In Fig. 6 Brinkman number also contributes to enhance the temperature profile of the fluid. Similarly, nanofluid is further heated due to first order Eyring-Powell parameter in Fig. 7. Nevertheless, quite an opposite trend in the temperature profile is observed, in Fig. 8 against \({K}_{6}\).

Effects of emerging parameters on concentration of nano particles is shown in Figs. 9, 10, 11, 12. It is seen that concentration of nano species increases subject to rise in concentration scale parameter \(n\) in Fig. 9. Similarly, higher concentration of nano particles is observed in Fig. 10. It is noted that number density of species rises due to increase Brownian motion parameter \({K}_{b}\).

An opposite phenomenon is examined in Fig. 11 when numerical value of thermophoretic parameter is variated. By enhancing \({K}_{t}\) in Fig. 11 concentration of tiny particles declines. The contribution of another significant number is depicted in the next graph. Schmidt number has the same effects on concentration of particles as \({K}_{t}\) in Fig. 12.

4.2 Generalized Couette flow

Unlike the above case nano flow of non-Newtonian fluid through the horizontal channel subject to motion of upper plate along with the contribution of constant pressure gradient is given in Figs. 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24. The flow behaviour against each pertinent parameter does not alter, for the flow is generated mainly, by top wall. However, the role of constant pressure gradient augments its impacts which are evident through the graphs. Figure 13 gives the effects first order Eyring Powell parameter. Like in the previous case, nano fluid finds hard to travel through the channel due to shear thickening effects which add to the physical property of the base liquid. In the same way, influence of pressure gradient is more prominent near the upper wall of the channel which further drifts the nano fluid across the channel. The suction Reynolds number brings different enhances effects on the velocity of nanofluid. Increase in \({K}_{2}\) expedites the nanoflow through porous channel in Fig. 14. Basically, rise in suction in channel enhances the dimensionless number which eventually, makes nanofluid with heat transfer rapid. Same increasing behaviour is witnessed for second order Eyring-Powell parameter in Fig. 15. Since, the introduction of pressure gradient brings promising effects on the flow that can be evinced from Fig. 16. Presence of constant pressure gradient support nanofluid as increase makes the flow faster, gradually against higher pressure gradient.

Fig. 13
figure 13

Velocity profile for different values of first order Eyring-Powell parameter

Full size image
Fig. 14
figure 14

Velocity profile for different values of Reynolds number

Full size image
Fig. 15
figure 15

Velocity profile for different values of second order Eyring Powell parameter

Full size image
Fig. 16
figure 16

Velocity profile for different values of pressure gradient parameter

Full size image

Thermal profile is depicted in Figs. 17, 18, 19, 20. Couple stresses in the fluid give rise to Peclet number which leads to higher temperature correspondingly, as to be seen in Fig. 17. In Fig. 18 Brinkman number augments heat in the system by intensifying viscous dissipation. Nevertheless, increase in friction between the molecules generates some extra heat, as \({K}_{1}\) is varied Fig. 19. Unlike above dimensionless quantities reduction in heat subject to \({K}_{6}\) is examined in Fig. 20.

Fig. 17
figure 17

Temperature profile for different values of Peclet

Full size image
Fig. 18
figure 18

Temperature profile for different values of Brinkman number

Full size image
Fig. 19
figure 19

Temperature profile for different values first order Eyring Powell parameter

Full size image
Fig. 20
figure 20

Temperature profile for different values of third order Eyring Powell parameter

Full size image

Concentration profile nano particles against the four significant quantities is given in Figs. 21, 22, 23, 24. Concentration scale parameter \(n\) increases the saturation of nano particles near the upper portion of the channel as to be seen in Fig. 21. By increasing Brownian motion parameter \({K}_{b}\) nano particles start moving haphazardly in channel. During the process collisions take place which not only rises the temperature, but also increases the concentration as observed in Fig. 22. Thermophoretic parameter reacts differently in Fig. 23. Higher thermophoretic force causes the reduction in concentration of nano species. At last, in Fig. 24 mass transfer attenuates for higher Schmidt number.

Fig. 21
figure 21

Concentration profile for different values of concentration scale parameter

Full size image
Fig. 22
figure 22

Concentration profile for different values of Brownian motion parameter

Full size image
Fig. 23
figure 23

Concentration profile for different values of thermophoresis parameter

Full size image
Fig. 24
figure 24

Concentration profile for different values Schmidt number

Full size image

5 Discussion

Since, the velocity of Eyring-Powell fluid reduces against increase in \({K}_{1}\). Increase in the concerned parameter causes additional shear thickness effects which hampers the flow velocity. Flow enhances due to suction Reynolds number. It is important to know that rise in Reynolds number reduces the viscosity of fluid. This translates to an increase in nano flow of Eyring-Powell fluid by aggravating inertial forces. Presence of constant pressure gradient support nanofluid as increase makes the flow faster, gradually against higher pressure gradient. Temperature profile of increases against Peclet number. Higher values of dimensionless number aggravate the couple stresses in the base liquid which generate extra heat into the system. Brinkman number also enhances the temperature profile of the fluid. Higher Brinkman number signifies that effects of viscous dissipation are more dominant as compared to heat transported by molecular conduction. More heat emerges in the system due to first order Eyring-Powell parameter as the flow is resisted by \({K}_{1}\). This intensifies the force of friction between adjacent fluid particles and temperature rises. Effects of emerging parameters on concentration of nano particles reveals that uncertain movement of tiny particles allow them to collide with each other. This collision not only rises the temperature, but also accumulates the particles beyond the lower plate. However, strong thermophoretic force entice to move from a region of higher temperature to region of lower region in the horizontal channel. Therefore, number density of nano particles declines along axial direction of the channel for \({K}_{t}\) and Same Schmidt number.

6 Comparison with previous study

Numerical data obtained by using Range-Kutta method with shooting technique is compared with the one obtained by Gupta and Massoudi [11], for the case of uniform viscosity model in Table 1. The previous study discussed the generalized second grade fluid between two heated walls for the case of Newtonian and non-Newtonian \((m\ne 0)\) fluid under the consideration of constant and variable viscosity models. For comparison purpose, we have presented the values of velocity and temperature gradients against the variation of pressure gradient and viscous dissipation parameters for limiting case \(\left({K}_{3}=m=0\right)\) in Table 1 and noted that the obtained solutions are in full coherence with the solutions obtained by Gupta and Massoudi [11]. However, numerical values of Nusselt number against different parameters are tabulated in Table 2. It is noted that more heat transfer rate is significant for the case of plane Couette nanofluid flow. On the other hand, transfer is nano species more prominent for the case of Generalized Couette flow. Variation of Sherwood number against Schmidt number, Brownian motion parameter and thermophoresis parameter in Table 3. The data indicates that Sherwood number attains higher numerical values corresponding to Schmidt number and thermophoresis parameter. However, Sherwood number reduces against Brownian motion parameter. Eventually, Generalized Couette flow generates greater Sherwood number as compared to plane Couette flow with respect to each dimensionless quantity.

Table 1 Comparison of current findings with previous results [11]
Full size table
Table 2 Variation of Nusselt Number versus different parameters
Full size table
Table 3 Variation of Sherwood number versus different parameters
Full size table

7 Conclusions

An incompressible flow of Eyring-Powell fluid is investigated through a porous channel. The two dimensional nano fluid is caused by the uniform motion of upper surface in axial direction and due to the constant suction velocity in transverse direction. A set of highly nonlinear and coupled differential equations that describes the heat and mass transfer of non-Newtonian fluid is obtained with the help of “Perturbation method”. The analytic solution is further compared with numerical solution as well, and found both solution in great agreement. Parametric study reveals that nano flow Eyring-Powell fluid due to moving plate and constant pressure gradient is more prominent than merely moving wall flow. It is noted that effects of constant pressure gradient on nano flow are more prominent away from the lower wall of the channel. Moreover, viscous dissipation introduces additional heat into the system whereas, heat expunges due to third Eyring-Powell parameter. Finally, thermophoretic force and Brownian motion act differently on particle concentration.