Stochastic dynamics of a non-linear cable–beam system

Abstract

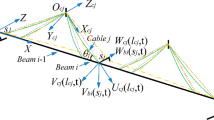
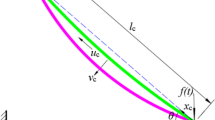
Cable-stayed bridges and guyed towers are examples of structures extensively used in Civil Engineering. The uniform tension in the cable may change during service life due to various causes. Thus, uncertainty studies appear desirable to provide information about the effect of the parameter variations on the structure dynamics. The non-linear dynamic behavior of a cable-beam system, as a simplified model of a guyed structure, is studied. The beam behavior is assumed linear, while the cable is modeled with non-linear equations accounting for the extensibility and an initial deformed state. The deterministic equations are linearized about the reference configuration and then frequencies and modes are calculated. The modes are later used to construct a reduced order model. The non-linear equations are discretized by finite elements with a Galerkin procedure. Afterwards, a stochastic model is stated with the cable tension and beam stiffness assumed as random variables and appropriate probability density functions (PDFs) are derived through the Principle of Maximum Entropy. A numerical analysis is carried out using Monte Carlo techniques for simulations. Some unexpected features, such as multimodality of the PDFs, are observed. The structural model seems to be more sensitive to the cable tension uncertainty than to the beam stiffness.

Appendix

The constants of Eq. 5 are listed next. For the sake of brevity, a compact notation is introduced. For instance, if one needs to calculate $d_{211},$ then, as stated in the fourth line, $L^2=d,$ and afterwards, in the sixth line, $L_{jkk}^i$ with $i=2$, $j=2$ and $k=1$ gives $L_{211}^2=d_{211}$.

$$\begin{aligned} m_i= & {} m_b\int _{0}^{L_b} \phi _{b_vi}'^2 + \phi _{b_ui}'^2 dx_b + m_c\int _{0}^{L_c}\phi _{c_vi}'^2 + \phi _{c_ui}'^2 {\mathrm{d}}x_c \\ a_i= & {} c_b\int _{0}^{L_b} \phi _{b_vi}'^2 + \phi _{b_ui}'^2 dx_b + c_c\int _{0}^{L_c} \phi _{c_vi}'^2 + \phi _{c_ui}'^2 {\mathrm{d}}x_c \\ p_i= & {} \int _{0}^{L_b} P_{b_vi}\phi _{b_vi} + P_{b_ui}\phi _{b_ui} dx_b + \int _{0}^{L_c} P_{c_vi}\phi _{c_vi} + P_{c_ui}\phi _{c_ui} {\mathrm{d}}x_c \\ L^1= & {} c , L^2 = d \\ L_{kkk}^i= & {} \frac{1}{2}EA_c \int _{0}^{L_c} \phi _{c_vk}'^3 \phi _{c_vi}' {\mathrm{d}}(x_c) \\ L_{jkk}^i= & {} \frac{3}{2}EA_c \int _{0}^{L_c} \phi _{c_vk}'^2 \phi _{c_vj}'^2 \phi _{c_vi}' {\mathrm{d}}(x_c) \\ L_{i}^i= & {} \int _{0}^{L_b}\Big \{ EI \phi _{b_vi}''^2 + EA_b\phi _{b_ui}'^2 \Big \}dx_b + \int _{0}^{L_c}\Big \{ H \phi _{c_vi}'^2 + EA_c \phi _{c_ui}'^2 \\&+ \, 2 EA_c Y_c' \phi _{c_ui}' \phi _{c_vi}' + 2 EA_c Y_c'^2 \phi _{c_vi}'^2 \Big \} {\mathrm{d}}x_c \\ L_j^i= & {} \int _{0}^{L_c} EA_c \bigg ( Y_c' \phi _{c_uj}' \phi _{c_vi}' + Y_c'^2 \phi _{c_vj}' \phi _{c_vi}' + \phi _{c_vj}' \phi _{c_ui}' \bigg ) {\mathrm{d}}x_c \\ L^i_{12}= & {} \int _{0}^{L_c}\bigg \{ EA_c\Big ( 3 Y_c' \phi '_{c_v1}\phi '_{c_v2}\phi '_{c_vi} + \phi '_{c_u1}\phi '_{c_v2}\phi '_{c_vi} + \phi '_{c_u2}\phi '_{c_v1}\phi '_{c_vi}\\&+\, Y'_c \phi '_{c_v1}\phi '_{c_v2}\phi '_{c_ui}\Big ) \bigg \} {\mathrm{d}}x_c \\ L_{jj}^i= & {} \int _{0}^{L_c} EA_c \bigg ( \frac{3}{2} Y_c' \phi _{c_vj}'^2 \phi _{c_vi}' + \phi _{c_vj}'\phi _{c_uj}' \phi _{c_vi}' + \frac{1}{2}\phi _{c_vj}'^2 \phi _{c_ui}'\bigg ) {\mathrm{d}}x_c \quad {\text{ with}} \quad i, j, k=1,2. \end{aligned}$$