The first frequency of cantilevered bars with geometric effect: a mathematical and experimental evaluation

Abstract

In engineering, a large number of structures may be modeled as cantilevers. Due to their intrinsic characteristics, some of these structures are sensitive to dynamic actions. Gusts of wind are dynamic excitations for which the fundamental frequency of vibration is an important factor when calculating the structural response. Modeling the effects of the axial force on the natural frequencies of a structure usually results in systems of differential equations that are not solvable from a practical engineering perspective. This article develops a simple mathematical expression for calculating the fundamental frequency of cantilevered structures, within small ranges, that considers the presence of an axial demand. This expression has been validated by dynamic laboratory testing.

1 Introduction

In general, studies of isolated bars are frequently related to analyzing the stability of structural systems, Gambhir [13]. As mentioned by Mailybaev and Seyranian [23], the influence of vibration on the stability of elastic systems is important in engineering theory and applications. Cano and Ochoa [6] maintain that the stability and dynamic behavior of beams and beam-columns are of great importance in structural dynamics, aerospace and earthquake engineering. The vibration analysis and seismic response of framed structures modeled as beams and columns have been studied by many researchers and continue to be treated extensively in the literature. Among these are problems dealing with vibration of bars and studies done by Goel [14, 15], Ferreira and Ewins [12] can be cited. Soares Filho et al. [26] presented work concerned with the dynamic elastic analysis of semi-rigid plane frames subjected to wind pressures, where the frame was considered as a set of contiguous bar elements, connected by rotational springs.

Systems consisting of cantilevered columns are useful both for analyzing stability and for calculating the wind forces in buildings. The standard procedure associates the building with a discrete model of a column inlaid into the base. The standards used for analyzing wind effects are based on the natural frequency and modes of vibration, principally the first mode.

Due to their characteristics, structures such as chimneys, tall reservoirs and telecommunication poles are sensitive to dynamic actions. When undergoing this type of excitation, they can resonate with the load. Typically, these are tall slim structures or structures subjected to high axial loads. The axial compression forces reduce the stiffness and influence the natural frequencies of the structure and they cannot be ignored in many cases. In this regard, Wilson and Habibullah [30] stated that further consideration of the normal force in structural dynamics is a viable technique for calculating the second-order effects because the effect is linearized and the solution to the problem is obtained directly and accurately, without interactions. It is valid for situations where the vertical force due to the structure’s weight and external loads remain constant during structural movement and for situations where the lateral displacements are small compared to the size. Structures are subject to effects that they need to resist. In general, they should stay reasonably close to their specifications during induced movements. In other words, the movements of a structure around their specification should be small. Therefore, a dynamic analysis of geometric non-linearities constrained by geometric stiffness is perfectly reasonable.

Specific studies on the effect of normal force on the vibration of structural systems were presented by Laurence [20]. Other researchers concerned with the issue were Howson and Williams [16] who studied the natural frequencies of frames with axially loaded Timoshenko members. Mian and Zhi-da [24] evaluated the second-order effect of an elastic circular shaft and by using asymptotic expansion methods they confirm that the effect of axial elongation and distortion of plane cross-section exists in an elastic circular shaft during large torsion and give the expressions of the axial force and the torque. For your turn, Banerjeea and Williams [3] showed studies that evaluate the change in vibrations modes for the first five natural frequencies of axially loaded tapered members.

The objective of this article is to evaluate the influence of axial force on the fundamental frequency of isolated bars and to present a safe way to calculate the fundamental frequency of any structure that can be satisfactorily modeled as an element of a simple cantilever bar. This process will result in a viable engineering solution. Although the expressions developed in this paper will be familiar to those accustomed to dealing with mechanical vibrations, their final presentation is a bit unusual. Its simplicity allows us to simultaneously consider the effect of an external force applied upon the free extremity of the structure and the structure’s self-weight, which produces a practical engineering solution.

It is important to highlight that many engineering models are complex and use expensive tools. In most practical applications of engineering, the use of concise and feasible models can lead to similar and even better results.

This work is a preliminary investigation that assesses the analytical results of a simplified mathematical solution by comparison with dynamic laboratory tests. The method developed here will be applied to determine the fundamental frequency of real structures and will motivate both comparative studies of other analytical methods, such as the finite elements method, and experimental field investigations.

2 Mathematical model

The analytical formulation developed here is based on the principle of virtual work combined with a technique similar to that of Rayleigh [25]. Rayleigh assumed that a system containing infinite degrees of freedom can be replaced by a finite single degree of freedom (SDOF) system that approximates their frequency.

Applications of the Rayleigh technique to mechanical systems with vibration problems are found in a wide range of scientific papers. Some of them are dedicated to the study of plate vibrations, which was one of the problems addressed by Rayleigh in his principal publication. Biancolini et al. [4] applied the method to approximate the frequencies of orthotropic plates using and merging the results obtained by other researchers who used a simple numerical procedure employing a particular formulation of the Rayleigh method. Cheung and Zhou [8] studied the free vibration of thin orthotropic rectangular plates with intermediate line supports in one or two directions. They used a new set of admissible functions, which are the static solutions of a point-supported beam under a series of sine loads. Chiba and Sugimoto [9] used the so-called Rayleigh–Ritz method for the problem of a cantilever plate attached to a ‘spring–mass’ system. They systematically clarified the coupled vibration characteristics of the system by thoroughly studying the effects of the ‘spring–mass’ attachment. Hu et al. [17] studied the problem of the vibration characteristics of shells subjected to axial forces, such as centrifugal forces, and used algebraic polynomial functions as the functional form. Laura et al. [19] used the Rayleigh–Ritz method to address the problem of vibrations in a circular plate. Kandasamy and Singh [18] analyzed the free vibration of isotropically skewed open circular cylindrical shells using a modified version of the Rayleigh–Ritz method.

Problems similar to the study of vibrations of bars were addressed by Wang [29] using a new displacement field applied to the Euler–Bernoulli theory. Wang concluded that it was an efficient unified approach for studying the free vibration and buckling problems of both thick and thin beams and plates. For their part, Zhou and Cheung [32] used the Rayleigh method to calculate the frequencies of a tapered Timoshenko beam under a Taylor series of static load and the Rayleigh–Ritz method is applied to derive the eigenfrequency equation.

It is important to observe that the technique developed by Rayleigh and presented in his first book was only used to calculate the fundamental frequency. Leissa [21] claims that the precision obtained through this method depends entirely on the functional form that is used to represent the free vibration mode. If the exact shape were assumed, the exact corresponding frequency would be generated by this method. Moreover, she adds that the technique developed by Rayleigh can be used to obtain frequencies for modes higher than the Fundamental. Form functions were addressed by Leung et al. [22] when using the dynamic stiffness method in a harmonic vibration analysis of a Timoshenko column.

It is interesting to note that the Ritz or Rayleigh–Ritz method, which Leissa [21] considers to be an inappropriate name, is considered to be an extension of Rayleigh’s method and is used to obtain both fundamental and higher vibration modes.

The basic concept behind the Rayleigh method is the principle of conservation of energy in mechanical systems; therefore, it is applicable to linear and non-linear structures, according to Clough and Penzien [10]. According to Temple and Bickley [27], the fundamental principles developed by Rayleigh are applied both to systems with finite degrees of freedom and to continuous systems. The purpose is to determine the fundamental period of vibration and to analyze the stability of the elastic systems with the precision required for engineering problems. To do this, the virtual works principles must be described by adequate chosen of generalized coordinates at the top of the bar and by a functional form that describes the first mode of vibration. At the end of the calculation, the movement equation is written in terms of the generalized coordinate, from which one can extract the generalized elastic and geometric properties of the system.

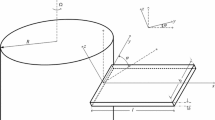
Consider a system containing just the horizontal degree of freedom that is in undamped free movement with the parameters shown in Fig. 1. This system is composed of a prismatic bar made from an elastic-linear material embedded in the base bearing its own weight and a mass on the free extremity that is representative of the bodies fixed to its top. The movement of the system does not alter the orientation of the normal force N(x), which has to be taken into consideration. A similar mathematical development can be found in Clough and Penzien [10].

Fig. 1

Parameters for developing the mathematical model

The work done by the external forces over the virtual displacement is:

$$ \delta W_{\text{E}} = - \int\limits_{0}^{L} {f_{\text{I}} (x)\delta v(x){\text{d}}x} + N(x)\delta e $$

(1)

where $f_{\text{I}} (x) = m_{1} (x)\mathop v\limits^{..} (x,t)$ represents the inertial force. The work of the virtual internal forces is given by:

$$ \delta W_{\text{I}} = \int\limits_{0}^{L} {M(x,t)\delta v^{\prime\prime}(x){\text{d}}x} $$

(2)

where $\delta v^{\prime\prime}(x) = \frac{{\partial^{2} v(x)}}{{\partial x^{2} }}.$

To be able to find the axial displacement e(t), it is necessary to take an infinitesimal element of the elastic line of the bar. Then the shortening of the axis due to the axial displacement will be:

$$ {\text{d}}s - {\text{d}}x = \sqrt {{\text{d}}x^{2} + {\text{d}}v^{2} } - {\text{d}}x = {\text{d}}x\sqrt {1 + \left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{2} } - {\text{d}}x. $$

(3)

The binomial development yields:

$$ \left( {1 + \left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = 1 + \frac{{\left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{2} }}{2} - \frac{{\left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{4} }}{8} + \frac{{\left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{6} }}{16} - \cdot \cdot \cdot $$

Because the superior order terms $\left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{2}$ are small when compared to the unit, $\left( {1 + \left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = 1 + \frac{{\left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{2} }}{2}$ is an acceptable approximation, which allows Eq. (3) to be rewritten as:

$$ {\text{d}}s - {\text{d}}x = {\text{d}}x\left[ {1 + \frac{1}{2}\left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{2} } \right] - {\text{d}}x = \frac{1}{2}\left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{2} . $$

(4)

By integrating Eq. (4) into the entire beam, the following equation is obtained:

$$ e(t) = \frac{1}{2}\int\limits_{0}^{L} {\left[ {v^{\prime}(x,t)} \right]^{2} } {\text{d}}x. $$

(5)

Because the parameters necessary for the solution of the problem may be expressed as functions of the generalized coordinate q and a form function $\phi (x),$

$$ \begin{array}{*{20}c} \begin{gathered} v\left( {x,t} \right) = \phi (x)q(t) \, \hfill \\ v^{\prime}(x,t) = \phi^{\prime}(x)q(t) \hfill \\ v^{\prime\prime}(x,t) = \phi^{\prime\prime}(x)q(t) \hfill \\ \ddot{v}(x,t) = \phi (x)\ddot{q}(t) \hfill \\ \dot{v}^{\prime\prime}(x,t) = \phi^{\prime\prime}(x)\dot{q}(t) \hfill \\ \end{gathered} & \begin{gathered} \delta v(x,t) = \phi (x)\delta q(t) \hfill \\ \delta v^{\prime}(x,t) = \phi (x)^{\prime}\delta q(t) \hfill \\ \delta v^{\prime\prime}(x,t) = \phi (x)^{\prime\prime}\delta q(t) \hfill \\ \delta e = \int\limits_{0}^{L} {v^{\prime}(x,t)\delta v^{\prime}(x){\text{d}}x} \hfill \\ \end{gathered} \\ \end{array} $$

(6)

is obtained.

Conveniently replacing Eqs. (5) and (6) in Eqs. (1) and (2) yields

$$ \delta W_{\text{E}} = \left[ { - \ddot{q}(t)\int\limits_{0}^{L} {m_{1} \left( {\phi (x)} \right)^{2} {\text{d}}x} + q(t)\int\limits_{0}^{L} {N(x)\left( {\phi^{\prime}(x)} \right)^{2} {\text{d}}x} } \right]\delta q $$

(7)

and

$$ \delta W_{\text{I}} = \left[ {q(t)\int\limits_{0}^{L} {EI\left( {\phi^{\prime\prime}(x)} \right)^{2} {\text{d}}x} } \right]\delta q $$

(8)

Equating Eqs. (7) and (8), the undamped free movement equation may be written in terms of the generalized coordinate:

$$ \prod \ddot{q}(t) + K_{0} q(t) - K_{g} q(t) = 0 $$

(9)

where $\prod$, $K_{0}$ and $K_{g}$ are the generalized mass and stiffness described by a function of a chosen form function, as can be seen here.

To consider the mass on the top of the column, the total generalized mass is given by:

$$ \prod = m_{0} + m_{2} $$

(10)

with:

$$ m_{2} = \int\limits_{0}^{L} {m_{1} } \left( {\phi (x)} \right)^{2} $$

(11)

The elastic and geometrical stiffnesses are:

$$ K_{0} = \int\limits_{0}^{L} {EI\left( {\frac{{{\text{d}}^{2} \phi (x)}}{{{\text{d}}x^{2} }}} \right)^{2} {\text{d}}x} $$

(12)

$$ K_{g} = \int\limits_{0}^{L} {N(x)\left( {\frac{{{\text{d}}\phi (x)}}{{{\text{d}}x}}} \right)^{2} {\text{d}}x} $$

(13)

respectively.

For the model in Fig. 1, $N(x) = \left[ {m_{0} + m_{1} (L - x)} \right]g$, with N(x) being the distributed normal internal force.

Assuming that the well-known trigonometric function

$$ \phi (x) = 1 - \cos \left( {\frac{\pi x}{2L}} \right) $$

(14)

which can be found in Clough and Penzien [10] and Timoshenko [28], represents the first buckling mode of the model exactly, its validity is restricted to the surroundings of the reference configuration.

Numerically solving the integrals in Eqs. (11) through (13), the outcomes are the total generalized mass, the generalized elastic stiffness, and the matrix of the geometric stiffness, respectively, where m ₁ is the mass per length unit and m ₀ is the concentrated mass on the top of the bar:

$$ \prod = m_{0} + \frac{1}{2}Lm_{1} \frac{3\pi - 8}{\pi } $$

(15)

$$ K_{0} = \frac{{\pi^{4} EI}}{{32L^{3} }} $$

(16)

and

$$ K_{g} = \frac{1}{16}g\frac{{2\pi^{2} m_{0} + \left( {\pi^{2} - 4} \right)m_{1} L}}{L} $$

(17)

The total generalized stiffness of the system is therefore:

$$ K = K_{0} + K_{g} $$

(18)

The natural frequency is given by:

$$ \omega = \sqrt {\frac{K}{\prod }} $$

(19)

Using Eqs. (15) through (17) in Eq. (19) yields a frequency equation that considers the influence of the axial force, in Hertz:

$$ f = \frac{1}{2\pi }\left( {\frac{{\frac{{\pi^{4} }}{32}\frac{EI}{{L^{3} }} + \left[ {\frac{{\pi^{2} }}{16}\left( {\frac{{2m_{0} + m_{1} L}}{L}} \right) - \frac{1}{4}m_{1} } \right]g}}{{m_{0} + \frac{3\pi - 8}{2\pi }Lm_{1} }}} \right)^{\frac{1}{2}} $$

(20)

In Eq. (20), E is the modulus of elasticity of the material, L is the length of the bar, I is the minor inertial moment of the section and g is the acceleration due to gravity, whose signal should be negative when the force is compressive. It is obvious that the effects of the shear force on the deflection of the bar were not considered in the previous development. Two observations deserve some comment here. If other masses exist within the system, they logically have to be considered, thus adjusting Eq. (20). In cases where there is variation in the geometry or in the elastic properties of the structure, it is necessary to solve the integrals from Eqs. (11) through (13) within the limits established for each interval.

The recent work of Yaman [31], the Adomian decomposition method is used to determine the vibrations of the beam/column with a variable rotation relative to the initial straight axis, obtaining results that are compatible with the finite elements method. Using Eq. (20) with the parameters given by Yaman yields 3.2840 Hz, compared to his results of 3.2532 Hz (a difference of less than 1 %).

3 Dynamic laboratory tests

Electrical strain gages and piezoelectric accelerometers were used. The former were manufactured by Excel Sensors [11] and the latter by Brüel & Kjaer [5]. The arrangement adopted for connecting the extensometers to the data acquisition system and the characteristics of the equipment are given in Table 1.

Table 1 Characteristics of sensors

The accelerometers were calibrated using a Brüel & Kjaer type 4294 manual caliper driver and connected to the acquisition system through a differential tension configuration with a gain of 1.

The connection of the accelerometers to the data acquisition system was preceded by the connection of the accelerometer to the Brüel & Kjaer type 2525 amplifier.

The ADS-2000 automatic data acquisition system AqDados [1] was used with the AI-2161 conversing plates, an AC-2122VA controlling plate (LYNX Informatics) and 16-bit resolution. The interface with the microcomputer was achieved through ethernet networking. The connection of the sensors to the data acquisition system was achieved through input connectors located at the rear of the equipment.

The test sample consisted of a nominally 1/2″ (12.70 mm) by 1/8″ (3.17 mm) flat metal bar that had two metallic masses fixed to its free extremity by lateral pressure. Its mass and the masses of the accelerometers and their magnetic bases resulted in a total of 1,595 g on the top of the rod.

Because the model of longitudinal elasticity was a steel piece, it was assumed to be 205 GPa. The density of the rod material was experimentally determined in the PCC/USP materials laboratory using the helium pycnometry technique. The relative density obtained was 8.19 (8,190 kg/m³). The other masses involved were measured using an electronic scale.

The test sample was instrumented with three extensometers and two accelerometers, according to the layout in Fig. 2. The extensometers were glued to the extension of the bar, and the accelerometers were attached to the magnetic bases.

Fig. 2

Instrumentation of the test sample and the details of the accelerometer settings

With the metallic masses added to the rod, three positions were adopted to simulate the possible influences of the axial load on the stiffness of the system. The first position took the influence of the axial compressive force into consideration. The set was positioned to compress the bar with its own weight and with the vertical load produced by the mass on the top. The second position considered the influence of the axial traction force. The set was positioned to generate traction force in the system, and the test sample was inverted from the first position. The third position analyzed the effect of no axial load upon the fundamental frequency of the model, and the set was installed in the horizontal position as a cantilever beam. Figure 3 illustrates the three positions used.

Fig. 3

Positions adopted in the tests

The test sample was fixed to the supporting device by metal clamps. The same fixation pattern was used for all the models. The contact surface of the inertial base was carefully prepared to reduce imperfections and roughness. The accelerometer cables were fixed to prevent interference with the signal reading. The support ensemble provided safe inertial conditions for carrying out the tests. Before excitation, the models were vertically leveled. The support ensemble provided safe inertial conditions for carrying out the tests.

The reference experimental length was visually controlled and measured using a metallic tapeline (Fig. 4) to compensate for the uncertainty in the real fixation point of the models on the base and in the real position where the axial force was applied. The same references were maintained for the different positions. The length varied by 5 cm up to the physical limit of the possible fixation or up to the maximum position consistent with the stability of the ensemble.

Fig. 4

Inferior reference length of the models

In both tests, models with different positions and lengths were excited by a random force of sufficient magnitude to set the system into oscillatory motion. After the excitation, the systems oscillated around the initial deformed position.

The signals in the time response were recorded and subsequently analyzed. The fundamental frequency of the models was obtained using the Fourier transform in the AqDAnalysis 7 [2] program. The auto-spectrum of the program was configured as follows: a Hanning-type compensation window; a data window for calculating the average spectrum; a fast-Fourier transform zoom equal to 1; and the maximum resolution possible for the number of samples.

It is important to note the conclusions of Carneiro [7], who states that for small amplitudes, both experience and theoretical solutions show the influence of the initial displacement in relation to body length to be negligible and that the influence of damping on the vibration period can generally be ignored.

4 Results and conclusion

The objective of this work was to evaluate the influence of axial forces on the first vibration frequency of isolated columns and to establish a relatively simple mathematical procedure to calculate this frequency. In other words, this work deals with the identification of the first natural frequency in cantilevered bars with non-linearities caused by geometric effects.

Using this single-calculation procedure it is possible to consider the influence of the normal force located on the free extremity of the bar and the weight of the bar itself, making it a simple and practical solution for use in routine engineering applications without requiring sophisticated computing resources. To validate the equation, a set of dynamic tests was conducted in the laboratory.

The effect of a normal force on the frequency of a column can be perceived through the numerical results obtained using Eq. (20). For this purpose, we used the elastic and geometric parameters of the bodies of the test sample used in the laboratory tests and varied the length from 0.15 to 5 m at short intervals. We plotted the graph in Fig. 5, which relates the frequencies of the column with the nature of the axial force.

Fig. 5

Numerical simulation of the influence of the axial force

The first factor to consider in this simulation goes back to the effects of a compressive force and the requirement for stability in the compressed bars. The highlighted aspect is the instability of the bar that occurs when the frequency is zero. This condition holds when it reaches a length of 1.1 m. If the effect of the compressive force were to be ignored, the curve would follow the horizontal axis asymptotically. The opposite occurs in the case of a tractive effort because this effort favors stiffness, thus stabilizing the system and increasing the frequency. The stiffness of the structure is not modified in the absence of normal stress, resulting in an intermediate curve between the two.

Table 2 shows the frequency variation of the column according to the different levels of axial force. The intensity of the normal force in these cases was obtained by varying the generalized mass, according to Eqs. (10) and (11). This variation produces a change both in strength and in the generalized mass of the system, which reduces the frequency of the bar while both the strength and the generalized mass of the system increase. Compared to the effort of compression, traction produces a higher frequency. The second column of Table 2 shows the frequency variation with the slenderness of the column, which becomes unstable when it reaches slenderness close to 1964.

Table 2 Influence of the axial load by analytical model

To evaluate the sole influence of the axial force on the first frequency of the column, the overall mass of the system was kept unchanged. Only the intensity of the normal force varied and was not associated, in this case, with gravitational action. By varying the intensity of the tensile force, an effort five times a variation of 0.46 % was noted in the frequency of the smallest element, while changing the force by a factor of 20 produced an increase close to 35 % on the longest element. The results can be seen in Table 3.

Table 3 Influence of the axial load intensity

The analytical and experimental results are available in Table 4. The graph in Fig. 6 shows the effect of the normal force upon the frequency of the physical models.

Table 4 Experimental and simplified mathematical model results

Fig. 6

Influence of a normal force on the experimental frequencies

The graphs in Figs. 7, 8 and 9 compare experimental results with mathematical models for each influence position of axial force.

Fig. 7

Compressive force: experimental results and mathematical model

Fig. 8

Tension force: experimental results and mathematical model

Fig. 9

Without normal force: experimental results and mathematical model

We conclude that the mathematical expression presented in this article predicts the fundamental frequency of a column inlaid in a base with an acceptable error of 3 %. It is important to note that for the longer models, which are subject to compression and act as beams, the initial reference configuration deviates from the assumptions of the mathematical model. In these cases, it is necessary to consider the normal force component that acts on the deflection of the bent bar. Moreover, it is interesting to note that the experimental activities carry uncertainties such as the imperfect conditions of support, clamping pressure of models, centralizations and uprights, initial deformations of the samples, among others.

A rich comparison that can be made to demonstrate the validity of the simplified process is a study using analysis by finite element method (FEM). For FEM the equivalent situation studied in this work correspond to a non-linear dynamic analysis using the geometric portion in the complete stiffness matrix of the system. This approach can be seen in Table 5.

Table 5 Finite element method and simplified mathematical model results

In conclusion, it was demonstrated that simplified modeling with non-linear effects can obtain similar or better results than the complex model. It is interesting to note that the ease of access to sophisticated computational tools has always given the impression that it is necessary to model finite element by using CAD/CAE/CFD, giving many degrees of freedom. However, many engineers often forget that the basic physical fundamentals are able to provide simple and inexpensive results, which can be very effective for analysis.

Studies are being carried out to apply Eq. (20) to actual structures. The results show that it is possible to use Eq. (20) in real structures as long as the weighing criteria are adapted to the geometry of the structure. Moreover, it is possible to adapt Eq. (20) to cases where there are discrete masses positioned along the length.