1 Introduction

In the field of geophysical investigations, the principal focus is decoding the subsurface structure of the earth based on data procured from or near the earth’s surface. The amassed data usually correlate with one or several significant features of the earth, thereby enabling a feasible determination of these physical properties by addressing an inverse problem. When a model of the subterranean area of interest is built, the inverse problem can be managed to deduce probable parameter values for the model. The end goal of geophysical inversion is to construct an earth model, characterized by an array of physical quantities that align with collected observational data. As data acquisition techniques advance incessantly, there emerges a pressing need for cutting-edge data processing methods. The central aim of this study is to develop innovative data processing algorithms by applying inverse theory to Fourier transformations for geophysical applications. In signal processing, the transfer of data from the time domain to the frequency domain is a conventional operation. The Discrete Fourier Transformation (DFT) algorithm is typically employed to discern the discrete frequency constituents of a regularly sampled time-domain dataset. However, the processing method’s vulnerability to noise is a crucial consideration, as noise recorded in the time domain is effectively transformed into the frequency domain. To significantly reduce the impact of data noise and outliers during data processing, a more robust method known as Iteratively Reweighted Least Square Fourier Transformation (IRLS-FT) was introduced by Dobróka et al. 2015. The efficacy of the algorithm was evaluated across various facets, including its application to a magnetic dataset (Dobróka et al. 2017) to affirm its noise-reducing capability. By integrating the IRLS algorithm with Cauchy-Steiner weights, the Fourier transformation was treated as a robust inverse problem, with the Fourier spectrum discretized using Hermite function-based series expansion (H-IRLS-FT). This methodology has proven successful in processing gravity data (Dobróka and Völgyesi 2010), well logging data (Dobróka et al. 2016; Szabó 2004), and Induced Polarization data (Turai et al. 2010). As the Hermite functions are eigenfunctions of the Fourier transform the H-IRLS-FT method is quick and accurate with a disadvantageous need of a preliminarily knowledge of a scale factor involved in the Hermite functions. To avoid this disadvantage we propose in this paper a new inversion-based Fourier transform using Chebyshev polynomials as the fundamental functions, thereby discretizing the Fourier spectrum through series expansion. Building on these contemporary advancements, we introduce the Chebyshev-Polynomials Least-Squares Fourier Transformation (C-LSQ-FT), and its robust version, the Chebyshev-Polynomials Iteratively Reweighted Least Squares Fourier Transformation (C-IRLS-FT). By employing this technique, we determine the expansion coefficients by solving an overdetermined inverse problem. Furthermore, the Iteratively Reweighted Least-Squares method was integrated to enhance the process’s robustness. In our framework, each data point contributes to the solution based on its error margin, achieved by iteratively weighting individual data points using Cauchy-Steiner weights, consequently crafting an algorithm resilient to data outliers, especially those sparsely scattered. By comparing this method with the traditional DFT algorithm in magnetic data’s pole reduction, we demonstrated the superior robustness and resistance of the C-IRLS-FT algorithm. These methods are initially tested on synthetic datasets, specifically configured with two types of noise, to assess the method’s robustness under varying conditions. Subsequently, the refined method is applied to actual exploration datasets, offering an opportunity to examine its effectiveness in real-world scenarios. By combining the analysis of synthetic and real-world datasets, the research aims to not merely further the development of the C-IRLS-FT method but also perform an exhaustive evaluation of its advanced features. The ultimate goal is to validate the enhanced performance of this method in processing geophysical data. Emphasis is placed on demonstrating its superior robustness, resilience to noise, and overall effectiveness, especially when juxtaposed with traditional techniques such as Discrete Fourier Transformation (DFT). Through the amalgamation of theory, innovation, and practical application, this study strives to contribute significantly to the field of geophysical data processing, providing researchers and industry professionals with a refined tool that enhances the quality and reliability of subsurface data interpretation.

2 Chebyshev polynomials as basis functions

The Chebyshev polynomials (Fig. 1) of the first kind fulfill the differential equation:

$$ \left(1-{x}^{2}\right){y}^{{\prime }{\prime }}-x{y}^{{\prime }}+{n}^{2}y=0$$
(1)

where \( \left|x\right|\) ≤ 1 and n represent integer numbers. They can also be generated by using the recurrence equations

$$ {T}_{0}\left(x\right)=1$$
(2)
$$ {T}_{1}\left(x\right)=x$$
(3)
$$ {T}_{n}\left(x\right)=2x{T}_{n-1}\left(x\right)-{T}_{n-2}\left(x\right), n\ge 1$$
(4)

The first five Chebyshev polynomials of the first kind are plotted in Fig. 1. It can be seen that these functions fulfill the symmetry conditions

$$ {T}_{n}\left(-x\right)={(-1)}^{n}{T}_{n}\left(x\right)$$
(5)

and on the interval − 1 ≤ x ≤ 1 all of the extrema have values that are either − 1 or 1:

$$ {T}_{n}\left(1\right)=1, {T}_{n}\left(-1\right)={(-1)}^{n}$$
(6)

In applying these polynomials as basis functions in a series expansion, the extrema features can result in resolution problems at large n values because \( T\left(n,x\right)\) and \( T\left(n+2,x\right)\) are close to each other near x=(+/-) 1. Because of this reason, we will apply also the Chebyshev polynomials of the second kind which fulfill the differential equation

$$ \left(1-{x}^{2}\right){y}^{{\prime }{\prime }}-3x{y}^{{\prime }}+n(n+2)y=0$$
(7)

and can be generated by the recurrence formulae.

Fig. 1
figure 1

Chebyshev polynomials - first type

Full size image
$$ {U}_{0}\left(x\right)=1$$
(8)
$$ {U}_{1}\left(x\right)=2x$$
(9)
$$ {U}_{n}\left(x\right)=2x{U}_{n-1}\left(x\right)-{U}_{n-2}\left(x\right),n\ge 1$$
(10)

The first five Chebyshev polynomials of the second kind are plotted in Fig. 2.

Fig. 2
figure 2

Chebyshev polynomials - second type

Full size image
Fig. 3
figure 3

The generated noise-free wave

Full size image

It can be seen that these functions fulfill the symmetry conditions

$$ {U}_{n}\left(-x\right)={(-1)}^{n}{U}_{n}\left(x\right)$$
(11)

and on the interval − 1 ≤ x ≤ 1 the extrema have different values

$$ {U}_{n}\left(1\right)=n+1$$
(12)

and

$$ {U}_{n}\left(-1\right)={\left(-1\right)}^{n}\left(n+1\right)$$
(13)

The Chebyshev polynomials have important orthogonality properties. The first kind of polynomials considers orthogonal on the interval \( -1\le x\le 1\) with weight function \( w\left(x\right)=\frac{1}{\sqrt{1-{x}^{2}}}\)

$$ {\int }_{-1}^{1}\frac{{T}_{n}\left(x\right){T}_{m}\left(x\right)}{\sqrt{1-{x}^{2}}}dx= \left\{\begin{array}{c}0 if n \ne m \\ \pi if n=m=0\\ \frac{\pi }{2} if n=m\ne 0. \end{array}\right.$$
(14)

Also, the Chebyshev polynomials of the second kind can be considered orthogonal on the interval \( -1\le x\le 1\) with weight function \( w\left(x\right)=\sqrt{1-{x}^{2}}\)

$$ {\int }_{-1}^{1}{U}_{n}\left(x\right){U}_{m}\left(x\right)\sqrt{1-{x}^{2}}dx= \left\{\begin{array}{c}0 if n \ne m\\ \frac{\pi }{2} if n=m\end{array}\right.$$
(15)

2.1 The C-LSQ-FT and C-IRLS-FT algorithms in 1D

As is well known, the traditional Fourier transformation is highly noise-sensitive. On the other hand, inverse problem theory encompasses a variety of noise rejection methods. So it is straightforward to expect, that by formulating the Fourier transform as an inverse problem, the noise sensitivity can be appreciably reduced. This idea was followed at the Department of Geophysics (University of Miskolc). Concerning the selection of the basis functions, two kinds of inversion-based Fourier transform algorithms were developed: Hermite function-based (H-LSQ-FT and H-IRLS-FT) method (Dobróka et al. 2012, 2015; Szegedi and Dobróka 2014) and the Legendre polynomial-based (L-LSQ-FT and L-IRLS-FT) algorithm (Nuamah and Dobroka 2019; Nuamah et al. (2021). As it was mentioned above, the H-LSQ-FT and the H-IRLS-FT methods have the disadvantage of the appropriate selection of a scale factor. The L-LSQ-FT and L-IRLS-FT procedures have some stability and resolution problems (similar to the Chebyshev polynomials of the first kind) because the symmetry conditions

$$ {P}_{n}\left(-x\right)={(-1)}^{n}{P}_{n}\left(x\right)$$

on the interval − 1 ≤ x ≤ 1 resulting in the extrema having values that are either − 1 or 1:

$$ {P}_{n}\left(1\right)=1, {P}_{n}\left(-1\right)={(-1)}^{n}$$

As a third possibility in this chapter, we formulate inversion-based Fourier transformation algorithms employing the Chebyshev polynomials of the second kind for the discretization of the continuous Fourier spectra. A new 1D Fourier transformation algorithm, the Chebyshev Polynomial Least-Squares Fourier Transformation (C-LSQ-FT), is presented together with the robust Chebyshev Polynomial Iteratively Reweighted Least-Squares Fourier Transformation (C-IRLS-FT).

Data conversion from the time domain to the frequency domain can be established using a Fourier transform. For the one-dimensional case, the \( D\left(\omega \right)\) Fourier transform of the time-dependent \( d\left(t\right)\) function is defined as

$$ D\left(\omega \right)= \frac{1}{\sqrt{2\pi }} {\int }_{-\infty }^{\infty }d\left(t\right){e}^{-j\omega t}dt $$

where \( t\) denotes the time, \( \omega \) is the angular frequency and \( j\) is the imaginary unit. The inverse Fourier transform ensures a return from the frequency domain to the time domain:

$$ d\left(t\right)= \frac{1}{\sqrt{2\pi }} {\int }_{-\infty }^{\infty }D\left(\omega \right){e}^{j\omega t}d\omega. $$

In the framework of the inversion-based Fourier transformation the \( D\left(\omega \right) \)frequency spectrum should be discretized using a finite series expansion

$$ D\left(\omega \right)=\sum _{n=1}^{M}{{{B}_{n} \psi }_{n}\left(\omega \right)}_{}$$
(16)

Where the parameter \( {B}_{n}\) is a complex-valued expansion coefficient and \( {\psi }_{n}\)is a member of an accordingly chosen set of real-valued basis functions. Using the terminology of (discrete) inverse problem theory, the theoretical value of time-domain data in the k-th sampling time \( {t}_{k}\) (forward problem) can be given by the inverse Fourier transform

$$ d\left({t}_{k} \right)={d}_{k}^{theor} = \frac{1}{\sqrt{2\pi }} {\int }_{-\infty }^{\infty }D\left(\omega \right){e}^{j\omega {t}_{k}}d\omega $$

Inserting the expression given in Eq. (16) one finds that

$$ {d}_{k}^{theor}= \sum _{n=1}^{M}{B}_{n}{G}_{k,n}$$
(17)

where the Jacobi matrix is introduced

$$ {G}_{k,n}= \frac{1}{\sqrt{2\pi }} {\int }_{-\infty }^{\infty }{\psi }_{n}\left(\omega \right){e}^{j\omega {t}_{K}}d\omega $$

as the inverse Fourier transform of the \( {\psi }_{n}\) basis function:

$$ {G}_{k,n}= {\mathcal{F}}_{k}^{-1}\left\{\left.{\psi }_{n}\left(\omega \right)\right\}\right.$$
(18)

In our present approach, the Chebyshev polynomials serve as the model’s basis function for parameterization using \( {U}_{n}\left(\omega \right)\) for the second kind

$$ {G}_{k,n}= {\mathcal{F}}_{k}^{-1}\left\{\left.{U}_{n}\left(\omega \right)\right\}\right.$$
(19)

.

To calculate the elements of the Jacoby matrix we can use a standard inverse DFT procedure:

$$ {G}_{k,n}= {IDFT}_{k}\left\{\left.{U}_{n}\left(\omega \right)\right\}\right.$$
(20)

(Note, that the IDFT acts on noise-free theoretical data of the Chebyshev polynomials.) In this case, the deviation vector can be formed like this:

$$ {e}_{k}={d}_{k}^{meas}-{d}_{k}^{theor}={d}_{k}^{meas}-\sum _{N=1}^{M}{B}_{n}{G}_{Kn}$$
(21)

where \( {d}_{k}^{meas}\) represent the measurement signal. The normal equation of the Gaussian Least Squares method, after using the L2-norm to measure the misfit and minimize it, can be written as:

$$ \overrightarrow{\varvec{B}}= {\left({\varvec{G}}^{T}\varvec{G}\right)}^{-1}{\varvec{G}}^{T}{\overrightarrow{d}}^{meas}$$
(22)

With the knowledge of the expansion coefficients the estimated spectrum can be given as the following:

$$ {D}^{est}\left(\omega \right)=\sum _{n=1}^{M}{B}_{n}{T}_{n}(\omega )$$
(23)

The previous equations rely on the inversion-based Fourier Transformation method, which uses Chebyshev polynomials based on the Least Square Fourier Transformation method (C-LSQ-FT). However, this method only works effectively with data sets that have noise that is distributed in a regular pattern. In cases where the data contains outliers, the procedure has less efficiency in processing them. As Barnett and Lewis (1994) stated, outliers are different from the remaining data, and LSQ will not give acceptable results. Outliers can appear as abnormal, deviant, incongruous, or anomalous (Aggarwal 2013), leading to serious problems such as high error variance in statistical power, decreased normality in the data, and corrupting the true relationship between exposure and outcome in model bias (Osborne and Overbay 2004). To solve this problem, we used the Iterative Reweighted Least Squares method that minimizes the deviation vector via Cauchy-Steiner weights (Steiner 1997) in combination with the Fourier transform using Chebyshev polynomials as basis functions for discretization, creating a robust algorithm, C-IRLS-FT.

From Eq. (19), which shows the Jacobian matrix derived from the inverse FT, and indicates the calculation of the theoretical value of the signal in Eq. (17), we can use the IRLS inversion algorithm as described by Dobróka et al. (2012), and write the weighted norm as:

$$ {E}_{w}=\sum _{k=1}^{N}{w}_{k}{e}_{k}^{2}$$
(24)

where Cauchy-Steiner weights represent the term \( {w}_{k}\) and can be defined as the following where the order of magnitude of \( \epsilon \) is changed during the iteration from \( {10}^{-1} to {10}^{-8}\):

$$ {w}_{k}=\frac{{\epsilon }^{2}}{{\epsilon }^{2}+{e}_{k}^{2}}$$
(25)

Scales and Gersztenkorn (1988) show that the problem of a nonlinear inverse problem caused by a non-quadratic misfit function can be solved by applying the IRLS method. As a first step, the misfit function:

$$ {E}_{w}^{0}=\sum _{K=1}^{N}{e}_{k}^{2}$$

can be minimized in a linear set of normal equations:

$$ {\overrightarrow{B}}^{0}={\left({\varvec{G}}^{T}\varvec{G}\right)}^{-1}{\varvec{G}}^{T}{\overrightarrow{d}}^{meas}$$
(26)

and the deviation error:

$$ {e}_{k}^{0}={d}_{k}^{meas}-\sum _{n=1}^{M}{B}_{n}^{0}{G}_{kn}$$
(27)

The weight equation can be written like this:

$$ {w}_{k}^{0}=\frac{{\epsilon }^{2}}{{\epsilon }^{2}+{\left({e}_{k}^{0}\right)}^{2}}$$
(28)

and the new misfit function takes the form:

$$ {E}_{w}^{1}=\sum _{k=1}^{N}{w}_{k}^{0}{\left({e}_{k}^{1}\right)}^{2}$$
(29)

The minimization of Eq. (29) in a linear set of equations can be solved where the weighting matrix \( {\varvec{W}}^{0} \)is independent of \( {\overrightarrow{B}}^{1}\):

$$ {\overrightarrow{B}}^{1}={\left({\varvec{G}}^{T}{\varvec{W}}^{0}\varvec{G}\right)}^{-1}{\varvec{G}}^{T}{\varvec{W}}^{0}{\overrightarrow{d}}^{meas}$$
(30)

This will be in an iterative loop until it matches the stop criterion; thus, it’s called the Chebyshev polynomials-based Iteratively-Reweighted Least Square Fourier Transform method (C-IRLS-FT).

2.2 The C-IRLS-FT algorithm in 2D

The advancement in signal processing has led to remarkable improvements in the extraction and analysis of vital information from various sources, as we can see before. One-dimensional (1D) noise reduction methods are being extensively utilized for their simplicity and computational efficiency. However, the inherent limitations of 1D techniques have prompted us to explore higher-dimensional approaches, offering improved performance and adaptability. We introduce a new algorithm C-IRLS-FT that enhances the existing 1D noise reduction techniques by extending their applicability to two-dimensional (2D) signals. Many papers discussed noise reduction in 2D geophysical data sets like gravity and magnetic (Dobróka et al. 2017; Nuamah and Dobroka (2019); Abdelaziz and Dobróka, (2020; Nuamah et al. 2021) using the Hermite function or Legendre polynomials as basis function. This innovative use of Chebyshev polynomials for the first time offers several advantages over traditional 1D methods, including improved noise reduction capabilities, better handling of complex data structures, and enhanced adaptability to various signals and data types.

Furthermore, the proposed 2D method incorporates advanced signal decomposition techniques, adaptive filtering, and intelligent thresholding mechanisms, collectively contributing to its superior performance. In particular, the method’s ability to exploit the spatial and spectral correlations present in 2D signals enables it to effectively suppress noise while preserving the underlying data’s essential features and details. This is achieved through the use of inversion-based 2D Fourier transform 2D-IRLS-FT that are designed to automatically identify and eliminate noise components while retaining the informative elements of the signal.

Data conversion from the space domain to the space-frequency domain can be established using a 2D Fourier transform. For the two-dimensional case, the \( D({\omega }_{x},{\omega }_{y})\) Fourier transform of the space-dependent \( d\left(x,y\right)\) function is defined as

$$ D({\omega }_{x},{\omega }_{y})= \frac{1}{2\pi } \underset{-\infty }{\overset{\infty }{\iint }}d\left(x,y\right){e}^{-j({\omega }_{x}x+{\omega }_{y}y)}dxdy $$
(31)

where \( \left(x,y\right)\) denote the space coordinates, \( ({\omega }_{x},{\omega }_{y})\) are the (angular) space frequencies in 2D and \( j\) is the imaginary unit. The inverse Fourier transform ensures a return from the space-frequency domain to the space domain:

$$ d\left(x,y\right)= \frac{1}{2\pi } \underset{-\infty }{\overset{\infty }{\iint }}D\left({\omega }_{x},{\omega }_{y}\right){e}^{j({\omega }_{x}x+{\omega }_{y}y)}d{\omega }_{x}d{\omega }_{y} $$
(32)

In the framework of the inversion-based Fourier transformation the \( D\left({\omega }_{x},{\omega }_{y}\right) \)frequency spectrum should be discretized using a finite series expansion

$$ D\left({\omega }_{x},{\omega }_{y}\right)= \sum _{n=1}^{N}\sum _{m=1}^{M}{{B}_{n,m} \psi }_{n}\left({\omega }_{x}\right){ \psi }_{m}\left({\omega }_{y}\right)$$
(33)

where the parameters \( {B}_{n,m}\) are complex-valued expansion coefficients, \( {\psi }_{n} \)and \( {\psi }_{m} \) are members of an accordingly chosen set of real-valued basis functions. Using the terminology of (discrete) inverse problem theory, the theoretical values of spatial domain data in the \( \left({x}_{k},{x}_{l}\right)\) sampling point (forward problem) can be given by the inverse Fourier transform

$$ d\left({x}_{k},{x}_{l}\right)={d}_{k,l}^{theor} = \sum _{n=1}^{N}\sum _{m=1}^{M}{{B}_{n,m} {G}_{k,l}^{n,m}}_{}$$
(34)

where the Jacobi matrix is introduced as

$$ {G}_{k,l}^{n,m}= \frac{1}{\sqrt{2\pi }} {\int }_{-\infty }^{\infty }{\psi }_{n}\left({\omega }_{x}\right){e}^{j{\omega }_{x}{x}_{k}}d{\omega }_{x}\frac{1}{\sqrt{2\pi }} {\int }_{-\infty }^{\infty }{\psi }_{m}\left({\omega }_{y}\right){e}^{j{\omega }_{y}{y}_{l}}d{\omega }_{y}$$

The Jacobian matrix is the inverse Fourier transform of the basis function \( {\psi }_{n}\) and \( {\psi }_{m}\).

In our investigations the Chebyshev polynomials of the second kind (\( {U}_{n}\)) serve as the model’s basis function for parameterization using Eq. (9) for the first kind and Eq. (15) for the second one:

$$ {G}_{k,l}^{n,m}= \frac{1}{\sqrt{2\pi }} {\int }_{-1}^{1}{U}_{n}\left({\omega }_{x}\right){e}^{j{\omega }_{x}{x}_{K}}d{\omega }_{x.}\frac{1}{\sqrt{2\pi }} {\int }_{-1}^{1}{U}_{m}\left({\omega }_{y}\right){e}^{j{\omega }_{y}{y}_{l}}d{\omega }_{y }$$
(35)

Or in another form:

$$ {G}_{k,l}^{n,m}= {\mathcal{F}}_{k}^{-1}\left\{\left.{U}_{n}\left({\omega }_{x}\right)\right\}\right.. {\mathcal{F}}_{l}^{-1}\left\{\left.{U}_{m}\left({\omega }_{y}\right)\right\}\right.$$
(36)

The reason for creating a new Fourier Transformation method revolves around creating a 2D inversion-based version of Eq. (35). To accomplish this, we will use a standard 2D inverse DFT process:

$$ {G}_{k,l}^{n,m}= {IDFT}_{k}\left\{\left.{U}_{n}\left({\omega }_{x}\right)\right\}\right.. {IDFT}_{l}\left\{\left.{U}_{m}\left({\omega }_{y}\right)\right\}\right.$$
(37)

We can create the theoretical data at the sampling points \( \left({x}_{k},{x}_{l}\right)\):

$$ {d}_{k,l}^{theor}= \sum _{n=1}^{N}\sum _{m=1}^{M}{B}_{n,m}{G}_{k,l}^{n,m}$$
(38)

The programming of the algorithm is more simple after using the transformation of the indices.

\( i=n+\left(m-1\right)N, s=k+\left(l-1\right)K\). With these notations, the total number of the unknown expansion coefficient is \( I=N+\left(M-1\right)N=NM\) and that of the measurement data is \( S=K+\left(L-1\right)K=KL\). The theoretical data can be calculated as

$$ {d}_{s}^{theor}=\sum _{i=1}^{M}{B}_{i}{G}_{si}$$

In this case, the deviation vector takes the form:

$$ {e}_{s}={d}_{s}^{meas}-{d}_{s}^{theor}={d}_{s}^{meas}-\sum _{i=1}^{M}{B}_{i}{G}_{si}$$
(39)

The normal equation of the Gaussian Least Squares method, after using the L2-norm to measure the misfit of the function and minimizing it, can be written as:

$$ \overrightarrow{\varvec{B}}= {\left({\varvec{G}}^{T}\varvec{G}\right)}^{-1}{\varvec{G}}^{T}{\overrightarrow{d}}^{meas}$$
(40)

where the estimated spectrum can be given as the following:

$$ {D}^{est}\left({\omega }_{x},{\omega }_{y}\right)=\sum _{n=1}^{N}\sum _{m=1}^{M}{B}_{n,m}{U}_{n}({\omega }_{x}){U}_{m}\left({\omega }_{y}\right)$$
(41)

The previous equations rely on the inversion-based Fourier Transformation method, which uses Chebyshev polynomials based on the Least Square Fourier Transformation method (C-LSQ-FT) as we saw in the 1D case. Also, this method only works effectively with data sets that have noise that is distributed in a regular pattern. In cases where the data contains outliers, the procedure has less efficiency in processing them. To solve this problem, we used the Iteratively Reweighted Least Squares method that minimizes the deviation vector via Cauchy-Steiner weights in combination with the Fourier transform using Chebyshev polynomials as basis functions for discretization, creating a robust algorithm, C-IRLS-FT.

As in the 1D case from Eq. (34), which shows the Jacobian matrix derived from the inverse FT, and indicates the calculation of the theoretical data, we can use the IRLS inversion algorithm as described by Dobróka et al. 2012; and write the weighted norm as:

$$ {E}_{w}=\sum _{s=1}^{S}{w}_{s}{e}_{s}^{2}$$
(42)

where Cauchy-Steiner weights represent with term \( {w}_{s}\) and can be defined as the following:

$$ {w}_{s}=\frac{{\epsilon }^{2}}{{\epsilon }^{2}+{e}_{s}^{2}}$$
(43)

Scales and Gersztenkorn (1988) show that the problem of a nonlinear inverse problem caused by a non-quadratic misfit function can be solved by applying IRLS. As a first step, the misfit function:

$$ {E}_{w}^{0}=\sum _{s=1}^{S}{e}_{s}^{2}$$

can be minimized in a linear set of normal equations:

$$ {\overrightarrow{B}}^{0}={\left({\varvec{G}}^{T}\varvec{G}\right)}^{-1}{\varvec{G}}^{T}{\overrightarrow{d}}^{me}$$
(44)

and the deviation error:

$$ {e}_{s}^{0}={d}_{s}^{meas}-\sum _{i=1}^{I}{B}_{i}^{0}{G}_{si}$$
(45)

The weight equation can be written like this:

$$ {w}_{s}^{0}=\frac{{\epsilon }^{2}}{{\epsilon }^{2}+{\left({e}_{s}^{0}\right)}^{2}}$$
(46)

and the misfit function:

$$ {E}_{w}^{1}=\sum _{s=1}^{S}{w}_{s}^{0}{\left({e}_{s}^{1}\right)}^{2}$$
(47)

The minimization of Eq. (29) in a linear set of equations can be solved where the weighting matrix \( {\varvec{W}}^{0} \)is independent of \( {\overrightarrow{B}}^{1}\):

$$ {\overrightarrow{B}}^{1}={\left({\varvec{G}}^{T}{\varvec{W}}^{0}\varvec{G}\right)}^{-1}{\varvec{G}}^{T}{\varvec{W}}^{0}{\overrightarrow{d}}^{meas}$$
(48)

This will be in an iterative loop until it matches the criteria; thus, it’s called the Chebyshev polynomials-based Iteratively-Reweighted Least Square Fourier Transform method (2D C-IRLS-FT).

3 Numerical testing

As we mentioned earlier, the new algorithms should be applied to synthetic data first to test them. For that, we create a wave loaded with different types of noise (Gaussian and Cauchy noise) to qualify the noise reduction capability of the introduced 1D and 2D algorithms.

3.1 Testing the 1D algorithm

We start with the following equation to create the data set:

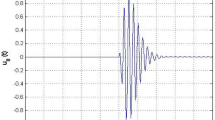
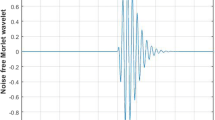
$$ d\left({t}_{k}\right)=c{t}_{k}^{n}{e}^{-\lambda {t}_{k}}\text{s}\text{i}\text{n}(\omega {t}_{k}+\gamma )$$
(49)

and the items n = 1, \( \lambda =20\), \( \omega =40\pi \), c = 739, and \( \gamma =\pi /4\) are the parameters of the generated wave. The sample rate of the generated waveform is Δt=0.0005 sec. Within the interval of [-1,1], as shown in Fig. 3.

The DFT method was applied to generate the real and imaginary parts of the Fourier transform without any noise contamination. In the same step, the C-IRLS-FT for the first and second kinds of Chebyshev polynomials were also applied, as shown in Fig. 4.

The DFT, C-LSQ-FT, and C-IRLS-FT methods produced similar results for the real and imaginary parts of the Fourier-transformed spectrum. Furthermore, in the inversion-based method for high-quality discretization, we use Chebyshev polynomials of the order up to M = 150. In summary, demonstrated methods are highly suitable for datasets without noise.

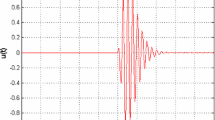
Gaussian and Cauchy’s noise are respectively loaded onto the previous waveform to test the algorithms separately and see the efficiency, as demonstrated in Fig. 5.

Fig. 4
figure 4

The spectrum of the noise-free signal in the frequency domain using (A) DFT, (B) C-IRLS-FT

Full size image
Fig. 5
figure 5

Generated noisy waveform with (A) Gaussian noise and (B) Cauchy noise in the time domain

Full size image

Gaussian noise is generally considered a type of random noise that follows a normal distribution with a zero mean and a specified variance. It is often utilized as a model for external noise in signal processing. It is considered additive, meaning that it does not depend on the signal and can be added to it without altering the signal’s distribution. Due to its properties, it is commonly used to simulate the effects of real-world noise in simulations and performance evaluations of signal processing algorithms. It is very important to reduce its impact on the interpretation of the real signal. This includes the development of filters using various transforms such as the Wavelet Transform (Deighan and Watts 1997), S-Transform (Askari and Siahkoohi 2008), and Fourier Transform (Dobróka et al. 2012). For testing purposes, the parameters of the applied Gaussian noise are the mean = 0 and \( \sigma \) = 0.01. As we can see in Fig. 6 A, the DFT method was applied to the Gaussian noisy data sets to demonstrate the efficiency of the presented algorithm. Furthermore, C-IRLS-Ft was also applied to the same data. To quantify the results, we used data distance:

$$ {{\Delta }}^{data}= \sqrt{\frac{1}{N}\sum _{k=1}^{N}{\left({d}_{k}^{noisy}-{d}_{k}^{noise-free}\right)}^{2}}$$
(50)

and the spectral distance

$$ {{\Delta }}^{spect}= \sqrt{\frac{1}{N}\sum _{i=1}^{N}Re{\left({u}_{i}^{noisy}-{u}_{i}^{noise-free}\right)}^{2}+Im{\left({u}_{i}^{noisy}-{u}_{i}^{noise-free}\right)}^{2}}$$
(51)

Figure 6B shows that the present algorithms C-IRLS-FT second kind have effective results in reducing Gaussian noise in synthetic data compared to the traditional DFT.

When conducting a comparison between different methods, it is important to consider the level of error associated with each approach. In the case of methods C-LSQ-FT, C-IRLS-FT, and conventional Discrete Fourier transform method (DFT), notable differences in error levels can be observed. Upon analyzing a Gaussian noisy data set, the data distance between the noisy and noise-free data is 0.1032 (Figs. 3 and 5 A). The conventional DFT displays a spectrum distance of 0.0103 (Fig. 6A) and method C-IRLS-FT displays a spectrum distance of 0.0077 for the second one (Fig. 6B). Note that there is a slight improvement using the second type of Chebyshev polynomials, probably due to the different extrema (Eqs. (12), (13)). Processing speed is a critical factor in many computational tasks, and various methods have been developed to enhance it because serial processing involves executing one task at a time, which can be time-consuming and limit overall processing speed. The method C-IRLS-FT consumes slightly more time (between 14 and 20 s) in both types than the C-LSQ-FT (between 8 and 11 s). This is related to the more computing procedure in IRLS. This data highlights that method C-IRLS-FT is likely the most accurate approach among the DFT method, which exhibits progressively higher (28–29%) spectrum distance.

Fig. 6
figure 6

The result of noisy data (Gaussian noise) after applying (A) DFT (B) C-IRLS-FT

Full size image

In the case of Cauchy noise, Fig. 7 compares the presented algorithms C-IRLS-FT with the traditional DFT. It reveals a significant reduction in noise and spikes when compared to conventional ones. The data distance between noisy and noise-free data sets is 0.414. As we compared previous methods in the Gaussian noise data set, we applied the same procedure and observed that the conventional DFT displays a spectrum distance of 0.0416 (Fig. 7A). The method C-IRLS-FT shows an improvement of around 60% in the spectrum distance of 0.0131 for the second one (Fig. 7B).

Fig. 7
figure 7

The result of noisy data (Cauchy noise) after applying (A) DFT, (B) C-IRLS-FT method

Full size image
Fig. 8
figure 8

The Noise-free 2D data set

Full size image

This greatly highlights the limitations of traditional DFT in effectively eliminating randomly occurring outliers and recursive random noise from a waveform compared with C-IRLS-FT.

3.2 Testing the 2D algorithm

To test the proposed method, we create a 2D noise-free data set consisting of a rectangular region with the dimensions [-1,1] units for directions x and y. In addition, this data set contains an anomaly in the middle with dimensions [-0.2,0.2] units also in directions x and y. For the sampling intervals, we set it to equal 0.04 units for both directions, creating 101*101 data points (Fig. 8).

We started with a noise-free data set in comparison to the previously mentioned method. The 2D Fourier spectrum of the data set was computed using 2D DFT, 2D C-LSQ-FT, and 2D C-IRLS-FT algorithms.

Figure 9 demonstrates the amplitude spectrum using 2D DFT, 2D C-LSQ-FT, and 2D C-IRLS-FT methods. All approaches give similar results without any significant difference, which indicates the effectiveness in processing noise-free datasets. The 2D C-LSQ-FT and 2D C-IRLS-FT used Chebyshev polynomials with M = 35 order.

The efficacy of the three methods was confirmed when applied to the noise-free surface. To test real-world scenarios, the surface was contaminated with Gaussian and Cauchy noise as two separate scenarios, producing much rougher areas as depicted in Figs. 10 and 12.

To accurately quantify the results, we propose the Root Mean Square (RMS) distance as a measure between the data sets (a) and (b) in the space domain:

Fig. 9
figure 9

The 2D Amplitude Spectrum for noise-free data set. (A) Using 2D DFT method (B) Using 2D C-LSQ-FT (C) using 2D C-IRLS-FT

Full size image
Fig. 10
figure 10

The noisy data set contaminated with Gaussian noise

Full size image
$$ {{\Delta }}^{data}= \sqrt{\frac{1}{N}\sum _{i=1}^{{N}_{x}}\sum _{j=1}^{{N}_{y}}{\left[{u}^{noisy}\left({x}_{i},{y}_{j}\right)-{u}^{noisefree}\left({x}_{i},{y}_{j}\right)\right]}^{2}}$$
(52)

and the model distance:

$$ {{\Delta }}^{Spectrum}= \sqrt{\begin{array}{c}\frac{1}{N}\sum _{i=1}^{{N}_{x}}\sum _{j=1}^{{N}_{y}}{\left({Re [U}^{noisy}\left({\omega }_{xi},{\omega }_{yj}\right)]-{Re[U}^{noisefree}\left({\omega }_{xi},{\omega }_{yj}\right)]\right)}^{2}\\ + \frac{1}{N}\sum _{i=1}^{{N}_{x}}\sum _{j=1}^{{N}_{y}}{\left({Im [U}^{noisy}\left({\omega }_{xi},{\omega }_{yj}\right)]-{Im[U}^{noisefree}\left({\omega }_{xi},{\omega }_{yj}\right)]\right)}^{2}\end{array}}$$
(53)

In the Gaussian noise scenario, shown in Fig. 10, the data distance between the noise-free and noisy data sets is 0.0501. On the other hand, the model distance between the 2D DFT spectrum of the noisy and noise-free data sets is 0.0017. Moving to the introduced methods, the data distance using the 2D C-LSQ-FT method is 0.0176, and the model distance is 7.33e-04. The 2D C-IRLS-FT showed similar results with a data distance equal to 0.0178; the model distance is 7.32e-04. From above, we can summarize that the 2D C-LSQ-FT and 2D C-IRLS-FT demonstrate high noise reduction to random noise compared to the 2D DFT method (Fig. 11). Also, both methods have similar outputs for amplitude spectrums. This result refers to the power of using Chebyshev polynomials as an alternative basis function in the inversion method.

Fig. 11
figure 11

The 2D Amplitude Spectrum for noisy data set (Gaussian noise). (A) using 2D DFT method (B) using 2D C-LSQ-FT (C) Using 2D C-IRLS-FT

Full size image

In the Cauchy noise scenario as shown in Fig. 12, the addition of random Cauchy noise generated outliers with sharp spikes.

Figure 13 showcases the noise reduction capabilities of the 2D DFT, 2D C-LSQ-FT, and 2D C-IRLS-FT methods, through processing Cauchy’s noisy data set. The output spectrums demonstrate that the 2D C-IRLS-FT method suppresses Cauchy noise considerably more effectively than the traditional 2D DFT method and 2D C-LSQ-FT. The 2D DFT method proves inadequate in eliminating the introduced noise, as evidenced by the spread of data noise in its output Fourier spectrums.

Fig. 12
figure 12

The Noisy data set contaminated with Cauchy noise

Full size image
Fig. 13
figure 13

The 2D Amplitude Spectrum for noisy data set (Cauchy noise). (A) Using 2D DFT method (B) Using 2D C-LSQ-FT (C) Using 2D C-IRLS-FT

Full size image

The data distance between the noise-free and noisy data sets is 0.0958. On the other hand, the model distance between the 2D DFT spectrum of the noisy and noise-free data sets is 0.0034. Moving to the introduced methods, the data distance using the 2D C-LSQ-FT method is 0.0253, and the model distance is 0.0009. The 2D C-IRLS-FT showed similar results with a data distance equal to 0.0161; the model distance is 6.69e− 04. Upon examination of the data, it became evident that the 2D C-LSQ-FT and 2D C-IRLS-FT techniques offered superior noise reduction capabilities relative to the traditional 2D DFT approach. Nonetheless, it is essential to establish a more resilient and effective method for filtering out random noise and outliers, given the susceptibility of the Least Squares and 2D DFT methods. Thus, it is strongly advised to consider utilizing the 2D C-IRLS-FT method.

4 Applying the 2D-C-IRLS-FT to filter field data set

For this research, a comprehensive field dataset was utilized. The dataset was derived from the Bureau Gravimétrique International (BGI), an organization working under the umbrella of the International Association of Geodesy (IAG). The BGI database comprises a rich collection of gravimetric measurements from various locations worldwide, making it a reliable source for in-depth research and analyses in the realm of geodesy. For our specific research, the parameters utilized from this dataset include minimum and maximum latitude (30° and 45°) and minimum and maximum longitude (33° and 45°). This data was used to define the specific geographical bounds of our study. Latitude and longitude values provided us with the precise locations of our field data points as shown in Fig. 14 as 3D and Fig. 15 as 2D.

Fig. 14
figure 14

The 3D Bouguer gravity anomaly data set

Full size image
Fig. 15
figure 15

2D Bouguer gravity anomaly

Full size image

We demonstrate the application of a two-dimensional low-pass Butterworth filter on gravity data. After converting the data to double precision, a 2D C-IRLS-FT is applied. A grid for the low-pass Butterworth filter is created, with its size defined by the dimensions of the data. The filter parameters, such as the normalized cutoff frequency and filter order, are set to 0.1 and 2, respectively. The low-pass Butterworth filter, which is a function of the distances from the center point of the grid, is then applied to the gravity data in the frequency domain (Butterworth 1930). The filtered data is then shifted back, and the inverse procedure is applied to convert it back to the spatial domain as a part of the 2D C-IRLS-FT method. Finally, low-pass filtered gravity data are visualized, as shown in Fig. 16. The Fourier Transform, using 2D C-IRLS-FT, a key component in this procedure, allows for the decomposition of the gravity data into its frequency components, enabling the application of the low pass filter in the frequency domain.

Fig. 16
figure 16

(A) represent the real data. (B) represent the Low pass filtered for Gravity data

Full size image

5 Conclusion

The paper revolves around the persistent challenge of noise and outlier contamination in geophysical data, specifically focusing on gravity measurements, as well as in other 2D images that encompass geophysical data. Noise and outliers in geophysical datasets can originate from various sources, such as instrumental errors, environmental factors, and processing artifacts. The presence of these unwanted signals can significantly impact the accuracy and reliability of interpretations and output results, ultimately affecting our understanding of subsurface structures, resource exploration, and hazard assessment. This, in turn, may lead to suboptimal decision-making in the context of natural resource management, environmental protection, and infrastructure development. We aim to contribute to this area of research by exploring novel techniques and algorithms for noise and outlier detection and reduction by assessing their performance in various geophysical applications. We recognize the importance of Fourier transformation as a widely utilized tool in geophysical data processing, particularly for enhancing the quality of datasets and providing a comprehensive picture of subsurface geology, but the traditional Discrete Fourier Transform (DFT) approaches have limitations in processing outlier noisy data. From this point, to address these challenges, this paper introduces an inversion-based 1D and 2D Fourier transformation (C-IRLS-FT) algorithm. These research findings demonstrated significant improvements in both the space and frequency domains, providing a strong foundation for the development and application of the C-IRLS-FT algorithm in the context of noise and outlier detection and reduction in geophysical data. We centered around reducing the sensitivity to outliers by implementing the inversion-based Fourier transformation on synthetic 1D and 2D datasets, as well as real field measurements. The overarching aim is to improve the reliability and accuracy of geophysical data interpretation, paving the way for more informed decision-making in resource exploration. To achieve this goal, the proposed C-IRLS-FT inversion approach is primarily grounded in the iteratively reweighted least-squares Fourier transformation. This iterative process allows for the fine-tuning of the analysis and enhances the ability to address noise and outlier-related issues. The series expansion technique is employed to discretize the Fourier frequency spectrum, which provides a more manageable and computationally efficient representation of the data. The expansion coefficients are then estimated as the solution to the over-determined inverse problem, further refining the analysis and ensuring that the method is robust in the face of diverse challenges. The Chebyshev polynomials are used as basis functions for this approach. This choice enables rapid and accurate computation of the elements of the Jacobian matrix, streamlining the overall process and increasing the method’s efficiency. Furthermore, the most frequent value (MFV) method is employed to address the issue of scale parameters, which can be a critical factor in the analysis of geophysical data. By iteratively determining the Cauchy-Steiner weights through an internal iteration loop, the MFV method minimizes data loss and contributes to the robustness of the C-IRLS-FT method. Overall, this carefully crafted combination of methods and techniques results in a powerful and effective approach to handling noise and outlier challenges in geophysical datasets. The superior performance of the C-IRLS-FT method in addressing noise and outlier contamination underscores its potential for improving the accuracy and dependability of geophysical data interpretation across various applications.