Multi-sensor Attitude Estimation using Quaternion Constrained GNSS Ambiguity Resolution and Dynamics-Based Observation Synchronization

Abstract

Recently, high accuracy and low-cost navigation hardware is becoming increasingly available that can be efficiently used for the control of autonomous vehicles. We present a sensor fusion method providing tightly coupled integration of pseudorange, carrier phase, and Doppler satellite measurements taken at multiple vehicle-mounted GNSS antennas with onboard inertial sensor observations. The key of accurate GNSS position and orientation estimation is the successful integer ambiguity resolution. We propose a method that uses the quaternion states as constraints to improve ambiguity resolution and to increase the accuracy of the GNSS based attitude determination. Generally, the low-cost hardware neither allows a hardware-level time synchronization between the GNSS receivers due to a lack of a common external oscillator nor provides the clock steering function available in geodetic GNSS receivers. The lack of observation synchronization causes several degrees of error in attitude estimation. To eliminate this effect, a dynamics-based solution is presented that synchronizes the observations by taking the dynamics of the moving platform into account. Compared to common external oscillator based sensor setups, our solution allows to increase both the number of rover receivers on the platform and the baselines between them easily, thus it opens up new possibilities in the attitude determination of large vehicles. We validate our approach against a tactical grade inertial navigation system. The results show that our approach using low-cost sensors provides the ambiguity success rate of 100% for the moving baselines, and the positioning and attitude error reached the centimeter and half a degree level, respectively.

1 Introduction

The current trends show that autonomous vehicles represent the future of road transport. Modern vehicles are equipped with multiple sensors like Global Navigation Satellite System (GNSS), Inertial Navigation System (INS), magnetometers, barometers, and odometers which monitor the motion parameters and are applied in driving assistance systems. Highly accurate and reliable positioning and attitude estimation are very important for safe autonomous driving. Thus, sensor fusion techniques are used to optimally combine these observations. INS helps to provide position solutions in intervals between GNSS samples and in case of GNSS outage, while multiple GNSS receivers forming moving baselines on the platform aid the elimination of sensor bias and drift in INS. To enable the spread of this technology, the development of low-cost hardware and the accompanying processing algorithms are necessary. The research area of autonomous vehicle positioning and orientation is currently very active. Chen et al. (2021) published an open-source software that implements a post-processing technique for the fusion of GNSS and INS sensors with several methods of GNSS/INS integration. However, these do not include the opportunity of moving baseline processing. Henkel and Iafrancesco (2014) used low-cost single-frequency GPS only receivers, gyroscopes, and accelerometer sensors to estimate position and attitude data with tightly coupled sensor fusion with the restoration of the integer property of double difference GNSS carrier phase ambiguities. Low-cost GNSS receivers have significantly evolved recently. Sensors observe multiple constellations, i.e., GPS, GLONASS, Galileo, and Beidou using multiple measurement frequencies. Eling et al. (2013) presented their GNSS/MEMS (Micro-Electromechanical Systems) attitude determination system for urban area application. They used GPS L1/L2 observations for multiple moving baselines and implemented the ambiguity function method (AFM) searching technique (Counselman and Gourevitch 1981; Remondi 1991) for the GPS-attitude determination. Accurate GNSS based attitude determination requires the successful resolution of phase ambiguity parameters. Teunissen (2006) modified the Least-square AMBiguity Decorrelation Adjustment (LAMBDA) technique for GPS based attitude determination. He used the baseline length of the moving baseline in the minimization as a constraint. Later Teunissen et al. (2011) further developed the optimization for a rotation-matrix-based attitude estimation constraint.

We had published the first version of our Extended Kalman Filter (EKF) for tightly coupled (TC) sensor integration algorithm for multiple low-cost GNSS receivers, accelerometers, gyroscopes (Farkas et al. 2019). We further developed this approach to involve all of the available satellite data and to include magnetic and barometric sensor measurements to enhance the reliability and the robustness of the estimation. Furthermore, we introduce a dynamic model for eliminating the effect of the observation latency. Our solution considers a full dynamic model of the moving platform and applies varying Dynamics-Based Observations Synchronization (DBOS) corrections to synchronize base and rover receiver observations, which is more pronounced when one uses low-cost GNSS receivers without clock-steering function.

We developed a quaternion constrained version of the MLAMBDA method by Chang et al. (2005) based on the constrained integer ambiguity resolution (IAR) method (Teunissen 2006; Giorgi and Teunissen 2010). We apply the quaternion representation for the attitude estimation due to its better numerical stability and use the quaternion constraint for integer ambiguity resolution on the moving baselines.

We validated our algorithm at the ZalaZone Automotive Proving Ground, Zalaegerszeg, Hungary (Szalay et al. 2019) under ideal, open sky conditions with a dedicated measurement platform using three low-cost GNSS receivers, a low-cost inertial, magnetic, and a barometric measurement unit as well as a tactical grade unit as a reference.

First, we present the background of the multi-baseline GNSS processing method including the sensor setup, the measurement platform, and the associated clock bias issues. The tightly coupled navigation EKF filter setup, the sensor models, and the DBOS model are discussed in the following sections. The subsequent section presents the integer ambiguity resolution steps in the position estimation and quaternion constrained attitude estimation cases followed by a section discussing the validation measurements and the results. The subsequent section contains the validation measurement descriptions and the results. Application of the DBOS method shows an ambiguity resolution success rate increase of 21.98% and a significant improvement on the estimation of yaw angles compared to the state-of-the-art velocity-based correction case. Finally, we conclude our article and discuss the applicability of our low-cost sensor position and attitude measurement system.

2 Multi-baseline GNSS and inertial sensor integration

The aim of sensor fusion in the navigation field is to establish a robust, high sample rate, and high accuracy localization estimation. The sensor integration can be implemented in two ways. First, the loosely coupled sensor integration, that uses the estimates (position and velocity solution of the GNSS receiver, attitude angles and body acceleration from INS sensor, etc.) from independent sensors and integrates them to the navigation algorithm. This integration can be implemented quickly and the computational load is low. However, the sensor errors are difficult to determine, as only estimates and their reliability are used. The second sensor integration method is the tightly coupled fusion, that uses the unprocessed measurements of the different sensors. All of the sensor models have to be implemented and the sensor related error terms are estimated by the localization algorithm. This setup has higher computational load, but the sensor errors can be handled more efficiently exploiting differences in operating principles of the applied sensors. This section presents the background of the tightly coupled sensor integration of the multiple GNSS receivers, inertial, magnetic, and barometric sensors. The following subsections explains the multi-baseline setup and the measurement platform built for testing the proposed algorithm.

2.1 Multi-baseline GNSS setup

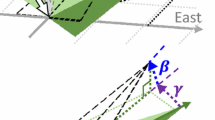
Real-time kinematic GNSS navigation technology is normally used to determine the position of a static rover, but it can be used also to calculate the precise position of a moving rover antenna onboard a vehicle. Placing several antennas on the platform even enables us to determine the attitude of the platform. The latter one is associated with the moving baseline processing technique. Multi-baseline processing combines both the aforementioned positioning methods (Fig. 1). The accurate time synchronisation between the moving base and the rover is the key of the high accuracy attitude estimation.

Fig. 1

Moving base setup for precise heading and precise absolute position of the rover. u-blox AG (2020)

The clock bias errors of the receivers at the moving baseline highly influence the attitude estimation. The clock bias represents the time difference between the clock of the satellites of a GNSS constellation and the clock of the receiver. The clocks of the satellites are atomic clocks with a stable drift, while the clocks of the receivers are generally implemented using a quartz crystal, sometimes compensated in temperature (TCXO - Temperature Compensated Crystal Oscillator), whose stability cannot compete with atomic clocks, and they vary from receiver to receiver. To eliminate this effect one may use a common external oscillator to synchronize the observations on the hardware level. Another solution is to use the clock steering function of high-end GNSS receivers, since they are capable to continuously adjust their internal clocks to the GPS system time within a couple of nanoseconds. However the clocks of the low-cost GNSS receivers are not synchronized to GPS time with this precision. Clock bias errors derived from single point positioning of four different low-cost u-blox GNSS receivers are depicted in Fig. 2. for a common 130 min long observation. The clock bias values range between $-$0.004 and 0.009 s and the clock drifts are significantly different, too.

Fig. 2

Clock biases of low-cost GNSS receivers during a 130-minutes-long observation

The reason for these differences lies in the internal oscillator supporting- both the operation of the radio signal processing units and used for timing during the signal processing. U-blox receivers subdivide the oscillator signal to provide a 1-kHz reference clock signal, which is used to drive many of the receiver’s processes. In particular, the measurement of satellite signals is arranged to be synchronized with the ticking of this 1-kHz clock signal (u-blox AG 2022). Thus, these receivers are unable to steer their internal clock at the nanosenconds level. Due to this, either hardware based or software based clock synchronization is needed between the receivers on the moving platform.

Next we show the details of the test platform, which is used to provide the measurement data to analyze the performance of the algorithm.

2.2 Measurement platform

A passenger vehicle environment was chosen to test the proposed algorithm because it provides enough opportunities to install multiple sensors with geometrically different setups. In the current study we used three low-cost u-blox F9P dual-frequency multi GNSS receivers and an ultra low-cost PixFalcon flight control computer. The F9P receivers were logging dual-frequency code-, Doppler delay and carrier phase observations of the GPS L1C/L2C, GLONASS L1OF/L2OF, Galileo E1B/E5b and Beidou B1I/B2I signals. The PixFalcon unit provided the accelerometer, the gyroscope, the magnetometer and the barometer data. The inertial sensors of the PixFalcon were sampled with 50 Hz, while the barometer and the magnetometer collected data with a 10 Hz measurement rate. The GNSS receivers were set to 10 Hz measurement rate and logged data from all the available constellations. The reference position and attitude data are derived from a tactical grade KVH GEO-FOG 3D Dual navigation system, which is equipped with a Trimble MB-Two dual GNSS receiver for GNSS heading solution, high accuracy accelerometer, fiber-optic gyroscope, magnetometer, and pressure sensors. The sensor placement is summarized in Fig. 3, and Table 1.

Fig. 3

Sensor placement setup

The antennas of the ZED-F9P receivers (UBX₁, UBX₂, UBX₃) were placed in a triangular form to achieve the best Euler-angle representation. The antennas of the KVH system (KVH₁, KVH₂) were placed diagonally to maximize the baseline length. The PixFalcon (PXF) and the KVH units were fixed in the trunk of the car. The permanent base receiver (PRM) had short baseline length ($\le$10 km) to the moving base receiver. The collected data is post-processed, however we developed the structure of the algorithm so, that it would work in real time, too.

Table 1 Lever arms between the applied sensors in meters

To keep the consistency between the low-cost system and the reference unit, we use broadcast ephemeris data from the receivers and all of the receivers use the same RTCM corrections, too.

We introduce our position and attitude estimation algorithm in the next section, where the estimated states, the filter steps, the sensor models, and the proposed dynamics-based observation synchronization technique are detailed.

3 Position and attitude estimation algorithm

The following section includes the theoretical description of the estimation filter design, the sensor models, the dynamics-based observations synchronization, and the integer ambiguity resolution steps.

The position and the attitude estimation of the moving platform is based on an Extended Kalman Filter algorithm tailored to the characteristics of asynchronous low-cost GNSS and INS sensors (Farkas et al. 2019, Vanek et al. (2023)).

The estimated state vector ($\textbf{x}$) contains the navigation related and sensor error states, which are

• Position ($\mathbf {X_{M}}$), velocity ($\mathbf {V_{M}}$) and acceleration ($\mathbf {A_{M}}$) of the Moving Base antenna in Earth-Centered Earth-Fixed (ECEF) Coordinate system

• Orientation quaternions ($\textbf{q}$), angular velocities ($\mathbf {\omega }$)

• Accelerometer bias error ($\mathbf {b_a}$), gyroscope bias error ($\mathbf {b_\omega }$), magnetometer bias error ($\mathbf {b_m}$), barometer bias error ($\mathbf {b_b}$)

• Local magnetic field ($\textbf{M}$)

• GNSS receiver clock biases for every receiver ($\delta _{i}^{GPS}, \delta _{i}^{GAL}, \delta _{i}^{GLO}, \delta _{i}^{BDS}$)

• GNSS receiver clock drifts for every receiver ($\dot{\delta }_{i}^{GPS}, \dot{\delta }_{i}^{GAL}, \dot{\delta }_{i}^{GLO}, \dot{\delta }_{i}^{BDS}$)

• Single differenced GLONASS system related receiver inter-channel biases for every baseline ($\mathbf {ICB_r}_{i-j}$)

• Single differenced integer ambiguities for every baseline and every satellite ($\textbf{N}_{i-j}$).

We prioritised the robust state space representation over less adaptive dynamic applicability, and therefore the acceleration and angular velocity variables describing the dynamics were also included as states in the state vector.

We present the simplified structure of the EKF algorithm in Fig. 4, where the relations between the measurements and the updated estimated states are presented by the color-coded notation. Take the example of the double differenced (DD) pseudorange, carrier phase, and Doppler delay measurements between the base station and the moving base receiver with the color of green on the left side. These measurements contribute to the update of the position and velocity states, the receiver dependent SD inter-channel biases (ICBs), and the baseline dependent SD integer ambiguity states on the right side of the figure. The other color codes follow a similar logic.

Fig. 4

Measurements-states relationship of the EKF based estimation algorithm in a single measurement epoch

The EKF prediction of the states ($\mathbf {\hat{x}}_{t}$) and their covariance matrix ($\mathbf {\hat{P}}_t$) from the previously updated epoch ($\textbf{x}_{t-1}$, $\textbf{P}_{t-1}$) are

$$\begin{aligned} \mathbf {\hat{x}}_{t}&=\textbf{F}_{t-1}^t \textbf{x}_{t-1} \end{aligned}$$

(1)

$$\begin{aligned} \mathbf {\hat{P}}_t&=\textbf{F}_{t-1}^t \textbf{P}_{t-1} \textbf{F}_{t-1}^{t^T}+\textbf{Q}_t. \end{aligned}$$

(2)

The $\textbf{F}_{t-1}^t$ is the state transition matrix, which is the partial derivative of the dynamic model based on slowly changing accelerations and angular velocities, and $\textbf{Q}_t$ is the process noise covariance matrix. The Kalman gain ($\textbf{K}_t$) is calculated as:

$$\begin{aligned} \textbf{K}_t&=\mathbf {\hat{P}}_t \textbf{H}_t^T(\textbf{H}_t \mathbf {\hat{P}}_t \textbf{H}_t^T+\textbf{R}_t)^{-1}, \end{aligned}$$

(3)

where $\textbf{H}_t$ is the observation equations derived Jacobian matrix and $\textbf{R}_t$ is the measurement noise matrix. The updated state vector ($\textbf{x}_t$) and covariance matrix ($\textbf{P}_t$) are the following:

$$\begin{aligned} \textbf{x}_t&=\mathbf {\hat{x}}_t+\textbf{K}_t(\textbf{z}_t-\textbf{h}(\mathbf {\hat{x}}_t)),\end{aligned}$$

(4)

$$\begin{aligned} \textbf{P}_t&=(\textbf{I}-\textbf{K}_t \textbf{H}_t)\mathbf {\hat{P}}_t, \end{aligned}$$

(5)

where the innovation residual vector ($\textbf{z}_t-\textbf{h}(\mathbf {\hat{x}}_t)$) contains the the measurements model vector ($\textbf{h}(\mathbf {\hat{x}}_t)$) and observation vector ($\textbf{z}_t$).

To illustrate the complexity of the filter, in case of three GNSS baselines on two frequencies with twenty available satellites, an inertial, a magnetic, and a barometric sensor the number of the estimated states is 180, and the size of the measurement vector in a GNSS processing epoch can reach 154.

The EKF algorithm uses the double differenced carrier-phase, pseudorange and Doppler-delay measurements of the given receivers of the baselines, the inertial, magnetic, and barometric sensor measurements. When GNSS measurements are available in the current epoch, then the filter update step is followed by the integer ambiguity resolution on all of the baselines. LAMBDA method is applied for the integer ambiguity resolution on the baseline between the permanent and the moving base receivers. The moving baseline based estimation allows to extend the optimization with attitude related constraint (Teunissen 2006; Giorgi 2011; Giorgi and Teunissen 2010; Wang et al. 2009). The attitude estimation in our approach is based on the quaternion representation, accordingly the constraint is the norm of the quaternions, as in previous works (Farkas et al. 2019; Vanek et al. 2023). The brief descriptions of the sensor models used are discussed in the following subsections and also available in our previous article (Vanek et al. 2023), which focuses on the cycle slip detection based on comparison of the triple differenced raw measurements and the predicted values of the estimation filter. Detection of cycle slip and its proper handling in the estimation procedure is key to reliable GNSS phase measurement based position and attitude determination. The proposed method performed more robust in urban canyon environment compared to the Melbourne-Wübbena and TurboEdit methods.

3.1 GNSS observations

The estimation algorithm uses the pseudorange, the carrier-phase and the Doppler-delay measurements of the permanent base, the moving base and the moving rover receivers (Fig. 3). The non-differenced measurement equations (6-8) are based on Hofmann-Wellenhof et al. (2012).

$$\begin{aligned} \varrho ^s_r&= \rho _r^s + c \left( \delta _r - \delta ^s - \delta ^{rel} - \delta ^{GD} \right) + I + T + \eta _{\varrho } \end{aligned}$$

(6)

$$\begin{aligned} \lambda ^s\phi ^s_r&= \rho _r^s + c \left( \delta _r - \delta ^s - \delta ^{rel} - \delta ^{GD} \right) - I + T + \lambda ^s\left( ICB_r + N^s\right) + \eta _{\phi } \end{aligned}$$

(7)

$$\begin{aligned} \lambda ^sd_r^s&= -\mathbf {E_r^s}(\mathbf {v_r}-\mathbf {v^s}) + c(\dot{\delta _r}-\dot{\delta ^s}) + \eta _d \end{aligned}$$

(8)

where $\rho _r^s$ is the norm of receiver ($\textbf{x}_r$) - satellite ($\textbf{x}^s$) position vector (9), $\mathbf {E_r^s}$ is the line of sight vector (10)

$$\begin{aligned} \rho _r^s&=\Vert \textbf{x}_r - \textbf{x}^s \Vert \end{aligned}$$

(9)

$$\begin{aligned} \mathbf {E_r^s}&= \frac{\textbf{x}_r - \textbf{x}^s}{\rho _r^s} , \end{aligned}$$

(10)

c is the speed of light, $\delta _r$ and $\dot{\delta }_{r}$ are the clock bias and drift of the receiver, $\delta ^s$ and $\dot{\delta }^s$ are the clock bias and drift of the satellite, $\delta ^{rel}$ and $\delta ^{GD}$ are the relativistic and the group delay of the satellite. The ionospheric and tropospheric delays are denoted by I and T. The inter-channel bias error ($ICB_r$) associated with the GLONASS system is given in the carrier-phase equation. This term is equal to zero in the case of other constellations. The non-differenced integer ambiguity is $N^s$ and $\lambda ^s$ is the wavelength of the given satellite measurement. The velocity of the given receiver and the satellite are $\mathbf {v_r}$ and $\mathbf {v^s}$. The pseudorange, the carrier-phase, and the Doppler-delay measurements are denoted by $\varrho _r^s$, $\phi _r^s$, and $d_r^s$ respectively. Error terms not modelled are included in the respective $\eta$ terms. The proposed estimation algorithm use the following differentiated GNSS measurements. Single differencing (SD) is realised between the common satellite observations of the receivers on the given baseline thus the satellite correlated errors (satellite clock bias and drift, atmospheric delays) can be reduced

$$\begin{aligned} \phi _{rb}^j = \phi _r^j-\phi _b^j. \end{aligned}$$

(11)

A pivot satellite - usually the one with the highest elevation - by constellations and frequencies is chosen and its SD observations are deducted from the SD observations to the other satellites. This gives the receiver dependent error-free (receiver clock bias and drift, inter-channel bias, hardware delay) double differenced (DD) values

$$\begin{aligned} \phi _{rb}^{jk} = \phi _{rb}^{j}-\phi _{rb}^{k}. \end{aligned}$$

(12)

The triple differencing (TD) is realised between the consecutive DD values in time

$$\begin{aligned} \phi _{rb\hspace{1mm}t-1} ^{jk\hspace{1mm} t} = \phi _{rb\hspace{1mm} t}^{jk} - \phi _{rb\hspace{1mm} t-1}^{jk}. \end{aligned}$$

(13)

The TD measurements include the position changes of the receiver, and the effect of cycle slips in case of carrier-phase measurements.

3.2 Inertial, magnetic and barometric sensors

The position and attitude estimation method uses the raw acceleration and gyroscope data of the INS system, too. The equation of the measured acceleration ($\textbf{a}$) is the one given by Henkel and Iafrancesco (2014) transformed to the quaternion representation introduced by Vanek et al. (2023)

$$\begin{aligned} \begin{aligned} \textbf{a}&={\mathbf {R_{body}^{ecef}}}^T \mathbf {A_{M}} -\textrm{skew}(\mathbf {\omega })\textrm{skew}(\mathbf {\omega })\mathbf {b_{{M}_{body}}^{INS}}+\\&+ \mathbf {b_a}-{\mathbf {R_{body}^{nav}}}^T \begin{bmatrix} 0\\ 0\\ g\\ \end{bmatrix}+{\mathbf {R_{body}^{ecef}}}^T (2\textrm{skew}\left( \begin{bmatrix} 0\\ 0\\ \varOmega _E\\ \end{bmatrix}\right) \textbf{V}_{M})+\eta _a, \end{aligned} \end{aligned}$$

(14)

where $\mathbf {R_{body}^{ecef}}$ is to rotation matrix from body to Earth-Centered Earth-Fixed (ECEF) coordinate system, $\mathbf {A_{M}}$ is the estimated acceleration of the moving base receiver, $\mathbf {\Omega }$ is the estimated angular velocity, $\mathbf {b_{M_{body}}^{INS}}$ is the lever arm between the moving base antenna and the INS sensor in body coordinate system, $\mathbf {b_a}$ is the estimated accelerometer sensor bias, $\mathbf {R_{body}^{nav}}$ is the body to navigational transformation matrix, g is the local gravity, $\varOmega _E$ is the angular velocity of Earth’s rotation, and $\textbf{V}_{M}$ is the velocity state vector of the moving-base receiver. The equation of the measured angular velocity ($\mathbf {\Omega }$) is

$$\begin{aligned} \begin{aligned} \mathbf {\Omega }&=\mathbf {\omega }+ \mathbf {b_{\omega }} + \mathbf {R_{body}^{ecef}}^T \begin{bmatrix} 0\\ 0\\ \varOmega _E\\ \end{bmatrix}+ {\mathbf {R_{body}^{nav}}}^T\mathbf {\omega _{{ecef}_{nav}}^{nav}}+\eta _{\omega }, \end{aligned} \end{aligned}$$

(15)

where $\mathbf {\omega }$ is the estimated angular velocity vector, $\mathbf {b_{\omega }}$ is the gyroscope sensor bias, $\mathbf { \omega _{ecef_{nav}}^{nav}}$ is the angular rates of the navigation coordinate system with respect to the ECEF coordinate system (Henkel and Iafrancesco 2014). The magnetometer measurement ($\textbf{m}$) model equation consists of terms as the navigational to body transformation matrix ($\mathbf {R_{body}^{nav}}^T$), the local magnetic field vector ($\textbf{M}$), and the magnetometer bias ($\mathbf {b_m}$)

$$\begin{aligned} \begin{aligned} \textbf{m} = \mathbf {R_{body}^{nav}}^T \textbf{M} + \mathbf {b_m} + \eta _m. \end{aligned} \end{aligned}$$

(16)

The barometric sensor model (b) is the following based on the formula of U.S. Standard Atmosphere (United States National Oceanic and Atmospheric Administration, United States Air Force 1976)

$$\begin{aligned} b = P_b\left[ \frac{T_b +(h(\mathbf {X_{M}})-h_b(\mathbf {X_{M}})-b_b)L_b}{T_b}\right] ^{\frac{-gM_E}{R^*L_b}} + \eta _b \end{aligned}$$

(17)

where $P_{b}$ is the reference pressure, $T_{b}$ is the reference temperature, $L_{b}$ is the temperature lapse rate, $h(\mathbf {X_{M}})$ is the height of the moving base receiver’s antenna ($\mathbf {X_{M}}$), $h_b(\mathbf {X_{M}})$ height of reference level, $b_b$ is the barometer sensor bias term, $R^{*}$ is the universal gas constant, g is the gravitational acceleration, and $M_E$ is the molar mass of air. The $\eta$ terms in the equations are the non-modeled errors as already described in the introduction of the GNSS observation equations.

4 Dynamics-based observations synchronization

Due to the different clock biases, the observation time of the moving base (M) can differ by several milliseconds from the rover (R), as shown in Fig. 2 above. This time lag causes errors in the estimated baseline length and attitude angles (Fig. 5), particularly in highly dynamic situations.

Fig. 5

Baseline length distortion due the time asynchronicity and the dynamic of the moving baseline

Consider a coordinated turn of a small unmanned aerial vehicle (UAV) moving with 60 degrees of bank angle, at 20 m/s velocity, leading to 50 deg/s yaw rate. Figure 6 depicts the norms of GNSS based attitude errors as a function of the measurement time differences using a six degrees of freedom simulation, assuming one meter GNSS baseline length. For better understanding the diagram includes the effects from only the rotation, the linear, and the full movement. The higher effect comes from the velocity, but it is also clear that the coupling of the velocity and the angular velocity can result to even higher errors.

Fig. 6

Absolute attitude errors and maximal DD residuals due to the dynamic effects with 1 m moving baseline length

There are specific hardware on the market with available single board integrated dual antenna setup (e.g. Trimble MB-Two receiver, which is used in the reference KVH GEO-FOG 3D Dual system), where time synchronization is solved at the hardware level. There are modular solutions such as u-blox ZED-F9P units (u-blox AG 2020) where stand-alone receivers can also function in moving base mode via a wired or wireless data communication link, but the time synchronization realization is not implemented at all.

We propose the Dynamics-Based Observations Synchronization (DBOS) method to eliminate the effect of the asynchronous observations of the low-cost receivers and increase the versatility and the robustness of the moving baseline measurement setup. The corrections are applied to the satellite-receiver phase and code ranges using both the velocity and the angular velocity states from the estimation algorithm:

$$\begin{aligned} c_{AoD}^s=\delta t_{AoD}E_M^s(V_M+R_{body}^{ecef}\textrm{skew}(\omega )b_{M_{body}}^R) \end{aligned}$$

(18)

The value of the satellite-dependent correction, $c_{AoD}^s$ includes the time difference ($\delta t_{AoD}$) between the rover and the moving base, the line-of-sight vector of the moving base antenna ($E_M^s$), the velocity of the moving base ($V_M$), and the transformed velocity component obtained by multiplying the angular velocity states ($\omega$) and the lever arm vector ($b_{M_{body}}^R$). This range correction is applied to the single differenced pseudorange and carrier phase measurements (6, 7) for the moving baselines. The effectiveness of the DBOS correction method is explained later in the measurement results section.

5 Integer ambiguity resolution

The key of the high accuracy GNSS carrier-phase measurement based positioning is the integer ambiguity resolution. The most widely used resolution method is LAMBDA, introduced by Teunissen (1995). Through the decorrelation, ambiguity transformation is capable of reducing the search space of the ambiguities and gives improvement in both positioning precision and resolution time. Chang et al. (2005) improved the reduction by a symmetric pivoting strategy in computing the $LDL^T$ factorization of the covariance matrix and shrinking the ellipsoidal region during the search. These improvements result in a significant running time improvement. The initial minimization problem is:

$$\begin{aligned} \breve{N}=\textrm{arg} \min _{N\in \mathbb {Z}^m}\left\Vert N-\hat{N}\right\Vert {_{P_{\hat{N}\hat{N}}}}^2 \end{aligned}$$

(19)

where $\breve{N}$ is the optimal solution of the potential integer ambiguity vectors (N). The $\hat{N}$ term is double-differenced float integer ambiguity vector from estimation of the Extended Kalman Filter update step, $P_{\hat{N}\hat{N}}$ is the covariance matrix of $\hat{N}$ vector.

5.1 Quaternion constrained integer ambiguity resolution

Based on Park and Teunissen (2003),Teunissen (2006) presented the baseline-length constrained integer ambiguity resolution in connection with a GNSS compass. Later, Giorgi and Teunissen (2010) published a rotation-matrix-based constraint in the ambiguity resolution. Wang et al. (2009) presented a method for the ambiguity resolution in attitude determination using trigonometric and baseline-length constraints to shrink the search space and to reduce the search time during each epoch. The extraction of the attitude information using baseline based estimation method is cumbersome. The rotation based method relies on the orthogonal nine element direction cosine matrix (DCM) which is composed of three independent matrix multiplication. In practice the estimation errors can accumulate and the matrix ceases to be orthogonal and becomes harder to reconstruct into a proper orthogonal form.

In comparison the quaternion representation is more compact with the four element estimation and after the normalization it represents an orthogonal rotation matrix. It also avoids the singularity of the Euler angle representation. Because of these advantages we propose to use quaternions for the attitude representation in the EKF estimation. Accordingly, the constrained integer ambiguity resolution method is also modified to use the quaternion norm as a constraint. The modified non-convex optimization problem for the integer ambiguity resolution:

$$\begin{aligned} \breve{N} = \textrm{arg} \min _{N\in \mathbb {Z}^m} \left\Vert {N-\hat{N}}\right\Vert {_{P_{\hat{N}\hat{N}}}}^2 + \left\Vert {\hat{q}(N)-\breve{q}(N)}\right\Vert {_{P_{\hat{q}(N)\hat{q}(N)}}}^2 \end{aligned}$$

(20)

where $\breve{N}$, $\hat{N}$ and $P_{\hat{N}\hat{N}}$ terms are the same as in the case of the unconstrained LAMBDA. The second term gives the cost of the ambiguity conditioned quaternion normalization, where $\hat{q}(N)$ is the conditional quaternion vector in the function of a possible integer ambiguity vector based on the estimated quaternion states (q). $P_{\hat{q}(N)\hat{q}(N)}$ is the conditional quaternion covariance matrix which is calculated by the quaternion covariance matrix ($P_{\hat{q}\hat{q}}$), the ambiguity covariance matrix ($P_{\hat{N}\hat{N}}$), and the off-diagonal matrices ($P_{\hat{q}\hat{N}}$, $P_{\hat{N}\hat{q}}$):

$$\begin{aligned} \hat{q}(N)&= \hat{q}-P_{\hat{q}\hat{N}}P_{\hat{N}\hat{N}}^{-1}(N-\hat{N})\end{aligned}$$

(21)

$$\begin{aligned} P_{\hat{q}(N)\hat{q}(N)}&= P_{\hat{q}\hat{q}}-P_{\hat{q}\hat{N}}P_{\hat{N}\hat{N}}^{-1}P_{\hat{N}\hat{q}} \end{aligned}$$

(22)

The $\breve{q}(N)$ term in 20 is the normalized conditional quaternion vector, that is a result of a second optimization:

$$\begin{aligned} \breve{q}(N) = \textrm{arg}\min _{\left\Vert q\right\Vert ^2=1}\left\Vert \hat{q}(N)-q\right\Vert ^2_{P_{\hat{q}(N)\hat{q}(N)}} \end{aligned}$$

(23)

where we are looking for the optimal quaternion vector, which has the smallest cost in $P_{\hat{q}(N)\hat{q}(N)}$ metric and its norm is equal to one. The computational load of this optimization is very high. We use the search technique in the constrained mode, which finds the best integer valued vector set in the original unconstrained search space using the MLAMBDA method by Chang et al. (2005). To reduce computational time of the the non-convex search we bound the search space according to Farkas et al. (2019).

After the integer ambiguity resolution step we apply an ambiguity ratio validation test, which computes the ratio of the second best and the best solution’s cost function values. When this ratio is over a predefined threshold value, the resolution is successful, and we use the integer ambiguity vector in the further epoch as pseudo measurements to fix the ambiguities until the next cycle slip or signal loss occurs.

6 Open-sky test

A measurement campaign was organized in 2020 at the ZalaZone automotive test track (Szalay et al. 2019). During this campaign, we had the opportunity to test our measurement setup with an ideal sky-view and high dynamics. The permanent GNSSNet.hu-ZALA GNSS base station was tracking the GPS and GLONASS systems on L1 and L2 with the measurement rate of 1 Hz. The distance between the base station and the moving base was approximately 6 kms. The GNSS correction stream was provided in an RTCM format to both the KVH and the u-blox receivers in real-time. The position and the attitude solutions of the moving base u-blox receiver and the KVH sensor were used for the validation of our EKF algorithm.

Fig. 7

Trajectory of the test

We drove our vehicle in the Smart City Zone, where we could record data with high dynamic cornering, braking and several figure-eight maneuvers. The trajectory of the drive is depicted in Fig. 7, and the total measurement time was 850 s. The raw measurement set and the KVH reference data are available on the link of Farkas (2023).

7 Results

The asynchronous time effects due to using low-cost GNSS receivers were presented in Sect. 4. It is clear that ignoring the sampling effect can lead to large errors in estimation. Figure 2 also showed, that the clock of the receivers can be delayed or advanced due to the time-varying receiver clock bias. In real-time applications the practice is to use the most recent base measurement at the instance of obtaining a new rover receiver sample (Takasu et al. 2013).

Since rover and base clock bias are both changing over time, in real-time implementation the corresponding base measurement delay could vary between 0 and 1 sample time of the base GNSS reveiver, which is in our case 100 ms.

Our application currently works in post-processing, but our aim is to demonstrate the efficiency of our DBOS method taking into account real-time implementation aspects. Due to this we present the nominal case (no delay between base and rover) and a modified epoch pairing (resembling real-time implementation) for the moving baselines ($Bl_2$=UBX₂-UBX₁, $Bl_3$=UBX₃-UBX₁). A constant offset of 1 sample on the base measurements, roughly 0.1 second (one sample time of the base receiver), is introduced artificially to represent a particular scenario showcasing real-time implementation related performance of our algorithm.

We ran our algorithm in two different modes to demonstrate the robustness and the performance of our proposed correction method: first, the only velocity based correction (TC v) was applied described by the first term of (18) which is similar to the age of differential correction method (Takasu et al. 2013) usually applied in relative kinematic positioning; second, the velocity and angular velocity corrections (TC DBOS) were applied using (18). The measurement data was also processed with the DBOS method with no delay, to present a low-cost sensors based reference. The real-time KVH sensor results are used as an absolute reference for comparing other solutions and statistical indicators.

The reference KVH sensor reported 100% ambiguity success rate on the position estimation baseline ($Bl_1$) in the observation period (Table 2), while it was 88.53% for the u-blox moving base solution calculated by the internal software of the receiver. The undelayed tightly coupled DBOS based EKF algorithm also processed the measurement data with almost 100% ambiguity success rate on all of the baselines which proves the efficiency of our algorithm in term of ambiguity success ratios, since it performs significantly better than the internal solution of the UBX receivers.

Table 2 Ambiguity success rates of the different baseline solutions (The percentage of deviation below five centimeters are shown in the brackets)

The integer ambiguity success ratio using the only velocity based correction is 78.02%. The table also contains the ratio below five centimeter error, since above 5 cm error we can assume a false fix. This value is only 23.66%, which is much lower than the total fixed ration the algorithm reports. The reason for this is the falsely resolved integer ambiguities, which also distort the position differences between the reference measurement (see Fig. 3 below). The estimation algorithm uses the fix and hold technique at the successfully resolved integer ambiguities, which uses the resolved ambiguities as pseudo measurements in the EKF estimation. There were no disturbing objects in the measurement environment therefore the number of cycle slips were minimal. The two aforementioned features result the low number of the integer ambiguity states re-initializations and the relatively high success rate.

Using the TC DBOS method, however the algorithm reported 100% ambiguity success rate on $Bl_1$ baseline. Taking into account the previous case, the position differentiation check has been carried out. In the 5% of the measurement time the errors were higher than 5 cms. However, this value is much lower than the 54.36% achieved by the TC v method. This proves that the more sophisticated dynamic model makes the DBOS method more robust, and it is capable to correct even large time offsets between the observations either caused by asynchronous clocks or the highly dynamic motion of the platform. One can also observe that even large time offsets do not affect the ambiguity success rates of the moving baselines. We could resolve all the ambiguities using the TC algorithm that can be explained by the short length of the moving baselines. The position result and the difference from the KVH unit are depicted in Fig. 8. The higher float rate and the effect of the falsely resolved integer ambiguities by the TC v based solution can also be seen on the position differences.

Fig. 8

Position results and the differences from the reference system

The statistical values of the differences from the position solutions of the KVH sensor as reference are summarized in Table 3. The statistics are separately calculated for ambiguity resolved (both fixed) and the unresolved (at least one of them in float) solution epochs.

Table 3 Mean, standard deviation, maximal absolute, median absolute, 95% percentile values between the position solution of the TC algorithm and the reference sensor

The velocity-only solution shows high errors in all direction. The false integer ambiguities and resulting positions degrades the estimation of the other sensor errors which entail inadequate convergence on the level of the whole state vector, which is also proved by Table 2. Hence the coordinate errors of the float intervals are also high, the errors are the order of meters. In comparison the DBOS correction performances low differences from the reference. The mean, the standard deviation, and the median values are on the order of centimeter, which are on the same low level as the no delay TC solution. This implies that the estimation based on the full dynamic compensation is more efficient and results in a proper state vector and covariance matrix for the correct integer ambiguity resolution. However, the maximum values show the effect of the 5% false resolved integer ambiguity interval.

The attitude angle (roll–$\phi$, pitch–$\theta$, yaw–$\psi$) results are depicted in Fig. 9. The differences also come from the comparison between the TC sensor fusion algorithm results and the KVH 4sensor results as references. The numerical values are depicted in Table 4.

Fig. 9

Attitude angle results and the differences from the reference system

Table 4 Mean, standard deviation, maximal absolute, median absolute, 95% percentile values between the attitude solution of the TC algorithm and the reference sensor

The roll angle results show no significant differences between TC v and TC DBOS methods. The proposed correction method improved the standard deviation value and the 95% percentile value with 40% in case of the pitch angle, but there are no major differences. The most significant improvement in terms of standard deviation between the velocity-only and the DBOS method could be observed in the estimated yaw angles. Observing the time series of the residuals on Fig. 9 and Table 4 the DBOS method shows a factor of 2.4$-$3.2 times lower standard deviation, median, 95% percentile and maximal values for the yaw angle compared to the TC v correction processing. The yaw angle estimated with lower errors using the DBOS method has significant effects on the accuracy of position estimation (Table 2 and Table 3) due to the better convergence of the estimation filter.

8 Conclusion

We presented our tightly coupled sensor integration algorithm for positioning and attitude estimation using multi-constellation, multi-receiver GNSS, accelerometer, gyroscope, magnetometer, barometer data processing. The estimation is based on an Extended Kalman Filter. We introduced the filter configuration in details, including the estimated states, state transitions and the sensor models used. To fully exploit the accuracy of the phase range observations, we developed a quaternion constrained MLAMBDA integer ambiguity resolution algorithm for the moving baseline. We tested our algorithm with real observations collected using low-cost hardware. The sensors were installed on an automobile platform with a KVH GEO-FOG 3D Dual unit as a reference. We compared the results of the developed algorithm with the solution of the tactical grade KVH unit and the u-blox internal solution.

Since the relative positioning technique used for the attitude determination requires simultaneous phase range observations taken by all the GNSS receivers on the moving platform, the time synchronisation of the observations must be solved. This is usually done using common oscillators on a hardware level, requiring cable or wireless communication between the receivers. We presented a dynamics-based observation synchronization approach, handling large clock biases, that takes into consideration the full dynamic model of the moving platform, including not only the velocity estimated, but also the angular velocities of the platform. The proposed full dynamic DBOS correction method successfully eliminated the effect of hardware delays between the GNSS receivers on the moving baseline, and lead to significantly higher success rates in the ambiguity resolution for the position estimation baseline, too. The positioning and attitude estimation results obtained with a low-cost sensor system showed remarkably good agreement with the reference values obtained by the KVH GEO-FOG 3D tactical grade unit. The obtained position and attitude results fulfills the requirements of automated lane changing. The proposed method can also be used in real time position and attitude determination and provides a good alternative for the hardware based time synchronization of onboard GNSS receivers in large moving platforms.