Transformation from a global spherical to an adjusted local rectangular harmonic model

Abstract

This work presents a technique to transform a global spherical to an adjusted local rectangular harmonic model. First, the mathematical form of a global spherical harmonic model is presented. Second, the necessary conversion from global (geocentric) into local rectangular coordinates is given. Third, Laplace’s equation is solved by the method of separation of variables in local rectangular coordinates and its solutions in different functional forms are presented. Then, the estimation of the coefficients of these mathematical models by a least squares’ adjustment process is described, using as data the values of the disturbing potential of the Earth’s gravity field. The strategy for the selection of the best mathematical model for a successful transformation is described and validated in different case studies. These refer to areas in Greece, China and Germany and include comparisons with other models or methods. The results show the applicability of the presented transformation and confirm its advantages.

1 Introduction

For the representation of the Earth’s global (geomagnetic or gravity) field, spherical harmonics are widely used, which are solutions of Laplace’s equation found by the method of separation of variables. Nowadays, the functionals of the geopotential can be computed from spherical harmonic models which are mainly derived from satellite measurements and become more and more detailed and accurate (Barthelmes 2013). On the other hand, for the representation of a local or regional field, Spherical Cap Harmonic Analysis (SCHA) (e.g. Haines 1985) and Rectangular Harmonic Analysis (RHA) (e.g. Alldredge 1981) are the preferred alternative techniques over the last decades. In comparison to classical spherical harmonic models, the resulting harmonic models from the above two techniques have two important advantages: First, the local or regional field represented by an analytical model needs much less parameters (coefficients) and has less memory requirements in computation and storage than a spherical harmonic model. Second, these models can be easily enhanced using new data of different kinds (e.g. gravity anomalies, geoid undulations), leading to a further refinement of the local field. For these reasons, the two techniques are now being used more and more in numerous problems of the geoscientific community.

A comprehensive and systematic review of the SCHA literature is presented by Torta (2020), underlining the respective merits and weaknesses of the ways in which the technique has been used since it was first proposed in the context of a regional geomagnetic field modeling by Haines (1985). Several works followed, where the main problem of this approach was the computation of the associated Legendre functions with non-integer degree (e.g. De Santis 1992; Younis 2013). To overcome this problem, a new approach, called Adjusted Spherical Cap Harmonics (ASCH), was proposed by De Santis (1992) using the well-known integer order and degree Legendre functions. In order to avoid the same problem, another new approach, called Virtual Spherical Harmonics (VSH), was proposed by Wang and Wu (2019) in regional geoid modeling. An application of modeling regional gravity fields in an integrated approach, using ASCH by a least squares’ estimation of the coefficients of the mathematical model, was presented by Younis (2013). Also, the transformation from a global spherical to an adjusted local spherical cap harmonic model was developed by Younis et al. (2013).

RHA was first introduced by Alldredge (1981) and it has been used in geomagnetic and gravity field modeling (e.g. Alldredge 1981, 1982, 1983; Nakagawa and Yukutake 1985; Nakagawa et al. 1985; Haines 1989, 1990a, 1990b; Malin et al. 1996; Jiang et al. 2014). In the works of Alldredge (1981, 1982, 1983), Nakagawa and Yukutake (1985) and Nakagawa et al. (1985), RH is applied only in geomagnetic fields.

In this approach, Laplace’s equation is solved by the method of separation of variables in local rectangular coordinates. As mentioned in Jiang et al. (2014), the computation of the trigonometric basis functions of the RH is more stable and efficient at high degree expansion than that of the associated Legendre functions of the SCH. The mathematical properties of rectangular harmonic expansions are studied in the works of Haines (1989, 1990a, 1990b). Malin et al. (1996) re-examined Alldredge’s method of rectangular harmonic analysis and modified the functional form of the mathematical model. In the work of Jiang et al. (2014), a mathematical model of the disturbing potential of the gravity field and its functionals (gravity anomaly and disturbance, geoid undulation, deflection of the vertical) was derived and a strategy was proposed in order to reduce the edge effects caused by periodic continuation in RH. Additional recent applications of RH include an iterative procedure of the weighted least squares’ prediction, which was used by Zhang et al. (2017) for merging the land, altimetric, shipborne and airborne gravity data. Also, Feizi et al. (2021) investigated the problem of local gravity field modeling over Tanzania mountainous regions using RH of vector airborne gravity data.

In this study, a global spherical geopotential model is transformed to a rectangular harmonic expansion, over a relatively small area, by a least squares’ adjustment process, using as input data values of the disturbing potential of the Earth’s gravity field. In contrast to previous works on RH, here we use the most general solution of Laplace’s equation, including the term corresponding to the case in which the constants of the separation of variables are zero. Then, we apply different conditions and derive additional mathematical models which can be validated through a numerical process. The strategy for the selection of the best mathematical model for such an application and, specifically, the selection of expansion degree and extension parameter of a model, is described in different case studies.

Although this work resembles the work of Jiang et al. (2014), there are two important differences between the two works: First, here we provide the different functional forms of the solution of Laplace’s equation and we develop a strategy for the selection of the best mathematical model for a successful transformation. Second, the final models of the two works (Eq. (8) in the work of Jiang et al. (2014) and Eq. (17) in this work) are formally different and for this reason the models are validated through a numerical process for the same data (Sect. 6.2). Comparing the results, the model used here achieves better performance, a result that is also justified by the different number of parameters between the two models. Specifically, the model of Eq. (8) in the work of Jiang et al. (2014) consists of $1+2N+2M+4NM$ terms, whereas Eq. (17) of this work contains $8+4N+4M+4NM$. The $7+2N+2M$ non-periodic extra terms are included for two reasons: (i) The general functional form is essentially an interpolating function and the non-trigonometric terms (such as linear trends) or the exponential term are retained in order to keep down the problems associated with the rectangular approximation of the spherical geometry of the problem, as pointed out in Haines (1990a) (ii) These terms limit the problems of an ill-posed system of normal equations, as proved through the presented numerical tests and other tests that may be worked out using the uploaded code.

This work is organized as follows: Sect. 2 describes the global spherical harmonic models used to compute the required data (values of the disturbing potential). Section 3 presents the necessary transformation from global (geocentric) into local rectangular coordinates, in which Laplace’s equation is expressed. The solutions of this partial differential equation are determined by the usual method of separation of variables, leading to a combination of functions and thus in different mathematical models. Section 4 describes the adjustment process for the estimation of the coefficients of these functional models. Section 5 evaluates the proposed adjusted local rectangular harmonic models. Section 6 presents various case studies, demonstrating and validating the performance of this methodology. Finally, Sect. 7 presents our conclusions.

2 Global spherical harmonic models

The Earth’s gravitational potential $V$ at any point, with spherical coordinates $\left(r,\phi ,\lambda \right)$ on or above the Earth’s surface, is conveniently expressed on a global scale by summing up over degree $n$ and order $m$ of a spherical harmonic expansion as follows:

$$V\left( {r,\phi ,\lambda } \right) = \frac{{GM}}{r}\sum\limits_{{n = 0}}^{{n_{{\max }} }} {\sum\limits_{{m = 0}}^{n} {\left( {\frac{R}{r}} \right)^{n} } } P_{{nm}} \left( {\sin \phi } \right)\left( {C_{{nm}} \cos m\lambda + S_{{nm}} \sin m\lambda } \right)$$

(1)

where $GM$ is the product of gravitational constant and mass of the Earth, $R$ is the reference radius, ${P}_{nm}$ are the Legendre functions and ${C}_{nm}$, ${S}_{nm}$ are Stokes’ coefficients. Hence, a global spherical harmonic model of the gravitational potential consists of ${\left({n}_{max}+1\right)}^{2}$ coefficients and the two values for $GM$ and $R$ to which the coefficients relate (Barthelmes 2013).

On the other hand, the normal gravitational potential $\overline{V }$ at any point with oblate spheroidal coordinates $\left(u,\beta ,\lambda \right)$ outside the level spheroid, is given by the following formula (Heiskanen and Moritz 1967):

$$\overline{V }\left(u,\beta \right)=\frac{GM}{E}{\mathrm{tan}}^{-1}\frac{E}{u}+\frac{1}{2}{\omega }^{2}{a}^{2}\frac{q}{{q}_{0}}\left({\mathrm{sin}}^{2}\beta -\frac{1}{3}\right)$$

(2)

where

$$q=\frac{1}{2}\left[\left(1+3\frac{{u}^{2}}{{E}^{2}}\right){\mathrm{tan}}^{-1}\frac{E}{u}-3\frac{u}{E}\right]$$

(3)

$${q}_{0}=\frac{1}{2}\left[\left(1+3\frac{{b}^{2}}{{E}^{2}}\right){\mathrm{tan}}^{-1}\frac{E}{b}-3\frac{b}{E}\right]$$

(4)

and $E=\sqrt{{a}^{2}-{b}^{2}}$ is the linear eccentricity of the spheroid with semi-axes $a$ and $b$ and $\omega$ is its angular velocity. Also, the transformations between the global (geocentric) rectangular coordinates $\left(X,Y,Z\right)$ and spherical $\left(r,\phi ,\lambda \right)$, spheroidal $\left(u,\beta ,\lambda \right)$ and geodetic $\left(\varphi ,\lambda ,\overline{h }\right)$ coordinates can be found e.g. in Heiskanen and Moritz (1967).

Finally, the disturbing potential $T$ at any point with global rectangular coordinates $\left(X,Y,Z\right)$ outside the masses is given by

$$T\left(X,Y,Z\right)=V\left(X,Y,Z\right)-\overline{V }\left(X,Y,Z\right)$$

(5)

which does not contain the centrifugal potential and is a harmonic function.

3 Laplace’s equation in local rectangular coordinates and its solutions

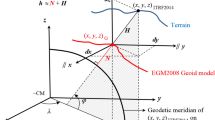
The disturbing potential may also be expanded into a series of rectangular harmonics. To find them, we introduce local rectangular coordinates $x$, $y$ and $z$. The $z$-axis is taken upward and the $y$-axis and $x$-axis northward and eastward, respectively, on the plane normal to a line which is perpendicular to an oblate spheroid (e.g. WGS84) at the center $\left({\varphi }_{0},{\lambda }_{0}\right)$ of the area under investigation. The global (geocentric) rectangular coordinates $\left(X,Y,Z\right)$ of a point are transformed into these local rectangular coordinates $\left(x,y,z\right)$ by the following relations:

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}-\mathrm{sin}{\lambda }_{0}& \mathrm{cos}{\lambda }_{0}& 0\\ -\mathrm{sin}{\varphi }_{0}\mathrm{cos}{\lambda }_{0}& -\mathrm{sin}{\varphi }_{0}\mathrm{sin}{\lambda }_{0}& \mathrm{cos}{\varphi }_{0}\\ \mathrm{cos}{\varphi }_{0}\mathrm{cos}{\lambda }_{0}& \mathrm{cos}{\varphi }_{0}\mathrm{sin}{\lambda }_{0}& \mathrm{sin}{\varphi }_{0}\end{array}\right]\left[\begin{array}{c}X-{X}_{0}\\ Y-{Y}_{0}\\ Z-{Z}_{0}\end{array}\right]$$

(6)

where $\left({X}_{0},{Y}_{0},{Z}_{0}\right)$ are the global coordinates and $\left({\varphi }_{0},{\lambda }_{0},{\overline{h} }_{0}\right)$ are the corresponding geodetic coordinates of the origin of the local coordinate system.

It can be shown that Laplace’s equation for the disturbing potential $T$, in local rectangular coordinates, is given by

$$\Delta T\equiv \frac{{\partial }^{2}T}{\partial {x}^{2}}+\frac{{\partial }^{2}T}{\partial {y}^{2}}+\frac{{\partial }^{2}T}{\partial {z}^{2}}=0$$

(7)

We shall attempt to solve this equation by separating the variables $x$, $y$, $z$ by means of the trial substitution

$$T\left(x,y,z\right)=f\left(x\right)g\left(y\right)h\left(z\right)$$

(8)

where $f$ is a function only of $x$, $g$ is a function only of $y$ and $h$ is a function only of $z$. Performing this substitution in Eq. (7) and dividing by $fgh$, we obtain

$$\frac{1}{f}\frac{{\partial }^{2}f}{\partial {x}^{2}}+\frac{1}{g}\frac{{\partial }^{2}g}{\partial {y}^{2}}+\frac{1}{h}\frac{{\partial }^{2}h}{\partial {z}^{2}}=0$$

(9)

which leads to the following three equations

$$\frac{{d}^{2}f}{d{x}^{2}}+{p}^{2}f=0$$

(10)

$$\frac{{d}^{2}g}{d{y}^{2}}+{q}^{2}g=0$$

(11)

and

$$\frac{{d}^{2}h}{d{z}^{2}}-\left({p}^{2}+{q}^{2}\right)h=0$$

(12)

where $p$ and $q$ could be any numbers (including zero).

Solutions of Eqs. (10) and (11) may be given by the functions

$${f}_{0}={A}_{0}+{B}_{0}x, p=0 \,\, \mathrm{and} \,\, {f}_{p}={A}_{p}\mathrm{cos}\left(px\right)+{B}_{p}\mathrm{sin}\left(px\right), p>0$$

(13)

$${g}_{0}={C}_{0}+{D}_{0}y, q=0 \,\, \mathrm{and} \,\, {g}_{q}={C}_{q}\mathrm{cos}\left(qy\right)+{D}_{q}\mathrm{sin}\left(qy\right), q>0$$

(14)

On the other hand, solution of Eq. (12) may be given by

$${h}_{00}={E}_{00}+{F}_{00}z, p=q=0 \,\, \mathrm{and} \,\, {h}_{pq}={F}_{pq}{e}^{-z\sqrt{{p}^{2}+{q}^{2}}}, p>0 \mathrm{or} q>0$$

(15)

which, for $p$ or $q$ positive, tends to zero when $z$ tends to infinity. Since the potential cannot diverge at large values of $z$, the positive exponent will be absent. Moreover, negative values of $p$ and $q$ are meaningless due to the periodicity in Eqs. (13) and (14) and the presence of squares in Eq. (15), therefore we only distinguish cases of zero and positive values. Also, to make the above solutions meet the needs of the problem under consideration, we replace the values $p$ and $q$ with (Alldredge 1981)

$${p}_{n}=n\frac{2\pi }{{D}_{x}} \,\, \mathrm{and} \,\, {q}_{m}=m\frac{2\pi }{{D}_{y}}$$

(16)

where $n$ (degree) and $m$ (order) are integers and ${D}_{x}$ and ${D}_{y}$ are the overall lengths in the $x$ and $y$ directions, respectively, that cover the entire area where the data are located.

Thus, the most general solution for the disturbing potential, as linear combination of the solutions (13), (14) and (15), in terms of truncated series at maximum degree $N$ and order $M$, is expressed in the form

$$T\left(x,y,z\right)={T}_{00}\left(x,y,z\right)+{T}_{n0}\left(x,y,z\right)+{T}_{0m}\left(x,y,z\right)+{T}_{nm}\left(x,y,z\right)$$

(17)

where

$${T}_{00}\left(x,y,z\right)={T}_{0}+{T}_{x}x+{T}_{y}y+{T}_{z}z+{T}_{xy}xy+{T}_{xz}xz+{T}_{yz}yz+{T}_{xyz}xyz$$

(18)

$${T}_{n0}\left(x,y,z\right)=\sum_{n=1}^{N}\left[{C}_{n0}\mathrm{cos}\left({p}_{n}x\right)+{S}_{n0}\mathrm{sin}\left({p}_{n}x\right)+{c}_{n0}y\mathrm{cos}\left({p}_{n}x\right)+{s}_{n0}y\mathrm{sin}\left({p}_{n}x\right)\right]{e}^{-z{p}_{n}}$$

(19)

$${T}_{0m}\left(x,y,z\right)=\sum_{m=1}^{M}\left[{C}_{0m}\mathrm{cos}\left({q}_{m}y\right)+{S}_{0m}\mathrm{sin}\left({q}_{m}y\right)+{c}_{0m}x\mathrm{cos}\left({q}_{m}y\right)+{s}_{0m}x\mathrm{sin}\left({q}_{m}y\right)\right]{e}^{-z{q}_{m}}$$

(20)

$${T}_{nm}\left(x,y,z\right)=\sum_{n=1}^{N}\sum_{m=1}^{M}\left[{CC}_{nm}\mathrm{cos}\left({p}_{n}x\right)\mathrm{cos}\left({q}_{m}y\right)+{CS}_{nm}\mathrm{cos}\left({p}_{n}x\right)\mathrm{sin}\left({q}_{m}y\right)+\,{SC}_{nm}\mathrm{sin}\left({p}_{n}x\right)\mathrm{cos}\left({q}_{m}y\right)+{SS}_{nm}\mathrm{sin}\left({p}_{n}x\right)\mathrm{sin}\left({q}_{m}y\right)\right]{e}^{-z\sqrt{{p}_{n}^{2}+{q}_{m}^{2}}}$$

(21)

This general solution (say model M0) has ${n}_{RHC}=8+4N+4M+4NM$ Rectangular Harmonic Coefficients (RHC). However, we can restrict the terms of the infinite series in Eq. (17) and obtain five additional models (M1 to M5), which are presented in Table 1, along with the number of the corresponding RHC.

Table 1 Functional forms of the mathematical models, along with the number of Rectangular Harmonic Coefficients

The spatial resolution represented by the above models, which is characterized in terms of half wavelength, can be computed from $N$ and $M$ as (Jiang et al. 2014):

$${\lambda }_{x}=\frac{{D}_{x}}{2N} \,\, \mathrm{and} \,\, {\lambda }_{y}=\frac{{D}_{y}}{2M}$$

(22)

Finally, the RHC in each of the previous models can be estimated by the method of least squares, as described in the next section.

4 Adjustment process of the transformation

Using the method of least squares (see e.g. Ghilani and Wolf (2006)) we can estimate the RHC of the models of Table 1 and, therefore, to transform a global spherical to an adjusted local rectangular harmonic model, which is practically an interpolating function. To do this, a 3D grid of $k$ points is generated over the area under investigation, where the number of points ($k$) is larger than the number of RHC (${n}_{RHC}$). Then, the values of the disturbing potential, at the grid points, are computed by Eq. (5) using a global spherical harmonic model and the function of the normal gravitational potential, for the same oblate spheroid of reference. These values are used as observations for an arbitrary point $i$, where $i=1,\dots ,k$. Then, we set up the linear observation equation e.g. for the model M0:

$${T}_{00}\left({x}_{i},{y}_{i},{z}_{i}\right)+{T}_{n0}\left({x}_{i},{y}_{i},{z}_{i}\right)+{T}_{0m}\left({x}_{i},{y}_{i},{z}_{i}\right)+{T}_{nm}\left({x}_{i},{y}_{i},{z}_{i}\right)={T}_{i}+{\upsilon }_{i}$$

(23)

where n = 1, 2, ... , N and m = 1, 2, ... , M. Similar equations can be written for the other models, although here we describe the process for the general model M0. Hence, the system of $k$ linear equations is represented in matrix form as

$$\mathbf{A}\widehat{\mathbf{x}}=\mathbf{y}+{\varvec{\upupsilon}}$$

(24)

where the $k\times {n}_{RHC}$ (design) matrix $\mathbf{A}$ contains the derivatives with respect to the elements of the ${n}_{RHC}\times 1$ vector of unknowns

$$\mathbf{x}={\left[\begin{array}{cccccccccccccccccc}{T}_{0}& {T}_{x}& {T}_{y}& {T}_{z}& {T}_{xy}& {T}_{xz}& {T}_{yz}& {T}_{xyz}& {C}_{10}& {S}_{10}& {c}_{10}& {s}_{10}& \cdots & {C}_{01}& {S}_{01}& {c}_{01}& {s}_{01}& \cdots \end{array}\right]}^{\mathrm{T}}$$

(25)

The $k\times 1$ vector of observations $\mathbf{y}$ contains the values of the disturbing potential and ${\varvec{\upupsilon}}$ is a $k\times 1$ vector of residuals. The solution of the adjustment is given by

$$\widehat{\mathbf{x}}={\left({\mathbf{A}}^{\mathrm{T}}\mathbf{P}\mathbf{A}\right)}^{-1}{\mathbf{A}}^{\mathrm{T}}\mathbf{P}\mathbf{y}$$

(26)

where the weight matrix $\mathbf{P}$, which is diagonal if the observational errors are uncorrelated, is computed from the variances of the observations. Furthermore, the variance factor ${\widehat{\sigma }}_{0}^{2}$ is computed by

$${\widehat{\sigma }}_{0}^{2}=\frac{{{\varvec{\upupsilon}}}^{\mathrm{\rm T}}\mathbf{P}{\varvec{\upupsilon}}}{k-{n}_{RHC}}$$

(27)

while the vector of residuals from Eq. (24). Also, from the residuals, we can compute the statistical index Root Mean Square (RMS)

$$\mathrm{RMS}=\sqrt{\frac{{{\varvec{\upupsilon}}}^{\mathrm{\rm T}}\mathbf{P}{\varvec{\upupsilon}}}{k}}$$

(28)

Finally, the variance–covariance matrix of the estimated parameters is given by

$${\widehat{\mathbf{V}}}_{\widehat{\mathbf{x}}}={\widehat{\sigma }}_{0}^{2}{\left({\mathbf{A}}^{\mathrm{T}}\mathbf{P}\mathbf{A}\right)}^{-1}$$

(29)

In this work, the values of disturbing potential (observations) are assumed unweighted and uncorrelated and thus the weight matrix is equal to the identity matrix, i.e. $\mathbf{P}=\mathbf{I}$. Also, following the suggestion of Jiang et al. (2014), in order to avoid the edge effects, we extend the sizes ${D}_{x}$ and ${D}_{y}$ of the data domain (only the sizes, not the data domain) to ${D}_{x}+{d}_{x}$ and ${D}_{y}+{d}_{y}$, respectively, although numerical instabilities may occur in the adjustment process. Then, Eq. (16) is modified as

$${p}_{n}=n\frac{2\pi }{{D}_{x}+{d}_{x}} \mathrm\;{and }\;{q}_{m}=m\frac{2\pi }{{D}_{y}+{d}_{y}}$$

(30)

Clearly, in order to minimize the RMS, which is influenced for a specific model (e.g. M0) by the maximum degree $N$ and order $M$ (expansion degree and order) and the sizes of ${d}_{x}$ and ${d}_{y}$ (extension sizes), we have to examine this dependence for various values of these parameters. However, for simplicity reasons, we assume $N=M$, ${d}_{x}=\rho d$ and ${d}_{y}=d$, where $\rho$ is a known real positive number, so that we only have to examine the values of the two parameters $N$ and $d$, which minimize the RMS of the disturbing potential, as we show in the following case studies. As an upper bound of the extension parameter $d$, for the restriction of numerical problems, should be used the size of the data domain. Furthermore, for the inversion of the symmetric matrix in Eq. (26), we use the method of Cholesky, which has been widely accepted in adjustments. Initially, we have to select the best mathematical model among the different functional forms presented in Table 1.

5 Validation of different adjusted local rectangular harmonic models

In order to select the best mathematical model (M0 to M5) which minimizes the RMS of the disturbing potential, we conduct numerical experiments based on data generated from the geopotential model EGM2008 with maximum degree 2190 (Pavlis et al. 2012). A 3D grid of $k=6724$ points in Greece, with spatial resolution $3' \times 3'$, was generated over a $2^\circ \times 2^\circ$ area from $\left(\varphi ,\lambda \right)=\left(37^\circ ,22^\circ \right)$ to $\left(\varphi ,\lambda \right)=\left(39^\circ ,24^\circ \right)$. The values of the disturbing potential were computed at four ellipsoidal height levels (0 m, 100 m, 1000 m and 2000 m) via the ICGEM online platform (Ince et al. 2019). The WGS84 reference ellipsoid was used to compute the normal gravity field parameters while maintaining the model’s defined tidal system. Gaussian filtering was not applied and the zero-degree term was taken into consideration. Then, the global (geocentric) rectangular coordinates $\left(X,Y,Z\right)$ of these points were transformed into the corresponding local rectangular coordinates $\left(x,y,z\right)$ through Eqs. (6), using as origin of the local coordinate system the point $\left({\varphi }_{0},{\lambda }_{0},{\overline{h}}_{0}\right)=\left(38^\circ ,23^\circ ,0\right)$. Also, the parameters of Eq. (30) were ${D}_{x}=180$ km and ${d}_{x}=0.80d$, while ${D}_{y}=220$ km and ${d}_{y}=d$.

Starting with model M0, we examined the performance for different values of expansion degree or order ($N=M$) and extension parameter $d$. The resulting RMS values and the execution time for each adjustment process are shown in Table 2. The minimum RMS value for the disturbing potential was produced with degree $N=20$ and extension parameter $d=125$ km.

Table 2 RMS values for the disturbing potential (in ${\mathrm{m}}^{2}/{\mathrm{s}}^{2}$) from the adjustments of model M0 for different values of expansion degree $N$ and extension parameter $d$ in an area $2^\circ \times 2^\circ$ in Greece

We repeated the same process for the other models (M1 to M5) and different values of expansion degree and extension parameter. The results of minimum RMS values are shown in Table 3. The experiment reveals that the RMS value of model M0 is smaller compared to those of the other models. Concluding, the numerical results confirm that the functional form M0 is able to provide a reliable and precise adjusted local model for the representation of a local gravity field, as we demonstrate and in the following case studies.

Table 3 Results of minimum RMS values for the disturbing potential from the adjustments of models M0 to M5 for different values of expansion degree and extension parameter in an area $2^\circ \times 2^\circ$ in Greece

The execution times reported in the tables correspond to a single adjustment (one combination of $N$ and $d$ values). The computations were performed on a personal computer running a 64-bit Linux Debian 5.9 operating system. The main characteristics of the hardware were: i7-5820 K CPU (with 6 cores-12 threads, clocked at 4.0 GHz) and 16 GB of RAM. All algorithms were implemented in C ++ and compiled using the GNU Compiler Collection version 10.2 at optimization level 3. We also employed the open-source “libquad-math”, the GCC Quad-Precision Math Library, which provides a precision of 33 decimal digits.

6 Case studies and numerical results

6.1 Local rectangular harmonic model in Greece

Having selected the model M0, we extended the previous area in Greece and a 3D grid of $k=26244$ points, with spatial resolution $3' \times 3'$, was generated over a $4^\circ \times 4^\circ$ area, from $\left(\varphi ,\lambda \right)=\left(36^\circ ,21^\circ \right)$ to $\left(\varphi ,\lambda \right)=\left(40^\circ ,25^\circ \right)$. The values of the disturbing potential were again computed at four ellipsoidal height levels (0 m, 100 m, 1000 m and 2000 m) via the ICGEM online platform (Ince et al. 2019). Here, the parameters of Eq. (30) were ${D}_{x}=350$ km and ${d}_{x}=0.80d$, while ${D}_{y}=440$ km and ${d}_{y}=d$. The resulting RMS values and the time for each adjustment process are shown in Table 4, where the symbol “-” indicates that the corresponding adjustment was omitted. The minimum RMS value for the disturbing potential was produced with degree $N=35$ and extension parameter $d=125$ km and from these values we produced Fig. 1. The values of the residuals plotted against the distance from the system origin are shown in Fig. 2 (Left).

Table 4 RMS values for the disturbing potential (in ${\mathrm{m}}^{2}/{\mathrm{s}}^{2}$) from the adjustments of model M0 for different values of expansion degree $N$ and extension parameter $d$ in an area $4^\circ \times 4^\circ$ in Greece

Fig. 1

The histogram of residuals for the disturbing potential (in ${\mathrm{m}}^{2}/{\mathrm{s}}^{2}$) from the adjustment of model M0 with expansion degree $N=M=35$ and extension parameter $d=125$ km in an area $4^\circ \times 4^\circ$ in Greece

Fig. 2

From the adjustment of model M0 with expansion degree $N=M=35$ and extension parameter $d=125$ km in $4^\circ \times 4^\circ$ area in Greece: Residuals of the disturbing potential (Left) and differences of disturbing potential between the values from the global and local model at the validation points (Right), as a function of the distance from the origin

In order to validate the resulting local model, a new grid of 6400 evaluation points was created in the same area. These were located intermediate to the adjustment points and had a single height value, corresponding to the actual height of the topography (for points in the sea, we used the corresponding height of the geoid). The differences of the values of the disturbing potential between the reference global and the local model are presented in Fig. 2 (Right).

The histogram of residuals of the disturbing potential, presented in Fig. 1, and the maximum values of residuals (Fig. 2—Left) correspond to $\pm 0.1$ mm precision of geoidal heights, which indicates that the model is successfully transformed. As it is known, the geoid undulation N is related to the disturbing potential T through the Bruns formula $N=T/\gamma$, where $\gamma$ is the normal gravity $(\approx 10\space\mathrm{m}/{\mathrm{s}}^{2})$. Furthermore, the differences of the disturbing potential between the values from the global and local model, at the grid of validation points (Fig. 2—Right), reflect the reliability and accuracy of the local model. Comparing the above results with those achieved for the smaller ($2^\circ \times 2^\circ$) area of Greece, with the same origin of the local coordinate system, we observe that the minimum RMS value was produced by the same extension parameter $d=125$ km but by a much greater expansion degree (from $N=20$ to $N=35$) which had a huge impact on execution time (from 4.17 min to 2.53 h per adjustment).

6.2 Local rectangular harmonic model in China

For a comparison with another mathematical model of RH, in this case study we generated the grid described in the work of Jiang et al. (2014). The $5^\circ \times 5^\circ$ data area in China is limited by the parallels of 29° and 34° northern latitude and by the meridians of 108° and 113° eastern longitude, with ${D}_{x}=470$ km, ${D}_{y}=551$ km and extension parameter ${d}_{x}={d}_{y}=d$. The data area was sampled with 14,641 points, spaced by $2.5' \times 2.5'$ in latitude and longitude and at the corresponding height of the geoid.

The RMS values for the disturbing potential from the adjustment of model M0 with different degrees and extension parameters are given in Table 5. From these values, we select the expansion degree $N=M=40$ and extension parameter $d=75$ km. The results are shown in Fig. 3.

Table 5 RMS values for the disturbing potential (in ${\mathrm{m}}^{2}/{\mathrm{s}}^{2}$) from the adjustments of model M0 for different values of expansion degree $N$ and extension parameter $d$ in an area $5^\circ \times 5^\circ$ in China

Fig. 3

From the adjustment of model M0 with expansion degree $N=M=40$ and extension parameter $d=75$ km in $5^\circ \times 5^\circ$ area in China: Residuals of the disturbing potential (Left) and differences of disturbing potential between the values from the global and local model at the validation points in a $3^\circ \times 3^\circ$ area (Right), as a function of the distance from the origin

We note that, as in the previous case study, we validated the model using 5184 points, located at intermediate positions of the adjustment points, in the area between parallels of 30° and 33° northern latitude and meridians of 109° and 112° eastern longitude.

It can be seen from Fig. 3 (Left) that the residuals of the disturbing potential (corresponding to $\pm 10 \, \space\mathrm{\mu m}$ precision of geoidal heights) and the differences of the disturbing potential between the values from the global and local model at the validation points (Fig. 3—Right), both reflect the reliability and accuracy of the successfully transformed local model. Comparing the above results (Table 5) with those achieved by Jiang et al. (2014), presented in Table 1 of mentioned paper, we obtain better results for the disturbing potential because of the use of a different general mathematical model (M0). In the case of the 5°×5° area, the RMS values related to the values of extension parameter d (last column of Table 1 in Jiang et al. (2014)) are significantly greater than the RMS values computed for different expansion degree N and the same values of parameter d in our Table 5, converted in terms of geoid undulation using Bruns formula. In addition, the RMS values in Table 5, in terms of geoid undulation, are the same order of magnitude as the RMS values referring to the smaller area 3°×3° in Table 1 presented in Jiang et al. (2014). Finally, it is worth noting that the number of coefficients in the model used by Jiang et al. (2014) equals to (2N+1)(2M+1).

6.3 Local rectangular harmonic model in Germany

For a comparison with the method of ASCH by a least squares’ estimation of coefficients of the mathematical model, in this case study we generated almost the same grid which was used in the work of Younis (2013). Thus, a 3D grid of $k=11163$ points, with spatial resolution $3' \times 3'$, was generated over a $3^\circ \times 3^\circ$ area in Germany, from $\left(\varphi ,\lambda \right)=\left(47^\circ ,7.5^\circ \right)$ to $\left(\varphi ,\lambda \right)=\left(50^\circ ,10.5^\circ \right)$, using as origin of the local coordinate system the point $\left({\varphi }_{0},{\lambda }_{0},{\overline{h}}_{0}\right)=\left(48.5^\circ ,9.0^\circ ,0 \mathrm{m}\right)$. The values of the disturbing potential were computed at ellipsoidal height levels of 0 m, 1000 m and 2000 m. The parameters of Eq. (30) are ${D}_{x}=220$ km and ${d}_{x}=0.66d$, while ${D}_{y}=330$ km and ${d}_{y}=d$.

The RMS values for the disturbing potential from the adjustment of model M0 with different degrees and extension parameters are given in Table 6. From these values, we select the expansion degree $N=M=25$ and extension parameter $d=125$ km and create Fig. 4.

Table 6 RMS values for the disturbing potential (in ${\mathrm{m}}^{2}/{\mathrm{s}}^{2}$) from the adjustments of model M0 for different values of expansion degree $N$ and extension parameter $d$ in an area $3^\circ \times 3^\circ$ in Germany

Fig. 4

From the adjustment of model M0 with expansion degree $N=M=25$ and extension parameter $d=125$ km in $3^\circ \times 3^\circ$ area in Germany: Residuals of the disturbing potential (Left) and differences of disturbing potential between the values from the global and local model at the validation points (Right), as a function of the distance from the origin

As in the previous cases, we validated the model using 3600 points, located at intermediate positions of the adjustment points and at the actual height of the topography.

It can be seen from Fig. 4 (Left) that the residuals of the disturbing potential correspond to $\pm 0.1$ mm precision of geoidal heights and the differences of the disturbing potential at the validation points (Fig. 4—Right) are generally small and increase with the distance from the origin. However, from Table 6 we ascertain some problems of numerical instability (NaN) for larger values of expansion degree $N$ and extension parameter $d$, i.e. the system of normal equations becomes unstable or even ill-posed. For the solution of this problem, any regularization method (Truncated SVD, Tikhonov etc.) may be applied, as in Jiang et al. (2014). In this work, we did not apply such methods because, as presented in Tables 2, 4, 5 and 6, the RMS value is smallest within the range of the parameters where the proposed transformation is still applicable and the numerical problems have not appeared.

Comparing the above results with those achieved by Younis (2013), from the same data, we obtain better results for the potential, mainly because of the use of rectangular harmonics instead of spherical cap harmonics. Furthermore, since the gravitational potential of the normal gravity field can be given analytically by Eq. (2), we find preferable to transform the disturbing potential rather than the gravitational potential. As already stated in the Introduction, spherical cap harmonics have their own problems and, additionally, they demand a gravitational constant of the Earth $GM$ and a selected reference radius $R$.

7 Conclusions

A global spherical harmonic model requires a very high number of coefficients to represent the gravitational potential, even in a local area. In contrast, a local rectangular harmonic model requires less coefficients and hence memory requirements in computation and storage. For example, the global model EGM2008, with maximum degree 2190, includes 4,800,481 coefficients, while the corresponding local model produced in this work, for instance in a $4^\circ \times 4^\circ$ area in Greece with maximum degree 35, includes only 5188 coefficients and the disturbing potential is accurately reproduced. Therefore, the transformation from a global spherical to an adjusted local rectangular harmonic model, as presented in this work, offers an advantage. This transformation is based on a mathematical model (M0), derived in this work, and uses a least squares’ adjustment process for the estimation of the rectangular harmonic coefficients of the model.

The results in the various case studies demonstrate the reliability and accuracy of the successfully transformed local model. The derived model of the potential is simpler to implement than other analyses (e.g. SCH, VSH) and, in addition, one can also calculate its functionals, such as gravity anomaly and disturbance, height anomaly, geoid undulation and deflection of the vertical. On the other hand, a limitation of the rectangular harmonic model is that it cannot be extrapolated, as evidenced by the increased errors in the edge of the region constrained by the data. However, the main drawback of the method for a larger area, known as edge effects (Jiang et al. 2014), may be alleviated using advanced least squares’ adjustment techniques.

The examination of the behavior of the residuals and their distributions, such as the statistical significance of the estimated parameters, should be an object of further study that could include measurements of the same or of a different kind, aiming at the refinement of the local model. On the other hand, the regional improvement of a global geopotential model using modern data such as GNSS/Leveling data leads to instabilities, such as the leakage effect (for details see the work of (Mosayebzadeh et al. (2019)). In any case, the first step is the transformation which has been presented in this study.