1 Introduction

Three dimensional models are fundamental in all branches of Earth Sciences, especially in solid Earth geophysics where structural variations can be significant but means of verification are limited. Since most of Earth’s interior cannot be sampled by drilling, it is by observing how seismic waves are reflected, converted, sped up, or delayed that images at depth are constructed. The overwhelming majority of studies employ P waves as well as tomographic methods to image volumetric velocity variations (e.g. Aki et al. 1977; Iyer and Hirahara 1993; Nolet 1987; Rawlinson et al. 2008).

A passive seismological method that is complementary to classical tomography is based on the conversion between P and S waves. Commonly known as the receiver function (RF) technique, this method images primary discontinuities, sharp velocity changes such as the Moho (crust – mantle) and the Conrad (upper crust – lower crust) interface, low-velocity zones, and mantle transition zone discontinuities. While this method started from single station applications (e.g. Langston 1977a, 1977b, 1979) and is a rapid tool to provide crustal thickness and average crustal Vp/Vs ratios (Chevrot and Van der Hilst 2000; Zhu and Kanamori 2000), it had the limitation of an assumed Vp for the whole crust. Single-station inversions for Vs as a function of depth, for example with the Neighbourhood Algorithm (Sambridge 1999a, 1999b), represent a step forward, but 3-D outcomes have only been obtained by the interpolation of such results (e.g. Kalmár et al. 2021). With station arrays and networks, time-to-depth migration such as the common conversion point technique (CCP, Dueker and Sheehan 1997) have often been employed to create 2D cross-section of the lithosphere, with the limitation of the applied velocity model.

The approach adopted in this study represents a new, alternative way to use receiver function and demonstrates a step forward over traditional techniques. It overcomes most of the earlier limitations by simultaneously performing the velocity model determination and migration for structural mapping. In practice, the 3-D velocity structure including discontinuities at interfaces and velocity gradients across layers are inverted from the seismic data.

This is achieved by stepping away from the currently widespread implementations to recover 3-D velocity variations in the lithosphere through the parametrization of the seismological model. Parametrizations driven by tomography are typically defined as single velocity values assigned to nodes at a given spacing, and interpolated velocity values in-between. This prevents an easy definition of sharp discontinuities that would generate converted waves and allow testing these models with receiver functions. Therefore, we here propose a novel parametrization with flexible node depths and a dual definition of velocities above and below each interface. This step increases the number of variables to invert, but allows to map simultaneously Moho depth and shear-wave velocity (including the Vp/Vs ratio variations) in three dimensions.

Beyond the aim of seismological imaging in 3-D, the goal of this research is also to provide a new tool to obtain models of Vs, which is commonly less studied than the imaging provided by P-wave alone. One reason is connected to the increased difficulty to pick S arrivals on a seismogram with respect to P arrivals, although recently ambient noise tomography (ANT) has become popular to invert for 3-D Vs structure (e.g. Campillo and Paul 2003; Shapiro et al 2005; Weaver 2005; Yang et al 2007). This method is based on largely horizontally propagating waves, and a relatively large aperture seismic network is required to image at depth.

The new method represents a powerful tool to be added to the palette of computational seismology, especially to better constrain seismic velocity at depth. The structure of the paper below is the following. After a detailed description of the new methodology developed for 3-D Vs model construction – mainly the novel model parametrization allowing for the presence of both discontinuities and velocity gradients, as well as the inversion scheme, we present the practical implementation for the first case study on the Central Alps, using the recently collected broadband seismic dataset of the AlpArray Seismic Network (Hetényi et al 2018a). The spacing of seismic stations provides a suitable target to carry out this first, real scenario inversion, while the complex tectonic history and variability of Moho depth and dip provide a challenging testing ground. The 3-D inversion results for the Alpine case (depth discontinuities and velocities) are shown through several maps and cross sections while in the Discussion section are also compared with the results obtained with the interpretation of geological profiles and ambient noise investigations.

2 Methods: 3-D crustal Vs-model inversion

2.1 Receiver functions

The new method is based on P-to-S converted waves, commonly called receiver function (RF), which is a way to image the Earth’s interior and its boundaries through the information inferred from teleseismic earthquakes recorded at a three-component seismograph (receiver). The investigated structure includes the depth of velocity discontinuities, as well as the local velocity conditions, especially the velocity change across the discontinuities. The RFs computation from real data requires 3-component sensors, as well as sub-vertically arriving waves thus teleseismic earthquakes and broadband instruments. Thanks to the sub-vertically propagating waves, the new method proposed here allows an easier application in areas characterized by low seismicity and over the full lateral and depth extent of a dense seismic network.

A seismogram can be viewed as a combination of the source time function of the earthquake, the Earth’s structure impulse response and the instrument’s impulse response. This combination represents the convolution which allows us to get the Z-R-T components of the seismogram (respectively vertical, radial and transverse), which are obtained by rotating the original Z-N-E component data into a coordinate system pointing towards the earthquake. In RF techniques, two deconvolution methods are commonly used: the frequency-domain spectral deconvolution, and the time-domain iterative deconvolution. In this study, we use the latter type of deconvolution, where the difference between predicted and observed horizontal seismogram is assured through the least squares technique. At the end of a number of pre-set iterations the series of spikes represent the best transfer function between the vertical and horizontal signals, thus the receiver function.

There is a broad literature available on the method and its application, we therefore refer to e.g., Owens and Crosson (1988), Ammon et al (1990), Cassidy (1992), Sambridge (1999a), Frederiksen and Bostock (2000), Park and Levin (2000) and Zhu and Kanamori (2000).

Our newly developed method employs RFs in a fully 3-D manner. The raypath of each source – receiver pair is computed according to a 3-D velocity model. Synthetic RFs are computed by extracting individual 1-D velocity models for each trace, and by calculating the corresponding theoretical RF response using the method of Shibutani et al. (1996). This is an efficient and reliable tool, where the S-wave velocity in each layer is constructed by linearly connecting the values at the upper and lower boundaries, in order to give a sequence of constant velocity gradient segments separated by velocity discontinuities.

2.2 Model parametrization

In seismology, the model parametrization is a simplified representation of a seismic structure by a set of model parameters, typically coordinates and wavespeeds. The main factors that interact with the choice of a particular model parametrization include the forward solver, the inversion algorithms, the a priori knowledge of Earth’s structure and the resolution capability of the available dataset (Kissling et al. 2001). A large portion of models to express the 3-D structure of the Earth’s interior employ grids or meshes creating 3-D blocks which are widespread in tomographic applications (e.g., Rawlinson et al. 2010; Thurber and Eberhart-Phillips 1999; Zhao et al. 1992; Zhao 2009).

The typical parametrization used in classical tomography for a 3-D domain is shown in Fig. 1a. This parametrization commonly consists in a rectangular grid with fixed node positions in space. A single velocity value is assigned to each block (or node), and velocities elsewhere are typically linearly interpolated from the defined values. Although this setup is convenient to manage numerically, physically the fixed block geometry does not allow to closely follow and constrain variable-depth interfaces such as the Moho discontinuity. To counter this drawback, very high resolution grids are necessary, which significantly increase the computational task. Without that, such model parametrization may be too simplistic to represent sharp interfaces which thus remain poorly resolved.

Fig. 1
figure 1

Evolution of model parametrization from classical tomography to the newly developed 3-D RF approach. a Typical model parametrization used in classical tomography: block boundaries are fixed in space; velocity values represent a volume. b The newly developed model parametrization using RFs for 3-D Vs tomography: layer boundaries are flexible in depth, while velocity profiles belong to a grid node distributed laterally, allowing the velocity jumps at discontinuities and also gradients across layers. Figure is not to scale

Full size image

To surmount these limitations and to allow 3-D Vs imaging by RFs which better reflects the structural complexity at depth, we define a new type of model parametrization, shown in Fig. 1b. Three main features characterize this setup:

  1. (1)

    vertical nodes are added only at velocity discontinuities;

  2. (2)

    the sharp velocity change is defined by assigning two velocity values at each node: a velocity above and a velocity below the discontinuity;

  3. (3)

    while the horizontal coordinates are fixed as before, the depth of the nodes (defining a discontinuity) is itself a variable.

All these characteristics together allow mapping the shape of the discontinuity as if it was with a flexible blanket, while simultaneously allowing sharp velocity changes at discontinuities and velocity gradients across layers. This model parametrization means 5 independent parameters per layer to invert for, a number that can be reduced upon simplifying assumptions for particular case studies. This two- to four-fold increase of velocity parameters is an additional computational burden, however the spatial resolution does not need to be as high as local earthquake or ambient noise tomography models, therefore the overall costs are lower. In fact, for each iteration, the computational cost is approximately 1000 core hours on Froggy architecture for an ANT study from Lu et al. 2020, while the time spent for 1 full inversion round with our model (4000 iterations) is about 31 hours, using a MacBook Pro with 8 GB of RAM and a 3.1 GHz Intel Core i7 processor.

2.3 Ray tracing

Ray propagation geometry is connected to the surrounding velocity conditions: for P-to-S converted waves, this is often approximated to the geometry of the teleseismic ray between the source and the receiver, with either the mantle (propagation from source) or the crustal side (migration from the receiver) being correct, but the remaining part not. Only a few studies attempted to match both at Moho depth (e.g. Singer et al. 2017). Here too the challenge is mainly computational, and since we aim at the construction of a 3-D Vs model, we implement ray tracing as close as possible to reach the target.

In the past few decades, numerous grid- and ray-based procedures have evolved, one of the most common methods being ray tracing (Julian and Gubbins 1977; Um and Thurber 1987; Virieux and Farra 1991; Červeny 2001). Commonly, ray tracing methods are grouped in two broad categories: shooting and bending.

Here we use a shooting approach for its relatively simple implementation and high accuracy. The propagation of the P-wave in a global 1-D velocity model (IASP91 by Kennett and Engdahl, 1991) is calculated using the TTBOX software (Knapmeyer 2004, 2005). In the original version, ray paths and travel times are computed only for a 1-D spherical isotropic velocity model and TTBOX uses the flat Earth transformations to evaluate both epicentral distance and travel time as functions of the ray parameter. The solution accuracy depends on the quality of the depth sampling (Knapmeyer, 2005) since velocity models may be defined by a list of depth samples or piecewise continuously by layer polynomials. The ray parameter needed to arrive at a given epicentral distance, and is returned which allows hitting the target distance within about 100 m.

For our purposes, in order to simulate the crustal propagation of P- and S-waves between the Moho and the surface, we implement our own ray-based method which follows the 3-D velocity-variations and Snell’s law at velocity discontinuities. The crustal ray-propagator is used for two reasons:

  1. 1.

    To make rays arriving precisely at the stations by correcting the teleseismic ray-parameter (see example in Fig. 2);

  2. 2.

    By recalculating ray geometries when the 3-D velocity models are updated during inversion procedure.

Fig. 2
figure 2

Implementation of the 3-D ray tracing procedure for a sample station (red triangle), before and after correction from teleseismic P to appropriate P-S converted raypath. a Teleseismic P-ray propagation with a shooting scheme from a source to a station using a 1-D spherical global velocity model, e.g. IASP91 (Kennett and Engdahl 1991). b P-to-S converted-wave arrival points near the station at the surface, following from teleseismic P-ray. c Scheme of the corrected P-to-S converted ray shooting, considering the Moho local dip and local crustal velocities, which arrives precisely to the station. The initial shooting is shown in dashed lines, the corrected in thick lines. The yellow dots represent piercing points at the Moho. d S-wave arrival points near the station at the surface, after correction, shown at the same scale as in b

Full size image

Figure 2 shows an example of the 3-D ray tracing procedure for a sample station. The location of the conversion point at Moho depth is computed as the intersection between the teleseismic P-wave and the discretized Moho surface using the Möller-Trumbore (1997) ray-triangle intersection algorithm (Fig. 2a), which represents a fast method for computing the intersection of the P-wave raypaths and a triangle in 3-D.

Then, the 3-D S-wave propagation in the crustal domain is performed with the actual velocity model with fine upward steps in depth and velocities interpolated based on inverse squared distance weighting of the 8 enclosing defined velocity points (4 nodes above and 4 below within the crustal column). At any discontinuity on the way, Snell’s law is applied to update the ray parameter, and the ray intersection with that discontinuity is calculated as above. The overall ray geometry is physically correct, but the first shooting produces a ray that is not reaching the surface near the station due to the incorrect initial ray-parameter computed from the epicentral distance (Fig. 2b).

In order to find the P-to-S converted ray geometry that reaches the station, we perform a second, corrected shooting, where the correction for each ray is given by the distance between the station and the ray’s initial arrival position at the surface. This operation allows to adjust the initial ray-parameter which makes the teleseismic P-wave arrive at the Moho and cause a converted crustal S-wave leg that reaches the surface much closer to the station (Fig. 2c).

Figure 2d shows the position of rays arriving at the surface after the corrected shooting: the distance to the station are significantly reduced compared to the initial shooting, but are not equal to zero as the crustal Vs model is itself 3-D and therefore the ray-shape is not identical with respect to the first shooting.

For the example presented in Fig. 2, in the first shooting the distribution of distances between the arriving S-waves and the station has a mean of 3 km (with a median of 2.4 km); after the adjustment of the ray parameter and second shooting, these values are reduced to 180 m and 60 m, respectively. This represents a good performance for this tool, and also the computation time is reasonable (about 0.04 s for each trace).

2.4 Inversion scheme

The flowchart of the general inversion procedure we developed is shown in Fig. 3. The starting model is builds on a priori information regarding velocities, number and geometry of discontinuities, as well as grid spacing. In general, Vs, Vp and discontinuity depths at each node are variables, and the user can assign a range of parameter search or even fix them. This determines the total number of parameters to invert and hence the computational load.

Fig. 3
figure 3

Flowchart of the inversion approach developed in this work, with dashed grey lines that represents the different phases of the proposed procedure. Parallelograms represent an input (green), an output (red) or a plot (grey). Blue rectangles are the main phases of computation; the diamond indicates a decision. The box with Vs is white because it represents an input for which the inversion is not computed directly, but it takes into account a fixed Vp/Vs ratio and an initial Vp value (green box)

Full size image

The total number of independent parameters at each node is maximum 5 × N, where N is the number of layers. For example, for a 2-layer model, N is equal to 10: 2 depths (Moho and Conrad), and 2 velocities (Vp and Vs) at 4 positions: at the surface, above and below the Conrad, and above the Moho discontinuity (values of velocities are fixed below the Moho). Good a priori data and simplifications (e.g. assuming layer-wise Vp/Vs) can reduce the number of parameters to invert.

The next step is the calculation of the forward model, which in our case is constituted by the ray tracing operation (Sect. 2.3). The synthetic RFs are then compared with RFs computed from observed seismograms that have passed several quality controls. We apply a stochastic inversion procedure using the simulated annealing (SA) technique and a pattern search solver searching across the range of all variables while minimizing misfit calculated with L2-norm between observed and computed RFs amplitude through a defined number of iterations. After that, the three-dimensional model is updated, ray geometries are recalculated, and a new round of iterations follow until satisfactory convergence.

This scheme is general and its details can be adapted according to the richness and quality of a priori information, data coverage and inversion targets.

2.5 Future methodology and application prospects

The newly developed approach is applicable to other regions where a dense network of broadband seismometers exists, such as Japan, the USArray and the IberArray areas, as well as the forthcoming AdriaArray. Further implementation developments could be the parallelization of the inversion itself, taking away the need to reduce the number of parameters that are inverted at each node.

Our methodology can be readily extended to future joint inversion taking advantage that other seismological techniques (e.g. traveltime tomography, Ammon et al. 2004; Kiselev et al. 2008; ambient noise studies, Chen et al. 2019; Guo et al. 2015; Mroczek and Tilmann 2021; surface wave dispersion, Bodin et al. 2012; Chen and Niu 2016; Julià et al. 2000; Shen et al. 2012) and gravity data (e.g. Basuyau and Tiberi 2011; Scarponi et al. 2021; Tiberi et al. 2003) are complementary in terms of resolution area and sensitivity to the only receiver functions investigations.

3 Data and application to the Central Alps

The Central Alps are a suitable testing ground of the new method thanks to its spatially dense station deployment and its tectonic complexity. For these reasons, we first implement the inversion over this area. In order to focus on the inversion performance and not on the computational challenge, a number of simplifying steps have been introduced. These and all practical details are described in the following sub-sections.

3.1 Practical implementation to the Central Alps

Given the station coverage and a priori information availability in the Central Alps, the horizontal spacing of grid nodes has been selected at 25 km distance. With this spacing, the entire area of investigation fits into a rectangular box spanned by 24×19 nodes, that is 575 km east–west and 450 km north–south distance.

With up to 10 parameters to invert at 456 nodes, the inverse problem is extremely large; we have therefore simplified the model parametrization and the inversion scheme in a computationally feasible manner for this case study.

3.1.1 Model parametrization

The model parameterization has been simplified to 4 parameters per node instead of 10. These are: the Moho discontinuity depth (\(zM\)), the Conrad discontinuity depth (\(zC\)), the Vp velocity change at the Conrad (\(\Delta vPc\)), and the overall Vp/Vs of the crust. The initial Vp values are fixed according to the 3-D local earthquake tomography by Diehl et al. 2009, and \(\Delta vPc\) is centered on the a priori Vp value at the Conrad.

We note that other options exist to reduce the number of parameters to invert per node, depending on the availability and quality of a priori data. A set of reasonable possibilities is shown in Supplementary Table 1.

3.1.2 Spatial separation of the inverse problem

For the inversion strategy, we take advantage of the sub-vertically propagating raypaths, as only the nearest RFs to a given node, which belong to the same portion of the surface defined by ray tracing operation, affect the model properties there. In other terms, the matrix linking model and data is extremely sparse. This allows to run the inversion locally at each node, instead of computing a very large inversion for the entire model domain. In practice, this requires visiting every node going from neighbour to neighbour along a given path, updating the model parameters according to Fig. 3.

To stabilize the results of the inverted parameters (\(zM\), \(zC\), Vp/Vs, \(\Delta vPc\)) and to make them independent of the pathway chosen when visiting the nodes, we perform at least 2 such iterations. The pathways are selected through the Travelling Salesman Problem (TSP) technique (Biggs 1986; Lawler 1985; Lin and Kernighan 1973), an algorithm tasked with finding the shortest route connecting a set of points in which all locations must be visited. In our application, the TSP creates paths that visit every node exactly once and proceeds from node to node by neighbours. In order to make the solution independent of the route taken by the TSP, and because the model geometry is a regular mesh in map view, we imposed different visit paths for each inversion round, which creates either spiral or zig-zag pathways. By performing at least two rounds of different TSP pathways, we expect the solution to improve as any disparities remaining between neighbouring nodes will be better resolved by re-considering the RFs constraining the node-wise parameters. In our application, the TSP enables the spatial separation of the node-wise inversion, to local subsets of the matrix.

3.1.3 Inversion at a node

At each node, the ray tracing of each RF is re-computed with the most up-to-date 3-D model. We then invert simultaneously for the number of parameters that vary (4 in the case of the Central Alps) and within an allocated range of values. In order to explore deeply the parameter space, we adopt the stochastic technique of optimization based on Simulated Annealing (SA). Simulated annealing (Kirkpatrick et al. 1983; Geman and Geman 1987) is a numerical method based on Metropolis sampling algorithm, using an analogy between the process of physical annealing and the mathematical problem of obtaining the global minimum of a function that may have local minima. In SA the distance to the new point is based on a probability distribution proportional to a parameter, which is the objective function. SA accepts all new points that have a lower value of the objective function as currently, and even – with a certain probability – those points that increase the objective function value. The SA represents the local inversion at a node, improving the set of parameters characterizing the model in that area (see Sect. 3.1.4).

The implementation of this approach was done through built-in functions in Matlab software, including a built-in pattern search solver. Beyond the number and variation range of parameters as well as the number of iterations, the objective function needed to be defined. The objective function is calculated by comparing the misfit between observed and synthetic RFs. The misfit calculation itself follows the L2-norm, but the time window over which the misfit is computed is a function of the Moho depth: we ensure that the multiples (PpPs and PpSs + PsPs reverberations) are included in the compared time frames. Then all RF misfits contributing to a given node’s inversion are averaged (for grouped rays: weighted by the number of rays in the group), and that provides the current misfit at that node. A few individual RF fits are shown in the SI 2. To demonstrate the overall improvement of fit across the entire study area for all nodes, we represent the misfit reduction \(mR\) as a relative ratio of improvement of the current misfit \(mC\) over the initial misfit m0 of the current round of TSP pathway:

$$mR = \frac{mC}{{m0}}$$
(1)

Values just below 1 indicate slight misfit reduction, and closer to 0 significant reduction, and it is represented as a relative improvement for each round (Fig. 6). The misfit improvement for the final model demonstrates that a few rounds of inversions clearly improve the overall misfit, and that the mean and median values of node-wise misfit reductions, less and less as the iteration rounds proceed, suggest convergence towards a stable solution.

3.1.4 Synthetic recovery tests

Synthetic recovery tests show that the method performs well in relation to our target. The SA inversion alone does not always provide a satisfactory result, but with the application of the pattern search solver (Lewis and Torczon 1999; Powell 1973) the solution recovers the initial parameter extremely closely (see Fig. 4 and SI 1). These same tests also enabled finding the number of iterations in each TSP round so that the solution can be considered stable.

Fig. 4
figure 4

Exploration of parameter space for some parameters for a synthetic recovery test. a Moho depth and Conrad depth; b Moho depth and Vp/Vs for the upper crust; c Moho depth and Vp/Vs for the lower crust; d Moho depth and P-velocity jump across the Conrad. Scatter points represent the value of the objective function to minimize before applying the pattern search solver. Other synthetic tests are available in the Supplementary Information SI 1

Full size image

In these synthetic recovery tests, we have generated receiver functions for a known structural and velocity model, and we have observed how quickly and how well the inversion process recovers the initial model from a very different starting point. For one of the ultimate tests we have performed, at each node the model had 5 parameters to invert (Moho depth, Conrad depth, Vp/Vs ratio in the upper and in the lower crust, and the Vp change across the Conrad discontinuity). In order to visualize the exploration of the parameter space during the Simulated Annealing (SA) and the Pattern Search (PS) inversion approach, the plots in Fig. 4 show some tested parameter sets colored according to their misfit in the SA phase, and the initial and final parameter sets value. In all plots, the starting value is shown by a green star, which is away from the set of 5 values of the model to recover. The solution found with the SA algorithm alone after 500 iterations is shown with the yellow star, while the ultimate solution, involving a combined approach between SA and PS, is represented by a red star.

As it can be seen by the distribution of dots, which represent each step of the SA phase, the randomness of the SA process covers the parameter space fairly well and the objective function value is smaller near the solution. In many cases, the SA phase alone provide a solution close to the true one (e.g. for Moho depth vs \(\Delta vPc\), Fig. 4d), nevertheless the PS phase is certainly useful and further improves the recovery of the initial values, improving the SA solution if it was not close to the initial value (e.g. Conrad depth in, Fig. 4a).

3.2 Data selection for the Central Alps

Two main reasons led to selecting the Central Alps as a testing ground: it is a tectonically and therefore structurally complex natural laboratory with three lithospheric plates (Europe, Adria, Liguria) and dipping structures at depth, and it is covered over the last several years by a dense, homogeneously distributed broadband seismological array. The structure of the Alpine crust has been studied for decades, with various methods such as local earthquake tomography (e.g., Diehl et al. 2009; Paul et al. 2001; Scafidi et al. 2016; Solarino et al. 2018) and several other tomographic approaches, including the most recently employed ambient noise tomography techniques (e.g., Guidarelli et al. 2017; Li et al. 2010; Lu et al. 2018; Molinari et al. 2015; Stehly et al. 2009; Verbeke et al. 2012). New advances in Alpine seismological imaging have been made possible thanks to the AlpArray Seismic Network (Hetényi et al. 2018a), which represents a joint effort of observatories’ permanent station development and research institutions’ temporary station deployment towards a large-aperture, uniformly spaced, broadband seismic network. The bulk of this network has been operational since 2016, and no point in the Alpine domain is farther than 30 km away from a station, which follows a hexagonal compact pattern on the map. The data has been collected by the AlpArray Working Group and distributed centrally via European Integrated Data Archive (EIDA, http://www.orfeus-eu.org/data/eida/).

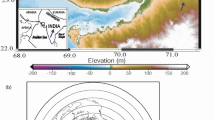
For our study, we download original Z-N-E component data in the rectangular box comprising the Central Alps, spanning from 5° to 12° E and from 45° to 48.5° N (Fig. 5a). In parallel, we take the catalogue of teleseismic events from the ANSS ComCat catalogue provided by the US Geological Survey (https://earthquake.usgs.gov/earthquakes/search/) with magnitudes M > 5.2 that occurred since May 1995 (start of the earliest selected station) to June 2018 (Fig. 5b). The epicentral distance was set between 25° and 95° with respect to the reference point located in Lausanne, Switzerland. This provides a total of 6,450 events recorded at 150 broadband stations, yielding a total of 287,414 three-component records.

Fig. 5
figure 5

a Broadband seismological stations used in the investigated area. Two-letter abbreviations in the legend represent the seismic network codes, see acknowledgements and references. b Distribution of teleseismic earthquakes considered for this work; yellow star shows the reference point in the Central Alps

Full size image

For the RF computation, we used the iterative time-domain deconvolution method following the algorithm by Ligorría and Ammon (1999), which is widely used in several crustal investigations (e.g. Abt et al. 2010; Beck and Zandt 2002; Zor et al. 2003). We perform the deconvolution with 100 iterations using the original traces that are Butterworth-filtered (order 2) in the frequency band between 0.125 and 0.5 Hz. The obtained series of spikes are then convolved with a Gaussian filter of order 2.

Considering the amount of data to analyze, it is not possible to perform a visual inspection of the entire dataset at each trace to check their quality. For this reason, a semi-automatic approach proposed by Hetényi (2007) and applied in several RF studies (e.g., Hetényi et al. 2015, 2018b; Kalmár et al. 2021; Subedi et al. 2018) is used to select the highest quality seismic records based on Z-N-E component data impulsiveness and similarity between stations for each event, as well as location and amplitude of the most prominent peak in the computed RFs. After having tested quality control parameters of various strictness, we retained 28,494 traces, which represents the top ca. 10% of our initial dataset.

3.2.1 Spatial grouping of rays

The newly developed inversion method is able to treat as many RFs as wanted in a dataset. However, for more efficient computation, a reasonable reduction of data is to group rays whose geometry is similar into a bundle. This operation is similar to stacking, that allows to increase signal-to-noise ratio (e.g. Kumar et al. 2010; Sippl et al. 2017), but here it is performed for grouping rays with clearly overlapping Fresnel zones, and not for all RFs of a given station. This way, the 3-D imaging capability is preserved.

In our application, two ways of grouping are combined: one is sub-dividing the inversion grid into horizontal sub-blocks at Moho depth, and the other follows back-azimuth ranges to define sectors. The tightness or broadness of grouping can be selected according to ray density. For our case, we chose 5 × 5 sub-blocks (25 such sub-blocks in the 25 × 25 km blocks spanned by nodes) as well as 6 sectors of 60° back-azimuth each, which provides a good compromise between an acceptable resolution and a reasonable computation time. The selection being done at Moho level, the latter criteria ensures that rays propagate along similar geometries through the crust.

Supplementary Information SI 3 shows one example for a station with 531 initial RFs represented with the piercing points at Moho depth, reflecting the spatial distribution of the contributing teleseismic earthquakes. Following the division described above, 13 new bundles (grouped RFs) and further 3 individual RFs are kept for the inversion. In a bundle, the waveforms are averaged, the same as ray parameters to compute the corresponding synthetic RFs. If wished, a data coverage criterion can be introduced by setting the minimum number of rays in a bundle. Consequently, for the misfit calculation, the weight to such grouped RFs is proportional to the number of bundled rays.

3.3 Starting model for the Central Alps

Following from key geological results (e.g., Escher et al. 1997; Schmid et al. 2017) and geophysical a priori information (see below) on the Central Alps, we build a 2-layer model of the crust considering 3 interfaces: the surface, an intra-crustal boundary (possible Conrad discontinuity) and the Moho discontinuity.

For the initial topography of the Moho, we take the depth maps of Spada et al. (2013) as a starting model, covering the Europe, Adria and Liguria plates. For the depth of the intra-crustal discontinuity, based on the geological profiles (Escher et al. 1997; Schmid et al. 2017), we set the initial value so that the lower crustal thickness is 12 km everywhere. As mentioned above, the depth of these two interfaces evolve independently during the inversion. For the definition of the surface, the elevation of the highest station (at 3000 m above sea level) is chosen to define velocities, but rays propagate to the actual elevation of the corresponding station.

The P-wave velocity model of the crust is fixed to the values provided in the 3-D local earthquake tomography of Diehl et al. (2009). The choice of this model is justified because it features both large spatial coverage over the Alps and the best resolution available in that entire domain, which is 25 × 25×15 km in the two horizontal and the vertical directions. The initial value of the Vp change across the Conrad discontinuity is derived from the IASP91 model (Kennett and Engdahl 1991), and is set to 0.7 km/s. The starting value of crustal Vp/Vs is set to 1.73.

We set our coordinate system’s center at 10°E longitude and 46°N latitude; then we resample the input models on the new grid following the new model parametrization described above.

3.4 Towards the final selected model for the Central Alps

Based on numerous inversion-parameter trials and synthetic recovery tests, the final inversion towards the 3-D Vs structure of the Central Alps was performed with three successive rounds of node-wise inversions following different TSP pathways. At each node, the simulated annealing and pattern search inversion was carried out, using 4000 iterations in the first round and 1500 iterations for the two subsequent rounds. The model is continuously updated and the ray tracing recomputed at each round. The relative misfit evolution in the three rounds are shown in Fig. 6. We show relative misfit reductions for each inversion round instead of absolute misfit values because the bundles are recomputed in each round, and, therefore, a given node considers different set of receiver functions. We can observe that in the first round, misfit is reduced by 20–25% for the median and average respectively, by 7–9% in the second, and by 4–6% in the third, which we considered as satisfactory convergence of the results.

Fig. 6
figure 6

Misfit reduction in the three subsequent iteration rounds of the inversion. The lines in the graph show the misfit reduction \(mR\) at each node as the ratio of final and initial misfit for the given round of iteration. Values of misfit reduction close to 1 indicate a slight improvement, while values closer to 0 show major improvements. Filled circles represent the mean of misfit reduction after the 1st (0.7702), the 2nd (0.9076) and the 3rd (0.9349) round of inversion; empty circles represent the corresponding medians (0.7925, 0.9298, 0.9715). The decreasing amount of misfit reduction represents convergence of the solution

Full size image

To put bounds on the range of variation of each inverted parameter, the Moho and the Conrad depth could vary within a ± 12 km and respectively ± 10 km range compared to the initial value in that round. From the second round onwards, an absolute constraint was added: \(zM\) within the 15–65 km and \(zC\) within the 10–55 km depth range. In all three rounds, the average crustal Vp/Vs could vary between 1.6 to 1.9 at each node, whereas \(\Delta vPc\) between -0.35 and 1.05 km/s.

Regarding spatial grouping of rays (Sect. 3.1.4), beyond the 5 × 5 km sub-blocks and 60° wide sectors, a threshold of at least 7 rays per bundle was imposed in the final inversion. Figure 7a represents the ray coverage map of the study area at the Moho level for the selected RFs respective Fresnel zones (defined as \(F\)) over the Moho depth starting model related to the rays’ concentration available in each area. Considering all the depths of the piercing points, the Fresnel radius considering the S-wave propagation goes between 9.3 and 15 km. Figure 7b represent the final ray coverage map at the Moho after the grouping of rays, representing a total of 631 bundles with 16,226 included RFs, corresponding to more than 80% of the RFs computed from observed and quality-controlled seismograms.

Fig. 7
figure 7

a Moho depth starting model (from Spada et al. 2013) and ray coverage of the final RF dataset in this study. White-shaded circles represent the position of piercing points for the final crustal S-wave at Moho depth; the radii of the circles are proportional to the Fresnel zone. b Number of contributing rays crossing each block in the study area at the Moho depth level after bundling. White cells are crossed by less than 7 rays, cells between 7 and 20 rays are shown with the yellow–red color scale, while cells in red are crossed by at least 20 rays

Full size image

4 Results

With the selected dataset and inversion parameters, the results converged to a solution that we consider representative for the 3-D Vs structure of the Central Alps. This is based on the convergence of the model through the iterations, as well as on the comparison to previous geophysical and geological results. Given the spatial distribution of rays, 218 nodes could be inverted. Most of these feature have good misfit levels, however some present  relatively high misfit value (because of noisy stations, or lower ray coverage near the edge of the model) therefore we impose a threshold above which results are not accepted.

The choice of this value, which for our application corresponds to 0.0025, was made by looking at the distribution of misfit, sorted by value. We choose a cut-off when there was a sharp increase in the absolute misfit compared to a large group of near-median values; this operation discards about 16% of the nodes. At these as well as at unresolved nodes surrounded by newly resolved results we employed an interpolation scheme based on the surrounding nodes and weighted by inverse-squared-distance. At nodes outside the resolved area we kept the starting parameters.

As a result of the inversion procedure, the selected model is represented through several maps and cross-sections. The maps (Figs. 8–10) provide point-wise information on the interface depths and velocity conditions. The cross-sections (Figs. 12–16) run across the Alps and are constructed from the values obtained at each node which are projected onto the transects; these are marked with points colored according to their newly constrained, interpolated or initial-value status. Between points and for each layer (upper crust, lower crust), velocity values are interpolated from the nearest neighbouring nodes; this layerwise procedure ensures that an intra-crustal discontinuity can be properly represented. The mantle is plotted at a constant velocity, at the value used in the inversion. Topography was part of the inversion but is only shown schematically above the results, and colored according to the tectonic plate. Finally, along all selected profiles, we also show Vs cross-sections obtained by 3-D ambient-noise tomography by Lu et al. (2018). This comparison is highly interesting as the two methods operate with mostly orthogonally propagating rays: RF with sub-vertical and ANT with mostly horizontal direction. For one of the profiles, two geological cross-sections are also presented for reference and comparison.

Fig. 8
figure 8

Depth of discontinuity results for the Conrad (a) and Moho (b). Colored points without an edge are the direct results from the inversion, blue edge represents interpolated value at unresolved nodes, green edge represents interpolated value following misfit-based quality control. Filled grey area shows the Alpine arc above its smoothed 800 m elevation line, whereas the filled cyan area represents the geological Ivrea Verbano Zone (IVZ). Thin double lines indicate the plate boundaries; red dashed line denotes the study area. The color scale spans the range of permitted depth values for each discontinuity during the inversion

Full size image

5 Discussion of the results

5.1 Discontinuities

As RFs are classically used to recover the depth of sharp discontinuities, one can expect that the crustal structure with the Moho and Conrad interface depths are the most reliable features that may result from this inversion (Fig. 8a and b). The Moho map (Fig. 8b) very clearly shows the deepening of the European crust-mantle limit towards the S-SE, until the plate boundary with Adria. Depths exceeding 40 km characterize the Alpine orogen itself, while the maximum depth reaches 60 km, representing the root of the mountain belt. On the Adria side, the Moho depth varies along plate boundary from very shallow near the Ivrea-Verbano zone to deeper going eastwards and reaching similar depths as Europe at the eastern border of the area resolved here. In the northern part of the map, Moho depth values get to as shallow as 25 km depth, representing the northern European foreland.

These features mimic past geophysical results, e.g. of Spada et al. (2013), yet local variations with respect to that (our starting model) can be seen in Supplementary Information 6. These show that our 3-D approach suggests locally deeper values than that of Spada et al. (2013), yet the order of differences is similar or slightly larger than the uncertainty of their map (± 3, ± 6 and ± 10 km for different quality RFs and similar values in their final map).

Looking at the intra-crustal discontinuity depth (Fig. 8a), we observe that it roughly follows the pattern of Moho depth, with up to 35 km depth in the Alps and even 45 km close to the plate boundary on the European side. Outside the Alpine arc, most of the values are in the 15–25 km depth range. This means that orogenic thickening essentially happens by increasing upper crustal thickness, and that the lower crust should more or less retain its thickness during orogeny. A cross-sectional example is presented in Sect. 5.3.

5.2 Velocities

The two other, directly inverted parameters for the Central Alps have been the average Vp/Vs of the crust (Fig. 9a), and the Vp change across the Conrad discontinuity \(\Delta vPc\) (Fig. 9b). There is somewhat more point-wise scatter compared to crustal-scale maps shown in Figs. 7 and 8. From these maps, we observe a clear trend, with lower (1.60–1.70) Vp/Vs values in the foreland and northern part, and higher values (1.80–1.90) inside the Alpine orogen. Lombardi et al. (2008) has also pointed at higher Vp/Vs values in the central arc of the Alps (see SI 4–5).

Fig. 9
figure 9

a Final Vp/Vs map for the entire crust (a) and final map (b) of P-wave velocity jump across the Conrad discontinuity (\(\Delta vPc\)). Colored points without an edge are the direct results from the inversion, black edge represents interpolated value at unresolved nodes, blue a and red b edge represents interpolated value following misfit-based quality control. Filled grey area shows the Alpine arc above its smoothed 800 m elevation line, whereas the filled cyan area represents the geological Ivrea Verbano Zone (IVZ). Thin double lines indicate the plate boundaries; red dashed line denotes the study area. The color scale spans the range of permitted values for Vp/Vs c and \(\Delta vPc\) d during the inversion

Full size image

The map of the velocity changes across the intra-crustal discontinuity (Fig. 9b) suggests higher values (> 0.7 km/s) both inside and outside the Alpine arc, with locally small, null and even negative values (decrease of Vp with depth). This would be an advance on earlier RF studies, which have not found a clear Conrad discontinuity, and would echo active seismic survey results which did image a more reflective lower crust with respect to the upper crust. In this regard, we have to stated that the concept of Conrad discontinuity is a specific issue that has a finding in the scientific literature with particular reference to the Alps (and Himalaya) orogen. Unlike the Moho interface, which has a distinct meaning as a change in rock chemistry, the Conrad (e.g. Litak and Brown 1989) is not always easily identifiable and followed with continuity.

However, we remain rather cautious because of the way \(\Delta vPc\) was implemented (symmetrically shifted Vs values above and below the interface, with a fixed middle point as in the initial Vp model). Moreover, in the generic formulation, our method allows to handle a global Vp/Vs value for each layer. For the specific Alpine case, we reduce the number of parameters to invert for and, if there is a Vp jump at the Conrad, there will also be a Vs jump in our inversion. A more flexible implementation as well as layer-wise Vp/Vs could provide more realistic results.

From these important parameters obtained with the newly developed methodology, one can represent the 3-D velocity structure of the crust in map view (Fig. 10). Receiver functions are more sensitive to relative velocity variations rather than to absolute S-waves velocities, moreover these values have been derived from a fixed Vp model and varying Vp/Vs as well as \(\Delta vPc\), therefore the maps from the inversion results are not necessarily simple to interpret. At the surface (Fig. 10a), Vs exhibits lower values (2.8–3.0 km/s) in the Alpine arc with respect to the European plate (3.0–3.2 km/s) without thickening. Figure 10b and c which represent shear-wave velocity maps above and below Conrad respectively, are both complex to read, since there is more local variability. The only feature that is clearly detected is that high velocities (> 4.2 km/s) are found in the European plate very close to the Europe-Adria plate boundary and that these values extend along and beneath the Alpine arc, more on the Vs map below the Conrad. This trend of higher velocities is confirmed and is much more pronounced on the map of Vs above the Moho discontinuity (Fig. 10d), where high velocities are found beneath the Alps (4.3–4.5 km/s), while lower velocities (3.6–3.8 km/s) are present in the northern part. This may represent the petrological changes of lower crustal material due to increasing pressure and temperature (metamorphism).

Fig. 10
figure 10

Final shear-wave velocity map at each interface: a Vs below the surface; b Vs above the Conrad; c Vs below the Conrad; d Vs above the Moho. Colored points without an edge are the direct results from the inversion, black edge represents interpolated value at unresolved nodes, red edge represents interpolated value following misfit-based quality control. The color scale is common to all four maps; other features are as in Fig. 8 and Fig. 9

Full size image

5.3 Cross-orogen profiles

The obtained 3-D structural results are presented here in the form of several cross-section and compared to previous investigations, mainly Vs profiles from ambient noise tomography as provided by Lu et al. (2018). The profiles’ locations are shown in Fig. 11.

Fig. 11
figure 11

Map of selected cross-sections shown in this work. Red box is the study area, filled light grey area shows the Alpine arc’s smoothed 800 m altitude line. Dashed red, blue and green lines represent the boundary of Europe, Adria and Liguria plates, from the model of Spada et al. (2013). Thin black dashed lines represent the contours of the country borders

Full size image

The labels of the shown sections are: AA’: ECORS – CROP, BB’: Jura mountains – Po plain, CC’: NFP-20 West, DD’: Vosges – West Po basin, EE’: Basel – Chiasso, FF’: European GeoTraverse, GG’: TRANSALP.

Profile A-A’ (Fig. 12) runs along the former ECORS-CROP project (e.g., Finetti 2005; Nicolas et al. 1990; Thouvenot et al. 1990) line across the Western Alps. The three newly constrained nodes point at a local high in the Moho topography, which resembles the step imaged by ANT. This could either be inherited structure or a result of collisional deformation. Beyond that, velocity variations appear reasonable and structurally similar to those retrieved by ANT, except for the low-velocity sediments of the Po plain at the eastern and of the profile.

Fig. 12
figure 12

Vs cross-sections along profile A-A’ (ECORS-CROP: Lon 5.0°, Lat 46.5°; Lon 8.5°, Lat 44.58°) with vertical exaggeration of 2:1. a Results obtained in this study: background velocities represent the result of the inversion, where dots show the projection of the model nodes. Green points are directly and well-resolved, grey points are not resolved directly. Red solid line represents the topography over the European plate, blue solid line the topography over the Adriatic plate, black solid vertical line the plate boundary between the two plates. b Vs cross-section obtained by ambient noise tomography by Lu et al. (2018)

Full size image

Profile B-B’ runs from W-NW to E-SE between the Jura mountains and the Po plain (Fig. 13). Seven nodes are newly constrained, covering the European plate and the plate boundary to Adria, one point has been discarded due to high misfit but fits the general structural picture. The deepening of the European plate is clearly visible and mimics the ANT results, the same as the significantly thinner crust on the Adriatic side of the plate boundary. The Po plain sediments are well imaged in the ANT results but do not show up in the 3-D RF Vs inversion results. These sediments are much lower velocity than the upper crust and cannot be fitted with a linear velocity gradient. Horizontal velocity variations within the European upper crust are likely not all real (e.g. node et 130 km distance), yet the Moho and Conrad boundaries are more suitably imaged to calculate RFs than in the ANT results.

Fig. 13
figure 13

Vs cross-sections along profile B-B’ (Jura mountains – Po plain: Lon 5.8°, Lat 46.7°; Lon 10.5°, Lat 45.15°) with vertical exaggeration of 2:1. a Results obtained in this study: background velocities represent the result of the inversion, where dots show the projection of the model nodes. Green points are directly and well-resolved, red points are poorly-resolved and therefore interpolated (for these two, the size of the circle is proportional to the absolute misfit), grey points are not resolved directly. Red solid line represents the topography over the European plate, blue solid line the topography over the Adriatic plate, black solid vertical line the plate boundary between the two plates. b Vs cross-section obtained by ambient noise tomography by Lu et al. (2018)

Full size image

Figure 14 shows the results along the NW–SE-oriented NFP-20 West profile that has been investigated in the past (e.g. Kissling et al. 2006; Pfiffner et al. 1997; Schmid et al. 2017). Six newly constrained nodes and one discarded but fitting node results from our converted-wave tomography model. These are all on the European plate, and image the thickening of the crust more smoothly than in the ANT results. The major step in Moho depth that corresponds to the Europe–Adria plate boundary is from the initial model on the Adriatic side, and corresponds to the Ivrea Geophysical Body (IGB), with its shallow-lying high-velocity anomaly. After that point, the Adriatic Moho depth gently increases to the South East. While this feature is well resolved both by our and the ANT results, the plate boundary and IGB zone (Scarponi et al. 2020, 2021), at ca. 200–300 km distance, is better resolved using our sub-vertical rays, and it appears less clearly and shifted or smeared to the SE in the Lu et al. (2018) model together with too-deep reaching low-velocities. When comparing our results with two geological transects (Schmid et al. 2017 in Fig. 14c and Escher et al., 1997 in Fig. 14d), we can observe a good match not only in crustal thickening, but also, more interestingly, in lower crustal thickness: this remains fairly constant all along the European plate, and is only resolved by 3-D RF Vs inversion, not by ANT. Horizontal Vs variation within the crust appears locally too important, as in the previous profile.

Fig. 14
figure 14

Comparison of two Vs results in cross-section view with geological results along closely located profiles, the NFP-20 West (Lon 6.25°, Lat 47.0°; Lon 10.0°, Lat 44.0°). a and b are Vs cross-sections obtained in this study and respectively from ambient noise tomography by Lu et al. (2018), presented as in Fig. 10, green topographic line represents the Liguria plate. Red dashed boxes show the location of the NFP 20-West profile. c NFP 20-West geological cross-section by Schmid et al. (2017). d The parallel but slightly offset geological profile by Escher et al. (1997) through the Western Swiss-Italian Alps from the Mont Tendre (Jura) in the NW to the Val Sesia in the SE. Note that the two geological profiles are not exaggerated vertically, and cover a shorter length than the seismic cross-section

Full size image

Profile D-D’ (Fig. 15 a-b) crosses and touches the two previous profiles, and runs from N-NW to S-SE between the Vosges mountains and the western Po Plain, with seven newly constrained nodes and one with higher misfit. The Moho itself is more sharply resolved in 3-D RF inversion, not only by definition but also compared to some of the more poorly defined parts in ANT results. A steeper deepening at 180 km distance in the European plate looks suspicious but is also present in the ANT results. The Europe–Adria plate boundary is also more sharply resolved in our results compared to ANT. Finally, there are no important horizontal Vs variations within the crust. Interestingly, at the deepest portion of the European crust (250 km distance), the velocity is a smooth gradient all across the crust and its root, without any sharp change.

Fig. 15
figure 15

a-b Vs cross-sections along profile D-D’ (Vosges – West Po: Lon 6.5°, Lat 48.0°; Lon 8.85°, Lat 45.0°); c-d Vs cross-sections along profile F-F’ (European GeoTraverse: Lon 9.30°, Lat 48.5°; Lon 9.30°, Lat 44°) and e–f Vs cross-sections along profile G-G’ (TRANSALP: Lon 11.6°, Lat 48.2°; Lon 11.6°, Lat 45.6°) presented as in Fig. 13

Full size image

Profile F-F’ (Fig. 15 c-d) crosses the Alps straight in N-S direction at the longitude of the former European GeoTraverse (Blundell et al. 1992), with 6 newly constrained nodes and further two less well-constrained. Most of these are on the European plate and image a smooth and then a bit more steepening to the south, similarly to ANT results. The Moho depth step across the plate boundary is clear and exceeds 20 km, while it is imaged in a rather smooth and continuous way by Lu et al. (2018). Here too, the low Vs sediments in the Po plain are not imaged by our results. Horizontal Vs variations are relatively smooth.

Profile G-G’ runs along the former TRANSALP line, in a N-S direction across the eastern domain of our study area (Fig. 15 d-e). While only 3 newly constrained nodes contribute to this image, the comparison is worth ANT and with TRANSALP project results (Castellarin et al. 1992; Kummerow et al 2004; Lippitsch et al 2003; Lüschen et al 2004; TRANSALP WG. 2002). Our 3-D RF results are directly compared with the 2D RF migration and interpretation of Kummerow et al. (2004) (Fig. 15d). Two main differences are visible. First, compared to the 10–15 km Moho step between the two plates seen by TRANSALP, our results show comparable Moho depths on the two sides, with slightly deeper structures on the European side. This is mainly due to the thicker crust imaged on the Adriatic side. Second, within the European plate at ca. 90 km distance, a sharper deepening is revealed in our results. This may look suspicious, but the ANT results also image a rather steeply descending Moho there and provide independent constraints on the European plate structure. The ANT results on the Adriatic side are too smooth to pick a Moho discontinuity, which echoes the results of previous investigations (Finetti 2005). Here too there are some horizontal Vs variations, which could be explained by the presence of a continuous vertical Vs gradient at the deepest part (ca. 55 km depth) of the orogenic root, as in profile D-D’.

Two further cross-sections are presented in the supplement, but provide only partial updates compared to the initial model.

Finally, profile E-E’ (Fig. 16) between Basel and Chiasso, parallel to but slightly to the East of profile D-D’, features 5 newly constrained nodes on the European side. The structure of this plate appears more variable than seen in ANT, and the deepening towards the orogen steeper. There is no Moho depth jump across the plate boundary, as in ANT, as this profile is east of the termination of the IGB. Horizontal Vs variations are smooth but miss imaging the sedimentary basin.

Fig. 16
figure 16

Vs cross-sections along profile E-E’ (Basel – Chiasso: Lon 7.23°, Lat 48.0°; Lon 10.39°, Lat 44.0°) presented as in Fig. 12, green topographic line represents the Liguria plate

Full size image

5.4 Lower crustal earthquakes related to inheritance?

One particular feature of the European plate in and near northern Alpine foreland is the occurrence of lower crustal earthquakes (e.g. Deichmann 1992) that have been recently re-assessed in Singer et al. (2014). We focus on this area in Fig. 17 and report the node-wise average crustal Vp/Vs results together with these seismic events. While the majority of the Alpine arc shows relatively high Vp/Vs values, this zone of the European foreland has a contiguous area with consistently lower Vp/Vs ratios below 1.70. By drawing lateral limits to the Vp/Vs ≤ 1.70 zone, it turns out that about 95% of the lower crustal earthquakes are located within those bounds, and they do not seem to align along well definable faults or fault zones. The western bound of this area is roughly along the Bern-Biel-Porrentruy-Belfort line; this is further NE than the shallow-lying and seismically active Fribourg Lineament (Vouillamoz et al. 2017).

Fig. 17
figure 17

Average crustal Vp/Vs map after interpolation of not resolved and poor quality nodes (extracted from Fig. 7c) together with lower crustal seismicity (yellow circles) in the northern Central Alpine region as reported by Singer et al. (2014). The size of the yellow circles is proportional to the magnitude of the event. Black squares show the location of the main cities in the study area, grey solid lines are national borders, while two magenta dashed line segments delimit the Vp/Vs ≤ 1.70 sector in the Alp’s northern foreland. See text for interpretation

Full size image

The eastern bound starts on the oriental side of Lindau, crosses NE of Ravensburg, and has a projected end between Albstadt and Tübingen. There is no primary geological boundary at the surface, according to the Geological Map of Switzerland (1:500,000 scale, published by the Swiss Federal Office of Topography). On the other hand, the nature of the lower crust is not well known, and it can be that this segment of the European plate with lower crustal earthquakes and relatively low Vp/Vs values is inherited. Several possibilities of inheritance can be invoked, such as composition that is related to Vp/Vs, permeability that is related to fluid flow and earthquakes, and others, but due to the lack of palpable evidence, only hypotheses can be emitted here. In general, inherited structures can play a key role in controlling strain localization on a local scale, during early stages of rifting (Piqué and Laville 1996; Tommasi and Vauchez 2001) and also in orogeny as reactivated structures. If the inheritance is compositional, even the lower crust should be of intermediate composition as it is difficult to balance a density sorted, mafic lower crust with Vp/Vs > 1.75 (e.g. Barton 1986; Christensen 1996; Zandt and Ammon 1995) to average crustal Vp/Vs of 1.70 or less. If the composition is different, that can affect other properties such as the thermal state or local stresses, but none of these can be ascertained here without deeper investigations into the history of Alpine and pre-Alpine evolution.

5.5 Limitations

Facing the complexity of the inverse problem, we have made several simplifications for the first application of this method, and here we discuss related limitations.

Regarding data processing and forward models, we rely on only two external scripts. One is TTBOX that satisfies our needs. The other is the synthetic RF calculator that uses frequency-domain deconvolution, while our data is processed using iterative time-domain deconvolution. This latter is much better adapted for crustal-scale investigations as it carries on less noise, while frequency-domain deconvolution is much more rapid for synthetics while not suffering from noise. In that sense, we feel confident of our choices but there can be slight discrepancies between small artifacts generated by the deconvolutions. The level of waveform fit (Supplementary Material 2) shows very similar wave shapes in general.

The major limitation in our implementation for the Central Alps was the reduction of the number of parameters to resolve from 10 to 4. This way, the Vs change across the Conrad discontinuity was flexible in amplitude only (to which RFs are more sensitive), not in absolute value. The use of locally vertically-averaged (but spatially variable) Vp/Vs for the entire crust was a limitation, and the inversions would benefit from layer-wise values: this would also lead to closer comparison with geological information and composition of these layers. Finally, at the cost of further increase in the number of parameters to invert, each Vs value could be taken independently (see Table S1), although with some reasonable constraints with respect to Vp, within given Vp/Vs bounds. Nevertheless, these have been limitations due to the implementation, and not the methodology itself.

For the Central Alps application, two major points emerged that could be improved in the future. One is to include the possibility of a third layer, in order to image sedimentary basins. This also brings the requirement to employ higher frequency RFs to resolve those structures with vertically propagating rays, and that choice may add more noise. Finally, several cross-sections featured horizontal Vs variations that seemed to be more rapid than reasonably imaginable. This point should be tested whether these remain when more than 4 inverted parameters per node are used.

Two major developments remain in terms of methodology. One is the simultaneous inversion of all nodes, eliminating the need for the spatial separation described in sub-Sect. 3.1.2. The other is the development of an uncertainty estimate of the obtained results: while here we obtain convergence throughout 3 rounds and a total of 7000 iterations per node, a quantitative assessment could be developed in future work.

6 Conclusions

In the first part of this work, we have presented a newly developed inversion procedure that yields a fully 3-D velocity and structural model of the crust based on receiver functions, and in the second part we have implemented it, with some adaptations, to the Central Alps, an area characterized by complex tectonics and a dense seismic network.

Among the methodological developments, one key pillar of this research was the definition of a new model parametrization, which allows including sharp discontinuities as well as discontinuities of variable depth during the inversion. This comes with an additional computational cost (although our procedure, from a computational point of view, proved to be more efficient than other tomographic methods, as e.g. Lu et al. 2020), but the two features combined overcome the long-standing inherent limitations of classical tomography approaches. Another key element was the accurate P-to-S converted ray propagator that links sources with receivers and respects Snell’s law in 3-D both across discontinuities and across areas characterized by velocity gradients at any geometry. The requirement for this new inversion method to image the crust in 3-D is the characteristic seismological station spacing at the surface, which should be comparable to the expected Moho depth.

In the Central Alps’ context, station density was ensured thanks to the AlpArray Seismic Network, which has provided a wealth of high-quality data to image this area with three different plates and dipping Moho areas. The implementation of our new method to this zone required some simplifications, so that the final results at each node are given by Moho depth, Conrad depth, average crustal Vp/Vs, as well as Vp change across the Conrad. The inversion at each node followed a stochastic procedure, combining simulated annealing and a pattern search algorithm while minimizing misfit between observed and synthetic receiver functions. The 3-D inversion results show that crustal thickness reflects well the roots of the Alpine orogen, and its jump between the European and Adriatic plates, including the Ivrea Geophysical Body. Average crustal Vp/Vs ratios are relatively higher beneath the orogen, while a low Vp/Vs area in the European foreland correlates with lower crustal earthquakes, which we interpret as mechanical differences in rock properties, most likely inherited.