1 Introduction

Between February 16 and April 5, 2019, an earthquake sequence took place in Somogy county, Hungary. During this 7 weeks, 9 earthquakes were recorded around the village of Somogyszob. The mainshock occurred on March 7 with a local magnitude \(M_L=4.0\) and epicentral intensity of 5 on the European Macroseismic Scale (EMS). It was preceded by 4 foreshocks with \(1.6 \le M_L \le 2.6\), and followed by 4 aftershocks with \(1.3 \le M_L \le 2.3\). The largest foreshock (\(M_L=2.6\)) was also felt in the epicentral region. Its macroseismic intensity was as large as 4 EMS.

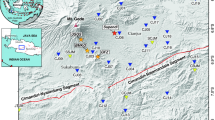
Seismic activity in Hungary can be characterized as moderate. The seismicity pattern shows that earthquakes mainly occur in the upper part of the crust and, due to the general weakness of the lithosphere beneath the Pannonian basin, the epicenters are distributed all around the country (Fig. 1). However, there are certain areas where seismicity is higher and where significant, destructive earthquakes with magnitude \(M>~5\) occurred in the last centuries (Zsíros 2000; Bondár et al. 2018).

Fig. 1
figure 1

Seismicity of Hungary and its surroundings for the period of 1900–2017 (gray dots) after Zsíros (2000) and Bondár et al. (2018). Only earthquakes with magnitude 3 or greater are shown. The local and regional seismic stations that were operational at the time of the Somogyszob earthquake (star) are also indicated (triangles: Hungarian National Seismological Network (HNSN) permanent stations, inverted triangles: permanent stations outside Hungary, circles: AlpArray Seismic Network (AASN) temporary stations). The region encircled by black rectangle is enlarged in Fig. 2. (Color figure online)

Full size image
Fig. 2
figure 2

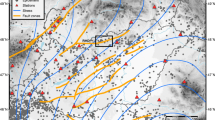
The epicentral region of the Somogyszob earthquake sequence (star) with the surrounding seismic stations. For location, see Fig. 1. Station codes and epicenters of earlier \(M \ge 4\) events (diamonds) are also indicated. Temporary stations BELGA and DARVA (squares) were operated after the mainshock to better record the aftershocks. For other symbols, see the caption of Fig. 1. (Color figure online)

Full size image

Somogy county does not belong to the most seismically active areas in Hungary. Although the Hungarian Earthquake Catalog (Zsíros 2000) contains events since 456 AD, there are only 15 known events with magnitude \(M \ge 3\) within 30 km vicinity of the Somogyszob mainshock. The first known earthquake in the region occurred in 1875 and the most significant one happened in 1925 near Nagykanizsa with a magnitude of 4.2. Besides this event, three more ones with \(M>4\) occurred before 2019 (Nagyatád, 1875, \(M=4.1\); Surd, 1876, \(M=4.1\); Répás, 1998, \(M=4.1\), Fig. 2). These numbers illustrate that the 2019 Somogyszob earthquake sequence studied in this paper represents uncommon seismic activity in the Somogy region.

In 2015, the Kövesligethy Radó Seismological Observatory (KRSO) joined the international AlpArray project (http://www.alparray.ethz.ch). AlpArray is a European collaborative project with involvement of some 55 institutes from 17 countries (Hetényi et al. 2018). The objective of the project is to study the lithospheric structure and geodynamics of the greater Alpine region using mainly seismological methods. Up to this date, the AlpArray Seismic Network (AASN) is one of the largest passive seismic experiment in Europe. Officially, it was operated between January 1, 2016 and March 31, 2019. At the time of the investigated Somogyszob earthquake sequence, the KRSO operated 14 temporary broadband AlpArray stations in Hungary (Fig. 1), in addition to the Hungarian National Seismological Network (HNSN) of 15 permanent broadband stations (Gráczer et al. 2018). Therefore, the 2019 Somogyszob earthquake sequence is the first remarkable one in the region that was recorded by a significant number of high-quality broadband digital seismographs, providing a good opportunity to study earthquake sources in an area where we have little knowledge about fault parameters and small-scale tectonic structure.

In this paper we analyze all available seismic data for the 2019 Somogyszob earthquake sequence. After a brief review of the data sources used in this study, we determine the hypocenter locations of the events applying a multiple-event location algorithm. Then we estimate their scalar moments, source radii and static stress drops from spectral analysis and determine the source mechanisms (moment tensors) of the three largest events using probabilistic waveform inversion methods. Reliable knowledge of earthquake source properties helps us to better understand the present-day geodynamic processes in the source area. The presented research also gives us an opportunity to show that our recently developed waveform inversion methods (Wéber 2006, 2018) are suitable to estimate the source mechanism for low-magnitude local earthquakes.

2 Waveform data

At the time of the Somogyszob earthquake sequence, the HNSN operated by the KRSO comprised 15 permanent broad-band stations. Moreover, we had access to waveforms recorded by the temporary broadband AASN (Hetényi et al. 2018; Gráczer et al. 2018, Figs. 1, 2).

After the mainshock, on March 8, 2019, two temporary stations (BELGA and DARVA, Fig. 2) were also operated by the KRSO in order to better record the aftershocks. The BELGA station was equipped with a Lennartz 3D seismometer with natural period of 5 s, whereas the DARVA station with a Guralp CMG-3ESPCDE seismometer with natural period of 60 s. Waveform data were also available from the neighboring countries and international agencies.

3 Event location

The mainshock was well recorded on all seismic stations in Hungary, as well as in the neighboring countries. The nearest recording station was about 17 km from the epicenter. Due to the high station density around the epicentral region (Fig. 2), the foreshocks and aftershocks were also detected by several stations in the country. P-wave and S-wave arrival times were manually picked from the observed three-component data.

Routine event processing at the KRSO uses the SeisComp3 software, where the default locator is LocSat (Bratt and Bache 1988). For the published Hungarian National Seismological Bulletin (HNSB), the magnitudes and locations are recalculated with the iLoc location algorithm (Bondár and Storchak 2011) using the three-dimensional (3D) Regional Seismic Travel Time (RSTT) velocity model (Myers et al. 2010) since 2014 (Bondár et al. 2018).

The iLoc is a single-event location algorithm that applies a priori estimation of the full data covariance matrix to take correlated travel time prediction errors due to unmodeled structures into account (Bondár and McLaughlin 2009). Ignoring these errors leads to underestimation of the uncertainties in determining hypocenter parameters (error-ellipse) and may result in systematic location bias. It has been shown earlier that iLoc gives significantly improved locations (Bondár and Storchak 2011; Bondár et al. 2018; Czecze and Bondár 2019). The locations can be further improved by multiple-event location methods that simultaneously locate an entire event cluster. The main assumption in most multiple-event algorithms is that the distance between two connected hypocenters is small compared to the event-station distance. We use the hypoDD Double-Difference Algorithm (Waldhauser 2001; Waldhauser and Ellsworth 2000) that can combine absolute arrival time picks and differential times from waveform cross-correlation. HypoDD is a linearized multiple-event location algorithm, therefore it requires the most accurate initial hypocenter estimates. Since the HNSB has not been published yet for 2019, we relocated the SeisComp3 locations obtained for the Somogyszob earthquake sequence with iLoc using the RSTT global 3D crust and upper mantle velocity model to provide the most accurate initial locations for hypoDD, even if hypoDD is not able to use a 3D velocity model.

After creating the initial locations by iLoc, we obtained the P and S differential times between event pairs by waveform cross-correlation at each station. We used the predicted first-arriving P and S travel times from a local velocity model (Gráczer and Wéber 2012) to determine the start time and the length of the windows for the cross-correlation computation. The differential time is the lag between the two waveforms that maximizes the correlation function. The similarity between two events is quantified by the correlation coefficient. We only kept differential times with correlations above 0.6 and we manually removed the noise correlations at every station.

One of the implicit requirements for successful multiple-event locations is that the cluster should be well-connected, that is each event be recorded by many stations and each station record many events. To satisfy this requirement we analyzed the data and created a network of connected event pairs and removed the outliers. Altogether, we collected 297 P and 174 S arrival times, and 166 P and 133 S differential times, producing 290 P-phase pairs and 316 S-phase pairs.

In the hypoDD analysis we solved the equations with Singular Value Decomposition (SVD). We used every available data within a radius of 400 km around the epicenter. The a priori weights of the differential times were their correlation coefficients, while in the case of the absolute travel times it was dependent on the phase (1.0 for P and 0.5 for S phases). In the first two sets of iterations, the phase picks were given more weight, and the differential times were down-weighted. In the remaining set of iterations, the weights were reversed and the differential times dominated. As hypoDD uses a 1D velocity model, we applied the 1D local velocity model of Gráczer and Wéber (2012). After nearly 30 iterations we obtained convergent solutions.

Table 1 Hypocentral parameters obtained from the hypoDD relocations of the events
Full size table

Figure 3 depicts the epicentral distribution of the Somogyszob earthquakes as initially located by the iLoc single-event locator and as determined by the hypoDD multiple-event location algorithm (Table 1). Note that there are 9 events in the cluster and the hypoDD determined only 8 events (due to the dynamic re-weighting schemes, Event 7 in Table 1 lost the connection during the iterations because of large residuals.) The initial iLoc epicenters show relatively high scatter with an apparent linear trend. The final hypoDD solutions, on the other hand, are confined to a small region and their distribution does not show any particular trend. Table 1 shows that all events occurred at around 13–14 km depth.

Fig. 3
figure 3

Epicentral distribution of the investigated events. Green triangles represent the iLoc single-event initial locations using the RSTT 3D velocity model. Red circles represent the hypoDD multiple-event solutions using differential times and catalog data with the Gráczer velocity model (Gráczer and Wéber 2012). Star denotes the mainshock (green: iLoc; red: hypoDD). The iLoc–hypoDD epicenter pairs are connected by gray lines. (Color figure online)

Full size image

4 Static source parameters

In order to estimate the static source parameters of the investigated earthquakes, we analyzed the displacement spectra of P- and S-wave seismograms with respect to the standard \(\omega ^2\) model of Brune (Brune 1970). We followed the methodology described in Süle and Wéber (2013). We analyzed the vertical component seismograms for P-waves and transverse component seismograms for S-waves separately.

After base-line correction, tapering and instrumental correction, the displacement amplitude spectrum U(f, R) at a hypocentral distance R can be described as

$$\begin{aligned} U(f,R) = G(R) \cdot \exp \left( -\frac{\pi f t}{Q(f)} \right) \cdot \exp (-\pi f \kappa ) \cdot \frac{A_0}{1+ \left( \frac{f}{f_c}\right) ^2} \end{aligned}$$
(1)

where f is the frequency, t is the travel time, and G(R) is the attenuation due to geometrical spreading. The second term in the right-hand side of the equation is the effect of path-dependent attenuation with frequency-dependent quality factor Q(f), the third therm is the near-surface attenuation characterized by the \(\kappa\) parameter (Singh et al. 1982), whereas the fourth term is the source spectrum with low-frequency spectral level \(A_0\) and corner frequency \(f_c\) (Brune 1970; Hanks and Wyss 1972). In this research we used the average attenuation models of \(Q_{P}(f)=154f^{0.92}\) and \(Q_{S}(f)=77f^{0.92}\) for P- and S-waves, respectively (Kiszely 2000; Süle and Wéber 2013). In a previous study, Süle and Wéber (2013) thoroughly investigated the near-surface attenuation by analyzing seismograms of low-magnitude events recorded at short hypocentral distances to estimate the average \(\kappa\) values for Hungary. Here we applied their average values of \(\kappa ^P=0.03\) and \(\kappa ^S=0.04\) for P- and S-waves, respectively.

After obtaining the best-fitting spectral parameters \(A_0\) and \(f_c\) by applying a grid search algorithm (Süle and Wéber 2013), we first calculated the scalar seismic moment \(M_0\) for each event-station pair. Then, for each event, we computed the average values and the multiplicative error factors for \(M_0\) and \(f_c\) following the equations proposed by Archuleta et al. (1982):

$$\begin{aligned}&{\overline{x}} = \mathrm {alog} \left( \frac{1}{N} \sum _{i=1}^{N} \log x_i \right) \end{aligned}$$
(2)
$$\begin{aligned}&\mathrm {StDev} [\log {\overline{x}}] = \left( \frac{1}{N-1} \sum _{i=1}^{N} (\log x_i - \log {\overline{x}})^2\right) ^{1/2} \end{aligned}$$
(3)
$$\begin{aligned}&E {\overline{x}} = \mathrm {alog} (\mathrm {StDev} [\log {\overline{x}}]) \end{aligned}$$
(4)

where x stands for \(M_0^{P,S}\) or \(f_c^{P,S}\), \({\overline{x}}\) denotes the mean of x, N is the number of the stations used, \(\mathrm {StDev}[.]\) is the standard deviation of the argument, and \(E {\overline{x}}\) is the multiplicative error factor for \({\overline{x}}\). Source parameters like source radius r, moment magnitude \(M_w\) and static stress drop \(\varDelta \sigma\) were calculated from the average values of \(M_0\) and \(f_c\) considering P- and S-wave data separately.

Tables 2 and 3 summarize all of the obtained average source parameters and multiplicative error factors. For two low-magnitude aftershocks (Events 6 and 7) the spectral analysis was unsuccessful due to the low SNR. In three cases (Events 1, 2 and 8, \(M_w<2.0\)) we were unable to determine \(f_c^P\) because the SNR for the P-wave was too low and/or the sampling rate was not sufficient to reliably estimate the high P corner frequency.

For the mainshock, we obtained moment magnitudes of \(M_w^P=3.7\) and \(M_w^S=3.8\). The retrieved corner frequencies are \(f_c^P=3.53\) Hz and \(f_c^S=3.07\) Hz, the source radii are \(r^P=509\) m and \(r^S=400\) m, and the static stress drops are \(\varDelta \sigma ^P=1.19\times 10^6\) Pa and \(\varDelta \sigma ^S=4.00\times 10^6\) Pa. As expected, \(f_c^P\) is larger than \(f_c^S\) for each event. Seismic moments and source radii estimated from P- and S-waves agree well. The average ratio of both \(M_0^P/M_0^S\) and \(r_P/r_S\) is close to one. The obtained results of the spectral analysis fit well into the data set of previously published source parameters of 74 earthquakes occurred in Hungary (Süle and Wéber 2013; Wéber and Süle 2014).

Table 2 Spectral seismic moments and moment magnitudes
Full size table
Table 3 Spectral source parameters
Full size table

5 Source mechanism

In this section we estimate the source mechanism for the three largest events of the Somogyszob earthquake sequence: the \(M_L=4.0\) mainshock, the \(M_L=2.6\) foreshock, and the \(M_L=2.3\) aftershock (Table 1). We first briefly summarize the inversion methods applied in this study. Then we analyze the selected events and discuss the obtained source mechanisms in detail.

5.1 Method

To determine the seismic moment tensor for the selected earthquakes, we applied the Monte Carlo Moment Tensor (MCMT) inversion method (Wéber 2006, 2009). It has already been successfully applied for studying the source mechanism of both local and near-regional events in the Pannonian basin (Wéber and Süle 2014; Wéber 2016a, b). Here we provide a brief description of the method.

We describe a general seismic point source by a moment tensor (MT) and a source time function (STF). If the STF is known or assumed to be known, the MT is calculated by deconvolving the Green’s functions (GFs) from the observed seismograms. For the generation of the synthetic GFs, we employed a frequency–wavenumber integration method (Wang and Herrmann 1980; Herrmann and Wang 1985; Herrmann 2013), which allows calculating the entire wavefield for horizontally layered earth structures. In this study, we used the same 1D velocity model as that used for event location.

In the MCMT inversion, we estimate the overall uncertainties of the retrieved MT using a Monte Carlo simulation technique (Rubinstein and Kroese 2008). Monte Carlo simulation determines how random variation in the input data affects the uncertainty of the output. In our problem, the simulation generates many new realizations of input data sets by randomly generating new hypocenters and waveforms according to their respective distributions. Then each generated input data set is inverted for MT (output). The distribution of the obtained set of MT solutions approximates well the posterior probability density (PPD) of the MT. In this study, we performed 10,000 Monte Carlo simulations and thus generated 10,000 MTs according to its posterior distribution. The final estimate for the best MT is given by the maximum likelihood point.

After obtaining an ensemble of MT solutions, we calculate the principal axes for each member mechanism of the ensemble. We adopt the convention of Sipkin (1993) that the P and T axes always point upwards and the principal axes form a right-handed coordinate system. Then we construct the two-dimensional histograms of the principal axes on the focal sphere and determine the confidence zones for the 50, 68, 90 and 95% confidence levels. The confidence contours of the P and T principal axes are then plotted on top of the beach ball representation of the maximum likelihood mechanism.

Additionally, each MT in the ensemble is decomposed into a double-couple (DC), a compensated linear vector dipole (CLVD), and an isotropic (ISO) component (Jost and Herrmann 1989). To assess the relative amounts of these components in a MT, we calculate their percentages as well.

When inverting for the mechanism of low-magnitude local events, the observed waveforms can be successfully modeled in 1D velocity models only at near-source stations. Unfortunately, the number of the high-quality near-station seismograms is usually not enough for successful waveform inversion. Using polarity data and waveforms together can be a remedy to this problem. In this study we apply the Joint Waveform and Polarity (JOWAPO) inversion technique (Wéber 2018) when the analyzed earthquake does not have the required number of high-quality near-station seismograms for pure waveform inversion.

The JOWAPO method is able to estimate the DC mechanism of the studied earthquake. It defines a likelihood function for both polarities and waveforms, and then performs Bayesian sampling. Bayesian sampling generates an ensemble of DC focal mechanisms whose members are distributed according to the PPD of the model parameters. Using waveforms in the inversion makes it possible to estimate the seismic scalar moment and its uncertainty as well. The method can utilize any type of first-motion data (P, SV and SH polarities) and can invert polarities without waveforms or vice versa.

For full details of the MCMT and JOWAPO inversion methods, the reader is referred to Wéber (2006, 2016a, b, 2018).

5.2 Waveform processing

To reliably estimate earthquake focal mechanisms by waveform inversion, it is necessary to use as low inversion frequency band as possible with high enough signal-to-noise ratio (SNR). So we first carefully analyzed the frequency-dependent SNR for each component of each observing seismic station in order to select the waveforms suitable for inversion, together with their optimal frequency band.

After selecting the waveforms, we converted them to displacement. Then, according to the previously selected frequency band, we applied a Butterworth band-pass filter to the displacement seismograms. The same filter was applied to the displacement GFs. Since the inversion frequency band was chosen well below the corner frequency of the events, we assumed that the STF was an impulse. Our simple 1D earth model (Gráczer and Wéber 2012) is able to model satisfactorily only the beginning of the P- and S-wave trains, so in the inversion we used first-arrival body waves only. The processed time window was chosen accordingly. The synthetic GFs were windowed in the same way as the observed seismograms. Our 1D velocity model is not able to accurately predict the arrival times of the different seismic phases, so to obtain the maximum correlation between the synthetics and the data, we applied a time shift between them before inversion. We allowed different time shifts for the P-phase and the S-phase.

5.3 Mainshock

The mainshock of the Somogyszob earthquake sequence was recorded by many stations in and outside Hungary. The inspection of the SNR of the recorded seismograms, however, revealed that those recorded at epicentral distances greater than about 100 km are too noisy for waveform inversion. At shorter distances the noise is still too large at longer (>2 s) periods and the most usable frequency band ranges between about 0.5 and 1.5 Hz with SNR \(\ge 3\). After all, we selected 14 waveforms of 6 stations to estimate the focal mechanism of the mainshock.

The obtained focal mechanism is presented in Fig. 4 and Table 4 (Event 5). The figure shows the beach ball representation of the deviatoric part of the full moment tensor solution together with the 50, 68, 90 and 95% confidence contours for the P and T principal axes. For verification purposes, P-wave polarities are also indicated on top of the beach ball. However, polarities were not used in the inversion. In addition, we also present the histograms of the DC, CLVD and ISO percentages constructed from the whole ensemble of Monte Carlo solutions (10,000 MTs in our case).

Fig. 4
figure 4

Left panel: Beach ball representation of the source mechanisms obtained for the three largest events of the Somogyszob earthquake sequence using waveform inversion. Compressional quadrants of the optimal solutions are shaded. Contours represent the 50, 68, 90 and 95% confidence zones for the P (triangle) and T (inverse triangle) principal axes. First-arrival P-wave polarities are indicated as well (solid circle: compression; open circle: dilatation; large circle: upgoing ray; small circle: downgoing ray). Equal area projection of lower hemisphere is used. Right panel: Histograms of the DC, CLVD and ISO percentages constructed from the whole ensemble of Monte Carlo solutions (10,000 MTs in our case). For Event 9 a pure DC mechanism, whereas for Event 3 a deviatoric mechanism has been determined. (Color figure online)

Full size image

Since we believe that the hypoDD epicenter estimated earlier is accurate enough for waveform inversion, in the MCMT inversion we only searched for hypocentral depth. For the mainshock, the optimum centroid depth is 11 km (Table 4). The retrieved thrust faulting mechanism is in good agreement with the available first-arrival P-wave polarities (Fig. 4). The DC component of the moment tensor is 93%. The histograms of the DC, CLVD and ISO percentages suggest that the non-DC components of the mechanism are statistically insignificant and a pure DC mechanism can characterize the mainshock. Both the P and T axes are strongly clustered around well-defined directions. The azimuth of the sub-horizontal P axis is \(214^\circ\) (Table 5). The obtained seismic moment is \(M_0=5.443 \times 10^{14}\) Nm that corresponds to moment magnitude \(M_w=3.79\) (Hanks and Kanamori 1979).

Figure 5 compares the observed seismograms and synthetic waveforms computed using the optimum focal depth and MT. Two quantities are given for each seismogram: the normalized correlation coefficient c and the variance reduction \(vr=1-\sum _ir_i^2/\sum _id_i^2\), where \({\mathbf {r}}\) and \({\mathbf {d}}\) are the residual vector and the data vector, respectively. The correlation values are mostly above 0.9 indicating that the synthetics and the data are usually highly correlated. However, the achieved vr values show that waveform amplitudes are not always modeled very well. Nevertheless, we obtained acceptable waveform matching.

Fig. 5
figure 5

Waveform comparison for the Somogyszob mainshock. The observed seismograms (grey lines) are band-pass filtered with cut-off frequencies of 0.5 and 1.5 Hz. The synthetic waveforms (black lines) are computed using the moment tensor obtained by waveform inversion. On the left-hand side of each seismogram, station code, component and phase are indicated. The numbers above the waveforms represent epicentral distance in km (d), normalized correlation (c), variance reduction (vr) and peak amplitude in nm (a). Waveforms are normalized individually. For station locations see Fig. 2

Full size image

5.4 Foreshock

On February 17, 2019 an \(M_L=2.6\) foreshock preceded the mainshock (Table 1). After carefully analyzing the spectra of the observed seismograms, it turned out that the frequency band most suitable for waveform inversion ranges between 0.7 and 2.0 Hz. After all, we selected 8 waveforms of 5 stations to estimate the focal mechanism of the event. Unfortunately, at 2 stations the first P-wave arrival was obscured by ambient noise.

The selected 8 waveforms were not enough to obtain a well-constrained full MT solution. In order to stabilize the inversion, we decreased the number of the model parameters from 6 to 5 by restricting the desired focal mechanism to a deviatoric one. The obtained deviatoric MT represents a thrust faulting mechanism with well-defined principal axes (Event 3 in Fig. 4 and Tables 4 and 5). The sub-horizontal P axis has an azimuth of \(211^\circ\), very similar to that of the mainshock. The optimum depth of the centroid is again 11 km. The mechanism has a moment magnitude \(M_w=2.58\) with 83% DC component. The solution is in agreement with the observed first-arrival P-wave polarities (not included in the inversion).

Table 4 Centroid depths and source mechanisms of the Somogyszob mainshock, a foreshock and an aftershock
Full size table
Table 5 Scalar moments and principal axes of the source mechanisms
Full size table

5.5 Aftershock

From waveform inversion point of view, the April 5, 2019 \(M_L=2.3\) aftershock was best recorded by the two temporary seismic stations BELGA and DARVA that were deployed after the mainshock to better record the aftershocks (Fig. 2). The selected 6 waveforms of 3 stations had a good SNR between 1 and 2 Hz. This data set is definitely not enough for pure waveform MT inversion. However, using the waveforms together with 9 observed P-wave polarities, the JOWAPO method made it possible to retrieve a well-defined DC thrust faulting mechanism (Event 9 in Fig. 4 and Tables 4 and 5). The azimuth of the sub-horizontal P axis is \(2^\circ\), slightly different from that of the mainshock and foreshock. The obtained seismic moment is \(M_0=1.197 \times 10^{13}\) Nm that corresponds to moment magnitude \(M_w=2.69\). The optimum depth of the event, where the synthetics fit best to the observed seismograms, is 11 km.

The estimated uncertainty of the resulting focal mechanisms largely depends on the data covariance matrix describing both data (waveform) errors and modeling errors. In this study we used a simple diagonal covariance matrix. Assuming uncorrelated noise, however, can underestimate the uncertainties of the achieved model parameters. To reduce this undesirable effect we used conservative estimates on data and modeling errors and adopted the conclusion of Zahradník and Custódio (2012) that realistic data errors have the same order of magnitude of the data itself, mostly due to inaccurate crustal models. More specifically, in this study the diagonal elements of the data covariance matrix corresponding to a given waveform were chosen to be the mean squared value of that waveform. Nevertheless, the confidence zones of the principal axes presented in Fig. 4 probably represent the lower limit of the uncertainty of the obtained mechanisms. It is especially true for the aftershock, because the JOWAPO inversion method estimates the uncertainty of the DC solution at the best fitting depth only, that is the effect of the uncertain focal depth is not taken into account.

6 Conclusions

In this paper we analyzed all available seismic data for the Somogyszob earthquake sequence in order to estimate the source parameters of the observed events.

We have estimated the hypocenters of the earthquakes using the hypoDD multiple-event location algorithm. The epicenter of the mainshock was at (17.302\(^{\circ }\) E, 46.307\(^{\circ }\) N) with an origin time of 2019-03-07 19:07:54 UTC. The foreshocks and aftershocks were confined to a small region next to the mainshock. The events occurred in a narrow depth range around 13–14 km. Thus, we can conclude that the earthquakes studied in this paper belong to a single small-scale seismogenic zone.

We have estimated the moment magnitude of the mainshock in two different ways giving \(M_w=3.79\) from waveform inversion and \(M_w=3.75\) from spectral analysis. The two estimates agree very well. For the other events whose spectral analysis was successful, moment magnitude varies between 1.7 and 2.6.

We have also estimated the spectral source parameters from displacement source spectra. The estimated source radius is about 500 m for the mainshock and varies between 67 and 212 m for the other events. The derived static stress drop spans from \(0.63\times 10^5\) to \(40.0\times 10^5\) Pa. These results fit well into the data set of previously published source parameters of 74 earthquakes occurred in Hungary (Süle and Wéber 2013; Wéber and Süle 2014). The obtained stress drop values are significantly less than 10 MPa suggested by Kanamori and Anderson (1975) for intraplate earthquakes. This observation may be attributed to the general weakness of the lithosphere beneath the inner part of the Pannonian basin.

We have successfully estimated the focal mechanism for the mainshock, a foreshock and an aftershock using our recently developed probabilistic waveform inversion techniques. The moment tensor solutions displayed in Fig. 4 reveal that the T principal axis is sub-vertical, whereas the P axis is sub-horizontal pointing towards N-NE. According to the classification scheme of Zoback (1992), all of the investigated earthquakes have thrust faulting mechanism. The amount of the resulting non-DC components are insignificant.

Bada et al. (2007) investigated the present-day stress pattern in the Pannonian basin. In the epicentral region of the Somogyszob earthquake sequence, the authors suggest an approximately NNE-SSW striking maximum horizontal stress direction. The P axes of the focal mechanisms retrieved in this study show similar orientations. Thus, our focal mechanism solutions are in good agreement with the present-day stress field derived by Bada et al. (2007). The obtained mechanisms also give further support to the hypothesis that the Pannonian basin is currently experiencing a compressional regime of deformation (Bada et al. 1999, 2001, 2007).