Abstract
The deformation pattern in active orogens is in general diffuse and distributed, and is expressed by spatially scattered seismicity and fault network. We select two relating datasets in the region encompassing Switzerland and analyse how they compare with each other. The datasets are not complete but are the best datasets currently available which fully cover the investigated area at a uniform scale. The distribution of distances from each earthquake to the nearest fault suggests that about two-thirds of the seismicity occurs near faults, yet about 10% occurs far from known faults. These numbers are stable for various selections of earthquakes and even when considering location uncertainties. Earthquake magnitudes in the catalogue are smaller than what could be expected from faults lengths. This suggests that the deep fracture pattern is more segmented than the superficial one, or mostly partial rupture during earthquakes, and (partly) the impropriety of the scaling law. Statistics on the distances from each fault to the nearest earthquake reveal that all supposedly-active faults in Switzerland have experienced a typically felt (magnitude 2.5 or larger) event, and only one out of six has not done so in the past four decades. Future applications of the presented approach to more complete or comprehensive fault databases may result in revised numbers regarding the connection between deep and superficial fracture patterns, representative of the stress regime of the region. The public and educational message: (1) in the region of Switzerland, earthquakes can happen in areas without known or mapped faults; (2) not all faults produce earthquakes within a human lifetime, but they seem to do so over long times.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and motivation
General knowledge of geoscientists holds that earthquakes occur on faults, and faults are created by brittle failure. While this can be clearly demonstrated for homogeneous media at relatively small scales, reality can be more complex due to various scales and material heterogeneities. This is especially true in an orogenic environment with a long deformation history such as the Alps. Switzerland and surrounding areas host a wealth of identified faults at surface which reflect the integrated time history of fracturing events, and a long catalogue of earthquakes which reflect the geologically most recent fracture pattern at depth. We here perform a comparison of these two datasets to analyse and quantify how much of the seismicity is related to known faults, and how much of it is relatively distant from known faults.
This analysis is relevant for several reasons.
-
1.
The central Alpine region is an area of distributed deformation, therefore—unlike in classical plate boundary settings—it is not obvious where fractures concentrate and whether the patterns at the surface and at depth correlate.
-
2.
The calculations for the current Swiss earthquake hazard model (Wiemer et al. 2016) do not include faults as seismogenic sources due to the sparse coverage and uncertain parameters in the considered databases (Wiemer et al. 2016, page 38).
-
3.
Another seismic hazard analysis project, focusing on Swiss nuclear power plant sites (project PEGASOS; Abrahamson et al. 2004) has identified the Reinach and Fribourg faults as potentially active. However, they found that the seismic hazard is dominated by magnitude 6–7 events at short distances. As a result, their analyses—while they serve well their purpose—is far from being complete for Switzerland and for the database of known faults and earthquakes.
-
4.
In Switzerland there is no clearly identified seismogenic zone database, as it is the case in Italy (DISS Working Group 2015). The along-strike segmentation of the Alps is also not as clear as that of the Himalayas, where there is a structural control on the extent of large earthquakes (Hetényi et al. 2016), but moderate to small seismicity still varies significantly along the arc (Diehl et al. 2017).
There is, therefore, a gap in the comparison of currently available geological and geophysical information related to fracture patterns at surface and at depth. In this paper we analyse (1) tectonic faults mapped at the surface and (2) the earthquake catalogue in the same region. These two datasets are constructed fully independently and method-wise very differently. Although we do not think that all earthquakes (especially at depths exceeding few kilometres) can be directly connected to faults at the surface, we argue that the analysis of the physical connection between zones of deep and of superficial fractures in an orogen, connected by the stress field, is of interest. Their correlation allows to quantify near-fault and off-fault seismicity, at least to a minimum level, considering the current fault and earthquake completeness. This baseline comparison can be improved in the future (see the Sects. 4 and 5), and the result can have practical applications for seismic hazard assessment.
2 Geodynamic and seismological setting
The Alpine orogenic system has formed by the interaction of the European and the Adriatic plates. The latter is one of several microplates of continental and oceanic provenance whose evolution between two large converging plates, Europe and Africa, has given rise to the tectonically complex Alpine–Mediterranean mountain belts (e.g., Handy et al. 2015). The Alps comprise significant along-strike differences in their structure and dynamics (e.g., Schmid et al. 2017). One of the reasons for this is the counter-clockwise rotation of Adria around a pole in NW Italy, causing currently little deformation in the Western Alps and frontal collision in the Eastern Alps (Weber et al. 2010). This is well reflected in the pattern of the major historical earthquakes in the Alps (Fig. 1, Table 1), the majority of which occurred at the southern front of the Eastern Alps.
Location of the 12 largest earthquakes in the Alpine region in the last millennium (red circles), with details listed in Table 1. The grey circles show the location of events outside the Alpine region. The white dashed line is the approximate contour of the Adriatic microplate according to Weber et al. (2010). The yellow corners define the frame of the study area shown in subsequent figures
Seismicity in Switzerland is moderate, but the level of analysis is detailed and comprehensive. The yearly earthquake reports with a long tradition (Deichmann et al. 2012 and references therein; Diehl et al. 2018 and references therein) discuss the main recent events and their tectonic interpretation. The ECOS-09 catalogue integrates thoroughly compiled and homogenized historical and instrumental data (Fäh et al. 2011). The regional stress field derived from fault plane estimates (Kastrup et al. 2004) points out perturbations with respect to the general European stress field in the vicinity of the Alps. On the regional scale, the uplift rate’s spatial gradient was proposed to drive seismicity as well as landslide loci (Jaboyedoff et al. 2003).
Yet most of the undertaken analyses focus mostly on the largest seismic events, leaving ample space for an overall comparison including smaller earthquakes and all, currently known faults.
3 Data and methods
3.1 Data
3.1.1 Earthquake catalogue
For this study we download the entire earthquake catalogue held at the Swiss Seismological Service, from the earliest event (250 AD) to the end of 2017, counting 25,638 events between magnitudes − 0.6 and 6.6. For the main analysis we use data downloaded using the command fdsnws-event. For the uncertainty analysis (see Sect. 4.2), we download the ECOS-09 (Fäh et al. 2011) dataset, which includes predefined location, depth and magnitude uncertainty categories until the end of 2008. For the analysis of more recent events, we download event data in XML output format for M ≥ 2.0 earthquakes, which include individual location, depth and magnitude uncertainty for each (633 events, but not all have all these information). Data are available and download procedures are described on the Swiss Seismological Service website http://www.seismo.ethz.ch (last accessed 15 February 2018).
Figure 2 shows the full catalogue in map view. This includes all historical events as described in ECOS-09. Then it contains events from the historical to analogue transition period, 1964–1974, where the magnitude of completeness decreased from 3.3 to 2.0. The analogue instrumental period lasted from 1975 to 1983, after which the analogue to digital transition period followed from 1984 to 2001. From 2002 the catalogue is fully based on digital instrumental records (Fäh et al. 2011).
a Map view of the full earthquake catalogue held at the Swiss Seismological Service from 250 AD to the end of 2017. b Map view of the full fault database on the 1:500,000 Geological Map of Switzerland held by the Swiss Federal Office of Topography. Supposedly-active and supposedly-inactive faults are shown in magenta and grey colour. The green box on both figures highlight the study area, shown from Fig. 3 onwards. The political boundaries of Switzerland and the ten largest lakes are shown for reference. Co-ordinates are shown in the Swiss grid in km
3.1.2 Fault catalogue
We chose to use the Geological Map of Switzerland at the 1:500,000 scale as it is the highest resolution map with complete fault information in the study area. The map (version 1.3) is available in digital format from the Swiss Federal Office of Topography (Swisstopo). This database was assembled primarily from academic research and mapping projects carried out by geologists for over a century, and revised two times. The “Tectonic Accidents” (transcriptions from French) sheet contains 12,737 faults with a total length of 28,328 km in a rectangular area encompassing Switzerland (Fig. 3). The database includes individual fault co-ordinates, fault length, and different faults categories. These categories are important to distinguish between “supposedly-active” (“faults” and “tectonic lineaments”: ID codes 21–24) and geologically old, “supposedly-inactive” faults (ID codes 11–18). These categories are based on the initial maps used to compile the database. We perform our analysis with the supposedly-active faults (total length: 10,906 km, of which 3644 in or touching Switzerland) and then test the sensitivity of our results with respect to this selection.
This selection of faults does not allow to distinguish whether they are truly active tectonic faults, or related to gravitational processes or to postglacial differential uplift (Persaud and Pfiffner 2004; Ustaszewski et al. 2008; Ustaszewski and Pfiffner 2008). While such compilations exist over areas of smaller extent, they are not available over our entire study area, where the selected 1:500,000 scale tectonic map is considered as the most complete. Future improvements of the fault database and application of the approach presented here will provide updates on quantifying the relationship between faults and earthquakes.
3.2 Methods
We perform two main calculations: (1) for each earthquake, the distance to the nearest fault; (2) for each fault, the distance to the nearest earthquake. We employ Euclidean distance calculations between earthquake epicenters and faults vertices using their X and Y co-ordinates in the Swiss grid. We chose to compute this distance horizontally as the dip information of the faults is generally not available, but we consider the earthquake depth information in the figures and in the interpretation. The comparison of earthquake focal mechanism and potentially related fault is performed for a few events yearly, and is discussed in annual reports of the Swiss Seismological Service (e.g., Diehl et al. 2018 and earlier).
As the distance calculations are simple, further details on their purpose is explained with each result presented in subsequent sections; in this section we discuss basic prior verifications.
The fault lengths in the fault database are verified for each fault by adding its individual digitized segments’ recalculated lengths, and is found to be matching within 0.11%. The digitized vertices defining these segments are typically (90% of the cases) < 1 km from each other and only 1% has > 2 km spacing, hence discretization artefacts are small.
To avoid artefacts in the comparison of the earthquake catalogue and the fault database near their coverage’s edge, we limit the selection of earthquakes to a narrower box, as shown on Fig. 2. In some cases, we only consider data within Switzerland, also represented on figures with the boundaries.
Earthquake depths, provided below sea-level, are converted to depth below surface using the elevation data at the earthquake location using the SRTM topography model (Farr et al. 2007) at 6 arc-seconds (180 m) horizontal resolution.
In general, we make no distinction between the types of earthquake magnitudes in the catalogue, unless specified below. We use ML for events since 2009 and Mw for event before that time, accounting for ca. One and three quarters of the catalogue, respectively. The difference between the two magnitudes is negligible for the range investigated in most of this study (M > 2.5) and becomes relevant only for small (M < 1) events. For a comparison of Mw and ML between small and large events we refer to Deichmann (2017), and for an empirical scaling relation in Switzerland to Goertz-Allmann et al. (2011).
To compare fault lengths with magnitudes, we follow the scaling relation proposed by Wells and Coppersmith (1994) who fitted a regression line between magnitude M and surface rupture length LRUP on data from 77 earthquakes with magnitudes 5.2–8.1 worldwide:
and the regression line fitted by changing the axes is:
In this comparison, the longest fault segment in the database with 62 km length could theoretically—if rupturing along its total length—host a M7.16 earthquake.
4 Results and discussion
4.1 Distance from earthquake to nearest fault
4.1.1 Reference result
We compute for each earthquake epicenter the distance to the nearest fault d in kilometres. For the reference case, we chose earthquakes since 1975 (beginning of the instrumental period), with magnitudes 2.5 and above (typically felt events) in the entire study area. This selection and the supposedly-active faults are shown on Fig. 3.
The distribution of calculated horizontal distances is shown on Fig. 4a. While the majority of events are within 5 km of a supposedly-active fault, there is a non-negligible part farther away, up to 30 km distance. We fit a probability density function (PDF) to the distance distribution in the form
where α (km−1) is the single parameter characterizing the PDF so that the integral of the function (of the probabilities) is 1. We use 60 bins (0.5 km bin width) so that the discrete function is well resolved but still has enough data in each bin. The best fit PDF for the reference case has α = 0.25 km−1, and we analyse this parameter as a function of selected earthquakes.
Results for the reference case. a Histogram of earthquake-to-nearest-fault distances. b The same distance plotted against hypocentral depth for each event. Green lines dipping at 60° and 30° angles allow defining “close” and “far” events, quantified in red in the lower left corner. Circle size and colour scales with magnitude. Events shown in grey at zero depth do not have hypocentre information and are not included in the statistics. c Comparison of reported against hypothetical magnitudes assuming full rupture on the nearest fault and scaling according to Wells and Coppersmith (1994). The red line is equality. Magnitudes scaled from fault length could be reduced when using stress-drop based estimates, but would need additional assumptions on stress-drop
A better evaluation of these distances can be made by adding the depth of the events relative to the surface (Fig. 4b). To quantitatively distinguish earthquakes that are “close” to and “far” from the nearest fault, we show two lines dipping at 60° and at 30° from the origin. These dip angles correspond to idealized normal and thrust faults, respectively (Anderson 1905), whereas idealized strike-slip faults would dip at 90°. As the real geometry of faults is likely more complicated and does not necessarily reach as deep as the earthquakes, these two lines are chosen to characterize the fracture patterns at depth and at surface. In the reference case, 63% of the earthquakes are below the 60° dipping line and are therefore labelled “close” events, and 11% are above the 30° dipping line and are “far” events. The sensitivity of the results on the earthquake and fault selection, as well as considerations on the uncertainties are discussed below.
We also compare the magnitude of each event with a hypothetical magnitude calculated using the fault length and the scaling law in Eq. (1). This represents a hypothetical scenario in which the full length of the nearest fault ruptures during an event. The comparison (Fig. 4c) reveals that the reported magnitude is always less than it could be by fully rupturing the nearest fault. This discrepancy may be reduced for M < 3 earthquakes when seismic source dimensions would be estimated using stress-drop, instead of the global scaling law based on M 5.2–8.1 earthquakes, however a notable difference remains. This means that rupture during these earthquakes is shorter, or partial compared to the nearest fault’s length if it continues at depth.
4.1.2 Sensitivity to selected data
The calculations performed for the reference case above are done for other selections of earthquakes to analyse the results’ sensitivity. The numbers for the tested cases are detailed in Table 2 and summarized in Table 3.
With respect to the reference case, we varied the time window of earthquakes, the minimum magnitude of the selection, and the chosen area. Two examples are shown on Figs. 5 and 6: M ≥ 0.5 events between 2002 and 2017 (fully digital seismic recordings) in the entire area, and all typically felt events (M ≥ 2.5) in Switzerland since the beginning of the catalogue (250 AD).
Map view and results for M ≥ 0.5 events in the time window 2002–2017 in the entire study area, with respect to supposedly-active faults. Display as on Figs. 3 and 4, map co-ordinates are shown in the Swiss grid in km. The smallest magnitudes (M 0.5 to 2.0) in d could be shifted to the right (by ca. 0.75 to 0.2 ± 0.15 units, respectively) as a result of ML–Mw correction
The example on Fig. 5 shows that the results are similar to the reference case considering a large number of events and even if magnitudes below the magnitude of completeness are included. The earthquakes highlight some features known tectonically, like the double earthquake band in the Valais, the Fribourg Lineament, but also the northern Alpine front, except a central segment. The distance distribution can be fitted with a PDF of parameter α = 0.24 km−1. The percentage of close, respectively far events is slightly lower (58%), respectively higher (15%), than in the reference case. The earthquake magnitudes are all lower than the hypothetical magnitudes scaled from the nearest fault’s length, like in the reference case. Only a small portion of the difference (ca. 0.6 of several units at M = 1) can be accounted for by the Mw − ML difference.
Figure 6 includes the entire historical catalogue of felt events within Switzerland. The Valais, the Grisons/Graubünden and the Basel area appear clearly. Western Switzerland shows a distributed seismicity which is more important than commonly believed. The PDF fitted on the distance distribution has α = 0.22 km−1. The earthquakes are on average slightly closer to faults than in the reference case (65% close, 8% far). The magnitude comparison reveals several events that are larger than the magnitude scaled from the nearest fault’s length. The majority of these have magnitudes above 5, and the difference with respect to the equality line is larger than the magnitude uncertainty in the ECOS-09 catalogue (typically < 0.5 when this information is provided). These can be explained by their exceptional nature, as the 1356 millennial Basel earthquake, the large location uncertainty of historical events causing wrong nearest-fault associations, or simply blind faults.
As a summary of the sensitivity tests (Table 3), the range of close events is 57–66%, while the range of far events is 8–16%, depending on the choice of earthquakes. The numbers point to slightly more closeness when only the typically felt events (M ≥ 2.5) are considered. To demonstrate that the results are distinct from those of a random distribution, we computed the “close” and “far” percentage numbers considering a random distribution of events in the study area and in the first 15 km depth of the crust. The average of ten such tests (Table 3) proves the distinct nature of real data: while the latter show between 3/5 to 2/3 close events and 1/12 to 1/6 far events, random distributions show ca. 1/2 and 1/5 to 1/4, respectively. A significant change in our results can only be produced when a much broader set of faults, i.e. both the supposedly-active and the supposedly-inactive, are considered (Table 2). This means that the close and far percentages obtained here for supposedly-active faults, ca. 62% and ca. 10% on average, are related to the geometrical distribution of these faults in the study area. The same can be concluded from the PDF fitted on the distribution of distances. The parameter α is largely similar for the cases where active faults are selected (0.21–0.35 km−1), and is significantly different when all faults are taken into account (0.73 km−1). The variability of α is listed in Table 2 and shown in Online Resource 1.
4.2 Uncertainty analysis
4.2.1 Faults
The uncertainty of fault location is virtually zero, and the discretization of fault vertices is mostly less than 1 km (see Sect. 3.2).
4.2.2 Earthquake locations
The location uncertainty of earthquakes relates to the precision of location determination and is not an absolute accuracy. An important element defining this is the velocity model used during the location process. It is beyond the scope of this paper to discuss the quality of the velocity model, but the seismological network and earthquake catalogue of Switzerland are generally considered to be of high quality.
As in most catalogues, the uncertainties tend to be worse with the age of earthquakes. This is the case of the ECOS-09 catalogue, which includes 19,275 events, and predefined categories for the north–south, east–west and vertical uncertainties such as “≤ 20 km” or “≤ 50 km” (see Fäh et al. 2011 for details). While the uncertainties generally decrease with time, especially with the beginning of the instrumental record (see Online Resource 2), it remains ambiguous to perform a quantitative assessment.
We therefore take the most recent part of the catalogue (2009 onwards) in which earthquakes have individually determined horizontal and vertical uncertainties and perform two analyses.
In the first, we start with a computation as above and obtain 57% close and 13% far faults (Fig. 7a). We then create a heat map to take into account the uncertainties, by associating a 2-D Gaussian at the location of each event on the same distance–depth diagram. The semi-axes of the ellipse at the base of the Gaussian are 3σ of the individual horizontal and the vertical uncertainty values. The total weight of each Gaussian is 1, so better located events will have a more focused trace in the heat map. The parts of ellipses that reach over to the other side of the nearest fault are folded over the ordinate (depth axis). Finally, we sum the individual, ellipse-shape weights and obtain the heat map on Fig. 7b. The “close” and “far” percentage are obtained by integrating the heat map below the 60° and above the 30° dipping lines. We obtain 56 and 15%, respectively, which is very close to the initial results. While the initial result seems robust, this approach considers only the nearest fault to each earthquake. However, in reality, the location uncertainty may bring the earthquake closer to another fault.
Uncertainty analysis of the results, for M ≥ 2.0 earthquakes in the time window 2009–2017. a Distance to nearest fault against earthquake depth, displayed as on earlier figures. b Same display in form of a heat map (relative intensity), considering horizontal and vertical uncertainties of each event. The close and far statistics are very close to the initial numbers. See text for description. c Magnitude uncertainties (1σ) added on a comparative magnitude figure as shown on earlier figures
To test this scenario as well, we perform 10 tests in which the location of each earthquake is shifted in a random horizontal direction by a random amount, following a Gaussian distribution whose width scales with the horizontal uncertainty. Each event is also shifted in depth in the same random way. The “close” and “far” percentages remain in a narrow range and show a slight improvement with respect to the initial numbers. Close events are in the 58–61% range (compared to 57% initially), and the far events are in the 9–11% range (initially 13%). This means that the random shift of earthquake locations actually brought the events slightly closer to their nearest or another fault.
In summary, our two tests that consider earthquake location uncertainties, without and with other faults, do not reveal any strong bias in our initial results and put confidence that they are robust.
4.2.3 Earthquake magnitudes
For the same selection of earthquakes as above, we also add the magnitude uncertainty information, where available, on the usual diagram (Fig. 7c). The uncertainty values are typically less than one magnitude unit, and none of them crosses the equality line. Thus they confirm the general trend in which earthquake magnitudes are lower than what could be expected from full rupture of the nearest fault.
4.3 Fracture length distributions
A striking feature of the above comparisons is the generally lower earthquake magnitude compared to the nearest fault’s length (Figs. 4c, 5d, 7c). Except for relatively large, historical events (Fig. 6d), the faults seem to be able to produce larger events than those occurring in reality, supposing they break their entire length mapped at the surface.
To verify whether this is a coincidence or a general feature of the study area, we analyse the two databases without connecting individual earthquakes and faults, and compare the distribution of all earthquakes’ magnitudes with that of all fault’s lengths. To represent these on the same scale, we homogenize them using the right and respectively left side of Eq. 2, the scaling relation proposed by Wells and Coppersmith (1994). The histogram on Fig. 8 shows that the fault length and earthquake magnitude distributions contained in the databases are different, despite each of them having a maximum near their centre. The faults are generally longer with respect to the length scale corresponding to earthquakes’ rupture lengths.
Comparison of the fault database with the earthquake catalogue in terms of characteristic length, homogenized using Eq. 2. Faults in general seem to be longer than earthquake rupture lengths, even if the discrepancy would partly reduce when stress-drop based magnitude—source-dimension equations would be used. See text for further details. Units on the horizontal axis are as indicated to the right of the colour legend. The histogram counts are shown in natural logarithm simply for representation purposes
We see two interpretations for this discrepancy.
Either the scaling law, calibrated on larger events globally, cannot be applied to background seismicity and to an integrated faulting history as that of Switzerland. If this is the case, the scaling law is seriously wrong, as demonstrated by the ca. 2 units of difference in the location of maxima on Fig. 8, corresponding to a difference of ca. 3 in magnitudes or a multiplication factor of ca. 100 in fault lengths. These differences would partly reduce when stress-drop based magnitude—earthquake source dimension relationships would be used, however the extent of reduction depends on the assumed stress-drop and we chose not to speculate on its value.
Therefore at least part of the results have a tectonic meaning: they suggest that the fracture pattern and depth, mirrored by the seismicity, is clearly more fragmented than the fracture pattern at surface, mirrored by the fault map. This can be a physical state of the fracture patterns, or, if the mapped fault segments at surface are comparable in length to those at depth, it may also mean that the earthquakes do not rupture the full, available fault length. It may also be that faults mapped at the surface are curvilinear, and therefore longer than what single earthquakes can rupture. Further analysis is required on both databases, especially to see whether their respective completeness levels and temporal sampling (geological for the faults, within the seismic cycle for earthquakes) play a biasing role in this result.
4.4 Distance from fault to nearest earthquake
In an exercise opposite to the previous, we compute for each fault the distance to the nearest earthquake. The goal is to see whether one can draw any conclusion about faults being active or inactive over a considered time window.
4.4.1 Reference result
As a reference case we consider faults in Switzerland only, to avoid any bias from the region to the NW (French Jura, Franche Comté) with a dense fault network but few earthquakes. We select the same earthquakes as in the other reference case (Sect. 4.1): M ≥ 2.5 events since 1975. We than calculate the percentage of faults that are more than 10, 15 and 20 km away from any earthquake. We also calculate their cumulative length as a percentage of the total length of considered faults.
For the reference case, 16, 4 and 2% of faults are more distant from earthquakes than 10, 15 and 20 km, respectively, and they make up 15, 5 and 1% of the fault network length. The ca. 1/6 of the faults in Switzerland that satisfy the 10-km-distance criteria are highlighted on Fig. 9. They show the southern part of the canton of Ticino, several faults in the Jura in Western Switzerland and Lake Geneva area, and the northern front of the Alps in the central segment of the country. Surprisingly, a few short faults are also highlighted in the Simplon area and in the Valais.
4.4.2 Sensitivity to selected data
We analyse the sensitivity of the results as a function of selected data, primarily the earthquakes, but also the faults. As in the reference case above, we compute the number N and cumulative length L of faults more distant from earthquakes than 10, 15 and 20 km. The results are presented in Table 4 as percentages rounded to the nearest integer.
The tests reveal a strong dependence of the results on the selected earthquakes. All, supposedly-active faults have seen a typically felt earthquake (M ≥ 2.5) occurring at less than 10 km distance since the beginning of the catalogue (250 AD). This can be a key element to include in hazard analysis. The results depend strongly on magnitude. At higher thresholds (e.g., M 3.3–3.5), 10% of the faults have never experienced an earthquake closer than 10 km, and this rate is more than 50% for the past half century. At lower thresholds (e.g., M 1.5), almost all faults have seen an event in the past 16 years. Considering the supposedly-inactive faults within Switzerland as well does not decrease the percentages significantly. However, extending the area to the entire box shown on Fig. 9 causes a comparatively larger increase.
While these results do not account for location uncertainties, they underline another way of comparing faults with earthquakes, in which the selection criteria such as time, magnitude and area, play an important role.
5 Avenues for future research
The following sections describe possible future studies to continue the analyses presented here.
5.1 More fault data
The 1:500,000 tectonic map was chosen as it is currently the only map covering the entire study region at uniform resolution. The fault database can be further improved by adding subsurface fault information, for example from the Seismic Atlas of Switzerland (Sommaruga et al. 2012) and from project GeoMol (Allenbach et al. 2017). For the end of 2019, Swisstopo plans the completion of the 1:25,000 scale geological maps across Switzerland, which will bring a new level of details for analyses. Furthermore, the revision of active versus non-active faults can lead to a better picture of faults–earthquakes relationship. Nevertheless, our approach presented here can be applied directly to new datasets.
5.2 Focused fault analysis
With denser field instrumentation and state-of-the-art seismic techniques, the active but slowly moving fault in the Alpine region can be further characterized. An outstanding example is the work on the Fribourg Lineament (Vouillamoz et al. 2017), and the ongoing effort around the Rawil depression (T. Diehl, pers. comm.). While this approach is not conceivable across the entire country, it will bring more certainty for seismic hazard assessment through the characterization of important active faults.
5.3 Kinematic comparison
Our analysis could be brought further by comparing the strike, dip and rake from seismic focal mechanism (FM) solutions and fault characteristics. The strike of the FM should lie close to the fault orientation. The FM dip and rake information could be plotted on figures as our distance–depth graphs (e.g. Fig. 4b), to see whether the fault nearest to an earthquake can reasonably regarded as the respective host fault. Mapped faults can be compared to the a compilation of focal mechanisms and the derived stress map (Kastrup et al. 2004), and included either as input or as control of 3-D numerical models of geodynamic evolution which can quantify the 3-D stress and strain field (e.g., Lechmann et al. 2014; von Tscharner et al. 2016). Such models would further characterize the relationship between stress and strain fields in Switzerland, which has been recently analysed by Houlié et al. (2018).
5.4 Comparison with geology
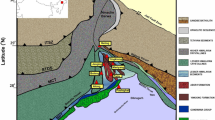
As demonstrated above, the depth information is crucial in the analysis of earthquake loci with respect to faults. Further insights can be gained when plotting the earthquake locations in the vicinity of geological profiles on these latter. Examples are presented on Fig. 10 across the Jura Mountains and the Western Swiss Alps.
Earthquakes plotted on geological profiles across the Western Alps. a Profile by Escher et al. (1997). b Profile NFP20-West as interpreted in Schmid et al. (2017). We refer to the original publications for the colour codes. Both profiles run NW–SE near the eastern end of Lake Geneva, the latter is ca. 25 km to the NE and horizontally offset by ca. 50 km. On all figures only those earthquakes are shown that are located less than 30 km distance from the profile, with known magnitude, known vertical uncertainty, and known horizontal uncertainty for events since 2009, and, for events until 2008 (ECOS-09), when the largest of the E–W and N–S uncertainties is ≤ 20 km. The size of the circles is proportional to the local magnitude (ML) of events
In the Alps, where geological structures are highly non-cylindrical and strongly plunging, meaningful correlation with foci projected horizontally on cross-sections is challenging. However, by combining map and cross-section view of earthquakes, a link with structures associated to the Rhône-Simplon fault-system can be postulated. Developing a 3-D model should help to confirm this hypothesis and similar ones elsewhere.
Movements in front and below the external crystalline massifs propagating towards the basal thrust of the Prealps and the Subalpine Molasse can be the source of several earthquakes.
In the basement below the Jura and the Molasse Basin, earthquakes are located below the Jura detachment. The connection with faults observed at the surface is not possible. On classical cross-sections such as Fig. 10, the basement is pictured as a homogeneous formation. It is obviously not the case in an area so strongly pre-structured by the Variscan orogeny and the Mesozoic extensional phases. For instance, the possible role of late Variscan structures such as the faults bounding Permo-Carboniferous troughs should be examined more closely and in 3-D.
5.5 Improving seismic hazard assessment?
It seems to be a good idea to take all faults with low earthquake-to-fault distances, and incorporate them in seismic hazard assessment. However, this is simply smearing the already available information on the spatial distribution of earthquakes towards the faults. It also disregards the fact that the earthquake catalogue is incomplete, both in time (for large events) and in space (for small events, too).
The same problem arises if one calculates the cumulative moment liberated on each fault from the earthquakes to which they are closest. The seismic cycle in a slowly deforming orogen is likely longer than the time period covered by the seismic catalogue, and we do not have good constraints on the time scales of transients.
In an inverse approach, one can highlight those faults that have low fault-to-earthquake distances. While this also relies on earthquake loci, it allows to quantify how relevant is the fault dataset for the given earthquake catalogue. As mentioned above, for M ≥ 2.5 events and long times, all faults have seen an event occurring within 10 km distance. This assessment can be done for smaller events and shorter time periods to map already ruptured against not-yet ruptured zones, given that the earthquake catalogue is complete for that magnitude.
5.6 Numerical modelling
It is clear that both the fault map, available at the surface, and the earthquake catalogue, available over geologically short time scales, are incomplete. For an improved understanding of a region’s seismotectonics it is essential to include the depth information and the long-term evolution of the stress and strain field. To this end 3-D numerical modelling that includes brittle-plastic, ductile and elastic deformation behaviour with pressure-and temperature-dependent flow laws, reliable thermal fields, and high numerical resolution is necessary, to name a few key elements. 3-D numerical models are also important to understand the relation between faults and seismicity because the fault type (normal, strike-slip or thrust) depends on the 3-D stress state, which can vary significantly spatially and temporally during crustal deformation.
6 Conclusions
We carried out a baseline comparison between two different yet physically connected databases in Switzerland and neighbouring regions: faults and seismicity. They are linked by the stress regime and express the active fracture pattern at the surface and at depth, respectively.
By calculating the distance from each earthquake to the nearest known and supposedly-active fault, we observe that about two-thirds of the earthquakes can be considered as being close to a fault, yet about 10% are far. This match is surprisingly good considering the very disparate construction of the databases, but still deviates from the general knowledge that earthquakes occur on faults. Although both databases are likely incomplete—earthquakes in time, faults if they are blind, or covered by sediments or snow,—sensitivity tests and considerations about earthquake location uncertainties do not affect these general results.
The comparisons of earthquake magnitude with hypothetical magnitudes obtained from fault lengths show a discrepancy, both in general for the database, and also when earthquakes and respective nearest faults are paired. A smaller part of this discrepancy would vanish when assumptions on stress-drop would be made. The remaining discrepancy means either that earthquakes rupture is partial with respect to the fault’s extent, or the deep fracture pattern is clearly more segmented than the superficial one.
The two-third overlap in deep and superficial fracture patterns, and the 10% remote seismicity are the first of such quantifications in an orogenic zone, which typically deforms in a distributed manner. The analysis of results by close comparison to geological data, especially at depth, as well as state-of-the art numerical modelling integrating field data and rheological characteristics can shed light on how stress and strain evolve in a broadly, and in this case slowly deforming system.
Finally, statistics on faults’ distance to the nearest earthquake reveal results that strongly depend on the selection criteria. All supposedly-active faults in Switzerland have experienced a M 2.5 or larger earthquake according to currently available data, and only one-sixth have not done so in the past 42 years, since the beginning of instrumental earthquake detection.
Further work can be done to complete the databases, and to rightly choose which elements of the analysis presented here can be reasonably included in earthquake hazard assessment.
The message for educators: the general knowledge taught in schools must be taken with a pinch of salt. Earthquakes can happen in areas without (known or mapped) faults, and not all faults produce earthquakes within a human lifetime, but they seem to do so over long times.
References
Abrahamson NA, Coppersmith KJ, Koller M, Roth P, Sprecher C, Toro GR, Youngs R (2004) Probabilistic Seismic Hazard Analysis for Swiss Nuclear Power Plant Sites (PEGASOS Project). Final report, vol 1, text. NAGRA, Wettingen, 362 pp. Available online at www.swissnuclear.ch/upload/cms/user/PEGASOSProjectReportVolume1-new.pdf
Allenbach R, Baumberger R, Kurmann E, Michael CS, Reynolds L (2017) GeoMol: geologisches 3D-modell des Schweizer Molassebeckens. Rapports du Service géologique national 10 (ISBN: 978-3-302-40109-6)
Anderson EM (1905) The dynamics of faulting. Trans Edinb Geol Soc 8:387–402. https://doi.org/10.1144/transed.8.3.387
Deichmann N (2017) Theoretical basis for the observed break in ML/Mw scaling between small and large earthquakes. Bull Seismol Soc Am 107:505–520. https://doi.org/10.1785/0120160318
Deichmann N, Clinton J, Husen S, Edwards B, Haslinger F, Fäh D et al (2012) Earthquakes in Switzerland and surrounding regions during 2011. Swiss J Geosci 105:463–476. https://doi.org/10.1007/s00015-012-0116-2
Diehl T, Singer J, Hetényi G, Grujic D, Giardini D, Clinton J, Kissling E, GANSSER Working Group (2017) Seismotectonics of Bhutan: evidence for segmentation of the Eastern Himalayas and link to foreland deformation. Earth Planet Sci Lett 471:54–64. https://doi.org/10.1016/j.epsl.2017.04.038
Diehl T, Clinton J, Deichmann N et al (2018) Earthquakes in Switzerland and surrounding regions during 2015 and 2016. Swiss J Geosci 111:221–244. https://doi.org/10.1007/s00015-017-0295-y
DISS Working Group (2015) Database of individual seismogenic sources (DISS), Version 3.2.0: a compilation of potential sources for earthquakes larger than M 5.5 in Italy and surrounding areas. http://diss.rm.ingv.it/diss/, Istituto Nazionale di Geofisica e Vulcanologia. https://doi.org/10.6092/INGV.IT-DISS3.2.0
Escher A, Hunziker JC, Marthaler M, Masson H, Sartori M, Steck A (1997) Geologic framework and structural evolution of the western Swiss-Italian Alps. In: Pfiffner OA, Lehner P, Heitzmann P, Mueller S, Steck A (eds) Deep structure of the Swiss Alps. Birkäuser, Basel, pp 205–222
Fäh D, Giardini D, Kästli P, Deichmann N, Gisler M, Schwarz-Zanetti G, Alvarez-Rubio S, Sellami S, Edwards B, Allmann B, Bethmann F, Wössner J, Gassner-Stamm G, Fritsche S, Eberhard D (2011) ECOS-09 earthquake catalogue of Switzerland release 2011 report and database. Public catalogue, 17.4.2011. Swiss Seismological Service ETH Zurich, Report SED/RISK/R/001/20110417
Farr TG, Rosen PA, Caro E, Crippen R, Duren R, Hensley S, Kobrick M, Paller M, Rodriguez E, Roth L, Seal D, Shaffer S, Shimada J, Umland J, Werner M, Oskin M, Burbank D, Alsdorf D (2007) The shuttle radar topography mission. Rev Geophys 45:RG2004. https://doi.org/10.1029/2005rg000183
Goertz-Allmann B, Edwards B, Bethmann F, Deichmann N, Clinton J, Fäh D, Giardini D (2011) A new empirical magnitude scaling relation for Switzerland. Bull Seismol Soc Am 101:3088–3095. https://doi.org/10.1785/0120100291
Handy MR, Ustaszewski K, Kissling E (2015) Reconstructing the Alps–Carpathians–Dinarides as a key to understanding switches in subduction polarity, slab gaps and surface motion. Int J Earth Sci 104:1–26. https://doi.org/10.1007/s00531-014-1060-3
Hetényi G, Cattin R, Berthet T, Le Moigne N, Chophel J, Lechmann S, Hammer P, Drukpa D, Sapkota SN, Gautier S, Thinley K (2016) Segmentation of the Himalayas as revealed by arc-parallel gravity anomalies. Sci Rep 6:33866. https://doi.org/10.1038/srep33866
Houlié N, Woessner J, Giardini D, Rothacher M (2018) Lithosphere strain rate and stress field orientations near the Alpine arc in Switzerland. Sci Rep 8:2018. https://doi.org/10.1038/s41598-018-20253-z
Jaboyedoff M, Baillifard F, Derron MH (2003) Preliminary note on uplift rates gradient, seismic activity and possible implications for brittle tectonics and rockslide prone areas: the example of western Switzerland. Bull Soc Vaud Sc nat 88(3):401–420
Kastrup U, Zoback ML, Deichmann N, Evans KF, Giardini D, Michael AJ (2004) Stress field variations in the Swiss Alps and the northern Alpine foreland derived from inversion of fault plane solutions. J Geophys Res 109:B01402. https://doi.org/10.1029/2003JB002550
Lechmann SM, Schmalholz SM, Hetényi G, May DA, Kaus BJP (2014) Quantifying the impact of mechanical layering and underthrusting on the dynamics of the modern India–Asia collisional system with 3-D numerical models. J Geophys Res 119:616–644. https://doi.org/10.1002/2012JB009748
Persaud M, Pfiffner OA (2004) Active deformation in the eastern Swiss Alps: post-glacial faults, seismicity and surface uplift. Tectonophysics 385:59–84. https://doi.org/10.1016/j.tecto.2004.04.020
Schmid SM, Kissling E, Diehl T, van Hinsbergen DJJ, Molli G (2017) Ivrea mantle wedge, arc of the Western Alps, and kinematic evolution of the Alps–Apennines orogenic system. Swiss J Geosci 110:581–612. https://doi.org/10.1007/s00015-016-0237-0
Sommaruga A, Eichenberger U, Marillier F (2012) Seismic atlas of the Swiss Molasse Basin. Edited by the Swiss Geophysical Commission. Matér Géol Suisse Géophys 44
Stucchi M, Rovida A, Gomez Capera AA et al (2012) The SHARE European earthquake catalogue (SHEEC) 1000–1899. J Seismol 17:523–544. https://doi.org/10.1007/s10950-012-9335-2
Ustaszewski M, Pfiffner OA (2008) Neotectonic faulting, uplift and seismicity in the central and western Swiss Alps. In: Siegesmund S, Fügenschuh B, Froitzheim N (eds) Tectonic aspects of the Alpine–Dinaride–Carpathian system, vol 298. Geological Society London Special Publications, London, pp 231–249. https://doi.org/10.1144/SP298.12
Ustaszewski M, Hampel A, Pfiffner OA (2008) Composite faults in the Swiss Alps formed by the interplay of tectonics, gravitation and postglacial rebound: an integrated field and modelling study. Swiss J Geosci 101:223–235. https://doi.org/10.1007/s00015-008-1249-1
von Tscharner M, Schmalholz SM, Epard JL (2016) 3-D numerical models of viscous flow applied to fold nappes and the Rawil depression in the Helvetic nappe system (western Switzerland). J Struct Geol 86:32–46. https://doi.org/10.1016/j.jsg.2016.02.007
Vouillamoz N, Mosar J, Deichmann N (2017) Multi-scale imaging of a slow active fault zone: contribution for improved seismic hazard assessment in the Swiss Alpine foreland. Swiss J Geosci 110:547–563. https://doi.org/10.1007/s00015-017-0269-0
Weber J, Vrabec M, Pavlovčič-Prešeren P, Dixon T, Jiang Y, Stopar B (2010) GPS-derived motion of the Adriatic microplate from Istria Peninsula and Po Plain sites, and geodynamic implications. Tectonophysics 483:214–222
Wells DL, Coppersmith J (1994) New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull Seismol Soc Am 84:974–1002
Wiemer S, Danciu L, Edwards B, Marti M, Fäh D, Hiemer S, Wössner J, Cauzzi C, Kästli P, Kremer K (2016) Seismic hazard model 2015 for Switzerland. Swiss Seismol Serv Rep 1:45. https://doi.org/10.12686/sed/networks/2a
Acknowledgements
The authors acknowledge all people who have contributed to the compilation and maintenance of the earthquake catalogue at the Swiss Seismological Service and of the tectonic map at Swiss Federal Office of Topography (Swisstopo), as well as these two institutions for making the data available. We thank Pauline Baland (Swisstopo) for her support, and Stefan Schmid for his encouragement. We warmly thank Nicholas Deichmann for his thoughtful review, an anonymous Swiss geologist reviewer and an anonymous third reviewer. We are grateful to the Swiss National Science Foundation for funding project OROG3NY (Grant PP00P2_157627).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hetényi, G., Epard, JL., Colavitti, L. et al. Spatial relation of surface faults and crustal seismicity: a first comparison in the region of Switzerland. Acta Geod Geophys 53, 439–461 (2018). https://doi.org/10.1007/s40328-018-0229-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40328-018-0229-9