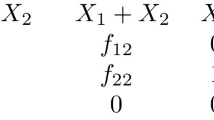Persistent competition models between healthy cells and cancer cells in a tissue

Abstract

In this paper, we mainly construct and analyze a model of competition between two populations of cells for the glucose in a tissue. We first study the existence and global asymptotic stability of a positive equilibrium point of the model with one population of cells. After that, the sufficient conditions are established for uniform persistence of the competition model from what proceeds and by the mean of the Thieme-Zhao Theorem. Finally, we also give some numerical simulations to illustrate these results and conclusions.

Appendix A

Let $F:{\mathbb {R}}_{+}^{n}\rightarrow {\mathbb {R}}^{n}$ be locally Lipschitz and consider the ordinary differential system

$$\begin{aligned} {\dot{x}}=F(x). \end{aligned}$$

(A.1)

Definition A.1

We assume that X is a positively invariant subset of ${\mathbb {R}}_{+}^{n}$ for the system (A.1), $X=X_{1}\cup X_{2}$ and $X_{1}\cap X_{2}=$Ø with $X_{2}$ being a closed subset of X and $X_{1}$ positively invariant. Let $Y_{2}\subseteq X_{2}$.

1.:

$Y_{2}$ is called a weak repeller for $X_{1}$ if

$$\begin{aligned} \limsup _{t \rightarrow +\infty } d(x(t),Y_{2})>0, \end{aligned}$$

for all solutions x(t) of (A.1) with $x(0)\in X_{1}$.

2.:

$Y_{2}$ is called a uniform strong repeller for $X_{1}$ if there exists some $\varepsilon >0$ such that

$$\begin{aligned} \liminf _{t \rightarrow +\infty } d(x(t),Y_{2})>\varepsilon , \end{aligned}$$

for all solutions x(t) of (A.1) with $x(0)\in X_{1}$.

Definition A.2

Assume that $X=X_{0}\cup \partial X_{0}$ with $X_{0}$ being open in X. The system (A.1) is said to be uniformly persistent with respect to $(X_{0},\partial X_{0})$ if there exists some $\varepsilon >0$ such that

$$\begin{aligned} \liminf _{t \rightarrow +\infty } d(x(t),\partial X_{0})>\varepsilon , \end{aligned}$$

for all solutions x(t) of (A.1) with $x(0)\in X_{0}$.

Definition A.3

We assume that X is a positively invariant subset of ${\mathbb {R}}_{+}^{n}$ and $M\subseteq X$ an invariant set for the system (A.1). M is called an isolated invariant set in X if there exists some open subset U containing M such that $U\cap {\mathbb {R}}_{+}^{n}$ contains no invariant subset other than M.

Definition A.4

Let $Y\subset {\mathbb {R}}_{+}^{n}$. Let $x^{*}$ and $y^{*}$ be two equilibrium points of the system (A.1) in Y.

1.:

The point $x^{*}$ is said to be chained in Y to $y^{*}$, written $x^{*}\overset{Y}{\leadsto }y^{*}$, if there exists a solution x(t) of (A.1) which is defined for all $t\in {\mathbb {R}}$ and takes all its values in Y such that $x(t)\rightarrow x^{*}$ as t $\rightarrow -\infty$ and $x(t)\rightarrow y^{*}$ as t $\rightarrow +\infty$ and there exists some $t\in {\mathbb {R}}$ such that $x(t)\ne$ $x^{*}$ and $x(t)\ne$ $y^{*}$.

2.:

A set M of equilibria of (A.1) in Y is called cyclic in Y if there exists some $x^{*}\in M$ with $x^{*}\overset{Y}{\leadsto }x^{*}$ or if there exist $x_{1}^{*},\cdots ,x_{k}^{*}$ in M such that $x_{1}^{*}\overset{Y}{\leadsto }x_{2}^{*}\overset{Y}{\leadsto }\cdots \overset{Y}{\leadsto }x_{k}^{*}\overset{Y}{\leadsto }x_{1}^{*}$, and acyclic in Y if it is not cyclic in Y.

Theorem A.5

(Thieme–Zhao [8, 9]) Let $X\subseteq {\mathbb {R}}_{+}^{n}$ be closed, $F:X\rightarrow {\mathbb {R}}^{n}$ be locally Lipschitz and continuous. Assume that X is positively invariant for the system (A.1) which is supposed to be dissipative on X. Let $X=X_{1}\cup X_{2}$, $X_{1}\cap X_{2}=$Ø, with $X_{2}$ being a closed subset of ${\mathbb {R}}^{n}$and $X_{1}$ positively invariant. Let M be a finite set of equilibria of (A.1) in $X_{2}$. Assume that:

C1.:

Every solution that starts in $X_{2}$ and stays in $X_{2}$ for all forward times converges to one of the equilibria in M,

C2.:

Every equilibrium in M is an isolated invariant set in X and a weak repeller for $X_{1}$,

C3.:

M is acyclic in $X_{2}$.

Then $X_{2}$ is a uniform strong repeller for $X_{1}$. Moreover, if $X_{1}$ is convex, there exists at least one equilibrium point in $X_{1}$.