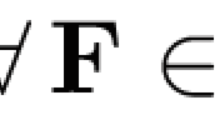Numerical approximation of the scattering amplitude in elasticity

Abstract

We propose a numerical method to approximate the scattering amplitudes for the elasticity system with a non-constant matrix potential in dimensions $d=2$ and 3. This requires to approximate first the scattering field, for some incident waves, which can be written as the solution of a suitable Lippmann-Schwinger equation. In this work we adapt the method introduced by Vainikko (Res Rep A 387:3–18, 1997) to solve such equations when considering the Lamé operator. Convergence is proved for sufficiently smooth potentials. Implementation details and numerical examples are also given.

1 Introduction

The scattering of time-harmonic elastic waves in $\mathbb {R}^d$ ($d=2,3$) is described through the solutions of the Lamé equation

$$\begin{aligned} \Delta ^{*}\mathbf {u}(x)+\omega ^{2}\mathbf {u}(x) = Q(x)\mathbf {u} (x), \qquad \qquad \omega >0,\ x\in \mathbb {R}^{d}, \end{aligned}$$

(1)

where $\mathbf {u}: \mathbb {R}^{d} \rightarrow \mathbb {R}^{d}$ is the displacement vector, $\omega >0$ is the frequency and

$$\begin{aligned} \Delta ^{*}\mathbf {u}(x) = \mu \Delta \mathrm {I} \mathbf {u}(x)+(\lambda +\mu )\nabla div\,\mathbf {u}(x), \end{aligned}$$

(2)

with $\Delta \mathrm {I}$ denoting the $d\times d$ diagonal matrix with the Laplace operator on the diagonal. The constants $\lambda$ and $\mu$ are known as the Lamé parameters and depend on the underlying elastic properties. Throughout this paper we will assume that $\mu >0$ and $2\mu +\lambda >0$ so that the operator $\Delta ^{*}$ is strongly elliptic. The square matrix Q represents the action of some live loads on a bounded region. This can also represent inhomogeneities in the density of the elastic material $\rho (x)$. In this case, Q takes the particular form $Q=\omega ^2 (1-\rho (x))I$. Here we assume that each component of Q, $q_{\alpha \beta }(x)$, $\alpha ,\beta =1,...,d$, is real, compactly supported and belongs to $L^{r}(\mathbb {R}^{d})$ for some $r>d/2$.

When $Q=0$ a solution of (1) is expressed as the sum of its compressional part $\mathbf {u}^{p}$ and the shear part $\mathbf {u}^{s}$

$$\begin{aligned} \mathbf {u}=\mathbf {u}^{p}+\mathbf {u}^{s}, \end{aligned}$$

(3)

where

$$\begin{aligned} \mathbf {u}^{p}=-\frac{1}{k_{p}^{2}}\nabla div\,\mathbf {u}\quad \text {and} \quad \mathbf {u}^{s}=\mathbf {u}-\mathbf {u}^{p} \end{aligned}$$

(4)

with

$$\begin{aligned} \displaystyle k_{p}^{2}=\frac{\omega ^{2}}{(2\mu +\lambda )} \qquad \mathtt {\mathrm {and}} \qquad k_{s}^{2}=\frac{\omega ^{2}}{\mu }. \end{aligned}$$

They are solutions of the vectorial homogeneous Helmholtz equations

$$\begin{aligned} \Delta \mathrm {I}\mathbf {u}^{p}(x)+k_{p}^{2}\mathbf {u}^{p}(x)=\mathbf {0}, \quad \text{ and } \quad \Delta \mathrm {I}\mathbf {u}^{s}(x)+k_{s}^{2}\mathbf {u}^{s}(x)=\mathbf {0}, \end{aligned}$$

respectively. The values $k_{p}$ and $k_{s}$ are known as the associated speed of propagation of longitudinal waves (p-waves) and transverse waves (s-waves) respectively. Note that compressional waves satisfy $\nabla \times \mathbf {u}^{p}=0$ while for the transverse ones we have $div \; \mathbf {u}^{s}=0$.

When $Q\ne 0$ solutions $\mathbf {u}$ of (1) can be interpreted as perturbations of the homogeneous ones, i.e. we write

$$\begin{aligned} \mathbf {u}(x)=\mathbf {u}_{i}(x)+\mathbf {v}(x), \end{aligned}$$

(5)

where $\mathbf {u}_{i}$ is the incident wave, a solution of the homogeneous Lamé equation (i.e. with $Q=0$), and $\mathbf {v}$ the scattered solution.

Unicity of scattered solutions $\mathbf {v}$ is obtained from radiation conditions when $|x|\rightarrow \infty$. A natural choice is to assume that there are no reflections coming from infinity. As Q is compactly supported this condition coincides with the analogous imposed to solutions of $\Delta ^{*}\mathbf {v}(x)+\omega ^{2} \mathbf {v}(x)=\mathbf {0}$ in an exterior domain. These are known as the outgoing Kupradze radiation conditions and they are equivalent to make both $\mathbf {v}^{p}$ and $\mathbf {v}^{s}$ (according to the decomposition (3) and (4)) satisfy the corresponding outgoing Sommerfeld radiation conditions for the Hemholtz equation, that is,

$$\begin{aligned} (\partial _{r}-ik_{p})\mathbf {v}^{p}&=\mathbf {o}(r^{-(d-1)/2}),\quad r=|x|\rightarrow \infty , \end{aligned}$$

(6)

$$\begin{aligned} (\partial _{r}-ik_{s})\mathbf {v}^{s}&=\mathbf {o}(r^{-(d-1)/2}),\quad r=|x|\rightarrow \infty . \end{aligned}$$

(7)

It is known that, with certain conditions in Q, the system (1), (5) together with the outgoing Kupradze radiation conditions (6) and (7) has a unique solution $\mathbf {u}$ (see Theorem 2.1 and Proposition 3.1 of [3] and chapter 5 in [9]).

Problem (1), (6) and (7) and (5) is equivalent to the integral equation

$$\begin{aligned} \mathbf {u}=\mathbf {u}_i + \int _{\mathbb {R}^d} \Phi (x-y) Q(y)\mathbf {u}(y) \; dy, \end{aligned}$$

(8)

where $\Phi (x)$ is the fundamental tensor of the Lamé operator $\Delta ^*+\omega ^2 I$. This tensor is well-known for dimension $d=2,3$ (see [2, 12]). We give its expression in Sect. 7 below.

The implicit integral equation for $\mathbf {u}$ in (8) is known as a Lippmann–Schwinger equation. A trigonometrical collocation method was proposed in [15] for the numerical approximation of this equation, when considering the scalar case and the fundamental solution of the Hemholtz equation, (we used this method in [5] to give approximations of the potential in the inverse quantum scattering problem). A similar collocation method, but without trigonometric polynomials, was proposed in [13]. In this paper we adapt the method in [15] to approximate the solutions of (8). Apart of the fact that we are dealing with a more complex vector problem, there are two main difficulties arising. The first one comes from the asymptotic bound for the Fourier coefficients of a suitable truncation of the Green tensor field associated to the Lamé operator (see Lemma 2 below). This is required to prove the convergence of the method. The second one comes from the fact that we slightly change the point of view in [15] where the numerical method gives an approximation of the product $Q \mathbf {u}$, and therefore $\mathbf {u}$ can be computed only in the support of Q. As described in [15], the solution $\mathbf {u}$ can be extended to $\mathbb {R}^d$ but the estimate of the numerical approximation blows up in the proximity of the boundary of the support of Q. In our approach we solve the problem directly on $\mathbf {u}$ and therefore we obtain a global approximation in $\mathbb {R}^d$.

As an application we approximate scattering amplitudes. Let us briefly describe what these objects are and their interest. As incident waves we usually consider plane waves either transverse (plane s-waves)

$$\begin{aligned} \mathbf {u}^{s}_{i}(\omega , \theta , \varphi ,x)=e^{ik_{s}\theta \cdot x}\varphi , \end{aligned}$$

(9)

with polarization vector $\varphi \in \mathbb {S}^{d-1}$ orthogonal to the wave direction $\theta \in \mathbb {S}^{d-1}$, or longitudinal plane waves (plane p-waves)

$$\begin{aligned} \mathbf {u}^{p}_{i}(\omega ,\theta ,x)=e^{ik_{p}\theta \cdot x}\theta . \end{aligned}$$

(10)

Note that transversal waves depend on an extra angle parameter $\varphi$, not determined by $\theta$, only for $d=3$. From now on, we omit the dependence on $\varphi$ when considering the specific case $d=2$.

If $\mathbf {u}_p$ is the solution of (1) with $\mathbf {u}_p=\mathbf {u}_i^p+\mathbf {v}_p$, $\mathbf {v}_p$ the scattered solution satisfying the outgoing Kupradze radiation condition, then $\mathbf {v}_p=\mathbf {v}^p_p+\mathbf {v}^s_p$ and we have the asymptotic as $|x|\rightarrow \infty$ (see section 2 of [3] or [4]),

$$\begin{aligned} \mathbf {v}^{p}_p(x)&= c\ k_{p}^{\frac{d-3}{2}}\,\frac{e^{ik_{p}|x|}}{|x|^{(d-1)/2}}\,\mathbf {v}_{p,\infty }^p\left( \omega ,\theta , x/|x|\right) + \mathbf {o}\left( |x|^{-(d-1)/2}\right) , \end{aligned}$$

(11)

$$\begin{aligned} \mathbf {v}^{s}_p(x)&= c\ k_{s}^{\frac{d-3}{2}}\,\frac{e^{ik_{s}|x|}}{|x|^{(d-1)/2}}\,\mathbf {v}_{p,\infty }^s\left( \omega ,\theta , x/|x|\right) + \mathbf {o}\left( |x|^{-(d-1)/2}\right) , \end{aligned}$$

(12)

where $\mathbf {v}_{p,\infty }^p$ and $\mathbf {v}_{p,\infty }^s$ are known as the longitudinal and transverse scattering amplitudes of $\mathbf {u}_p$ respectively. Note that the last argument in $\mathbf {v}_{p,\infty }^p\left( \omega ,\theta , x/|x|\right)$ corresponds to a direction in $\mathbb {S}^{d-1}$. This is interpreted as the direction in which the scattering amplitude is observed.

In a similar way, if $\mathbf {u}_s$ is the solution of (1) with $\mathbf {u}_s=\mathbf {u}_i^s+\mathbf {v}_s$, $\mathbf {v}_s$ the scattered solution satisfying the outgoing Kupradze radiation condition then $\mathbf {v}_s=\mathbf {v}^p_s+\mathbf {v}^s_s$ and we obtain the similar asymptotic to (11) and (12) and the longitudinal and transverse scattering amplitudes of $\mathbf {u}_s$,

$$\begin{aligned} \mathbf {v}_{s,\infty }^p(\omega ,\theta ,\varphi , x/|x|), \qquad \mathbf {v}_{s,\infty }^s(\omega ,\theta ,\varphi ,x/|x|). \end{aligned}$$

(13)

Note that the scattering amplitudes are d-dimensional vector fields. However their directions are not completely free. In particular, longitudinal scattering fields are in the direction of the last argument x/|x| while transverse scattering fields are orthogonal to this direction (see [3, 4] and formulas (33) and (34) below).

Scattering amplitudes can be easily measured in practice with seismographs situated far away from the support of the potential Q. Thus, a natural question is if we can derive information of the elastic material from these scattering amplitudes, [3, 4, 6, 8, 10] for numerical results. This is known as the inverse scattering problem in elasticity, (analogous problems arise in quantum scattering, acoustic or electromagnetic obstacle scattering, [7]). In our case, the inverse problem would be to obtain information about the matrix Q.

To understand the problem let us mention how much information we can derive from these data. We can define 2 scattering amplitudes coming from longitudinal incident waves $\mathbf {u}^{p}_{i}$. They depend on the variables $\left( \omega ,\theta , x/|x|\right) \in \mathbb {R}^+\times \mathbb {S}^{d-1} \times \mathbb {S}^{d-1}$. This gives us $2d-1$ free parameters for each amplitude. They are vector waves but the direction is not completely free, as we mentioned above. The amplitude coming from the longitudinal wave has a known direction, and therefore it only depends on a scalar function, while the one coming from the transverse wave is orthogonal to this known direction, and therefore it depends on $d-1$ scalar functions. Globally, scattering amplitudes coming from longitudinal incident waves can be represented with d scalar functions depending on $2d-1$ variables. Concerning transverse incident waves $\mathbf {u}^{s}_{i}$ we can define $2(d-1)$ different scattering amplitudes. Each one depends now on the variables $\left( \omega ,\theta ,\varphi , x/|x|\right) \in \mathbb {R}^+\times \mathbb {S}^{d-1} \times \mathbb {S}^{d-2} \times \mathbb {S}^{d-1}$. We have now $3d-3$ variables for each vector wave. Once again, the amplitudes are vector fields but the directions are not free. There are $d-1$ scattering amplitudes coming from longitudinal waves that are characterized by a single scalar function while the others require $d-1$ scalar functions. Thus, we have $(d-1)+(d-1)^2=d(d-1)$ scalar functions depending on $3d-3$ variables. In the particular case $d=2$ we obtain 4 different scalar amplitudes depending on 3 parameters, while in dimension $d=3$ we have 3 scalar functions depending on 5 variables and 6 more depending on 6 variables.

Now, if we want to determine Q from these scattering amplitudes we have to compute $d^2$ functions depending on d coordinates. In dimension $d=2$ this requires information of 4 functions depending on 2 variables, while for $d=3$, 9 functions depending of 3 variables are involved. We see that, in principle the inverse problem consisting in recovering the matrix Q from scattering data is overdetermined since the scatering amplitudes depend on more variables than the components of the potential. Of course, some of these scattering amplitudes may not be independent and, in practice, we cannot measure all these parameters accurately but it is reasonable to think that we can combine part of this information to recover Q. Then, it is natural to restrict the scattering data. In the linear elasticity problem, it is most usual to deal with either fixed-angle or backscattering data. In the first case we fix the direction of the incident waves $\theta$ (which is no longer a free parameter) and in the latter, only scattering amplitudes with the last entry fixed as $x/|x|=-\theta$ are considered. Whether the scattering amplitudes allow to recover the potential Q in these cases is widely open. There are some results only for some particular situations as for instance if $Q(x)=q(x)I$, or when $\lambda +\mu =0$, where the Lamé operator can be reduced to a system of two independent vector Hemholtz equations, [3].

When reconstruction is not known, or difficult to obtain, it is sometimes possible to define approximations of Q from scattering amplitudes (see [4] for backscattering data and [3] for fixed angle data). Let us give an example in dimension $d=2$. Note that scattering amplitudes for transversal incident waves will not depend on the angle $\varphi$ in this case and we omit this variable in the following. We define the Fourier transform of the $2\times 2$ matrix $Q_b$ (that we denote $\widehat{Q_b}$) from scattering amplitudes as follows. For $\xi \in \mathbb {R}^2$ with $\xi =-2 \omega \theta$, $\omega >0$ and $\theta \in \mathbb {S}^1$,

$$\begin{aligned} \widehat{Q_b}(\xi )e_i=(\theta \cdot e_i) \mathbf {v_{p,\infty }}( \omega , \theta ,-\theta )+ (\theta ^\perp \cdot e_i) \mathbf {v_{s,\infty }}( \omega , \theta ,-\theta ) , i=1,2, \end{aligned}$$

where $\mathbf {v_{p,\infty }}$ (resp. $\mathbf {v_{s,\infty }}$) is a linear combination of $\mathbf {v^p_{p,\infty }}(\omega _{pp}, \theta ,-\theta )$ and $\mathbf {v^s_{p,\infty }}(\omega _{ps},\theta , -\theta )$, for certain energies $\omega _{pp}$ and $\omega _{ps}$ (resp. $\mathbf {v^p_{s,\infty }}(\omega _{pp}, -\theta )$ and $\mathbf {v^s_{s,\infty }}(\omega _{ps}, -\theta )$), and $\{e_1,e_2\}$ is the canonical basis in $\mathbb {R}^2$. The matrix $Q_b$ is known as the Born approximation of Q for backscattering data. There are not estimates on how good is the Born approximation in general. Most of the results involve asymptotic estimates for their Fourier tranforms, that allows to deduce that the Born approximation $Q_b$ and Q share the same singularities. In other words, we can use the Born approximation to recover the singularities of Q, [4].

It is worth mentioning that here we are restricting ourselves to the recovering of Q from scattering data. However, similar problems can be stated for more general situations as to recover the Lamé coefficients or other quantities depending on the elastic properties, [8]. This is a field where there are few results.

As we mentioned before, we apply the numerical approximation of the Lippmann–Schwinger equation (8) to simulate scattering amplitudes. In fact, as we show below (Sect. 6) the scattering amplitudes can be recovered from the potential and the scattering solutions of (8) for the different incident waves. This allows to construct synthetic scattering amplitudes from numerical approximation of (8). In particular, we can test reconstruction algorithms and compute Born approximations that can be compared with the potential Q. This will be done in a forthcoming publication.

The rest of the paper is divided as follows: In Sect. 2 we reduce the Lippmann–Schwinger equation (8) to a multiperiodic problem by localizing and periodic extension. In Sect. 3 we introduce the finite trigonometric space used in the discretization. In Sect. 4 we derive the trigonometric collocation method. Convergence is proved in Sect. 5. In Sect. 6 we show how to approximate the scattering amplitudes. In Sect. 7 we estimate the Fourier coefficientes of the Green function involved in the multiperiodic version of (8). Finally, in Sect. 8 we include some numerical examples that illustrate the convergence of the method and the approximation of some scattering amplitudes.

2 Reduction to a multiperiodic problem

We first write the Lippmann–Schwinger equation (8) in terms of the scattered solution $\mathbf{v}$,

$$\begin{aligned} \mathbf {v}= & {} \int _{\mathbb {R}^d} \Phi (x-y) Q(y)\mathbf {u}_i(y) \; dy+\int _{\mathbb {R}^d} \Phi (x-y) Q(y)\mathbf {v}(y) \; dy \nonumber \\= & {} \mathbf {f} +\int _{\mathbb {R}^d} \Phi (x-y) Q(y)\mathbf {v}(y) \; dy, \end{aligned}$$

(14)

where we have written the first term in the right hand side as a generic smooth function $\mathbf {f}:\mathbb {R}^d\rightarrow \mathbb {R}^d$.

From now on we assume that, for some $\rho >0$, the components of Q, $Q_{\alpha \beta }$, and those of $\mathbf {f}=(f_1,f_2,...,f_d)^T$ satisfy,

$$\begin{aligned} supp \; Q_{\alpha \beta } \subset \overline{B}(0,\rho ), \; \; Q_{\alpha \beta }\in W^{\nu ,2}(\mathbb {R}^d), \; \; f_\alpha \in W^{\nu ,2}_{loc}(\mathbb {R}^d), \; \; \nu >d/2. \end{aligned}$$

(15)

In particular this guarantees that the components of Q and $\mathbf {f}$ are continuous functions.

Given $R>2\rho$, we define

$$\begin{aligned} G_R=\left\{ x=(x_1,x_2,...,x_d)\in \mathbb {R}^d \; : \; |x_k|<R,\; k=1,2,..,d \right\} . \end{aligned}$$

Problem (14) on $G_R$ is equivalent to the following: given $\mathbf {f}$ and the $d\times d$ matrix function Q, find $\mathbf {v}:G_{R}\rightarrow \mathbb {R}^d$ solution of

$$\begin{aligned} \mathbf {v}=\mathbf {f}+\int _{G_R} \Phi (x-y) Q(y)\mathbf {v}(y) \; dy ,\qquad (x\in G_R). \end{aligned}$$

(16)

Solving (16) in $x\in G_R$ allows us to obtain $\mathbf {v}$ in $G_R$ . Once this is known, the solution in $\mathbb {R}^d\backslash G_R$ can be obtained by simple integration using (8). This allows us to localize the problem to the bounded domain $G_R$.

The idea now is to use (16) to approximate the solution $\mathbf {v}$ in the smaller ball $x\in \overline{B}(0,\rho )\subset G_R$. For those points, only the values of $\Phi$ in the ball $\overline{B}(0,2\rho )$ are involved and therefore, changing $\Phi$ outside this ball does not affect to the solution $\mathbf {v}(x)$. This allows us to localize the Green tensor function to a compact support function in $G_R$ without changing the solution. We consider a smooth cutting of the form

$$\begin{aligned} K(x)=\Phi (x) \psi (|x|), \quad x\in G_R, \quad R>2\rho , \end{aligned}$$

(17)

where $\psi :[0,\infty )\rightarrow \mathbb {R}$ satisfy the conditions

$$\begin{aligned} \psi \in C^\infty [0,\infty ), \quad \psi (r)=1 \text{ for } 0\le r \le 2\rho \text{, } \quad \psi (r)=0 \text{ for } r\ge R\text{. } \end{aligned}$$

Analogously, we truncate $\mathbf {f}$ by considering $\mathbf {f}(x)\psi (|x|)$, that we still denote $\mathbf {f}$ to simplify.

A more drastic cutting using the characteristic function of the ball B(0, R) is also possible but this is more convenient as we comment below.

Once localized the problem we extend $\mathbf {v},$ $\mathbf {f}$, the components of the matrixes Q and K to R-periodic functions for which we still use same notation. Thus, we change (16) by a multiperiodic integral equation

$$\begin{aligned} \mathbf {v}=\mathbf {f}+\int _{G_R} K (x-y) Q(y)\mathbf {v}(y) \; dy ,\qquad (x\in G_R). \end{aligned}$$

(18)

The smooth cutting of $\mathbf {f}$ and $\Phi (x)$ guarantees a smooth periodic extension from $G_R$ to $\mathbb {R}^d$.

The solvability of (18) is obviously deduced from the one of (16). Moreover, once solved (18) we obtain the solution of (16) in $B(0,\rho )$ and we can extend $\mathbf {v}$ to $\mathbb {R}^d$ by

$$\begin{aligned} \mathbf {v}=\mathbf {f}+\int _{B(0,\rho )} \Phi (x-y) Q(y)\mathbf {v}(y) \; dy ,\qquad x\in \mathbb {R}^d, \end{aligned}$$

(19)

where $\mathbf {f}$ in (19) represents the original function, i.e. before cutting and periodizing.

3 Finite dimensional trigonometric space

The family of exponentials

$$\begin{aligned} \varphi _j(x)=\frac{e^{i\pi j \cdot x/R}}{(2R)^{d/2}}, \quad j=(j_1,j_2,...,j_d)\in \mathbb {Z}^d, \end{aligned}$$

(20)

constitutes an orthonormal basis on $L^2(G_R)$ with the norm

$$\begin{aligned} \Vert u \Vert _0^2=\int _{G_R}|u(x)|^2 dx. \end{aligned}$$

We also introduce the space $H^\eta =H^\eta (G_R)$ which consists of $dR-$multiperiodic functions (distributions) having finite norm

$$\begin{aligned} \Vert u \Vert _\eta =\left( \sum _{j\in \mathbb {Z}^d}(1+ |j|)^{2\eta } |\hat{u}(j)|^2 \right) ^{1/2} , \end{aligned}$$

with

$$\begin{aligned} \hat{u}(j)= \int _{G_R} u(x)\overline{\varphi _j(x)} dx, \quad j\in \mathbb {Z}^d, \end{aligned}$$

the Fourier coefficients of u.

We now introduce a finite dimensional approximation of $H^\eta$. Let us consider $h=2R/N$ with $N\in \mathbb {N}$ and a mesh on $G_R$ with grid points jh, $j\in \mathbb {Z}_h^d$ and

$$\begin{aligned} \mathbb {Z}_h^d=\left\{ j=(j_1,j_2,...,j_d)\in \mathbb {Z}^d \; : \; -\frac{N}{2} \le j_k < \frac{N}{2}, \; k=1,2,...,d \right\} . \end{aligned}$$

We also consider $\mathcal {T}_h$ the finite dimensional subspace of trigonometric polynomials of the form

$$\begin{aligned} v_h=\sum _{j\in Z_h^d} c_j \varphi _j, \qquad c_j\in \mathbb {C}. \end{aligned}$$

Any $v_h\in \mathcal {T}_h$ can be represented either through the Fourier coefficients or the nodal values,

$$\begin{aligned} v_h(x)=\sum _{j\in Z_h^d} \hat{v}_h(j) \; \varphi _j(x)=\sum _{j\in Z_h^d} v_h(jh) \; \varphi _{h,j}(x), \end{aligned}$$

where $\varphi _{h,j}(kh)=\delta _{jk}$, more specifically

$$\begin{aligned} \varphi _{h,j}(x)=\frac{h^d}{(2R)^d}\sum _{k\in \mathbb {Z}_h^d} e^{i\pi k \cdot (x-jh)/R}. \end{aligned}$$

For a given $v_h \in \mathcal {T}_h$, the nodal values $\bar{v}_h$ and the Fourier coefficients $\hat{v}_h$ are related by the discrete Fourier transform $\mathcal {F}_h$ as follows,

$$\begin{aligned} \hat{v}_h =h^d\mathcal {F}_h \bar{v}_h, \qquad \bar{v}_h =\frac{1}{h^d}\mathcal {F}_h^{-1} \hat{v}_h, \end{aligned}$$

where, as usual, $\mathcal {F}_h$ relates the sequence x(n) ($n=(n_1,n_2,...,n_d)$) with X(j) according to

$$\begin{aligned} X(j)= & {} \sum _{n_1,n_2,...,n_d=-N/2}^{N/2-1} x(n)e^{-i2\pi n\cdot j /N}, \qquad j=(j_1,j_2, ...,j_d), \\&j_k=-N/2,-N/2+1,...,N/2-1 . \end{aligned}$$

This definition coincides with the usual one in numerical codes (as MATLAB) up to a translation, since it considers instead $j_k=0, ..., N-1$. This must be taken into account in the implementation.

The orthogonal projection from $H^\eta$ to $\mathcal {T}_h$ is defined by the formula

$$\begin{aligned} P_h v=\sum _{j\in Z_h^d} \hat{v}(j) \varphi _j, \end{aligned}$$

while the interpolation projection $S_hv$ is defined, when $\eta >d/2$, by

$$\begin{aligned} S_hv\in \mathcal {T}_h, \quad (S_hv)(jh)=v(jh), \quad j\in \mathbb {Z}^d_h. \end{aligned}$$

(We need that v is continuous in order to be able to define $S_hv$. Since $H^\eta \subset W^{\eta , 2}_{loc}(\mathbb {R}^d)$, a function $v \in H^\eta$ with $\eta >d/2$ is continuous).

For a vector valued function $\mathbf {v}= (v^1, v^2,...,v^d)^T$ we maintain the same notation, i.e.

$$\begin{aligned} P_h \mathbf {v}= & {} \left( P_h(v^1), P_h(v^2),...,P_h(v^d) \right) ^T \in \mathcal {T}_h^d,\\ S_h \mathbf {v}= & {} \left( S_h(v^1), S_h(v^2),...,S_h(v^d) \right) ^T \in \mathcal {T}_h^d, \end{aligned}$$

and analogously for the discrete Fourier transform $\mathcal {F}_h$ of a vector $\mathbf {v_h} \in (\mathcal {T}_h)^d$. $\mathbf {v} \in (H^\eta )^d$ if

$$\begin{aligned} \Vert \mathbf {v}\Vert _\eta =\max _{k=1,2, ...,d }\Vert v^k\Vert _\eta < \infty . \end{aligned}$$

4 Trigonometric collocation method

The trigonometric collocation method to solve (18) reads,

$$\begin{aligned} \mathbf {v_h}=\mathbf {f_h}+S_h(\mathcal {K}(Q\mathbf {v_h})), \quad \mathbf {v_h} \in (\mathcal {T}_h)^d, \end{aligned}$$

(21)

where $\mathbf {f_h}=S_h \mathbf {f}$ and

$$\begin{aligned} \mathcal {K}(\mathbf {w_h})(x)=\int _{G_R} K (x-y) \mathbf {w_h}(y) \; dy, \quad \mathbf {w_h} \in (\mathcal {T}_h)^d. \end{aligned}$$

(22)

Note that here K and Q are $d\times d$ matrixes while $\mathbf {w_h}$ is a column vector with each component $w^i_h \in \mathcal {T}_h$. The integral applies to each component of the integrand vector function.

From the numerical point of view there is a difficulty in the discrete formulation (21) since $Q\mathbf {v_h}\notin (\mathcal {T}_h)^d$ and should be approximated. Therefore we modify the discrete formulation as follows,

$$\begin{aligned} \mathbf {v_h}=\mathbf {f_h}+\mathcal {K}(S_h(Q\mathbf {v_h})), \quad \mathbf {v_h} \in (\mathcal {T}_h)^d. \end{aligned}$$

(23)

The operator $\mathcal {K}$ leaves invariant the subspace $(\mathcal {T}_h)^d$ and (23) is consistent.

Since each one of the components in the matrix K is a periodic function the eigenfunctions of the associated convolution operator are known to be $\varphi _j$, defined in (20), while their eigenvalues $\widehat{K}_{\alpha \beta }(j)$ are the Fourier coefficients, i.e.

$$\begin{aligned} \int _{G_R} K_{\alpha \beta } (x-y) \; \varphi _j (y) \; dy = \widehat{K}_{\alpha \beta }(j) \varphi _j (x), \quad j\in \mathbb {Z}^d. \end{aligned}$$

(24)

We can write (23) in matrix form too. Let us interpret $\mathbf {v_h}=(v_h^1,v_h^2,...,v_h^d)^T$ and $\mathbf {f_h}=(f_h^1,f_h^2,...,f_h^d)^T$ as $dN^d$-column vectors with the node values of the d components respectively. We also write the matrix form of the discrete Fourier transform as $\mathcal {F}_h$ and observe that $S_h(Q\mathbf {v_h})$ can be interpreted as the vector obtained by the product of the components of the node values of Q. We obtain the matrix formulation,

$$\begin{aligned} \mathbf {v_h}=\mathbf {f_h}+\mathcal {F}_h^{-1}\widehat{K}_h \mathcal {F}_h \; (Q_h)_{diag} \mathbf {v_h}, \end{aligned}$$

(25)

where $(Q_h)_{diag}$ is the $dN^d\times dN^d$ matrix whose components are the $N^d\times N^d$ matrixes $diag(S_h(Q_{\alpha \beta })),$ $\alpha ,\beta =1,...,d,$ contain the nodal values of $S_h(Q_{\alpha \beta })$ in the diagonal. Here $\widehat{K}_h$ is also a $dN^d \times dN^d$ square matrix with components $K_{\alpha \beta }$, $\alpha ,\beta =1,...,d,$ where each $\hat{K}_{\alpha \beta }$ is a diagonal $N^d\times N^d$ matrix with the Fourier coefficients of $K_{\alpha \beta }$.

Thus, the matrix form of the collocation method at the nodes reads,

$$\begin{aligned} A_h\mathbf{v_h} = \mathbf{f_h}, \quad A_h=I-\mathcal {F}_h^{-1}\widehat{K}_h \mathcal {F}_h \; (S_h)_{diag}, \end{aligned}$$

(26)

and at the Fourier coefficients,

$$\begin{aligned} \widehat{A}_h\mathbf{\widehat{v}_h} = \mathbf{\widehat{g}_h}, \quad \widehat{A}_h=I-\widehat{K} \mathcal {F}_h \; (S_h)_{diag}\mathcal {F}_h^{-1}, \quad \mathbf{\widehat{g}_h}=\mathcal {F}_h \mathbf{f_h} . \end{aligned}$$

(27)

5 Convergence of the trigonometric collocation method

In this section we prove a convergence result for the collocation method described above. The proof requires three preparatory lemmas.

Lemma 1

Let $\eta > d/2$ be.

• 1. If $u,v \in H^\eta$ then $uv \in H^\eta$ and $\Vert uv \Vert _\eta \le c_\eta \Vert u\Vert _\eta \Vert u\Vert _\eta$.

• 2. $\Vert \mathbf {v}-S_h \mathbf {v}\Vert _\nu \le c_{\nu , \eta , R} h^{\eta - \nu }\Vert \mathbf {v} \Vert _\eta \quad \text {for } 0 \le \nu \le \eta , \;\; \mathbf {v} \in (H^\eta )^d$.

The proof of this Lemma can be found in [15] or [14] (dimension two) and [11].

Lemma 2

The Fourier coefficients of the components of the matrix K defined in (17) satisfy the following estimate

$$\begin{aligned} |\widehat{K}_{\alpha \beta }(j)| \le c |j|^{-2} \log |j|, \quad j\in \mathbb {Z}^d, \quad |j|\ne 0, \quad d=2,3, \end{aligned}$$

(28)

for some constant $c>0$ that depends only on $\omega$, $\lambda$, $\mu$, R, $\rho$ and d.

We prove this lemma in Sect. 7 below.

Lemma 3

Assume that all the components in Q satisfy $Q_{\alpha \beta }\in H^\eta$, with $\eta > d/2$ and let $\varepsilon > 0$ be such that $\eta \ge 2-\varepsilon$ Then,

$$\begin{aligned} \Vert \mathcal {K}(Q \cdot ) - \mathcal {K}(S_h(Q \cdot )) \Vert _{\mathcal {L}((H^\eta )^d,(H^\eta )^d)} \le c_{\eta , \varepsilon ,R,Q}h^{2-\varepsilon }, \end{aligned}$$

(29)

where $\mathcal {L}((H^\eta )^d,(H^\eta )^d)$ denotes the space of linear and continuous functions in $(H^\eta )^d$ (of course the constant $c_{\eta , \varepsilon ,R,Q}$ also depends on the constant of the Lemma 2) .

Proof

As a consequence of Lemma 2 we have that $\mathcal {K} \in \mathcal {L} ((H^{\eta -(2-\varepsilon )})^d,(H^{\eta })^d)$ for any $\eta \in \mathbb {R}$ and $\varepsilon >0$. Assume that $\mathbf {v} \in (H^\eta )^\eta$. By Lemma 1,

$$\begin{aligned} \Vert \mathcal {K}(Q \mathbf {v} ) - \mathcal {K}(S_h(Q \mathbf {v} )) \Vert _\eta\le & {} c\Vert Q \mathbf {v}-S_hQ \mathbf {v} \Vert _{\eta -(2-\varepsilon )} \le c_{\eta , \varepsilon ,R}h^{2-\varepsilon } \Vert Q \mathbf {v}\Vert _\eta \\\le & {} c_{\eta , \varepsilon ,R} \max _{\alpha , \beta }{\Vert Q_{\alpha \beta }} \Vert _\eta h^{2-\varepsilon } \Vert \mathbf {v} \Vert _\eta \le c_{\eta , \varepsilon ,R,Q}h^{2-\varepsilon } \Vert \mathbf {v} \Vert _\eta . \end{aligned}$$

We have the following result

Theorem 4

Assume that Q and $\mathbf {f}$ satisfy (15) and the homogeneous problem (8) with $\mathbf {u}_i=0$ has only the trivial solution. Then, equation (18) has a unique solution $\mathbf {v} \in (H^\nu )^d$, $\eta > d/2$, and the collocation equation (23) has also a unique solution $\mathbf {v_h} \in (\mathcal {T}_h)^d$ for sufficiently small h. Moreover,

$$\begin{aligned} \Vert \mathbf {v_h} -\mathbf {v} \Vert _\eta \le c_{\eta , \nu , R, Q} \Vert \mathbf {v} - S_h \mathbf {v} \Vert _\eta \le c_{\eta , \nu , R, Q} \Vert \mathbf {v} \Vert _\nu h^{\nu -\eta }, \; \; \nu \ge \eta . \end{aligned}$$

(30)

Proof

This is a generalization of the analogous proof for the scalar case in [15]. From Lemmas 1 and 2 we have $\mathcal {K}(Q \cdot ) \in \mathcal {L}((H^\eta )^d,(H^\eta )^d)$ since

$$\begin{aligned} \Vert \mathcal {K} Q \mathbf {v}\Vert _\eta \le c \Vert Q \mathbf {v}\Vert _{\eta } \le c_\eta \max _{\alpha , \beta }\Vert Q_{\alpha \beta }\Vert _\eta \Vert \mathbf {v}\Vert _{\eta } \le c_{\eta , Q} \Vert \mathbf {v}\Vert _{\eta }. \end{aligned}$$

The existence and uniqueness for (18) is easily deduced from the inverse of the operator $I-\mathcal {K}(Q \cdot ) \in \mathcal {L}((H^\eta )^d,(H^\eta )^d)$. In fact this inverse exists since $\mathcal {K}(Q \cdot )$ is compact and the homogeneous integral equation (18) with $\mathbf {f}=0$ has only the trivial solution, since if there were a non-zero solution $\mathbf {v}$, it would be a solution of (8) with $u_i=0$ in $B(0,\rho )$ and extend to $\mathbb {R}^d$.

Concerning the collocation equation (23), we write

$$\begin{aligned} I-\mathcal {K}(S_hQ \cdot )=I-\mathcal {K}(Q \cdot )+\mathcal {K}(Q \cdot )-\mathcal {K}(S_hQ \cdot ). \end{aligned}$$

$I-\mathcal {K}(Q \cdot )$ admits an inverse in $\mathcal {L}((H^\eta )^d,(H^\eta )^d)$. On the other hand by (29) we have

$$\begin{aligned} \Vert \mathcal {K}(Q \cdot ) -\mathcal {K}(S_h Q \cdot ) \Vert _{\mathcal {L}(H^\eta )^d, (H^\eta )^d)} \le c_{\eta , \varepsilon , R, Q} h^{2-\varepsilon }, \;\; \eta >d/2 \; \text { and } \eta \ge 2-\varepsilon , \end{aligned}$$

then if we take h such that

$$\begin{aligned} \Vert \mathcal {K}(Q \cdot ) -\mathcal {K}( S_hQ \cdot ) \Vert _{\mathcal {L}(H^\eta )^d, (H^\eta )^d)}\le & {} c_{\eta , \varepsilon , R, Q} h^{2-\varepsilon } \\< & {} \frac{1}{\Vert (I-\mathcal {K}(Q\cdot ))^{-1} \Vert _{\mathcal {L}((H^\eta )^d, (H^\eta )^d)}} , \end{aligned}$$

then we can guarantee the existence of the inverse of the operator $I-\mathcal {K}(S_hQ \cdot )$ in $\mathcal {L}((H^\eta )^d, (H^\eta )^d)$, (see Corollary 1.1.2 of [14]), and therefore the existence and uniqueness of solution $\mathbf {v}$ of (23) in $(H^\eta )^d$. But if $\mathbf {v}$ is a solution of (23), then $\mathbf {v}$ is necessarily in $(\mathcal {T}_h)^d$.

We now obtain (30). First of all observe that from (18) and (23) we obtain

$$\begin{aligned}{}[I-\mathcal {K} (S_h Q \; \cdot )] (\mathbf{v}- \mathbf{v_h})= & {} \mathbf{v} - \mathcal {K} (S_h Q \; \mathbf{v}) - \mathbf{f_h} + S_h \mathcal {K} ( Q \; \mathbf{v}) - S_h\mathcal {K} ( Q \; \mathbf{v})\\= & {} \mathbf{v}-S_h\mathbf{v} + S_h \mathcal {K} ( Q \; \mathbf{v}) - \mathcal {K} (S_h Q \; \mathbf{v}). \end{aligned}$$

As $[I-\mathcal {K} (S_h Q \; \cdot )]$ is invertible in $\mathcal {L}((H^\eta )^d,(H^\eta )^d)$, for sufficiently small h, it is enough to estimate the second hand term in this last expression. For the first two terms, by Lemma 1, we have,

$$\begin{aligned} \Vert \mathbf{v}-S_h\mathbf{v} \Vert _\eta \le c_{\eta , \mu ,R}h^{\nu -\eta } \Vert \mathbf{v} \Vert _\nu , \quad \eta \le \nu . \end{aligned}$$

(31)

Now we estimate $S_h \mathcal {K} - \mathcal {K}S_h$ as a linear operator in $(H^\eta )^d$. Note that the projector operator $P_h$ commutes with $\mathcal {K}$. To simplify we prove it only for the case $d=2$. For $\mathbf{w}= \sum _{j\in \mathbb {Z}^2}(w^1(j),w^2(j))^T \varphi _j$, we have

$$\begin{aligned} \mathcal {K} P_h \mathbf{w}= & {} \mathcal {K} \sum _{j\in \mathbb {Z}_h^d} \left( \begin{array}{c} \widehat{w}^1(j) \\ \widehat{w}^2(j) \end{array} \right) \varphi _j \\= & {} \sum _{j\in \mathbb {Z}_h^d} \left( \begin{array}{cc} \widehat{K}_{11}(j) &{} \widehat{K}_{12}(j) \\ \widehat{K}_{21} (j) &{} \widehat{K}_{22} (j) \end{array} \right) \left( \begin{array}{c} \widehat{w}^1(j) \\ \widehat{w}^2(j) \end{array} \right) \varphi _j \\= & {} P_h \sum _{j\in \mathbb {Z}^d} \left( \begin{array}{cc} \widehat{K}_{11}(j) &{} \widehat{K}_{12}(j) \\ \widehat{K}_{21} (j) &{} \widehat{K}_{22} (j) \end{array} \right) \left( \begin{array}{c} \widehat{w}^1(j) \\ \widehat{w}^2(j) \end{array} \right) \varphi _j = P_h \mathcal {K} \mathbf{w} . \end{aligned}$$

In particular, $(S_h \mathcal {K}-\mathcal {K} S_h)=0$ on $(\mathcal {T}_h)^d$. Therefore,

$$\begin{aligned}&\Vert (S_h \mathcal {K}-\mathcal {K} S_h) ( Q \; \mathbf{v})\Vert _\eta \le \Vert (S_h \mathcal {K}-\mathcal {K} S_h) ( P_h(Q \; \mathbf{v}))\Vert _\eta \\&\qquad + \Vert (S_h \mathcal {K}-\mathcal {K} S_h) ( (I-P_h)(Q \; \mathbf{v}))\Vert _\eta \\&\quad = \Vert (S_h \mathcal {K}-\mathcal {K} S_h) ( (I-P_h)(Q \; \mathbf{v}))\Vert _\eta \le \Vert S_h \mathcal {K} ( (I-P_h)(Q \; \mathbf{v}))\Vert _\eta \\&\qquad + \Vert \mathcal {K} S_h ( (I-P_h)(Q \; \mathbf{v}))\Vert _\eta . \end{aligned}$$

The two terms here are estimated in a similar way. For the first one, let $\varepsilon$ be such that $0<\varepsilon <2$,

$$\begin{aligned}&\Vert S_h \mathcal {K} ( (I-P_h)(Q \; \mathbf{v}))\Vert _\eta \le \Vert \mathcal {K} ( (I-P_h)(Q \; \mathbf{v}))\Vert _\eta \\&\quad \le c_R \Vert (I-P_h)(Q \; \mathbf{v})\Vert _{\eta -(2-\varepsilon )} \le c_{\eta , \nu ,R} h^{2- \varepsilon +\nu -\eta } \Vert Q \; \mathbf{v}\Vert _\nu \\&\quad \le c_{\eta , \nu , R,Q} h^{2-\varepsilon +\nu -\eta } \Vert \mathbf{v}\Vert _\nu . \end{aligned}$$

From the above inequality and (31) we obtain (30).

The trigonometric collocation provides a numerical method to approximate the solution of (18), which coincides with the solution of (8) in $x\in B(0,\rho )$. Outside this ball we can approximate the solution of (8) by a suitable discretization of formula (19). For example, with the trapezoidal rule we obtain,

$$\begin{aligned} \mathbf {v}(x)=\mathbf {f}(x)+h^d\sum _{j \in \mathbb {Z}^d_h} \Phi (x-jh) Q(jh)\mathbf {v_h}(jh),\quad |x|>B(0,\rho ). \end{aligned}$$

(32)

The error can be easily estimated from Theorem 4,

$$\begin{aligned} | \mathbf {v_h}(x) - \mathbf {v}(x) | \le c(x) h^{\nu } \Vert \mathbf {v} \Vert _\nu , \quad \nu >2, \end{aligned}$$

where $c(x)=c|x|^{-(d-1)/2}$, c independent of x and h and $|x|^{-(d-1)/2}$ comes from the fundamental tensor of Lamé operator (see Sect. 7) and the asymptotic behaviour of $H^{(1)}_\nu (r)$ when $r\rightarrow \infty$.

Note that c(x) does not blow up as $|x|\rightarrow \rho$, even if $\Phi (x-jh)$ becomes singular for some values of j. This is due to the fact that $B(0,\rho )$ has compact support included in Q and therefore the terms $\Phi (x-jh) Q(jh)$ in (32) vanish for those j. This is in contrast with the method in [15], where the error bound is lost for $|x|\rightarrow \rho$.

6 Numerical approximation of scattering data

As we said in the introduction we usually consider incident waves as plane waves either transverse (plane s-waves) or longitudinal (plane p-waves). For an incident p-wave $\mathbf {u}_i^p$ in the form (10) we can define two different scattering amplitudes given in (11) and (12). These can be written as (see [3] or [4])

$$\begin{aligned} \mathbf {v}_{p,\infty }^p\left( \omega , \theta , x/|x|\right)&=\frac{1}{2\mu +\lambda }\,\Pi _{x/|x|}\widehat{Q\mathbf {u}_p}\left( k_{p}x/|x|\right) , \end{aligned}$$

(33)

$$\begin{aligned} \mathbf {v}_{p,\infty }^s\left( \omega , \theta , x/|x|\right)&=\frac{1}{\mu }\,(\mathrm {I}-\Pi _{x/|x|})\widehat{Q\mathbf {u}_p}\left( k_{s}x/|x|\right) , \end{aligned}$$

(34)

where $\mathbf {u}_p$ is the solution of (8) with $\mathbf {u}_i=\mathbf {u}_i^p$. Here $\Pi _{x/|x|}$ is the orthogonal projection onto the line defined by the vector x.

Analogously, for an incident s-wave in the form (9) we can define two different scattering amplitudes given in (13). These can be written as

$$\begin{aligned} \mathbf {v}_{s,\infty }^p\left( \omega , \theta ,\varphi , x/|x|\right)&=\frac{1}{2\mu +\lambda }\,\Pi _{x/|x|}\widehat{Q\mathbf {u}_s}\left( k_{p}x/|x|\right) , \end{aligned}$$

(35)

$$\begin{aligned} \mathbf {v}_{s,\infty }^s\left( \omega , \theta ,\varphi , x/|x|\right)&=\frac{1}{\mu }\,(\mathrm {I}-\Pi _{x/|x|})\widehat{Q\mathbf {u}_s}\left( k_{s}x/|x|\right) , \end{aligned}$$

(36)

where now $\mathbf {u}_s$ is the solution of (8) with $\mathbf {u}_i=\mathbf {u}_i^s$.

Natural approximations of these scattering amplitudes are given by,

$$\begin{aligned} \mathbf {v}_{p,\infty , h}^p( \omega ,\theta ,\theta ' )= & {} \frac{1}{2\mu +\lambda }\, h^d \sum _{j\in \mathbb {Z}_h^d} e^{-i k_p\theta ' \cdot j h}\left( Q\mathbf {u}_{p,h}( jh) \cdot \theta '\right) \theta ', \\ \mathbf {v}_{p,\infty ,h}^s( \omega ,\theta , \theta ')= & {} \frac{1}{\mu }\, h^d \sum _{j\in \mathbb {Z}_h^d} e^{-i k_s\theta ' \cdot j h}\left[ Q\mathbf {u}_{p,h}( jh) - \left( Q\mathbf {u}_{p,h}( jh) \cdot \theta '\right) \theta ' \right] , \\ \mathbf {v}_{s,\infty , h}^p( \omega ,\theta ,\varphi ,\theta ' )= & {} \frac{1}{2\mu +\lambda }\, h^d \sum _{j\in \mathbb {Z}_h^d} e^{-i k_p\theta ' \cdot j h}\left( Q\mathbf {u}_{s,h}( jh) \cdot \theta '\right) \theta ', \\ \mathbf {v}_{s,\infty ,h}^s( \omega ,\theta ,\varphi , \theta ')= & {} \frac{1}{\mu }\, h^d \sum _{j\in \mathbb {Z}_h^d} e^{-i k_s\theta ' \cdot j h}\left[ Q\mathbf {u}_{s,h}( jh) - \left( Q\mathbf {u}_{s,h}( jh) \cdot \theta '\right) \theta ' \right] , \end{aligned}$$

where $\omega >0$ and $\theta ,\theta '\in \mathbb {S}^{d-1}$, $\varphi \in \mathbb {S}^{d-2}$ and

$$\begin{aligned} Q\mathbf {u}_{r,h}( jh) =(S_h (Q\mathbf {u}_r))( jh)=Q(jh)\mathbf {u}_r(jh) , \mathbf {r}=\mathbf {p} \text { or } \mathbf {s}. \end{aligned}$$

7 Fourier coefficients of the Green function

In this section we prove Lemma 2. We divide this section in two sections where we consider separately the cases $d=2$ and $d=3$.

7.1 The case $d=2$

The fundamental solution when $d=2$ is given by (see [12]),

$$\begin{aligned} \Phi (x)=\Phi _1(|x|) I+\Phi _2(|x|) J(x), \end{aligned}$$

where for $x\in \mathbb {R}^2\backslash \{0\}$ (identified with a matrix $1 \times 2$) the matrix J is given by

$$\begin{aligned} J(x)=\frac{x^Tx}{|x|^2}, \end{aligned}$$

and for each $v>0$, the functions $\Phi _1$ and $\Phi _2$ are given by

$$\begin{aligned} \Phi _1(v)= & {} \frac{i}{4\mu } H^{(1)}_0 (k_s v)-\frac{i}{4\omega ^2v}\left[ k_s H^{(1)}_1 (k_s v)- k_p H^{(1)}_1 (k_p v) \right] ,\\ \Phi _2(v)= & {} \frac{i}{4\omega ^2}\left[ \frac{2k_s}{v} H^{(1)}_1 (k_s v)- k_s^2H^{(1)}_0 (k_s v) \right. \\&\left. - \frac{2k_p}{v} H^{(1)}_1 (k_p v)+ k_p^2H^{(1)}_0 (k_p v) \right] , \end{aligned}$$

with $H^{(1)}_k$ the Hankel function of first kind and order k. For $v\rightarrow 0$, $\Phi _1 \sim - (k_s^2+k_p^2)/(4\pi \omega ^2) \log v$, while $\Phi _2 \sim (k_p^4-k_s^4)/(16\pi \omega ^2)v^2\log (v)$, so that the integral in (8) is weakly singular. Thus, we can write

$$\begin{aligned} \Phi _n(v)=\frac{1}{\pi } \log v \Psi _n(v)+ \Upsilon _n (v), v >0, \; \; n=1,2, \end{aligned}$$

(37)

where $\Psi _n, \Upsilon _n \in C^\infty [0,\infty )$, $n=1,2$, are even functions.

On the other hand, we remind that

$$\begin{aligned} K_{\alpha \beta }(x)= \left( \Phi _1(|x|)\delta _{\alpha \beta } + \Phi _2(|x|)\frac{x_\alpha x_\beta }{|x|^2} \right) \psi (|x|), \quad \alpha ,\beta =1,2. \end{aligned}$$

(38)

Let $a>0$ be a number to be determined later, $j \in \mathbb {Z}^2$ and we assume that $|j|^{-a } \le \min \{1/2, \rho \}$. From now on C indicates a positive and universal constant which depends only on $\omega$, $\Phi _n$ $n=1,2$, $\lambda$, $\mu$, $\rho$, R, d and a.

We can write

$$\begin{aligned} \widehat{K}_{\alpha \beta }(j)=\int _{B(0,|j|^{-a})} K_{\alpha \beta }(x)\varphi _{-j}(x)dx+\int _{|j|^{-a} \le |x| \le R} K_{\alpha \beta }(x)\varphi _{-j}(x)dx. \end{aligned}$$

(39)

We start by estimating the first integral in (39), essentially by using the size of the ball $B(0,|j|^{-a})$. From (37) and (38)

$$\begin{aligned} \left| \int _{B(0,|j|^{-a})} K_{\alpha \beta }(x)\varphi _{-j}(x)dx \right| \le C \int _{B(0, |j|^{-a})} | \log |x|| dx \le C\frac{ \log |j|}{|j|^{2 a}}. \end{aligned}$$

Note that this first term satisfies the bound in (28) as soon as $a\ge 1$.

To deal with the second integral in (39) we use that $\varphi _j=-\frac{R^2}{\pi ^2|j|^2}\Delta \varphi _j$ and Green’s formula,

$$\begin{aligned}&\int _{|j|^{-a} \le |x| \le R} K_{\alpha \beta }(x)\varphi _{-j}(x)dx\\&\quad =- \frac{R^2}{\pi ^2|j|^2}\int _{|j|^{-a} \le |x| \le R} K_{\alpha \beta }(x)\Delta \varphi _{-j}(x)dx \\&\quad =-\frac{R^2}{\pi ^2|j|^2}\int _{|j|^{-a} \le |x| \le R} \Delta K_{\alpha \beta }(x) \varphi _{-j}(x)dx \\&\qquad + \frac{R^2}{\pi ^2|j|^2}\int _{|x|=R} \left( K_{\alpha \beta }(x)\frac{ \partial \varphi _{-j}}{\partial r}(x) -\varphi _j(x)\frac{\partial K_{\alpha \beta }}{\partial r}(x) \right) d \sigma (x) \\&\qquad - \frac{R^2}{\pi ^2|j|^2}\int _{|x|=|j|^{-a}} \left( K_{\alpha \beta }(x)\frac{ \partial \varphi _{-j}}{\partial r}(x) -\varphi _j(x)\frac{\partial K_{\alpha \beta }}{\partial r}(x) \right) d \sigma (x). \end{aligned}$$

Note that we only have to prove that the three integrals in the right hand side of the second equality above can be bounded by $C \log |j|$. The second one is obviously bounded since $K_{ \alpha \beta }$ is $C^\infty$ in $0 < |x | \le R$. The same argument applies to the first integral in the annulus $\rho \le |x | \le R$, so that we can reduce ourselves to the subregion $|j|^{-a}<|x|<\rho$. Thus, we only have to show that

$$\begin{aligned} \left| \int _{|j|^{-a} \le |x| \le \rho } \Delta \Phi _{\alpha \beta }(x) \varphi _{-j}(x)dx \right| \le C \log |j|, \end{aligned}$$

(40)

and

$$\begin{aligned} \left| \int _{|x|=|j|^{-a}} \left( \Phi _{\alpha \beta }(x)\frac{ \partial \varphi _{-j}}{\partial r}(x) -\varphi _j(x)\frac{\partial \Phi _{\alpha \beta }}{\partial r}(x) \right) d \sigma (x) \right| \le C \log |j|, \end{aligned}$$

(41)

where we have used that $K_{\alpha \beta }$ is equal to $\Phi _{\alpha \beta }$ in $B(0,\rho )$.

A straightforward computation shows that

$$\begin{aligned} \Delta \Phi _{\alpha \beta }(x)= & {} \Delta \Phi _1(|x|) \delta _{\alpha \beta }+ \Delta \Phi _2 (|x|) \frac{x_\alpha x_\beta }{|x|^2}+(-1)^{\frac{\alpha +\beta }{2}}\Phi _2(|x|)2\frac{x_1^2-x_2^2}{|x|^4}\delta _{\alpha \beta }\nonumber \\&-2\Phi _2(|x|) \frac{x_1x_2}{|x|^4}(1-\delta _{\alpha \beta }), \end{aligned}$$

(42)

and

$$\begin{aligned} \frac{\partial \Phi _{\alpha \beta }}{\partial r}(x)= \left( \nabla \Phi _1(|x|) \cdot \frac{x}{|x|}\right) \delta _{\alpha \beta }+\left( \nabla \Phi _2(|x|) \cdot \frac{x}{|x|}\right) \frac{x_\alpha x_\beta }{|x|^2} , \end{aligned}$$

(43)

where for $n=1,2$ we have

$$\begin{aligned} \nabla \Phi _n(|x|)= & {} \left( \frac{1}{\pi |x|} \Psi _n(|x|)+ \frac{\log |x|}{\pi }\Psi '_n(|x|)+\Upsilon '(|x|) \right) \frac{x}{|x|}, \end{aligned}$$

(44)

$$\begin{aligned} \Delta \Phi _n(|x|)= & {} \frac{2+\log |x|}{\pi |x|}\Psi '_n(|x|)+\frac{\log |x| }{\pi } \Psi ''_2(|x|)+\frac{1}{|x|}\Upsilon '_n(|x|)+\Upsilon ''_n(|x|). \end{aligned}$$

(45)

From (42) and (45) we have that

$$\begin{aligned} \left| \Delta \Phi _{\alpha \beta }(x) \right| \le C \left( \frac{| \log |x||}{|x|}+\frac{1}{|x|^2} \right) \le \frac{C}{|x|^2}, \end{aligned}$$

and

$$\begin{aligned} \left| \int _{|j|^{-a} \le |x| \le \rho } \Delta \Phi _{\alpha \beta }(x) \varphi _{-j}(x)dx \right| \le C \int _{|j|^{-a}}^\rho \frac{dt}{t} \le C \log |j|, \end{aligned}$$

so (40) holds.

Finally, to prove estimate (41) we observe that $\frac{\partial \varphi _{-j}}{\partial r}(x)=-\frac{i \pi }{R} (j \cdot x) \varphi _{-j}(x)$, and the following

$$\begin{aligned} \left| \Phi _n(|x|) \right| \le C (1+ \log |j|), \left| \nabla \Phi _n(|x|) \right| \le C ( 1+ \log |j| + |j|^{a}), |x|=|j|^{-a}, \end{aligned}$$

for $n=1,2$, which are easily obtained from (44) and (37). Therefore,

$$\begin{aligned}&\left| \int _{|x|=|j|^{-a}} \left( \Phi _{\alpha \beta }(x)\frac{ \partial \varphi _{-j}}{\partial r}(x) -\varphi _j(x)\frac{\partial \Phi _{\alpha \beta }}{\partial r}(x) \right) d \sigma (x) \right| \\&\quad \le C\left( (1+ \log |j|)|j| + ( 1+ \log |j| + |j|^{a}) \right) |j|^{-a} \\&\quad \le C \left( 1 + |j|^{1-a} \log |j|+ |j|^{-a} \log |j| \right) . \end{aligned}$$

If we take $a =1$, the above estimate gives (41).

7.2 The case $d=3$

The proof is analogous to the case $d=2$ so that we omit some details. The fundamental solution in dimension $d=3$ is given by (see [1])

$$\begin{aligned} \Phi (x)= \Phi _1(|x|)I+\Phi _2(|x|)J(x) , \end{aligned}$$

and as in the case $d=2$, $J(x)=\frac{x^Tx}{|x|^2}$, where for $v>0$

$$\begin{aligned} \Phi _1(v) =\frac{k_s^2}{4\pi \omega ^2}\frac{e^{ik_s v}}{v} + \frac{1}{4\pi \omega ^2}\left( \frac{ik_s e^{ik_s v} - ik_pe^{ik_p v}}{v^2} - \frac{e^{ik_s v}-e^{ik_p v}}{v^3} \right) , \end{aligned}$$

and

$$\begin{aligned} \Phi _2(v)= & {} \frac{1}{4\pi \omega ^2}\left( -\frac{k_s^2e^{ik_sv}-k_p^2e^{ik_pv}}{v} - 3\frac{ik_se^{ik_sv}-ik_pe^{ik_pv}}{v^2} \right. \\&\left. + 3\frac{e^{ik_sv}-e^{ik_pv}}{v^3}\right) . \end{aligned}$$

It can be seen that

$$\begin{aligned} \Phi _1(v)= & {} \frac{k_s^2}{4\pi \omega ^2}\frac{e^{ik_sv}}{v}+ \frac{k_p^2-k_s^2}{8\pi \omega ^2v}+\Psi _1(v) , \end{aligned}$$

(46)

$$\begin{aligned} \Phi _2(v)= & {} \frac{k_s^2-k_p^2}{8\pi \omega ^2v}+\Psi _2(v), \end{aligned}$$

(47)

where $\Psi _1$ and $\Psi _2$ are in $C^\infty [0,\infty )$ and null when $k_p=k_s$.

From (46) and (47) we have

$$\begin{aligned} \Phi _{\alpha \beta }(x)= & {} \left( \frac{k_s^2 e^{ik_s|x|}}{4 \pi \omega ^2|x|}+ \frac{k_p^2-k_s^2}{8\pi \omega ^2|x|}+\Psi _1(|x|) \right) \delta _{\alpha \beta } \\&+\left( \frac{k_s^2-k_p^2}{8\pi \omega ^2|x|}+\Psi _2(|x|) \right) \frac{x_\alpha x_\beta }{|x|^2}. \end{aligned}$$

Again C will indicate a universal constant, depending on the same parameters as in the case $d=2$. Let $j\in \mathbb {Z}^3$, $a>0$ to be chosen later and we assume that $|j|^{-a} \le \min \{ 1/2, \rho \}$.

$$\begin{aligned} \widehat{K_{\alpha \beta }}(j) =\int _{B(0,|j|^{-a})}K_{\alpha \beta }(x)\varphi _{-j}(x)dx +\int _{|j|^{-a} \le |x| \le R}K_{\alpha \beta }(x)\varphi _{-j}(x)dx. \end{aligned}$$

(48)

For the first integral we observe that

$$\begin{aligned} K_{\alpha \beta }(x) \le C \left( 1+ \frac{1}{|x|} \right) , x \in B(0,R). \end{aligned}$$

Therefore,

$$\begin{aligned} \left| \int _{|x| \le |j|^{-a}}K_{\alpha \beta }(x)\varphi _{-j}(x)dx \right| \le C \int _{0}^{|j|^{-a}} \left( t +t^2 \right) dt \le \frac{C}{|j|^{2 a}}. \end{aligned}$$

(49)

For the second integral in (48) we proceed as in the case $d=2$

$$\begin{aligned}&\int _{|j|^{-a} \le |x| \le R}K_{\alpha \beta }(x)\varphi _{-j}(x)dx\nonumber \\&\quad =-\frac{R^2}{\pi ^2|j|^2}\int _{|j|^{-a} \le |x| \le R}K_{\alpha \beta }(x ) \Delta \varphi _{-j}(x)dx \nonumber \\&\quad =-\frac{R^2}{\pi ^2|j|^2}\int _{|j|^{-a} \le |x| \le R} \Delta K_{\alpha \beta }(x ) \varphi _{-j}(x)dx \nonumber \\&\qquad +\int _{|x|=R} \left( K_{\alpha \beta }(x) \frac{\partial \varphi _{-j}}{\partial r}(x)- \varphi _{-j}(x) \frac{\partial K_{\alpha \beta }}{\partial r}(x) \right) d \sigma (x) \nonumber \\&\qquad -\int _{|x|=|j|^{-a}} \left( K_{\alpha \beta }(x) \frac{\partial \varphi _{-j}}{\partial r}(x)- \varphi _{-j}(x) \frac{\partial K_{\alpha \beta }}{\partial r}(x) \right) d \sigma (x) . \end{aligned}$$

(50)

$K_{\alpha \beta }$ is a $C^\infty$ function in $\min \{ 1/2, \rho \} \le |x| \le R$, so $\Delta K_{\alpha \beta }$ in bounded in this region. Since $\psi (|x|)=1$ in $B(0,\rho )$, it will be sufficient to show that

$$\begin{aligned} \left| \int _{|j|^{-a} \le |x| \le \frac{1}{2} }\Delta \Phi _{\alpha \beta }(x ) \varphi _{-j}(x)dx \right| \le C \log |j|, \end{aligned}$$

(51)

and

$$\begin{aligned} \left| \int _{|x|=|j|^{-a}} \left( \Phi _{\alpha \beta }(x) \frac{\partial \varphi _{-j}}{\partial r}(x)- \varphi _{-j}(x) \frac{\partial \Phi _{\alpha \beta }}{\partial r}(x) \right) d \sigma (x) \right| \le C \log |j|. \end{aligned}$$

(52)

A simple calculation gives us for $|x| \in [|j|^{-a},\frac{1}{2}]$ and $n=1,2$ that

$$\begin{aligned} |\Phi _n(|x|)| \le \frac{C}{|x|},\quad |\nabla \Phi _n(|x|)|\le \frac{C}{|x|^2}, \quad \left| \frac{\partial \Phi _n}{\partial r}(|x|)\right| , \le \frac{C}{|x|^2},\quad |\Delta \Phi _n(|x|)|\le \frac{C}{|x|}. \end{aligned}$$

Moreover, if $g_{\alpha \beta }(x)=\frac{x_\alpha x_\beta }{|x|^2}$ then $|\nabla g_{\alpha \beta }(x)| \le \frac{C}{|x|}$ and $|\Delta g_{\alpha \beta }(x)| \le \frac{C}{|x|^2}$.

Table 1 Experiment 1: error estimate as h decreases.

From these estimates we obtain

$$\begin{aligned} \left| \Phi _{\alpha \beta } \right| \le \frac{C}{|x|}, \left| \nabla \Phi _{\alpha \beta }(x) \right| \le \frac{C}{|x|^2}, \left| \Delta \Phi _{\alpha \beta }(x) \right| \le \frac{C}{|x|^3} , \left| \frac{\partial \Phi _{\alpha \beta }}{\partial r}(x) \right| \le \frac{C}{|x|^2}. \end{aligned}$$

We start by estimating (51) by using the above estimates

$$\begin{aligned} \left| \int _{|j|^{-a} \le |x| \le \frac{1}{2}} \Delta \Phi _{\alpha \beta }(x ) \varphi _{-j}(x)dx \right| \le C \int _{|j|^{-a}}^{1/2} \frac{1}{t}d t \le C \log |j|. \end{aligned}$$

Fig. 1

Numerical results of experiment 2: $Re\; (\mathbf{v}_s( x)\cdot \theta ^\perp )$ corresponding to a transverse incident wave with incident angle $\theta =(\cos \pi /4, \sin \pi /4)$ and $\omega =50$, both in the computational domain (left) and the subdomain where the approximation to the continuous solution holds (right)

To study (52) we use the same estimates we used to obtain (51) and $\frac{\partial \varphi _{-j}}{\partial r}(x)=-i \frac{\pi }{R}\frac{j \cdot x}{|x|} \varphi _{-j}(x).$ We have

$$\begin{aligned} \left| \int _{|x|=|j|^{-a}} \Phi _{\alpha \beta }(x) \frac{\partial \varphi _{-j}}{\partial r}(x) d \sigma (x) \right| \le C |j|^{1+a}\int _{|x|=|j|^{-a}}d\sigma (x) \le C |j|^{1-a}, \end{aligned}$$

and

$$\begin{aligned} \left| \int _{|x|=|j|^{-a}} \varphi _{-j}(x) \frac{\partial \Phi _{\alpha \beta }}{\partial r}(x) d \sigma (x) \right| \le C |j|^{2 a} \int _{|x|=|j|^{-a}} d \sigma (x)\le C. \end{aligned}$$

If we take $a =1$, from the inequalities above, (48), (49), (50), (51) and (52) we obtain estimate (28).

8 Implementation and numerical experiments

The discretization of the Lippmann–Schwinger equation (14) reduces to the finite dimensional implicit system (25). The solution requires,

• 1. An approximation of the Fourier coefficients $\hat{K}_h$.

• 2. A solver for the linear system. Here we use the gmres routine in MATLAB.

To approximate the Fourier coefficients $\hat{K}_{\alpha \beta }$ we consider the trapezoidal rule. This can be interpreted as the discrete Fourier transform of $K_{\alpha \beta }$ in a suitable uniform mesh centered in the origin. Therefore we use the fft algorithm in MATLAB.

Fig. 2

Numerical results of experiment 2: We show transverse $Re\; (\mathbf{v}_s( x)\cdot \theta ^\perp )$ (left) and longitudinal $Re\; (\mathbf{v}_p(x)\cdot \theta )$ (right) waves corresponding to a transverse incident wave with incident angle $\theta =(\cos \pi /4, \sin \pi /4)$ and different frequencies $\omega =10, 50$ and 100

Fig. 3

Numerical results of experiment 2: We show transverse $Re\; (\mathbf{v}_s( x)\cdot \theta ^\perp )$ (left) and longitudinal $Re\; (\mathbf{v}_p(x)\cdot \theta )$ (right) waves corresponding to a longitudinal incident wave with incident angle $\theta =(\cos \pi /4, \sin \pi /4)$ and different frequencies $\omega =10,50$ and 100

We must be careful since the Green function is singular at the origin. This affects to the numerical approximation of the Fourier coefficients in (24), where the Green tensor appears in the integrand. In particular, if we use the trapezoidal rule to approximate the integral, we obtain a singular value for this integral. To avoid this problem we simply replace the value at the origin by zero. This does not affect significantly to the accuracy of the trapezoidal rule. For example, in dimension $d=2$ the functions in the Green tensor have a logarithmic singularity at the origin. The error derived by our choice affects the quadrature formula only near $x=0$. More precisely, it affects the ball centered at $x=0$ and radius h (the mesh size) B(0, h). The real value of the integral in this ball is easily estimated by

$$\begin{aligned} \int _{B(0,h)} \log |x| dx =2\pi \int _0^h r \log (r) \; dr \sim h^2 \log h. \end{aligned}$$

Thus, if we replace the integral by the value obtained with the trapezoidal rule and our choice, the error is basically the same as the one associated to the trapezoidal rule for smooth functions.

Now we show some numerical experiments that illustrate the convergence of the numerical method in dimension $d=2$ and provide numerical approximations of scattering data.

Experiment 1  In this first experiment we illustrate the convergence of the solution of the Lippmann-Schwinger equation by considering an analytical solution. We define the vector function

$$\begin{aligned} \mathbf{g} (x)=\chi _{|x|<1}(1-|x|^2)^4(1, 1). \end{aligned}$$

Then, $\mathbf{v}=(\Delta ^*+\omega ^2I)\mathbf{g}$, $\mathbf{f}=\mathbf{v}-\mathbf{g}$ and $Q=I$ solve the Lippmann-Schwinger equation (14). In table 1 we illustrate the convergence of the solution as N grows.

Fig. 4

Numerical results of experiment 2: scattering amplitudes corresponding to a transverse incident wave with incident angle $\theta =(\cos \pi /4, \sin \pi /4)$ (upper simulations), and longitudinal incident wave with the same incident angle $\theta =(\cos \pi /4, \sin \pi /4)$ (lower simulations). The horizontal axis corresponds to the angle $\theta _a'\in [0,2\pi )$ such that $\theta '=(\cos \theta _a',\sin \theta _a')\in \mathbb {S}^1$ and the vertical axis is the frequency $\omega \in (0,100)$

Experiment 2  Here we show an example of the scattering fields and amplitudes that can be obtained with the numerical method presented in this paper. We focus on dimension $d=2$. Unfortunately we do not have analytical solutions in this case to compare the approximation.

We consider the Lamé parameters $\lambda =1$, $\mu =4$ and the potential given by

$$\begin{aligned} Q(x)=q(x)\; I, \quad q(x)=\chi _{0.6<|x|<0.8}+1.2 \chi _{|x_1|+|x_2|<0.2} \end{aligned}$$

which has compact support in B(0, 1).

We fix the angle of an incident transverse wave $\theta =(\cos \pi /4, \sin \pi /4)$ and compute $\mathbf{v}_h$, by approximating (14), that we decompose into the longitudinal and transverse waves $\mathbf{v}_h = \mathbf{v}_{h,s}+\mathbf{v}_{h,p}$. To compute $\mathbf{v}_{h,p}$ and $\mathbf{v}_{h,s}$ we use (4). In fact, for any vector field $\mathbf{v}_h \in \mathcal {T}_h$,

$$\begin{aligned} \mathbf{v}_h= & {} \sum _{j\in \mathbb {Z}^d_h} \left( \begin{array}{c} \hat{v}_h^1(j) \\ \hat{v}_h^2 (j) \end{array}\right) \varphi _j(x), \quad \mathbf{v}_{h,s}= \mathbf{v}_{h}-\mathbf{v}_{h,p}\\ \mathbf{v}_{h,p}= & {} - \frac{1}{k_p^2} \nabla div \; \mathbf{v}_h = \frac{\pi ^2}{R^2 k_p^2} \sum _{j\in \mathbb {Z}^2_h} j\otimes j \left( \begin{array}{c} \hat{v}_h^1(j) \\ \hat{v}_h^2 (j) \end{array}\right) \varphi _j(x) \in \mathcal {T}_h. \end{aligned}$$

In Fig. 1 we show the real part of the transverse wave $Re\; (\mathbf{v}_s(x)\cdot \theta ^\perp )$ (here $\theta ^\perp =(\cos 3\pi /4, \sin 3\pi /4)$) for $\omega =50$ both in the computational domain $[-2.1,2.1]\times [-2.1,2.1]$ and the domain where the approximation converges to the solution of the real continuous equation $[-1,1]\times [-1,1]$. In the computational domain the solution is periodic, due to the trigonometric basis that we use. Of course, this is not the case for the inner subdomain where we approximate the real solution.

Now we compare both the real parts of the longitudinal $Re\; (\mathbf{v}_p(x)\cdot \theta )$ and transverse $Re (\;\mathbf{v}_s(x)\cdot \theta ^\perp )$ solutions for transverse incident waves at different frequencies and the same angle $\theta =(\cos \pi /4, \sin \pi /4)$. Note that here the incident wave $u^s_i= e^{ik_s \theta \cdot x}\theta ^\perp$ is complex and so it is the scattered field. The real part (resp. imaginary part) corresponds to the real part (resp. imaginary part) of the incident wave. In particular, we observe how larger incident frequencies provide more complicated solutions. A similar comparison for the longitudinal incident wave $u^s_i= e^{ik_s \theta \cdot x}\theta$ is given in Fig. 3.

Finally, in Fig. 4 the sinogram with the scattering amplitudes corresponding to the real part of the transverse waves $Re\; (\mathbf{v}^s_s(\omega ,\theta ,\theta '))$ and longitudinal ones $Re \;(\mathbf{v}^s_p(\omega ,\theta ,\theta '))$, for a traverse incident wave $\mathbf{u_i^s}=e^{ik_s \theta } \theta ^\perp$, with $\theta =(\cos \pi /4, \sin \pi /4)$, different frequencies $\omega >0$ and angles $\theta '\in \mathbb {S}^1$ (upper simulations). In the lower simulations, we show the analogous sinograms corresponding to a longitudinal incident wave $\mathbf{u_i^p}=e^{ik_p \theta } \theta$, with $\theta =(\cos \pi /4, \sin \pi /4)$.

When considering a transverse incident wave (upper simulations in Fig. 4) we observe that transverse amplitudes are more concentrated for $\theta '=\theta =(\cos \pi /4, \sin \pi /4)$ and larger $\omega$ while longitudinal ones have smaller amplitude for $\theta '=\theta =(\cos \pi /4, \sin \pi /4)$ and $\theta '=\theta ^\perp =(\cos 3\pi /4, \sin 3\pi /4)$. On the other hand, for a longitudinal incident wave (lower simulations in Fig. 4) we observe the opposite phenomenon, i.e. transverse amplitudes have smaller amplitude for $\theta '=\theta =(\cos \pi /4, \sin \pi /4)$ and $\theta '=\theta ^\perp =(\cos 3\pi /4, \sin 3\pi /4)$, while longitudinal ones are more concentrated for $\theta '=\theta =(\cos \pi /4, \sin \pi /4)$ and larger $\omega$.