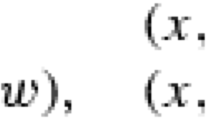Skip to main content
SpringerLink
Log in

Complex Lambda Length as Parameter for \(\mathrm{SL}(2,{\mathbb {C}})\) Representation Space of Punctured Surface Groups

  • Published:
Computational Methods and Function Theory Aims and scope Submit manuscript

Abstract

We introduced in Nakanishi and Näätänen (J Lond Math Soc 70:383–404, 2004) complex \(\lambda \)-lengths after Penner’s paper (Commun Math Phys 113:299–339, 1987) to give global coordinate systems for an \(\mathrm{SL}(2,{\mathbb {C}})\)-representation space of a punctured surface group. However, there the \(\lambda \)-lengths are defined only for a restricted class of ideal arcs in the surface. In this paper, we define complex \(\lambda \)-lengths for arbitrary ideal arcs in pursuit of a full analogy of Penner’s theory on the Teichmüller space.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Kra, I.: On lifting Kleinian groups to SL\((2,{\mathbb{C}})\). In: Differential Geometry and Complex Analysis, pp. 181–193. Springer, Berlin (1985)

  2. Maclachlan, C., Reid, A.W.: The Arithmetic of Hyperbolic 3-Manifolds, Graduate Texts in Math, vol. 219. Springer, Berlin (2003)

    Book  Google Scholar 

  3. Mosher, L.: A user’s guide to the mapping class group: once punctured surfaces, Geometric and computational perspectives on infinite groups (Mineapolis, MN and New Brusswick, NJ, 1994), DIMACS Ser. Discrete Math. Theoret. Comput. Sci., vol. 25, pp. 101–174. Amer. Math. Soc., Providence, RI (1996)

  4. Nakanishi, T., Näätänen, M.: The Teichmüller space of a punctured surface represented as a real algebraic space. Michigan Math. J. 42, 235–258 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  5. Nakanishi, T., Näätänen, M.: Complexification of lambda length as parameter for SL\((2,{\mathbb{C}})\) representation space of punctured surface groups. J. Lond. Math. Soc. 70, 383–404 (2004)

    Article  MATH  Google Scholar 

  6. Nakanishi, T.: A trace identity for parabolic elements of SL\((2,{\mathbb{C}})\). Kodai Math. J. 30, 1–18 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Penner, R.C.: The decorated Teichmüller space of punctured surfaces. Commun. Math. Phys. 113, 299–339 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  8. Penner, R.C.: Weil-Petersson volumes. J. Differ. Geom. 35, 559–608 (1992)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors wish to thank Tapani Kuusalo for a careful reading of the manuscript and for his many suggestions.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, University of Helsinki, PL 68 (Gustaf Hällströmin katu 2B), 00014 , Helsinki, Finland

    Marjatta Näätänen

  2. Department of Mathematics, Shimane University, Matue , 690-8504, Japan

    Toshihiro Nakanishi

Authors
  1. Marjatta Näätänen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Toshihiro Nakanishi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Toshihiro Nakanishi.

Additional information

Communicated by Bruce Palka.

Dedicated to the memory of Professor F. W. Gehring.

T. Nakanishi is supported by JSPS KAKENHI Grant Number 22540191.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Näätänen, M., Nakanishi, T. Complex Lambda Length as Parameter for \(\mathrm{SL}(2,{\mathbb {C}})\) Representation Space of Punctured Surface Groups. Comput. Methods Funct. Theory 14, 559–575 (2014). https://doi.org/10.1007/s40315-014-0077-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40315-014-0077-8

Keywords

Mathematics Subject Classification (2010)

Search

Navigation