The distributed no-idle permutation flowshop scheduling problem with due windows

Abstract

The distributed no-idle permutation flowshop scheduling problem has gained significant attention as a prominent area of research in recent years, particularly in industries where setup operations are so expensive that reactivating the machines is not cost-effective. This study addresses an extension of the distributed permutation flowshop scheduling problem with no-idle and due window constraints. The aim is to determine the job assignments to the factories and their sequences in each factory that provide the minimum total weighted earliness and tardiness (TWET) penalties considering due windows. This study is the first to formulate this problem, offering four different mathematical models, and presents a benchmark to examine different problem cases that may arise in practical applications. Furthermore, to effectively solve the diverse problem instances, two hybrid metaheuristic algorithms based on the Iterated Greedy are proposed. These metaheuristics exhibit promising capabilities, enabling the solution of problem instances involving up to 500 jobs. To assess the effectiveness of the proposed models and algorithms, extensive numerical experiments are conducted, facilitating a thorough evaluation and comparison of their performances.

1 Introduction

With the rise of decentralized and globalized economies, multi-factory manufacturing environments have gained significant importance. The prevalence of supply chains with multiple plants and the presence of duplicate production lines within single factories have further driven the need to allocate products among distributed resources (Fernandez-Viagas and Framinan 2015; Naderi and Ruiz 2010, 2014). Consequently, distributed manufacturing has emerged as a prominent research avenue within the scheduling field, offering intriguing theoretical properties and practical applications (Ying et al. 2017). In this regard, the Distributed Permutation Flowshop Scheduling Problem (DPFSP) has drawn significant attention in the scheduling literature and is an active field in Operational Research (OR) (Perez-Gonzalez and Framinan 2023). The main goal of the DPFSP is to assign jobs to specific flowshops and determine their sequencing in order to minimize certain criteria in the context of multiple flowshops where jobs can be processed. Cao and Chen (2003) were the first to address the DPFSP, which they referred to as the parallel flowshop scheduling problem. However, the formalization and comprehensive treatment of the DPFSP began with the seminal work of Naderi and Ruiz (2010).

The DPFSP involves the processing of n jobs within f identical factories, each equipped with a flowshop comprising of m machines. The problem deals with two primary decisions, namely the assignment of jobs to factories and the determination of the processing order within each factory. The objective is to minimize the makespan across all factories.

The DPFSP introduces a significant level of complexity compared to its origin, the Permutation Flowshop Scheduling Problem (PFSP). In PFSP a production sequence defined for the given set of jobs, and it is assumed that the same job permutation remains consistent across all machines. This simplification effectively prohibits the passing of jobs between machines, reducing the solution space from $(n!)^m$ to n!. However, in the DPFSP, the assignment of jobs to factories adds an additional layer of complexity to the problem, necessitating the construction of a distinct schedule for each factory. Moreover, the DPFSP becomes NP-Complete when the number of jobs, n, exceeds the number of factories, f (Naderi and Ruiz 2010).

When no idle times are allowed at machines, we deal with the distributed no-idle permutation flowshop scheduling problem (DNIPFSP). This constraint models an important practical situation that arises when expensive machinery is employed. Idling on such expensive equipment is often not desired. Clear examples are the steppers used in the production of integrated circuits by means of photolithography. Other examples come from sectors where less expensive machinery is used but where machines cannot be easily stopped and restarted. Ceramic roller kilns, for example, consume large quantities of natural gas when in operation. Idling is not an option because it takes several days to stop and restart the kiln due to very large thermal inertia. In all such cases, idling must be avoided (Ruiz et al. 2009). Additionally, meeting job due date requirements is essential, as failure to complete a job within the specified due window may result in customer compensation penalties while finishing a job too early increases final inventory costs. The notion of due windows has been employed to define the due date requirements of jobs in these industries (Jing et al. 2020; Pan et al. 2017).

This study focuses on the distributed no-idle permutation flowshop scheduling problem with due windows (DNIPFSPDW), which serves as an extension to the DPFSP by incorporating no-idle constraints and due windows. The primary objective of the DNIPFSPDW is to minimize the total weighted earliness and tardiness (TWET) of job completions. Following the well-established three-field notation introduced by (Graham et al. 1979) for scheduling problems, the DNIPFSPDW can be represented as $DF_{m}|prmu, no-idle|TWET$. To the best of our knowledge, the DNIPFSPDW has not been thoroughly explored in the existing literature, and there is a lack of computational investigations on this specific problem.

In this study, we propose four mathematical formulations to model the DNIPFSPDW. Due to the inclusion of a total weighted tardiness objective, which is known to be NP-hard in the flowshop scheduling problem (FSP) (Lawler 1977), the DNIPFSPDW inherits its computational complexity and also falls under the NP-hard category. Consequently, exact solution approaches are inefficient when solving large-scale instances of the problem. For such complex problems, metaheuristic approaches prove to be more suitable as they can obtain high-quality solutions within reasonable computation times. In particular, the iterated greedy (IG) metaheuristic has demonstrated its effectiveness for a majority of PFSPs (Ruiz and Stützle 2007; Fernandez-Viagas et al. 2017). Hence, we develop two hybrid iterated greedy algorithms specifically tailored for the DNIPFSPDW.

This study offers several contributions to the existing literature, which can be summarized as follows:

• Development of four mathematical models to tackle the DNIPFSPDW;

• Proposal of effective hybrid metaheuristic approaches designed specifically for the DNIPFSPDW;

• Introduction of a novel fitness evaluation procedure that accounts for the no-idle and due date requirements of the DNIPFSPDW;

• Provision of a comprehensive benchmark instance set specifically designed for evaluating the performance of DNIPFSPDW algorithms.

The remainder of this paper is organized as follows. Section 2 briefly explores relevant literature. Section 3 introduces the DNIPFSPDW and proposes the mathematical models. Section 4 presents the proposed solution approach. Section 5 provides the computational study and the obtained numerical results. Finally, Sect. 6 concludes the study and provides some suggestions for further studies.

2 Literature review

This section reviews the development of different studies extending the basic DPFSP. It also analyses the objective function, constraints, and solution approaches introduced in the different extensions.

Following the preliminary study of Cao and Chen (2003), there was a noticeable time gap in the literature concerning the DPFS until the pivotal work of Naderi and Ruiz (2010). Naderi and Ruiz (2010) comprehensively addressed the $PFm|prmu|C_{\text {max}}$ problem, introducing six alternative MIP models, based on different approaches to characterizing the problem variables and two factory-assignment rules known as the NEH1 and NEH2 heuristics. Subsequently, several studies have successfully strived to improve the solution quality in terms of objective value and computation time. These improvements have been addressed by devising various solution methodologies (e.g. Variable Neighborhood Descent (VND) (Gao and Chen 2011a), hybrid genetic algorithm (HGA) with a local search (Gao and Chen 2011b), and the Tabu Search-Enhanced Local Search (Gao et al. 2013)). Lin et al. (2013) were the pioneers in employing versions of the IG algorithm by Ruiz and Stützle (2007) for the distributed flowshop problem. Naderi and Ruiz (2014) enhanced the leading solutions for the DPFSP instances through the introduction of a scatter search algorithm. In parallel, Fernandez-Viagas and Framinan (2015) realized similar improvements using an IG algorithm, offering theoretical results embedded in different local search methods trying to reduce the solution space. In another study, Bargaoui et al. (2017) proposed a chemical reaction optimization algorithm outperforming the Naderi and Ruiz (2010) and Fernandez-Viagas and Framinan (2015) methods. Later, Ruiz et al. (2019) developed two IG algorithms, drawing on the VNS algorithm from Naderi and Ruiz (2010). The first algorithm incorporates a local search enhancement, while the second adopts a two-stage approach, initially applying IG to the entire layout and subsequently focusing on the factory dictating the makespan.

Building on the pivotal study of Naderi and Ruiz (2010), the scope of research on the DPFSP has expanded, exploring new objective functions. Fernandez-Viagas et al. (2018) and Ali et al. (2021) studied the total flowtime criterion addressing $PFm|prmu|\sum C_{j}$ problem. Meanwhile, Jing et al. (2020), addressed the PFm|prmu|TWET problem which included an idle time insertion procedure to satisfy the due window constraints. Additionally, Khare and Agrawal (2021) studied the total tardiness criterion, investigating the $PFm|prmu|\sum T_{j}$ problem.

Lin and Ying (2016) and Komaki and Malakooti (2017) both focused on the distributed permutation flowshop scheduling problem with no-wait constraints ($PFm|prmu,no-wait|C_{\text {max}}$). The first proposed a MIP model and developed an Iterated Cocktail Greedy (ICG) algorithm. The latter introduced a new MIP model that considers the delay on the first machine to maintain a no-wait sequence and employed a General Variable Neighborhood Search (GVNS) for larger problems. In a recent study, Avci et al. (2022) investigated the same problem proposing an exact branch-and-cut (BC) technique employing a heuristic algorithm to obtain high-quality upper bounds.

Another extension of the DPFSP is the distributed no-idle permutation flowshop scheduling problem (DNIPFSP) in which no idle time is allowed between the processing of each pair of consecutive jobs on each machine. Ying et al. (2017) pioneered research on the $PFm|prmu, no-idle|C_{\text {max}}$ problem by proposing a MIP model and an iterated reference greedy (IRG) metaheuristic. Subsequent research by Ling-Fang et al. (2018) employed a two-stage memetic algorithm (TSMA) to address this problem, while Chen et al. (2019) expanded the scope to a bi-objective model that considered both makespan and energy consumption, introducing a collaborative optimization algorithm (COA) to enhance solution diversity and quality. Meanwhile, Cheng et al. (2019) expanded upon the original problem by incorporating mixed no-idle constraints and solved this problem by developing an IG-based algorithm. Later, Li et al. (2021) addressed the $PFm|prmu,mixed no-idle|C_{j}$ problem proposing a mathematical formulation and an adaptive iterated greedy (AIG) algorithm enhanced with swap-based local search. In a recent study, Li et al. (2022) examined the distributed assembly mixed no-idle permutation flowshop scheduling problem with a total tardiness objective and proposed an improved IG algorithm called referenced iterated greedy (RIG).

To sum up, there is a considerable research effort in modeling and solving the DPFSP and its extensions. The majority of the related studies consider the makespan minimization objective, while there are a few studies considering other objectives, such as total flow time (Fernandez-Viagas et al. 2018; Pan et al. 2019; Li et al. 2021), total tardiness (Deng and Wang 2017; Ribas et al. 2019; Shao et al. 2020; Li et al. 2022), TWET (Jing et al. 2020; Pan et al. 2017). However, there exists no study investigating no-idle requirements between jobs with due windows. Our study closes this gap by considering TWET objective for the DNIPFSP.

3 Problem definition and formulation

The DNIPFSPDW involves a set of jobs, $J=\{1,2,3,\ldots ,|J|\}$ to be processed in $F=\{1,2,3,\ldots ,|F|\}$ available factories. Each factory consists of $I=\{1,2,3,\ldots ,|I|\}$ machines set in series, where job $j \in J$ on machine $i \in I$ is processed in $p_{ji}$ time units. Each job must be assigned to a single factory, and each machine can process at most one job at a time. Furthermore, a job cannot be processed by more than one machine simultaneously. The processing order of jobs on the machines is predetermined and fixed, and preemption is not allowed. Additionally, the machines cannot have idle time between processing of any pair of jobs. Each job $j \in J$ is associated with a due window represented by $[d_{j}^{-},d_{j}^{+}]$. Let $c_{j}$ denote the completion time of job $j \in J$ on the last machine. The amounts of earliness and tardiness for job $j \in J$ are calculated as $e_{j}=$max$\{d_{j}^{-}-c_{j},0\}$ and $t_{j}=$max$\{c_{j}-d_{j}^{+},0\}$, respectively. The objective of the DNIPFSPDW is to minimize TWET, which is calculated as follows:

$$\begin{aligned} TWET=\sum _{j \in J} (w_{j}^{e} e_{j}+w_{j}^{t} t_{j}) \end{aligned}$$

(1)

where $w_{j}^{e}$ and $w_{j}^{t}$ represent unit penalties for earliness and tardiness of job $j\in J$, respectively.

A problem instance including five jobs and two factories each equipped with three machines is shown as follows:

$$\begin{aligned}{} & {} \begin{pmatrix} w_{j}^{e} \\ w_{j}^{t} \end{pmatrix} = \begin{pmatrix} 8 &{}\quad 3 &{}\quad 7 &{}\quad 4 \\ 4 &{}\quad 7 &{}\quad 6 &{}\quad 9 \end{pmatrix}, \quad p_{ji} = \begin{pmatrix} 14 &{}\quad 15 &{}\quad 50 \\ 3 &{}\quad 59 &{}\quad 1 \\ 77 &{}\quad 65 &{}\quad 77 \\ 71 &{}\quad 56 &{} \quad 21 \end{pmatrix}, \quad \nonumber \\{} & {} \begin{pmatrix} d_{j}^{-}\\ d_{j}^{+} \end{pmatrix} = \begin{pmatrix} 126 &{} \quad 143 &{} \quad 137 &{} \quad 165\\ 189 &{} \quad 174 &{} \quad 177 &{} \quad 201 \end{pmatrix} \end{aligned}$$

(2)

Figure 1 depicts a feasible solution for this problem, displaying the start and finish times of each job on the different machines at the assigned factory. The objective function value for this solution is $TWET = 46 \times 7 + 42 \times 6 = 574$

Fig. 1

Gantt chart representing the solution of the example problem

In the following subsections, we present four alternative models for DNIPFSPDW, namely sequence-based model ($M_{seq}$), minimal sequence-based model ($M^{'}_{seq}$), position-based model ($M_{pos}$), and reduced position-based model ($M^{'}_{pos}$). These models offer different approaches to represent the job factory assignment, ranging from models that require a significant number of additional binary variables to more efficient models that eliminate the need for additional variables. The first two proposed models, $M_{seq}$ and $M'_{seq}$, focus on capturing the sequence of jobs, where the $M'_{seq}$ reduces the size of $M_{seq}$ model by eliminating the factory index from the formulation. In contrast, the $M_{pos}$ model considers the position of jobs in the production plan at each factory, rather than their explicit sequence. This alternative approach provides a different perspective on the problem. To improve the efficiency of the $M_{pos}$ model, we introduce $M'_{pos}$, which significantly reduces the number of variables at the expense of adding some constraints. The details of these proposed models, along with the corresponding notation, are described in the subsequent subsections. For easy reference, Table 1 provides an overview of the notation used in the proposed models.

Table 1 The notation for the mathematical models

3.1 Sequence-based model ($M_{seq}$)

The Sequence-based Model ($M_{seq}$) employs a set of binary decision variables to represent the relative sequences of the jobs. Each sequence begins with a dummy job, $j=0$ with zero processing time. Therefore, a dummy job is added to job set J ($J' = J \cup {\{0\}}$). To formulate the problem, we define the binary variable $y_{jf}$, which indicates whether job $j \in J$ is assigned to factory $f \in F$ ($y_{jf}=1$), or not ($y_{jf}=0$). Additionally, the binary variable $x_{j'jf}$ indicates whether job $j \in J$ is processed immediately after $j' \in J', j' \ne j$ in factory $f \in F$ ($x_{j'jf}=1$), or not ($x_{j'jf}=0$). Moreover, the continuous variable $c_{j'if}$ represents the completion time of job $j' \in J'$ on machine $i \in I$ in factory $f \in F$. Regarding $\Gamma$ as a sufficiently big number, $M_{seq}$ for the DNIPFSPDW is as follows:

$$\begin{aligned}&\text {Objective function: Eq.}~(1) \nonumber \\&\text {Subject to:}{} & {} \nonumber \\&\sum _{f \in F} y_{jf} = 1{} & {} \forall j \in J \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{j' \in J':j'\ne j} \sum _{f \in F} x_{j'jf} = 1{} & {} \forall j \in J \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{j \in J} x_{0jf} \le 1{} & {} \forall f \in F \end{aligned}$$

(5)

$$\begin{aligned}&\sum _{j'\in J':j'\ne j} (x_{j'jf}+x_{jj'f}) \le 2y_{jf}{} & {} \forall j\in J,f \in F \end{aligned}$$

(6)

$$\begin{aligned}&\sum _{i\in I} c_{jif} \le \Gamma y_{jf}{} & {} \forall j\in J', f\in F \end{aligned}$$

(7)

$$\begin{aligned}&c_{jif} \ge c_{j(i-1)f} + p_{ji} - \Gamma (1-y_{jf}){} & {} \forall i\in I\backslash \{1\},j\in J,f \in F \end{aligned}$$

(8)

$$\begin{aligned}&c_{jif} \ge c_{j'if}+p_{ji}+\Gamma (x_{j'jf}-1){} & {} \forall i\in I,j\in J,j'\in J': j \ne j',f\in F \end{aligned}$$

(9)

$$\begin{aligned}&c_{jif} \le c_{j'if} + p_{ji} + \Gamma (1-x_{j'jf}){} & {} \forall i\in I\backslash \{1\}, j\in J,j' \in J':j\ne j',f \in F \end{aligned}$$

(10)

$$\begin{aligned}&e_j \ge d_j^- - \sum _{f \in F} c_{j|I|f}{} & {} \forall j\in J \end{aligned}$$

(11)

$$\begin{aligned}&t_{j} \ge \sum _{f \in F} c_{j|I|f} - d_{j}^{+}{} & {} \forall j\in J \end{aligned}$$

(12)

$$\begin{aligned}&y_{jf}, x_{j'jf} \in \{0,1\}{} & {} \forall j\in J,j'\in J': j \ne j',f\in F \end{aligned}$$

(13)

$$\begin{aligned}&c_{jif} \ge 0{} & {} \forall i\in I,j\in J,f\in F \end{aligned}$$

(14)

$$\begin{aligned}&e_{j}, t_{j} \ge 0{} & {} {\forall j \in J} \end{aligned}$$

(15)

Constraints (3) force each job $j \in J$ to be assigned to only one factory. Constraints (4) guarantee that each job $j \in J$ is preceded by only one job. Constraints (5) and (6), guarantee that each job $j \in J$ assigned to factory $f \in F$ has exactly one successor and one predecessor assigned to the same factory. Constraint set (7) states that completion time of a job $j\in J$ in factory $f\in F$ can be positive if and only if job $j\in J$ is assigned to factory $f\in F$. Constraint set (8) determines the completion time of each job $j \in J$ on each machine $i \in I$. Constraints (9) and (10) prevent the machines from having idle time. Constraints (11) and (12) calculate earliness and tardiness values for each job $j \in J$. Constraints (13–15) specify the domain of the decision variables.

3.2 Minimal sequence-based model ($M^{'}_{seq}$)

In this model, the index for the factories (i.e. f) is removed from the decision variables, and dummy jobs insertion is used to divide the complete sequence into |F| parts, corresponding to each factory. Therefore, |F| repetitions of the dummy job 0 within the sequence alongside the other jobs are incorporated. Consequently, the model explores a search space that encompasses a sequence of length $|J|+|F|$. The first repetition of the dummy job 0 occurs at the beginning of the sequence. Subsequently, all the jobs following this repetition until the second occurrence of the dummy job 0 are scheduled within factory 1 while preserving their relative order. The jobs between the second and third repetitions of the dummy job 0 are allocated to factory 2. This pattern repeats for all subsequent occurrences of the dummy job 0. Finally, the jobs listed after the $|F|^{\text {th}}$ occurrence of the dummy job 0 correspond to those assigned to factory |F|.

In this model, the binary decision variable $x_{j'j}$ indicates whether job $j' \in J'$ is processed immediately before the job $j \in J$ ($x_{j'j}=1$), or not ($x_{j'j}=0$). The continuous variable $c_{j'i}$ demonstrates the completion time of job $j' \in J'$ on machine $i \in I$.

$M^{'}_{seq}$ for the DNIPFSPDW is as follows:

$$\begin{aligned}&\text {Objective function: Eq.}~(1) \nonumber \\&\text {Subject to: Eq.}\ (15){} & {} \nonumber \\&\sum _{j' \in J': j' \ne j} x_{j'j} = 1{} & {} \forall j \in J \end{aligned}$$

(16)

$$\begin{aligned}&\sum _{j \in J: j \ne j'} x_{j'j} \le 1{} & {} \forall j' \in J' \end{aligned}$$

(17)

$$\begin{aligned}&\sum _{j \in J} x_{0j} = |F|{} & {} \end{aligned}$$

(18)

$$\begin{aligned}&\sum _{j \in J} x_{j0} = |F| - 1{} & {} \end{aligned}$$

(19)

$$\begin{aligned}&x_{j'j} + x_{jj'} \le 1{} & {} \forall j \in J,j' \in J':j' < j \end{aligned}$$

(20)

$$\begin{aligned}&c_{j0} \ge p_{j0} x_{0j}{} & {} \forall j \in J \end{aligned}$$

(21)

$$\begin{aligned}&c_{ji} \ge c_{j(i-1)} + p_{ji}{} & {} \forall i \in I\backslash \{1\},j \in J \end{aligned}$$

(22)

$$\begin{aligned}&c_{ji} \ge c_{j'i} + p_{ji} + \Gamma (x_{j'j}-1){} & {} \forall i \in I,j \in J, j'\in J': j' \ne j \end{aligned}$$

(23)

$$\begin{aligned}&c_{ji} \le c_{j'i} + p_{ji} - \Gamma (x_{j'j}-1){} & {} \forall i \in I,j \in J, j'\in J': j' \ne j \end{aligned}$$

(24)

$$\begin{aligned}&e_{j} \ge d_{j}^{-} - c_{j|I|}{} & {} \forall j \in J \end{aligned}$$

(25)

$$\begin{aligned}&t_{j} \ge c_{j|I|} - d_{j}^{+}{} & {} \forall j \in J \end{aligned}$$

(26)

$$\begin{aligned}&x_{j'j} \in \{0,1\}{} & {} \forall j \in J,j' \in J': j \ne j' \end{aligned}$$

(27)

$$\begin{aligned}&c_{j'i} \ge 0{} & {} \forall i \in I,j'\in J' \end{aligned}$$

(28)

The constraints (16) guarantee that each job $j\in J$ has exactly one predecessor. Constraints (17) ensure that each job $j'\in J'$ has at most one successor. Constraints (18) and (19) divide the entire sequence of the jobs into |F| subsets by dummy jobs. Constraints (20) prohibit job $j \in J$ from simultaneously being a successor and a predecessor of job $j' \in J'$. Constraint sets (21) and (22) calculate the completion time of each job $j\in J$ on each machine $i\in I$. Constraints (23) and (24) are the no-idle constraints. Constraints (26) and (25) calculate earliness and tardiness values for each job $j \in J$. Finally, Constraints (27) and (28) define the bounds of the decision variables.

3.3 Position-based model ($M_{pos}$)

Position-based model ($M_{pos}$) employs a set of binary decision variables which represent the positions occupied by the jobs in factories. Let $L=\{1,\ldots ,|J|\}$ be the set of available positions in each factory. The binary decision variable, $x_{jlf}$, indicates whether job $j \in J$ is processed at position $l \in L$ in factory $f \in F$ ($x_{jlf}=1$) or not ($x_{jlf}=0$). The continuous variable, $c_{lif}$, presents the completion time of a job assigned to position $l \in L$ on machine $i \in I$ in factory $f \in F$. Regarding the defined decision variables, the $M_{pos}$ for the DNIPFSPDW is as follows:

$$\begin{aligned}&\text {Objective function: Eq.}~(1) \nonumber \\&\text {Subject to: Eq.} \ (15){} & {} \nonumber \\&\sum _{l \in L} \sum _{f \in F} x_{jlf} = 1{} & {} \forall j \in J \end{aligned}$$

(29)

$$\begin{aligned}&\sum _{j \in J} x_{jlf} \le 1{} & {} \forall l \in L,f \in F \end{aligned}$$

(30)

$$\begin{aligned}&\sum _{j \in J} x_{j(l+1)f} \ge \sum _{j \in J} x_{jlf}{} & {} \forall f \in F, l \in L \backslash \{|J|\} \end{aligned}$$

(31)

$$\begin{aligned}&\sum _{j \in J} \sum _{l' \in L:l' \le l} x_{jl'f'} \ge \sum _{j \in J} \sum _{l' \in L:l' \le l} x_{jl'f}{} & {} \forall l \in L, f,f' \in F : f > f' \end{aligned}$$

(32)

$$\begin{aligned}&c_{l1f} \ge \sum _{j\in J} x_{jlf} p_{j1}{} & {} \forall l \in L, f \in F \end{aligned}$$

(33)

$$\begin{aligned}&c_{lif} \ge c_{l(i-1)f}+ \sum _{j\in J} x_{jlf} p_{ji}{} & {} \forall l \in L,i \in I \backslash \{1\},f \in F \end{aligned}$$

(34)

$$\begin{aligned}&c_{lif} = c_{(l-1)if}+ \sum _{j \in J} x_{jlf} p_{ji}{} & {} \forall l \in L\backslash \{1\},i \in I,f\in F \end{aligned}$$

(35)

$$\begin{aligned}&e_{j} \ge d_{j}^{-} - c_{l|I|f} - \Gamma (1-x_{jlf}){} & {} \forall j \in J, l \in L, f \in F \end{aligned}$$

(36)

$$\begin{aligned}&t_{j} \ge c_{l|I|f} - d_{j}^{+} - \Gamma (1-x_{jlf}){} & {} \forall j \in J, l \in L, f \in F \end{aligned}$$

(37)

$$\begin{aligned}&x_{jlf} \in \{0,1\}{} & {} \forall j \in J, l \in L, f \in F \end{aligned}$$

(38)

$$\begin{aligned}&c_{lif} \ge 0{} & {} \forall l \in L,i \in I, f \in F \end{aligned}$$

(39)

Constraint set (29) enforces that each job $j \in J$ is assigned to exactly one position in a factory. Constraints (30) stipulate that each position $l \in L$ in a factory $f \in F$ is occupied by at most one job. Constraints (31) prevent the occupation of position $l+1$ unless a job is assigned to position $l \in L$ in factory $f \in F$. Similarly, Constraint set (32) prevents the occupation of position $l' \in L$ in factory $f \in F$ unless a job has been assigned to position $l' \in L$ in the previous factory $f' \in F$. Thus, we can characterize both Constraint sets (31) and (32) as symmetry-breaking constraints. Constraints (33) and (34) determine the completion time of a job assigned to position $l\in L$ on machine $i\in I$. Constraints (35) prevent the machines from having idle time between processing of any pair of jobs. Constraints (36) and (37) specify the earliness and tardiness values of each job $j \in J$, respectively. Finally, Constraints (38) and (39) indicate the domain of the decision variables.

3.4 Reduced position-based model ($M^{'}_{pos}$)

This model maintains a position-based approach similar to $M_{pos}$. In the previous position-based model, a single variable with three indices is used to handle both decision aspects of the DNIPFSPDW. This means that the assignment of jobs to factories and the sequencing of jobs within each factory are combined into a set of binary variables with three indexes ($x_{jlf}$). However, $M^{'}_{pos}$ aims to further reduce the number of both binary and continuous variables, even though it involves introducing additional constraints. To achieve this, we defined binary variables $x_{jl}$ indicating whether job $j \in J$ occupies position $l \in L$ ($x_{jl}=1$), or not ($x_{jl}=0$) and $y_{lf}$ indicating whether the job in position $l \in L$ is assigned to factory $f \in F$ ($y_{lf}=1$), or not ($y_{lf}=0$). As a result of this strategy, the number of possible job positions is reduced from $|J|^2\times |F|$ to $|J|^2+|J|\times |F|$. Furthermore, the continuous variable $c_{li}$ indicates the completion time of the job on position $l \in L$ on machine $i \in I$. Regarding the defined variables the $M^{'}_{pos}$ for the DNIPFSPDW is as follows:

$$\begin{aligned}&\text {Objective function: Eq.}~(1) \nonumber \\&\text {Subject to: Eq} .\ (15){} & {} \nonumber \\&\sum _{l \in L} x_{jl} = 1{} & {} \forall j \in J \end{aligned}$$

(40)

$$\begin{aligned}&\sum _{j \in J} x_{jl} = 1{} & {} \forall l \in L \end{aligned}$$

(41)

$$\begin{aligned}&\sum _{f \in F} y_{lf} = 1{} & {} \forall l \in L \end{aligned}$$

(42)

$$\begin{aligned}&y_{1f} + y_{|L|f} \le 1{} & {} \forall f \in F \end{aligned}$$

(43)

$$\begin{aligned}&y_{l(f+1)} \le 2 - y_{(l-1)f} - y_{(l+1)f}{} & {} \forall f \in F\backslash \{|F|\}, l \in L \backslash \{1,|L|\} \end{aligned}$$

(44)

$$\begin{aligned}&y_{l1} \le y_{(l-1)1}{} & {} \forall l \in L \backslash \{1\} \end{aligned}$$

(45)

$$\begin{aligned}&y_{lf} \le \sum _{f' \in F: f' \le f} y_{l'f'}{} & {} \forall l, l' \in L: l' < l, f \in F \end{aligned}$$

(46)

$$\begin{aligned}&c_{l1} \ge \sum _{j \in J} x_{jl} p_{j1}{} & {} \forall l \in L \end{aligned}$$

(47)

$$\begin{aligned}&c_{li} \ge c_{l(i-1)} + \sum _{j \in J} x_{jl} p_{ji}{} & {} \forall l \in L, i \in I \backslash \{1\} \end{aligned}$$

(48)

$$\begin{aligned}&c_{li} \le c_{(l-1)i} + \sum _{j \in J} x_{jl} p_{ji} \ + \Gamma (1-y_{lf}) + \Gamma (1-y_{(l-1)f}){} & {} \forall l \in L \backslash \{1\}, i \in I, f\in F \end{aligned}$$

(49)

$$\begin{aligned}&c_{li} \ge c_{(l-1)i} + \sum _{j \in J} x_{jl} p_{ji} \ - \Gamma (1-y_{lf}) - \Gamma (1-y_{(l-1)f}){} & {} \forall l \in L \backslash \{1\}, i \in I, f\in F \end{aligned}$$

(50)

$$\begin{aligned}&e_{j} \ge d_{j}^{-} - c_{l|I|} - \Gamma (1-x_{jl}){} & {} \forall j \in J, l \in L \end{aligned}$$

(51)

$$\begin{aligned}&t_{j} \ge c_{l|I|} - d_{j}^{+} - \Gamma (1-x_{jl}){} & {} \forall j \in J, l \in L \end{aligned}$$

(52)

$$\begin{aligned}&x_{jl} \in \{0,1\}{} & {} \forall l \in L, j \in J \end{aligned}$$

(53)

$$\begin{aligned}&c_{li} \ge 0{} & {} \forall l\in L, i \in I, j \in J \end{aligned}$$

(54)

The constraints (40) enforce that each job $j \in J$ must occupy only one position. The constraint set (41) mandates that each position $l \in L$ be allocated precisely once. Constraints (42) ensure that each job $j \in J$ is allocated to precisely one factory $f \in F$. Constraint set (43) ensures that the first and last positions cannot be in the same factory. The constraints (44) ensure the consistency between positions and factories, guaranteeing that the current position must belong to the same factory when both the previous and the next positions do. Constraints (45) and (46) act as symmetry-breaking constraints, ensuring that job $j \in J$ can only be allocated to position $l \in L$ in factory $f \in F$ if and only if all prior positions in all preceding factories are occupied. Constraints (47) control the completion time of jobs on the first machine. Constraints (48) guarantee that each job cannot begin until the preceding job assigned to the same machine in the same factory has been finished. Constraints (49) and (50) prevent machines from having idle time. Constraints (51) and (52) calculate the earliness and tardiness values of each job $j \in J$. Constraints (53)–(54) define the decision variables domain.

4 Solution approaches

Given that the single machine problem with due windows is already known to be NP-Hard (Pan et al. 2017), the DNIPFSPDW is, therefore, an NP-Hard problem. Solving the DNIPFSPDW poses additional challenges due to the presence of multiple factories. To tackle this challenging problem, metaheuristic algorithms have proven to be as a highly promising approach (Jing et al. 2020). In this study, we present a hybrid metaheuristic algorithm to solve the DDNIPFSPDW. Since this problem has not been previously addressed in the literature, we selected a widely used algorithm from the existing literature for comparison purposes. The subsequent sections provide a detailed explanation of the proposed algorithm.

4.1 Solution representation and evaluation

Let S denote a solution for the DNIPFSPDW with |F| factories, representing the permutation in factory $f\in F$ as $\pi ^f=(\pi _1^f, \dots , \pi _{n_f}^f)$ where $\pi _q^f$ is the $q^{\text {th}}$ job in the permutation, and $n_f$ is the number of jobs assigned to factory f. However, representing the solution in this form fails to completely describe the completion time of jobs regarding no-idle constraints and due windows. In order to determine the optimal completion time and achieve an efficient schedule for jobs, certain timing adjustments are necessary to ensure optimal job waiting times. To address this, we have developed the No-idle adjustment and the Gap insertion methods to calculate the optimal timing schedule for a given permutation $\pi _q$.

To better illustrate the characteristics of the methods, an example problem with two jobs and three machines is presented for one factory in Fig. 2. Figure 2a displays the completion time of jobs using the conventional forward calculation method, wherein the completion time is accomplished by sequentially adding the process times of subsequent jobs on the next machine as soon as they become available. Figure 2a depicts 56 units of idle time between jobs 1 and 2 on machine two, and similarly, 62 units of idle time for machine three. It is inferred from Fig. 2a that the conventional forward calculation method alone is inadequate for evaluating the fitness of solutions in the DNIPFSPDW.

Fig. 2

Gantt chart for illustrating No-idle adjustment and Gap insertion

To address this constraint, a forward-backward completion time method, referred to as the No-idle adjustment, is proposed.

No-idle adjustment: Let $p(\pi ^f_q,i)$ represent the processing time, and $c'(\pi ^f_q,i)$ denote the completion time of job $\pi ^f_q$ on machine $i\in I$ at factory $f\in F$. The calculation of $c'(\pi ^f_q,i)$ follows the conventional forward calculation approach, as outlined below:

$$\begin{aligned} c'(\pi ^f_q,i)=\left\{ \begin{array}{ll} p(\pi ^f_q,i),&{}\quad \text {if } i=1,q=1\\ c'(\pi ^f_{q-1},i)+p(\pi ^f_q,i),&{}\quad \text {if } i=1,q>1\\ \max {(c'(\pi ^f_{q},i-1),c'(\pi ^f_{q-1},i))}+p(\pi ^f_q,i),&{}\quad \text {otherwise.} \end{array}\right. \end{aligned}$$

(55)

If $c'(\pi ^f_{q},i-1)>c'(\pi ^f_{q-1},i)$, machine $i\in I$ remains idle until the completion of $\pi ^f_{q}$ on machine $i-1$. To address this issue, it is necessary to adjust the completion times of the preceding jobs to accommodate the no-idle constraints. To ensure compliance with the no-idle constraints, a specific adjustment procedure is proposed, outlined in Algorithm 1. The procedure begins with the completion times calculated using the conventional forward calculation method (Eq. (55)). Then, starting with the completion time of the last job on each machine $i\in I$ in $f\in F$, the procedure ensures that the makespan of the related factory remains unchanged while eliminating idle times between each pair of jobs. By working through the job permutation in reverse order, the completion times obtained from the no-idle adjustment procedure satisfy the no-idle constraints. This ensures that there are no-idle times between jobs, and the adjusted completion times reflect the optimal scheduling solution.

Algorithm 1

No-idle adjustment

Gap insertion: In practical operational settings, it is often challenging for all jobs to be completed exactly within their designated time windows due to various constraints. Consequently, an effective production plan strives to finish jobs as closely to their due dates as possible, minimizing any additional penalties. To have no-idle time between two consecutive jobs, it is necessary to introduce gaps on each machine before commencing the production process. A question that naturally arises is to what extent it is worth adding a gap to obtain the best objective function value. Several methods for gap insertion have been proposed in the relevant literature (Tseng and Liao 2008; Pan et al. 2017; Rossi and Nagano 2020; Zhu et al. 2022). However, given the similarities in the nature of the problems, this study develops an adapted version of the gap insertion approach based on Jing et al. (2020) to determine the ideal completion time for jobs. It is worth noting that these methods are commonly referred to as “idle time insertion” in the literature. However, to avoid any confusion with machine idle time, the term “gap insertion” is employed in this study.

Idle time can potentially be inserted to each machine of every factory. However, for the purpose of evaluating a solution, it is sufficient to only consider the last machine. Therefore, this paper specifically addresses the insertion of idle time to the last machine of each factory. When examining the last machine, we can partition the jobs or consecutive blocks of jobs based on their completion time status. Let $S_M$ represent the jobs on the last machine. We can then define three subsets as follows:

• $S_{E}$: The early jobs ($S_{E}=\{j \in S_{M}|e_{j}>0\}$)

• $S_{T}$: The tardy jobs ($S_{T}=\{j \in S_{M}|t_{j}>0\}$)

• $S_{D}$: The jobs that are completed on time ($S_{D}=\{j \in S_{M}|e_{j}=t_j=0\}$)

The gap insertion procedure is outlined in Algorithm 2. During each iteration of the procedure, the subsets $S_E$, $S_T$, and $S_D$ are updated accordingly. If the total earliness weight of early jobs exceeds the total tardiness weight of tardy jobs, inserting a gap before the operations will yield a better fitness value. However, this insertion may lead to tardiness in some jobs belonging to $S_D$. To mitigate this, a maximum allowable gap, denoted as $\theta$, is calculated. If the total earliness weight of early jobs surpasses the total tardiness weight of on-time jobs, a gap can be inserted up to the minimum earliness value. Conversely, the maximum allowable gap is bounded by $\min _{j\in S_{D}}(d_{j}^{+}-C_{j|I|})$. At the end of each iteration, the completion times, earliness, and tardiness values of the jobs are updated. This procedure is repeated for all jobs in each factory.

Algorithm 2

Gap insertion

As depicted in Fig. 2b, the idle times between jobs 1 and 2 for both machines two and three are zero using the suggested gap insertion method. However, the completion times of the jobs do not align with their respective due windows. To minimize this discrepancy, the proposed method inserts a 20-unit gap, as shown in Fig. 2c. The overall fitness evaluation procedure developed in this study is summarized in Algorithm 3.

Algorithm 3

Fitness evaluation

4.2 Hybrid iterated greedy algorithm (HIG)

IG is a single solution-based metaheuristic algorithm, characterized by its simplicity and effectiveness, first proposed by Ruiz and Stützle (2007) for scheduling problems. It consists of two fundamental phases, known as the destruction and reconstruction phases. IG offers great flexibility as it can be easily integrated with local evade procedures and other metaheuristic algorithms, enabling further enhancements in solution quality (Stützle and Ruiz 2018). In this regard, the present study introduces two hybrid metaheuristic algorithms that combine the IG algorithm with either Tabu Search (Glover 1989, 1990) or Local Search as intermediate search schemes at specific stages. The incorporation of these intermediate search techniques is intended to achieve a synergistic improvement in the overall performance and effectiveness of the algorithms.

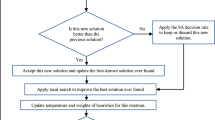
The proposed hybrid Iterated Greedy (HIG) algorithms consist of four phases: initialization, destruction, reconstruction, and intermediate search. The algorithm starts by generating an initial solution denoted as S, by a variant of the NEH heuristic. Then, the destruction phase removes some of the jobs from the original permutation, and the reconstruction phase reinserts the removed jobs into the partial solution to produce a new complete one. The intermediate search scheme is activated when the best-so-far solution does not improve over a certain number of iterations. To determine whether a new solution overrides the current solution, an acceptance criterion is considered. The algorithm incorporates a temperature parameter temp, which controls the acceptance probability of the new solutions. If the update results in a better objective value compared to the current solution, it is accepted unconditionally. Otherwise, the acceptance probability is determined using the formula $e\frac{f(S^*)-f(S')}{temp}$, where $f(S^*)$ and $f(S')$ represent the objective function value of best-so-far and new solution, respectively. The temperature value starts with the objective value of the initial solution and exponentially decreases to zero during the iterations.

The algorithms check for the equilibrium condition, which occurs when there is no improvement in the best solution over a certain number of iterations. When the equilibrium condition is met, the temperature is reduced by multiplying it with a cooling rate coefficient between [0,1]. The algorithms terminate under three conditions: reaching the maximum number of iterations, reaching the maximum number of consecutive iterations without improvement, or exceeding the time limit, which is calculated as $timeLimit=\min (|F|) \times |J|$. The detailed steps of the HIG algorithm are illustrated in Algorithm 4.

Algorithm 4

Hybrid Iterated Greedy (HIG)

4.2.1 Initialization

In this study, a variant of the NEH heuristic is employed as the initial solution generation method. The NEH heuristic requires a seed sequence to construct a solution. To obtain the seed sequence, the Earliest Due Date-Weighted Earliness Tardiness (EDDWET) method is utilized, as it has been suggested as the most effective heuristic by Jing et al. (2020). Algorithm 5 provides a depiction of the EDDWET method.

The EDDWET method begins by creating two sets, $G_{w}^{e}$ and $G_{w}^{t}$, for the jobs based on their unit earliness and tardiness weights. If $w_{j}^{t}>w_{j}^{e}$, it is included in $G_{w}^{t}$; otherwise, it is added to $G_{w}^{e}$. The jobs in $G_{w}^{e}$ are then sorted in a non-decreasing order of their $w_{j}^{e}$ values to create an incomplete sequence denoted as $\tau _{w}^{e}$. Conversely, the jobs in $G_{w}^{t}$ are sorted in a non-increasing order of their $w_{j}^{t}$ values, forming another incomplete sequence $\tau _{w}^{t}$. Next, the initial jobs from each partial sequence are selected and compared based on their $d^{+}$ values. The job with the smallest $d^{+}$ is removed from its associated list and added to the end of the seed sequence, $\tau$. This process continues until one of the partial sequences ($\tau _{w}^{t}$ or $\tau _{w}^{e}$) is depleted. In such a case, the remaining jobs from the other partial sequence are added to the end of $\tau$. The first |F| jobs in $\tau$ are then distributed to be the first job of each factory. Subsequently, the remaining jobs are assigned to the factories one by one, following the order of the seed sequence $\tau$. Each job is assigned to the factory that yields the smallest incremental penalty in the objective function when the new job is added.

Algorithm 5

EDDWET

4.2.2 Destruction

In the destruction stage, a certain number of jobs, denoted by r, are randomly selected and removed from the current solution S. This process creates a partial solution, while the removed jobs are stored in a separate list called R.

The number of removed jobs at the destruction phase remains constant throughout the iterations of the algorithm. In this study, four distinct destruction strategies have been implemented, and they are randomly selected for each destruction attempt. This approach ensures variability and introduces different dynamics to the destruction phase of the algorithm.

• Random selection: This method is the simplest approach, which randomly selects and removes r jobs from an existing incumbent solution S.

• Factory-based selection: The factory-based operator aims to achieve a balanced distribution of jobs by reducing the workload on factories with high penalty costs. This operator deletes one random job from up to r factories with the highest TWET value. If $r > |F|$, the remaining $r -|F|$ jobs are randomly eliminated.

• Greedy selection: A promising approach to reducing the objective value is to replace jobs that contribute the most to the penalty. Greedy selection intends to remove $\frac{r}{2}$ jobs with the greatest tardiness and the other $\frac{r}{2}$ with the highest earliness penalties.

• Block selection: To effectively explore the neighboring solution space, this operator employs a block-based selection technique, in which a consecutive series of jobs from a random factory’s sequence ($Q^{f}$) is picked from a random position. The size of the block takes an integer number between [1,$\min (r,|Q^{f}|)$]. To ensure that the desired number of jobs are deleted (r), this operator is applied multiple times on different factory sequences.

4.2.3 Reconstruction

The reconstruction operators create a complete solution by incorporating the partial solution ($S^{D}$) and the list of removed jobs (R) obtained from the destruction stage. The followings are the four different reconstruction operators which are utilized randomly for each reconstruction attempt.

• Order selection: Since the destruction phase frequently eliminates certain jobs based on the heuristics, maintaining the same order avoids making large jumps to distant neighboring solutions. To construct a complete solution, the algorithm examines all potential positions for each removed job, regarding their removal order. For each given job, it identifies a subset of positions that result in the lowest increase in the objective value. Then, a position is picked using a Roulette Wheel approach, to insert a given job on each attempt until all the removed jobs are treated.

• Random selection: To further investigate the unexplored regions of solution space, the removed jobs are reinserted one at a time in a random manner.

• Greedy selection: Each removed job is iteratively inserted into all positions of a partial solution, and the insertion that results in the minimum increment of the objective value is selected. This process continues until all the removed jobs have been reinserted.

• k-regret: This study employs the idea of regret function with some modifications to fit into the current problem’s concept. The present k-regret function attempts to compute the regret value, which represents the difference between the value of inserting a job into its first best position and its $k^{\text {th}}$ best position ($k>1$). For a given value of k, the regret is computed as follows:

  $$\begin{aligned} \Delta \lambda _{j} = \lambda _{j}^{1} + \sum _{n=2}^{k} (\lambda _{j}^{n} - \lambda _{j}^{1}){} & {} \forall \ j \in J \end{aligned}$$

  (56)

  Where $\lambda _{j}^{n}$ denotes the objective value for the $n^{\text {th}}$ best insertion position of job j. Then, the job with the highest $\Delta \lambda _{j}$ is inserted in the position with minimum insertion cost until all removed jobs are placed.

4.3 Intermediate search (IS)

The IG algorithm and its variants include an intermediate search strategy to systematically explore the solution space. This intermediate search procedure, as an optional phase, can be applied to the solution derived from the reconstruction process, aiming to enhance its quality. This study introduces two distinct techniques, namely Tabu Search and Local Search, as the intermediate search schemes within the IG algorithm. These techniques are employed to further refine the solutions and improve the overall performance of the algorithm.

4.3.1 Tabu search (TS)

In the context of a search strategy, TS refers to the process of transitioning from one feasible solution to another within each iteration. In the case of PFSP, the TS algorithm is often structured, to begin with a sequence and evolves consecutively through neighboring solutions to find a better one. A “Tabu List (TL)” allows TS to avoid going back to the same solutions from which it recently emerged. By doing so, the solution space is comprehensively explored, and trapping in locally optimal solutions is avoided. In this regard, recently evaluated solutions are declared tabu for a certain number of iterations. A move made in iteration Iter is called tabu until iteration $(Iter+\delta )$ where $\delta$ is the prespecified tabu tenure (TT) value.

TL can be seen as a short-term memory that keeps track of recent moves in order to prevent revisiting previously explored sequences. In this study, a customized version of the TL generation technique proposed by Ying and Lin (2017) is employed, taking into account the inclusion of $\alpha$ jobs. The generation of TL involves constructing sets $\mathscr {A}_{1}$ and $\mathscr {A}_{2}$. For each factory, the job with the lowest earliness, not already present in TL, is added to $\mathscr {A}_{1}$. Similarly, $\mathscr {A}_{2}$ consists of the jobs with the lowest tardiness from each factory, excluding those already in TL. Initially, the jobs included in TL are composed of the union of $\mathscr {A}_{1}$ and $\mathscr {A}_{2}$. The remaining $\alpha - |\mathscr {A}_{1} \cup \mathscr {A}_{2}|$ distinct jobs are randomly selected from the input solution and added to set $\mathscr {A}_{3}$.

TS algorithm proposed in this study starts with the best-found solution obtained from the initial IG-based procedure and sets it as the bestGlobal solution. Similar to the destruction phase, r jobs are randomly selected from the bestGlobal solution to be destroyed. Then the new solution is reconstructed using the k-regret operator.

After generating a set of neighboring solutions based on the bestGlobal, each new solution is identified to be either forbidden or free. If a move is recognized as forbidden according to the TL, it is not approved unless it meets the aspiration criterion. The aspiration criterion serves as a condition to override the tabu status of a move once this move leads to a solution better than the best found.

Next, the best of forbidden and free solutions is determined to specify the best solution for the current iteration (bestIter). If there exists a best-free solution (bestFree), bestIter is updated to it even if the objective of the best-forbidden solution (bestForbiden) is better. The aspiration criterion, however, allows the bestForbiden to be considered if it improves the bestGlobal. Subsequently, the TT for all jobs in the TL is decreased by one. At the same time, the bestIter is compared with bestGlobal, and in case of offering a better objective value, the bestGlobal is updated accordingly. The TL is then updated based on the new bestGlobal. This procedure will go on until the number of unimproved consecutive iterations exceeds maxNoImprove. Algorithm 6 explains different steps of the proposed TS algorithm in detail.

Algorithm 6

Tabu search

4.3.2 Local search (LS)

As another alternative solution approach, this study also adopts the classic Iterated Greedy algorithm with Local Search (IG-LS). In order to ensure a fair comparison of results, IG-LS adopts the same initial solution, destruction, and reconstruction procedures as employed in the proposed IG-TS algorithm. Additionally, IG-LS incorporates a Local Search (LS) technique that utilizes three search methods in a sequential manner. The LS process begins with the first neighborhood and continues until no better solution is found, at which point the best-found solution is passed on to the next operator. This process continues until the final operator fails to find a better solution and stagnates at its local optimum. The following provides a summary of the sequential application of the local search operators within the algorithm.

• Single Insertion: As one of the most used operators in FSPs, it improves a given solution by relocating a job and reinserting it into another position. First, a job is randomly selected from factories that have more than one job. Then, it is reinserted into a random position in another factory. The selection of the new position is determined by a Roulette Wheel, which assigns a higher probability to the best factory and position in terms of the objective value.

• Block Insertion: In this operator all the removed jobs are reinserted as a block into a randomly selected factory with a randomly assigned location with no change in the sequence of jobs within the block.

• Exchange: This operator randomly chooses and exchanges two distinct jobs of an incumbent solution from two randomly selected factories.

5 Computational study

This section provides a summary of the conducted computational experiments, using the benchmark developed in this study. A detailed description of the benchmark creation process is presented in Sect. 5.1. The analysis of the proposed mathematical models is discussed in Sect. 5.2. Furthermore, the calibration of the algorithm’s parameters is explained in Sect. 5.3. Finally, the performance evaluation of the developed algorithms is presented in Sect. 5.4.

5.1 Benchmark and experimental setting

Despite the availability of benchmarks for traditional FSP, the unique characteristic of incorporating due windows in the context of DNIPFSPDW necessitates a specific focus on due dates. To address this, the DPSP data proposed by Naderi and Ruiz (2010) was extended by introducing three additional parameters: T (tardiness factor), W (width of the due window), and R (due date range). Based on these parameters, two sets of benchmark instances, namely small and large, were generated. The instance generation process involves six parameters: the number of machines (I), jobs (J), factories (F), tardiness factor (T), due date range (R), and the width of the due window with respect to the due date (W). The processing time data from Naderi and Ruiz (2010) was utilized to construct the instance data. The unit earliness and tardiness weights were generated using a uniform distribution within the range U [1, 9]. The due dates were randomly generated using a uniform distribution, employing the method proposed in equation (57), where $\lfloor X \rceil$ denotes rounding X to the nearest integer and P indicates the makespan upper bound calculated by the NEH2 heuristic developed by Naderi and Ruiz (2010).

$$\begin{aligned}&d_{j} = \text {max}(0, U[\lfloor P(1-T-R/2)\rceil , \lfloor P(1-T+R/2)\rceil ]) \end{aligned}$$

(57)

The calculated due dates vary from simple to difficult to fulfill depending on the parameters of T and R. The due windows are generated centered around $d_{j}$ with $W\%$ width of $d_{j}$ as follows: $d_{j}^{-} = \text {max}(0, \lfloor d_{j}-d_{j} \times H/100 \rceil )$ and $d_{j}^{+} = \text {max}(0, \lfloor d_{j}+d_{j} \times H/100 \rceil )$ where $H=[1,W]$. The benchmark instances are generated with the following parameter combinations: $F={2, 4}$, $I={3, 4, 5}$, and $J={4, 10, 16}$ for small-sized instances, and $F={4, 7}$, $I={5, 10, 20}$, and $J={20, 50, 100, 200, 500}$ for large-sized instances. Each combination is replicated five times with different seeds, resulting in a total of 720 small instances and 960 large instances. All instances, along with the best complete solutions found in this paper, and their objective value are available to download at 10.17632/yr5tyyk8ds.4. Furthermore, Table 2 presents the time limit considered for each problem size:

Table 2 Time limit values for each problem size

Both algorithms were implemented in Java, and the mathematical models were solved in Python using the Gurobi solver 9.0. All the computational tests have been carried out on a computer with Intel(R) Core (TM) i3-7130U CPU @ 2.70GHz and 8 GB of RAM, using the Microsoft Windows 10 operating system. The computational CPU time for Gurobi is limited to 3600 s (1 h) in the experiments.

5.2 The performance of the proposed mathematical models

Table 3 shows the computational results of the proposed mathematical models for small-sized instances with 2 and 4 factories, where the number of jobs is 4, 10, and 16. The column labeled “UB” demonstrates the upper bound found by the Gurobi solver, whereas the “Gap” column indicates the gap between Gurobi’s best bound and lower bound. The “Opt Num” column displays the number of instances solved to optimality, and the column “Time” shows the average CPU time in seconds. Analyzing Table 3, it can be observed that all of the models exhibit similar performance for instances with four jobs in terms of computational time and optimality gap.

When the number of jobs increases to 10 or more, the computational complexity of the models also increases, resulting in longer CPU times to solve the instances. Based on the comparison of the models presented in Table 3 for instances with ten jobs and two factories, it is evident that $M^{'}{seq}$, M pos, and $M^{'}{pos}$ outperform M seq by obtaining optimal solutions for all cases. However, $M_{pos}$ is able to achieve these results within a relatively shorter time than $M^{'}_{seq}$, but with a CPU time that is fairly comparable to $M^{'}_{pos}$. For instances with 16 jobs and two factories, a similar performance is observed, with $M^{'}_{pos}$ emerging as the best model, achieving the optimal solution for 31 out of 120 instances. Furthermore, considering the Gap column for instances with 16 jobs, it can be inferred that $M^{'}_{pos}$ exhibits better performance in terms of finding lower bounds compared to the other models.

Based on the results presented in Table 3, it can be observed that the performance of the models varies for instances with ten jobs and four factories. $M_{seq}$ achieves optimal solutions for only 55 out of 120 instances, whereas $M^{'}{pos}$ successfully identifies optimal solutions for 113 out of 120 instances. The other two models are able to find optimal solutions for all cases. In terms of CPU time, $M^{'}{seq}$ demonstrates higher performance, requiring an average of 6.5 s to solve instances with ten jobs. On the other hand, M pos and $M^{'}{pos}$ exhibit significantly longer CPU times. The superior performance of $M^{'}_{seq}$ is not limited to instances with ten jobs, as it continues to deliver better results for instances with 16 jobs by finding optimal solutions for 24 out of 120 instances in an average time of 2908.01 s. Furthermore, considering the quality of lower bounds, $M^{'}_{seq}$ also outperforms the other models, as indicated by the Gap column in Table 3 for instances with four factories.

Table 3 The average results for the small-sized instances

Table 3 illustrates that solving instances with four factories using $M^{'}_{seq}$ requires far less computational time compared to other models. This suggests that $M^{'}{seq}$ is more efficient in exploring and evaluating the solution space for instances with a higher number of factories.

In general, $M_{seq}$ does not demonstrate satisfactory performance in terms of lower bound quality, incumbent solution, and CPU time across all cases under study. The performance of the other models is highly dependent on the number of factories present in a given instance. While M pos may exhibit slightly poor performance for instances with four factories compared to $M^{'}{seq}$, it demonstrates significantly better performance for cases with two factories. On the other hand, the performance of $M^{'}{pos}$ is relatively similar for instances with two factories, but its performance deteriorates as the number of factories increases to four. Therefore, to analyze the effect of other parameters, the performance of the $M_{pos}$ will be investigated as it delivers a better overall performance compared to others.

To determine the effect of the contributing parameters of the problem on the performance of $M_{pos}$, an ANOVA test was conducted with a significance level of 0.05. The findings indicate that the number of factories has a statistically significant effect on the performance of the model, as determined by the P-value of 0.02.

The results also indicate that tighter values for W demand more time to converge to the optimal solution. The conducted ANOVA test with a significance level of 0.05 for W as a fixed variable in response to the gap for $M_{pos}$ model also confirms the effect of W on decreasing objective value and elapsed time with a P-value of 0. For different values of R, the variation of the optimality gap and computational time is significant. An increase in R reduces the optimality gap and computational time. By performing a similar ANOVA test with the fixed variable R in response to the gap, a P-value of 0.001 demonstrates the significant effect of R in increasing objective value and CPU time. A totally different observation is detected while changing the value of T. These results imply that larger values of T narrow down the due date of jobs, which in return, increases the complexity of solution space, requiring the model to spend more time investigating the solution space. Similarly, in the ANOVA test for variable T, a P-value of 0.001 confirms that T has a noticeable effect on increasing both CPU time and objective value. Although the number of machines in each factory does not have a direct impact on the model, its variation impacts the average computational gap and mean CPU time. The performed ANOVA test confirms the significance of the number of machines on the performance of $M_{pos}$ with a P-value of 0.026.

5.3 Calibration of algorithm parameters

To achieve the best performance of the algorithm, it is necessary to calibrate its input parameters. Therefore, a Taguchi experiment employing the L27 orthogonal array was conducted. The experiment involved randomly selecting eight instances and defining three levels for each parameter. Each instance was then executed 15 times to ensure reliable and robust results. The proposed algorithm contains eight parameters $\alpha$, r, TSMaxNoImprove, maxNeighbor, TT, activTabu, tabuMaxIter, and maxNoImprove. The specific values used for each parameter are presented in Table 4, providing a comprehensive overview of the parameter configuration employed in the calibration process. The values assigned to each parameter were chosen based on existing literature.

Table 4 Considered values for each parameter

The main effects of S/N ratios on IG-TS parameter levels are presented in Fig. 3. As one can infer from the Fig. 3, the best parameter levels of the algorithm are $tabuMaxNoImprove = 10$, $tabuMaxNeighbor = 80$, $TT = 3$, $\alpha = 0.25\times |J|$, $r = 7$, $activTabu = 40$, $tabuMaxIter = 30$, and $maxNoImprove = 120$.

Fig. 3

Main effects of S/N ratios for IG-TS parameters

Given the substantial count of calibrated parameters in the proposed algorithm, a variance analysis is carried out on the key parameters as identified by linear regression. Additionally, the interaction among these parameters is examined to assess the robustness of the algorithm. In the regression analysis under discussion, the principal aim was to explore the influence of involving parameters on the Relative Percentage Deviation (RPD). The P-values associated with these parameters (independent variables) are as follows: $TSMaxNoImprove= 0, maxNeighbor= 0, TT= 0.773, \alpha = 0.49, r = 0, activTabu = 0, tabuMaxIter = 0.963,$ and $maxNoImprove = 0.001$. Based on these P-values, all parameters except for $TT, \alpha ,$ and tabuMaxIter show statistical significance, having P-values less than the 0.05 threshold. These variables, hence, are identified as key parameters.

Figure 4 demonstrates the interaction among the key parameters within the algorithm, highlighting four distinct interactions. An uptick in the parameter r, which signifies the number of removed jobs, prompts the algorithm to search for improved solutions in expanded neighboring solutions. This exploration associated with r prevents the algorithm from converging to near-optimal solutions. This oversight becomes more pronounced if combined with a late activation of the TS, which can compromise the search for quality solutions and affect the algorithm’s robustness. Furthermore, a lower r value constrains both the TS and IG methods’ ability to escape the local optima due to their shared reliance on r. Such a restriction, especially when TS is activated early, forces the hybrid algorithm to rely more heavily on the TS, adversely impacting the robustness. Observations indicate that the interaction between the parameters r and maxNoImprove is consistent with the behavior of r as previously stated. On the other hand, a low setting for maxNoImprove can prematurely halt the search process, preventing it from converging to a high-quality solution. In contrast, a high maxNoImprove does not guarantee the evasion of local optima if r remains small, despite allowing more iterations. However, allowing more iterations by increasing maxNoImprove could enable convergence towards an improved solution, provided that r is adjusted to avoid excessively distant leaps in the solution space. Examining the parameter maxNoImprove as shown in the last column of Fig. 4, interactions with two additional parameters, activeTabu, and maxNeighbor, are evident. The plot detailing the interplay between maxNoImprove and activTabu suggests that early initiation of the TS may diminish the solution’s robustness. In contrast, a higher activTabu value, when paired with an increased maxNoImprove, can enhance the search process’s ability to move beyond local optima by affording additional iterations for exploration. Additionally, in the context of the $maxNeighbor - maxNoImprove$ parameter pairing, an increase in the number of neighboring solutions does not necessarily lead to higher robustness. Nonetheless, it is noteworthy that at a maxNoImprove level of 80, there is a display of robust performance when the count of maximum neighboring solutions remains low. This configuration allows for iterations within a near-optimal solution space, avoiding the leap to overly distant solutions.

Fig. 4

Interaction plot of IG-TS key parameters

5.4 Performance analysis of algorithms

The evaluation of the proposed meta-heuristic algorithms incorporates an extensive statistical comparison. These algorithms are applied to solve both 720 small and 960 larger instances. We conduct a comparative analysis of the proposed IG-TS and IG-LS algorithms against three established algorithms sourced from relevant literature, with a focus on the objective function and the no-idle constraint. The algorithms under comparison include Adaptive Iterated Greedy (Li et al. 2021), Iterated Greedy (Jing et al. 2020), and Iterated Local Search (Pan et al. 2017) which, have been adapted to suit the objective function, the suggested No-idle adjustment, and the Gap insertion requirements of the problem under study. Notably, the time limit termination criterion, as advised in the referenced algorithms, was deemed insufficient for a fair comparison. Therefore, we standardized the time limit in line with that of the proposed algorithms as depicted in Table 2. Moreover, one of the search operators in the Adaptive Iterated Greedy algorithm proved to be inapplicable, owing to the distinctive nature of the problems.

Table 5 illustrates the computational results of heuristic methods applied to small-sized instances, categorized by factories, machines, and jobs. The “RPD” column displays the average Relative Percentage Deviation (RPD) value for each group of instances computed as ($\frac{SomeSol-BestSol}{BestSol}$) with respect to the best-known solution (the best obtained among all heuristics and MIP models). Additionally, the “Time” column details the average CPU time required by the algorithms to solve each problem configuration over 10 multiple runs.

As can be seen, all algorithms successfully identify the optimal solution for instances involving two factories and four jobs, with IG-TS achieving this in a shorter average computation time. For instances of 10 jobs with two factories, the proposed IG-TS algorithm finds the optimal solution in a relatively small CPU time compared to the mathematical model. These findings highlight the better performance of IG-TS, even for small-sized instances. Similarly, the IG-LS algorithm solves the instances to optimality in the same CPU time as IG-TS does. On the other hand, it is inferred from the obtained RPD values that AIG, IG, and, ILS are unable to identify the optimal solution for all of the mentioned instances. Furthermore, as the job count increases to 16, the IG-TS algorithm demonstrates its capability to either find or improve upon the solutions obtained by the Gurobi solver within a significantly lower CPU time. While IG-LS also delivers solutions faster than IG-TS, it occasionally falls short of the best solutions found by IG-TS, as reflected in the mean RPD values. Conversely, the other three algorithms demonstrate weaker performance in these instances, as evidenced by their RPD values.

Table 5 The average results for the small-sized instances

Table 6 The average results for the large-sized instances

The findings in Table 5 highlight the robust performance in determining optimal solutions for small-sized instances, regardless of the number of factories. Notably, both IG-TS and IG-LS algorithms exhibit even shorter average computation times for instances involving four factories than those with two. AIG, IG, and ILS also successfully identified optimal solutions in scenarios with four factories and four jobs. Moreover, the RPD values reveal that while these three algorithms did not always find the best solution in certain instances, their performance improved compared to the two factory instances. This can be attributed to the increased flexibility offered by a larger number of potential job placement locations, enabling more possible production planning.

The results from the application of the heuristic algorithms on large-sized instances with four and seven factories are presented in Table 6. Given the lack of known optimal solutions or reliable MIP bounds the obtained RPD values for each group of instances are computed concerning the best-known solution across all heuristic methods. The IG-TS algorithm clearly demonstrates its ability to consistently generate high-quality solutions for all large instances. The impact of increasing the number of jobs on the time and RPD of both IG-TS and IG-LS algorithms is noteworthy. With an increase in the number of jobs, the time needed for the IG-TS and IG-LS algorithms to converge to a solution also rises, due to the demanding computational efforts required in each iteration. However, the time difference between both algorithms for a given instance is substantial. This time difference can be attributed to the specific operators utilized in both algorithms, particularly the k-regret method. The k-regret method examines and evaluates a considerable number of potential insertions of removed jobs at each attempt, thus requiring more time to reach a conclusive solution at each iteration. Despite the longer processing time, the IG-TS algorithm consistently delivers solutions that significantly outperform the IG-LS algorithm. Conversely, despite AIG, IG, and ILS being given more exploration time than their original implementation, they generally fail to achieve better solutions compared to IG-TS in most instances.

It is observed that an increase in the number of factories has a significant impact on the computational time and quality of the solution. As the quantity of factories increases, the computational time and RPD decrease. This phenomenon can be attributed to the increased availability of potential job placement locations, which reduces the complexity of terminating a solution.

6 Conclusions

This study addresses the distributed no-idle permutation flowshop scheduling problem with due windows. It involves two interconnected decisions: the initial job assignments to factories and the subsequent sequencing of these assigned jobs. Four variants of mathematical models were proposed to address this concept in the flowshop scheduling problem aiming to minimize the total weighted earliness and tardiness penalties. The proposed position-based mathematical model was found to be the most efficient among the four formulations evaluated. An ANOVA test was conducted to assess the impact of input parameters on the model’s performance. The results indicated that increasing jobs, machines, and factories increases the complexity, reflected in either longer computation time or larger gaps in the obtained solution. This finding highlights the importance of considering the complexity of the model and emphasizes the need for efficient algorithms to handle large-sized problems. In this context, two hybrid algorithms were developed as solution approaches and subsequently compared with three well-established algorithms from existing literature. The first hybrid algorithm, which incorporates the tabu search scheme, effectively identified the optimal solution and outperformed the Gurobi solver for small-sized instances. Additionally, the proposed IG-TS algorithm demonstrated significant improvements over the benchmark IG-LS algorithm. Moreover, both proposed algorithms were able to obtain better solutions in comparison to the other three heuristics when handling larger instances. This demonstrates the effectiveness of the hybrid approach in finding optimal or near-optimal solutions for both small and large-sized instances and also highlights the potential of combining different optimization techniques to enhance the performance of a given algorithm. Furthermore, the computational research was conducted on benchmarks developed based on Naderi and Ruiz (2010) data.

This study solves the problem with up to 500 jobs for the first time. Several research avenues remain unexplored in terms of solution approaches and the problem itself. Other combinatorial heuristics seem to be applicable to solve this problem for comparison purposes, like the Genetic algorithm. Additionally, other mathematical models with different sequence representative variables can be developed to solve the problem for larger sizes. Furthermore, the cutting planes can be devised to enhance the mathematical models’ performance by accelerating the lower-bound growth.