1 Introduction

According to the most recent published papers, the fuzzy differential equation was introduced in 1978. Moreover, Kandel (1980) and Byatt and Kandel (1978) present the fuzzy differential equation and have rapidly expanded literature. First-order linear fuzzy differential equations emerge in modeling the uncertainty of dynamical systems. The solutions of first-order linear fuzzy differential equations have been widely considered (e. g., see Chalco-Cano and Roman-Flores 2008; Buckley and Feuring 2000; Seikkala 1987; Diamond 2002; Song and Wu 2000; Allahviranloo et al. 2009; Zabihi et al. 2023; Allahviranloo and Pedrycz 2020).

The most famous numerical solutions of order fuzzy differential equations are investigated and analyzed under the Hukuhara and gH-differentiability (Safikhani et al. 2023). It is widely believed that the common Hukuhara difference and so Hukuhara derivative between two fuzzy numbers are accessible under special circumstances (Kaleva 1987; Diamond 1999, 2000). The gH-derivative, however, is available in less restrictive conditions, even though this is not always the case (Dubois et al. 2008). To overcome these serious defects of the concepts mentioned above, Bede and Stefanini (Dubois et al. 2008) describe g-derivative. In 2007, Allahviranloo used the predictor–corrector under the Seikkala-derivative method to propose a numerical solution of fuzzy differential equations (Allahviranloo et al. 2007).

Here, we investigate the Adams–Bashforth method to solve fuzzy differential equations focusing on g-differentiability. We restrict our study on normal, convex, upper semicontinuous, and compactly supported fuzzy sets in \(\mathbb {R}^n\).

This paper has been arranged as mentioned below: firstly, in Sect. 2, we recall the necessary definitions to be used in the rest of the article, after a preliminary section in Sect. 3, which is dedicated to the description of the Adams–Bashforth method to fix the purposed equation. The convergence theorem is formulated and proved in Sect. 4. For checking the accuracy of the method, three examples are presented. In Sect. 5, their solutions are compared with the exact solutions. In the last section, some conclusions are given.

2 Preliminaries

Definition 2.1

(Mehrkanoon et al. 2009) A fuzzy subset of the real line with a normal, convex, and upper semicontinuous membership function of bounded support is a fuzzy number \(\tilde{w}\). The family of fuzzy numbers is indicated by F.

We show an arbitrary fuzzy number with an ordered pair of functions \((\underline{w}(\gamma ),\overline{w}(\gamma ))\), \(0\le \gamma \le 1\) which provides the following:

  • \(\underline{w}(\gamma )\) is a bounded left continuous non-decreasing function over [0, 1], corresponding to any \(\gamma \).

  • \(\overline{w}(\gamma )\) is a bounded left continuous non-decreasing function over [0, 1], corresponding to any \(\gamma \).

    $$\begin{aligned} \underline{w}(\gamma )\le \overline{w}(\gamma ),\quad \textrm{where} ~~ \gamma \in [0,1]. \end{aligned}$$
    (1)

Then, the \(\gamma \)-level set

$$\begin{aligned}{}[w]^{\gamma }=\{s|u(s)\ge \gamma \}, \qquad 0\le \gamma \le 1, \end{aligned}$$
(2)

is a closed bounded interval, which is denoted by:

$$\begin{aligned}{}[w]^{\gamma }=[\underline{w}\ ,\overline{w}]. \end{aligned}$$
(3)

Definition 2.2

(Bede and Stefanini 2013) The g-difference is defined as follows:

$$\begin{aligned}{}[w \ominus _g z]^{\gamma }= [\textrm{inf}_{\theta \ge \gamma } \textrm{min} \{\underline{w}_{\theta }-\underline{z}_{\theta }, \overline{w}_{\theta }-\overline{z}_{\theta }\}, \textrm{sup}_{\theta \ge \gamma } \textrm{max} \{\underline{w}_{\theta }-\underline{z}_{\theta }, \overline{w}_{\theta }- \overline{z}_{\theta }\}]. \end{aligned}$$
(4)

In Bede and Stefanini (2013), the difference between g-derivative and q-derivative has been fully investigated.

Definition 2.3

(Bede and Stefanini 2013; Diamond 1999, The Hausdorff distance) The Hausdorff distance is defined as follows:

$$\begin{aligned} D(w,z)=\sup _{\gamma \in [0,1]}\{||[w]^{\gamma } \circleddash _{gH} [z]^{\gamma }||_*\}=|| w \circleddash _g z||,\quad \forall w, z \in R_F, \end{aligned}$$
(5)

where \(|| \cdot ||=D(\cdot , \cdot )\) and the gH-difference \(\circleddash _{gH}\) is with interval operands \([u]^\gamma \) and \([v]^\gamma \)

By definition, D is a metric in \(R_F\) which has the subsequent properties:

  1. 1.

    \(D(w+t, z+t)=D(w,z ) \qquad \forall w, z, t \in R_F\),

  2. 2.

    \(D(rw,rz)=|r|D(w,z)\qquad \forall w, z\in \ R_F, r\in R\),

  3. 3.

    \(D(w+t,z+d)\le D(w,z)+ D(t, d)\qquad \forall w, z, t, d \in R_F\).

Then, \((D, R_F)\) is called a complete metric space.

Definition 2.4

(Bede and Stefanini 2013) Neumann’s integral of \(k{:}\, [m, n] \rightarrow R_F\) is defined level-wise by the fuzzy

$$\begin{aligned} \bigg [\int ^n_m k(y)\textrm{d}y\bigg ]^\gamma = \int ^m_n[k(y)]^{\gamma }\textrm{d}y. \qquad \gamma \in [0,1]. \end{aligned}$$
(6)

Definition 2.5

(Bede and Stefanini 2013) Suppose \(k{:}\, [m,n] \rightarrow R_F\) is a function with \([k(y)]^{\gamma }=[\underline{k}_{\gamma }(y), \overline{k}_{\gamma }(y)]\). If \(\underline{k}_{\gamma }(y)\) and \(\overline{k}_{\gamma }(y)\) are differentiable real-valued functions with respect to y, uniformly for \(\gamma \in [0, 1]\), then k(y) is g-differentiable and we have

$$\begin{aligned}{}[k'_g(y)]^{\gamma }=\left[ \mathrm{inf~min}_{\theta \ge \gamma } \{(\underline{k}_{\theta })'(y),(\overline{k}_\theta )'(y)\}, \mathrm{sup~ max}_{\theta \ge \gamma }(\{\underline{k}_{\theta })'(y),(\overline{k}_{\theta })'(y)\}\right] . \end{aligned}$$

Definition 2.6

(Bede and Stefanini 2013) Let \(y_0 \in [m, n]\) and t be such that \(y_0+t \in ]m, n[\), then the g-derivative of a function \(k{:}\, ]m, n[ \rightarrow R_F\) at \(y_0\) is defined as

$$\begin{aligned} k'_g(y_0)=\lim _{t\rightarrow 0} \frac{1}{t}[k(y_0+t)\circleddash _g k(y_0)]. \end{aligned}$$
(7)

If there exists \(k'_g(y_0)\in R_F\) satisfying (7), we call it generalized differentiable (g-differentiable for short) at \(y_0\). This relation depends on the existence of \(\circleddash _g\), and there exists no such guarantee for this desire.

Theorem 2.7

Suppose \(k{:}\,[m,n]\rightarrow R_F\) is a continuous function with \([k(y)]^{\gamma }=[k^{-}_{\gamma }(y), k^{+}_{\gamma }(y)]\) and g-differentiable in [m, n]. In this case, we obtain

$$\begin{aligned} \int ^n_m{k'_g}(y)\textrm{d}y=k(n){\circleddash }_g k(m). \end{aligned}$$
(8)

Proof

To show the assertion, it is enough to show their equality in level-wise form, suppose k is g-differentiable, so we have

$$\begin{aligned}&\bigg [\int ^n_m k'_g(y)\textrm{d}y\bigg ]^\gamma = \int ^n_m [k'_g(y)]^\gamma \textrm{d}y\nonumber \\&\quad =\int ^{n}_{m}[\mathrm{inf~min}_{\theta \ge \gamma }\{(k^{-}_{\theta }){'}(y),(k^{+}_{\theta }){'}(y)\}, \mathrm{sup~ max}_{\theta \ge \gamma }\{(k^{-}_{\theta }){'}(y),(k^{+}_{\theta }{'}(y)\}]\textrm{d}y\nonumber \\&\quad = \left[ \inf ~\textrm{min}_{\theta \ge \gamma }\left\{ \int ^n_m(k^{-}_{\theta })'(y)\textrm{d}y,\ \int ^n_m(k^{+}_{\theta })'(y)\textrm{d}y\right\} ,\mathrm{sup~max}_{\theta \ge \gamma } \left\{ \int ^n_m(k^{-}_{\theta })'(y)\textrm{d}y, \int ^n_m (k^{+}_{\theta })'(y)\textrm{d}y\right\} \right] \nonumber \\&\quad =\bigg [\inf ~\textrm{min}_{\theta \ge \gamma }\left\{ k^{-}_{\theta }(n)-k^{-}_{\theta }(m),k^{+}_{\theta }(n)-k^{+}_{\theta }(m)\right\} , \mathrm{sub~ max} \left\{ k^{-}_{\theta }(n)-k^{-}_{\theta }(m), k^{+}_{\theta }(n)-k^{+}_{\theta }(m)\right\} \bigg ]\nonumber \\&\quad =k(n){\circleddash }_g k(m). \end{aligned}$$
(9)

\(\square \)

Definition 2.8

(Kaleva 1990, fuzzy Cauchy problem) Suppose \(x'_g(s)=k(s,x(s))\) is the first-order fuzzy differential equation, where y is a fuzzy function of s, k(s, x(s)) is a fuzzy function of the crisp variable s, and the fuzzy variable x and \(x'\) is the g-fuzzy derivative of x. By the initial value \(x(s_0)=\gamma _0\), we define the first-order fuzzy Cauchy problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} x'_g(s)=k(s,x(s)), \qquad s_0\le s \le T, \\ x(s_0)=\gamma _0. \end{array}\right. } \end{aligned}$$

Proposition 2.9

Suppose \(\textit{k, h}{:}\, [\textit{a}, \textit{b}] {\rightarrow } R_F\) are two bounded functions, then

$$\begin{aligned}{} & {} {{\textrm{sup}}_A( k+\ h)\ }\le {{\textrm{sup}}_A k\ }+{{\textrm{sup}}_A h,\ }\ \\{} & {} {{\textrm{inf}}_A( k+h)\ }\ge {{\textrm{inf}}_A k\ }+{{\textrm{inf}}_A h.\ }\ \end{aligned}$$

Proof

Since \(k(y)\le \textrm{sup}_A k\) and \(k(y)\le \textrm{sup}_A k\) for every \(y \in [m,n]\), one can obtain \(k(y)+h(y)\le \textrm{sup}_A k+\textrm{sup}_A h\). Thus, \(k+h\) is bounded from above by \(\textrm{sup}_A k+\textrm{sup}_A h\), so \(\textrm{sup}_A( k+h) \le \textrm{sup}_A k+ \textrm{sup}_A h\). The proof for the infimum is similar. \(\square \)

Definition 2.10

Let \(\{\widetilde{q}_m\}^\infty _{m=0}\) be a fuzzy sequence. Then, we define the backward g-difference \(\nabla _g \widetilde{q}_m\) as follows

$$\begin{aligned} \nabla _g\widetilde{q}_m =\widetilde{q}_m{\circleddash }_g \widetilde{q}_{m-1} \qquad \textrm{for} ~m \ge 1. \end{aligned}$$
(10)

So, we have

$$\begin{aligned} \nabla _g^2\widetilde{q}_m&=\nabla _g(\nabla _g\widetilde{q}_m)=\nabla _g(\widetilde{q}_m{\circleddash }_g \widetilde{q}_{m-1})=\nabla _g \widetilde{q}_m{\circleddash }_g \nabla _g \widetilde{q}_{m-1}\nonumber \\&= (\widetilde{q}_m{\circleddash }_g \widetilde{q}_{m-1}) {\circleddash }_g (\widetilde{q}_{m-1}{\circleddash }_g \widetilde{q}_{m-2})=\widetilde{q}_m{\circleddash }_g 2 \widetilde{q}_{m-1}\oplus \widetilde{q}_{m-2}. \end{aligned}$$
(11)

Consequently,

$$\begin{aligned} \nabla _g^k\widetilde{q}_n=\nabla _g^{k-1}(\nabla _g\widetilde{q}_m), \quad ~ \textrm{for} ~ k \ge 2. \end{aligned}$$
(12)

Proposition 2.11

For a given fuzzy sequence \({\left\{ {\widetilde{q}}_m\right\} }^{\infty }_{m=0}\), by supposing backward g-difference, we have

$$\begin{aligned} \nabla _g^k \widetilde{q}_m=h^k \widetilde{q}^{(k)}_{m_g}. \end{aligned}$$
(13)

Proof

We prove proposition by induction that, for all \(n \in \mathbb {Z}^+\),

Using Definition 2.10, for base case, \(n = 1\), we have

$$\begin{aligned} \nabla _g\widetilde{q}_m&=\widetilde{q}_m{\circleddash }_g \widetilde{q}_{m-1}=h\times \frac{\widetilde{q}_m{\circleddash }_g\widetilde{q}_{m-1}}{h}=h \widetilde{q}'_{m_g}, \nonumber \\ \nabla _g^2 \widetilde{q}_m&=\nabla \widetilde{q}_m{\circleddash }_g\ \nabla \widetilde{q}_{m-1}=h \widetilde{q}'_{m_g}{\circleddash }_g h \widetilde{q}'_{{m-1}_g}=h\times \frac{h \widetilde{q}'_{m_g}\circleddash _{g}h\widetilde{q}'_{{m-1}_g}}{h}=h^2 \widetilde{q}^{''} _{m_g}. \end{aligned}$$
(14)

Induction step: Let \( k \in \mathbb {Z}^+\) be given and suppose (14) is true for \(n=k\). Then,

$$\begin{aligned} \nabla ^{k+1}\widetilde{q}_m&=\nabla ^k\widetilde{q}_m\circleddash _g \nabla ^k \widetilde{q}_{m-1}=h^k \widetilde{q}^{(k)}_{m_g}\circleddash _g h^k \widetilde{q}^{(k)}_{m_g} \\&= h \times \frac{h^k \widetilde{q}^{ (k )}_{m_g}\circleddash _gh^k\widetilde{q}^{(k)}_{m_g}}{h}=h^{k+1} \widetilde{q}^{(k+1)}_{m_g}. \end{aligned}$$

Conclusion: For all \(m\in \mathbb {Z}^+\), (14) is correct, by the principle of induction. \(\square \)

Definition 2.12

(Switching Point) The concept of switching point refers to an interval where fuzzy differentiability of type-(i) turns into type-(ii) and also vice versa.

3 Fuzzy Adams–Bashforth method

To derivative of a fuzzy multistep method, we consider the solution of the initial-value problem:

$$\begin{aligned} \widetilde{x}'(s)=\widetilde{k}\ (s,\widetilde{x}(s)),\quad s_0\le s\le S.\quad \widetilde{x}(s_0)=\widetilde{\gamma }_0. \end{aligned}$$
(15)

To obtain the approximation \(t_{j+1}\) at the mesh point \(s_{j+1}\), where initial values

$$\begin{aligned} {\widetilde{t}}_0={\widetilde{\gamma }}_0,\quad {\widetilde{t}}_1={\widetilde{\gamma }}_1,\quad \cdots \quad {\widetilde{t}}_{n-1}={\widetilde{\gamma }}_{n-1} \end{aligned}$$
(16)

are assumed.

If integrated over the interval \([s_j,s_{j+1}]\), we get

$$\begin{aligned} \widetilde{x}(s_{j+1}){\circleddash }_g \widetilde{x}(s_j)=\int ^{s_{j+1}}_{s_j}\widetilde{x}'(s) \textrm{d}s= \int ^{s_{j+1}}_{s_j}{\widetilde{k}(s, \widetilde{x}(s))\textrm{d}s}, \end{aligned}$$
(17)

but, without knowing \(\widetilde{x}(s)\), we cannot integrate \(\widetilde{k}(s,\widetilde{x}(s))\), one can apply an interpolating polynomial \(\widetilde{q}(s)\) to \(\widetilde{k}(s, \widetilde{x}(s))\), which is computed by the data points \(\left( s_0, {\widetilde{t}}_0\right) , \left( s_1,{\widetilde{t}}_1\right) ,\ldots \left( s_j,{\widetilde{t}}_j\right) \). These data were obtained in Sect. 2.

Indeed, by supposing that \(\widetilde{x}\left( s_j\right) \approx \ {\widetilde{t}}_j\ \), Eq. (17) is rewritten as

$$\begin{aligned} \widetilde{x}\left( s_{j+1}\right) {\circleddash }_g{\widetilde{t}}_j\approx \int ^{s_{j+1}}_{s_i}{\widetilde{q}(s) \textrm{d}s}. \end{aligned}$$
(18)

To take a fuzzy Adams–Bashforth explicit m-step method under the notion of g-difference, we construct the backward difference polynomial \({\widetilde{q}}_{n-1}(s)\),

$$\begin{aligned} (s_j,\widetilde{k}(s_j,\widetilde{x}(s_j))), (s_{j-1},\widetilde{k}(s_{j-1},\widetilde{x}(s_{j-1}))), \ldots , \left( s_{j+1-n}, \widetilde{k}(s_{j+1-n},\widetilde{x}(s_{j+1-n}))\right) . \end{aligned}$$
(19)

We assume that the nth derivatives of the fuzzy function k exist. This means that all derivatives are g-differentiable. As \({\widetilde{q}}_{n-1}(s)\) is an interpolation polynomial of degree \(n-1\), some number \({\xi }_j\) in \(\left( s_{j+1-n}, s_j\right) \) exists with

$$\begin{aligned} \widetilde{k}(s,\widetilde{x}(s))={\widetilde{q}}_{n-1}\left( s\right) \oplus \frac{{\widetilde{k}}^{\left( n\right) }_g\ (s, \widetilde{x}(s))}{n!}\odot \ (s- s_j)\ (s- s_{j-1})\cdot \cdot \cdot \ \left( s- s_{j+1-n}\right) , \end{aligned}$$
(20)

where the corresponding notation \({\widetilde{k}}^{(n)}_g (s, \widetilde{x}(s)),n\in \mathbb {N},\) exists. Moreover, it can be mentioned that the existence of this corresponding formula based on the existence of \({\circleddash }_g\), and while \({\circleddash }_g\) exist this relation always exists.

We introduce the \(s=s_j+\beta h\), with \(\textrm{d}s=h \textrm{d}\beta \), substituting these variable into \({\widetilde{q}}_{n-1}(s)\) and the error term indicates

$$\begin{aligned} \int ^{s_{j+1}}_{s_j}{\widetilde{k}\ (s,\widetilde{x}(s)\textrm{d}s}&=\int ^{s_{j+1}}_{s_j}{\sum ^{n-1}_{k=0}{({-1)}^k\left( \genfrac{}{}{0.0pt}{}{-\beta }{k}\right) \nabla ^k_g}\widetilde{k}\ (s_j,\widetilde{x}(s_j) \textrm{d}s}\nonumber \\&\quad \oplus \int ^{s_{j+1}}_{s_j}{\frac{\widetilde{k}^{(m)}_g (s,\widetilde{x}(s))}{n!}\odot \ (s-\ s_j)(s-\ s_{j-1}) \cdots (s-\ s_{j+1-n})\ \textrm{d}s} \nonumber \\&=\sum ^{n-1}_{k=0}{\nabla }^k_g\widetilde{k}\ (s_j, \widetilde{x}(s_j)\ h\ ({-1)}^k\ \int ^1_0{\left( \genfrac{}{}{0.0pt}{}{-\theta }{k}\right) \textrm{d}\beta } \nonumber \\&\quad \oplus \frac{h^{n+1}}{n!}\int ^1_0{\ \beta \ \left( \beta +1\right) \cdots \left( \beta +n-1\right) \ {\widetilde{k}}^{(n)}_g\ \left( {\xi }_j, \widetilde{x}\left( {\xi }_j\right) \right) \textrm{d}\beta }. \end{aligned}$$
(21)

So, we will get

$$\begin{aligned} \int ^{s_{j+1}}_{s_j}{\widetilde{k} (s,\widetilde{x}(s))\ \textrm{d}s}&=h\ [\widetilde{k}({(s}_j,\widetilde{x}(s_j))\oplus \frac{1}{2}{\nabla }_g\widetilde{k}({(s}_j,\widetilde{x}(s_j))\oplus \frac{5}{12}{{\nabla }^2}_g\widetilde{k}(\left( s_j, \widetilde{x}(s_j)\right) + \cdots ] \nonumber \\ {}&\quad \oplus \frac{h^{n+1}}{n!}\int ^1_0{ \beta \left( \beta +1\right) \cdots \left( \beta +n-1\right) {\widetilde{k}}^{(n)}_g\ \left( {\xi }_j, \widetilde{x}\left( {\xi }_j\right) \right) \textrm{d}\beta }. \end{aligned}$$
(22)

Obviously, the product of \(\beta \ \left( \beta +1\right) \cdots \left( \beta +n-1\right) \) does not change sign on [0, 1], so the Weighted Mean Value Theorem for some number \({\mu }_j\), where \(s_{j+1-n}< {\mu }_j< s_{j+1}\), can be applied to the last term in Eq. (22), hence it becomes

$$\begin{aligned} \frac{h^{n+1}}{n!}&\int ^1_0{\ \beta \ (\beta +1)\cdots (\beta +n-1)\ {\widetilde{k}}^{(n)}_g\ ({\xi }_j,\widetilde{x}({\xi }_j))\textrm{d}\beta }\ \nonumber \\ {}&=\frac{h^{m+1}\ {\widetilde{k}}^{(n)}_g\ ({\mu }_j, \widetilde{x}({\mu }_j ))}{n!}\int ^1_0{\beta (\beta +1)\cdots (\beta +n-1)\ \textrm{d}\beta . }\ \end{aligned}$$
(23)

So, it simplifies to

$$\begin{aligned} h^{n+1}\ {\widetilde{k}}^{(n)}_g\ \left( {\mu }_j, \widetilde{x}\left( {\mu }_j\right) \right) {(-1)}^n\ \int ^1_0{\ \left( \genfrac{}{}{0.0pt}{}{-\beta }{n}\right) \textrm{d}\beta }, \end{aligned}$$
(24)

whereas

$$\begin{aligned} \widetilde{x}\left( s_{j-1}\right) {\circleddash }_g\ \widetilde{x}\left( \ s_j\right) =\ \int ^{s_{j+1}}_{s_j}{\widetilde{k}\ \left( s,\ \widetilde{x}\left( s\right) \right) \ \textrm{d}s}. \end{aligned}$$
(25)

So, Eq. (20) is written as

$$\begin{aligned} \widetilde{x}\left( s_{j-1}\right) {\circleddash }_g\ \widetilde{x}\left( s_j\right)&=\ h\ \left[ \widetilde{k}\left( \left( s_j,\widetilde{x}\left( s_j\right) \right) \right) \oplus \ \frac{1}{2}{\nabla }_g\widetilde{k}\left( \left( s_j,\widetilde{x}\left( s_j\right) \right) \right) \oplus \frac{5}{12}{{\nabla }^2}_g\widetilde{k}\left( \left( s_j,\ \widetilde{x}\left( s_j\right) \right) \oplus \cdots \right) \right] \ \nonumber \\&\quad \oplus \ h^{n+1}\ {\widetilde{k}}^{(n)}_g\ \left( {\mu }_j, \widetilde{x}\left( {\mu }_j\right) \right) {(-1)}^n\ \int ^1_0{\ \left( \genfrac{}{}{0.0pt}{}{-\beta }{n}\right) \textrm{d}\beta }. \end{aligned}$$
(26)

It is also worth mentioning that the notions \(\Delta _{g}\) and \(\oplus \) are extensively utilized solving the problems of sup and inf existence.

To illustrate this method, we discuss solving the fuzzy initial value problem \({\widetilde{x}}'\left( s\right) =\widetilde{k}(s,\widetilde{x}\left( s\right) )\) by Adams–Bashforth’s three-step method. To derive the three-step Adams–Bashforth technique, with \(n= 3\), We have

$$\begin{aligned} {\widetilde{t}}_0&=\ {\widetilde{\gamma }}_0, \quad {\widetilde{t}}_1=\ {\widetilde{\gamma }}_1, \quad {\widetilde{t}}_2=\ {\widetilde{\gamma }}_2,\nonumber \\ {\widetilde{t}}_{n+1}{\circleddash }_g{\widetilde{t}}_n&= {h}\int ^{{1}}_0{\left( {\widetilde{\textrm{k}}}_{\textrm{m}}\oplus {\beta }{{\nabla }}_g{\widetilde{{k}}}_{{m}}\oplus \frac{{\beta }\left( {\beta }+1\right) }{{2}}{{{\nabla }}^{{2}}}_g{\widetilde{{k}}}_{{m}}\right) \textrm{d}\beta }. \end{aligned}$$
(27)

For \(m=2, 3,\ldots , N-1.\) So

$$\begin{aligned} {\left[ {\widetilde{t}}_{m+1}{\circleddash }_g{\widetilde{t}}_m\right] }_{\gamma }={\left[ {h}\int ^{{1}}_0{\left( \widetilde{{k}}_{{m}}\oplus \ \beta {\nabla }_g{\widetilde{{k}}}_{{m}}\oplus \frac{{\beta }\left( {\beta }{+1}\right) }{{2}}{{{\nabla }}^{{2}}}_g{\widetilde{{k}}}_{{m}}\right) \ \textrm{d}\beta }\right] }^{{\gamma }}. \end{aligned}$$
(28)

Here, we also describe our model as introduced models \(\Delta _{g}\) and \(\oplus \).

By considering

$$\begin{aligned} {\left[ {{\nabla }}_g{\ }{\widetilde{k}}_i\right] }^{\gamma }= & {} \left[ {\textrm{infmin}}_{{\theta }{\ge }{\gamma }}{\ }\left\{ {{k}}^{-}_{j\theta }-{\ }k^{-}_{j-1.\beta }{,\ }{{k}}^+_{j\theta }-{\ }k^{+}_{j-1.\theta }\right\} ,\right. \\ {}{} & {} \left. {\ \textrm{sup}\ }{{\textrm{max}}}_{{\theta }{\ge }{\gamma }}\left\{ {{k}}^{-}_{j\theta }-{\ }k^{-}_{j-1.\theta }{\,\ }{{k}}^+_{j\theta }-{\ }k^{+}_{j-1.\theta }\right\} \ \right] .\end{aligned}$$

As a consequence

(29)

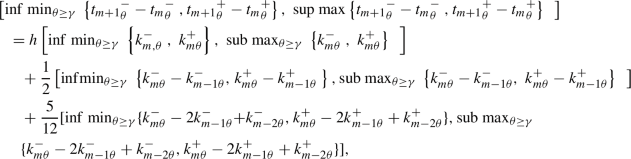
from which we obtain

$$\begin{aligned} \textrm{inf} ~\textrm{min}_{\theta \ge \gamma }&\{t_{m+1_\theta }^{-} -t_{m_\theta }^{-},t_{m+1_\theta }^+-t_{m_\theta }^+\} \le \end{aligned}$$
(30)
$$\begin{aligned} \mathrm{inf ~min}_{\theta \ge \gamma }&\left\{ h\left( \frac{23}{12}k^{-}_{m\beta }-\ \frac{16}{12}k^{-}_{m-1 \theta }+\ \frac{5}{12}k^{-}_{m-2 \theta }\right) ,\ h\left( \frac{23}{12}\ k^{+}_{m\theta }-\frac{16}{12}\ k^{+}_{m-1 \theta }+\ \frac{5}{12}\ k^{+}_{m-2 \theta }\right) \ \right\} . \end{aligned}$$
(31)

And

(32)

From (24) and (29), we get

$$\begin{aligned}&\left\{ h \left( \frac{23}{12}k^-_{m\theta }-\frac{16}{12}k^{-}_{m-1\theta }+\frac{5}{12} k^-_{m-2\theta }\right) , h\left( \frac{23}{12} k^+_{m\theta }-\frac{16}{12} k^+_{m-1\theta }+ \frac{5}{12} k^+_{m-2\theta } \right) \right\} \nonumber \\&\quad \subseteq \left\{ t_{m+1}^-{_{\theta }}-t_m^-{_{\theta }}, t_{m+1}^+{_{\theta }}-t_m^+{_{\theta }}\right\} , \end{aligned}$$
(33)

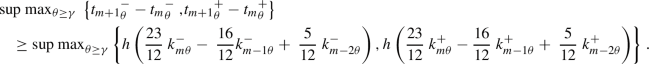
if we suppose that

Case 1:

$$\begin{aligned} \textrm{inf}~{\textrm{min}}_{{\theta }{\ge }{\gamma }} \left\{ {t_{m+1}}^{-}_{\theta }-{t_m}^{-}_{\theta }{\ },{\ }{t_{m+1}}^+_{\theta }-{t_m}^+_{\theta }\right\} ={t^{-}}_{m+1 \alpha }-{t^{-}}_{m \alpha }, \quad \alpha \in \ \left[ \theta , 1\right] \end{aligned}$$
(34)

and

$$\begin{aligned}&{\textrm{inf}~{\textrm{min}}_{{\theta }{\ge }{\gamma }}\ \left\{ h\left( \frac{23}{12}{\ k}^{-}_{m\theta }-\frac{16}{12}k^{-}_{m-1 \theta }\mathrm {+\ }\frac{5}{12}{\ k}^{-}_{m-2 \theta }{\ }\right) ,h\left( \frac{23}{12}\ k^{+}_{m\theta }-\frac{16}{12} k^{+}_{m-1 \theta }+\ \frac{5}{12}\ k^{+}_{m-2 \theta }\right) \ \right\} \ }\nonumber \\&\quad = h\ \left( \frac{23}{12}\ k^{-}_{m\alpha }\ -\frac{16}{12}\ k^{-}_{m-1 \alpha }+\ \frac{5}{12} k^{-}_{m-2 \alpha }\right) . \end{aligned}$$
(35)

So

$$\begin{aligned} \textrm{sup} \ {\textrm{max}}_{\theta \ge \gamma }\ \left\{ {t_{n+1}}^{-}_{\theta }-{t_n}^{-}_{\theta },{t_{n+1}}^+_{\theta }-{t_n}^+_{\theta }\right\} = {t^+}_{n+1 \gamma } - {t^+}_{n \alpha }, \alpha \in [\theta , 1], \end{aligned}$$
(36)

and

$$\begin{aligned}&{\textrm{sup} ~{\textrm{max}}_{\theta \ge \gamma }\ \left\{ h\ \left( \frac{23}{12}{\ k}^{-}_{m\theta }-\frac{16}{12}k^{-}_{m-1 \theta }+\ \frac{5}{12}{\ k}^{-}_{m-2 \theta }\right) , h\left( \frac{23}{12}\ k^{+}_{m\theta }-\frac{16}{12}\ k^{+}_{m-1 \theta }+\ \frac{5}{12}\ k^{+}_{m-2 \theta }\ \right) \right\} \ }\nonumber \\&\quad = h\left( \frac{23}{12}\ k^{+}_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1 \alpha }+\ \frac{5}{12}{\ k}^+_{m-2 \alpha }\right) . \end{aligned}$$
(37)

Then, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} {t^{-}}_{m+1 \alpha }\ -\ {t^{-}}_{m \alpha }\le \ \frac{23}{12}\ {\ k}^{-}_{m\alpha }\ -\frac{16}{12}\ {\ k}^{-}_{m-1 \alpha }+\ \frac{5}{12}{\ k}^{-}_{m-2\alpha },\ \\ {t^+}_{m+1 \alpha }\ -\ {t^+}_{m \alpha }\ge \ \ \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1\alpha }+\ \frac{5}{12}{\ k}^+_{m-2 \alpha }. \end{array}\right. } \end{aligned}$$
(38)

Hence,

$$\begin{aligned} {\left\{ \begin{array}{ll} {t^{-}}_{m+1 \alpha }\ \ \le {t^{-}}_{m \alpha }+h\left( \frac{23}{12}\ {\ k}^{-}_{m\alpha }\ -\frac{16}{12}\ {\ k}^{-}_{m-1 \alpha }+\ \frac{5}{12}{\ k}^{-}_{m-2 \alpha }\right) ,\ \\ {t^+}_{m+1 \alpha }\ \ \ge {t^+}_{m \alpha }+h\left( \ \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1 \alpha }+\ \frac{5}{12}{\ k}^+_{m-2 \alpha }\right) . \end{array}\right. } \end{aligned}$$
(39)

We follow

$$\begin{aligned}&\left[ {t^{-}}_{m \alpha }+h\left( \frac{23}{12} k^{-}_{m\alpha }\ -\frac{16}{12} k^{-}_{m-1 \alpha }+ \frac{5}{12} k^{-}_{m-2 \alpha }\right) , t^+_{m \alpha }+h\left( \frac{23}{12} k^{+}_{m\alpha }-\frac{16}{12} k^{+}_{m-1 \alpha }+ \frac{5}{12} k^{+}_{m-2 \alpha }\right) \ \right] \nonumber \\&\quad \subseteq \left[ {t^{-}}_{m+1 \alpha },{\ }{t^+}_{m+1 \alpha }\ \right] , \end{aligned}$$
(40)

Similarly, we have

Case 2:

$$\begin{aligned} \textrm{inf}\ {\textrm{min}}_{{\theta }{\ge }{\gamma }} \left\{ {t_{m+1}}^{-}_{\theta }-{t_m}^{-}_{\theta },{t_{m+1}}^+_{\theta }-{t_m}^+_{\theta }\right\} = {t^+}_{m+1 \alpha } - {t^+}_{m \alpha }, \alpha \in \left[ \theta , 1\right] , \end{aligned}$$
(41)

and

$$\begin{aligned}&{\textrm{inf} {\textrm{min}}_{{\theta }{\ge }{\gamma }}\ \left\{ h\left( \frac{23}{12}{\ k}^{-}_{m\theta }-\frac{16}{12}k^{-}_{m-1 \theta }+\ \frac{5}{12}{\ k}^{-}_{m-2 \theta }\right) , h\left( \frac{23}{12}\ k^{+}_{m\theta }-\frac{16}{12}\ k^{+}_{m-1 \theta }+\ \frac{5}{12}\ k^{+}_{m-2 \theta }\right) \right\} \ }\nonumber \\&\quad = h\left( \frac{23}{12}\ {\ k}^{-}_{m\alpha }\ -\frac{16}{12}\ {\ k}^{-}_{m-1 \alpha }+\ \frac{5}{12}{\ k}^{-}_{m-2 \alpha }\right) . \end{aligned}$$
(42)

So,

$$\begin{aligned} \textrm{sup}{{\ \textrm{max}}}_{{\theta }{\ge }{\gamma }}\ \left\{ t_{m+1}^{-}{_{\theta }}-t_m^{-}{_{\theta }}\ ,t_{m+1}^+{_\theta }-t_m^+{_{\theta }}\right\} =t^{-}_{m+1 \alpha }-t^{-}_{m \alpha }, \quad \alpha \in \ \left[ \theta , 1\right] \end{aligned}$$
(43)

and

$$\begin{aligned}&{\textrm{sup} {\textrm{max}}_{{\theta }{\ge }{\gamma }}\ \left\{ h\left( \frac{23}{12}{\ k}^{-}_{m\theta }-\frac{16}{12}k^{-}_{m-1 \theta }+\frac{5}{12}{\ k}^{-}_{m-2 \theta }\right) ,h\left( \frac{23}{12}\ k+_{m\theta }-{\frac{16}{12}\ k}^+_{m-1 \theta }+\ \frac{5}{12}\ k^{+}_{m-2 \theta }\right) \right\} \ }\nonumber \\&\quad = k\left( \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1 \alpha }+\ \frac{5}{12}{\ k}^+_{m-2 \alpha }\right) . \end{aligned}$$
(44)

Thus,

$$\begin{aligned} {\left\{ \begin{array}{ll} {t^+}_{m+1 \alpha }\ -\ {t^+}_{m \alpha }\le h\left( \frac{23}{12}\ {\ k}^{-}_{m\alpha }\ -\frac{16}{12}\ {\ k}^{-}_{m-1\alpha }+\ \frac{5}{12}{\ k}^{-}_{m-2 \alpha }\right) \ \\ {t^{-}}_{m+1 \alpha }\ -\ {t^{-}}_{m \alpha }\ge h\left( \ \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1\alpha }+\ \frac{5}{12}{\ k}^+_{m-2 \alpha }\right) . \end{array}\right. } \end{aligned}$$
(45)

So that,

$$\begin{aligned} {\left\{ \begin{array}{ll} {t^+}_{m+1 \alpha }\ \ \le {t^+}_{m \alpha }+h\left( \ \frac{23}{12}\ {\ k}^{-}_{m\alpha }\ -\frac{16}{12}\ {\ k}^{-}_{m-1 \alpha }+\ \frac{5}{12}{\ k}^{-}_{m-2 \alpha }\right) \ \\ {t^{-}}_{m+1 \alpha }\ \ \ge \ \ {t^{-}}_{m \alpha }+h\left( \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1 \alpha }+\ \frac{5}{12}{\ k}^+_{m-2 \alpha }\right) . \end{array}\right. } \end{aligned}$$
(46)

Then, we can say

$$\begin{aligned}&\left[ {t^+}_{m \alpha }+h\left( \frac{23}{12}\ k^{-}_{m\alpha }\ -\frac{16}{12}\ k^{-}_{m-1 \alpha }+\ \frac{5}{12}k^{-}_{m-2 \alpha }\right) ,{t^{-}}_{m \alpha }+h\left( \frac{23}{12}\ k^{+}_{m\alpha }\ -\frac{16}{12}\ k^{+}_{m-1 \alpha }+\ \frac{5}{12}k^{+}_{m-2 \alpha }\right) \right] \nonumber \\&\quad \subseteq \left[ {t^+}_{m+1 \alpha }\ ,\ {t^{-}}_{m+1 \alpha }\ \ \right] . \end{aligned}$$
(47)

Case 3:

$$\begin{aligned} \mathrm{inf \ min}_{\theta \ge \gamma }\ \left\{ {t_{m+1}}^{-}_{\theta }-{t_m}^{-}_{\theta },{t_{m+1}}^+_{\theta }-{t_m}^+_{\theta }\right\} ={t^+}_{m+1 \alpha } - {t^+}_{m \alpha },\alpha \in \ \left[ \theta , 1\right] \end{aligned}$$
(48)

and

$$\begin{aligned}&\left[ {\textrm{inf} \ {\textrm{min}}_{\theta \ge \gamma }\ \left\{ h\left( \frac{23}{12}{\ k}^{-}_{m\theta }-\frac{16}{12}k^{-}_{m-1 \theta }+\ \frac{5}{12} k^{-}_{m-2 \theta }\right) ,h\left( \frac{23}{12}\ k^{+}_{m\theta }-\frac{16}{12} k^{+}_{m-1 \theta }+\ \frac{5}{12}\ k^{+}_{m-2 \theta }\right) \ \right\} \ }\right. \nonumber \\&\left. \quad = \frac{23}{12}\ k^{+}_{m\alpha }\ -\frac{16}{12}\ k^{+}_{m-1 \alpha }+\ \frac{5}{12} k^{+}_{m-2 \alpha }\right] . \end{aligned}$$
(49)

So,

$$\begin{aligned} {\textrm{sup}\ \textrm{max}}_{\theta \ge \gamma }\ \left\{ t_{m+1}^{-}{_{\theta }}-t_m^{-}{_{\theta }},t_{m+1}^+{_{\theta }}-t_m^+{_{\theta }}\right\} =t^{-}_{m+1 \alpha } - t^{-}_{m \alpha },\quad \alpha \in \left[ \theta , 1\right] \end{aligned}$$
(50)

and

$$\begin{aligned}&{\textrm{sup} \ {\textrm{max}}_{\theta \ge \gamma }\ \left\{ h\left( \frac{23}{12}{\ k}^{-}_{m\theta }-\frac{16}{12}k^{-}_{m-1 \theta }+\ \frac{5}{12}{\ k}^{-}_{m-2 \theta }\right) , h\left( \frac{23}{12}\ k^{+}_{m\theta }-\frac{16}{12}\ k^{+}_{m-1 \theta }+\ \frac{5}{12}\ k^{+}_{m-2 \theta }\right) \right\} \ }\nonumber \\ {}&\quad = h\left( \frac{23}{12}{\ k}^{-}_{m\alpha }\ -\frac{16}{12}\ {\ k}^{-}_{m-1 \alpha }+\ \frac{5}{12}{\ k}^{-}_{m-2 \alpha }\right) . \end{aligned}$$
(51)

So,

$$\begin{aligned} {\left\{ \begin{array}{ll} {t^+}_{m+1 \alpha }\ -\ {t^+}_{m \alpha }\le h\left( \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1 \alpha }+\ \frac{5}{12}{\ k}^+_{m-2\alpha }\right) \ \\ {t^{-}}_{m+1 \alpha }\ -\ {t^{-}}_{m \alpha }\ge h\left( \ \frac{23}{12}\ {\ k}^{-}_{m\alpha }\ -\frac{16}{12}\ {\ k}^{-}_{m-1 \alpha }+\ \frac{5}{12}{\ k}^{-}_{m-2 \alpha }\right) .\end{array}\right. } \end{aligned}$$
(52)

Then,

$$\begin{aligned} {\left\{ \begin{array}{ll} {t^+}_{m+1 \alpha }\ \le {t^+}_{m \alpha }+h\left( \ \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1 \alpha }+\ \frac{5}{12}{\ k}^+_{m-2 \alpha }\right) \ \\ {t^{-}}_{m+1 \alpha }\ \ge \ \ {t^{-}}_{m \alpha }+h\left( \frac{23}{12}\ {\ k}^{-}_{m\alpha }\ -\frac{16}{12}\ {\ k}^{-}_{m-1 \alpha }+\ \frac{5}{12}{\ k}^{-}_{m-2 \alpha }\right) . \end{array}\right. } \end{aligned}$$
(53)

So, we have

$$\begin{aligned}&\left[ {t^+}_{m \alpha }+h\left( \frac{23}{12}\ k^{+}_{m\alpha }-\frac{16}{12}\ k^{+}_{m-1 \alpha }+\frac{5}{12}{\ k}^+_{m-2 \alpha }\right) ,{t^{-}}_{m \alpha }+h\left( \frac{23}{12}\ k^{-}_{m\alpha }-\frac{16}{12}\ k^{-}_{m-1 \alpha }+\ \frac{5}{12}k^{-}_{m-2 \alpha }\right) \ \right] \nonumber \\ {}&\quad \subseteq \left[ {t^+}_{m+1 \alpha }, {t^{-}}_{m+1 \alpha }\ \right] . \end{aligned}$$
(54)

Case 4:

$$\begin{aligned} \ {\textrm{inf} ~\textrm{min}}_{{\theta }{\ge }{\gamma }}\ \left\{ {t_{m+1}}^{-}_{\theta }-{t_m}^{-}_{\theta },{t_{m+1}}^+_{\theta }-{t_m}^+_{\theta }\right\} ={t_{m+1}}^{-}_{\theta }-{t_m}^{-}_{\theta }, \end{aligned}$$
(55)

and

$$\begin{aligned}&{\textrm{inf} \ {\textrm{min}}_{{\theta }{\ge }{\gamma }}\ \left\{ h\left( \frac{23}{12}{\ k}^{-}_{m\theta }-\frac{16}{12}k^{-}_{m-1\theta }+\frac{5}{12} k^{-}_{m-2 \theta }\right) \ ,h\left( \frac{23}{12}\ k^{+}_{m\theta }-\frac{16}{12}\ k^{+}_{m-1 \theta }+\ \frac{5}{12}\ k^{+}_{m-2 \theta }\right) \right\} \ } \nonumber \\&\quad = h\left( \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1 \alpha }+\ \frac{5}{12}{\ k}^+_{m-2 \alpha }\right) ,\quad \alpha \in \left[ \theta , 1\right] . \end{aligned}$$
(56)

So,

$$\begin{aligned} \textrm{sup} \ {\textrm{max}}_{\theta \ge \gamma }\ \left\{ {t_{m+1}}^{-}_{\theta }-{t_m}^{-}_{\theta },{t_{m+1}}^+_{\theta }-{t_m}^+_{\theta }\right\} ={t_{m+1}}^+_{\theta }-{t_m}^+_{\theta }, \end{aligned}$$
(57)

and

$$\begin{aligned}&{\textrm{sup} \ {\textrm{max}}_{\theta \ge \gamma }\ \left\{ h\left( \frac{23}{12}{\ k}^{-}_{m\theta }-\frac{16}{12}k^{-}_{m-1 \theta }+\frac{5}{12}{\ k}^{-}_{m-2 \theta }\right) ,h\left( \frac{23}{12}\ k^{+}_{m\theta }-\frac{16}{12}\ k^{+}_{m-1 \theta }+\ \frac{5}{12}\ k^{+}_{m-2 \theta }\right) \ \right\} \ }\nonumber \\ {}&\quad = h\left( \frac{23}{12}\ {\ k}^{-}_{m\alpha }\ -\frac{16}{12}\ {\ k}^{-}_{m-1 \alpha }+\ \frac{5}{12}{\ k}^{-}_{m-2 \alpha }\right) . \end{aligned}$$
(58)

And so,

$$\begin{aligned} {\left\{ \begin{array}{ll} {t_{m+1}}^{-}_{\theta }-{t_m}^{-}_{\theta }\le h\left( \frac{23}{12}\ {\ t}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1 \alpha }+\ \frac{5}{12}{\ k}^+_{m-2 \alpha }\right) \ \\ {t_{m+1}}^+_{\theta }-{t_m}^+_{\theta }\ge h\left( \ \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1\alpha }+\ \frac{5}{12}{\ k}^+_{m-2\alpha }\right) . \end{array}\right. } \end{aligned}$$
(59)

Then,

$$\begin{aligned} {\left\{ \begin{array}{ll} {t^{-}}_{m+1 \alpha }\ \le {t^{-}}_{m \alpha }+h\left( \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1 \alpha }+\ \frac{5}{12}{\ k}^+_{m-2\alpha }\right) \ \\ {t^+}_{m+1 \alpha }\ \ge \ {t^+}_{m \alpha }+h\left( \ \frac{23}{12}\ {\ k}^+_{m\alpha }\ -\frac{16}{12}\ {\ k}^+_{m-1 \alpha }+\ \frac{5}{12}{\ k}^+_{m-2 \alpha }\right) . \end{array}\right. } \end{aligned}$$
(60)

We follow:

$$\begin{aligned}&\left[ {t^{-}}_{m \alpha }+h\left( \frac{23}{12}\ k^{+}_{m\alpha }-\frac{16}{12}\ k^{+}_{m-1 \alpha }+\ \frac{5}{12}k^{+}_{m-2 \alpha }\right) ,{t^+}_{m \alpha }+h\left( \frac{23}{12}\ k^{-}_{m\alpha }\ -\frac{16}{12}\ k^{-}_{m-1 \alpha }+\frac{5}{12}k^{-}_{m-2 \alpha }\ \right) \right] \nonumber \\ {}&\quad \subseteq \left[ {t^{-}}_{m+1 \alpha }\ ,{t^+}_{m+1 \alpha }\ \ \right] . \end{aligned}$$
(61)

4 Convergence

We begin our dissection with definitions of the convergence of multistep difference equation and consistency before discussing methods to solve the differential equation.

Definition 4.1

The differential fuzzy equation with initial condition

$$\begin{aligned} {\widetilde{x}}'\left( s\right)&=\widetilde{k}\ (s,\widetilde{x}\left( s\right) ),\quad s_0\le s\le S, \nonumber \\ \tilde{x}_{s_{0}}&=\lim _{s\longrightarrow s_{0}}\tilde{x}'(s)=\tilde{\gamma }_{0} \end{aligned}$$
(62)

and similarly, the other models can be derived as

$$\begin{aligned} \tilde{t}_{i}=\tilde{\gamma }_{i},\quad i=0,1,\dots , n-1, \end{aligned}$$
(63)

in which

$$\begin{aligned} {\widetilde{t}}_{j+1}=\ {\widetilde{t}}_j+h\ \phi \left( s_j, \widetilde{t}\left( s_j\right) \right) \end{aligned}$$
(64)

is the \(\left( j+1\right) \)st step in a multistep method. At this step, it has a fuzzy local truncation error as follows

$$\begin{aligned} {\widetilde{\nu }}_{j+1}\left( h\right) =\ \frac{\widetilde{x}\left( s_{j+1}\right) {\circleddash }_g\widetilde{x}\left( s_j\right) }{h}{\circleddash }_g\phi \left( s_j,\widetilde{x}\left( s_j\right) ,h\right) . \end{aligned}$$
(65)

Exists N that for all \(j= n-1, n, \ldots N-1\), and \(h=\frac{b-a}{N}\), where

$$\begin{aligned} \phi \left( s_j,\widetilde{x}\left( s_j\right) ,h\right)&= \widetilde{k}\left( {(s}_j,\widetilde{x}\left( s_j\right) \right) \oplus \ \frac{h}{2}{\nabla }_g\widetilde{k}\left( {(s}_j,\widetilde{x}\left( s_j\right) \right) \oplus \frac{5h}{12}{{\nabla }^2}_g\widetilde{k}\left( {(s}_j, \widetilde{x}\left( s_j\right) \right) \oplus \cdots \nonumber \\&\qquad {\oplus \ ((-1)}^n\ \int ^1_0{\ \left( \genfrac{}{}{0.0pt}{}{-\beta }{n}\right) \textrm{d}\beta })\ h\ {{\nabla }^n}_g\widetilde{k}\left( {(s}_j, \widetilde{x}\left( s_j\right) \right) . \end{aligned}$$
(66)

And \(\widetilde{x}\left( s_j\right) \) indicates the exact value of the solution of the differential equation. The approximation \({\widetilde{t}}_j\) is taken from the different methods at the jth step.

Definition 4.2

A multistep method with local truncation error \({\widetilde{\nu }}_{j+1}\left( h\right) \) at the \((j+1)\)th step is called consistent with the differential equation approximation if

$$\begin{aligned}&\lim _{h\rightarrow 0}|\widetilde{\nu }_j(h)|=0,\quad \forall j= n, n+ 1,\ldots , N, \end{aligned}$$
(67)
$$\begin{aligned}&\lim _{s_j\rightarrow 0}|\widetilde{\gamma }_j-\widetilde{x} (s_j)| =0,\quad \forall j = 1, 2, \ldots , n -1. \end{aligned}$$
(68)

Theorem 4.3

Let the initial-value problem

$$\begin{aligned} {\widetilde{x}}'\left( s\right)&=\widetilde{k}\ (s,\widetilde{x}\left( s\right) ),\qquad s_0\le s\le S,\qquad \widetilde{x}\left( s_0\ \right) =\ {\widetilde{\gamma }}_0,\nonumber \\ {\widetilde{x}}_0&={\widetilde{\gamma }}_0,\quad {\widetilde{t}}_1={\widetilde{\gamma }}_1,\quad \ldots \quad , {\widetilde{t}}_{n-1}={\widetilde{\gamma }}_{n-1} \end{aligned}$$
(69)

be approximated by a multistep difference method:

$$\begin{aligned} {\widetilde{t}}_{j+1}=\ {\widetilde{t}}_j\oplus h\ \phi \left( s_j,\widetilde{t}\left( s_j\right) \right) . \end{aligned}$$
(70)

Let a number \(h_0>0\) exist, and \(\phi \left( s_j,\widetilde{t}\left( s_j\right) \right) \) be continuous, with meets the constant Lipschitz T

$$\begin{aligned} E=\ \left\{ \left( s, \widetilde{t},h\right) \big |{\ s}_0\le s\le S\ and\ \widetilde{t}\in R_F, \ 0\le h\le h_0\right\} . \end{aligned}$$
(71)

Then, the difference method is convergent if and only if it is consistent. It is equal to

$$\begin{aligned} \phi \left( s,\widetilde{x},0\right) =\widetilde{k}\left( s, \widetilde{x}\right) ,\qquad \forall s_0\le s\le S. \end{aligned}$$
(72)

We are aware of the concept of convergence for the multistep method. As the step size approaches zero, the solution of the difference equation approaches the solution to the differential equation. In other words

$$\begin{aligned} \lim _{h\rightarrow 0} \left| {\widetilde{t}}_j{\circleddash }_g\ \widetilde{x}\left( s_j\right) \right| =0. \end{aligned}$$
(73)

For the multistep fuzzy Adams–Bashforth method, we have seen that

$$\begin{aligned}&{\widetilde{\nu }}_{j+1}\left( h\right) \nonumber \\&\quad =\frac{\widetilde{x}\left( s_{j+1}\right) {\circleddash }_g-\widetilde{x}\left( s_j\right) }{h}{\circleddash }_g[\widetilde{k}\left( {(s}_j, \widetilde{x}\left( s_j\right) \right) \oplus \ \frac{h}{2}{\nabla }_g\widetilde{k}\left( {(s}_j,\widetilde{x}\left( s_j\right) \right) \oplus \frac{5h}{12}{{\nabla }^2}_g\widetilde{k}\left( {(s}_j,\widetilde{x}\left( s_j\right) \right) +\cdots \nonumber \\&\quad {\oplus \ ((-1)}^n\ \int ^1_0{\ \left( \genfrac{}{}{0.0pt}{}{-\theta }{n}\right) \textrm{d}\theta })\ h\ {{\nabla }^n}_g\widetilde{k}\left( {(s}_j, \widetilde{x}\left( s_j\right) \right) ] \end{aligned}$$
(74)

using Proposition 2.11, \(\nabla ^l_g{\widetilde{k}}_m=h^l\widetilde{k}^{(l)}_{m_g}\), and substituting it in Eq. (66), we have

$$\begin{aligned} \phi (s_j,\widetilde{x}(s_j))&=\ \widetilde{k}({(s}_j,\widetilde{x}(s_j))\oplus \frac{h}{2}{\widetilde{k}}'({(s}_j,\widetilde{x}(s_j))\oplus \frac{5h^2}{12}\widetilde{k}''({(s}_j,\widetilde{x}(s_j))+\cdots \nonumber \\ {}&\quad +\, \left( (-1)^n\ \int ^1_0{\ \left( \left( {\begin{array}{c}-\beta \\ n\end{array}}\right) \right) \textrm{d}\beta }\right) h^n \widetilde{k}^{(n)}({(s}_j, \widetilde{x}(s_j)). \end{aligned}$$
(75)

So,

$$\begin{aligned} \widetilde{\nu }_{j+1}(h)&=\frac{x(s_{j+1}){\circleddash }_g-x(s_j)}{h}{\circleddash }_g\ \left[ \widetilde{k} \left( \left( s_j,\widetilde{x}(s_j )\right) \right) \oplus \ \frac{h}{2}{\widetilde{k}}'({(s}_j,\widetilde{x}(s_j ))+\cdots \right. \nonumber \\&\left. \oplus \ \left( (-1)^{n-1}\ \int ^1_0{\ \left( \genfrac{}{}{0.0pt}{}{-\beta }{n}\right) \textrm{d}\beta }\right) \ h^n\ {\widetilde{k}}^{(n)}\left( (s_j, \widetilde{x})\left( s_j\right) \right) \right] . \end{aligned}$$
(76)

Consequently,

$$\begin{aligned} \left| {\widetilde{\nu }}_{j+1}(h)\right| =\left| h^n\ {\widetilde{k}}^{(n)}({(s}_j,\ \widetilde{x}(s_j)) {((-1)}^{n-1}\ \int ^1_0{\ \left( \genfrac{}{}{0.0pt}{}{-\beta }{n}\right) \textrm{d}\beta })\right| \end{aligned}$$
(77)

under the hypotheses of paper, \(\widetilde{k}({(s}_j,\widetilde{x}(s_j))\in R_F\), and by definition g-differentiability \(\widetilde{k}^{(n)}({(s}_j,\widetilde{x}(s_j))\in R_F\) so by Definition 2.1\(\ {\widetilde{k}}^{(n)}\left( {(s}_j,\widetilde{x}\left( s_j\right) \right) \in R_F\) for \(j\ge 0\) are bounded, thus exists M such that

$$\begin{aligned} {\widetilde{k}}^{(n)}\left( {(s}_j,\widetilde{x}\left( s_j\right) \right) \le M. \end{aligned}$$
(78)

And hence,

$$\begin{aligned} {\widetilde{\nu }}_{j+1}\left( h\right) \le MZ, \end{aligned}$$
(79)

where

$$\begin{aligned} Z=\ {(-1)}^n\ \int ^1_0{\ \left( \genfrac{}{}{0.0pt}{}{-\beta }{n}\right) \textrm{d}\beta }\ h^n. \end{aligned}$$
(80)

When \(h\rightarrow 0\), we will have \(Z\rightarrow 0\) so

$$\begin{aligned} {\mathop {\textrm{lim}}_{h\rightarrow 0} \left| {\widetilde{\nu }}_j\left( h\right) \right| \ }=0. \end{aligned}$$
(81)

So, we see that it satisfied the first condition of Definition 4.2. The concept of the second part is that if the one-step method generating the starting values is also consistent, then the multistep method is consistent. So our method is consistent; therefore according to Theorem 4.3, this difference method is convergent.

5 Examples

Example 5.1

Consider the initial-value problem

$$\begin{aligned} \widetilde{x}'&= -\widetilde{x}\oplus s\oplus 1, \end{aligned}$$
(82)
$$\begin{aligned} \widetilde{x}^\gamma (0)&=(0.96+0.04 \gamma , 1.01+0.01 \gamma ). \end{aligned}$$
(83)

Obviously, one can check the exact solution as follows:

$$\begin{aligned} \tilde{x}(s)=(s-0.025 e^s+0.985 e^{-s},s+1 e^{-s}, s+0.025 e^s+0.985 e^{-s}). \end{aligned}$$

Indeed, the solution is a triangular number

$$\begin{aligned}&\underline{x}(s)=s-0.025 e^s+0.985 e^{-s},\\ {}&x'(s)=s+1e^{-s},\\&\overline{x}(s)=s+0.025 e^s+0.985 e^{-s}. \end{aligned}$$

So, the exact solution in mesh point \(s=0.01\) is

$$\begin{aligned} \tilde{x}(0.01)= & {} (0.01-0.025 e^{-0.01}+0.985 e^{-0.01}, 0.01 +e^{-0.01}, 0.01+0.025 e^{0.01}\\ {}{} & {} +0.985 e^{-0.01}). \end{aligned}$$

On the other hand with the proposed method, the approximated solution in \(s=0.01\) is as follows:

$$\begin{aligned} \tilde{t}^{\gamma } (0.01)= & {} (0.01+e^{-0.01}-(1-\gamma )(0.025 e^{0.01}+0.15e^{-0.01}, 0.01+e^{-0.01}\\ {}{} & {} +(1-\gamma )(0.025e^{0.01}-0.15 e^{-0.01}), \end{aligned}$$

where \(\tilde{t}^\gamma \) is a approximated of \(\tilde{x}\).

The maximum error in \(s=0.1\), \(s=0.2, \ldots , s=1\), also shows the errors (Table 1).

Table 1 The global truncation errors of Example 5.1
Full size table

Suppose

$$\begin{aligned} \tilde{y}'(t)=\tilde{f}(t)=-\tilde{y}(t)+t+1. \end{aligned}$$
(84)

Consider the initial-value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} y^{-}(t)=1-0.025e^t+0.985 e^{-t},\\ y'(t)=t+e^{-t},\\ y^+(t)=t+0.025e^t+0.985 e^{-t}, \end{array}\right. } \end{aligned}$$
(85)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} y^{-r}=t+e^{-t}-(1-r)(0.025e^t+0.015e^{-t}),\\ y^{+r}=t+e^{-t}+(1-r)(0.025e^t-0.015e^{-t}). \end{array}\right. } \end{aligned}$$
(86)

Thus, we have

$$\begin{aligned}&{\left\{ \begin{array}{ll} y^{-r}(0)=0.96+0.04 r\\ y^{+r}(0)=1.01+0.01 r \end{array}\right. }\end{aligned}$$
(87)
$$\begin{aligned} \Rightarrow&{\left\{ \begin{array}{ll} y^{-r}(0.01)=0.01+e^{-0.01}-(1-r)(0.025 e^{0.01}+0.015e^{-0.01})\\ y^{+r}(0.01)=0.01+e^{-0.01}+(1-r)(0.025 e^{0.01}-0.015e^{-0.01}) \end{array}\right. } \end{aligned}$$
(88)
$$\begin{aligned}&{\left\{ \begin{array}{ll} y^{-r}(0.02)=0.02+e^{-0.02}-(1-r)(0.025 e^{0.02}+0.015e^{-0.02})\\ y^{+r}(0.02)=0.02+e^{-0.02}+(1-r)(0.025 e^{0.02}-0.015e^{-0.02}) \end{array}\right. } \end{aligned}$$
(89)
$$\begin{aligned}&\vdots \nonumber \\&{\left\{ \begin{array}{ll} y^{-r}(0.1)=0.1+e^{-0.1}-(1-r)(0.025 e^{0.1}+0.015e^{-0.1})\\ y^{+r}(0.1)=0.1+e^{-0.1}+(1-r)(0.025 e^{0.1}-0.015e^{-0.1}), \end{array}\right. } \end{aligned}$$
(90)

where (90) are real values. Suppose

$$\begin{aligned} {\left\{ \begin{array}{ll} y^{-}{'}(t)=-y^+(t)+t+1, \\ y''(t)=-y'(t)+t+1,\\ y^{+}{'}(t)=-y^{-}{'}(t)+t+1. \end{array}\right. } \end{aligned}$$
(91)

Therefore,

$$\begin{aligned} {\left\{ \begin{array}{ll} f^{-}(t)-y^+(t)+t+1,\\ f'(t)=-y'(t)+t+1,\\ f^+(t)=-y^{-}(t)+t+1. \end{array}\right. } \end{aligned}$$
(92)

By (85), (86), (92), we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} f^{-r}(t)=-y'+t+1-(1-r)(0.025e^t-0.015 e^{-t})\\ =1-e^{-t}-(1-r)(0.025e^t-0.015 e^{-t}),\\ f^{+r}(t)=-y'+t+1+(1-r)(0.025e^t+0.015 e^{-t})\\ =1-e^{-t}+(1-r)(0.025e^t+0.015 e^{-t}). \end{array}\right. } \end{aligned}$$
(93)

According to the previous sections, this example has been solved by the two-step Adams–Bashforth method with \(t=0.1\) and \(N=10\). We use the following relations to solve it.

$$\begin{aligned}&\tilde{y}_{n+1}\ominus _g \tilde{y}_n =\frac{h}{2}[3\tilde{f}_n \ominus _g \tilde{f}_{n-1}],\\ {}&\textrm{inf} ~\textrm{min}_{r\ge \alpha }\left\{ y^{-}_{n+1,r}-y^{-}_{n,r},y^+_{n+1,r}-y^+_{n,r}\right\} =y^{-}_{n+1,\alpha }\ominus _g y^{-}_{n,\alpha },\\ {}&\textrm{sup} ~\textrm{max}_{r\ge \alpha }\left\{ y^{-}_{n+1,r}-y^{-}_{n,r},y^+_{n+1,r}-y^+_{n,r}\right\} =y^+_{n+1,\alpha }\ominus _g y^+_{n-1,\alpha },\\&\textrm{inf} ~\textrm{min}_{r\ge \alpha }\left\{ y^{-}_{n+1,r}-y^{-}_{n,r},y^+_{n+1,r}-y^+_{n,r}\right\} =\textrm{inf}~ \textrm{min}_{r\ge \alpha }\left\{ \frac{h}{2}(3f^{-}_{n,r}-f^{-}_{n-1,r}),\frac{h}{2}(3f^+_{n,r}-f^+_{n-1,r}),\right. \\&\textrm{sup} ~ \textrm{max}_{r\ge \alpha }\left\{ y^{-}_{n+1,r}-y^{-}_{n,r},y^+_{n+1,r}-y^+_{n,r}\right\} =\textrm{sup} ~ \textrm{max}_{r\ge \alpha }\left\{ \frac{h}{2}(3f^{-}_{n,r}-f^{-}_{n-1,r}),\frac{h}{2}(3f^+_{n,r}-f^+_{n-1,r}),\right. \\&{\left\{ \begin{array}{ll} y^{-r}(n+0.01)=(n+0.01)+e^{-(n+0.01)}-(1-r)(0.025e^{n+0.01}+0.015e^{-(n+0.01)}),\\ y^{-r}(n)=ne^{-n}-(1-r)(0.025e^n+0.015e^{-n}), \end{array}\right. }\\&{\left\{ \begin{array}{ll} y^{-r}(0)=0.96+0.04r,\\ y^{+r}(0)=1.01+0.01r, \end{array}\right. }\\&{\left\{ \begin{array}{ll} y^{+r}(n+0.01)=(n+1)+e^{-(n+0.01)}+(1-r)(0.025e^{(n+0.01)}-0.015e^{-(n+0.01)}),\\ y^{+r}(n)=ne^{-n}+(1-r)(0.025e^n-0.015e^{-n}), \end{array}\right. }\\&\quad f^{-r}(n)=1-e^{-n}-(1-r)(0.025e^n-0.015e^{-n}),\\ {}&\quad f^{-r}(n-0.01)=1-e^{-(n-0.01)}-(1-r)(0.025e^{(n-0.01)}-0.015e^{-(n-0.01)}). \end{aligned}$$

Example 5.2

Consider the initial-value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} x'_{H}(t)&{}=(1-s)x(s),0\le s\le 2,\\ x(0)&{}=(0,1,2).\\ \end{array}\right. } \end{aligned}$$

First, we solve the problem with the gH-differentiability. The initial-value problem on [0, 1] is \([(i)-gH]\)-differentiable and \([(i)-gH]\)-differentiable on (1, 2]. By solving the following system, the \([(i)-gH]\)-differentiable solution will be achieved

$$\begin{aligned} {\left\{ \begin{array}{ll} (x_{-})^{'}(s;\gamma )&{}= {\left\{ \begin{array}{ll} (1-s)&{}\quad x_{-}(s;\gamma ),0\le s\le 1,\\ (1-s)&{}\quad x^{+}(s;\gamma ),1\le s\le 2,\\ \end{array}\right. } \\ (x^{+})^{'}(s;\gamma )&{}= {\left\{ \begin{array}{ll} (1-s)&{}\quad y^{+}(s;\gamma ),0\le s\le 1,\\ (1-s)&{}\quad y_{-}(s;\gamma ),1\le s\le 2,\\ \end{array}\right. } \\ x(0;\gamma )&{}=[\gamma ,2-\gamma ].\\ \end{array}\right. } \end{aligned}$$

By solving the following system, the \([(ii)-gH]\)-differentiable solution will be achieved

$$\begin{aligned} {\left\{ \begin{array}{ll} (x_{-})^{'}(s;\gamma )&{}= {\left\{ \begin{array}{ll} (1-s)&{}\quad x^{+}(s;\gamma ),0\le s\le 1,\\ (1-s)&{}\quad x_{-}(s;\gamma ),1\le s\le 2,\\ \end{array}\right. } \\ (x^{+})^{'}(s;\gamma )&{}= {\left\{ \begin{array}{ll} (1-s)&{}\quad x_{-}(s;\gamma ),0\le s\le 1,\\ (1-s)&{}\quad x^{+}(s;\gamma ),1\le s\le 2,\\ \end{array}\right. } \\ 1 x(0;\gamma )&{}=[\gamma ,2-\gamma ].\\ \end{array}\right. } \end{aligned}$$

If we apply the Euler method to the approximate solution of the initial-value problem by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{0}&{}=(0,1,2),\\ x_{k+1}&{}=v_{k}\oplus h\odot ((1-s_{k})\odot v_{k}),\\ &{}0\le s_{k}\le 1,k=0,1,\dots ,\dfrac{N}{2}-1,\\ x_{k+1}&{}=x_{k}\ominus (-1)h\odot ((1-s_{k})\odot x_{k}),\\ &{}1<s_{k}\le 2, k=\dfrac{N}{2},\dots , N.\\ \end{array}\right. } \end{aligned}$$

The results are presented in Table 2.

Table 2 The global truncation errors of Example 5.2
Full size table

In the calculations of this method, we need to consider the \(i-gh\)-differentiability and \(ii-gH\)-differentiability. But when we use g-differentiability, we do not need to check the different states of the differentiability. To solve using the method mentioned in the article, we have:

$$\begin{aligned}&\tilde{x}'=(1-s)\tilde{x}(s),\\&\tilde{x}(0)=(0,1,2). \end{aligned}$$

Or we have \(x^\gamma (0)-[\gamma , 2-\gamma ]\). The exact solution is as follows:

$$\begin{aligned} x^\gamma (s)&=\left( \gamma e^{s-\frac{s^2}{2}}, (2-\gamma )e^{s-\frac{s^2}{2}}\right) ,\\ \tilde{\underline{k}}^\gamma (s)&=\gamma e^{s-\frac{s^2}{2}} -s(2-\gamma )e^{s-\frac{s^2}{2}},\\ \tilde{\overline{k}}^\gamma (s)&=(2-\gamma )e^{s-\frac{s^2}{2}}-s\gamma e^{s-\frac{s^2}{2}}. \end{aligned}$$

The results of the solution using the Adams–Bashforth two-step method for \(h = 1\) and calculating the approximate value of the solution and the error of the method can be seen in the Table 3.

Table 3 Error comparison table
Full size table

Consider the initial-value problem \(\tilde{x'}=(s\ominus 1)\odot \tilde{x}^2\), where \(s\in [-1,1]\)

$$\begin{aligned} \tilde{x}(0)=(0/999\oplus 0/001 \gamma , 1/001 \ominus 0/001 \gamma ), \end{aligned}$$

the exact solution is

$$\begin{aligned} x(s,\gamma )=\frac{-1}{\frac{s^2}{2}\ominus s\oplus (0/999\oplus 0/001 \gamma , 1/001\ominus 0/001 \gamma )}. \end{aligned}$$

6 Conclusion

In the present paper, the proposed method, which is based on the concept of g-differentiability, provides a fuzzy solution. This solution is related to a set of equations from the family of Adams-Bashforth differential equations, which coincide with the solutions derived by fuzzy differential equations.

The gH-difference is a powerful and versatile fuzzy differential operator that is more flexible, robust, and computationally efficient, making it a good choice for solving a wide range of fuzzy differential equations. It does not need i and ii-differentiability. In Examples, we compare g-differentiability and gH-differentiability.

G-differentiability allows for capturing gradual changes in a fuzzy-valued function. G-differentiable functions exhibit certain degrees of smoothness and continuity, which can be useful in modeling and analyzing fuzzy systems. The choice of the parameter g in g-differentiability is crucial and depends on the specific problem. Determining an appropriate value for g requires careful consideration and analysis. H-differentiability combines the gradual reduction of fuzziness (via the parameter g) with the Hukuhara difference (H-difference). It provides a more refined analysis of fuzzy-valued functions. gH-differentiability offers enhanced modeling capabilities by considering both the gradual reduction of fuzziness and the separation between fuzzy numbers or fuzzy sets. But gH-differentiability introduces an additional level of complexity compared to g-differentiability or H-differentiability alone. The combination of gradual reduction and H-difference requires careful understanding and analysis to ensure proper application.