1 Introduction

The fractional calculus (FC) has drawn much consideration from numerous researchers. In reality, many years ago, FC attracted interest in various fields, which include biology, chemistry, electricity, mechanics, physics, economy, biophysics, signal and photograph processing, control principle, aerodynamics, and blood float phenomena (Hilfer et al. 2010; Safaie et al. 2015; Yang et al. 2014).

The FC and tempered FC (TFC) notions were generalized in various manners, including variable-order FC (Yaghoobi et al. 2017; Yang and Machado 2017; Sabzikar et al. 2015; Moghaddam et al. 2018). Furthermore, the formulation of fractional integration involving exponential kernels and weak singular was provided (Buschman 1972). A new TFC class was developed (Sabzikar et al. 2015; Meerschaert and Sabzikar 2016; Zhang 2010; Kullberg and del Castillo-Negrete 2012) that describes Brownian motion, random walks, and tempered fractional differential equations (TFDEs).

TFDEs received less attention than other forms of fractional differential equations (FDEs), and the numerical algorithms for solving TFDEs are currently being developed. According to the global nature of the tempered fractional operator, it is frequently not easy to develop analytical and exact solutions for TFDEs. Therefore, using spectral methods to treat the TFDEs were widely studied throughout the last decade (Doha et al. 2013; Bhrawy et al. 2017; Zaky et al. 2016; Dabiri and Butcher 2017).

Spectral collocation methods are a highly accurate and efficient class of techniques for the solution of nonlinear PDEs and FDEs. The crux of these techniques is to expand the solution in terms of global basis functions, where the expansion coefficients are computed so that the differential equation is satisfied exactly at a set of collocation points. The fundamental unknowns are the solution values at these points. The expansion is mainly used for approximating the integral and derivative operators (Zeng et al. 2015, 2017). These methods have several advantages over common finite difference methods. For instance, they have the potential for rapidly convergent approximations. Moreover, they have low or non-existent phase and dissipation errors.

Spectral methods are stable, fast, and accurate for handling TFDEs (Zhao et al. 2016). These techniques were introduced in the 1970 s after the finite difference and finite element methods (Trefethen 2000), which are often based on discretizing variables in a finite set of basis functions, typically of the Jacobi type (Grandclément et al. 2011) and producing equations for these functions’ coefficients. Such techniques exhibit an exponential converging rate of solutions, especially for smooth functions. A sparse representation of equations has been produced recently in research, which is substantially well-conditioned and faster than traditional dense collocation approaches (Viswanath 2015; Miquel and Julien 2017; Burns et al. 2020). The aforementioned characteristics make spectral methods interesting to scientists in their attempts to examine a wide range of physical phenomena with high accuracy.

There were several matrices of differentiation and integration with various polynomial bases presented (Dabiri and Butcher 2017; Doha et al. 2011; Bhrawy et al. 2014; Lakestani et al. 2012). There are two types of techniques for producing operational matrices: direct and indirect (Dabiri and Butcher 2017). The size of the operational matrices produced by direct techniques is restricted, so that, they are unsuitable for solving TFDEs with highly oscillatory solutions. The most widely used algorithms for treating PDEs, FDEs, and TFDEs are the discrete implicit (Zhang et al. 2016), Petrov–Galerkin spectral (Zayernouri et al. 2015), Gegenbauer and Chebyshev pseudo-spectral (Dahy and Elgindy 2021; Elgindy and Dahy 2018; Aboelenen 2018; Hosny et al. 2020), finite difference algorithms (Kullberg and del Castillo-Negrete 2012), the predictor–corrector techniques employing the trapezoidal (Deng et al. 2017) and Jacobi–Gauss-Lobatto (Zhang 2010) in quadrature forms. Furthermore, the computational cost of numerically handling the tempered time-dependent problems is considerable, and the development of efficient and fast solutions is an important and vital issue.

The notion of tempered fractional derivatives (TFDs) is subdivided into several TFPDEs, such as the TFBE (Zhao et al. 2021b), the tempered fractional diffusion equations (Zhao et al. 2021a; Li and Deng 2016; Bu and Oosterlee 2021), the tempered fractional Fokker-Planck equation (Sun et al. 2017), and the TFADP (Guan and Cao 2021).

The recent numerical algorithms handling integer-order differential equations (Hesthaven et al. 2007; Kirby and Sherwin 2006) are difficult to adapt to the other fractional and TFDEs. According to its long-range history dependency, the computational cost of approximation is a critical limitation in simulating tempered fractional-order systems. The creation of numerical algorithms in this field, on the other hand, does not have a long record and has subsequently experienced fast development. The first rigorous work on tempered motions was begun by Meerschaert et al. (2008) and Garmendia (2008), who extended a time-space spectral technique to treat the time-dependent fractional diffusion problem. In accordance with their error analysis, they established an exponential convergence in their numerical tests.

In this brief paper, we develop an exponentially accurate and fast TFSCM for treating time-dependent and steady-state TFPDEs. That can be carried out successfully without any restrictions on the range of the initial and boundary conditions. The method is simple, easy to implement for non-tempering problems, and presents fully exponential convergence rates; moreover, the proposed extended method runs smoothly in the temporal direction as well.

The rest of the article is organized as follows: Sect. 2 is devoted to certain definitions and preliminaries of TFC. We state the current problem and introduce FLIs, which satisfy the KD property at the selected collocation nodes, and we derive the corresponding TFDMs in Sect. 3. Section 4 is devoted to treating a variety of linear and nonlinear TFPDEs in order to check the numerical efficiency of the TFSCM. Moreover, we examine steady-state problems such as the space-TFADP and generalized multiterm space-tempered fractional equations; furthermore, we examine time-dependent TFPDEs such as the time-space TFADP, the multi-term time-space TFPDEs, and finally the space-TFBE to illustrate the TFSCM’s exponential rate of convergence.

2 Preliminaries and definitions

This section represents some of the main properties and definitions of TFC (Sabzikar et al. 2015; Fernandez and Ustaoğlu 2020; Guo et al. 2019; Obeidat and Bentil 2021). Letting \(\Omega = [-1, 1]\), The left-sided fractional integrals of the tempered Riemann–Liouville (TRL) type associated with the fractional order \(0< \mu < 1\), and the tempering parameter \(\tau \ge 0\) are defined as:

$$\begin{aligned} \left( {{}_{{-1}}^{TRL} {\mathcal {I}}_x^{\mu ,\tau }f} \right) \left( x \right) = {e^{ - \tau x}}\left( {{}_{{-1}}^{RL}\textrm{I}_x^\mu {e^{\tau x}}f} \right) \left( x \right) = \frac{{{e^{ - \tau x}}}}{{\Gamma \left( \mu \right) }}\int _{-1}^x {\frac{{{e^{\tau s}}f\left( s \right) }}{{{{\left( {x - s} \right) }^{1 - \mu }}}}{\text {d}}s}, \; x > {-1}, \end{aligned}$$
(1)

and the corresponding right-sided TRL fractional integral defined by the expression

$$\begin{aligned} \left( {{}_x^{TRL} {\mathcal {I}}_{{1}}^{\mu ,\tau }f} \right) \left( x \right) = {e^{\tau x}}\left( {{}_{{x}}^{RL}\textrm{I}_{1}^\mu {e^{ - \tau x}}f} \right) \left( x \right) = \frac{{{e^{\tau x}}}}{{\Gamma \left( \mu \right) }}\int _{ x}^{1} {\frac{{{e^{ - \tau s}}f\left( s \right) }}{{{{\left( {x - s} \right) }^{1 - \mu }}}}{\text {d}}s}, \; x < {1}, \end{aligned}$$
(2)

and the associated TRL fractional derivative of order \(\mu \) with tempering parameter \(\tau \ge 0\) is given by

$$\begin{aligned} \left( {_{ - 1}^{TRL}\mathcal{D}_x^{\mu ,\tau }f} \right) \left( x \right) = {e^{ - \tau x}}\left( {{}_{ -1}^{RL}D_x^\mu {e^{\tau x}}f} \right) \left( x \right) = \frac{{{e^{ -\tau x}}}}{{\Gamma \left( {1 - \mu }\right) }}\frac{d}{{dx}}\int _{ - 1}^x{\frac{{{e^{\tau s}}f\left( s \right) }}{{{{\left( {x - s} \right) }^\mu }}}ds} ,\quad x > - 1, \end{aligned}$$
(3)
$$\begin{aligned} \left( {{}_x^{TRL}\mathcal{D}_1^{\mu ,\tau }f} \right) \left( x \right) = {e^{\tau x}}\left( {_x^{RL}D_1^\mu {e^{ - \tau x}}f} \right) \left( x \right) = {\frac{{{e^{\tau x}}}}{{\Gamma \left( {1 - \mu } \right) }}\frac{{\text {d}}}{{{\text {d}}x}}\int _x^1 {\frac{{{e^{ - \tau s}}f\left( s \right) }}{{{{\left( {s - x} \right) }^\mu }}}{\text {d}}s} } ,\; x < 1, \end{aligned}$$
(4)

where \(\textrm{I}\) and D are the usual RL fractional integral and derivative operators, respectively. An alternative pattern to define the TFDs according to the tempered Caputo (TC) derivative for left-sided of order \(0< \mu < 1\) with the same tempering parameter, defined as

$$\begin{aligned} \left( {{}_{{-1}}^{TC}{\mathcal {D}}_x^{\mu ,\tau }f} \right) \left( x \right) = {e^{ - \tau x}}\left( {{}_{{-1}}^CD_x^\mu {e^{\tau x}}f} \right) \left( x \right) = \frac{{{e^{ - \tau x}}}}{{\Gamma \left( {1 - \mu } \right) }}\int _{ - 1}^x {\frac{{{e^{\tau s}}f'\left( s \right) }}{{{{\left( {x - s} \right) }^\mu }}}{\text {d}}s}, \; x > {-1}, \end{aligned}$$
(5)

and the corresponding right-sided TC derivatives defined by the expression

$$\begin{aligned} \left( {{}_x^{TC}{\mathcal {D}}_{{1}}^{\mu ,\tau }f} \right) \left( x \right) = {e^{\tau x}}\left( {{}_x^CD_{{1}}^\mu {e^{ - \tau x}}f} \right) \left( x \right) = {\frac{{{e^{\tau x}}}}{{\Gamma \left( {1 - \mu } \right) }}\int _x^1 {\frac{{{e^{ - \tau s}}f'\left( s \right) }}{{{{\left( {s - x} \right) }^\mu }}}{\text {d}}s} }, \; x < {1}. \end{aligned}$$
(6)

Both RL and Caputo TFDs type are mainly related by the following useful relation:

$$\begin{aligned} \left( {{}_{ - 1}^{TRL}{\mathcal {D}}_x^{\mu ,\tau } f} \right) \left( x \right)&= \frac{{f\left( { - 1} \right) }}{{\Gamma \left( {1 - \mu } \right) {{\left( {1 + x} \right) }^\mu }}} + \left( {{}_{ - 1}^{TC}{\mathcal {D}}_x^{\mu ,\tau } f} \right) \left( x \right) , \end{aligned}$$
(7)
$$\begin{aligned} \left( {{}_x^{TRL}{\mathcal {D}}_1^{\mu ,\tau } f} \right) \left( x \right)&= \frac{{f\left( 1 \right) }}{{\Gamma \left( {1 - \mu } \right) {{\left( {1 - x} \right) }^\mu }}} + \left( {{}_x^{TC}{\mathcal {D}}_1^{\mu ,\tau } f} \right) \left( x \right) . \end{aligned}$$
(8)

These definitions will be matched together when vanishing the boundary-values. Moreover,the associated tempered fractional integrations by parts for the aforementioned TFDs are obtained as

$$\begin{aligned} {\left( {f\left( x \right) ,_{ - 1}^{TRL}\mathcal{D}_x^{\mu ,\tau }g\left( x \right) } \right) _\Omega }&= {\left( {g\left( x \right) ,_{ - 1}^{TC}\mathcal{D}_x^{\mu ,\tau }f\left( x \right) } \right) _\Omega } + \left. {f\left( x \right) _{ - 1}^{TRL}\mathcal{I}_x^{\mu ,\tau }g\left( x \right) } \right] _{x = - 1}^1, \end{aligned}$$
(9)
$$\begin{aligned} {\left( {f\left( x \right) ,_x^{TRL}\mathcal{D}_1^{\mu ,\tau }g\left( x \right) } \right) _\Omega }&= {\left( {g\left( x \right) ,_{ - 1}^{TC}\mathcal{D}_x^\mu f\left( x \right) } \right) _\Omega } - \left. {f\left( x \right) _x^{TRL}\mathcal{I}_1^{\mu ,\tau }g\left( x \right) } \right] _{x = - 1}^1. \end{aligned}$$
(10)

Also, we note an important property of the TRL fractional derivatives. Let \(0 < p \le 1\), \(0 < q \le 1\) and \(f(-1) = 0, x > -1\); then

$$\begin{aligned} {}_{ - 1}^{TRL}{\mathcal {D}}_x^{p + q}f\left( x \right) = \left( {{}_{ - 1}^{TRL}{\mathcal {D}}_x^p} \right) \left( {{}_{ - 1}^{TRL}{\mathcal {D}}_x^q} \right) f\left( x \right) = \left( {{}_{ - 1}^{TRL}{\mathcal {D}}_x^q} \right) \left( {{}_{ - 1}^{TRL}{\mathcal {D}}_x^p} \right) f\left( x \right) . \end{aligned}$$
(11)

The fractional-order derivative for \(t \in (0,1)\) defined by

$$\begin{aligned} {}_0^{TC}{\mathcal {D}}_t^{\mu ,\tau } {t^k} = \left\{ \begin{array}{ll} 0, &{}\quad k< \mu ,\\ \\ \frac{{\Gamma \left( {k + 1} \right) }}{{\Gamma \left( {k + 1 - \mu } \right) }}{e^{ - \tau t}}{t^{k - \mu }},&{} \quad 0< \mu < k, \end{array} \right. \end{aligned}$$
(12)

and the integer tempered order defined as

$$\begin{aligned} {}_{ - 1}{\mathcal {D}}^{\tau }_x f(x)= \left( {{e^{ - \tau x}}\frac{{\text {d}}}{{{\text {d}}x}}{e^{\tau x}}f} \right) (x). \end{aligned}$$
(13)

3 Problem statement and fractional Lagrange interpolants

The pivotal key for evaluating the inner products in Galerkin and pseudospectral Galerkin techniques is the interpolation operators in standard collocation methods. As a result, we employ a set of interpolation points \(\left\{ {{x_i}} \right\} _{i = 1}^N\) by which we get the associated Lagrange interpolants. Furthermore, in order to establish a collocation method, the residual must vanish on the same set of points, known as collocation nodes \(\left\{ {{y_i}} \right\} _{i = 1}^N\). Generally, these nodes do not have to be identical to the desired interpolation points. The current TFSCM is directly based on a spectral theory proposed for TFSLPs in (Deng et al. 2018; Zayernouri and Karniadakis 2013, 2014; Zayernouri et al. 2015), which we use to deal with

$$\begin{aligned} \begin{aligned} {\lambda _0}\frac{{\partial u\left( {x,t} \right) }}{{\partial t}}&= {}^{{\tau _x},{\tau _t}}{\mathcal{K}^{{\sigma _x},{\sigma _t}}}u\left( {x,t} \right) ,\quad - 1 \le x \le 1,\quad 0 \le t \le T,\\ u\left( {x,0} \right)&= h(x),\quad - 1 \le x \le 1,\\ u(x,t)&= 0,\quad x \in {\mathbb {R}}\backslash [ -1,1], \end{aligned} \end{aligned}$$
(14)

where \(\lambda _0 \in {\mathbb {R}}\), \({{}^{{\tau _x},{\tau _t}}\mathcal{K}^{{\sigma _x},{\sigma _t}}}\) represents the tempered fractional differential operator (TFDO), \(\sigma _x, \sigma _t\) are the greatest fractional orders of the spatial and temporal operators, respectively, and \(\tau _x, \tau _t \ge 0\) are the tempering parameters for x and t, respectively. We represent the solution to Problem (14) as a finite series of tempered fractal (nonpolynomial) basis functions, known as the generalized tempered Jacobi polyfractonomials, that are TFSLP’s eigenfunctions of the first kind, explicitly derived as

$$\begin{aligned} {}^ - {\mathcal {J}}_n^{\left( {\alpha , - \beta ,\mu ,\tau } \right) }\left( x \right) = {\left( {1 + x} \right) ^{ - \beta + \mu - 1}}{e^{ - \tau x}}J_{n - 1}^{\left( {\alpha - \mu + 1, - \beta + \mu - 1} \right) }\left( x \right) , \quad x \in \left[ { - 1,1} \right] , \end{aligned}$$
(15)

where \(J^{(\alpha -\mu + 1,-\beta + \mu -1)}_{n-1} (x)\) denotes the Jacobi polynomials with \(0< \mu < 1,\; \alpha \in \left[ { - 1,2 - \mu } \right) \), and \(\beta \left[ { - 1,\mu - 1} \right) \). Obviously, the eigenfunctions \({}^ - {\mathcal {J}}_n^{\left( {\alpha , - \beta ,\mu ,\tau } \right) }\left( x \right) \) with \(\alpha = \beta \), show the same properties of approximation when they are employed as basis functions. Thus, we employ these eigenfunctions associated with the parameters \(\alpha = \beta = -1\) as

$$\begin{aligned} ^ - {\mathcal J}_n^{(\mu ,\tau )}\left( x \right) = {\left( {1 + x} \right) ^\mu }{e^{ - \tau x}}J_{n - 1}^{( - \mu ,\mu )}\left( x \right) ,\quad x \in \left[ { - 1,1} \right] . \end{aligned}$$
(16)

By imposing the alternative tempered eigensolutions properties in Zayernouri and Karniadakis (2013), the left-sided TFD of Eq. (16), of both RL and Caputo type, is equated as

$$\begin{aligned} {}_{ - 1}{\mathcal {D}}_x^{\mu ,\tau }\left( {{}^ - {\mathcal {J}}_n^{\left( {\mu ,\tau } \right) }\left( x \right) } \right) = \frac{{\Gamma \left( {n + \mu } \right) }}{{\Gamma \left( n \right) }}{e^{ - \tau x}}J_{n - 1}^{\left( {0,0} \right) }\left( x \right) , \end{aligned}$$
(17)

where \(J^{(0,0)}_{n-1}( x )\) is Legendre polynomial of degree \(n - 1\). We strive to find the solutions

$$\begin{aligned} {u_N} \in V_N^{\mu ,\tau } = {\text {span}}\left\{ {^ - \mathcal{J}_n^{\left( {\mu ,\tau } \right) }\left( x \right) , \quad 1 \le n \le N} \right\} , \end{aligned}$$
(18)

\(x \in [ - 1,1], \mu \in \left( {0,1} \right) \) of the form

$$\begin{aligned} {u_N}\left( x \right) = \sum \limits _{i = 1}^N {{{{\hat{u}}}_N}\left( {{x_i}} \right) {}^ - {\mathcal {J}}_n^{\left( {\mu ,\tau } \right) }\left( x \right) }. \end{aligned}$$
(19)

This formal expansion can be written as a nodal expansion, as follows:

$$\begin{aligned} {u_N}\left( x \right) = \sum \limits _{i = 1}^N {{u_N}\left( {{x_i}} \right) \mathcal{L}_i^{\left( \mu \right) }\left( x \right) }, \end{aligned}$$
(20)

where \({\mathcal {L}}_n^{\left( {\mu } \right) }\) denotes the FLIs, they are defined through the interpolations points \(-1 = x_1< x_2< \dots < x_N = 1\). The interpolants \({\mathcal {L}}_i^{\left( {\mu } \right) }\) are all of the non-integer order \((N + \mu - 1)\) and given as

$$\begin{aligned} {\mathcal {L}}_i^{\left( \mu \right) }\left( x \right) = {\left( {\frac{{x - {x_1}}}{{{x_i} - {x_1}}}} \right) ^\mu }\mathop {\mathop \prod \limits ^N }\limits _{\begin{array}{*{20}{c}} {r = 1}\\ {r \ne i} \end{array}} \left( {\frac{{x - {x_r}}}{{{x_i} - {x_r}}}} \right) ,\quad 2 \le i \le N. \end{aligned}$$
(21)

Before solving Problem (14), we shall specify the superscripted interpolation parameter \(\mu \). It is assumed that the generalized form of TFPDE can be paired with various fractional orders \(\sigma _r,\; r = 1, 2, \dots ,M\) for some \(M \in {\mathbb {N}}\). We will then illustrate how to select \(\sigma \) using just the fractional differentiation orders \(\sigma _r\) provided in the test examples.

Remark 3.1

The boundary condition(s) in Problem (14) allow us to construct \({\mathcal {L}}_i^{\left( {\mu } \right) }\) only for \(i = 2, 3,\dots ,N\) when the greatest fractional order \(0<\sigma <1\), for which we set \(u_N(-1) = 0\). Furthermore, since \(0<\sigma < 2\), there are only \((N - 2)\) FLIs to construct \({\mathcal {L}}_i^{\left( {\mu } \right) }, i = 2, 3, \dots ,N - 1\), as we set \(u_N( \pm 1) = 0\).

The FLIs, defined in Eq. (21), satisfy \({\mathcal {L}}_i^{\left( {\mu } \right) } = \delta _{i,r}\) at interpolation nodes, where \(\delta _{i,r}\) is the KD function; Furthermore, they obviously differ as a polyfractonomial within \(x_r\)’s. We use the FLIs as fractional nodal basis functions in Eq. (20), for which they constitute the basic structure of the eigenfunctions Eq. (16), employed as fractional formal bases in Eq. (19).

3.1 Tempered fractional differentiation matrix \({\mathcal {D}}^{{\sigma ,\tau }},\; 0< \sigma < 1\)

In this part, we derive the TFDM \(\varvec{{\mathcal {D}}}^{{\sigma ,\tau }}\) with a generalized order \(0< \sigma < 1\). Substituting Eq. (21) into Eq. (20), then take the \(\sigma \)th order TFD for both sides, we obtain

$$\begin{aligned}{} & {} {}_{ - 1}\mathcal{D}_x^{\sigma ,\tau }{u_N}\left( x \right) { = _{ - 1}}\mathcal{D}_x^{\sigma ,\tau }\left[ {\sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) \mathcal{L}_i^{\left( \mu \right) }\left( x \right) } } \right] \nonumber \\= & {} \sum \limits _{i = 2}^N {{u_N}{{\left( {{x_i}} \right) }_{ - 1}}\mathcal{D}_x^{\sigma ,\tau }\left[ {{{\left( {\frac{ {1 + x} }{{1 + {x_i}}}} \right) }^\mu }\mathop \prod \limits _{\begin{array}{*{20}{c}} {r = 1}\\ {r \ne i} \end{array}}^N \left( {\frac{{x - {x_r}}}{{{x_i} - {x_r}}}} \right) } \right] } \nonumber \\= & {} \sum \limits _{i = 2}^N {{u_N}{{\left( {{x_i}} \right) }_{ - 1}}\mathcal{D}_x^{\sigma ,\tau }\left[ {{{\left( {1 + x} \right) }^\mu }{\Psi _i}} \right] {d_i},} \end{aligned}$$
(22)

where \(d_i = \frac{1}{(1 + x_i)^{\mu }}\), and \({\Psi _i} = \mathop {\mathop \prod \nolimits ^N }\nolimits _{\begin{array}{c} r = 1\\ r \ne i \end{array} }\left( {\frac{{x - {x_r}}}{{{x_i} - {x_r}}}} \right) ,\;i = 2,3, \ldots ,N\) they are all clearly polynomials of integer degree \(N - 1\), that we can express them as a finite series of Jacobi polynomials \(J^{(-\mu ,\mu )}_{n-1} (x)\) in the fashion

$$\begin{aligned} {\Psi _j} = \sum \limits _{n = 1}^N {\gamma _n^j{e^{ - \tau x}}J_{n - 1}^{(- \mu ,\mu )}\left( x \right) }, \end{aligned}$$
(23)

where the unknown coefficients \(\gamma _n^j\) can be easily obtained analytically. Imposing Eq. (23) into Eq. (22), we have

$$\begin{aligned} _{ - 1}\mathcal{D}_x^{\mu ,\tau }{u_N}\left( x \right)&= \sum \limits _{i = 2}^N {{u_N}{{\left( {{x_i}} \right) }_{ - 1}}\mathcal{D}_x^{\sigma ,\tau }\left[ {{{\left( {1 + x} \right) }^\mu }\sum \limits _{n = 1}^N {\gamma _n^i{e^{ - \tau x}}J_{n - 1}^{( - \mu ,\mu )}\left( x \right) } } \right] {d_i}} \nonumber \\&= \sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {d_i} {{\sum \limits _{n = 1}^N {\gamma _n^i} }_{ - 1}}\mathcal{D}_x^{\mu ,\tau }\left[ {{{\left( {1 + x} \right) }^\sigma }{e^{ - \tau x}}J_{n - 1}^{( -\mu ,\mu )}\left( x \right) } \right] } \texttt {by} (16)\nonumber \\&= \sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {d_i}{{\sum \limits _{n = 1}^N {\gamma _n^i} }_{ - 1}}\mathcal{D}_x^{\sigma ,\tau }\left[ {\mathcal{J}_n^{(\mu ,\tau )}\left( x \right) } \right] } \texttt {by} (17) \end{aligned}$$
(24)

  • Firstly, we study the specific case \(\sigma = \mu \in (0, 1)\). By imposing Eq. (17), we have

    $$\begin{aligned} _{ - 1}\mathcal{D}_x^{\sigma ,\tau }{u_N}\left( x \right) = \sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {d_i}\sum \limits _{n = 1}^N {\gamma _n^i} \left[ {\frac{{\Gamma \left( {n + \mu } \right) }}{{\Gamma \left( n \right) }}{e^{ - \tau x}}J_{n - 1}^{\left( {0,0} \right) }\left( x \right) } \right] }. \end{aligned}$$
    (25)

    As a result, we select the collocation and interpolation nodes to be identical. Then, recall Remark 3.1 and by calculating \({}_{ - 1}{\mathcal {D}}^{\mu ,\tau }_x u_N( x )\) at the collocation nodes \(\left\{ {x_j} \right\} _{j=2}^N\) we have

    $$\begin{aligned} {{{\left. {_{ - 1}\mathcal{D}_x^{\mu ,\tau }{u_N}\left( x \right) } \right| }_{{x_j}}}}&= \sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {d_i}\sum \limits _{n = 1}^N {\gamma _n^i} \left[ {\frac{{\Gamma \left( {n + \mu } \right) }}{{\Gamma \left( n \right) }}{e^{ - \tau {x_j}}}J_{n - 1}^{\left( {0,0} \right) }\left( {{x_j}} \right) } \right] }\nonumber \\&= \sum \limits _{i = 2}^N {{\mathcal {D}}_{ij}^{\mu ,\tau } {u_N}\left( {{x_i}} \right) ,} \end{aligned}$$
    (26)

    where \({\mathcal {D}}^{\mu ,\tau }_{ij}\) are the elements of the \((N - 1) \times (N - 1)\) TFDM \(\varvec{{\mathcal {D}}}^{\mu ,\tau }\), obtained as

    $$\begin{aligned} {\mathcal {D}}_{ij}^{\mu ,\tau } = \frac{1}{{{{\left( {1 + {x_i}} \right) }^\mu }}}\sum \limits _{n = 1}^N {\gamma _n^i\frac{{\Gamma \left( {n + \mu } \right) }}{{\Gamma \left( n \right) }}{e^{ - \tau {x_j}}}J_{n - 1}^{\left( {0,0} \right) }\left( {{x_j}} \right) }. \end{aligned}$$
    (27)

  • Finally, we study the general case \(0<\sigma <1\), which is essential for the TFDO when it is combined with various FDs of distinct order. To construct the TFDM in this case, we introduce the useful mapping \(z = (1 + x)/2\) from \(x \in [-1, 1]\) to \(z \in [0, 1]\) and rewrite Eq. (24) as

    $$\begin{aligned} {}_{ - 1}{\mathcal {D}}_x^{\sigma ,\tau } {u_N}\left( x \right)&= \sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {d_i}\sum \limits _{n = 1}^N {\gamma _n^i{}_{ - 1}{\mathcal {D}}_x^{\sigma ,\tau } \left[ {{}^ - {\mathcal {J}}_n^{(\mu ,\tau )}\left( {x\left( z \right) } \right) } \right] } },\nonumber \\&= \sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {d_i}\sum \limits _{n = 1}^N {\gamma _n^i{{\left( {\frac{1}{2}} \right) }^\sigma }{}_0{\mathcal {D}}_z^{\sigma ,\tau } \left[ {{}^ - {\mathcal {J}}_n^{(\mu ,\tau )}\left( {x\left( z \right) } \right) } \right] } }, \end{aligned}$$
    (28)

    where \({}^ - {\mathcal {J}}_n^{(\mu ,\tau ) }\left( {x\left( z \right) } \right) \) is the shifted basis, which can be written as

    $$\begin{aligned} ^ - \mathcal{J}_n^{(\mu ,\tau )}\left( {x\left( z \right) } \right) = {2^\mu }{e^{ - \tau \left( {2z - 1} \right) }}\sum \limits _{s = 0}^{n - 1} {\rho \left( {n,s,\mu } \right) {z^{s + \mu }}.} \end{aligned}$$
    (29)

    where

    $$\begin{aligned} \rho \left( {n,s,\mu } \right) = {\left( { - 1} \right) ^{n + s - 1}}\left( {\begin{array}{*{20}{c}} {n + s - 1}\\ s \end{array}} \right) \left( {\begin{array}{*{20}{c}} {n - \mu - 1}\\ {n - s - 1} \end{array}} \right) . \end{aligned}$$
    (30)

    By substituting Eq. (29) into Eq. (28), we obtain

    $$\begin{aligned} {_{ - 1}\mathcal{D}_x^{\sigma ,\tau }{u_N}\left( x \right) = {2^{\mu - \sigma }}\sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {d_i}\sum \limits _{n = 1}^N {\gamma _n^i\sum \limits _{s = 0}^{n - 1} {\rho \left( {n,s,\mu } \right) } {}_0\mathcal{D}_z^{\sigma ,\tau }\left[ {{e^{ - \tau \left( {2z - 1} \right) }}{z^{s + \mu }}} \right] } } },\nonumber \\ \end{aligned}$$
    (31)

    then, evaluate \({}_0{\mathcal {D}}_z^{\sigma ,\tau } \left[ {{e^{ - \tau \left( {2z - 1} \right) }}{z^{s + \mu }}} \right] \) using Eq. (12), and finally, via the inverse mapping transform, we have the \(\sigma \)-TFD of the approximation as

    (32)

    where is the ceiling function and

    $$\begin{aligned} {\eta _{n,s}} = {\left( {\frac{1}{2}} \right) ^s}\rho \left( {n,s,\mu } \right) \frac{{\Gamma \left( {s + \mu + 1} \right) }}{{\Gamma \left( {s + \mu - \sigma + 1} \right) }}. \end{aligned}$$
    (33)

    Similarly, by calculating \({}_{-1} {\mathcal {D}}^{\mu ,\tau }_{x} u_N( x )\) at the collocation points \(\left\{ {x_j} \right\} ^{N}_{j=2}\),

    (34)

    where \({\mathcal {D}}^{{\sigma ,\tau }}_{ij}\) are the elements of the \((N - 1) \times (N - 1)\) TFDM \(\varvec{{\mathcal {D}}}^{{\sigma ,\tau }}\), computed as

    (35)

3.2 Tempered fractional differentiation matrix \({\mathcal {D}}^{1 + \sigma ,\tau },\; 0< \sigma < 1\)

Similarly, we will subdivide this derivation into two cases.

  • When \(\sigma = \mu \). The TFDM \(\varvec{{\mathcal {D}}}^{{1+\sigma ,\tau }}\) can be directly generated via Eq. (11) and hence by applying the first tempered derivative of Eq. (25) as

    $$\begin{aligned} _{ - 1}{\mathcal {D}}_x^{1 + \mu ,\tau }{u_N}\left( x \right)&= \left( {_{ - 1}{\mathcal {D}}_x} \right) \left( {_{ - 1}{\mathcal {D}}_x^{\mu ,\tau } {u_N}\left( x \right) } \right) \nonumber \\&= \sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {d_i}\sum \limits _{n = 2}^N {\gamma _n^i\frac{{\Gamma \left( {n + \mu } \right) }}{{\Gamma \left( n \right) }}\left( {_{ - 1}{\mathcal {D}}{_x}} \right) \left[ {{e^{ - \tau x}}J_{n - 1}^{(0,0)}\left( x \right) } \right] } } \nonumber \\&= \sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {d_i}\sum \limits _{n = 2}^N {\gamma _n^i\frac{{\Gamma \left( {n + \mu } \right) }}{{\Gamma \left( n \right) }}{e^{ - \tau x}}\left[ {\frac{n}{2}J_{n - 2}^{(1,1)}\left( x \right) } \right] } }. \end{aligned}$$
    (36)

    Also, we can evaluate \({}_{ - 1}{\mathcal {D}}_x^{1 + \mu ,\tau } u_N( x )\) at the collocation points \(\left\{ {x_j} \right\} ^N_{j=1}\) to obtain

    $$\begin{aligned} {\left. {{}_{ - 1}\mathcal{D}_x^{1 + \mu ,\tau }{u_N}\left( x \right) } \right| _{{x=x_j}}}&= \sum \limits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {d_i}\sum \limits _{n = 2}^N {\gamma _n^i\frac{{\Gamma \left( {n + \mu } \right) }}{{\Gamma \left( n \right) }}{e^{ - \tau x}}\left[ {\frac{n}{2}J_{n - 2}^{(1,1)}\left( {{x_j}} \right) } \right] } }\nonumber \\&= \sum \limits _{i = 2}^N {{\mathcal {D}}_{ij}^{1 + \mu ,\tau }{u_N}\left( {{x_i}} \right) }, \end{aligned}$$
    (37)

    where \({\mathcal {D}}_{ij}^{1 + \mu ,\tau }\) are the entries of the TFDM \(\varvec{{\mathcal {D}}}^{1 + \mu ,\tau }\), provided as

    $$\begin{aligned} {\mathcal {D}}_{ij}^{1 + \mu ,\tau } = \frac{1}{{{{\left( {1 + {x_i}} \right) }^\mu }}}\sum \limits _{n = 2}^N {\gamma _n^i\frac{{\Gamma \left( {n + \mu } \right) }}{{\Gamma \left( n \right) }}{e^{ - \tau x}}\left[ {\frac{n}{2}J_{n - 2}^{(1,1)}\left( {{x_j}} \right) } \right] }. \end{aligned}$$
    (38)

  • For \(\sigma \ne \mu \), apply the first derivative of Eq. (32) in terms of x as follow:

    (39)

    by calculating the above equation at the collocation points, we get the following

    (40)

    in which \({\mathcal {D}}_{ij}^{1 + \sigma ,\tau }\) are the elements of \(\varvec{{\mathcal {D}}}^{1 + \sigma ,\tau }\), computed as

    (41)

3.3 Interpolation/collocation points

The interpolation and collocation nodes can theoretically be chosen at random. The appropriate selection of interpolation/collocation points from an alternative perspective is vital to constructing efficient methods that yield well-conditioned linear systems. For the TFDMs \(\varvec{{\mathcal {D}}}^{\sigma ,\tau }\) and \(\varvec{{\mathcal {D}}}^{1+\sigma ,\tau },\; \sigma \in (0, 1)\), we use five different sets of interpolation/collocation points. This is the case for the general TFODEs/TFPDEs, where both the above operators may appear. In order to combine both boundary points, we consider N Gauss-Lobatto collocation points. The five types of interpolation/collocation points, are listed as follows:

  • Fourier collocation points (Equidistant points), we denote them as

    $$\begin{aligned}{\mathcal {F}}_{{\mathcal {P}}_N} = \left\{ {{x_j}:{x_j} = - 1 + 2(j - 1)/(N - 1),\quad j = 1,2, \ldots ,N} \right\} .\end{aligned}$$

  • The polyfractonomial eigenfunctions zeros of \(\mathcal{J}_{N - 1}^{(\mu ,\tau )}(x)\) by adding the boundary point \(x = 1\). We denote them as \({}^ - {{\mathcal {J}}_{{{\mathcal {P}}_N}}}\).

  • Legendre polynomial \(L_{N-1}(x)\) roots, including the boundary points \(x = \pm 1\), and we denote them as \({L_{{{\mathcal {P}}_N}}}\), which are identically considered to be (fractional) extrema of the Jacobi polyfractonomials.

  • Chebyshev \(T_{N-1}(x)\) roots including the boundary points \(x = \pm 1\), we denote them as \({T_{{{\mathcal {P}}_N}}}\).

  • The extrema of Chebyshev \(T_{N+1}(x)\) roots, are denoted as \(T_{{P_N}}^{'}\).

We study the one-dimensional steady-state space-tempered fractional advection and diffusion equations, and time-dependent TFPDE to investigate the efficiency of each selection of interpolation/collocation points. In these test instances, we examine the resulting accuracy as well as the condition number of the related linear system for the five previously described interpolation/collocation point selections.

4 Numerical experiments

In this part, we examine the accuracy and applicability of the TFSCM by actually treating seven well-studied linear and nonlinear test problems in the literature having exact solutions. In fact, many applications involve TFDOs and others include several TFD terms of possibly different fractional order. The resulting linear algebraic systems were handled using the MATLAB mldivide method included with the MATLAB software. Furthermore, we corroborate our numerical conclusions by presenting the \(L^{\infty }\)-norm errors of the numerical solutions \({\left\| {E_N^u} \right\| _\infty }\) and the associated condition number \(\kappa (A) \) of the resulting linear algebraic system from each selection of the collocation points on the right side. Furthermore, we support our numerical results by exhibiting the absolute error matrix \(E^u_{N,N}\) for the two-dimensional examples, whose elements are defined by

$$\begin{aligned} \left( {E_{N,N}^u} \right) = | {{u_{exact}}\left( {x,t} \right) - {u_{approx}}\left( {x,t} \right) } |. \end{aligned}$$

Example 1

Firstly, consider a simple form of TFODE, the steady-state-tempered fractional advection equation of order \(\sigma \in (0, 1)\) and \(\tau \ge 0\):

$$\begin{aligned} {}_{ - 1}{\mathcal {D}}_x^{\sigma ,\tau } u\left( x \right) = f\left( x \right) , \quad - 1 \le x \le 1, \end{aligned}$$
(42)

subject to the initial condition \(u\left( { - 1} \right) = 0\). We’re seeking a solution to Eq. (42) in the pattern of \(\sum \nolimits _{i = 2}^N {{u_N}\left( {{x_i}} \right) {\mathcal {L}}_i^{\mu ,\tau }\left( x \right) } \) (with \(u_N(-1) = u_N(x_1) = 0\)). Then, by using one the interpolation/collocation points aforementioned in Sect. 3.3 and having the residual

$$\begin{aligned} Res_N\left( x \right) = {}_{ - 1}{\mathcal {D}}_x^{\sigma ,\tau }u\left( x \right) - f\left( x \right) , \end{aligned}$$
(43)

to decay to zero at the collocation points, and then set \(\sigma = \mu \), we have

$$\begin{aligned} \sum \limits _{i = 2}^N {{\mathcal {D}}_{ij}^{\mu ,\tau } {u_N}\left( {{x_i}} \right) } - f\left( {{x_j}} \right) = 0, \end{aligned}$$
(44)

and \(j = 2, 3, \dots ,N\). Then, the TFSCM resulting the linear algebraic system:

$$\begin{aligned} \varvec{{\mathcal {D}}}^{\sigma ,\tau } {\textbf{u}}_N = \textbf{f}, \end{aligned}$$
(45)

where \(\varvec{{\mathcal {D}}}^{\sigma ,\tau }\) is the corresponding \((N - 1) \times (N - 1)\) TFDM defined in Eq. (27). The analytical solution to Eq. (42) is \(u_{exact}(x) = {e^{ - \tau x}} (1 + x)^{101/12}\), which a tempered fractional-order function, corresponding to \(f(x) = \frac{{\Gamma (113/12)}}{{\Gamma (113/12 - \sigma )}}{e^{ - \tau x}}{(1 + x)^{101/12 - \sigma }}\). We exhibit the log-linear \({\left\| {E_N^u} \right\| _\infty }\) of the approximate solution to Eq. (42) on the left plots of Figs. 1, 2, and 3. And we show the resulting \(\kappa (A)\) from TFSCM versus N on the right side of the figures. We examine five distinct interpolation/collocation points defined in Sect. 3.3. We also test three different fractional orders, Fig. 1 is associated with the fractional order \(\sigma = \mu = 0.1\), Fig. 2 corresponds to \(\nu = \mu = 0.5\), and Fig. 3 corresponds to \(\nu = \mu = 0.9\). In each case, we demonstrate that the TFSCM yields an exponential convergence (decay of the \({\left\| {E_N^u} \right\| _\infty }\) to zero versus N). We also noted that the zeros of \({L_{{{\mathcal {P}}_N}}}\), are the best points among the five types. It is demonstrated that this selection not only results in the highest accuracy (lowest level of error) but also in the slowest increase of the \(\kappa (A)\) versus N.

Fig. 1
figure 1

The numerical results of Example 1 with fractional order \(\sigma \) using the TFSCM. The right and left figures show the \(L^{\infty }\)-error and its corresponding \(\kappa (A)\) using \(\sigma = \mu = 0.1\) for \(\tau = 1\) and \(N = \) 3:20

Full size image
Fig. 2
figure 2

The numerical results of Example 1 with tempered fractional order \(\sigma \) using the TFSCM. The right and left figures show the \(L^{\infty }\)-error and its corresponding \(\kappa (A)\) using \(\sigma = \mu = 0.5\) for \(\tau = 1\) and \(N = \) 3:20

Full size image
Fig. 3
figure 3

The numerical results of Example 1 with tempered fractional order \(\sigma \) using the TFSCM. The right and left figures show the \(L^{\infty }\)-error and its corresponding \(\kappa (A)\) using \(\sigma = \mu = 0.9\) for \(\tau = 1\) and \(N = \) 3:20

Full size image

Example 2

Then, we test a high order TFODE which is a space-tempered fractional diffusion equation of order \(1 + \sigma ,\; 0< \sigma <1\),

$$\begin{aligned} {}_{-1} {\mathcal {D}}^{1+\sigma ,\tau }_x u( x ) = f(x), \quad -1 \le x \le 1, \end{aligned}$$
(46)

subject to \(u(\pm 1) = 0\). We seek solutions to Eq. (46) in the form \({u_N}\left( x \right) = \sum \nolimits _{i = 2}^{N - 1} {u_N}\left( {{x_i}} \right) {\mathcal {L}}_i^{\mu ,\tau }\left( x \right) \), where \(u_N(x_1) = u_N(x_N) = u_N(\pm 1) = 0\) to check the efficiency of the higher differentiation matrices. Similarly, by allowing the residual to decay to zero at the collocation points and setting \(\mu = \sigma \), we have

$$\begin{aligned} \sum \limits _{i = 2}^N {{\mathcal {D}}_{ij}^{1 + \sigma ,\tau }{u_N}\left( {{x_i}} \right) } - f\left( {{x_j}} \right) = 0,\quad j = 2, 3,\dots ,N - 1, \end{aligned}$$
(47)

yields the linear algebraic system

$$\begin{aligned} \varvec{{\mathcal {D}}}^{1 + \sigma ,\tau }{\textbf{u}_N} = \textbf{f}, \end{aligned}$$
(48)

where \(\varvec{{\mathcal {D}}}^{1+\sigma ,\tau }\) is the associated \((N - 2) \times (N - 2)\) TFDM given in Eq. (38). By the same exact solution studied in Example 1 and via an identical style, we exhibit the log-linear \({\left\| {E_N^u} \right\| _\infty }\) of the numerical solution of u(x), versus N, On the left side of the Figs. 4, 5, and 6, and the corresponding \(\kappa (A)\) of the linear system obtained from each selection of interpolation/collocation points on the right side. We use different interpolation/collocation points. We also examine three different fractional orders, Fig. 4 associated with the fractional order \(\sigma = \mu = 0.1\), Fig. 5 corresponds to \(\nu = \mu = 0.5\), and Fig. 6 corresponds to \(\nu = \mu = 0.9\). In each case, we demonstrate that the TFSCM yields an exponential convergence (decay of the \({\left\| {E_N^u} \right\| _\infty }\) to zero versus N). We also noted that the zeros of \({L_{{{\mathcal {P}}_N}}}\), are the best points among the five types. It is demonstrated that this selection not only results in the highest accuracy (lowest level of error) but also in the slowest increase of \(\kappa (A)\) versus N.

Fig. 4
figure 4

The numerical results of Example 2 with tempered fractional order \(1 +\sigma \) using the TFSCM. The right and left figures show the \(L^{\infty }\)-error and its corresponding \(\kappa (A)\) using \(\sigma = \mu = 0.1\) for \(\tau = 1\) and \(N = \) 3:20

Full size image
Fig. 5
figure 5

The numerical results of Example 2 with tempered fractional order \(1 +\sigma \) using the TFSCM. The right and left figures show the \(L^{\infty }\)-error and its corresponding \(\kappa (A)\) using \(\sigma = \mu = 0.5\) for \(\tau = 1\) and \(N = \) 3:20

Full size image
Fig. 6
figure 6

The numerical results of Example 2 with tempered fractional order \(1 +\sigma \) using the TFSCM. The right and left figures show the \(L^{\infty }\)-error and its corresponding \(\kappa (A)\) using \(\sigma = \mu = 0.9\) for \(\tau = 1\) and \(N = \) 3:20

Full size image

Next, we discuss two linear steady-state TFODEs:

  • The space-TFADP.

  • The multi-term space TFODEs.

In this part, we attempt to illustrate that the TFSCM may be used to treat many models of TFODEs with almost the same flexibility.

Example 3

Consider the following two-term equation

$$\begin{aligned} {C_1}{}_{ - 1}{\mathcal {D}}_x^{{\sigma _1,\tau }}u\left( x \right) - {C_2}{}_{ - 1}{\mathcal {D}}_x^{1 + {\sigma _2,\tau }}u\left( x \right) = f\left( x \right) , \quad -1 \le x \le 1, \end{aligned}$$
(49)

which models the dynamics of the steady-state TFADP together with \(u\left( { \pm 1} \right) = 0\), where \({\sigma _1}\) and \({\sigma _2} \in \left( {0,1} \right) \).

Remark 4.1

The previous problems 1 and 2 were associated with a single fractional order \(\sigma \), so we perform the interpolation via Eq. (20). However, in Eq. (49), the TFDO in the general case is combined with two fractional orders. Thus, we have to determine a convenient fractional order, \(\sigma _{cov}\), to perform an interpolation procedure at the selected collocation nodes. The \(\sigma _{cov}\) can be easily chosen as the mean of the fractional orders in Eq. (49) or as the max/min\(\left\{ {\sigma _{1}, \sigma _{2}} \right\} \).

For the current problem, we seek the solution to Eq. (49) as \({u_N}\left( x \right) = \sum \nolimits _{i = 2}^{N - 1} {{u_N}\left( {{x_i}} \right) {\mathcal {L}}_i^{\mu ,\tau }\left( x \right) }\) setting \(\mu = \sigma _{cov}\), where \(u_N(x_1) = u(\pm 1) = u_N(x_N)\) due to the homogeneous boundary conditions. We construct \({\mathcal {L}}_i^{\mu ,\tau }\left( x \right) \) only for \(i = 2, 3, \dots , N - 1\). Then, at the collocation points \(\left\{ {{x_j}} \right\} _{i = j}^{N - 1}\), require the associated residual to decay to zero,

$$\begin{aligned} {C_1}\sum \limits _{i = 2}^{N - 1} {{\mathcal {D}}_{ij}^{{\sigma _1,\tau }}{u_N}\left( {{x_i}} \right) } - {C_2}\sum \limits _{i = 2}^{N - 1} {{\mathcal {D}}_{ij}^{1 + {\sigma _2,\tau }}{u_N}\left( {{x_i}} \right) } - f\left( {{x_j}} \right) = 0, \end{aligned}$$
(50)

we have the linear algebraic system

$$\begin{aligned} \varvec{{\mathcal {D}}}_{Join}^{\sigma ,\tau } {{\textbf{u}}_N} = \textbf{f}, \end{aligned}$$
(51)

where \(\varvec{{\mathcal {D}}}^{\sigma ,\tau }_{Join} = C_1\varvec{{\mathcal {D}}}^{\sigma _1,\tau } - C_2\varvec{{\mathcal {D}}}^{1 + \sigma _2,\tau }\) of size \((N - 2) \times (N - 2)\), in which \(\varvec{{\mathcal {D}}}^{1 + \sigma _2,\tau }\) is obtained from Eq. (38) or Eq. (41). To show the efficiency of the TFSCM of this problems, we consider

$$\begin{aligned} f\left( x \right) = {e^{ - \tau x}}\left( {\frac{{\Gamma \left( {113/12} \right) }}{{\Gamma \left( {113/12 - {\sigma _1}} \right) }}{{\left( {1 + x} \right) }^{101/12 - {\sigma _1}}} - \frac{{\left( {101/12 - {\sigma _2}} \right) \Gamma \left( {113/12} \right) }}{{\Gamma \left( {113/12 - {\sigma _2}} \right) }}{{\left( {1 + x} \right) }^{89/12 - {\sigma _2}}}} \right) ,\nonumber \\ \end{aligned}$$
(52)

where the analytical solution to Eq. (49) is obtained as \({u_{exact}} = e^{ - \tau x}{\left( {1 + x} \right) }^{101/12}\).

In Figs. 7, 8, and 9, we utilize distinct orders \(\sigma _1\) and \(\sigma _2\) to show the \(L^{\infty }\)-norm error of the approximate solution of u(x) versus N in log-linear style (on left plots). And we show the corresponding \(\kappa (A)\) of the resulting linear algebraic system from the TFSCM (on right plots). Figure 7 is corresponding to the fractional order \(\sigma _1 = \sigma _2 = \mu \), and Fig. 8 corresponds to the case where \(\sigma _1 < \sigma _2\), here we take the fractional interpolation parameter \(\mu \) as \(\sigma _{\max }\), \(\sigma _{\min }\), and \(\sigma _{mean}\), similarly, Fig. 9 corresponds to \(\sigma _1 < \sigma _2\) such that for this case \(\sigma _2 - \sigma _1\) becomes larger than that considered in Fig. 8.

Firstly, we observe that the TFSCM yields an exponential convergence due to (decay of the \({\left\| {E_N^u} \right\| _\infty }\) to zero versus N) in every case. In this case, we employ \({L_{{\mathcal{P}_N}}}\) points, as interpolation/collocation points. While the second useful observation is about the selected fractional parameter \(\mu \), we observe that among \(\mu = \sigma _{\max },\; \sigma _{\max }\), and \(\sigma _{mean}\), the mean value, i.e., \(\mu = \sigma _{mean}\), exhibits the fastest decay of \({\left\| {E_N^u} \right\| _\infty }\) to zero in the figures moreover shows the slowest increase of \(\kappa (A)\) versus N.

Fig. 7
figure 7

The numerical results of Example 3 with mixed fractional orders using the TFSCM. The right and left figures show the \(L^{\infty }\)-error and its corresponding \(\kappa (A)\) using various values of \(\sigma \) for \(\tau = 1\) and \(N = \) 3:20

Full size image
Fig. 8
figure 8

The numerical results of Example 3 with mixed tempered fractional orders using the TFSCM. The right and left figures show the \(L^{\infty }\)-error and its corresponding \(\kappa (A)\) using various values of \(\sigma \) for \(\tau = 1\) and \(N = \) 3:20

Full size image
Fig. 9
figure 9

The numerical results of Example 3 with mixed tempered fractional orders using the TFSCM. The right and left figures show the \(L^{\infty }\)-error and its corresponding \(\kappa (A)\) using various values of \(\sigma \) for \(\tau = 1\) and \(N = \) 3:20

Full size image

Example 4

Next, we study the generalized case of Eq. (42) as a multiterm linear TFDE in the form

$$\begin{aligned} \sum \limits _{k = 1}^{{M_1}} {{C_k}\left[ {{}_{ - 1}{\mathcal {D}}_x^{{\sigma _k,\tau }}u\left( x \right) } \right] } + \sum \limits _{l = 1}^{{M_2}} {{C_l}\left[ {{}_{ - 1}{\mathcal {D}}_x^{1 + \sigma _l,\tau }u\left( x \right) } \right] } + {\mathcal {M}}u\left( x \right) = f\left( x \right) , \quad -1 \le x \le 1,\nonumber \\ \end{aligned}$$
(53)

subject to \(u\left( { \pm 1} \right) = 0\), where \(\sigma _k\), and \(\sigma _l \in (0, 1)\). Moreover, \(\left\{ {{C_k}} \right\} _{k = 1}^{{M_1}},\left\{ {{C_l}} \right\} _{l = 1}^{{M_2}}\) also \({{\mathcal {M}}}\) are known real constants. By performing identical steps to seek a numerical solution to Eq. (53) as \({u_N}\left( x \right) = \sum \nolimits _{i = 2}^{N - 1} {{u_N}\left( {{x_i}} \right) {\mathcal {L}}_i^{\mu ,\tau }\left( x \right) } \) by setting \(\mu \) to some representative parameter \(\sigma \). Next, at the candidate collocation points \(\left\{ {{x_j}} \right\} _{j = 1}^{N - 1}\) (\(^ - {\mathcal{J}_{{\mathcal{P}_N}}}\) Points), the corresponding residual must decay to zero, we obtain

$$\begin{aligned} {\sum \limits _{k = 1}^{{M_1}} {{C_k}\left[ {{}_{ - 1}{\mathcal {D}}_x^{{\sigma _k,\tau }}u\left( x \right) } \right] } _{x = {x_j}}} + {\sum \limits _{l = 1}^{{M_2}} {{C_l}\left[ {{}_{ - 1}{\mathcal {D}}_x^{1 + \sigma _l,\tau }u\left( x \right) } \right] } _{x = {x_j}}} + {{\mathcal {M}}} u\left( {{x_j}} \right) - f\left( {{x_j}} \right) = 0.\nonumber \\ \end{aligned}$$
(54)

As a result, the collocated TFDE yields the linear algebraic system

$$\begin{aligned} \varvec{{\mathcal {D}}}_{Join}^{{\sigma _{k,l},\tau }}{{\textbf{u}}_N} = \textbf{f}, \end{aligned}$$
(55)

where \(\varvec{{\mathcal {D}}}_{Join}^{{\sigma _{k,l},\tau }} = \sum \nolimits _{k = 1}^{{M_1}} {\varvec{{\mathcal {D}}}^{{\sigma _k,\tau }}} + \sum \nolimits _{l = 1}^{{M_2}} {\varvec{{\mathcal {D}}}^{1 + {\sigma _l},\tau }} + {\mathcal {M}}\textbf{I}\) is the total TFDM of size \((N - 2) \times (N - 2)\), the TFDMs \(\varvec{{\mathcal {D}}}^{\sigma _k,\tau },\; k = 1, 2, \dots , M_1\), and \(\varvec{{\mathcal {D}}}^{1+\sigma _l,\tau },\; l = 1, 2, \dots ,M_2\), are resulted from Eqs. (35) and (41). and \(\textbf{I}\) denotes the identity matrix.

In Figs. 10 and 11, we exhibit the log-linear \({\left\| {E_N^u} \right\| _\infty }\) of the approximate solution to Eq. (53), versus N, using different \(\sigma _k\) and \(\sigma _l\) on the left, In this problem, we take the exact solution as \(u_{exact}(x) = {e^{ - \tau x}}\left( {{{(1 + x)}^{101/12}} - 2{{(1 + x)}^5}} \right) \). The observed results demonstrated again the TFSCM’s exponential convergence and officially confirmed that choosing the fractional parameter \(\mu \) to be the average of all fractional differential orders yields the fastest exponential convergence. The corresponding \(\kappa (A)\) obtained for such mean value, \(\mu \), also leads to a small increase versus N (reported on the right side of Figs. 10 and 11).

Fig. 10
figure 10

The numerical results of Example 4 employing various fractional orders using the TFSCM. The left and right figures show the \(L^{\infty }\)-error and the corresponding \(\kappa (A)\) of the resulting linear algebraic system respectively. Corresponding to the fractional orders \(\sigma _k = \sigma _1 = 0.2,\; \sigma _2 = 1/3\), and \(\sigma _3 = 5/7\), and corresponds to \(\sigma _l = \sigma _k\), where \(\sigma _1 = 0.2,\; \sigma _2 = 1/3,\; \sigma _3 = 5/7\). for \({\mathcal {M}} = 3, \tau = 1\) and \(N = \) 3:20

Full size image
Fig. 11
figure 11

The numerical results of Example 4 employing various fractional orders using the TFSCM. The left and right figures show the \(L^{\infty }\)-error and the corresponding \(\kappa (A)\) of the resulting linear algebraic system respectively. \(\sigma _k = \sigma _1 = 0.2,\; \sigma _2 = 0.5\), and \(\sigma _3 = 0.8\), and corresponds to \(\sigma _l = \sigma _k\), where \(\sigma _1 = 0.2,\; \sigma _2 = 0.5,\; \sigma _3 = 0.8\). for \({\mathcal {M}} = 3, \tau = 1\) and \(N = \) 3:20

Full size image

Following, we study time-dependent TFPDEs that include the spatial and temporal fractional orders within the differential terms. We specifically study

  • Time-space TFADP.

  • The multiterm time-space TFPDEs.

  • The nonlinear time-space TFBE.

Example 5

Consider the time-space TFADP:

$$\begin{aligned}{} & {} {}_0 {\mathcal {D}}_t^{\sigma _t,\tau _t} u\left( {x,t} \right) + C{}_{ - 1} {\mathcal {D}}_x^{{\sigma _1},\tau _x}u\left( {x,t} \right) - {\mathcal {M}}{}_{ - 1} {\mathcal {D}}_x^{1 + {\sigma _2},\tau _x}u\left( {x,t} \right) = f\left( {x,t} \right) ,\; \nonumber \\{} & {} \qquad -1 \le x \le 1,\; 0 \le t \le T, \end{aligned}$$
(56)

subject to the initial condition \(u\left( {x,0} \right) = 0\), associated with the fractional orders \(\sigma _t\), \(\sigma _1\), and \(\sigma _2 \in (0,1)\). We seek the solution in the fashion

$$\begin{aligned} {u_{{N_x},{N_t}}}\left( {x,t} \right) = \sum \limits _{i = 1}^{{N_x}} {\sum \limits _{k = 1}^{{N_t}} {{u_{{N_x},{N_t}}}\left( {{x_i},{t_k}} \right) {\mathcal {L}}_i^{\mu _x,\tau _x}\left( x \right) {\mathcal {H}}_k^{\mu _t,\tau _t}\left( t \right) } }, \end{aligned}$$
(57)

where \({\mathcal {L}}_i^{\mu _x,\tau _x}\left( x \right) \) denotes the fractional spatial Lagrange basis related to the fractional parameter \(\mu _x\), and \({\mathcal {H}}_k^{\tau ,{\mu _t}}\left( t \right) \) represents the associated temporal nodal basis related to the fractional parameter \(\mu _t\), constructed as

$$\begin{aligned} \mathcal{H}_k^{{\mu _t}}\left( t \right) = {\left( {\frac{t}{{{t_k}}}} \right) ^{{\mu _t}}}\prod _{\begin{array}{*{20}{c}} {q = 1}\\ {q \ne k} \end{array}}^{{N_t}}\left( {\frac{{t - {t_q}}}{{{t_k} - {t_q}}}} \right) , \quad 2 \le k \le {N_t}, \end{aligned}$$
(58)

in which the collocation nodes can be regarded as \(t_j = (x_j+1)T/2\), where \(x_j\) are the spatial collocation nodes, for \(0 = t_1< t_2< \dots < t_N = T\). Following identical steps as in Sect. 3.1 and choosing \(\sigma _t = \mu _t\), we can obtain the time-TFDM \(\varvec{{\mathcal {D}}}^{\mu _t,\tau _t}\), whose elements are given as

$$\begin{aligned} {\mathcal {D}}_{i,j}^{\mu _t,\tau _t} = \frac{1}{{{{\left( {{t_k}} \right) }^{{\mu _t}}}}}\sum \limits _{k = 1}^{{N_t}} {\frac{{\Gamma \left( {k + {\mu _t}} \right) }}{{\Gamma \left( k \right) }}\gamma _n^j{e^{ - \tau _t t}}J_{n - 1}^{(0,0)}\left( {x\left( {{t_i}} \right) } \right) }. \end{aligned}$$
(59)

Note that, the interpolants \(\mathcal{H}_k^{{\mu _t}}\left( t \right) \) still satisfy the KD property at the chosen time interpolation points. Moreover, the same \(\gamma _n^i\) evaluated for the space-TFDM is utilized in Eq. (59). Then, Plug Eq. (57) into Eq. (56) and employ the same interpolation points. Then, via the KD property for time-space FLIs we have

$$\begin{aligned} \mathbf{{U}}{\left( {{\varvec{{\mathcal D}}^{\sigma _t,\tau _t}}} \right) ^{T}} + \left[ {\mathbf{{C}}{\varvec{{\mathcal D}}^{\sigma _1,\tau _x}} - \mathcal{M}{\varvec{{\mathcal D}}^{1+\sigma _2,\tau _x}}} \right] \mathbf{{U}} = \mathbf{{F}}, \end{aligned}$$
(60)

where \(\textbf{U}\) and \(\textbf{F}\) represent the numerical solution and load matrices whose elements are \(u_{N_x,N_t} (x_i, t_k)\) and \(f(x_i, t_k)\), respectively. The linear algebraic system Eq. (60) considered to Lyapunov equation

$$\begin{aligned} \textbf{A}\textbf{U} + \textbf{U}\textbf{B} = \textbf{F}, \end{aligned}$$
(61)

where \(\textbf{A} = C \varvec{{\mathcal {D}}}^{\sigma _1,\tau _x} - {\mathcal {M}} \varvec{{\mathcal {D}}}^{1+\sigma _2,\tau _x}\) and \(\mathbf{{B}} = {\left( {{{\varvec{{\mathcal {D}}}}^{{\sigma _1},{\tau _t}}}} \right) ^T}\), the superscript \({}^T\) denotes the matrix transpose. The exact solution is given by \({u_{exact}}(x,t) = {e^{ - {\tau _x}x - {\tau _t}t}}\Big ( 2{{(1 + x)}^{94/17}} - {{(1 + x)}^{111/17}} \Big ){t^{20/3}}\).

The numerical results were reported in Figs. 12 and 13. We examined the temporal accuracy in plot (d) of Fig. 12. The aim here is to demonstrate the exponential convergence of the time-integration error versus N. In each plot of Figs. 12, we examine the time-fractional order \(\sigma _t= 1/3\) and \(\sigma _1 = \sigma _2=2/3\) for the space-fractional orders.

Figure 13 shows the log-linear \({\left\| {E_N^u} \right\| _\infty }\) of the numerical solution to Eq. (56), versus N, for the parameters \(\sigma _t = 0.02, \sigma _1 = \sigma _2 = 1/3, \mu _t = 0.02,\mu _x = 0.9, \tau _t =\tau _x = 1/3\) and \(N = 3:20\) in plot (a). While in plot (b) we exhibit \({\left\| {E_N^u} \right\| _\infty }\) of the approximate solution with N for the parameters \(\sigma _t = 0.6, \sigma _1 = \sigma _2 = 2/3, \mu _t = 0.6,\mu _x = 0.75, \tau _t =\tau _x = 1/3\) and \(N = 3:20\). We employ the five type points in Sect. 3.3 as the time interpolation points.

Fig. 12
figure 12

The numerical simulation of Example 5. a The exact solution on \((x,t)\in [-1,1] \times [0,1]\). b The numerical solution on the same region obtained using \(N = 20\), using Legendre points. c Exhibits the absolute errors at the Legendre nodes. d \({\left\| {E_N^u} \right\| _\infty }\) of the numerical solution versus N for the parameters \(\sigma _t = 1/3,\; \sigma _1 = \sigma _2 = 2/3,\; \mu _t = 1/3,\; \mu _x = 2/3,\; \tau _t = \tau _x = 1/3\) and \(N = \) 3:20

Full size image
Fig. 13
figure 13

The numerical simulation of Example 5. a The log-linear \({\left\| {E_N^u} \right\| _\infty }\) of the numerical solution versus N for the parameters \(\sigma _t = 0.02,\; \sigma _1 = \sigma _2 = 1/3,\; \mu _t = 0.02,\; \mu _x = 0.9,\; \tau _t =\tau _x = 1/3\) and \(N = 3:20\). b Exhibits the log-linear \({\left\| {E_N^u} \right\| _\infty }\) of the approximate solution versus N for the parameters \(\sigma _t = 0.6,\; \sigma _1 = \sigma _2 = 2/3,\; \mu _t = 0.6,\;\mu _x = 0.75,\; \tau _t =\tau _x = 1/3\) and \(N = \) 3:20

Full size image

Example 6

Here, we study a generalized case of the TFADP 5 to a multiterm linear TFPDE given as

$$\begin{aligned} \begin{aligned}&_0\mathcal{D}_t^{{\sigma _t},{\tau _t}}u\left( {x,t} \right) + \sum \limits _{k = 1}^{{M_1}} {{C_k}\left[ {_{ - 1}\mathcal{D}_x^{{\sigma _{1,k}},{\tau _x}}u\left( {x,t} \right) } \right] } + \sum \limits _{p = 1}^{{M_2}} {{K_p}\left[ {_{ - 1}\mathcal{D}_x^{1 + {\sigma _{2,p}},{\tau _x}}u\left( {x,t} \right) } \right] }\\&+ {{\mathcal {M}}}u\left( {x,t} \right) = f\left( {x,t} \right) , \quad -1 \le x \le 1, \quad 0 \le t \le T, \end{aligned} \end{aligned}$$
(62)

subject to the initial condition \({u\left( {x,0} \right) = 0}\), where \(K_{M_2} \ne 0,\; \sigma _t,\; \sigma _{1,k}\), and \(\sigma _{2,p} \in (0, 1)\). In addition, \(\left\{ {{C_k}} \right\} _{k = 1}^{{M_1}},\; \left\{ {{K_p}} \right\} _{p = 1}^{{M_2}}\), and \(\mathcal{M}\) are given real constants. Using a similar way as before in Sect. 5 yielding a further Lyapunov matrix equation

$$\begin{aligned} {{\tilde{\mathbf{{A}}}}}{} \mathbf{{U}} + \mathbf{{U}}{{\tilde{\mathbf{{B}}}}} = {{\tilde{\mathbf{{F}}}}}, \end{aligned}$$
(63)

which \({{\tilde{\mathbf{{A}}}}} = \sum \nolimits _{k = 1}^{{M_1}} {{C_k}{\varvec{{\mathcal {D}}}^{{\sigma _{1,k},\tau _x}}}} + \sum \nolimits _{p = 1}^{{M_2}} {{K_p}{\varvec{{\mathcal {D}}}^{1 + {\sigma _{2,p},\tau _x}}}} \) and \({{\tilde{\mathbf{{B}}}}} = \left( {{\varvec{{\mathcal {D}}}_t^{\sigma _t,\tau _t}}} \right) ^T\).

Figures 14 and 15 report our results of Eq. (62), where Fig. 14 shows the exact solution on \((x,t)\in [-1,1] \times [0,1]\), the numerical solution on the same region obtained using \(N = 20\), the absolute errors for employing \({{T^{'}}_{{\mathcal{P}_N}}}\) points, and the log-linear \({\left\| {E_N^u} \right\| _\infty }\) of the approximate solution versus N for various parameters. Moreover, we exhibit the \({\left\| {E_N^u} \right\| _\infty }\) of the approximate solution versus N. On the left side of Fig. 15 the fractional orders are chosen as \(\sigma _{1,k} = \sigma _{2,p},\; k\) and \(p = 1, 2, 3\), where \(\sigma _{1,1} = 0.2,\; \sigma _{1,2} = 1/3\), and \(\sigma _{1,3} = 5/7\), and the right side associated with the fractional orders are \(\sigma _{1,k} = \sigma _{2,p}\). We examine time fractional orders \(\sigma _t = 0.1\) and 0.9, considering the same exact solution chosen in the recent case with a different associated term f(x, t), produced by Eq. (12).

Fig. 14
figure 14

The numerical simulation of Example 6. a Exhibits the exact solution on \((x,t)\in [-1,1] \times [0,1]\). b Exhibits the numerical solution on the same region produced using \(N = 20\), using \({{T^{'}}_{{\mathcal{P}_N}}}\) points. c Exhibits the absolute errors for \({{T^{'}}_{{\mathcal{P}_N}}}\) points. d Exhibits the log-linear \({\left\| {E_N^u} \right\| _\infty }\) of the approximate solution versus N for the parameters \(\sigma _t = 1/3,\; \sigma _{1,k} = \sigma _{2,p} = 1/7\) for \(k,\; p = 1,2,3\), \(\mu _t = 1/3,\; \mu _x = 1/7,\; \tau _t =\tau _x = 1\), \({\mathcal {M}} = 3\) and \(N = \) 3:20

Full size image
Fig. 15
figure 15

The numerical simulation of Example 6. a Exhibits the log-linear \({\left\| {E_N^u} \right\| _\infty }\) of the approximate solution versus N for the parameters \(\sigma _t =1/3, \sigma _{1,k} = 0.2,\; \sigma _{2,p} = 5/7\) for \(k,p=1,2,3, \mu _t = 0.9,\;\mu _x = 1/7,\; \tau _t =\tau _x = 1, {\mathcal {M}} = 3\) and \(N = 3:20\). b The log-linear \({\left\| {E_N^u} \right\| _\infty }\) of the approximate solution versus N for the parameters \(\sigma _t = 1/3,\; \sigma _{1,k} =0.2, \sigma _{2,p} = 5/7\) for \(k,p=1,2,3, \mu _t = 0.1,\;\mu _x = 1/7, \tau _t = \tau _x = 1,\; {\mathcal {M}} = 3\) and \(N = \) 3:20

Full size image

Example 7

One of the most significant advantages of the TFSCM is the efficient numerical treatment of nonlinear tempered fractional differential terms in TFPDEs. Finally, we consider the nonlinear time-dependent space-TFBE.

$$\begin{aligned} \begin{aligned}&\frac{{\partial u}}{{\partial t}} + u\left( {x,t} \right) {}_{ - 1}{\mathcal {D}}_x^{{\sigma _1},\tau }u\left( {x,t} \right) - \upsilon {}_{ - 1}{\mathcal {D}}_x^{1 + {\sigma _2},\tau }u\left( {x,t} \right) = f\left( {x,t} \right) \\&\quad - 1 \le x \le 1,\quad 0 \le t \le T,\\ \end{aligned} \end{aligned}$$
(64)

subject to the initial condition \(u\left( {x,0} \right) = 0\), where \({\sigma _1}\) and \({\sigma _2} \in (0, 1)\). The spatial discretization style can be similarly done as shown in previous sections as

$$\begin{aligned} \frac{{d{{{\tilde{\mathbf{{u}}}}}_N}\left( t \right) }}{{dt}} = - {{\tilde{\mathbf{{u}}}}_N}\left( t \right) \circ {{\varvec{{\mathcal {D}}}}^{{\sigma _1},\tau }}{{\tilde{\mathbf{{u}}}}_N}\left( t \right) + \upsilon {{\varvec{{\mathcal {D}}}}^{1 + {\sigma _2},\tau }}{{\tilde{\mathbf{{u}}}}_N}\left( t \right) + {\tilde{\mathbf{{f}}}}\left( t \right) , \end{aligned}$$
(65)

where \({\tilde{{\mathbf{{u}}}}}_N\) are the components of the solution vector, and \(\circ \) denotes the Hadamard product (entrywise product). We perform the time discretization of the resulting system using a Runge-Kutta algorithm of order four (RK-4). Figure 16 reports the numerical simulations of Example 7. Table 1 exhibits the exponential convergence of \(L^{\infty }\)-norm error of the numerical solution to Eq. (64) with N, associated with the fractional orders \(\sigma _1 = \sigma _2 = 0.5\), and the simulation time \(T = 0.5\). We employ \(\Delta t = 5 \times 10^{-6}\) in our RK-4 multistage time-discretization algorithm. We have studied three different \(\upsilon \) values:

  • \(\upsilon = 0\) represents the inviscid TFBE.

  • \(\upsilon = 10^{-4}\) represents the viscous TFBE with small diffusivity.

  • \(\upsilon = 10^{-3}\) for the viscous TFBE with comparatively larger diffusivity.

For each case, the exact solution of this problem is \({u_{exact}}(x,t) = {e^{ - {\tau _x}x - (1 + {\tau _t})t}}(1 - x){(1 + x)^{94/17}}\) with the corresponding forcing term

$$\begin{aligned} \begin{array}{*{20}{l}} {f\left( {x,t} \right) = - \left( {{\tau _t} + 1} \right) {u_{exact}}\left( {x,t} \right) }\\ {\quad +\frac{{2\Gamma \left( {{q_0}} \right) }}{{\Gamma \left( {{q_0} - {\sigma _x}} \right) }}{e^{ - t\left( {{\tau _t} + 1} \right) - x{\tau _x}}}{{(1 + x)}^{{q_0} - {\sigma _x}}}{u_{exact}}\left( {x,t} \right) \left( {{{\left( {1 + x} \right) }^{ - 1}} - \frac{{\Gamma \left( {{q_0} + 1} \right) }}{{\Gamma \left( {{q_0} - {\sigma _x} + 1} \right) }}} \right) }\\ {\quad - \frac{{\upsilon \Gamma \left( {{q_0}} \right) }}{{\Gamma \left( {{q_0} - {\sigma _x}} \right) }}{e^{ - t\left( {{\tau _t} + 1} \right) - x{\tau _x}}}\left( {{{(1 + x)}^{{q_0} - {\sigma _x} - 2}}\left( {{q_0}(1 - x) - 2\left( {{\sigma _x} + 1} \right) } \right) } \right) ,} \end{array} \end{aligned}$$
(66)

where \(q_0 = 111/17\) (Figs. 16, 17, 18).

Fig. 16
figure 16

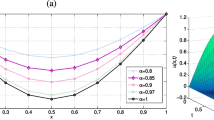
The numerical simulation of Example 7. a Exhibits the exact solution on \((x,t)\in [-1,1] \times [0,0.5]\). b The numerical solution on the same region obtained using \(N = 20\), using Jacobi points. c The absolute errors for \(^ - {\mathcal{J}_{{\mathcal{P}_N}}}\) points. d The \({\left\| {E_N^u} \right\| _\infty }\) of the approximate solution versus x for the parameters \(\mu _x =\sigma _1 = \sigma _2 = 9/17,\; \tau _t =\tau _x = 1,\; \upsilon = 10^{-3},\; \Delta t = 5 \times 10^{-6}\) and \(N = \) 3:20

Full size image
Fig. 17
figure 17

The three figures show the natural logarithm of the maximum absolute error vs N of Example 7, for \(\upsilon = 0, 10^{-3}\), and \(10^{-4}\) respectively. In all three cases, the data can be well fitted by an approximately straight line indicating exponential convergence of the scheme. The figures token for \(^ - {\mathcal{J}_{{\mathcal{P}_N}}}\) points at the parameters \(\mu _x =\sigma _1 = \sigma _2 = 9/17,\; \tau _t =\tau _x = 1,\; T = 0.5, \Delta t = 5 \times 10^{-6}\) and \(N = \) 7:16

Full size image
Table 1 The exponential decay of \(\left( {E_{N,N}^u} \right) \) of the approximate solution to Example 7 with N, corresponding to the fractional orders \(\mu = \sigma _1 = \sigma _2 = 9/17,\; \tau _x = \tau _t = 1\), and \(T = 0.5\)
Full size table
Fig. 18
figure 18

The elapsed times taken by the FSCM against various values of N of Examples 1,5, and 7, respectively. Plot a shows the time taken to construct the L.H.S matrix \(\varvec{{\mathcal {D}}}^{\sigma ,\tau }\), R.H.S. vector \(\textbf{f}\), and then solve the linear system (45). Plot b shows the time taken to construct the L.H.S Matrices \(\textbf{A}\), \(\textbf{B}\), and R.H.S. vector \(\textbf{F}\), and then solve the Lyapunov Eq. (61). While Plot c shows the time taken to construct the matrices \({{\varvec{{\mathcal {D}}}}^{{\sigma _1},\tau }}\), \({{\varvec{{\mathcal {D}}}}^{1 + {\sigma _2},\tau }}\), and then perform the spatial discretization Eq. (65)

Full size image

5 Conclusion

This paper presented an accurate exponential TFSCM for solving steady-state and time-dependent TFPDEs subject to initial and Dirichlet boundary conditions. We have extended this technique following a strategy of the spectral theory developed in Zayernouri and Karniadakis (2014) and Zayernouri and Karniadakis (2013) in order to handle the TFSLPs. We derived forms of the corresponding TFDMs and treated seven well-studied linear and nonlinear TFPDEs to illustrate the fast, exponential convergence and numerical efficiency of the TFSCM. For that purpose, we examined the effect of five distinct interpolation/collocation points at the convergence rate, we found that the exponential decay of \(L^{\infty }\)-norm error varies between them by numerical treatment of the test experiments, however, the category \({L_{{\mathcal{P}_N}}}\) see Fig. 17, \({T_{{\mathcal{P}_N}}}\) points, numerically exhibit a notable speed in accuracy and leading to minimal \(\kappa (A)\) in the resulting linear system compared to \({\mathcal{F}_{{\mathcal{P}_N}}}\), \(^ - {\mathcal{J}_{{\mathcal{P}_N}}}\), \({T_{{\mathcal{P}_N}}}\), and \({{T^{'}}_{{\mathcal{P}_N}}}\) points.

The proposed method enjoys the luxury of integrating five useful tools: (a) the superior advantages possessed by the family of spectral methods, (b) ease of implementation, (c) lower computational cost, (d) fast performance see Fig. 18, and (e) exponential accuracy.

In direct comparison to standard Galerkin projection techniques, our TFSCM did not employ quadratures. Furthermore, nonlinear terms may be treated in TFSCM with the same simplicity as linear terms. This matter is extremely vital as solving nonlinear TFPDEs via Galerkin techniques is still challenging. Furthermore, while using Galerkin techniques in linear TFPDEs becomes fundamentally similar to TFSCM, using Galerkin spectral methods by employing classical basis functions does not necessarily yield exponential convergence, as they do in our TFSCM. Another major limitation in Galerkin projection methods is the difficulty in handling multiterm TFPDEs, for which no direct variational form can be efficiently generated. In contrast, we have clearly demonstrated that using our TFSCM to solve such multiterm FPDEs involves no more work. Despite the advantages indicated above, the disadvantage of TFSCM is that there is no strict theoretical structure for collocation methods in general.