On the exact reproduction number in SIS epidemic models with vertical transmission

Abstract

This paper proposes a bi-variate competition process to describe the spread of epidemics of SIS type through both horizontal and vertical transmission. The interest is in the exact reproduction number, $\mathcal{R}_{\mathrm{{exact}},0}$, which is seen to be the stochastic version of the well-known basic reproduction number. We characterize the probability distribution function of $\mathcal{R}_{\mathrm{{exact}},0}$ by decomposing this number into two random contributions allowing us to distinguish between infectious person-to-person contacts and infections of newborns with infective parents. Numerical examples are presented to illustrate our analytical results.

1 Introduction

Vertical transmission of pathogens (Busenberg and Cooke 1992), such as viruses and bacteria, refers to generational transmission from colonized parents to their offspring. Several vertically transmitted infections are included in the term TORCH complex (see, e.g., Jaan and Rajnik 2021), which is related to congenital infections of Toxoplasmosis, Other infections (chickenpox caused by varicella zoster virus, chlamydia, hepatitis B, human immunodeficiency virus, parvovirus, syphilis, and Zika fever, among others), Rubella, Cytomegalovirus, and Herpes simplex. For some viruses—including human immunodeficiency viruses and hepatitis B virus—infections can occur by contact with or transfer of blood and body fluids (semen, vaginal fluids). This means that, in such cases, the generational transmission of the disease is possible at the same time that the person-to-person contact leads to the dissemination of the pathogen.

Motivated by the above-mentioned pathogens, a variety of epidemic models with vertical and horizontal transmission have been analyzed, mainly under the deterministic perspective, with special emphasis on global stability properties such as the asymptotic stability of the disease-free equilibrium and the endemic equilibrium. Without claiming an exhaustive list of deterministic epidemic models involving vertical and horizontal transmission, we can mention a susceptible-infectious (SI) model (Kang and Castillo-Chavez 2014) of host–parasite interactions incorporating Allee effects and horizontal and/or vertical transmission, under the assumption that infectious individuals can experience pathogen-induced reductions in reproductive ability; a susceptible-infectious-susceptible (SIS) model with quarantined individuals and Beddington–DeAngelis incidence (Chen and Zhao 2020); a susceptible-exposed-infectious-removed (SEIR) model (Li et al. 2001); a susceptible-exposed-infectious-removed-susceptible (SEIRS) model (Gou and Wang 2007); and susceptible-infectious-removed (SIR) models with pulse vaccination (D’Onofrio 2005; Gao et al. 2007; Lu et al. 2002), and with nonlinear incidence rate, treatment, and vaccination for newborns of susceptible and recovered individuals (Hu et al. 2012), among others. The model of Naji and Hussien (2016) considers two strains with infections of SIRS type and of SIS type that spread through both horizontal and vertical transmission in the host population; see also Ref. Bichara et al. (2014), where the authors consider SIS and SIR models with n different pathogen strains and vertical transmission, including the possibility of infants with passive immunity in the framework of the SIR model. In the setting of plant–virus epidemiology, we refer the reader to the paper by Jeger et al. (1998), where an SEIR-type epidemic for the plant host is linked to an susceptible-exposed-infectious (SEI) model with vertical transmission for the insect vector population. The model of Jeger et al. (1998) describes the interaction of the virus with the vector and possible control options, including the removal and destruction of diseased plants and reduction of the vector-population size, for example, by insecticide or vegetation management. A non-linear model is introduced by Naresh et al. (2006) to study the transmission of HIV/AIDS into a population with varying size with vertical transmission and other demographic and epidemiological aspects.

In an attempt to investigate how the unpredictability of person-to-person contact affects the spread of a disease, Kiouach and Sabbar (2018) assume that the contact rate is perturbed by Gaussian white noise and establish sufficient conditions for persistence and extinction of the disease in a stochastic SIRS model with vertical transmission and transfer from infectious to susceptible compartments. In the setting of the SIR model with vertical transmission and media coverage, stochastic perturbations are introduced by Wang et al. (2020), who prove existence and uniqueness of the positive solution, and extinction and persistence in mean. In analyzing random perturbations in the SIS model with vertical transmission and immigration of susceptible individuals, and emigration of susceptible and infectious individuals, Zhang et al. (2018) use suitably defined Lyapunov functions to derive an ergodic stationary distribution, and conditions for the extinction and persistence of the pathogen.

In this paper, we focus on a Markov chain model to describe the spread of epidemics of SIS type through both horizontal and vertical transmission. Accordingly, the underlying Markov chain is seen as a competition process (Iglehart 1964; Reuter 1961) on the positive orthant $\mathbb {N}_0\times \mathbb {N}_0$, where the point (i, s) represents the size of the subpopulations of infectious and susceptible individuals, and the one-step transitions from (i, s) are allowed only to a neighboring point $(i',s')\in \{(i-1,s),(i-1,s+1),(i,s-1),(i,s+1),(i+1,s-1),(i+1,s)\}$; as a result, this process can be thought of as the natural generalization of the uni-variate birth–death process arising from the standard SIS epidemic model. Specifically, the interest is in characterizing the probabilistic behavior of the exact reproduction number $\mathcal{R}_{\mathrm{{exact}},0}$ (Artalejo and Lopez-Herrero 2013; Economou et al. 2015, Section 3.3), which is decomposed here into two random contributions that record infectious contacts between individuals and infections of newborns with infectious parents. Our methodology is based on the use of finite quasi-birth–death (QBD) processes and related algorithms to evaluate their stationary vector (Akar et al. 2000; De Nitto Personè and Grassi 1996; Gaver et al. 1984, Section 2), first-passage times and sojourn times (Gaver et al. 1984, Sections 3–4; Gómez-Corral et al. 2020), and perturbation properties (Gómez-Corral and López-García 2018).

In the deterministic setting, the basic reproduction number $R_0$ is by far the most widely used index in mathematical epidemiology (Li et al. 2011; Roberts 2007), mainly due to the simplicity of its definition and the fact that it is usually a threshold value establishing that a disease persists only if $R_0>1$ (van den Driessche and Watmough 2002). It is also important to remark its role in the validity of the final size equation and the uniqueness of its solution (Ma and Earn 2006), and the control effort required to eradicate the pathogen, among other aspects. When a stochastic approach is adopted, it is well known (Artalejo and Lopez-Herrero 2013) that the value of $R_0$ overestimates the reproductive potential of a pathogen, especially when the involved community has a small size. An appropriate alternative to $R_0$—in particular, for Markov chain models in epidemics—is the exact reproduction number $\mathcal{R}_{\mathrm{{exact}},0}$, which is introduced in Artalejo and Lopez-Herrero (2013) by translating the definition of $R_0$ into a random variable. Among the most relevant features of $\mathcal{R}_{\mathrm{{exact}},0}$, compared to $R_0$, are that $\mathcal{R}_{\mathrm{{exact}},0}$ eliminates the effect of repeated infectious contacts; it is not necessarily defined at the time of invasion, but at any later time; and it provides a more accurate index to quantify the transmission of a disease. However, the analytical treatment of $\mathcal{R}_{\mathrm{{exact}},0}$ requires knowing a priori the underlying parameters of the epidemic model. In computing the mass function of $\mathcal{R}_{\mathrm{{exact}},0}$ and its moments, the most intensive effort lies in the inversion of matrices and related memory requirements, whence the numerical solution of $\mathcal{R}_{\mathrm{{exact}},0}$ may experience instability with a large population size. These features and limitations show the adequacy of $\mathcal{R}_{\mathrm{{exact}},0}$ to quantify, in a more realistic way than $R_0$, the transmission potential of a disease in small communities sharing confined spaces, such as families and intensive care units (Economou et al. 2015), a mini-community design to assert the indirect effect of vaccination (Fernández-Peralta and Gómez-Corral 2021), and hospital ward (Chalub et al. 2023), among others.

The organization of the paper is as follows. In Sect. 2, we first give the mathematical description of the SIS epidemic model with vertical and horizontal transmission, and then introduce a bi-variate competition process to describe the number of susceptible and infectious individuals at time t. In Sect. 3, we characterize the joint probability law of the exact number $\mathcal{R}_{\mathrm{{exact}},0}^H$ of secondary infections by contact between susceptible individuals and a (predetermined) initially infectious individual, and the number $\mathcal{R}_{\mathrm{{exact}},0}^V$ of infectious newborns with the initially infectious individual as parent. Based on the tridiagonal-by-blocks form of the underlying q-matrix, we derive an iterative procedure for computing the joint probability law of $(\mathcal{R}_{\mathrm{{exact}},0}^V,\mathcal{R}_{\mathrm{{exact}},0}^H)$ by using first-step analysis and block-Gaussian elimination. In Sect. 4, our analytical results are exemplified with some numerical experiments. A brief discussion is finally presented in Sect. 5.

2 The mathematical model description

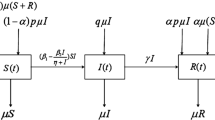
Consider a closed and homogeneously well-mixed population of N(t) individuals that can be partitioned into two compartments or subpopulations of susceptible (S), and infectious (I) individuals, with densities, respectively, denoted by S(t) and I(t) at time t; see Fig. 1. A susceptible individual is assumed to be healthy, but can become infectious by contact with an infectious individual according to a Poisson process of rate $\mu >0$ in such a way that it should remain infectious during an exponentially distributed time of parameter $\gamma _N>0$. The natural recovery period (with mean length $\gamma _N^{-1}$) of an infectious individual can be effectively shortened due to health-care actions with treatment function $\eta (i)=\gamma _T\min \{i,C\}$, where $\gamma _T\ge 0$ denotes the treatment rate,¹ and C is the threshold at which the health-care system reaches its maximal capacity. This means that treatment increases linearly with the number i of infectious individuals before reaching the maximum resources and is constant afterward.

Fig. 1

Diagram of transitions between compartments in the SIS epidemic model with vertical and horizontal transmission

The model incorporates the birth and the death of individuals, and the vertical transmission of the disease. Therefore, the total population size $N(t)=S(t)+I(t)$ is not constant, but it is assumed that $N(t)\in \{0,1,...,M\}$ in the sense that limited resources in the ecosystem prevent population growth above a certain maximum size $M<\infty$. An infectious individual gives birth to either a susceptible individual with rate $p\beta _I$ or an infectious one with rate $(1-p)\beta _I$, where $\beta _I>0$ is the birth rate and $p\in [0,1]$ represents the proportion of the offspring of infectious parents that are susceptible individuals. Only susceptible individuals are assumed to be born with susceptible parents, which occurs at rate $\beta _S>0$. There is a natural death rate $\alpha _S>0$ for susceptible individuals, and infectious individuals face death due to either natural causes or the disease with joint death rate $\alpha _I>0$. The underlying processes governing infectious contacts and infections of newborns, recovery times, and birth and death events are assumed to be mutually independent.

Fig. 2

Transitions from any state $(i,s)\in \mathcal{S}{\setminus } l(0)$

The birth rates $\beta _S$ and $\beta _I$ are not necessarily assumed equal, which will allow us to analyze the influence of birth control measures, for example, on the subpopulation of infectious individuals, taking decreasing values of $\beta _I$, for a fixed value of $\beta _S$. The choice $\alpha _I=\alpha '_I+\alpha ''_I$ allows us to distinguish between the death of infectious individuals due to natural causes or due to the disease, with $\alpha _S=\alpha '_I$ if the death of an individual does not depend on the compartment and, consequently, $\alpha _I>\alpha _S$ when the disease can cause the death of infectious individuals.

We note that the model coincides with the SIS epidemic model with demography if $p=1$, which results in a uni-variate birth–death process on the state space $\{0,...,M\}$. The standard SIS epidemic model (Allen 2003, Section 7.3.2) is derived when the births and deaths are ignored with the selection $\alpha _S=\alpha _I=\beta _S=\beta _I=0$.

The above Markovian formulation yields a bi-variate competition process $\mathcal{X}=\{(I(t),S(t)): t\ge 0\}$ (Reuter 1961) taking values in the finite reducible state space

$$\begin{aligned} \mathcal{S}= & {} \{(i,s)\in \mathbb {N}_0\times \mathbb {N}_0: i+s\in \{0,...,M\}\}, \end{aligned}$$

whose non-vanishing infinitesimal transition rates (Fig. 2) from state (i, s) to state $(i',s')$ are given by

$$\begin{aligned} q_{(i,s),(i',s')}= & {} \left\{ \begin{array}{ll} \alpha _I i, &{} \hbox {if }(i',s')=(i-1,s), \\ \alpha _S s, &{} \hbox {if }(i',s')=(i,s-1), \\ \gamma _N i+\eta (i), &{} \hbox {if }(i',s')=(i-1,s+1), \\ \mu is, &{} \hbox {if }(i',s')=(i+1,s-1), \\ (1-p) \beta _I i, &{} \hbox {if }(i',s')=(i+1,s), \\ \beta _S s+p \beta _I i, &{} \hbox {if }(i',s')=(i,s+1), \end{array}\right. \end{aligned}$$

for states $(i,s), (i',s')\in \mathcal{S}$ with $(i',s')\ne (i,s)$. These rates are related, respectively, to the death of an infectious individual, the death of a susceptible individual, the recovery of an infectious individual, an infectious contact between the compartments of susceptible and infectious individuals, the birth of an infectious individual, and the birth of a susceptible individual. We also consider the value $q_{(i,s),(i,s)}=-q_{(i,s)}$, where $q_{(i,s)}$ is the rate of the sojourn time of process $\mathcal{X}$ in state (i, s); that is

$$\begin{aligned} q_{(i,s)}= & {} (\alpha _I+(1-\delta _{i+s,M})\beta _I+\gamma _N)i+(\alpha _S+(1-\delta _{i+s,M})\beta _S)s+\eta (i)+\mu is, \end{aligned}$$

for $(i,j)\in \mathcal{S}$, where $\delta _{a,b}$ represents the Kronecker delta. Note that the state (0, 0) is absorbing, and $\mathcal{X}$ evolves as a birth–death process on the class $\{(0,s): s\in \{0,...,M\}\}$ of infection-free states, with birth parameters $\{\beta _S s: s\in \{1,...,M-1\}\}$ and death parameters $\{\alpha _S s: s\in \{1,...,M\}\}$.

For later use, we use a lexicographical ordering of states and decompose the state space $\mathcal{S}$ by levels into $\cup _{i=0}^M l(i)$, where the ith level is defined as the subset

$$\begin{aligned} l(i)= & {} \{(i,s): s\in \{0,...,M-i\}\}, \end{aligned}$$

for $i\in \{0,...,M\}$. This labeling of states allows to reformulate the process $\mathcal{X}$ as a finite QBD process (Gaver et al. 1984; Gómez-Corral et al. 2020) with q-matrix

$$\begin{aligned} Q= & {} \left( \begin{array}{ccccc} Q_{0,0} &{} Q_{0,1} &{} &{} &{} \\ Q_{1,0} &{} Q_{1,1} &{} Q_{1,2} &{} &{} \\ &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} Q_{M-1,M-2} &{} Q_{M-1,M-1} &{} Q_{M-1,M} \\ &{} &{} &{} Q_{M,M-1} &{} Q_{M,M} \end{array}\right) , \end{aligned}$$

(1)

where the sub-matrices $Q_{i,i'}$ are seen to be of dimension $(M-i+1)\times (M-i'+1)$, for integers $i'\in \{\max \{0,i-1\},i,\min \{i+1,M\}\}$ and $i\in \{0,...,M\}$. In particular, the non-vanishing entries of $Q_{i,i-1}$ are related to the removal of an infectious individual due to its recovery or death; the diagonal entries of $Q_{i,i}$ are given by $-q_{(i,s)}$ for states (i, s) with $s\in \{0,...,M-i\}$, whereas the non-vanishing off-diagonal entries of $Q_{i,i}$ are linked to the birth and the death of a susceptible individual; and the non-vanishing entries of $Q_{i,i+1}$ are associated with new infections due to the horizontal and the vertical transmission of the disease. Expressions for these sub-matrices are summarized in Appendix A.

An immediate consequence of the resource-limited condition (i.e., $N(t)\in \{0,1,...,M\}$ with $M<\infty$) is the fact that the length of an outbreak is a non-defective random variable. This means that, from any initial state $(i,s)\in \mathcal{S}$, process $\mathcal{X}$ will reach the class of infection-free states almost surely. Indeed, the mean time to the first entrance into the class of infection-free states is finite, regardless to the initial state $(i,s)\in \mathcal{S}$.

Remark 1

The dynamics of process $\mathcal{X}$ in the case $M=\infty$ is related to a QBD process with infinitely many states, for which further work must be done to study the occurrence of the first passage to the class $\{(0,s): s\in \mathbb {N}_0\}$ of infection-free states. While it is outside the scope of this work, we briefly point out here that, by Gómez-Corral et al. (2023, Theorem 1), the resulting QBD process with infinitely many states is always regular, whence inequalities $\max \{\beta _I,\beta _S\}<\min \{\alpha _I,\alpha _S\}$, and $\min \{\beta _I,\beta _S\}\le \alpha _I+\alpha _S$ if $\max \{\beta _I,\beta _S\}=\min \{\alpha _I,\alpha _S\}$, can be seen as sufficient for the first passage to the subset $\{(0,s): s\in \mathbb {N}_0\}$ of disease-free states to occur with certainty, and in a finite mean time, from any initial state $(i,s)\in \mathbb {N}_0\times \mathbb {N}_0$; see, e.g., Gómez-Corral et al. (2023, Theorem 3) and Reuter (1961, Theorems 2-3).

3 An exact measure of the disease spread

Let us consider an invasion time (i.e., $I(0)=1$ and $S(0)=s_0$ with $s_0\in \{0,...,M-1\}$) and define the exact number $\mathcal{R}_{\mathrm{{exact}},0}$ of secondary infections generated by the initially infectious individual before it recovers or dies (Artalejo and Lopez-Herrero 2013), which should occur at a certain random time $\tau$. Specifically, time $\tau$ is an exponentially distributed random variable with mean value $(\alpha _I+\gamma _N+(1-\delta _{C,0})\gamma _T)^{-1}$. The most remarkable feature of process $\mathcal{X}$ is the vertical and the horizontal transmission of the disease, whence we decompose $\mathcal{R}_{\mathrm{{exact}},0}$ into two random contributions $\mathcal{R}_{\mathrm{{exact}},0}^V$ and $\mathcal{R}_{\mathrm{{exact}},0}^H$ according to the fact that infections are linked, respectively, to infectious newborns with the initially infectious individual as parent and to infectious contacts between the compartment of susceptible individuals and the initially infectious individual, occurring both events before time $\tau$. To prevent transmission of the disease at the initiation of an outbreak, the decomposition of $\mathcal{R}_{\mathrm{{exact}},0}$ into $\mathcal{R}_{\mathrm{{exact}},0}^V$ and $\mathcal{R}_{\mathrm{{exact}},0}^H$ is suited to prioritize birth control measures, especially from infectious parents, over contingency measures against person-to-person contact—e.g., social distancing, and handwashing—or vice versa, and to analyze the subsequent consequences that limitations on these prophylactic interventions could cause on the relationships between individuals and even the survival of the population. For instance, when the magnitude of $\mathcal{R}_{\mathrm{{exact}},0}$—in terms of sample paths—or its expectation is greater than one, the values of $\mathcal{R}_{\mathrm{{exact}},0}^V$, and of $\mathcal{R}_{\mathrm{{exact}},0}^H$ will make it possible to quantify, in a differentiated way, the effects of specific interventions on the dynamics of the population. The probability $1-p$ of infectious offspring (Table 1) is closely related to the disease, whence no action can be taken on the value of $1-p$ in the framework of the above-mentioned interventions.

Table 1 Prevalence estimates of congenitally acquired disease, measured in terms of cases per 100 live births, for some TORCH diseases

Let $I^*$ denote the status of the initially infectious individual at time $\tau +0$ (i.e., immediately after time $\tau$). In particular, $I^*=D$ if the initially infectious individual dies before recovering; $I^*=N$ if it recovers due to natural causes; and $I^*=T$ if it recovers due to treatment. The aim is to characterize the joint probability law of $(\mathcal{R}_{\mathrm{{exact}},0}^V,\mathcal{R}_{\mathrm{{exact}},0}^H)$ by evaluating the conditional probabilities

$$\begin{aligned} P_{(1,s_0)}(i^*,r_V,r_H)= & {} P\left( \left. I^*=i^*, \mathcal{R}^V_{\mathrm{{exact}},0}=r_V, \mathcal{R}^H_{\mathrm{{exact}},0}=r_H \right| (I(0),S(0))=(1,s_0)\right) , \end{aligned}$$

for $i^*\in \{D,N,T\}$ and pairs $(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0$.

It is clear that $\mathcal{R}_{\mathrm{{exact}},0}^V$ and $\mathcal{R}_{\mathrm{{exact}},0}^H$ are inherently linked to events taking place during the time interval $[0,\tau )$ and, consequently, the conditional probabilities $P_{(1,s_0)}(i^*,r_V,r_H)$, for status $i^*\in \{D,N,T\}$ and pairs $(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0$, satisfy the equalities

$$\begin{aligned} \frac{\alpha _I}{\alpha _I+\gamma _N+(1-\delta _{C,0})\gamma _T}= & {} \sum _{(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0}P_{(1,s_0)}(D,r_V,r_H), \end{aligned}$$

(2)

$$\begin{aligned} \frac{\gamma _N}{\alpha _I+\gamma _N+(1-\delta _{C,0})\gamma _T}= & {} \sum _{(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0}P_{(1,s_0)}(N,r_V,r_H), \end{aligned}$$

(3)

$$\begin{aligned} \frac{(1-\delta _{C,0})\gamma _T}{\alpha _I+\gamma _N+(1-\delta _{C,0})\gamma _T}= & {} \sum _{(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0}P_{(1,s_0)}(T,r_V,r_H). \end{aligned}$$

(4)

These equalities are derived by observing that the left-hand side of (2)–(4) corresponds to the marginal mass function $\{P(I^*=i^* | (I(0),S(0))=(1,s_0)): i^*\in \{D,N,T\}\}$.

In evaluating the probability $P_{(1,s_0)}(i^*,r_V,r_H)$, for a predetermined status $i^*\in \{D,N,T\}$ and a fixed pair $(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0$, we first define, for states $(i,s)\in \mathcal{S}\setminus l(0)$ and any time $t<\tau$, the conditional probability $P_{(i,s)}(i^*,r_V',r_H')$ that the initially infectious individual gives birth to $r_V'$ infectious offspring and generates $r_H'$ infectious contacts with susceptibles during the residual interval $[t,\tau )$, and its status at time $\tau +0$ is $i^*$, given that (i, s) is the current state of $\mathcal{X}$ and the infectious period of the initially infectious individual is in process at time t. We then derive an iterative procedure that, starting from the families of conditional probabilities $\{P_{(i,s)}(i^*,0,0): (i,s)\in \mathcal{S}{\setminus } l(0)\}$, $\{P_{(i,s)}(i^*,r_V',0): r_V'\in \{1,...,r_V\}, (i,s)\in \mathcal{S}{\setminus } l(0)\}$ and $\{P_{(i,s)}(i^*,0,r_H'): r_H'\in \{1,...,r_H\}, (i,s)\in \mathcal{S}{\setminus } l(0)\}$, evaluates the conditional probabilities in $\{P_{(i,s)}(i^*,r_V,r_H): (i,s)\in \mathcal{S}{\setminus } l(0)\}$ in terms of $\{P_{(i,s)}(i^*,r_V-1,r_H): (i,s)\in \mathcal{S}{\setminus } l(0)\}$ and $\{P_{(i,s)}(i^*,r_V,r_H-1): (i,s)\in \mathcal{S}{\setminus } l(0)\}$, for every status $i^*\in \{D,N,T\}$ and pair $(r_V,r_H)\in \mathbb {N}\times \mathbb {N}$; see Fig. 3.

Fig. 3

An iterative procedure to compute the family of conditional probabilities $\{P_{(i,s)}(i^*,r_V,r_H): (i,s)\in \mathcal{S}{\setminus } l(0)\}$, for a predetermined status $i^*$ and a fixed pair $(r_V,r_H)$, in the special case $r_V=r_H+2$

3.1 A first-step analysis of process $\mathcal{X}$

We can derive a system of linear equations for the conditional probabilities $P_{(i,s)}(i^*,r_V,r_H)$, for $(i,s)\in \mathcal{S}{\setminus } l(0)$, $i^*\in \{D,N,T\}$ and $(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0$, using the first-step analysis. To be concrete, it is found that

$$\begin{aligned} P_{(i,s)}(D,0,0)= & {} \frac{\alpha _I}{q_{(i,s)}}+(1-\delta _{i,1})\frac{\alpha _I (i-1)}{q_{(i,s)}}P_{(i-1,s)}(D,0,0) \nonumber \\{} & {} +(1-\delta _{i,1})\frac{\gamma _N (i-1)+(1-\delta _{C,0})\gamma _T\min \{i-1,C-1\}}{q_{(i,s)}} P_{(i-1,s+1)}(D,0,0) \nonumber \\{} & {} +(1-\delta _{s,0})\frac{\alpha _S s}{q_{(i,s)}}P_{(i,s-1)}(D,0,0) \nonumber \\{} & {} +(1-\delta _{i,M})(1-\delta _{s,M-i})\frac{\beta _S s+p\beta _I i}{q_{(i,s)}}P_{(i,s+1)}(D,0,0) \nonumber \\{} & {} +(1-\delta _{i,1})(1-\delta _{s,0})\frac{\mu (i-1)s}{q_{(i,s)}}P_{(i+1,s-1)}(D,0,0) \nonumber \\{} & {} +(1-\delta _{i,1})(1-\delta _{i,M})\frac{(1-p)\beta _I (i-1)}{q_{(i,s)}}P_{(i+1,s)}(D,0,0), \end{aligned}$$

(5)

for states $(i,j)\in \mathcal{S}\setminus l(0)$. Similarly, the conditional probabilities $P_{(i,s)}(N,0,0)$ and $P_{(i,s)}(T,0,0)$, for $(i,j)\in \mathcal{S}\setminus l(0)$, are seen to satisfy (5) with the term $q^{-1}_{(i,s)}\alpha _I$ replaced by $q^{-1}_{(i,s)}\gamma _N$ and $q^{-1}_{(i,s)}(1-\delta _{C,0})\gamma _T$, respectively. For any status $i^*\in \{D,N,T\}$ and pairs $(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0{\setminus } \{(0,0)\}$, it is also seen that

$$\begin{aligned} P_{(i,s)}(i^*,r_V,r_H)= & {} (1-\delta _{i,1})\frac{\alpha _I (i-1)}{q_{(i,s)}}P_{(i-1,s)}(i^*,r_V,r_H) \nonumber \\{} & {} +(1-\delta _{i,1})\frac{\gamma _N (i-1)+(1-\delta _{C,0})\gamma _T\min \{i-1,C-1\}}{q_{(i,s)}} P_{(i-1,s+1)}(i^*,r_V,r_H) \nonumber \\{} & {} +(1-\delta _{s,0})\frac{\alpha _S s}{q_{(i,s)}}P_{(i,s-1)}(i^*,r_V,r_H) \nonumber \\{} & {} +(1-\delta _{i,M})(1-\delta _{s,M-i})\frac{\beta _S s+p\beta _I i}{q_{(i,s)}}P_{(i,s+1)}(i^*,r_V,r_H) \nonumber \\{} & {} +(1-\delta _{i,M})(1-\delta _{s,0})\frac{\mu s}{q_{(i,s)}}P_{(i+1,s-1)}(i^*,r_V,r_H-1) \nonumber \\{} & {} +(1-\delta _{i,1})(1-\delta _{s,0})\frac{\mu (i-1)s}{q_{(i,s)}}P_{(i+1,s-1)}(i^*,r_V,r_H) \nonumber \\{} & {} +(1-\delta _{i,M})\frac{(1-p)\beta _I}{q_{(i,s)}}P_{(i+1,s)}(i^*,r_V-1,r_H) \nonumber \\{} & {} +(1-\delta _{i,1})(1-\delta _{i,M})\frac{(1-p)\beta _I (i-1)}{q_{(i,s)}}P_{(i+1,s)}(i^*,r_V,r_H), \end{aligned}$$

(6)

for states $(i,j)\in \mathcal{S}\setminus l(0)$.

Equations (5) and (6) can be easily written in matrix form using column vectors $p_i (i^*,r_V,r_H)$, for $i\in \{1,...,M\}$, with $(1+s)$th entry $P_{(i,s)}(i^*,r_V,r_H)$ for integers $s\in \{0,...,M-i\}$, and a suitable decomposition of sub-matrices $Q_{i,i-1}$ and $Q_{i,i+1}$. Specifically, the rate sub-matrix $Q_{i,i-1}$ is written in terms of

$$\begin{aligned} Q_{i,i-1}= & {} Q^D_{i,i-1}+Q^N_{i,i-1}+Q^T_{i,i-1}+Q^*_{i,i-1},\quad i\in \{1,...,M\}, \end{aligned}$$

where $Q^D_{i,i-1}$, $Q^N_{i,i-1}$, and $Q^T_{i,i-1}$ consist of the infinitesimal transition rates from states (i, s) with $s\in \{0,...,M-i\}$ associated, respectively, with the death, the natural recovery, and the recovery due to treatment of the initially infectious individual, and $Q^*_{i,i-1}$ is related to transitions associated with the death and recovery of the remaining $i-1$ infectious individuals. The rate sub-matrix $Q_{i,i+1}$ is written in a similar manner as follows:

$$\begin{aligned} Q_{i,i+1}= & {} Q^V_{i,i+1}+Q^H_{i,i+1}+Q^*_{i,i+1},\quad i\in \{1,...,M-1\}, \end{aligned}$$

where $Q^V_{i,i+1}$ and $Q^H_{i,i+1}$ record the infinitesimal transition rates associated, respectively, with the vertical and the horizontal secondary infections generated by the initially infectious individual before time $\tau$, and $Q^*_{i,i+1}$ records the infinitesimal transition rates associated with secondary infections generated by the remaining $i-1$ infectious individuals.

In matrix form, Eqs. (5) and (6) are given by

$$\begin{aligned} -Q_{i,i}p_i(i^*,r_V,r_H)= & {} \delta _{(r_V,r_H),(0,0)}Q^{i^*}_{i,i-1}1_{M-i+2} \nonumber \\{} & {} \quad +(1-\delta _{(r_V,r_H),(0,0)})(1-\delta _{i,M}) \nonumber \\{} & {} \quad \times \Big ((1-\delta _{r_V,0})Q^V_{i,i+1}p_{i+1}(i^*,r_V-1,r_H)\nonumber \\{} & {} \quad +(1-\delta _{r_H,0})Q^H_{i,i+1}p_{i+1}(i^*,r_V,r_H-1)\Big ) \nonumber \\{} & {} \quad +(1-\delta _{i,1})Q^*_{i,i-1}p_{i-1}(i^*,r_V,r_H) \nonumber \\{} & {} \quad +(1-\delta _{i,1})(1-\delta _{i,M})Q^*_{i,i+1}p_{i+1}(i^*,r_V,r_H), \end{aligned}$$

(7)

for $i^*\in \{D,N,T\}$ and $i\in \{1,...,M\}$, where $1_a$ is the column vector of order a of ones; note that $Q^{i^*}_{i,i-1}1_{M-i+2}=\alpha _I 1_{M-i+1}$ if $i^*=D$, $\gamma _N 1_{M-i+1}$ if $i^*=N$, and $\gamma _T 1_{M-i+1}$ if $i^*=T$.

3.2 A general iterative scheme

It is important to note that, for a fixed pair $(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0$, we do not need solve (7) in the unknown vectors $p_i(D,r_V,r_H)$, $p_i(N,r_V,r_H)$ and $p_i(T,r_V,r_H)$, with $i\in \{1,...,M\}$, simultaneously, but only the matrix equations

$$\begin{aligned} -Q_{i,i}p_i(i^*,r_V,r_H)= & {} s_i(i^*,r_V,r_H)+(1-\delta _{i,1})Q^*_{i,i-1}p_{i-1}(i^*,r_V,r_H)\nonumber \\{} & {} +(1-\delta _{i,1})(1-\delta _{i,M})Q^*_{i,i+1}p_{i+1}(i^*,r_V,r_H), \end{aligned}$$

(8)

for $i\in \{1,...,M\}$, in the unknown vectors $p_i(i^*,r_V,r_H)$, for the predetermined selection $(i^*,r_V,r_H)$, with $s_i(i^*,r_V,r_H)=Q^{i^*}_{i,i-1}1_{M-i+2}$ if $(r_V,r_H)=(0,0)$, and $(1-\delta _{i,M})\left( Q^V_{i,i+1}p_{i+1}(i^*,r_V-1,r_H)+Q^H_{i,i+1}p_{i+1}(i^*,r_V,r_H-1)\right)$ if $(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0\setminus \{(0,0)\}$. Therefore, the application of block-Gaussian elimination to solve (8) results in

$$\begin{aligned} p_1(i^*,r_V,r_H)= & {} -Q^{-1}_{1,1}s_1(i^*,r_V,r_H), \end{aligned}$$

(9)

$$\begin{aligned} p_i(i^*,r_V,r_H)= & {} h_i(i^*,r_V,r_H)+H_ip_{i-1}(i^*,r_V,r_H),\quad i\in \{2,...,M\}, \end{aligned}$$

(10)

where $H_i=(-Q_{i,i}-(1-\delta _{i,M})Q^*_{i,i+1}H_{i+1})^{-1}Q^*_{i,i-1}$ and

$$\begin{aligned} h_i(i^*,r_V,r_H)= & {} \left( -Q_{i,i}-(1-\delta _{i,M})Q^*_{i,i+1}H_{i+1}\right) ^{-1} \\{} & {} \times \left( s_i(i^*,r_V,r_H)+(1-\delta _{i,M})Q^*_{i,i+1}h_{i+1}(i^*,r_V,r_H)\right) , \end{aligned}$$

for $i\in \{2,...,M\}$.

As a last remark, we note that, for a predetermined status $i^*\in \{D,N,T\}$ and a fixed pair $(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0$, Algorithm 1 evaluates the solution of the system of linear equations (5) and (6) using Algorithm 2 to derive the column vectors $\{p_i(i^*,r'_V,r'_H): i\in \{1,...,M\}\}$, for every pair $(r'_V,r'_H)\in \{0,\ldots ,r_V\} \times \{0,\ldots ,r_H\}$.

Algorithm 1

Computation of the column vectors $\{p_i(i^*,r'_V,r'_H): i \in \{1,\ldots ,M\},$ $(r'_V,r'_H)\in \{0,\ldots ,r_V\} \times \{0,\ldots ,r_H\}\}$, for a predetermined status $i^*\in \{D,N,T\}$ and a selected pair $(r_V,r_H)\in \mathbb {N}_0\times \mathbb {N}_0$.

Step 1: $j:=0$;

     $w:=\min \{r_V,r_H\}$.

Step 2: While $j\le w$, do

        $r'_V:=j$;

        $r'_H:=j$;

        while $r'_H\le r_H$, do

               compute $\{p_i(i^*,r'_V,r'_H): i \in \{1,\ldots ,M\}\}$ from Algorithm 2;

               $r'_H:=r'_H+1$;

        $r'_H:=j$;

        $r'_V:=j+1$;

        while $r'_V\le r_V$, do

               compute $\{p_i(i^*,r'_V,r'_H): i \in \{1,\ldots ,M\}\}$ from Algorithm 2;

               $r'_V:=r'_V+1$;

        $j:=j+1$.

Algorithm 2

Computation of the column vectors $\{p_i(i^*,r'_V,r'_H): i \in \{1,\ldots ,M\}\}$, for a predetermined status $i^*\in \{D,N,T\}$ and a fixed pair $(r'_V,r'_H)\in \{0,\ldots ,r_V\} \times \{0,\ldots ,r_H\}$.

Step 1: $i:=0$;

     while $i\le M-1$, do

        $i:=i+1$;

        $s_i(i^*,r'_V,r'_H):= \delta _{(r'_V,r'_H),(0,0)}Q^{i^*}_{i,i-1}1_{M-i+2}+(1-\delta _{(r'_V,r'_H),(0,0)})(1-\delta _{i,M})$

               $\times \Big (Q^V_{i,i+i}p_{i+1}(i^*,r'_V-1,r'_H)+Q^H_{i,i+i}p_{i+1}(i^*,r'_V,r'_H-1)\Big )$.

Step 2: While $i\ge 2$, do

        $H_i:=(-Q_{i,i}-(1-\delta _{i,M})Q^*_{i,i+1}H_{i+1})^{-1}Q^*_{i,i-1}$;

        $h_i(i^*,r'_V,r'_H):=(-Q_{i,i}-(1-\delta _{i,M})Q^*_{i,i+1}H_{i+1})^{-1}\Big (s_i(i^*,r'_V,r'_H)$

               $+(1-\delta _{i,M})Q^*_{i,i+1}h_{i+1}(i^*,r'_V,r'_H)\Big )$;

        $i:=i-1$.

Step 3: $p_i(i^*,r'_V,r'_H)=-Q^{-1}_{i,i}s_i(i^*,r'_V,r'_H)$;

     while $i\le M-1$, do

        $i:=i+1$;

        $p_i(i^*,r'_V,r'_H):=h_i(i^*,r'_V,r'_H)+H_i p_{i-1}(i^*,r'_V,r'_H)$.

4 Numerical work and discussion

Fig. 4

The mass function $\{P(\mathcal{R}_{\mathrm{{exact}},0}=r | (I(0),S(0))=(1,s_0)): r\in \{0,...,18\}\}$ versus the birth rate $\beta _I$, for Scenarios 1 ($\mu =1.0$), 2 ($\mu =2.5$), and 3 ($\mu =5.0$), at an invasion time with $s_0=20$

In this section, we present selected numerical results to explore the influence of the contact rate $\mu$ and the birth rate $\beta _I$ on the horizontal and vertical transmission of the disease during the early stages of an epidemic. We consider a population with maximum size $M=100$, which consists initially of one infective and twenty susceptible individuals. In our experiments, three scenarios are defined in terms of the contact rate $\mu$ in such a way that less and more frequent infectious contacts occur in Scenarios 1 and 3, respectively, and are related to the values $\mu =1.0$ and $\mu =5.0$, and Scenario 2 corresponds to $\mu =2.5$. Birth and death rates are related to each other through the relationships $\beta _S=2\beta _I$, $\alpha _S=\beta _S$, and $\alpha _I=2\alpha _S$, for values $\beta _I\in \{1.25, 2.5, 3.75, 5.0, 10.0\}$. Therefore, the subpopulation of susceptible individuals is assumed to behave stable over time in terms of the underlying birth and death rates; in contrast, births among infectious individuals are expected to occur less frequently than births among susceptibles, and infectious individuals are more likely to die than susceptible ones. The value $p=0.2$ is assumed, so that $80\%$ of newborns from infectious parents are expected to be infective. It is assumed that an infectious individual recovers from natural causes, on average, in 1.0 units of time; i.e., $\mu _N^{-1}=1.0$. The treatment function is defined from the rate $\mu _T=1.5$ and the threshold $C=10$.

In Figs. 4, 5 and 6, the marginal mass function of $\mathcal{R}_{\mathrm{{exact}},0}$, the joint mass function of $(\mathcal{R}_{\mathrm{{exact}},0}^V,\mathcal{R}_{\mathrm{{exact}},0}^H)$ and the marginal mass functions of $\mathcal{R}_{\mathrm{{exact}},0}^V$ and $\mathcal{R}_{\mathrm{{exact}},0}^H$, respectively, are plotted as a function of the contact rate $\mu$ and the birth rate $\beta _I$. The specific intervals on the ox axis in Figs. 4 and 6, and on the axes ox and oy in Fig. 5 are selected to accumulate at least $99\%$ of the probability of the corresponding probability distribution function. It is observed that, as intuition tells us, the higher the rate $\mu$ of contact between individuals, the more easily the pathogen spreads from the initially infectious individual to susceptible individuals at an early stage of the epidemic. This behavior is related to Fig. 4, where the marginal mass function of $\mathcal{R}_{\mathrm{{exact}},0}$ is seen to be more concentrated over the value $r=0$ and values close to it for small values of the contact rate $\mu$—as seen in Scenario 1, regardless of $\beta _I$-, while it becomes more concentrated over higher values of r—for example, $r=4$ in Scenario 3 for $\beta _I=1.25$—as $\mu$ increases. Unlike the behavior of the probability law of $\mathcal{R}_{\mathrm{{exact}},0}$ with respect to $\mu$, increasing values of the birth rate $\beta _I$ do not lead to further spread of the pathogen in our numerical experiments; for instance, the mass function of $\mathcal{R}_{\mathrm{{exact}},0}$ in Scenario 1 becomes more concentrated on the value $r=0$ and its surroundings as $\beta _I$ increases, contrary to what was expected. This apparently contradictory behavior can be explained by taking into account that births leading to infectious progeny from the initially infectious individual—that is, contributing to the value of $\mathcal{R}_{\mathrm{{exact}},0}$—are recorded during the time interval $[0,\tau )$ with expected length $(\alpha _I+\gamma _N+\gamma _T)^{-1}$, where $\alpha _I=4\beta _I$. Thus, the length of this time interval is likely to decrease as $\beta _I$ increases and, consequently, fewer births of infectious individuals from the initially infectious individual contribute to $\mathcal{R}_{\mathrm{{exact}},0}$, even though the birth rate $\beta _I$ is increasing. This makes the spread of the pathogen from the initially infectious individual to its progeny less likely with increasing values of $\beta _I$.

Fig. 5

The joint probabilities $\{P(\mathcal{R}^H_{\mathrm{{exact}},0}=r_H,\mathcal{R}^V_{\mathrm{{exact}},0}=r_V | (I(0),S(0))=(1,s_0)): (r_H,r_V)\in \{0,...,9\}\times \{0,...,9\}\}$ in the case $\beta _I=3.75$, for Scenarios 1 ($\mu =1.0$), 2 ($\mu =2.5$), and 3 ($\mu =5.0$), at an invasion time with $s_0=20$

Figures 5 and 6 show, in more detail, how secondary infections due to horizontal transmission—in terms of $\mathcal{R}_{\mathrm{{exact}},0}^H$—and due to vertical transmission—in terms of $\mathcal{R}_{\mathrm{{exact}},0}^V$—contribute each one to the probability law of $\mathcal{R}_{\mathrm{{exact}},0}$.² It is seen that the pathogen is more likely to be spread by person-to-person contact as fewer infectious progeny are given birth to by the initially infectious individual; i.e., on the set $\{\mathcal{R}_{\mathrm{{exact}},0}^V=r_V\}$ with $r_V\in \{0,1\}$ in Fig. 5. Note that, in such a case, the value of $\mathcal{R}_{\mathrm{{exact}},0}^H$ is expected to be higher as the number of person-to-person contacts increases. It is also remarkable that the number of person-to-person contacts has a notable influence on how the number of secondary infections due to vertical transmission can be predicted from the number of secondary infections due to horizontal transmission. This behavior can be observed by comparing Scenario 1 with Scenario 3 on $\{\mathcal{R}_{\mathrm{{exact}},0}^H=r_H\}$ for suitably selected integers $r_H$. Smaller values of $\mathcal{R}_{\mathrm{{exact}},0}^H$—in particular, $r_H\in \{0,1,2\}$—allow accurate prediction of small values of $\mathcal{R}_{\mathrm{{exact}},0}^V$ when the number of person-to-person contacts is small (Scenario 1), while larger values of $\mathcal{R}_{\mathrm{{exact}},0}^H$—that is, $r_H\in \{3,4,...\}$—do not. In contrast, an accurate prediction of the smaller values of $\mathcal{R}_{\mathrm{{exact}},0}^V$ is possible on a larger set $\{\mathcal{R}_{\mathrm{{exact}},0}^H=r_H\}$—for example, in the case $r_H\in \{0,...,6\}$—when the number of person-to-person contacts increases in our numerical experiments (Scenario 3).

Fig. 6

The marginal mass functions of $\mathcal{R}^H_{\mathrm{{exact}},0}$ (left) and of $\mathcal{R}^V_{\mathrm{{exact}},0}$ (right) versus the contact rate $\mu$ and the birth rate $\beta _I$, at an invasion time with $s_0=20$

In terms of the marginal probability laws of $\mathcal{R}_{\mathrm{{exact}},0}^H$ and of $\mathcal{R}_{\mathrm{{exact}},0}^V$, Fig. 6 shows that the marginal mass function of $\mathcal{R}_{\mathrm{{exact}},0}^H$ is strongly influenced against the changes of $\mu$ and $\beta _I$, while $\mathcal{R}_{\mathrm{{exact}},0}^V$ is not very sensitive with respect to the variation of these parameters. In particular, it is seen that the main contribution to $\mathcal{R}_{\mathrm{{exact}},0}$ in our experiments comes from the spread of the pathogen through person-to-person contacts.

To conclude, it is seen in Table 2 and Fig. 7 that the most likely value of $\mathcal{R}_{\mathrm{{exact}},0}$—denoted by $r_{\max }$—behaves, as expected, as an increasing function of $\mu$. Moreover, the corresponding conditional probability $P(\mathcal{R}_{\mathrm{{exact}},0}=r_{\max } | (I(0),S(0))=(1,s_0))$ starts decreasing toward its minimum value and then increases with increasing values of $\mu$, irrespectively of $\beta _I$. On the contrary, the values of $r_{\max }$ decrease with increasing values of $\beta _I$ in our numerical results, and the corresponding conditional probability does not have a common general behavior as a function of $\beta _I$ (Table 2).

Fig. 7

The conditional probability $P(\mathcal{R}_{\mathrm{{exact}},0}=r_{\max } | (I(0),S(0))=(1,s_0))$ versus the contact rate $\mu$ and the birth rate $\beta _I$, at an invasion time with $s_0=20$

5 Concluding remarks

In this paper, a Markov chain model to describe the spread of epidemics of SIS type through interactions between susceptible and infectious individuals, and generational transmission from colonized parents to their progeny has been presented. The analysis of the model requires the use of a bi-variate competition process $\mathcal{X}$, which can be seen as the natural generalization of the uni-variate birth–death process arising in the classical SIS epidemic model without vertical transmission. Since bi-variate competition processes can be formulated as QBD processes, a broad range of mathematical techniques for block-structured Markov chains have great potential in the epidemiological setting to evaluate well-known descriptors; among these descriptors, we can mention the limiting distribution of the number of susceptible and infectious individuals as the time index tends to infinite, the random length of an outbreak, extreme values, and perturbation properties. In analyzing how the pathogen spreads in an early stage of the epidemic, the exact reproduction number $\mathcal{R}_{\mathrm{{exact}},0}$ has been expressed in terms of two random contributions allowing us to quantify how many secondary infections are related to the dynamics of horizontal and vertical transmission from an initially infectious individual. The joint probability law of the resulting random numbers $\mathcal{R}_{\mathrm{{exact}},0}^H$ and $\mathcal{R}_{\mathrm{{exact}},0}^V$ has been characterized in terms of finite systems of linear equations, which can be solved in an iterative manner by block-Gaussian elimination. It is clear that, since secondary cases are related to an exponentially distributed time $\tau$, the probability law of $\mathcal{R}_{\mathrm{{exact}},0}$, and those of $\mathcal{R}_{\mathrm{{exact}},0}^H$ and $\mathcal{R}_{\mathrm{{exact}},0}^V$, are non-defective. This also holds in the case $M=\infty$, due to the regularity of the underlying QBD process with infinitely may states (Remark 1), and Eq. (8) is seen to remain valid for integers $i\in \mathbb {N}$.

A major problem relates to the understanding of mechanisms which are responsible for the dissemination of a pathogen at the person-to-person and generational level. The specialized versions $\mathcal{R}_{\mathrm{{exact}},0}^H$ and $\mathcal{R}_{\mathrm{{exact}},0}^V$ are useful to understand how, specially in the case of populations with stable size over time, the person-to-person behavior can influence the dynamics at an early stage of the epidemic more strongly than the generational transmission from a initially colonized parent to its progeny. Therefore, the decomposition of the exact reproduction number into $\mathcal{R}_{\mathrm{{exact}},0}^H$ and $\mathcal{R}_{\mathrm{{exact}},0}^V$ can be considered as a promising tool for the study of how the mechanisms of vertical transmission are important in modeling the epidemic. Under the particular circumstances that the marginal mass function of $\mathcal{R}_{\mathrm{{exact}},0}^V$ is seen to be essentially concentrated over the value $r_V=0$, the bi-variate process $\mathcal{X}$ could be appropriately replaced by a simple uni-variate birth–death process and, consequently, the corresponding analysis of related descriptors might be analytically simplified.

Table 2 Values of $r_{\max }$ versus the contact rate $\mu$ and the birth rate $\beta _I$, at an invasion time with $s_0=20$

Fig. 8

Diagram of transitions between compartments in an SIS epidemic model with vertical and horizontal transmission, and pre- and post-exposure vaccination

Other Markov chain models for epidemics of the SIS type with vertical transmission may be appropriately studied by adapting our methodology. By way of example, we consider here the possibility of enriching the model by allowing vaccination (Fig. 8), and we exemplify how the QBD formulation is the key in the derivation of the joint distribution of $(\mathcal{R}_{\mathrm{{exact}},0}^V,\mathcal{R}_{\mathrm{{exact}},0}^H$). A third compartment of vaccinated (V) individuals must be incorporated into the model, and the infinitesimal dynamics of the resulting three-variate competition process $\mathcal{X}'=\{(I(t),S(t),V(t)): t\ge 0\}$ (Iglehart 1964) are governed by the following non-vanishing transition rates from state (i, s, v) to state $(i',s',v')$:

$$\begin{aligned} q_{(i,s,v),(i',s',v')}= & {} \left\{ \begin{array}{ll} \alpha _I i, &{} \hbox {if }(i',s',v')=(i-1,s,v), \\ \alpha _S s, &{} \hbox {if }(i',s',v')=(i,s-1,v), \\ \alpha _V v, &{} \hbox {if }(i',s',v')=(i,s,v-1), \\ (1-\bar{p}'')(\gamma _N i+\eta (i)), &{} \hbox {if }(i',s',v')=(i-1,s+1,v), \\ \bar{p}''(\gamma _N i+\eta (i)), &{} \hbox {if }(i',s',v')=(i-1,s,v+1), \\ \lambda s, &{} \hbox {if }(i',s',v')=(i,s-1,v+1), \\ \mu is, &{} \hbox {if }(i',s',v')=(i+1,s-1,v), \\ (1-p) \beta _I i, &{} \hbox {if }(i',s',v')=(i+1,s,v), \\ \bar{p}(\beta _S s+\beta _V v)+\bar{p}' p \beta _I i, &{} \hbox {if }(i',s',v')=(i,s,v+1), \\ (1-\bar{p})(\beta _S s+\beta _V v)+(1-\bar{p}')p \beta _I i, &{} \hbox {if }(i',s',v')=(i,s+1,v),\end{array}\right. \end{aligned}$$

for states $(i,s,v),(i',s',v')\in \mathcal{S}'$ with $(i',s',v')\ne (i,s,v)$ and $\mathcal{S}'=\{(i,s,v)\in \mathbb {N}_0\times \mathbb {N}_0\times \mathbb {N}_0: i+s+v\in \{0,...,M\}\}$, and $q_{(i,s,v),(i,s,v)}=-q_{(i,s,v)}$, where

$$\begin{aligned} q_{(i,s,v)}= & {} (\alpha _I+(1-\delta _{i+s+v,M})\beta _I+\gamma _N)i+(\alpha _S+(1-\delta _{i+s+v,M})\beta _S+\lambda )s \\{} & {} +(\alpha _V+(1-\delta _{i+s+v,M})\beta _V)v+\eta (i)+\mu is, \end{aligned}$$

for $(i,s,v)\in \mathcal{S}'$. In these expressions, $\alpha _V$ is the death rate of vaccinated individuals, $\beta _V$ is the birth rate of healthy individuals from vaccinated parents, and $\lambda$ is the rate that a susceptible individual becomes vaccinated by administration of a therapeutic (post-exposure) vaccine. Probabilities $\bar{p}$ and $\bar{p}'$, with $\bar{p},\bar{p}'\in [0,1]$, are linked to prophylactic (pre-exposure) vaccination interventions at birth of healthy individuals from susceptible and vaccinated parents, and infectious parents, respectively, and probability $\bar{p}''$, with $\bar{p}''\in [0,1]$, is related to the use of a prophylactic vaccine after recovery of infectious individuals. Vaccines are assumed to be perfect; i.e., vaccines are fully effective and vaccinated individuals acquire lifelong immunity against the pathogen. As is the case of process $\mathcal{X}$, the q-matrix of $\mathcal{X}'$ is seen to have the structured form of Q in Eq. (1) using the labeling of states $\mathcal{S}'=\cup _{i=0}^M l'(i)$ with levels $l'(i)=\{(i,s,v): s+v\in \{0,...,M-i\}\}$, for $i\in \{0,...,M\}$. This means that, for process $\mathcal{X}'$, sub-matrices $Q_{i,i-1}$ and $Q_{i,i+1}$ in (1) record infinitesimal rates associated with the recovery and the death of infectious individuals, and new infections, respectively, and diagonal entries of $Q_{i,i}$ are specified by $-q_{(i,s,v)}$, for (i, s, v) with $s+v\in \{0,...,M-i\}$. Non-vanishing off-diagonal entries of $Q_{i,i}$ correspond to the birth and the death of susceptible and vaccinated individuals, and the therapeutic use of a vaccine on susceptible individuals. The column vectors $p_i(i^*,r_V,r_H)$ for process $\mathcal{X}'$, for integers $i\in \{1,...,M\}$ and $i^*\in \{D,N,T\}$, are defined as $p_i(i^*,r_V,r_H)$ in Section 3.1 with the probabilities $P_{(i,s)}(i^*,r_V,r_H)$ replaced by the conditional probabilities $P(I^*=i^*, \mathcal{R}_{\mathrm{{exact}},0}^V=r_V, \mathcal{R}_{\mathrm{{exact}},0}^H=r_H | (I(0),S(0),V(0))=(i,s,r))$, for states $(i,s,v)\in \mathcal{S}'{\setminus } l'(0)$. Equations (9) and (10) are then found to determine the joint probability law of $(\mathcal{R}_{\mathrm{{exact}},0}^V,\mathcal{R}_{\mathrm{{exact}},0}^H)$ by adapting our approach in Sections 3.1 and 3.2 to process $\mathcal{X}'$; in particular, matrices $Q_{i,i-1}$ (respectively, $Q_{i,i+1}$) for $\mathcal{X}'$ must be appropriately decomposed by distinguishing, in a similar manner to $\mathcal{X}$, between the death, the natural recovery, and the recovery due to treatment of the initially infectious individual (respectively, the vertical and the horizontal secondary infections generated by the initially infectious individual).

The use of any prophylactic or therapeutic vaccine will decrease the opportunities of the initially infectious individual to infect healthy individuals, whence model $\mathcal{X}'$ is expected to predict a lower transmission of the pathogen at an early state of the disease than model $\mathcal{X}$; i.e., events $\{\mathcal{R}_{\mathrm{{exact}},0}^V\in \{0,...,r'_V\}\}$ and $\{\mathcal{R}_{\mathrm{{exact}},0}^H\in \{0,...,r'_H\}\}$, for certain relatively small values $r'_V$ and $r'_H$, are expected to occur more likely in process $\mathcal{X}'$ than in process $\mathcal{X}$ and, on at least first observation, the tail of the distribution of $\mathcal{R}_{\mathrm{{exact}},0}^V$ (respectively, $\mathcal{R}_{\mathrm{{exact}},0}^H$) for process $\mathcal{X}$ is expected to be heavier than that of $\mathcal{R}_{\mathrm{{exact}},0}^V$ (respectively, $\mathcal{R}_{\mathrm{{exact}},0}^H$) for process $\mathcal{X}'$. Further work must be done to predict the effects of a prophylactic intervention—defined by the selection $\lambda =0$ and at least one strictly positive value of $\bar{p}$, $\bar{p}'$ and $\bar{p}''$—compared to a therapeutic intervention—defined by a strictly positive value of $\lambda$ and $\bar{p}=\bar{p}'=\bar{p}''=0$—especially to derive certain thresholds for the underlying probabilities $\bar{p}$, $\bar{p}'$ and $\bar{p}''$, and the rate $\lambda$ that make the use of a prophylactic vaccine preferable over the use of a therapeutic one, and vice versa.

In the Markov chain model, person-to-person contacts are governed by mutually independent Poisson processes of common rate $\mu$, regardless of whether they result in a new infection or not. This means that, since the Poisson process has independent and stationary increments (Kulkarni 2020, Chapter 5), individuals are assumed to together constitute a homogeneously well-mixed population with varying size over time. Another aspect of interest is how to preserve the Markovian formulation of the model when the exponential regime—governing infectious contacts, recovery times, and birth and death events—is generalized to non-exponential distributional assumptions. For instance, a Markov-modulated version of process $\mathcal{X}$ can be defined by replacing the exponentially distributed recovery times with mean $\gamma _N^{-1}$ by phase-type random variables (He 2014, Chapter 1) of order m. Instead of states (i, s) for $\mathcal{X}$, this results in states $(i,s;y')$ for an augmented process $(\mathcal{X},\mathcal{Y})$ with vector $y'=(y_1,...,y_m)$—with $\sum _{j=1}^m y_j=i$—recording the number $y_j$ of phase-type recovery times at phase j, for $j\in \{1,...,m\}$, at an arbitrary time; note that other Markov-modulated versions can be obtained from the replacement of exponentially distributed times until the occurrence of individuals’ birth and death by phase-type random variables, and/or the Poisson processes for infectious contacts by Markovian arrival streams (He 2014, Chapter 2). Although process $(\mathcal{X},\mathcal{Y})$ can be thought of as a finite QBD process and the approach in Section 3 can be readily adapted, the memory requirements are so demanding that the numerical solution for the mass function of $(\mathcal{R}_{\mathrm{{exact}},0}^V,\mathcal{R}_{\mathrm{{exact}},0}^H)$ will become rapidly prone to numerical instability due to the cardinality of the underlying state space, as observed in Ref. Almaraz and Gómez-Corral (2018) for the simpler SIR model. In analyzing the exact reproduction number in SIS epidemic models with vertical transmission and a general infection period distribution, the theory on piecewise-deterministic Markov processes will be requested in a similar manner to the study of secondary cases in the framework of the SIR model (Gómez-Corral and López-García 2017).

Appendix A: The q-matrix of process \(\mathcal{X}\)

We construct the structured q-matrix in Eq. (1) using a lexicographical labeling of states. This yields the following expressions for sub-matrices $Q_{i,i'}$, for $i'\in \{\max \{0,i-1\},i,\min \{i+1,M\}\}$:

• (i) For $i=0$, the sub-matrix $Q_{0,0}$ has the form

  $$\begin{aligned} Q_{0,0}= & {} \left( \begin{array}{cccccc} 0 &{} &{} &{} &{} &{} \\ \alpha _S &{} -q_{(1,0)} &{} \beta _S &{} &{} &{} \\ &{} 2\alpha _S &{} -q_{(2,0)} &{} 2\beta _S &{} &{} \\ &{} &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} &{} (M-1)\alpha _S &{} -q_{(M-1,0)} &{} (M-1)\beta _S \\ &{} &{} &{} &{} M\alpha _S &{} -q_{(M,0)} \end{array}\right) , \end{aligned}$$

  and, since l(0) is a closed class of states, $Q_{0,1}=0_{(1+M)\times M}$, where $0_{a\times b}$ denotes the null matrix of dimension $a\times b$.

• (ii) For $i\in \{1,...,M\}$, the sub-matrices $Q_{i,1-1}$ and $Q_{i,i}$ are given by

  $$\begin{aligned} Q_{i,i-1}= & {} \left( \begin{array}{ccccc} \alpha _I i &{} \gamma _N i+\eta (i) &{} &{} &{} \\ &{} \alpha _I i &{} \gamma _N i+\eta (i) &{} &{} \\ &{} &{} \ddots &{} \ddots &{} \\ &{} &{} &{} \alpha _I i &{} \gamma _N i+\eta (i) \end{array}\right) , \\ Q_{i,i}= & {} \left( \begin{array}{cccccc} -q_{(i,0)} &{} p\beta _I i &{} &{} &{} &{} \\ \alpha _S &{} -q_{(i,1)} &{} \beta _S+p\beta _I i &{} &{} &{} \\ &{} 2\alpha _S &{} -q_{(i,2)} &{} 2\beta _S+p\beta _I i &{} &{} \\ &{} &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} &{} (M-i-1)\alpha _S &{} -q_{(i,M-i-1)} &{} (M-i-1)\beta _S+p\beta _I i \\ &{} &{} &{} &{} (M-i)\alpha _S &{} -q_{(i,M-i)} \end{array}\right) . \end{aligned}$$

• (iii) For $i\in \{1,...,M-1\}$, the sub-matrix $Q_{i,i+1}$ is specified by

  $$\begin{aligned} Q_{i,i+1}= & {} \left( \begin{array}{ccccc} (1-p)\beta _I i &{} &{} &{} &{} \\ \mu i &{} (1-p)\beta _I i &{} &{} &{} \\ &{} 2\mu i &{} (1-p)\beta _I i &{} &{} \\ &{} &{} \ddots &{} \ddots &{} \\ &{} &{} &{} (M-i-1)\mu i &{} (1-p)\beta _I i \\ &{} &{} &{} &{} (M-i)\mu i \end{array}\right) . \end{aligned}$$