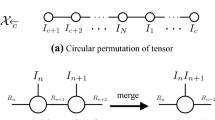
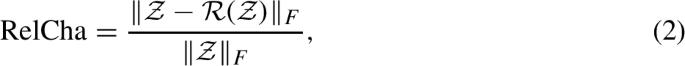Abstract
This paper proposes an algorithm based on defined scaled tri-factorization (STF) for fast and accurate tensor ring (TR) decomposition. First, based on the fast tri-factorization approach, we define STF and design a corresponding algorithm that can more accurately represent various matrices while maintaining a similar level of computational time. Second, we apply sequential STFs to TR decomposition with theoretical proof and propose a stable (i.e., non-iterative) algorithm named TR-STF. It is a computationally more efficient algorithm than existing TR decomposition algorithms, which is beneficial when dealing with big data. Experiments on multiple randomly simulated data, highly oscillatory functions, and real-world data sets verify the effectiveness and high efficiency of the proposed TR-STF. For example, on the Pavia University data set, TR-STF is nearly 9240 and 39 times faster, respectively, and more accurate than algorithms based on alternating least squares and singular value decomposition. As an extension, we apply sequential STFs to tensor train (TT) decomposition and propose a non-iterative algorithm named TT-STF. Experimental results demonstrate the superiority of the proposed TT-STF compared with the state-of-the-art TT decomposition algorithm.











Similar content being viewed by others
Data Availability
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Notes
This denotes the relative error between the given tensor and the approximated tensor.
The details of this data set can be found at https://www.github.com/clausmichele/CBSD68-dataset.
RelCha is defined by
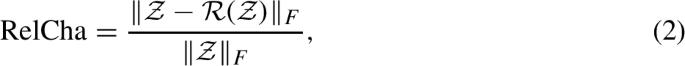
where \(\mathcal {Z}\) denotes the original image and \(\mathcal {R}(\mathcal {Z})\) is the reconstructed image. The smaller the RelCha, the better the result.
The details of this data set can be found at https://www.kaggle.com/jessicali9530/coil100.
References
Bozorgmanesh H, Hajarian M (2022) Triangular decomposition of CP factors of a third-order tensor with application to solving nonlinear systems of equations. J Sci Comput 90:74
Brachat J, Comon P, Mourrain B, Tsigaridas E (2010) Symmetric tensor decomposition. Linear Algebra Appl 433:1851–1872
Bro R (1997) PARAFAC. Tutorial and applications. Chem Intell Lab Syst 38(2):149–171
Cao X, Yao J, Xu Z, Meng D (2020) Hyperspectral image classification with convolutional neural network and active learning. IEEE Trans Geosci Remote Sens 58(7):4604–4616
Che M, Wei Y (2020) Multiplicative algorithms for symmetric nonnegative tensor factorizations and its applications. J Sci Comput 83:53
Che M, Wei Y, Yan H (2021) An efficient randomized algorithm for computing the approximate Tucker decomposition. J Sci Comput 88:32
Chen Y, Huang T-Z, He W, Yokoya N, Zhao X-L (2020) Hyperspectral image compressive sensing reconstruction using subspace-based nonlocal tensor ring decomposition. IEEE Trans Image Process 29:6813–6828
Cichocki A, Lee N, Oseledets A-H, Phan I, Zhao Q, Mandic DP (2016) Tensor networks for dimensionality reduction and large-scale optimization: part 1 low-rank tensor decompositions. Found Trends® Mach Learn 9:249–429
De Lathauwer L (2006) A link between the canonical decomposition in multilinear algebra and simultaneous matrix diagonalization. SIAM J Matrix Anal Appl 28(3):642–666
De Lathauwer L, De Moor B, Vandewalle J (2000) On the best rank-1 and rank-(R1,R2,. . .,RN) approximation of higher-order tensors. SIAM J Matrix Anal Appl 21(4):1324–1342
DE Silva V, Lim L-H (2008) Tensor rank and the ill-posedness of the best low-rank approximation problem. SIAM J Matrix Anal Appl 30:1084–1127
Dektor A, Rodgers A, Venturi D (2021) Rank-adaptive tensor methods for high-dimensional nonlinear PDEs. J Sci Comput 36:88
Deng L-J, Feng M, Tai X-C (2019) The fusion of panchromatic and multispectral remote sensing images via tensor-based sparse modeling and hyper-Laplacian prior. Inf Fusion 52:76–89
Deng L-J, Vivone G, Jin C, Chanussot J (2021) Detail injection-based deep convolutional neural networks for pansharpening. IEEE Trans Geosci Remote Sens 59(8):6995–7010
Deng L-J, Vivone G, Paoletti ME, Scarpa G, He J, Zhang Y, Chanussot J, Plaza A (2022) Machine learning in pansharpening: a benchmark, from shallow to deep networks. IEEE Geosci Remote Sens Mag 10(3):279–315
Deng S-Q, Deng L-J, Wu X, Ran R, Hong D, Vivone G (2023) PSRT: pyramid shuffle-and-reshuffle transformer for multispectral and hyperspectral image fusion. IEEE Trans Geosci Remote Sens 61:1–15. https://doi.org/10.1109/TGRS.2023.3244750
Dian R, Li S, Fang L (2019) Learning a low tensor-train rank representation for hyperspectral image super-resolution. IEEE Trans Neurral Netw Learn Syst 30(9):2672–2683
Ding M, Huang T-Z, Ji T-Y, Zhao X-L, Yang J-H (2019) Low-rank tensor completion using matrix factorization based on tensor train rank and total variation. J Sci Comput 81:941–964
Ding M, Huang T-Z, Zhao X-L, Ng MK, Ma T-H (2021) Tensor train rank minimization with nonlocal self-similarity for tensor completion. Inverse Probl Imaging 15(3):475–498
Fu X, Lin Z, Huang Y, Ding, X (2019) A variational pan-sharpening with local gradient constraints. In: Proceedings of IEEE conference on computer vision pattern recognition (CVPR), pp 10257–10266
Gnanasekaran DEA (2022) Hierarchical orthogonal factorization: sparse least squares problems. J Sci Comput 91:50
Goulart JHDM, Boizard M, Boyer R, Favier G, Comon P (2016) Tensor CP decomposition with structured factor matrices: algorithms and performance. IEEE J Sel Top Signal Process 10:757–769
Hashemizadeh M, Liu M, Miller J, Rabusseau G (2020) Adaptive tensor learning with tensor networks. In: Proceedings of NeurIPS 1st workshop on quantum tensor networks in machine learning
He W, Yokoya N, Yuan L-H, Zhao Q-B (2019) Remote sensing image reconstruction using tensor ring completion and total variation. IEEE Trans Geosci Remote Sens 57(11):8998–9009
He W, Yao Q, Chao L, Yokoya N, Zhao Q, Zhang H, Zhang L (2022) Non-Local Meets Global: an iterative paradigm for hyperspectral image restoration. IEEE Trans Pattern Anal Mach Intell 44(04):2089–2107
Hillar CJ, Lim L-H (2013) Most tensor problems are NP-hard. J ACM 60:1–39
Holtz S, Rohwedder T, Schneider R (2012) The alternating linear scheme for tensor optimization in the tensor train format. SIAM J Sci Comput 34(2):A683–A713
Huckle T, Waldherr K, Schulte-Herbriggen T (2013) Computations in quantum tensor networks. Linear Algebra Appl 438(2):750–781
Jiang J, Sanogo F, Navasca C (2022) Low-CP-rank tensor completion via practical regularization. J Sci Comput 91:18
Kolda TG, Bader BW (2009) Tensor decompositions and applications. SIAM Rev 51(3):455–500
Liu Y, Jiao LC, Shang F (2013) A fast tri-factorization method for low-rank matrix recovery and completion. Pattern Recogn 46(1):163–173
Luan Z, Ming Z, Wu Y (2023) Hankel tensor-based model and l1-tucker decomposition-based frequency recovery method for harmonic retrieval problem. Comput Appl Math 42:14
Orus R (2014) A practical introduction to tensor networks: matrix product states and projected entangled pair states. Ann Phys 349:117–158
Oseledets IV (2011) Tensor-train decomposition. SIAM J Sci Comput 33(5):2295–2317
Oseledets IV, Tyrtyshnikov EE (2009) Breaking the curse of dimensionality, or how to use SVD in many dimensions. SIAM J Sci Comput 31:3744–3759
Oseledets I, Tyrtyshnikov E (2010) TT-cross approximation for multidimensional arrays. Linear Algebra Appl 432(1):70–88
Qi L, Wang Q, Chen Y (2015) Three dimensional strongly symmetric circulant tensors. Linear Algebra Appl 482:207–220
Ran R, Deng L-J, Jiang T-X, Hu J-F, Chanussot J, Vivone G (2023) GuidedNet: a general CNN fusion framework via high-resolution guidance for hyperspectral image super-resolution. IEEE Trans Cybern. https://doi.org/10.1109/TCYB.2023.3238200
Shen Y, Wen Z, Zhang Y (2014) Augmented Lagrangian alternating direction method for matrix separation based on low-rank factorization. Optim Methods Softw 29(2):239–263
Sultonov A, Matveev S, Budzinskiy S (2023) Low-rank nonnegative tensor approximation via alternating projections and sketching. Comput Appl Math 42:68
Sun C-W, Huang T-Z, Xu T, Deng L-J (2023) NF-3DLogTNN: an effective hyperspectral and multispectral image fusion method based on nonlocal low-fibered-rank regularization. Appl Math Model 118:780–797
Tai X-C, Deng L-J, Yin K (2021) A multigrid algorithm for maxflow and Min-Cut problems with applications to multiphase image segmentation. J Sci Comput 101:87
The Singular Value Decomposition (SVD), chap. 4. Wiley, pp 261–288 (2002). https://doi.org/10.1002/0471249718.ch4. https://onlinelibrary.wiley.com/doi/abs/10.1002/0471249718.ch4
Tucker LR (1996) Some mathematical notes on three-mode factor analysis. Psychometrika 31(3):279–311
Wang Y, Yang Y (2022) Hot-svd: higher order t-singular value decomposition for tensors based on tensor-tensor product. Comput Appl Math 41:394
Wang H, Zhang F, Wang J, Huang T, Huang J, Liu X (2022) Generalized nonconvex approach for low-tubal-rank tensor recovery. IEEE Trans Neural Netw Learn Syst 33(8):3305–3319
Wang H, Peng J, Qin W, Wang J, Meng D (2023) Guaranteed tensor recovery fused low-rankness and smoothness. IEEE Trans Pattern Anal Mach Intell 1:1–17. https://doi.org/10.1109/TPAMI.2023.3259640
Wen Z, Yin W, Zhang Y (2012) Solving a low-rank factorization model for matrix completion by a non-linear successive over-relaxation algorithm. Math Program Comput 4:333–361
Xiao C, Yang C, Li M (2021) Efficient alternating least squares algorithms for low multilinear rank approximation of tensors. J Sci Comput 87:67
Xiao J-L, Huang T-Z, Deng L-J, Wu Z-C, Vivone G (2022) A new context-aware details injection fidelity with adaptive coefficients estimation for variational pansharpening. IEEE Trans Geosci Remote Sens 60:1–15
Xu C (2016) Hankel tensors, Vandermonde tensors and their positivities. Linear Algebra Appl 491:56–72
Xu T, Huang T-Z, Deng L-J, Zhao X-L, Huang J (2020) Hyperspectral image super-resolution using unidirectional total variation with Tucker decomposition. IEEE J Sel Top Appl Earth Obs Remote Sens 13:4381–4398
Xu T, Huang T-Z, Deng L-J, Yokoya N (2022) An iterative regularization method based on tensor subspace representation for hyperspectral image super-resolution. IEEE Trans Geosci Remote Sens 60:1–16. https://doi.org/10.1109/TGRS.2022.3176266
Xue J, Zhao Y, Liao W, Chan JC-W (2019) Nonlocal low-rank regularized tensor decomposition for hyperspectral image denoising. IEEE Trans Geosci Remote Sens 57(7):5174–5189
Xue J, Zhao Y, Liao W, Chan JC-W, Kong SG (2020) Enhanced sparsity prior model for low-rank tensor completion. IEEE Trans Neural Netw Learn Syst 31(11):4567–4581
Xue J, Zhao Y-Q, Bu Y, Liao W, Chan JC-W, Philips W (2021a) Spatial-spectral structured sparse low-rank representation for hyperspectral image super-resolution. IEEE Trans Image Process 30:3084–3097
Xue J, Zhao Y-Q, Huang S, Liao W, Chan JC-W, Kong SG (2021b) Multilayer sparsity-based tensor decomposition for low-rank tensor completion. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2021.3083931
Xue J, Zhao Y, Bu Y, Chan JC-W, Kong SG (2022) When Laplacian scale mixture meets three-layer transform: a parametric tensor sparsity for tensor completion. IEEE Trans Cybern 52(12):13887–13901. https://doi.org/10.1109/TCYB.2021.3140148
Zhao Q, Zhou G, Xie S, Zhang L, Cichocki A (2016) Tensor ring decomposition. arXiv:1606:05535
Zniyed Y, Boyer R, de Almeida ALF, Favier G (2020) A TT-based hierarchical framework for decomposing high-order tensors. SIAM J Sci Comput 42(2):822–848
Acknowledgements
The authors would like to thank the anonymous referees and editor for their valuable remarks, questions, and comments that enabled the authors to improve this paper. This research is supported by NSFC (12171072, 12271083), Natural Science Foundation of Sichuan Province (2022NSFSC0501), Key Projects of Applied Basic Research in Sichuan Province (Grant No. 2020YJ0216), and National Key Research and Development Program of China (Grant No. 2020YFA0714001).
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
There is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Xu, T., Huang, TZ., Deng, LJ. et al. TR-STF: a fast and accurate tensor ring decomposition algorithm via defined scaled tri-factorization. Comp. Appl. Math. 42, 234 (2023). https://doi.org/10.1007/s40314-023-02368-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-023-02368-w