Robust spectral treatment for time-fractional delay partial differential equations

Abstract

Fractional delay differential equations (FDDEs) and time-fractional delay partial differential equations (TFDPDEs) are the focus of the present research. The FDDEs is converted into a system of algebraic equations utilizing a novel numerical approach based on the spectral Galerkin (SG) technique. The suggested numerical technique is likewise utilized for TFDPDEs. In terms of shifted Jacobi polynomials, suitable trial functions are developed to fulfill the initial-boundary conditions of the main problems. According to the authors, this is the first time utilizing the SG technique to solve TFDPDEs. The approximate solution of five numerical examples is provided and compared with those of other approaches and with the analytic solutions to test the superiority of the proposed method.

1 Introduction

Unlike ordinary integration and differentiation, the non-local property of fractional calculus is the main aim of attracting many researchers in various fields to study its definitions, properties and applications (Kimeu (2009) and Dalir and Bashour (2010)). Also, due to the emergence of a large number of natural phenomena that have been described using fractional calculus such as fluid mechanics (Kulish and Jose (2002)), viscoelasticity (Meral et al. (2010)), thermoelasticity (Povstenko (2015)), media (Tarasov (2011)), continuum mechanics (Carpinteri and Mainardi (1997)), and other application (Podlubny (1999); Kilbas et al. (2006); Sun et al. (2018)), numerous researchers have been keen on concentrating on various types of fractional differential equations (FDEs), and looking for the solutions to these equations has become the goal of many mathematicians. Due to the tremendous difficulty of finding exact solutions for many types of FDEs, many researchers have been interested in obtaining analytical and numerical solutions for such problems. Some of them are the finite difference (Hendy et al. (2021)), predictor-corrector (Kumar and Gejji (2019)), wavelet operational matrix (Yi and Huang (2014)), Galerkin-Legendre spectral (Zaky et al. (2020)), fractional-order Boubaker wavelets (Rabiei and Razzaghi (2021)), fractional Jacobi collocation (Abdelkawy et al. (2020)) and artificial neural network (Pakdaman et al. 2017) methods. Because of the globality of fractional calculus, it is preferable to use global numerical techniques to solve FDEs of various types.

Over the last four decades, spectral methods have been developed rapidly for several advantages. The uses of spectral methods ensure that all calculations can be performed numerically with an arbitrarily large degree of accuracy. As a result, an accurate solution was obtained with a relatively small number of degrees of freedom and hence at a reasonable computational cost, especially for variable coefficients and nonlinear problems. The choice of trial functions is one of the features which distinguish spectral methods from finite-element and finite-difference methods. The trial functions for spectral methods are differentiable global functions that fit well with the nonlocal definition of fractional derivatives, making them promising candidates for solving different types of fractional differential equations.

Spectral techniques can be separated into three principal types: Galerkin, tau, and collocation. The choice of the appropriate utilized spectral method suggested for solving such differential equations depends certainly on the type of the differential equation and also on the type of the initial or boundary conditions governing it. Also, different trial functions lead to different spectral approximations, for instance, trigonometric polynomials for periodic problems; Chebyshev, Legendre, ultraspherical, and Jacobi polynomials for non-periodic problems; Jacobi rational and Laguerre polynomials for problems on the half line, and Hermite polynomials for problems on the whole line.

In the last few years, Several authors have expressed interest in utilizing various spectral approaches for solving ordinary and partial FDEs. Doha et al. (2013) applied the collocation and tau spectral approaches based on shifted Jacobi polynomials for solving linear and nonlinear FDEs, respectively. Alsuyuti et al. (2019) used a modification of the SG approach for solving a class of ordinary FDEs. Abd-Elhameed et al. (2022) used the third- and fourth-kinds Chebyshev polynomials as the basis function of the Petrov-Galerkin method for treating particular types of odd-order boundary value problems. Hafez et al. (2022) introduced two efficient SG algorithms for solving multi-dimensional time-fractional advection–diffusion-reaction equations based on fractional-order Jacobi functions. Ezz-Eldien et al. (2020) introduced a solution of two-dimensional multi-term time-fractional mixed sub-diffusion and diffusion-wave equation using the time-space spectral collocation (SC) method.

Sometimes, the current state is insufficient to describe the behavior of the process being considered. Still, information on the previous state can benefit the system’s behavior. These systems are called time-delay systems. In the last decades, much attention has been paid to time-delay systems because of its many applications in a large number of practical systems, such as economics, transportation, chemical processes, robotics, physics and engineering (Zavarei and Jamshidi (1987); Kuang (1993); Jaradat et al. (2022); Cai and Huang (2002); Bocharov and Rihan (2000); Ji and Leung (2002)). Searching for exact solutions for any system in the presence of delay is a complex process. Therefore, developing analytical and numerical techniques for various types of FDDEs has attracted the attention of many authors. Ezz-Eldien (2018) introduced the spectral tau technique for solving systems of multi-pantograph equations. Cheng et al. (2015) applied the reproducing kernel theory for solving the neutral functional-differential equation with proportional delays. Akkaya et al. (2013) introduced a numerical approach based on first Boubaker polynomials for solve FDDEs. Ahmad and Mukhtar (2015) applied the artificial neural network for the multi-pantograph differential equation. Ezz-Eldien and Doha (2019) used the SC for pantograph Volterra integro-differential equations. Otherwise, FDDEs have many applications in numerous scientific domains, such as population ecology, control systems, biology and medicine (Magin (2010); Jaradat et al. (2020); Wu (2012); Alquran and Jaradat (2019); Keller (2010)). A large number of numerical methods have been introduced to get the solutions to various types of FDDEs. The Haar wavelet (Amin et al. (2021)), reproducing kernel (Allahviranloo and Sahihi (2021)), Generalized Adams (Zhao et al. (2021)), Lagrange interpolations (Zuniga-Aguilar et al. (2019)), finite difference (Moghaddam and Mostaghim (2014)) and Legendre wavelet methods (Yuttanan et al. (2021)) have been applied for solving various types of FDDEs. Recently, spectral methods have been applied to solve different FDDEs. Hafez and Youssri (2022) used the Gegenbauer-Gauss SC method for fractional neutral functional-differential equations. Alsuyuti et al. (2021) used the Legendre polynomials as basis function of SG approach for solving a general form of multi-order fractional pantograph equations. Abdelkawy et al. (2020) used the Jacobi SC method for fractional functional differential equations of variable order. Ezz-Eldien et al. (2020) applied Chebyshev spectral tau method for solving multi-order fractional neutral pantograph equations.

The current study aims to develop an accurate numerical solution for the FDDEs and TFDPDEs. The numerical method offered in the spatial and temporal axes is based on the SG technique. Special properties of shifted Jacobi polynomials are exploited to generate new basis functions that meet the problem’s initial and boundary conditions. The elements of a system of algebraic equations are determined using advanced techniques and are represented as a matrix.

The following is a breakdown of the article’s structure. In Sect. 2, the SG approach is explained, along with a full explanation of how to solve FDDEs using the resulting system of algebraic equations. For TFDPDEs, the SG approach is used in Sect. 3. The convergence analysis and the stability of the proposed numerical scheme is investigated in Sect. 4. Section 5 presents numerical solutions to five test problems compared to those obtained using other algorithms to demonstrate the method’s superior performance. Section 6 concludes with some recommendations.

2 Fractional delay differential equations

In this section, we discuss the numerical approach for solving the FDDEs

$$\begin{aligned} D_t^{\nu _n}{} Y (t)+\sum _{k=0}^{n-1}\eta _k\,D_t^{\nu _k}{} Y (\alpha _k\,t+\beta _k)=p(t), \end{aligned}$$

(1)

subject to

$$\begin{aligned} Y ^{(k)}(0)=0,\qquad k=0(1)n-1, \end{aligned}$$

(2)

where $0\le t \le \tau ,$ $k-1< \nu _k \le k;(k=1(1)n)$ and $\nu _0=0,$ while $\eta _k,\alpha _k,\beta _k$ for $k=0(1)n-1,$ are given constants and $D_t^{\nu }{} Y (t)$ denotes the Caputo fractional (CF) derivative of order $\nu ,$ w.r.t. tPodlubny (1999), namely,

$$\begin{aligned} D_t^{\nu }{} Y (t)=\frac{1}{\Gamma (\lceil \nu \rceil -\nu )} \int _{0}^{t}\frac{Y ^{(\lceil \nu \rceil )}(z)}{(t-z)^{\nu +1-\lceil \nu \rceil }} dz,\quad t>0, \end{aligned}$$

where $\Gamma (.)$ and $\lceil .\rceil$ are the Gamma and Ceilling functions, respectively. As an SG approach, we define the following space

$$\begin{aligned} {\mathcal {J}}_{N_1}=\text {span}\{J^{(\rho ,\sigma )}_{0,\tau }(t),J^{(\rho ,\sigma )}_{1,\tau }(t),\ldots ,J^{(\rho ,\sigma )}_{N_1-n,\tau }(t)\}, \end{aligned}$$

(3)

and then we choose the basis function as follows:

$$\begin{aligned} \Omega _{N_1}=\{\psi (t)\,\in {\mathcal {J}}_{N_1}:\psi ^{(k)}(0)=0,\,k=0(1)n-1\}, \end{aligned}$$

(4)

where $J^{(\rho ,\sigma )}_{j,\tau }(t)$ denotes the shifted Jacobi polynomials defined on $[0,\tau ]$, have orthogonality relation is given by

(5)

where $\varsigma _{j,\jmath }$ is the well-known Kronecker delta function, and

$$\begin{aligned} \hbar _{j,\tau }^{(\rho ,\sigma )}=\frac{\tau ^{\lambda }\Gamma (j+\rho +1) \Gamma (j+\sigma +1)}{j! (2 j+\lambda ) \Gamma (j+\lambda )}, \end{aligned}$$

(6)

with

(7)

and

$$\begin{aligned}\lambda =\rho +\sigma +1.\end{aligned}$$

For more details about Jacobi polynomials, one can consult (Ezz-Eldien (2016); Alsuyuti et al. (2022)). Now, we assume that the solution of the FDDEs (1)–(2) is approximated by

$$\begin{aligned} Y _{N_1}(t)=\sum _{j=0}^{N_1-n}c_{j}\,\psi _j(t), \end{aligned}$$

(8)

where

$$\begin{aligned} \psi _j(t)=t^n \, J^{(\rho ,\sigma )}_{j,\tau }(t). \end{aligned}$$

(9)

Hence, the SG technique is to find $Y _{N_1}(t)\in \Omega _{N_1},$ such that

where

is the scalar inner product w.r.t. weighted space with . Using the approximation (8), we have

Let us denote

(10)

where $0\le \jmath \le N_1-n.$ Then, one can deduce that the main problem is equivalent to

$$\begin{aligned} \left( {\textbf{A}}+\sum _{k=0}^{n-1}\eta _k\,{\textbf{B}}_k\right) {\textbf{C}}={\textbf{P}}, \end{aligned}$$

(11)

where

$$\begin{aligned}{\textbf{C}}=\{c_{0},c_{1},\cdots ,c_{N_1-n}\}.\end{aligned}$$

Using (9) with the explicit analytic form of the shifted Jacobi polynomial $J^{(\rho ,\sigma )}_{j,\tau }(t),$ we have

$$\begin{aligned} \begin{aligned} \psi _j(t)&=\sum _{r=0}^j \frac{(-1)^{j-r} \Gamma (j+\sigma +1) \Gamma (j+r+\lambda )}{r! \tau ^r (j-r)! \Gamma (r+\sigma +1) \Gamma (j+\lambda )}\,t^{r+n},\\ \psi _j(\alpha \, t+\beta )&=\sum _{r=0}^j \frac{(-1)^{j-r} \Gamma (j+\sigma +1) \Gamma (j+r+\lambda )}{r! \tau ^r (j-r)! \Gamma (r+\sigma +1) \Gamma (j+\lambda )}\,\left( \alpha \, t+\beta \right) ^{r+n}. \end{aligned}\end{aligned}$$

(12)

Applying the CF-derivative, we get

$$\begin{aligned} \begin{aligned} D_t^\nu \psi _j(t)&=\sum _{r=0}^j \frac{(-1)^{j-r}(n+r)!\Gamma (j+\sigma +1) \Gamma (j+r+\lambda )}{r! \tau ^{r}(j-r)! \Gamma (r+\sigma +1) \Gamma (j+\lambda ) \Gamma (n+r-\nu +1)}\,t^{n+r-\nu },\\ D_t^\nu \psi _j(\alpha \, t+\beta )&=\sum _{r=0}^j \sum _{s=\lceil \nu \rceil }^{n+r}\frac{(-1)^{j-r} s! \alpha ^s \beta ^{n+r-s}\left( {\begin{array}{c}n+r\\ s\end{array}}\right) \Gamma (j+\sigma +1) \Gamma (j+r+\lambda )}{r! \tau ^{r}(j-r)! \Gamma (r+\sigma +1) \Gamma (s-\nu +1) \Gamma (j+\lambda )}\,t^{s-\nu }. \end{aligned} \end{aligned}$$

(13)

Making use of (12)–(13), and after performing some manipulations, we have

(14)

where

$$\begin{aligned} \begin{aligned} {\mathcal {T}}_{j,\jmath ,n,\nu }&=\sum _{r=0}^j \frac{({-}1)^{j{-}r} (n{+}r)! \Gamma (j{+}\sigma {+}1) \Gamma (\jmath {+}\rho {+}1) \Gamma (j{+}r{+}\lambda ) \Gamma (2 n{+}r{-}\nu {+}\sigma {+}1)(2 n{+}r{-}\jmath {-}\nu {+}1)_{\jmath }}{\tau ^{\nu {-}\lambda {-}2 n}\,r! \jmath ! (j{-}r)! \Gamma (j{+}\lambda ) \Gamma (r{+}\sigma {+}1) \Gamma (n{+}r{-}\nu {+}1) \Gamma (2 n{+}r{+}\jmath {+}\lambda {-}\nu {+}1)},\\ \widetilde{{\mathcal {T}}}_{j,\jmath ,\alpha ,\beta ,n,\nu }&=\sum _{r=0}^j\sum _{s=\lceil \nu \rceil }^{n{+}r}\frac{({-}1)^{j{-}r} s! \left( {\begin{array}{c}n{+}r\\ s\end{array}}\right) \Gamma (j{+}\sigma {+}1) \Gamma (\jmath {+}\rho {+}1)\Gamma (j{+}r{+}\lambda ) \Gamma (n{+}s{-}\nu {+}\sigma {+}1)(n{+}s{-}\jmath {-}\nu {+}1)_{\jmath }}{ \tau ^{r{-}\lambda {+}\nu {-}n{-}s}\alpha ^{{-}s}\,\beta ^{s{-}n{-}r}\,r! \jmath ! (j{-}r)! \Gamma (j{+}\lambda ) \Gamma (r{+}\sigma {+}1) \Gamma (s{-}\nu {+}1) \Gamma (n{+}s{+}\jmath {+}\lambda {-}\nu {+}1)}. \end{aligned}\nonumber \\ \end{aligned}$$

(15)

In virtue of (10) and (14), we have

$$\begin{aligned} {\textbf{A}}={\mathcal {T}}_{j,\jmath ,n,\nu _n},\qquad \qquad {\textbf{B}}_k=\widetilde{{\mathcal {T}}}_{j,\jmath ,\alpha _k,\beta _k,n,\nu _k}. \end{aligned}$$

(16)

Finally, we use a suitable solver to find the unknowns vector ${\textbf{C}}$.

3 Time-fractional delay partial differential equations

In this section, we apply the numerical method for the TFDPDEs

$$\begin{aligned}&D_t^{\nu }\,Y (x,t)+\mu _1\, D_t^{\nu }\,Y (x,\alpha _1\,t+\beta _1)\nonumber \\&\quad =\mu _2\, \partial _{xx}\,Y (x,t)+ \mu _3\,\partial _{xx}\,Y (x,\alpha _2\,t+\beta _2) +\mu _4\,Y (x,\alpha _3\,t+\beta _3)\nonumber \\&\qquad +\mu _5\,Y (\alpha _4\,x+\beta _4,t)+\mu _6 Y (\alpha _5\,x+\beta _5,\alpha _6\,t+\beta _6)+p(x,t), \end{aligned}$$

(17)

subject to

$$\begin{aligned} Y (x,0)=0,\qquad Y (0,t)=Y (\ell ,t)=0, \end{aligned}$$

(18)

where $0\le x \le \ell ,\ 0\le t \le \tau ,$ $0< \nu <1,$ while $\mu _\iota ,\alpha _\iota ,\beta _\iota$ for $\iota =1(1)6,$ are given constants, and $D_t^{\nu }\,Y (x,t)$ denotes the CF-derivative of order $\nu ,$ w.r.t. t. Defining the following spaces

$$\begin{aligned} \begin{aligned} \bar{{\mathcal {J}}}_{N_2}&=\text {span}\{J^{(\rho ,\sigma )}_{0,\ell }(x),J^{(\rho ,\sigma )}_{1,\ell }(x),\ldots ,J^{(\rho ,\sigma )}_{N_2-2,\ell }(x)\},\\ {\mathcal {J}}_{N_1}&=\text {span}\{J^{(\rho ,\sigma )}_{0,\tau }(t),J^{(\rho ,\sigma )}_{1,\tau }(t),\ldots ,J^{(\rho ,\sigma )}_{N_1-1,\tau }(t)\},\\ \end{aligned}\end{aligned}$$

(19)

and

$$\begin{aligned} \begin{aligned} \mho _{N_2}&=\{\phi (x)\,\in \bar{{\mathcal {J}}}_{N_2}: \phi (0)=\phi (\ell )=0\},\\ \Omega _{N_1}&=\{\psi (t)\,\in {\mathcal {J}}_{N_1}: \psi (0)=0\}. \end{aligned}\end{aligned}$$

(20)

As a time-space spectral method, we approximate the solution of the TFDPDE (17)–(18) by a truncated series of shifted Jacobi polynomials as follows

$$\begin{aligned} Y _{N_2,N_1}(x,t)=\sum _{i=0}^{N_2-2}\sum _{j=0}^{N_1-1}c_{ij}\,\phi _i(x)\,\psi _j(t), \end{aligned}$$

(21)

where

$$\begin{aligned} \begin{aligned} \phi _i(x)&=x\,(\ell -x)\,J^{(\rho ,\sigma )}_{i,\ell }(x),\\ \psi _j(t)&=t\,J^{(\rho ,\sigma )}_{j,\tau }(t). \end{aligned}\end{aligned}$$

(22)

Also, we have to find $Y _{N_2,N_1}(x,t)\in \mho _{N_2}\times \Omega _{N_1},$ such that

where

is the scalar inner product w.r.t. weighted space with

(23)

Using (21), we get

If we denote

(24)

where $0\le \imath \le N_2-2,\ 0\le \jmath \le N_1-1,$ then the main problem is equivalent to

$$\begin{aligned} \left( {\mathcal {A}}+{\mathcal {B}}+{\mathcal {D}}+{\mathcal {E}}+{\mathcal {F}}+{\mathcal {G}}+{\mathcal {H}}\right) {\mathcal {C}}={\mathcal {P}}, \end{aligned}$$

(25)

where

$$\begin{aligned}{\mathcal {C}}=\{c_{00},c_{01},\cdots ,c_{0N_1-1},c_{10},c_{11},\cdots ,c_{1N_1-1},\cdots ,c_{N_2-2N_1-1}\}.\end{aligned}$$

Using (22), we can write

$$\begin{aligned} \begin{aligned} \phi _i(x)&=\sum _{r=0}^i \frac{(-1)^{i-r} \Gamma (i+\sigma +1) \Gamma (i+r+\lambda )}{r! \ell ^r (i-r)! \Gamma (i+\lambda ) \Gamma (r+\sigma +1)}\,x\,(\ell -x),\\ \phi _i(\alpha \,x+\beta )&=\sum _{r=0}^i \frac{(-1)^{i-r} \Gamma (i+\sigma +1) \Gamma (i+r+\lambda )}{r! \ell ^r (i-r)! \Gamma (i+\lambda ) \Gamma (r+\sigma +1)}\,(\alpha \,x+\beta )^{r+1} (\ell -(\alpha \,x+\beta )), \end{aligned}\end{aligned}$$

(26)

hence,

$$\begin{aligned}{} & {} \frac{\partial ^{q}}{\partial x^q}\phi _i(x)=\sum _{r=0}^i \frac{(-1)^{i-r} \Gamma (i+\sigma +1) \Gamma (i+r+\lambda )}{r! \ell ^r (i-r)! \Gamma (i+\lambda ) \Gamma (r+\sigma +1)} \,x^{r-q+1} \nonumber \\{} & {} \quad \Big (\ell (r-q+2)_q-(r-q+3)_q\,x\Big ). \end{aligned}$$

(27)

In the same manner as in the previous section, we get

(28)

where

$$\begin{aligned} {\mathcal {X}}_{i,\imath ,q}=\sum _{r=0}^i \frac{(-1)^{i-r} \Gamma (i+\sigma +1) \Gamma (i+r+\lambda )}{r! \ell ^r (i-r)! \Gamma (r+\sigma +1) \Gamma (i+\lambda )}\,\Big (\ell \,\xi _{\imath ,r-1,q}-\xi _{\imath ,r,q}\Big ), \end{aligned}$$

(29)

and

$$\begin{aligned} \xi _{\imath ,r,q}=\frac{\ell ^{\lambda -q +r+4}\,\Gamma (\imath +\rho +1) \Gamma (r-q+\sigma +4)(r-\imath -q+5)_{\imath -1}(r-q+3)_{q}}{\imath !(\rho +(\rho +1) (r-q+3)-\imath (\lambda +\imath )+1)^{-1}\Gamma (r+\imath -q+\lambda +5)}, \end{aligned}$$

(30)

while

$$\begin{aligned} \widetilde{{\mathcal {X}}}_{i,\imath ,\alpha ,\beta }=\sum _{r=0}^i \frac{(-1)^{i-r} \Gamma (i+\sigma +1) \Gamma (i+r+\lambda )}{r! \ell ^r (i-r)! \Gamma (r+\sigma +1) \Gamma (i+\lambda )}\,\Big (\ell \, \zeta _{\imath ,r-1,\alpha ,\beta }-\zeta _{\imath ,r,\alpha ,\beta }\Big ), \end{aligned}$$

(31)

where

$$\begin{aligned} \zeta _{\imath ,r,\alpha ,\beta }=\sum _{s=0}^{r+2}\frac{\ell ^{\lambda +s+2}\alpha ^s\beta ^{r-s+2} \left( {\begin{array}{c}r+2\\ s\end{array}}\right) \Gamma (s+\sigma +2) \Gamma (\imath +\rho +1)(s-\imath +3)_{\imath -1}}{\imath ! \Gamma (s+\imath +\lambda +3)(\rho +(\rho +1) (s+1)-\imath (\lambda +\imath )+1)^{-1}}. \end{aligned}$$

(32)

In virtue of (26) and (32), we have

$$\begin{aligned} \begin{aligned} {\mathcal {A}}&={\mathcal {X}}_{i,\imath ,0}\,{\mathcal {T}}_{j,\jmath ,1,\nu },\\ {\mathcal {B}}&={\mathcal {X}}_{i,\imath ,0}\,\widetilde{{\mathcal {T}}}_{j,\jmath ,\alpha _1,\beta _1,1,\nu },\\ {\mathcal {D}}&={\mathcal {X}}_{i,\imath ,2}\,{\mathcal {T}}_{j,\jmath ,1,0},\\ {\mathcal {E}}&={\mathcal {X}}_{i,\imath ,2}\,\widetilde{{\mathcal {T}}}_{j,\jmath ,\alpha _2,\beta _2,1,0},\\ {\mathcal {F}}&={\mathcal {X}}_{i,\imath ,0}\,\widetilde{{\mathcal {T}}}_{j,\jmath ,\alpha _3,\beta _3,1,0},\\ {\mathcal {G}}&=\widetilde{{\mathcal {X}}}_{i,\imath ,\alpha _4,\beta _4}\,{\mathcal {T}}_{j,\jmath ,1,0},\\ {\mathcal {H}}&=\widetilde{{\mathcal {X}}}_{i,\imath ,\alpha _5,\beta _5}\,\widetilde{{\mathcal {T}}}_{j,\jmath ,\alpha _6,\beta _6,1,0}. \end{aligned} \end{aligned}$$

(33)

4 Theoretical analysis

This section aims to verify how effective the numerical solution of the suggested approach for problems (1) and (17). We start this section with a review of certain auxiliary lemmas that will be important later for the study of convergence and stability analysis for the proposed method.

4.1 Convergence analysis

Lemma 1

Alsuyuti et al. (2022) For any $\rho ,\sigma >-1$ and $j\ge nm;\,n,m\in \mathbb {N},$ then, the following nm-times repeated integration formula is valid

where is given in (7).

Lemma 2

Alsuyuti et al. (2022) For any non-negative number $j;\,j\ge nm$ and $\rho ,\sigma \ge -\frac{1}{2},$ the following inquality is valid

Lemma 3

Rainville (1971) For all non-negative number j and real number $\nu$, one has

$$\begin{aligned}\Gamma (j+\nu ) = {\mathcal {O}}(j^{\nu -1} j!). \end{aligned}$$

Lemma 4

Szegö (1975) If $\rho ,\sigma > -1$, then, $\mid J_{j,\tau }^{(\rho ,\sigma )}(t) \mid ={\mathcal {O}}(j^\iota ),$ where $\iota =\max (\rho ,\sigma ,-\frac{1}{2}).$

Theorem 1

If $Y (t)=t^n\,f(t)$ is expanded in infinite series of the basis functions $\psi _j(t)$ given as in (9), i.e.,

$$\begin{aligned} Y (t)=\sum _{j=0}^{\infty }c_{j}\,\psi _j(t),\quad t\in [0,\tau ]. \end{aligned}$$

(34)

Then this series converges uniformly to $Y (t),$ and the expansion coefficients $c_j$ satisfy the following inequality

$$\begin{aligned} \left| c_j\right| <{\mathcal {O}}\left( j^{1-nm}\right) ,\quad \forall j\ge nm+1, \end{aligned}$$

(35)

with $\left| f^{(nm)}(t)\right| \le \epsilon$ where $\epsilon$ is a positive constant.

Proof

Applying the orthogonality relation (5) to Eq. (34) under the assumption (9), then we can write

where $\hbar ^{(\rho ,\sigma )}_{j,\tau }$ and are given as in (6) and (7), respectively.

Now, if we assume that $Y (t)=t^n\,f(t),$ and with the aid of the relation (9), then we have

Applying the integration by parts nm-times, and in virtue of Lemma 1, we get

Hence,

Based on Lemmas 2 and 3, and after performing some manipulations, then we get (35), which ends the proof. $\square$

Theorem 2

If $Y (x,t)=t\,x\,(\ell -x)\,f(t)\,\hat{f}(x)$ is expanded in infinite series of the basis functions $\phi _i(x)$ and $\psi _j(t)$ given as in (22), respectively, i.e.,

$$\begin{aligned} Y (x,t)=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }c_{ij}\,\phi _i(x)\,\psi _j(t). \end{aligned}$$

(36)

Then this series converges uniformly to $Y (x,t),$ and the expansion coefficients $c_{ij}$ satisfy the following inequality

$$\begin{aligned} \left| c_{ij}\right| <{\mathcal {O}}\left( i^{1-2m}\,j^{1-m}\right) ,\quad \forall i\ge 2m+1,\,j\ge m+1, \end{aligned}$$

with $\left| \hat{f}^{(2m)}(x)\,f^{(m)}(t)\right| \le \varepsilon$ where $\varepsilon$ is a positive constant.

Proof

Applying the orthogonality relation (5) to Eq. (36), under the assumptions (22), then we can write

(37)

where $\hbar ^{(\rho ,\sigma )}_{j,\tau }$ and are given in (6) and (7), respectively.

Again, with the aid of Eq. (36) and the assumption $Y (x,t)=t\,x\,(\ell -x)\,f(t)\,\hat{f}(x)$, the coefficients $c_{ij}$ can be written as follows

where is given by (23), hence,

Applying the integration by parts 2m-times and m-times with respect to x and t,  respectively, and in virtue of Lemma 1, with the aid of Theorem 1 and Lemmas 2 and 3, and after performing some manipulations, we get

$$\begin{aligned} \left| c_{ij}\right| <{\mathcal {O}}\left( i^{1-2m}\,j^{1-m}\right) ,\quad \forall i\ge 2m+1,\,j\ge m+1, \end{aligned}$$

which ends the proof. $\square$

4.2 Stability analysis

Theorem 3

For the two consecutive approximations $Y _{N_1}(t)$ and $Y _{N_1+1}(t),$ we have the following estimate

$$\begin{aligned} \left| Y _{N_1+1}(t)-Y _{N_1}(t)\right| < {\mathcal {O}}(N_1^{\iota -nm+1}). \end{aligned}$$

Proof With the aid of Theorem 1 and Lemma 4, we have

$$\begin{aligned} \left| Y _{N_1+1}(t)-Y _{N_1}(t)\right|&=\left| \sum _{j=0}^{N_1-n+1} c_j\,\psi _j(t)-\sum _{j=0}^{N_1-n} c_j\,\psi _j(t)\right| \\&=\left| c_{N_1-n+1}\,\psi _{N_1-n+1}(t)\right| \\&\le \left| c_{N_1-n+1}\right| \,\left| \psi _{N_1-n+1}(t)\right| \\&< {\mathcal {O}}(N_1^{\iota -nm+1}). \end{aligned}$$

$\square$

Theorem 4

For the two consecutive approximations $Y _{N_2,N_1}(x,t)$ and $Y _{N_2+1,N_1+1}(x,t),$ we have the following estimate

$$\begin{aligned} \left| Y _{N_2+1,N_1+1}(x,t)-Y _{N_2,N_1}(x,t)\right| < {\mathcal {O}}\big (max(N_2^{\iota },N_1^{\iota })\big ), \end{aligned}$$

where $\iota =\max (\rho ,\sigma ,-\frac{1}{2}).$

Proof

Using a similar technique to that introduced for the proof of Theorem 3, we can prove this theorem. $\square$

5 Numerical verification

This section is confined to testing our proposed algorithm. For this purpose, we will present five numerical examples accompanied by presenting comparisons with some other techniques in the literature to demonstrate the efficiency and high accuracy of our proposed numerical algorithm.

Example 1

Consider the following FDDE (Amin et al. (2021))

$$\begin{aligned} D_t^{\frac{1}{2}}{} Y (t)=Y (t-1)-Y (t)+2t-1+\frac{8t^{\frac{3}{2}}}{3\sqrt{\pi }},\quad t\in [0,1], \end{aligned}$$

(38)

with $Y (0)=0$ and $Y (t)=t^2$ as the exact solution.

Amin et al. in Amin et al. (2021) raised this issue and used the SC method based on Haar wavelet and Gauss elimination techniques to reduce it into a system of linear algebraic equations. The best absolute errors achieved using the numerical approach presented in Amin et al. (2021) were around $10^{-7}$ with 2048 steps, see Table 1 in Amin et al. (2021). If we apply the numerical technique presented in Sect. 2 for solving the above problem with $N_1=4$ and $\{\rho ,\sigma \}=\{1,1\},$ then the approximate solution of $Y (t)$ might be composed as follows:

$$\begin{aligned} Y _{4}(t)=c_0\,t\, J^{(\rho ,\sigma )}_{0,\tau }(t)+c_1\, t\, J^{(\rho ,\sigma )}_{1,\tau }(t)+c_2\, t\, J^{(\rho ,\sigma )}_{2,\tau }(t)+c_3\, t\, J^{(\rho ,\sigma )}_{3,\tau }(t), \end{aligned}$$

(39)

and the vector ${\textbf{P}}$ can be expressed in writing as:

$$\begin{aligned}{\textbf{P}} = \left[ \frac{1}{60}+\frac{32}{297\sqrt{\pi }},\quad \frac{1}{30}+\frac{320}{3861\sqrt{\pi }},\quad \frac{1}{70}+\frac{32}{1287\sqrt{\pi }},\quad \frac{128}{65637\sqrt{\pi }} \right] ^T.\end{aligned}$$

Therefore, the FDDE (38) is identical to the system

$$\begin{aligned} \left( {\textbf{A}}-{\textbf{B}}_0+{\textbf{B}}_1\right) {\textbf{C}}={\textbf{P}}, \end{aligned}$$

(40)

where the matrices ${\textbf{A}},\ {\textbf{B}}_0$ and ${\textbf{B}}_1$ can be composed as follows:

$$\begin{aligned}{\textbf{A}}=\left( \begin{array}{ccccccc} \dfrac{8}{63\sqrt{\pi }} &{} &{} \dfrac{368}{2079\sqrt{\pi }} &{} &{} \dfrac{88}{819\sqrt{\pi }} &{} &{} \dfrac{11936}{225225\sqrt{\pi }} \\ &{} &{} &{} &{} &{} &{} \\ \dfrac{16}{231\sqrt{\pi }} &{} &{} \dfrac{5216}{27027\sqrt{\pi }} &{} &{} \dfrac{9808}{45045\sqrt{\pi }} &{} &{} \dfrac{35008}{255255\sqrt{\pi }} \\ &{} &{} &{} &{} &{} &{} \\ \dfrac{8}{1001\sqrt{\pi }} &{} &{} \dfrac{752}{9009\sqrt{\pi }} &{} &{} \dfrac{10408}{51051\sqrt{\pi }} &{} &{} \dfrac{1821216}{8083075\sqrt{\pi }} \\ &{} &{} &{} &{} &{} &{} \\ -\dfrac{32}{45045\sqrt{\pi }} &{} &{} \dfrac{21184}{2297295\sqrt{\pi }} &{} &{} \dfrac{1236832}{14549535\sqrt{\pi }} &{} &{} \dfrac{225664}{1119195\sqrt{\pi }} \\ \end{array} \right) ,\end{aligned}$$

$$\begin{aligned}{\textbf{B}}_0=\left( \begin{array}{ccccccccc} -\dfrac{1}{30} &{}&{} \dfrac{2}{15} &{}&{} -\dfrac{69}{140}&{}&{} \dfrac{28}{15}\\ &{}&{}&{}&{}&{}&{}\\ 0 &{}&{} -\dfrac{2}{105} &{}&{} \dfrac{1}{7}&{}&{} -\dfrac{50}{63}\\ &{}&{}&{}&{}&{}&{}\\ \dfrac{1}{140} &{}&{} -\dfrac{1}{35} &{}&{} \dfrac{13}{140}&{}&{} -\dfrac{9}{35}\\ &{}&{}&{}&{}&{}&{}\\ 0 &{}&{} \dfrac{2}{315} &{}&{} -\dfrac{1}{21}&{}&{} \dfrac{884}{3465}\\ \end{array} \right) ,\qquad {\textbf{B}}_1=\left( \begin{array}{ccccccccc} \dfrac{1}{20} &{}&{} \dfrac{1}{30} &{}&{} \dfrac{1}{140}&{}&{} 0\\ &{}&{}&{}&{}&{}&{}\\ \dfrac{1}{30} &{}&{} \dfrac{1}{21} &{}&{} \dfrac{1}{35}&{}&{} \dfrac{2}{315}\\ &{}&{}&{}&{}&{}&{}\\ \dfrac{1}{140} &{}&{} \dfrac{1}{35} &{}&{} \dfrac{11}{280}&{}&{} \dfrac{1}{42}\\ &{}&{}&{}&{}&{}&{}\\ 0 &{}&{} \dfrac{2}{315} &{}&{} \dfrac{1}{42}&{}&{} \dfrac{38}{1155}\\ \end{array} \right) .\end{aligned}$$

Solving the system (40) using any suitable solver, the unknown coefficients vector ${\textbf{C}}$ can be determined as follows:

$$\begin{aligned}{\textbf{C}}=\left[ \frac{1}{2},\quad \frac{1}{4},\quad 0,\quad 0\right] ^T,\end{aligned}$$

which leads to the exact solution

$$\begin{aligned}{} Y _4(t)=\frac{1}{2}\, t\, J^{(\rho ,\sigma )}_{0,\tau }(t)+\frac{1}{4}\, t\, J^{(\rho ,\sigma )}_{1,\tau }(t)=t^2.\end{aligned}$$

Example 2

Consider the fractional pantograph differential equation (Syam et al. 2021)

$$\begin{aligned} D_t^{\nu }\,Y (t)=Y (t)+\frac{1}{10}\,Y (\frac{1}{10}\, t)+p(t),\quad t\in [0,1],\, 0<\nu \le 1, \end{aligned}$$

where

$$\begin{aligned} p(t)=\frac{2\nu }{\Gamma (3-\nu )}\,t^{2-\nu }-\frac{11}{10}-\nu \, t^2-\frac{\nu }{1000}\,t^2, \end{aligned}$$

with $Y (0)=1$ and $Y (t)= 1+\nu \, t^2$ as the exact solution.

Syam et al. (2021) considered this problem and applied the modified operational matrix method (MOMM) for getting the numerical solution. Table 1 compares the absolute errors of $Y (t)$ at $\{\rho ,\sigma \}= \{0,0\}$ with distinct values of $\nu$ against the numerical results given by the MOMM (Syam et al. 2021).

Table 1 Absolute errors of $Y (t)$ at $\{\rho ,\sigma \}= \{0,0\}$ with distinct $\nu$ for Example 2

Example 3

Consider the following TFDPDE (Hosseinpour et al. 2018)

$$\begin{aligned} \begin{aligned} D^{\nu }_tY (x,t)&=\frac{\partial ^2}{\partial x^2}{} Y (x,t)+Y (x,t-1) +x^2\left( \frac{\Gamma (\frac{8}{3})t^{\frac{5}{3}-\nu }}{\Gamma (\frac{8}{3}-\nu )}+\frac{\Gamma (\frac{7}{3})t^{\frac{4}{3}-\nu }}{\Gamma (\frac{7}{3}-\nu )}\right) \\&\quad -2\left( t^{\frac{5}{3}}+t^{\frac{4}{3}}\right) -x^2\left( (t-1)^{\frac{5}{3}}+(t-1)^{\frac{4}{3}}\right) , \end{aligned} \end{aligned}$$

subject to

$$\begin{aligned} Y (x,0)=Y (0,t)=0,\quad Y (1,t)=t^{\frac{5}{3}}+t^{\frac{4}{3}}, \qquad x\in [0,1],\ t\in [0,2]. \end{aligned}$$

The exact solution is $Y (x,t)= x^2 \left( t^{\frac{5}{3}}+t^{\frac{4}{3}}\right) .$

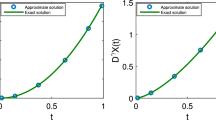
To approximate the solution to this problem, Hosseinpour et al. (2018) introduced two new numerical approaches based on the Pade approximation method with Legendre polynomial (PALP) and Muntz-Legendre polynomial (PAMLP). The authors in Hosseinpour et al. (2018) used the Pade approximation and two-sided Laplace transformations with the operational matrix of fractional derivatives to transform the main problem into a system of FPDEs without delay. In Table 2, we compare the absolute errors of $Y (x,t)$ achieved using the proposed approach against the PALP and PAMLP approaches at $\{N_2,N_1\}=\{5,5\}$ and $\nu =0.9.$ Fig. 1 obtain the approximate solution of Y(x, 1.8) at $\{N_2,N_1\}=\{5,5\},$ $\{\rho ,\sigma \}= \{0,0\}$ and $\nu =0.5$.

Table 2 Comparison of the absolute errors of Y(x, 1.8) using the new approach against the PALP and PAMLP methods (Hosseinpour et al. 2018) for Example 3

Example 4

Consider the time-fractional neutral delay parabolic equation (Usman et al. 2020)

$$\begin{aligned} \begin{aligned} D^{\nu }_t\,Y (x,t)+D^{\nu }_t\,Y (x,t-\frac{1}{10})=\frac{1}{2}\frac{\partial ^2}{\partial x^2}{} Y (x,t)+\frac{1}{2}\frac{\partial ^2}{\partial x^2}{} Y (x,t-\frac{1}{10}) +p(x,t), \end{aligned} \end{aligned}$$

subject to

$$\begin{aligned} Y (x,0)=0,\quad Y (0,t)=Y (1,t)=t^2, \qquad x\in [0,1],\ t\in [0,2], \end{aligned}$$

and select p(x, t) so that the exact solution is $Y (x,t)=t^2 \cos (\pi x).$

Usman et al. (2020) considered this problem and applied the SC approach for getting the numerical solution. They constructed the operational matrices of fractional-order integration and those of differentiation with the delay operational matrix based on shifted Gegenbauer polynomials to transform them into a system of algebraic equations. The most accurately results obtained by the SC approach (Usman et al. 2020) were around $10^{-15}$ using $(N_2=20)$, see Figures 6 and 7 in Usman et al. (2020). In Table 3, we list the maximum absolute errors of $Y (x,t)$ at $\nu =\{0.5,0.7,0.9\},\ \{\rho ,\sigma \}=\{0,0\}$ with $N_1=3$ and $N_2=\{4,6,8,10,12,14,16,18\}.$ Fig. 2 obtains the convergence of the new numerical approach in the perspective of the function $Log_{10}L_\infty$ for $Y (x,t)$ at $N_1=3,$ $\{\rho ,\sigma \}= \{0,0\}$ and $\nu =\{0.5,0.7,0.9\}$ with different values of $N_2$. Figure 3 obtain the approximate solution of $Y (x,t)$ at $\{N_2,N_1\}=\{6,6\},$ $\{\rho ,\sigma \}= \{1,1\}$ and $\nu =0.7$.

Fig. 1

Approximate solution of $Y (x,t)$ at $\{N_2,N_1\}=\{5,5\},$ $\{\rho ,\sigma \}= \{0,0\}$ and $\nu =0.5$ for Example 3

Table 3 Maximum absolute errors of $Y (x,t)$ at $\nu =\{0.5,0.7,0.9\}$ with $N_1=3$ and various choices of $N_2$ for Example 4

Fig. 2

$Log_{10}L_\infty$ of $Y (x,t)$ at $N_1=3,$ $\{\rho ,\sigma \}= \{0,0\}$ and $\nu =\{0.5,0.7,0.9\}$ with distinct values of $N_2$ for Example 4

Fig. 3

Approximate solution of $Y (x,t)$ at $\{N_2,N_1\}=\{6,6\},$ $\{\rho ,\sigma \}= \{1,1\}$ and $\nu =0.7$ for Example 4

Example 5

Consider the following TFDPDE (Dehestani et al. 2019)

$$\begin{aligned} \begin{aligned} D^{\nu }_t\,Y (x,t)&=\frac{\partial ^2}{\partial x^2}{} Y (x,t)-Y (x,t-1) +\frac{\Gamma (3)}{\Gamma (3-\nu )}(2x-x^2)t^{2-\nu }\\&\quad +2t^2+x(2-x)(t-1)^2, \end{aligned} \end{aligned}$$

subject to

$$\begin{aligned} Y (x,0)=Y (0,t)=Y (1,t)=0, \qquad x\in [0,2],\ t\in [0,1]. \end{aligned}$$

The exact solution is $Y (x,t)=t^2 (2x- x^2).$

To solve the current problem, Dehestani et al. (2019) applied the SC technique with the help of the Genocchi wavelet method. The most accurate results of absolute errors of $Y (x,t)$ given in Dehestani et al. (2019) were around $10^{-14}$, where the absolute errors achieved using our algorithm were around $10^{-16}$. Figures 4 and 5 obtain the absolute errors and approximate solution, respectively, of $Y (x,t)$ at $\{N_2,N_1\}=\{3,3\},$ $\{\rho ,\sigma \}= \{1,1\}$ and $\nu =0.7$.

Fig. 4

Absolute errors of $Y (x,t)$ at $\{N_2,N_1\}=\{3,3\},$ $\{\rho ,\sigma \}= \{1,1\}$ and $\nu =0.7$ for Example 5

Fig. 5

Approximate solution of $Y (x,t)$ at $\{N_2,N_1\}=\{3,3\},$ $\{\rho ,\sigma \}= \{1,1\}$ and $\nu =0.7$ for Example 5

6 Concluding remarks

In the current study, we developed a numerical method for solving the FDDEs. The suggested technique is based on the SG method and shifted Jacobi polynomials. A novel approach is used to convert the core problem into another by solving a system of algebraic equations. The SG approach is also applied for TFDPDEs in both temporal and spatial axes. Moreover, the convergence and stability of this scheme are rigorously established. To our knowledge, it is the first attempt to deal with TFDPDEs using the SG algorithm or shifted Jacobi polynomials. By providing five test problems and contrasting the outcomes with those obtained using alternative results and the exact solution, the effectiveness of the suggested approach is validated. The new results ensure that the suggested method is more accurate than the collocation Haar wavelet, Bernoulli wavelet operational matrix, Pade approximation Legendre polynomial, Pade approximation Muntz-Legendre polynomial, collocation Gegenbauer and collocation Genocchi wavelet methods. We also mention that the codes were written and debugged using Mathematica version 12 software using a PC machine, with Intel(R) Core(TM) i5-8500 CPU @ 3.00 GHz, 12.00 GB of RAM.