Abstract
This paper studies the efficiency assessment of Decision Making Units (DMUs) when their inputs and outputs are fuzzy sets. An axiomatic derivation of the fuzzy production possibility set is presented and a fuzzy enhanced Russell graph measure is formulated using a fuzzy arithmetic approach. The proposed approach uses polygonal fuzzy sets and LU-fuzzy partial orders, and provides crisp efficiency measures (and associated efficiency ranking) as well as fuzzy efficient targets. The proposed approach has been compared with other fuzzy DEA approaches on different datasets from the literature, and the results show that it has more discriminant power and more flexibility in modelling the input and output data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Assessing and improving efficiency is a widespread and important problem in today’s competitive marketplace. But not only firms but all types of organizations, including public bodies, need to make an efficient use of the limited resources available. And not only the benefits involve reduced costs and increased revenue but also reduced natural resources depletion, reduced pollution, and increased sustainability. Hence, the need to develop efficiency assessment models and tools that can be used in practical settings where uncertainty may be present in the data.
Data envelopment analysis (DEA) is the methodology most commonly used for assessing the relative efficiency of a set of Decision Making Units (DMUs). The first step in DEA is deriving a Production Possibility Set (PPS) from the input and output data of the observed DMUs and using certain axioms (such as envelopment, free disposability, and convexity). The non-dominated subset of the PPS corresponds to the efficient frontier. If a DMU lies on the efficient frontier it is said to be efficient. Otherwise, it is inefficient and the distance to the efficient frontier, which is a function of the potential input and output improvements (i.e., the input and output slacks), is used to compute an efficiency score. There are different ways to define the PPS (e.g., Constant Returns to Scale, CRS, Variable Returns to Scale, VRS) as well as different ways to compute the efficiency score. In this paper, we will use the enhanced Russell graph measure (ERM) proposed in Pastor et al. (1999), which, in the case of crisp data, is equivalent to the slacks-based measure of efficiency (SBM) of Tone (2001).
Although still a very active research field, the DEA methodology is very well developed in the case of crisp data. There are however situations in which there is uncertainty in the data. Dyson and Shale (2010) discusses possible sources of uncertainty in DEA and reviews different approaches for handling this uncertainty. A classic approach for handling data uncertainty is stochastic DEA methods, such as Chance Constrained DEA (Cooper et al. 2002, 2004) or Monte Carlo simulation (e.g., Kao and Liu 2009, 2019). These approaches assume that the input and output data are random variables whose joint distribution function is known (generally a multivariate normal) or can be fitted from historical data (e.g., a beta distribution). The resulting efficient frontier is random and so are the efficiency scores. Olesen and Petersen (2016) present a thorough review of stochastic DEA approaches, including Stochastic Frontier Analysis and Chance-constrained DEA. The reader is also referred to Salahi et al. (2019) and Izadikhah (2021) for examples of Robust optimization and Chance-constrained DEA approaches, respectively, that also use the ERM efficiency considered in this paper.
An alternative to considering random data is modelling data uncertainty using fuzzy sets. Thus, often, the data variability is not due to randomness. There can be multiple factors such as inherent data variability, effectiveness of measurement instruments, multiplicity of data sources, etc. data can lead to uncertainty in the input and output data. Take, for example, a typical input variable such as the number of employees of a certain company or business unit. That variable is not random, but can fluctuate from 1 month to another (or even from 1 week to another) along the year and it may not be easy to reach a single, crisp number to represent that variable. The same happens with typical output variables like the number of customers attended or the number of transactions processed in cases in which a strict and exhaustive counting of all inquiries and requests attended may not exist and the corresponding numbers are only known approximately. Fuzzy sets have proved very helpful to model these type of uncertainties. Hence, applying DEA to fuzzy data has been the subject of many studies [see Hatami-Marbini et al. (2011) and Emrouznejad et al. (2014) for a survey and a taxonomy], although many of the existing approaches have drawbacks (Soleimani-damaneh et al. 2006). A number of Fuzzy DEA (FDEA) approaches are based on the \(\alpha \)-level set (i.e., \(\alpha \)-cut) concept [e.g., Kao and Liu (2000), Saati et al. (2002)]. Another large group of FDEA studies use a fuzzy ranking approach [e.g., Guo and Tanaka (2001), León et al. (2003)], Ghasemi et al. (2015)]. Other researchers use a possibility [e.g., Lertworasirikul et al. (2003), or a fuzzy arithmetic approach [e.g., Wang et al. (2005)] or consider fuzzy random/type-2 fuzzy sets [e.g., Tavana et al. (2013)]. Another category of FDEA approaches, and which has been thoroughly reviewed in Peykani et al. (2021), is Fuzzy Chance-constrained DEA. Thus, it can be said that FDEA is a fruitful and growing area of efficiency analysis under uncertainty, with many new approaches and applications being reported [e.g., Kachouei et al. (2020), Ebrahimnejad and Amani (2021)]. And not only can FDEA be applied in efficiency analysis, but also it can be used to solve multiobjective fuzzy optimization problems (e.g., Bagheri et al. 2020, 2021a, b).
Most existing FDEA approaches use a radial metric and an input or an output orientation. There are many situations, however, in which both inputs and outputs should be improved and not necessarily in the same proportions. In those cases, a non-radial and non-oriented approach, like the proposed fuzzy ERM (FERM) model, is adequate. In this paper, an axiomatic approach to derive a Fuzzy PPS (FPPS) is presented and an FERM model is proposed. Only a few researchers have attempted to explicitly build a FPPS from the observations. Thus, Allahviranloo et al. (2007) use the Extension principle to define an FPPS, while Raei Nojehdehi et al. (2012) use a geometrical approach based on t-norms.
Table 1 summarizes the existing fuzzy ERM/SBM approaches together with other fuzzy DEA methods for comparison. As regards FERM approaches, note that a fuzzy ranking approach is used in Jahanshahloo et al. (2004), Ahmady et al. (2015) and Izadikhah et al. (2017). Hsiao et al. (2011) and Puri and Yadav (2013) use the \(\alpha \)-level set approach of Kao and Liu (2000), while Saati and Memariani (2009) use the \(\alpha \)-level set approach of Saati et al. (2002). Chen et al. (2013) also use \(\alpha \)-cuts and the Extension Principle. Both Hsiao et al. (2011) and Chen et al. (2013) also formulate a Fuzzy Super SBM model. Wu et al. (2015) proposed the \(\alpha \)-level set FERM approach with undesirable outputs. Izadikhah and Khoshroo (2018) also considered undesirable outputs and proposed a possibility approach to solve a super-efficiency FERM model. Finally, Azadi et al. (2015) proposed a possibility approach based on a multiplier ERM formulation.
As it can be seen in Table 1, the FERM approach proposed in this paper uses polygonal fuzzy numbers, an LU-fuzzy partial order, and an axiomatic derivation of the fuzzy PPS. With respect to polygonal fuzzy numbers, Stefanini et al. (2006) proposed using a uniform subdivision of the interval [0, 1] to get a finite number of \(\alpha \)-cuts. Báez-Sánchez et al. (2012) study the polygonal fuzzy numbers as a particular case of parametric representation of fuzzy numbers with linear interpolation. As an application of polygonal fuzzy numbers, Chen and Adam (2018) has recently proposed a new transformation-based weighted fuzzy interpolative reasoning method. In this paper, we consider polygonal fuzzy number to model or approximate inputs and outputs. No ranking functions or expected values on the polygonal fuzzy numbers are needed to formulate the corresponding crisp model.
Another difference between the existing and the proposed FERM approach is that we compute a crisp efficiency score instead of a fuzzy efficiency score. Fuzzy efficiency scores are more consistent with the fuzzy nature of the data, but the crisp efficiency scores are simpler to understand and apply for practitioners. In this paper, we have opted for crisp efficiency scores. Computing fuzzy efficiency scores using a fully fuzzy approach and LU-fuzzy partial orders is also possible (e.g., Arana-Jiménez et al. 2020), but the process is necessarily much more involved. In this paper, we have searched for a compromise between fuzziness/information loss and simplicity.
Therefore, the contributions of the proposed approach are several. One of them is the use of polygonal fuzzy numbers and a LU-fuzzy partial order. Another is the axiomatic derivation of the fuzzy production possibility set that contains all the fuzzy operating points that are deemed feasible. Using this fuzzy DEA technology, a simple fuzzy optimization model allows computing a crisp efficiency score and a fuzzy target for each production unit. To solve the proposed FERM model, a crisp optimization model is formulated that, although in principle is non-linear, can be appropriately linearized. In the end, we have a simple and effective FDEA approach for assessing the efficiency and projecting the production units.
The paper is organized as follows. In Sect. 2, the crisp DEA PPS and ERM model are reviewed. To consider and model the uncertainty in the data, in Sect. 3, polygonal fuzzy numbers are presented. Suitable notations and rules to deal with arithmetic operations and LU-fuzzy partial orders are also derived. Then, in Sect. 4, assuming that inputs and outputs are given by polygonal fuzzy numbers, the corresponding fuzzy PPS is derived, a fuzzy ERM model is formulated and a method to solve it is presented. Section 5 illustrates the proposed approach and compares it with existing approaches using different datasets from the literature. Finally, in Sect. 6, conclusions are drawn and further research outlined.
2 Crisp production possibility set and ERM model
Let us consider a set of n DMUs. For \(j\in J=\{1,\ldots ,n\}\), each \(DMU_j\) has m inputs \(X_j = (x_{1j},\ldots ,x_{mj}) \in {\mathbb {R}}^m\), produces s outputs \(Y_j = (y_{1j},\ldots ,y_{sj}) \in {\mathbb {R}}^s\). In the classic Charnes et al. (1978) DEA model, the production possibility set (PPS) or technology, denoted by T, satisfies the following axioms:
-
(A1)
Envelopment \((X_j,Y_j)\in T\), for all \(j\in J\).
-
(A2)
Free disposability \((x,y)\in T\), \((x',y')\in {\mathbb {R}}^{m+s}\), \(x'\geqq x\), \(y'\leqq y\Rightarrow (x',y')\in T\).
-
(A3)
Convexity \((x,y), (x',y')\in T\), then \(\lambda (x,y)+(1-\lambda )(x',y')\in T\), for all \(\lambda \in [0,1]\).
-
(A4)
Scalability \((x,y)\in T\Rightarrow (\lambda x,\lambda y)\in T\), for all \(\lambda \in {\mathbb {R}}_+\).
Following the minimum extrapolation principle (see Banker et al. 1984), the DEA PPS, which contains all the feasible input-output bundles, is the intersection of all the sets that satisfy axioms (A1)–(A4), and can be expressed as
In radial DEA models, see Charnes et al. (1978), the efficiency of a DMU\(_p\) is measured in two ways. One way is reducing all the inputs equi-proportionally without decreasing the outputs (input-oriented model), and then, the problem is formulated as \(\mathrm{min} \{\theta _p \in {\mathbb {R}}_{+} | (\theta _p x_p, y_p)\in T \}\). The second one consists in expanding all the outputs equi-proportionally without increasing the inputs (output-oriented model), i.e., \(\mathrm{max} \{\theta _p \in {\mathbb {R}}_{+} | (x_p, \theta _p y_P)\in T \}\).
There exist other DEA approaches in which the reductions of inputs and outputs are not equi-proportional. In particular, Pastor et al. (1999) proposed the following Enhanced Russell Graph Efficiency Measure (ERM):
where \(\lambda _j\), \(j=1,\ldots ,n\), are the intensity variable of each DMU\(_j\) for defining the corresponding efficient target of DMU\(_p\). R is interpreted as the the ratio between the average input reduction and the average output increase. Pastor et al. (1999) showed some interesting properties of ERM. Thus, \(0<R\le 1\), R is units invariant and a DMU\(_j\) is efficient if and only if \(R=1\).
3 Polygonal fuzzy numbers
In this paper, we model the uncertainty in the data, and hence on the production possibility set, by means of polygonal fuzzy numbers. In this regard, in this section, we present the definition of polygonal fuzzy numbers, corresponding arithmetic operations, and inequality relationships using LU-partial orders on fuzzy sets. Furthermore, we derive certain properties that facilitate the modelling of the corresponding PPS which we propose in Sect. 4. To this end, it is necessary to establish the following notation and results.
We denote by \({\mathcal {K}}_{C}=\left\{ \left[ {\underline{a}},{\overline{a}}\right] \;|\; {\underline{a}},{\overline{a}}\in {\mathbb {R}} \text{ and } {\underline{a}}\le {\overline{a}}\right\} \) the family of all bounded closed intervals in \({\mathbb {R}}\). A fuzzy set on \({\mathbb {R}}^{n}\) is a mapping \(u:{\mathbb {R}}^{n}\rightarrow [0,1]\). For each fuzzy set u, we denote its \(\alpha \)-level set as \([u]^{\alpha }=\{x\in {\mathbb {R}}^{n}\) | \(u(x)\ge \alpha \}\) for any \( \alpha \in (0,1]\), and its support as \( \mathrm{supp}(u)=\{x\in {\mathbb {R}}^{n}\) | \(u(x)>0\}\). The closure of \(\mathrm{supp}(u)\) defines the 0-level of u, i.e., \([u]^{0}=cl(supp(u))\) where cl(M) means the closure of the subset \(M\subset {\mathbb {R}}^{n}\). Following Dubois and Prade (1978, 1980), a fuzzy set u on \({\mathbb {R}}\) is said to be a fuzzy number if (i) u is normal, this is there exists \(x_0 \in {\mathbb {R}}\), such that \(u(x_0)=1\), (ii) upper semi-continuous function, (iii) convex, and (iv) \([u]^0\) is compact. \({\mathcal {F}}_{C}\) denotes the family of all fuzzy numbers. The \(\alpha \)-levels of a fuzzy number can be represented as \([u]^{\alpha }=\left[ {\underline{u}}_{\alpha }, {\overline{u}}_{\alpha }\right] \in {\mathcal {K}}_{C}\), \({\underline{u}}_{\alpha },{\overline{u}} _{\alpha }\in {\mathbb {R}}\). Although there are many parametrical families of fuzzy numbers [see Báez-Sánchez et al. (2012) and Hanss (2005) for a complete description of these families], two of the most used families of fuzzy numbers are triangular and trapezoidal fuzzy numbers, because of their easy modeling and interpretation [see, for instance, Dubois and Prade (1978, 1980), Kaufmann and Gupta (1985), Khan et al. (2013), Lotfi et al. (2009), Stefanini et al. (2006)]. As an extension of these two families of fuzzy numbers, and inspired in other definitions of parametric fuzzy numbers [see, for instance, Stefanini et al. (2006), Stefanini and Bede (2014), Hanss (2005), Báez-Sánchez et al. (2012)], below we review the concept of polygonal fuzzy numbers, introduced by Báez-Sánchez et al. (2012) as a particular case of polygonal fuzzy sets.
Definition 1
Given a partition of the interval [0, 1], \({\mathcal {P}}_k=\{\alpha _i:i=0,1\ldots ,k\}\), with \(0=\alpha _0< \alpha _1< ,\ldots ,<\alpha _k=1\), a fuzzy number \({\tilde{a}}\) is said to be a k-polygonal fuzzy number with respect to \({\mathcal {P}}_k\) if its \(\alpha \)-levels satisfy \([{\tilde{a}}]^{\alpha }=(1-\lambda )[{\tilde{a}}]^{\alpha _{i-1}}+\lambda [{\tilde{a}}]^{\alpha _{i}}\), where \(0\le \alpha _{i-1}<\alpha \le \alpha _{i}\le 1\) for some \(i=0,\ldots , k-1\) and \(\lambda =\lambda (\alpha )=(\alpha -\alpha _{i-1})/(\alpha _{i}-\alpha _{i-1})\).
In terms of their membership function instead of their \(\alpha \)-levels, a polygonal fuzzy number can alternatively be defined as follows.
Proposition 1
Given a partition of the interval [0, 1], \({\mathcal {P}}_k=\{\alpha _i:i=0,1\ldots ,k\}\), with \(0=\alpha _0< \alpha _1< ,\ldots ,<\alpha _k=1\), for \(k\in N\), a fuzzy number \({\tilde{a}}\) is a k-polygonal fuzzy number with respect to \({\mathcal {P}}_k\) if and only if there exist \(a^{-}_{0},a^{-}_{1},\ldots ,a^{-}_{k},a^{+}_{k},\dots , a^{+}_{1},a^{+}_{0}\in {\mathbb {R}}\) with \(a^{-}_{0}\le a^{-}_{1}\le \cdots \le a^{-}_{k}\le a^{+}_{k}\le \cdots \le a^{+}_{1}\le a^{+}_{0}\), such that its membership function is
A proof of Proposition 1 can be found in Appendix A. As a result of Proposition 1, we can denote a k-polygonal fuzzy number with respect to \({\mathcal {P}}_k=\{\alpha _i:i=0,1\dots ,k\}\) as \({\tilde{a}}=({a^{-}_{0},a^{-}_{1},\ldots ,a^{-}_{k},a^{+}_{k},\ldots , a^{+}_{1},a^{+}_{0}})\). For the sake of simplicity, in the sequel, we will assume that \(\alpha _i=\frac{i}{k}\), and then \({\tilde{a}}\) is said to be a regular k-polygonal fuzzy number. We denote the set of all regular k-polygonal fuzzy numbers as \(RPFN_k\). Thus, \({\tilde{a}}=(a^{-}_{0},a^{-}_{1},a^{+}_{1},a^{+}_{0})\) corresponds to a trapezoidal fuzzy number. And, if \(a^{-}_{1} = a^{+}_{1}\), then \({\tilde{a}}\) is a triangular fuzzy number, and it can be noted as \({\tilde{a}}=(a^{-}, a, a^{+})\). Finally, we denote \({\tilde{0}}\) and \({\tilde{1}}\) as the regular polygonal fuzzy numbers whose components are all 0 and 1, respectively. Figure 1 illustrates examples of both, a general k-polygonal fuzzy number, on the top, and regular 1-polygonal and 2-polygonal fuzzy numbers, on the bottom.
Representation for a general k-polygonal Fuzzy number \({\tilde{a}}=({a^{-}_{0},a^{-}_{1},\ldots ,a^{-}_{k},a^{+}_{k},\ldots , a^{+}_{1},a^{+}_{0}})\), with respect to a partition \(\alpha _0=0 < \alpha _1 \le \cdots \le \alpha _k=1\) (top) and some examples of \(k=1\), \(k=2\) and \(k=3\) regular polygonal fuzzy numbers (bottom)
Let us give the following definitions for two arithmetic operations, namely sum and multiplication by scalar, necessary for the derivation of the fuzzy PPS.
Definition 2
Given two regular k-polygonal fuzzy numbers \({\tilde{a}}=({a^{-}_{0},a^{-}_{1},\ldots ,a^{-}_{k},a^{+}_{k},\dots , a^{+}_{1},a^{+}_{0}})\) and \({\tilde{b}}=({b^{-}_{0},b^{-}_{1},\ldots ,b^{-}_{k},b^{+}_{k},\ldots , b^{+}_{1},b^{+}_{0}})\), the following basic arithmetical operations can be defined:
-
(i)
Addition
$$\begin{aligned} {\tilde{a}}+{\tilde{b}}= \left( a^{-}_{0}+b^{-}_{0},a^{-}_{1}+b^{-}_{1},\ldots ,a^{-}_{k}+b^{-}_{k}, a^{+}_{k}+b^{+}_{k},\ldots , a^{+}_{1}+b^{+}_{1},a^{+}_{0}+b^{+}_{0}\right) . \end{aligned}$$(3) -
(ii)
Multiplication by a scalar \(\lambda \in {\mathbb {R}}\)
$$\begin{aligned} {rCl} \lambda {\tilde{a}}= & {} \left\{ \begin{aligned}&\left( \lambda a^{-}_{0},\lambda a^{-}_{1},\ldots ,\lambda a^{-}_{k},a^{+}_{k},\ldots , \lambda a^{+}_{1},\lambda a^{+}_{0}\right)&\text{ if } \lambda \ge 0;\\&\left( \lambda a^{+}_{0}, \ldots , \lambda a^{+}_{k-1}, \lambda a^{+}_{k}, \lambda a^{-}_{k}, \lambda a^{-}_{k-1}, \ldots , \lambda a^{-}_{0}\right)&\text{ if } \lambda < 0. \end{aligned} \right. \end{aligned}$$(4)
Let us recall the LU-fuzzy partial orders, which are well known in the literature [see, e.g., Wu (2009), Stefanini and Arana-Jiménez (2019) and the references therein].
Definition 3
Given two fuzzy numbers \({\mu }, {\nu }\), we say that
-
(i)
 if and only if \({\underline{\mu }}_{\alpha }\le {\underline{\nu }}_{\alpha }\) and \({\overline{\mu }}_{\alpha }\le {\overline{\nu }}_{\alpha }\), for all \(\alpha \in [0,1]\),
if and only if \({\underline{\mu }}_{\alpha }\le {\underline{\nu }}_{\alpha }\) and \({\overline{\mu }}_{\alpha }\le {\overline{\nu }}_{\alpha }\), for all \(\alpha \in [0,1]\), -
(ii)
\(\mu \prec \nu \) if and only if \({\underline{\mu }}_{\alpha }< {\underline{\nu }}_{\alpha }\) and \({\overline{\mu }}_{\alpha }< {\overline{\nu }}_{\alpha }\), for all \(\alpha \in [0,1]\).
The relationships  and \(\mu \succ \nu \) mean
and \(\mu \succ \nu \) mean  and \(\nu \prec \mu \), respectively. In Arana-Jiménez (2018), a reformulation of the previous definition for triangular fuzzy numbers by means of the relationship between their parameters is presented. The following extends this result to regular k-polygonal fuzzy numbers.
and \(\nu \prec \mu \), respectively. In Arana-Jiménez (2018), a reformulation of the previous definition for triangular fuzzy numbers by means of the relationship between their parameters is presented. The following extends this result to regular k-polygonal fuzzy numbers.
Proposition 2
Given two regular k-polygonal fuzzy numbers \({\tilde{a}}=(a^{-}_{0},a^{-}_{1},\dots ,a^{-}_{k},a^{+}_{k}, \ldots , a^{+}_{1},a^{+}_{0})\) and \({\tilde{b}}=({b^{-}_{0},b^{-}_{1},\ldots ,b^{-}_{k},b^{+}_{k},\ldots , b^{+}_{1},b^{+}_{0}})\) with respect to \(\{\alpha _i:i=0,1\ldots ,k\}\), it follows that:
-
(i)
 if and only if \(a^{-}_{i}\le b^{-}_{i}\), and \(a^{+}_{i}\le b^{+}_{i}\), for all \(i=0,1,\ldots , k\).
if and only if \(a^{-}_{i}\le b^{-}_{i}\), and \(a^{+}_{i}\le b^{+}_{i}\), for all \(i=0,1,\ldots , k\). -
(ii)
\({\tilde{a}}\prec {\tilde{b}}\) if and only if \(a^{-}_{i}<b^{-}_{i}\), and \(a^{+}_{i}<b^{+}_{i}\), for all \(i=0,1,\ldots , k\).
Proof
The proof is similar to that given in Arana-Jiménez (2018). \(\square \)
We can also consider a natural extension of Definition 3 to vectors of fuzzy numbers. Thus, given two vectors of fuzzy numbers \(\mu =(\mu _1,\ldots ,\mu _H)\) and \(\nu =(\nu _1,\ldots ,\nu _H)\), we say that  if
if  for all h.
for all h.
4 Proposed fuzzy PPS and fuzzy ERM model
Let us consider a set of n DMUs, \(j\in J=\{1,\ldots ,n\}\), each DMU\(_j\) has m inputs \({\tilde{X}}_j = ({\tilde{x}}_{1j},\ldots , {\tilde{x}}_{mj}) \in \mathrm{RPFN}_k\times \cdots \times \mathrm{RPFN}_k= (\mathrm{RPFN}_k)^m_+\), produces s outputs \({\tilde{Y}}_j = ({\tilde{y}}_{1j},\ldots ,{\tilde{y}}_{sj}) \in (\mathrm{RPFN}_k)^s_+\). Let us consider the following axioms, which are analogous to (A1)–(A4) in Section 2 but considering fuzzy inputs and outputs and using the corresponding partial order introduced in Definition 3:
-
(B1)
Envelopment \(({\tilde{X}}_j,{\tilde{Y}}_j)\in T\), for all \(j\in J\).
-
(B2)
Free disposability \(({\tilde{x}},{\tilde{y}})\in T\),
 ,
,  , \(({\tilde{x}}',{\tilde{y}}')\in (\mathrm{RPFN}_k)^{m+s}_+ \Rightarrow ({\tilde{x}}',{\tilde{y}}')\in T\).
, \(({\tilde{x}}',{\tilde{y}}')\in (\mathrm{RPFN}_k)^{m+s}_+ \Rightarrow ({\tilde{x}}',{\tilde{y}}')\in T\). -
(B3)
Convexity \(({\tilde{x}},{\tilde{y}}), ({\tilde{x}}',{\tilde{y}}')\in T\), then \(\alpha ({\tilde{x}},{\tilde{y}})+(1-\alpha )({\tilde{x}}',{\tilde{y}}')\in T\), for all \(\alpha \in [0,1]\).
-
(B4)
Scalability \(({\tilde{x}},{\tilde{y}})\in T\Rightarrow (\alpha {\tilde{x}},\alpha {\tilde{y}})\in T\), for all \(\alpha \in {\mathbb {R}}_+\).
Following the minimum extrapolation principle, the fuzzy production possibility set is the intersection of all sets that satisfy axioms (B1)–(B4):

Theorem 1
Under axioms (B1), (B2), (B3), and (B4), \(T_\mathrm{FDEA}\) is the fuzzy production possibility set that results from the minimum extrapolation principle.
Proof
See Appendix B. \(\square \)
Given the above fuzzy production possibility set, we can present the following definition of efficiency.
Definition 4
\(({\tilde{x}},{\tilde{y}})\in T_\mathrm{FDEA}\) is said to be efficient if  ,
,  , for all \(({\tilde{x}}',{\tilde{y}}')\in T_\mathrm{FDEA}\).
, for all \(({\tilde{x}}',{\tilde{y}}')\in T_\mathrm{FDEA}\).
After the characterization result for the fuzzy PPS, given in Theorem 1, and to provide a measure for the efficiency of each DMU, we can formulate the following fuzzy ERM (FERM) model, as an extension of the corresponding crisp ERM model:

where the different inputs \({\tilde{x}}_{ij}\) and outputs \({\tilde{y}}_{rj}\) belong to \((\mathrm{RPFN}_k)_+\), that is
Note that one of the advantages of using k-polygonal fuzzy numbers is that you can have all the flexibility you need for modeling the fuzzy input and output data and yet be able to describe the whole membership function using a finite set of alpha values. Since the linear combination of the observed inputs and outputs is also k-polygonal fuzzy numbers, the above feature also applies to the constraints of the proposed model (5). That is why, according to Proposition 2, the following crisp model, which only considers a finite number of alpha values, is equivalent to model which considers all alpha values.
The above model above can be written in parameterized form as follows:
Note that FERM inherits some ERM properties such as that \(0<{R}^F\le 1\), and that \({R}^F\) is units invariant. Furthermore, it is not difficult to show that if \(\mathrm{DMU}_p\) is efficient, then \({R}^F({\tilde{X}}_p, {\tilde{Y}}_p)=1\). However, as shown in Example 1, unlike in the crisp case, \({R}^F({\tilde{X}}_p, {\tilde{Y}}_p)=1\) is not a sufficient condition for efficiency. Hence, model (6) needs to be modified to correct this, as argued below.
Example 1
This small and simple example aims to illustrate that \({R}^F({\tilde{X}}_p, {\tilde{Y}}_p)=1\) does not imply the efficiency of \(\mathrm{DMU}_p\) in the fuzzy case, as it occurs for the crisp model (1). Let us assume that there are only two DMUs that consume a single input and produce a single output and that the two same output value but different inputs. Specifically, let \({\tilde{X}}_1=({\tilde{x}}_1)\), where \({\tilde{x}}_1=(1,1.75,2.5,3.5,4.75,6)\), \({\tilde{X}}_2=({\tilde{x}}_2)\), where \({\tilde{x}}_2=(2,3,3,3.5,4.75,6)\) and \({\tilde{Y}}_1={\tilde{Y}}_2=({\tilde{y}})\). \(\mathrm{DMU}_1\) is efficient, but \(\mathrm{DMU}_2\) is not efficient, since it is clear that  , \({\tilde{Y}}_2 ={\tilde{Y}}_1\), as it is directly derived from Fig. 2, see left plot. However, according to model (6), not only \(\theta \) and \(\gamma \) are equal to one for both DMUs, but \({R}^F({\tilde{X}}_1, {\tilde{Y}}_1)=1\), and \({R}^F({\tilde{X}}_2, {\tilde{Y}}_2)=1\). In fact, all convex combinations of the two DMUs have \({R}^F({\tilde{X}}_p, {\tilde{Y}}_p)=1\), for \(p=1,2\). Therefore, an optimal value of unity for model (6) does not imply the efficiency of the DMU. Moreover, among all the alternative optimal targets for DMU\(_2\), \({\tilde{X}}_2^\mathrm{target}= \lambda _1{\tilde{X}}_{1} + \lambda _2{\tilde{X}}_{2}\), only one is truly efficient, namely \({\tilde{X}}_2^\mathrm{target}={\tilde{X}}_{1}\), which corresponds to \(\lambda _1=1\) and \(\lambda _2=0\). Hence, model (6) is not an adequate extension of the crisp case.
, \({\tilde{Y}}_2 ={\tilde{Y}}_1\), as it is directly derived from Fig. 2, see left plot. However, according to model (6), not only \(\theta \) and \(\gamma \) are equal to one for both DMUs, but \({R}^F({\tilde{X}}_1, {\tilde{Y}}_1)=1\), and \({R}^F({\tilde{X}}_2, {\tilde{Y}}_2)=1\). In fact, all convex combinations of the two DMUs have \({R}^F({\tilde{X}}_p, {\tilde{Y}}_p)=1\), for \(p=1,2\). Therefore, an optimal value of unity for model (6) does not imply the efficiency of the DMU. Moreover, among all the alternative optimal targets for DMU\(_2\), \({\tilde{X}}_2^\mathrm{target}= \lambda _1{\tilde{X}}_{1} + \lambda _2{\tilde{X}}_{2}\), only one is truly efficient, namely \({\tilde{X}}_2^\mathrm{target}={\tilde{X}}_{1}\), which corresponds to \(\lambda _1=1\) and \(\lambda _2=0\). Hence, model (6) is not an adequate extension of the crisp case.
An initial attempt to solve this discrepancy between a ratio value \({R}^F({\tilde{X}}_p, {\tilde{Y}}_p)=1\) and the DMU’s efficiency characterization, as discussed in Example 1, might be to consider a different variable \(\theta _{il}\) and \(\gamma _{rl}\), for each level \(l=0,\ldots ,k\), that is
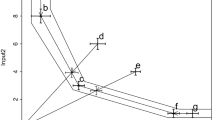
However, coming back to Example 1, the solution of model (7) for \(DMU_2\) input would be \(\theta _{0} = \theta _{0.5} = \theta _{1} = 1\), i.e., since the right limits for both \({\tilde{X}}_1\) and \({\tilde{X}}_2\) coincide, this leads to all three \(\theta _l\) (and \(\gamma _l\)) variables being equal to unity, and therefore to a modified (FERM) value \(R_m^F({\tilde{X}}_2, {\tilde{Y}}_2)=1\), which would be misleading as DMU\(_2\) is not efficient. See central plot of Fig. 2.
Consider two DMUs that consume a single input and produce a single and unit output. The inputs of \(\mathrm{DMU}_1\) and \(\mathrm{DMU}_2\) are \({\tilde{X}}_1=(1,1.75,2.5,3.5,4.75,6)\), and \({\tilde{X}}_2=(2,3,3,3.5,4.75,6)\), respectively. Left: DMU\(_2\) is clearly inefficient,  , \({\tilde{X}}_1\ne {\tilde{X}}_2\) and they have the same output, but when (6) is solved, we get that \(\theta =1\) and hence \(R^F({\tilde{X}}_2,{\tilde{Y}}_2)=1\). This is in contrast with the crisp case, where only efficient DMUs have an ERM efficiency score equal to unity. Center: If the variables \(\theta _l\) and \(\gamma _l\) are let free for each l-level, the issue remains. Since the right limits of both \({\tilde{X}}_1\) and \({\tilde{X}}_2\) coincide, the solution of model (7) would be \(\theta _{0}=\theta _{0.5}=\theta _{1}=1\) and \(R^F_m({\tilde{X}}_2,{\tilde{Y}}_2)=1\). Right: Using separate left and right variables \(\theta ^L_{l}\) and \(\theta ^R_{l}\), the modified (MFERM) model (8) computes \(R^F_M({\tilde{X}}_2,{\tilde{Y}}_2)<1\) and thus indicates that \(\mathrm{DMU}_2\) is inefficient
, \({\tilde{X}}_1\ne {\tilde{X}}_2\) and they have the same output, but when (6) is solved, we get that \(\theta =1\) and hence \(R^F({\tilde{X}}_2,{\tilde{Y}}_2)=1\). This is in contrast with the crisp case, where only efficient DMUs have an ERM efficiency score equal to unity. Center: If the variables \(\theta _l\) and \(\gamma _l\) are let free for each l-level, the issue remains. Since the right limits of both \({\tilde{X}}_1\) and \({\tilde{X}}_2\) coincide, the solution of model (7) would be \(\theta _{0}=\theta _{0.5}=\theta _{1}=1\) and \(R^F_m({\tilde{X}}_2,{\tilde{Y}}_2)=1\). Right: Using separate left and right variables \(\theta ^L_{l}\) and \(\theta ^R_{l}\), the modified (MFERM) model (8) computes \(R^F_M({\tilde{X}}_2,{\tilde{Y}}_2)<1\) and thus indicates that \(\mathrm{DMU}_2\) is inefficient
We have checked that in a fuzzy framework, both efficient and inefficient DMUs could have the same objective value of 1 for the straightforward extension of ERM model (6), or the modified (7). For example, if the upper/lower limits of the l-levels coincide, may lead to this case. This motivates the inclusion of left and right variables \(\{\theta _{l}^{L}\); \(\theta _{l}^{R}\); \(\gamma _{l}^{L}\); \(\gamma _{l}^{R}\}\), for each l-level
The advantage of model (8) over (5) is that, as shown below in Theorem 2, it has the efficiency indication property, i.e., \(R^F_M({\tilde{X}}_p,{\tilde{Y}}_p)\)=1 if and only if the \(DMU_p\) is efficient.
Note that, using separate left and right input reduction factors for each input and left and right output expansion factors for each output, all feasible input reductions and output increases are exhausted. Back to Example 1, not all the above variables \(\theta _{l}^{L}\) and \(\theta _{l}^{R}\) are equal to one for the inefficient DMU\(_2\), and \(R_M^F({\tilde{X}}_2, {\tilde{Y}}_2)<1\). This can be seen in the right panel of Fig. 2, which shows the optimal left and right values of the input reduction variables for the different alpha values.
Despite the objective function of (8) is non-linear, it is possible, following a similar procedure to that proposed by Pastor et al. (1999), to reformulate the problem and get an equivalent problem with a linear objective function as follows:
Reformulating (8) using (9), we have
The above optimization problem (LMFERM) is now a linear program whose feasibility region and objective function are equivalent to those given in (8), with the change of variables given in (9).
Theorem 2
\(({\tilde{x}},{\tilde{y}})\in T_\mathrm{FDEA}\) is efficient if and only if \(R^F_M({\tilde{x}},{\tilde{y}})\)=1.
Proof
See Appendix C. \(\square \)
Besides, this model provides the targets \(({\tilde{X}}_p^\mathrm{target},{\tilde{Y}}_p^\mathrm{target})\) associated with a \(\mathrm{DMU}_p\), given as
Note that above (MFERM) model, and equivalently model (LMFERM), computes the efficiency score of a \(\mathrm{DMU}_p\) and this is indicated in the arguments of \(R^F({\tilde{X}}_p,{\tilde{Y}}_p)\). It can, however, be used to project any feasible operating point \(({\tilde{x}},{\tilde{y}})\) to compute its efficiency \(R_M^F({\tilde{x}},{\tilde{y}})\). This will be useful for proving the following result.
Theorem 3
\(R^F_M({\tilde{X}}_p^\mathrm{target},{\tilde{Y}}_p^\mathrm{target})=1\).
Proof
See Appendix D \(\square \)
In summary, extending the conventional ERM efficiency, the proposed MFERM approach uses a linearizable, non-oriented, non-radial optimization model that exhausts all feasible input reductions and output expansions at all l-levels, providing crisp efficiency scores (and corresponding efficiency ranking) as well as fuzzy efficient targets.
5 Numerical examples
5.1 Triangular fuzzy numbers dataset
To illustrate the proposed fuzzy ERM model, consider the dataset from Arya and Yadav (2017) shown in Table 2 and which correspond to 12 Community Health Centers (CHCs) in Meerut district of Uttar Pradesh, India. The table shows the fuzzy input and output of each DMU. The first input is the total sum of doctors and staff nurses, while the second one is the number of pharmacists. The two outputs correspond to the number of inpatients and outpatients, respectively. All the inputs and outputs are given as triangular fuzzy numbers, which correspond to \(k=1\) regular polygonal fuzzy numbers.
The efficiency \(R^F_M({\tilde{X}}_p,{\tilde{Y}}_p)\) of each \(DMU_p\), \(p=1,\ldots ,12\), has been computed using (10), and is shown in the second column of Tables 2 and 3. It can be seen that DMUs H1, H2, H3, H8, and H12 are labelled efficient. In Table 3, we also add a ranking, based on this efficiency measurement, so that this ranking can be compared with those of other methods. Efficient DMUs are all ranked equal.
Table 2 shows the fuzzy targets computed for each DMU using (11) and (12). Due to horizontal space constraints, the structure of the table is unusual in the sense that for each DMU, there are two rows, each showing the data and the results for each of the two inputs and two outputs. Note that the target coincides with the observed data in the case of the efficient DMUs and dominate it, in the sense of the partial order introduced in Definition 3, in the case of inefficient DMUs.
For comparison purposes, Table 3 also shows the efficiency scores computed by other approaches from the literature. The fourth column shows the \(SBME_p\) efficiency score computed by the fuzzy SBM model of Arya and Yadav (2017). Note that their method labelled all DMUs as efficient except one, namely H11. Thus, it seems that the proposed FERM approach has, at least for this dataset, more discriminant power than this method. The fifth and sixth columns of Table 3 correspond to the results of the Fuzzy SBM model of Chen et al. (2013) and Hsiao et al. (2011). Since they use fuzzy slack variables, their efficiency scores are fuzzy. The corresponding \(\alpha \)-cuts for \(\alpha =0,1\) levels are shown. Note that the FERM efficiency scores are within the corresponding \(\alpha =0\) cut for all DMUs.
Finally, the two last columns of Table 3 correspond to the fuzzy ERM approach of Izadikhah et al. (2017), where a pair of models are used to generate upper and lower limits of interval efficiency score, based on the enhanced Russell model applied to interval data. The whole dataset is converted into intervals for applying this methodology, computing the nearest weighted interval approximation of fuzzy numbers, with the weighting function \((4a^3,4a^3)\). We use a preference degree measurement \(\rho _j\), see Izadikhah et al. (2017) for more details, to establish some partial order between intervals and ranking the DMUs. In this case, although at first sight, it appears that this method has more discriminant power from Izadikhah et al. (2017), we also remark the different efficiency interpretations. Izadikhah et al. (2017) approach computes an efficiency score interval (converting or approximating all data to intervals). Whereas the proposed method is based on technical efficiency within a fuzzy technology framework. According to the latter, the efficient DMUs are characterized by \(R^F_M({\tilde{X}}_p,{\tilde{Y}}_p)=1\) (see Theorem 2). In this regard, we found in some cases that efficient DMUs are ranked after inefficient ones by Izadikhah et al. (2017) approach. However, despite these differences, we see agreement between the results of both methods. Thus, except for DMU 12, \(R^F_M({\tilde{X}}_p,{\tilde{Y}}_p)\) always lies within the corresponding efficiency score interval. The level of agreement between the results of our approach and Izadikhah et al. (2017) has been tested using a Wilcoxon signed-rank test, which is a non-parametric paired difference test for matched pairs or dependent samples. With a p-value\( = 0.2146\), we cannot reject the null hypothesis of homogeneity, i.e., that the median difference is zero.
5.2 Modified dataset with 2-polygonal fuzzy numbers
In this section, we illustrate the proposed approach with fuzzy data that are not triangular fuzzy numbers. Actually, polygonal fuzzy numbers allow a great deal of flexibility in modelling the uncertainty in the input and output data. To keep things simple, however, we will just consider 2-polygonal fuzzy numbers, instead of triangular (1-polygonal). We have modified the inputs and outputs of the DMUs for getting RPFN\(_2\) data. The modifications have been randomly generated keeping the same closure; see Table 4.
As an example, Fig. 3 shows the input/output data for DMU H4, as well as the corresponding input and output targets. The black circles and solid lines show the observed 2-polygonal fuzzy inputs and outputs. The MFERM targets are represented with dashed lines and black squares. For example, for input 2, the corresponding variables are \(\{\theta _{2,0}^{L};\theta _{2,1}^{L};\theta _{2,2}^{L};\theta _{2,2}^{R};\theta _{2,1}^{R};\theta _{2,0}^{R}\}=\{0.525; 0.849; 1.000; 1.000; 0.683; 0.445\}\). In the case of output 1, the target support is significantly to the right of the observed data, implying a large inefficiency as regards that output. For the other inefficient DMUs, this separation between the targets and observed data values is even greater and happens mainly for output 2.
Observed and target 2-polygonal fuzzy inputs and outputs for DMU H4 for example in Sect. 5.2. The black circles and solid lines show the observed inputs, \({\tilde{x}}_{14}\) and \({\tilde{x}}_{24}\), and outputs, \({\tilde{y}}_{14}\) and \({\tilde{y}}_{24}\). The corresponding targets, \({\tilde{x}}_{i4}^\mathrm{target}\) and \({\tilde{y}}_{r4}^\mathrm{target}\), are represented with black squares and dashed lines. To compute the MFERM input and output targets, the observed data \({\tilde{x}}_{i4}\) and \({\tilde{y}}_{r4}\) are multiplied by the corresponding variables \(\{\theta _{il}^{L}; \theta _{il}^{R}; \gamma _{rl}^{L}; \gamma _{rl}^{R}\}\), at levels \(l=0,1,2\), thus exhausting all possible input and output improvements. In the case of output 1, the support of the observed data and the MFERM target differ significantly, and hence, the x-axis has been broken (the gap is marked with two vertical lines)
In addition to the fuzzy input and output for the example in Sect. 5.2, Table 4 shows the corresponding MFERM efficiency scores. In general, they show an improvement with respect to those of Example 5.1. The efficient or inefficient character of the DMUs remains the same, but the inefficient DMUs have improved their efficiency. This is not guaranteed to happen necessarily, although it is not strange. That is, because the use of a higher k-polygonal fuzzy numbers leads to an increased number of constraints (and hence a smaller feasibility region) in (PLFERM) model, which is a minimization problem.
The lower part of Table 4 also shows the computed MFERM targets. The efficient DMUs are projected onto themselves. For the inefficient DMUs, as graphically shown in Fig. 2 for DMU H4, the fuzzy targets always dominate the observed inputs and outputs and sometimes by a large amount.
The interpretation of the fuzzy targets is similar to that of the fuzzy data from which they derive. Thus, for each \(\alpha \)-level, the corresponding \(\alpha \)-cuts of the observed input and the corresponding target can be compared, and the same occurs with the observed output and the target output. The proposed approach guarantees that, for each \(\alpha \)-level, the lower limit of the target input is less than the lower limit of the observed input and that the upper limit of the target input is less than the upper limit of the observed input. Moreover, the relative difference between the two lower limits and between the upper limits must be at least the value of the corresponding \(\theta _{il}^{L}\), \(\theta _{il}^{R}\), \(\gamma _{rl}^{L}\) or \(\gamma _{rl}^{R}\) variable computed by the model (LMFERM) (10), and Eq. (9), which represents the maximum margin for improvement for that input or output.
Thus, for example, as indicated in Table 4 and shown in Fig. 3, the 0.0-level interval of input 1 of the observed DMU H4 is the interval [6, 11], while the 0.0-level interval for the corresponding target is [2.19, 3.38]. Assuming that the units of that input refer to full-time equivalents (FTE), the target indicates that, for that \(\alpha \)-level, the minimum value of the variable can be reduced to 3.81 FTE and the maximum value can be reduced 7.62 FTE. The same reasons that make the observed input uncertain and fuzzy apply to the corresponding target. The proposed approach does neither ignore nor eliminate those reasons. What is clear is that, at the 0.0-level, DMU H4 can reduce input 1 by at least 3.81 FTE. Note also the feasible reduction for the 0.5 level (from [6.7, 10.45] to [2.43, 3.22]), and for the 1.0 level (from [8, 8] to [2.9, 2.9]). Overall, \(\{\theta _{1,0}^{L};\theta _{1,1}^{L};\theta _{1,2}^{L};\theta _{1,2}^{R};\theta _{1,1}^{R};\theta _{1,0}^{R}\}=\{0.365; 0.364; 0.363; 0.363; 0.308; 0.307\}\) for this input. As it can be seen in Fig. 3, something similar happens in the case of input 2, leading in this case to \(\{{\theta _{1,0}^{L};\theta _{1,1}^{L};\theta _{1,2}^{L};\theta _{1,2}^{R};\theta _{1,1}^{R};\theta _{1,0}^{R}\}}=\{{0.525; 0.849; 1.000; 1.000; 0.683; 0.445\}}\). In the case of the outputs, the interpretation is similar. Thus, for output 1, number of inpatients, the 0.0-level, 0.5-level, and 1.0-level sets for corresponding observed and the target fuzzy numbers are [485, 500] vs. [1000.68, 1005.18], [486.62, 496.94] vs. [1001.65, 1004.75], and [492, 492] vs. [1003.05, 1003.05], respectively.
Therefore, for DMU H4, the increase in the number of inpatients is apparent and significant, as the value of the corresponding variables \(\{\gamma _{1,0}^{L};\gamma _{1,1}^{L}; \gamma _{1,2}^{L}; \gamma _{1,2}^{R};\gamma _{1,1}^{R};\gamma _{1,0}^{R}\}=\{2.063; 2.058; 2.039; 2.039; 2.022; 2.010\}\) computed by model (10) and equations (9), attests.
By contrast, for output 2, the number of outpatients, \(\{\gamma _{2,0}^{L}; \gamma _{2,0.5}^{L}; \gamma _{2,1}^{L}; \gamma _{2,1}^{R}; \gamma _{2,0.5}^{R}; \gamma _{2,0}^{R}\}=\{1.0005; 1.0005; 1.0002; 1.0002; 1.0001; 1.000\}\) because the upper limit of one of the 0.0-set cannot be increased, as it can be seen in Fig. 3. This leads to the corresponding MFERM efficiency score shown in Table 4
In summary, what the example in Sect. 5.2 illustrates is that the use of k-polygonal fuzzy numbers provides all the flexibility that be needed to represent the uncertainty in the data and that the proposed FERM approach can handle all those situations providing appropriate efficiency scores and the corresponding fuzzy targets.
5.3 Case study: electric power distribution company
This numerical example is taken from Izadikhah et al. (2017), where 17 Iranian suppliers of self-supporting cable for Markazi Province Electric Power Distribution Company (MPEPDC) in Iran are evaluated. There are 2 inputs, \(x_1 = \) the overall suppliers ranking (ordinal variable) and \(x_2 = \) unit price by considering volume discount (interval type). Furthermore, there are 6 outputs: \(y_1 = \) production capacity and \(y_2 =\) financial potential, both of interval type, and \(y_3 = \) environmental standards and regulations, \(y_4= \) research and developments for eco-design product, \(y_5 = \) safety and health standards, and \(y_6 = \) customer satisfaction. These last four outputs are fuzzy triangular numbers (see cf. Tables 10–14 in Izadikak for more details). Note that, since interval data \([a_1,a_2]\) correspond with trapezoidal fuzzy numbers \(({{x}^{-}_{0},{x}^{-}_{1},{x}^{+}_{1},{x}^{+}_{0}}) = (a_1,a_1,a_2,a_2)\), we model such type of data as \((RPFN_1)_+\). Recall also that the triangular fuzzy outputs are particular cases of the trapezoidal ones, where \({x}^{-}_{1}={x}^{+}_{1}\). We adopt the same approximation of the ordinal input \(x_1\) as an interval as done in Izadikhah et al. (2017).
Table 5 shows the results of applying the proposed (PLFERM) model to this dataset, and the comparison with the interval efficiency scores obtained by Izadikhah et al. (2017). The proposed approach identifies nine DMUs as efficient DMUs. This relatively high number is not surprising for a fuzzy problem with a such number of DMUs and variables. As already discussed above in Sect. 5.2, obviating the differences between efficiency interpretations in both methods, we find sufficient agreement, since most \(R^F_M({\tilde{X}}_p,{\tilde{Y}}_p)\) fall within the corresponding efficiency intervals. Moreover, if we apply a Wilcoxon signed-rank test of the results of our approach and Izadikhah et al. (2017), we get a p-value\( = 0.285\). This means that we cannot reject the null hypothesis of homogeneity, i.e., that the median difference is equal to zero, which supports the existence of sufficient agreement between both efficiency measurements. As in Sect. 5.1, Izadikhah et al. (2017) provides a ranking even between the efficient DMUs and, again, we find that in some cases, efficient DMUs are ranked after inefficient ones. The proposed approach is not able to discriminate between the efficient DMUs, but can easily rank the inefficient DMUs just sorting by their \(R_M^F(\tilde{X_p},\tilde{Y_p})\) value.
6 Conclusions
This paper presents a new approach for efficiency assessment and target setting when the input and output data are fuzzy. It is based on polygonal fuzzy numbers and LU-fuzzy partial orders. First, from the observed fuzzy data, and using simple axioms analogous to the ones considered in the crisp case, the fuzzy PPS containing all feasible operating points is inferred. Based on this PPS, a fuzzy ERM DEA model is proposed to compute, for each DMU, a crisp efficiency score, and a fuzzy target. The use of polygonal fuzzy numbers provides ample flexibility for modeling the uncertainty in the data. In addition, the non-radial approach used, which exhausts all possible input and output slacks, provides increased discriminant power.
The proposed approach has two main limitations. One is that it computes crisp efficiency scores. The second one is that it does not work (i.e., it leads to unbounded solutions) when the left limit of any input or output of a DMU is zero.
As regards topics for continuing this research, one is formulating a super-efficiency approach, so that the efficient DMUs can be classified into extreme efficient and non-extreme efficient and the former can be ranked. Another topic is fully fuzzy approach for computing fuzzy efficiency scores. Other interesting extensions of the proposed approach include handling negative data and undesirable outputs given as fuzzy sets. Finally, a meaningful comparison between fuzzy DEA and stochastic DEA is also due (see, e.g., Wanke et al. (2018)).
References
Ahmady N, Farzipoor Saen R, Ahmady E (2015) Developing a fuzzy enhanced Russell measure for media selection. Int J Bus Innov Res 9(4):470–485
Allahviranloo T, Hosseinzade Lotfi F, Adabitabar FM (2007) Fuzzy efficiency measure with fuzzy production possibility set. Appl Appl Math 2(2):152–166
Arana-Jiménez M (2018) Nondominated solutions in a fully fuzzy linear programming problem. Math Methods Appl Sci 41:7421–7430
Arana-Jiménez M, Sánchez-Gil MC, Lozano S (2020) Efficiency assessment and target setting using a fully fuzzy DEA approach. Int J Fuzzy Syst 22:1056–1072
Arya A, Yadav SP (2017) A fuzzy dual sbm model with fuzzy weights: an application to the health sector. Adv Intell Syst Comput 546:230–238
Azadi M, Jafarian M, Farzipoor Saen R, Mirhedayatian SM (2015) A new fuzzy DEA model for evaluation of efficiency and effectiveness of suppliers in sustainable supply chain management context. Comput Oper Res 54:274–285
Báez-Sánchez AD, Moretti AC, Rojas-Medar MA (2012) On polygonal fuzzy sets and numbers. Fuzzy Sets Syst 209:54–65
Bagheri M, Ebrahimnejad A, Razavyan S, Lofti FH, Malekmohammadi N (2020) Solving the fully fuzzy multi-objective transportation problem based on the common set of weights in DEA. J Intell Fuzzy Syst 39:3099–3124
Bagheri M, Ebrahimnejad A, Razavyan S, Lofti FH, Malekmohammadi N (2021a) Solving fuzzy multi-objective shortest path problem based on data envelopment analysis approach. Complex Intell Syst 7:725–740
Bagheri M, Ebrahimnejad A, Razavyan S, Lofti FH, Malekmohammadi N (2021b) Fuzzy arithmetic DEA approach for fuzzy multi-objective transportation problem. Oper Res. https://doi.org/10.1007/s12351-020-00592-4
Banker RJ, Charnes A, Cooper WW (1984) Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag Sci 30(9):1078–1092
Charnes A, Cooper WW, Rhodes E (1978) Measuring the efficiencies of DMUs. Eur J Oper Res 2(6):429–444
Chen SM, Adam SI (2018) Weighted fuzzy interpolated reasoning based on ranking values of polygonal fuzzy sets and new scale and move transformation techniques. Inf Sci 435:184–202
Chen YC, Chiu YH, Huang CW, Tu CH (2013) The analysis of bank business performance and market risk-applying fuzzy DEA. Econ Model 32(1):225–232
Cooper WW, Deng H, Huang Z, Li SX (2002) Chance constrained programming approaches to technical efficiencies and inefficiencies in stochastic data envelopment analysis. J Oper Res Soc 53:1347–1356
Cooper WW, Huang Z, Li SX (2004) Chance constrained DEA. In: Cooper, WW, Seiford LM, Zhu J (eds) Handbook on data envelopment analysis. Springer, Boston, MA, pp 229–264
Dubois D, Prade H (1978) Operations on fuzzy numbers. Int J Syst Sci 9(6):613–626
Dubois D, Prade H (1980) Fuzzy sets and systems: theory and applications. Academic Press, New York
Dyson RG, Shale EA (2010) Data envelopment analysis, operational research and uncertainty. J Opera Res Soc 61:25–34
Ebrahimnejad A, Amani N (2021) Fuzzy data envelopment analysis in the presence of undesirable outputs with ideal points. Complex Intell Syst 7:379–400
Emrouznejad A, Tavana M, Hatami-Marbini A (2014) The state of the art in fuzzy data envelopment analysis. Stud Fuzziness Soft Comput 309:1–45
Ghasemi MR, Ignatius J, Lozano S, Emrouznejad A, Hatami-Marbini A (2015) A fuzzy expected value approach under generalized data envelopment analysis. Knowl-Based Syst 89:148–159
Guo P, Tanaka H (2001) Fuzzy DEA: a perceptual evaluation method. Fuzzy Sets Syst 119:149–160
Hanss M (2005) Applied fuzzy arithmetic. Springer, Stuttgart
Hatami-Marbini A, Emrouznejad A, Tavana M (2011) A taxonomy and review of the fuzzy data envelopment analysis literature: two decades in the making. Eur J Oper Res 214(3):457–472
Hsiao B, Chern CC, Chiu YH, Chiu CR (2011) Using fuzzy super-efficiency slack-based measure data envelopment analysis to evaluate Taiwan’s commercial bank efficiency. Expert Syst Appl 38:9147–9156
Izadikhah M (2021) Developing a new chance constrained modified ERM model to measure performance of repair and maintenance groups of IRALCO. Int J Oper Res 41(2):226–243
Izadikhah M, Khoshroo A (2018) Energy management in crop production using a novel fuzzy data envelopment analysis model. RAIRO-Oper Res 52:595–617
Izadikhah M, Farzipoor Saen R, Ahmadi K (2017) How to assess sustainability of suppliers in volume discount context? A new data envelopment analysis approach. Transp Res Part D 51:102–121
Jahanshahloo GR, Hosseinzadeh Lotfi F, Moradi M (2004) Sensitivity and stability analysis in DEA with interval data. Appl Math Comput 156(2):463–477
Kachouei M, Ebrahimnejad A, Bagherzadeh-Valami H (2020) A common-weights approach for efficiency evaluation in fuzzy data envelopment analysis with undesirable outputs: application in banking industry. J Intell Fuzzy Syst 39:7705–7722
Kao C (2014) Network data envelopment analysis with fuzzy data. Stud Fuzziness Soft Comput 309:191–206
Kao C, Liu ST (2000) Fuzzy efficiency measures in data envelopment analysis. Fuzzy Sets Syst 113(3):427–437
Kao C, Liu ST (2009) Stochastic data envelopment analysis in measuring the efficiency of Taiwan commercial banks. Eur J Oper Res 196:312–322
Kao C, Liu ST (2019) Stochastic efficiency measures for production units with correlated data. Eur J Oper Res 273:278–287
Kaufmann A, Gupta MM (1985) Introduction to fuzzy arithmetic theory and applications. Van Nostrand Reinhold, New York
Khan IU, Ahmad T, Maan N (2013) A simplified novel technique for solving fully fuzzy linear programming problems. J Optim Theory Appl 159:536–546
León T, Liern V, Ruiz JL, Sirvent I (2003) A fuzzy mathematical programming approach to the assessment of efficiency with DEA models. Fuzzy Sets Syst 139:407–419
Lertworasirikul S, Fang SC, Joines JA, Nuttle HL (2003) Fuzzy data envelopment analysis (DEA): a possibility approach. Fuzzy Sets Syst 139(2):379–394
Liu ST (2016) Multi-period efficiency measurement with fuzzy data and weight restrictions. In: Hwang SN et al (eds) Handbook of operations analytics using data envelopment analysis. International Series in Operations Research & Management Science, vol 239. Springer, New York, pp 89–111
Lotfi FH, Allahviranloo T, Alimardani Jondabeh M, Alizadeh L (2009) Solving a fully fuzzy linear programming using lexicography method and fuzzy approximate solution. Appl Math Model 33:3151–3156
Momeni E, Tavana M et al (2014) A new fuzzy network slaceks-based DEA model for evaluating performance of supply chains with reverse logistics. J Intell Fuzzy Syst 27:793–804
Olesen OB, Petersen NC (2016) Stochastic data envelopment analysis—a review. Eur J Oper Res 251:2–21
Pastor JT, Ruiz JL, Sirvent I (1999) An enhanced DEA Russell graph efficiency measure. Eur J Oper Res 115:596–607
Peykani P, Lofti FH, Sadjadi SJ, Ebrahimnejad A, Mohammadi E (2021) Fuzzy chance-constrained data envelopment analysis: a structured literature review, current trends, and future directions. Fuzzy Optim Decis Mak 1:15. https://doi.org/10.1007/s10700-021-09364-x
Puri J, Yadav SP (2013) A concept of fuzzy input mix-efficiency in fuzzy DEA and its application in banking sector. Expert Syst Appl 40(5):1437–1450
Raei Nojehdehi R, Abianeh Maleki Moghadam P, Bagherzadeh Valami H (2012) A geometrical approach for fuzzy production possibility set in data envelopment analysis (DEA) with fuzzy input-output levels. Afr J Bus Manag 6(7):2738–2745
Saati S, Memariani A (2009) SBM model with fuzzy input-output levels in DEA. Aust J Basic Appl Sci 3(2):352–357
Saati S, Memariani A, Jahanshahloo GR (2002) Efficiency Analysis and Ranking of DMUs with Fuzzy Data. Fuzzy Optim Decis Mak 1:255–267
Salahi M, Toloo M, Hesabirad Z (2019) Robust Russell and enhanced Russell measures in DEA. J Oper Res Soc 70(8):1275–1283
Soleimani-damaneh M, Jahanshahloo GR, Abbasbandy S (2006) Computational and theoretical pitfalls in some current performance measurement techniques; and a new approach. Appl Math Comput 181:1199–1207
Stefanini L (2010) A generalization of Hukuhara difference and division for interval and fuzzy arithmetic. Fuzzy Sets Syst 161:1564–1584
Stefanini L, Arana-Jiménez M (2019) Karush-Kuhn-Tucker conditions for interval and fuzzy optimization in several variables under total and directional generalized differentiability. Fuzzy Sets Syst 362:1–34
Stefanini L, Bede B (2014) Generalized fuzzy differentiability with LU-parametric representation. Fuzzy Sets Syst 257:184–203
Stefanini L, Sorini L, Guerra ML (2006) Parametric representation of fuzzy numbers and application to fuzzy calculus. Fuzzy Sets Syst 157(18):2423–2455
Tavana M, Khanjani Shiraz R, Hatami-Marbini A, Agrell PJ, Paryab K (2013) Chance-constrained DEA models with random fuzzy inputs and outputs. Knowl Based Syst 52:32–52
Tone K (2001) A slacks-based measure of efficiency in data envelopment analysis. Eur J Oper Res 130(3):498–509
Wang YM, Chin KS (2011) Fuzzy data envelopment analysis: a fuzzy expected value approach. Expert Syst Appl 38(9):11678–11685
Wang YM, Greatbanks R, Yang JB (2005) Interval efficiency assessment using data envelopment analysis. Fuzzy Sets Syst 153:347–370
Wanke P, Barros CP, Emrouznejad A (2018) A comparison between stochastic DEA and fuzzy DEA approaches: revisting efficiency in Angolan banks. RAIRO Oper Res 52:285–303
Wu HC (2009) The optimality conditions for optimization problems with convex constraints and multiple fuzzy-valued objective functions. Fuzzy Optim Decis Mak 8:295–321
Wu J, Xiong B, An Q, Zhu Q, Liang L (2015) Measuring the performance of thermal power firms in China via fuzzy Enhanced Russell measure model with undesirable outputs. J Clean Prod 102:237–245
Acknowledgements
The first author was partially supported by the research project MTM2017-89577-P (MINECO, Spain). The second author was partially supported by Spanish Ministry of Economy and Competitiveness through grants AYA2016-75931-C2-1-P, and from the Consejería de Educación y Ciencia (Junta de Andalucía) through TIC-101. The third author acknowledges the financial support of the Spanish Ministry of Science, Innovation and Universities, grant PGC2018-095786-B-I00.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Marcos Eduardo Valle.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Proof of Proposition 1
Proof
Suppose that \({\tilde{a}}\) is a k-polygonal fuzzy number with respect to \({\mathcal {P}}_k\). Then, define \([a_i^-, a_i^+]=[{\tilde{a}}]^{\alpha _i}\), for \(i=0,\ldots , k\). Given \(x\in {\mathbb {R}}\), if \(x\not \in [{\tilde{a}}]^{\alpha _0}\), then \({\tilde{a}}(x)=0\); otherwise, there exists \(i\in \{1,\ldots , k\}\), such that \(a^{-}_{i-1}\le x < a^{-}_{i}\) or \(a^{-}_{k}\le x\le a^{+}_{k}\) or \(a^{+}_{i}< x\le a^{+}_{i-1}\). Consider the first case, that is, \(a^{-}_{i-1}\le x < a^{-}_{i}\). Following the reasoning given by Báez-Sánchez et al. (2012) with respect to the polygonal fuzzy numbers, we have that the membership function between the points \(a^{-}_{i-1}\) and \(a^{-}_{i}\) is linear. This means that if \(\alpha = {\tilde{a}}(x)\), then \(x=(1-\lambda )a^{-}_{i-1}+\lambda a^{-}_{i}\), with \(\lambda =(\alpha -\alpha _{i-1)}/(\alpha _{i}-\alpha _{i-1})\). Now, evaluate \({\tilde{a}}(x)\) by means of the expression (2), and it is derived that \({\tilde{a}}(x)=\alpha \). Therefore, the expression (2) is correct for the considered first case. The same for the other two cases \(a^{-}_{k}\le x\le a^{+}_{k}\) and \(a^{+}_{i}< x\le a^{+}_{i-1}\). Now, let us prove the reverse, and so, suppose that there exist \(a^{-}_{0},a^{-}_{1},\ldots ,a^{-}_{k},a^{+}_{k},\ldots , a^{+}_{1},a^{+}_{0}\in {\mathbb {R}}\) with \(a^{-}_{0}\le a^{-}_{1}\le \cdots \le a^{-}_{k}\le a^{+}_{k}\le \dots \le a^{+}_{1}\le a^{+}_{0}\), such that the membership function of a fuzzy number \({\tilde{a}}\) is given by (2). Given \(\alpha \in [0,1]\), there exists \(i\in \{1,\ldots , k\}\), such that \(0\le \alpha _{i-1}<\alpha \le \alpha _{i}\le 1\). Define \([{\tilde{a}}]^{\alpha }=[a_{\alpha }^-, a_{\alpha }^+]\). Since the \(\alpha \)-levels of a fuzzy number are nested, it is derived that \([{\tilde{a}}]^{\alpha _{i-1}}=[a^{-}_{i-1},a^{+}_{i-1}]\subseteq [{\tilde{a}}]^{\alpha }=[a_{\alpha }^-, a_{\alpha }^+]\subseteq [{\tilde{a}}]^{\alpha _{i}}=[a^{-}_{i},a^{+}_{i}]\). This implies that \(a^{-}_{i-1}\le a_{\alpha }^-\le a^{-}_{i}\) and \(a^{+}_{i}\le a_{\alpha }^+\le a^{-}_{i-1}\). The membership function is upper semi-continuous, so, on one hand, from expression (2), it follows that \(\alpha = u(a_{\alpha }^-)\), that is:
what is equivalent to
with \(\lambda =(\alpha -\alpha _{i-1})/(\alpha _{i}-\alpha _{i-1})\). On the other hand, and proceeding in a similar way from expression (2), it follows that \(\alpha = u(a_{\alpha }^+)\), and then:
what is equivalent to
with the same \(\lambda =(\alpha -\alpha _{i-1})/(\alpha _{i}-\alpha _{i-1})\). Therefore, from (A.2) and (A.4), it follows that:
As a consequence of (A.5), we have that the \(\alpha \)-levels of \({\tilde{a}}\) satisfy \([{\tilde{a}}]^{\alpha }=(1-\lambda )[{\tilde{a}}]^{\alpha _{i-1}}+\lambda [{\tilde{a}}]^{\alpha _{i}}\), where \(0\le \alpha _{i-1}<\alpha \le \alpha _{i}\le 1\) for some \(i=0,\dots , k-1\) and \(\lambda =\lambda (\alpha )=(\alpha -\alpha _{i-1})/(\alpha _{i}-\alpha _{i-1})\). Then, the proof is complete. \(\square \)
Appendix B: Proof of Theorem 1
Proof
Denote by \(T_\mathrm{true}\) the result of the minimum extrapolation principle axioms (B1), (B2), (B3), and (B4). To prove the theorem, it is necessary to show that \(T_\mathrm{FDEA}=T_\mathrm{true}\). To this end, let us divide the proof into two parts.
-
(i)
\(T_\mathrm{true}\subseteq T_\mathrm{FDEA}\). It is sufficient to prove that \(T_\mathrm{FDEA}\) satisfies (B1), (B2), (B3), and (B4), since this implies that \(T_\mathrm{FDEA}\) contains the intersection of all sets that satisfies the previous axioms, and, consequently, contains \(T_\mathrm{true}\). Therefore, let us check the axioms (B1), (B2), (B3), and (B4) by \(T_\mathrm{FDEA}\).
-
Check (B1). It is clear, since, given \(j\in J\), then \(({\tilde{X}}_j, {\tilde{Y}}_j)\), with \(\lambda _j=1\) and \(\lambda _i'=0\), for all \(i'\ne j\), satisfies conditions in \(T_\mathrm{FDEA}\).
-
Check (B2). Given \(({\tilde{x}},{\tilde{y}})\in T_\mathrm{FDEA}\),
 ,
,  , \(({\tilde{x}}',{\tilde{y}}')\in (RPFN_k)^{m+s}_+\), we have to prove that \(({\tilde{x}}',{\tilde{y}}')\in T_\mathrm{FDEA}\). By hypothesis, there exists \(\lambda \geqq 0\), such that
, \(({\tilde{x}}',{\tilde{y}}')\in (RPFN_k)^{m+s}_+\), we have to prove that \(({\tilde{x}}',{\tilde{y}}')\in T_\mathrm{FDEA}\). By hypothesis, there exists \(\lambda \geqq 0\), such that  (B.1)
(B.1)Combining (B.1) with
 ,
,  , it follows that:
, it follows that:  (B.2)
(B.2)Therefore, \(({\tilde{x}}',{\tilde{y}}')\in T_\mathrm{FDEA}\).
-
Check (B4). Given \(({\tilde{x}},{\tilde{y}})\in T_\mathrm{FDEA}\), there exists \(\lambda \geqq 0\), such that (B.1) holds. Given \(\alpha \in {\mathbb {R}}_+\), define \(\bar{\lambda }=\alpha \lambda =(\alpha \lambda _1,\dots ,\alpha \lambda _n)\geqq 0\). It follows that \((\alpha {\tilde{x}},\alpha {\tilde{y}})\in (\mathrm{RPFN}_k)^{m+s}_+\) and:
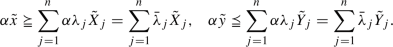
Therefore, \((\alpha {\tilde{x}},\alpha {\tilde{y}})\in T_\mathrm{FDEA}\).
-
Check (B3). Let us consider \(({\tilde{x}},{\tilde{y}}),({\tilde{x}}',{\tilde{y}}') \in T_\mathrm{FDEA}\), and \(\alpha \in [0,1]\). By hypothesis, there exist \(\lambda ,\lambda '\geqq 0\), such that
 (B.3)
(B.3) (B.4)
(B.4)Multiplying by \(\alpha \) each side in the first fuzzy inequality in (B.3), by \((1-\alpha )\) each side in the second fuzzy inequality in (B.3), and then combining the fuzzy inequalities, we get
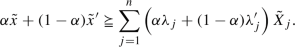 (B.5)
(B.5)Proceeding in a similar way with \({\tilde{y}}\) and \({\tilde{y}}'\) and inequalities (B.4), we have
 (B.6)
(B.6)Define \(\lambda ''=(\lambda ''_1,\dots ,\lambda ''_n)\), with \(\lambda ''_j=\alpha \lambda _j+(1-\alpha )\lambda '_j\ge 0\), for all \(j=1,\dots ,n\), and substitute them in expressions (B.5) and (B.6). It follows that \((\alpha {\tilde{x}}+(1-\alpha ){\tilde{x}}',\alpha {\tilde{x}}+(1-\alpha ){\tilde{y}}')=\alpha ({\tilde{x}},{\tilde{y}})+(1-\alpha ) ({\tilde{x}}',{\tilde{y}}')\in T_\mathrm{FDEA}\).
-
-
(ii)
\(T_\mathrm{FDEA}\subseteq T_\mathrm{true}\). We need to prove that every element of \(T_\mathrm{FDEA}\) belongs to \(T_\mathrm{true}\). To this purpose, consider \(({\tilde{x}},{\tilde{y}})\in T_\mathrm{FDEA}\), which means that there exists \(\lambda \geqq 0\), \(\lambda \in {\mathbb {R}}^n\), such that
 (B.7)
(B.7)We have that \(({\tilde{X}}_j,{\tilde{Y}}_j)\in T_\mathrm{true}\) by (B1), for all \(j\in J\). Then, by (B4), it follows that \((\lambda _j{\tilde{X}}_j,\lambda _j{\tilde{Y}}_j)\in T_\mathrm{true}\), for all \(j\in J\). Reasoning by induction, let us prove that
$$\begin{aligned} (\sum _{j=1}^{s}\lambda _j {\tilde{X}}_j, \sum _{j=1}^{s}\lambda _j {\tilde{Y}}_j)\in T_\mathrm{true},\quad s=1,\dots ,n. \end{aligned}$$(B.8)-
Check that in the case \(s=1\) it holds. This case is immediate, since \(({\tilde{X}}_1,{\tilde{Y}}_1)\in T_\mathrm{true}\), and then, by (B3), \((\lambda _1{\tilde{X}}_1,\lambda _1{\tilde{Y}}_1)\in T_\mathrm{true}\) .
-
Check that if cases \(s\le t\) are true, this implies that the case \(s=t+1\) is also true. We can write \( (\sum _{j=1}^{t+1}\lambda _j {\tilde{X}}_j, \sum _{j=1}^{t+1}\lambda _j {\tilde{Y}}_j)\) as the convex sum of two elements of \(T_\mathrm{true}\), multiplied by a scalar. Define \(\alpha =0.5\) and \(\alpha '=2\), then
$$\begin{aligned} \begin{array}{ll}\displaystyle &{} \left( \sum _{j=1}^{t+1}\lambda _j {\tilde{X}}_j, \sum _{j=1}^{t+1}\lambda _j {\tilde{Y}}_j\right) = \displaystyle \left( \sum _{j=1}^{t}\lambda _j {\tilde{X}}_j, \sum _{j=1}^{t}\lambda _j {\tilde{Y}}_j\right) + \left( \lambda _{t+1}{\tilde{X}}_{t+1},\lambda _{t+1}{\tilde{Y}}_{t+1}\right) \\ &{} \quad =\displaystyle \alpha ' \left( \alpha \left( \sum _{j=1}^{t}\lambda _j {\tilde{X}}_j, \sum _{j=1}^{t}\lambda _j {\tilde{Y}}_j\right) + (1-\alpha )\left( \lambda _{t+1}{\tilde{X}}_{t+1},\lambda _{t+1}{\tilde{Y}}_{t+1}\right) \right) . \end{array} \end{aligned}$$Then, by (B3) and (B4), it follows that \( (\sum _{j=1}^{t+1}\lambda _j {\tilde{X}}_j, \sum _{j=1}^{t+1}\lambda _j {\tilde{Y}}_j)\in T_\mathrm{true}\), and therefore, (B.8) holds.
As a consequence of (B.8), we have that \((\sum _{j=1}^{n}\lambda _j {\tilde{X}}_j, \sum _{j=1}^{n}\lambda _j {\tilde{Y}}_j)\in T_\mathrm{true}\). Since \(({\tilde{x}},{\tilde{y}})\) verifies (B.7), then by (B2), we conclude that \(({\tilde{x}},{\tilde{y}})\in T_\mathrm{true}\). Therefore, \(T_\mathrm{FDEA}\subseteq T_\mathrm{true}\) and the proof is complete.
-
\(\square \)
Appendix C: Proof of Theorem 2
-
(i)
Let us begin with the first part of the proof, that is, suppose that \(({\tilde{x}},{\tilde{y}})\in T_\mathrm{FDEA}\) is efficient and we have to prove that \(R^F_M({\tilde{x}},{\tilde{y}})\)=1. By contradiction, suppose that the statement is not true, i.e., \(R^F_M({\tilde{x}},{\tilde{y}})<1\). Let \((\theta ',\gamma ',\beta ,\lambda ')\) be the optimal solution for (LMFERM), and then, let \((\theta ,\gamma ,\lambda )\) be the corresponding optimal solution of model (MFERM). There must exist \(l_0\in \{0,\dots , k\}\), \(i_0\in \{1,\dots ,m\}\) and \(r_0\in \{1,\dots ,s\}\) such that \(\theta _{i_0l_0}^{L}<1\) or \(\theta _{i_0l_0}^{R}<1\) or \(\gamma _{r_0l_0}^{L}>1\) or \(\gamma _{r_0l_0}^{R}>1\). For the sake of simplicity, we continue the proof for the case \(\theta _{i_0l_0}^{R}<1\); the proof for the other cases is similar. From the constrains of (MFERM), it follows that \({\sum _{j=1}^{n}} \lambda _j {x}^{-}_{{ijl}} \le \theta _{il}^{L} {x}^{-}_{il}\le {x}^{-}_{il}\), \({\sum _{j=1}^{n}} \lambda _j {x}^{+}_{{ijl}} \le \theta _{il}^{R} {x}^{+}_{il}\le {x}^{+}_{il}\), \({\sum _{j=1}^{n}} \lambda _j {y}^{-}_{rjl} \ge \gamma _{rl}^{L} {y}^{-}_{rl}\ge {y}^{-}_{rl}\), \({\sum _{j=1}^{n}} \lambda _j {y}^{+}_{rjl} \ge \gamma _{rl}^{R} {y}^{+}_{rl}\ge {y}^{+}_{rl}\) for all i, l. In particular, \({\sum _{j=1}^{n}} \lambda _j {x}^{-}_{{i_0jl_0}} < \theta _{i_0l_0}^{L} {x}^{-}_{i_0l_0}\le {x}^{-}_{i_0l_0}\). Therefore,
 ,
,  , \(({\sum _{j=1}^{n}} \lambda _j {\tilde{X}}_{j},{\sum _{j=1}^{n}} \lambda _j {\tilde{Y}}_{j} )\ne ({\tilde{x}},{\tilde{y}})\), with \(({\sum _{j=1}^{n}} \lambda _j {\tilde{X}}_{j},\mathop {\displaystyle \sum \nolimits _{j=1}^{n}} \lambda _j {\tilde{Y}}_{j} )\in T_\mathrm{FDEA}\), contradicting the assumption that \(({\tilde{x}},{\tilde{y}})\) is efficient.
, \(({\sum _{j=1}^{n}} \lambda _j {\tilde{X}}_{j},{\sum _{j=1}^{n}} \lambda _j {\tilde{Y}}_{j} )\ne ({\tilde{x}},{\tilde{y}})\), with \(({\sum _{j=1}^{n}} \lambda _j {\tilde{X}}_{j},\mathop {\displaystyle \sum \nolimits _{j=1}^{n}} \lambda _j {\tilde{Y}}_{j} )\in T_\mathrm{FDEA}\), contradicting the assumption that \(({\tilde{x}},{\tilde{y}})\) is efficient. -
(ii)
For the second part of the proof, let us consider that \(R_M^F({\tilde{x}},{\tilde{y}})\)=1 and we have to prove that \(({\tilde{x}},{\tilde{y}})\in T_\mathrm{FDEA}\) is efficient. To this matter, suppose the contrary, that is, that \(({\tilde{x}},{\tilde{y}})\) is not efficient. This means that there exists \(({\tilde{x}}',{\tilde{y}}')\in T_\mathrm{FDEA}\), such that
 ,
,  and \(({\tilde{x}}',{\tilde{y}}')\ne ({\tilde{x}},{\tilde{y}})\). Then, there exist \(i_0\in \{1,\dots ,m\}\) or \(r_0\in \{1,\dots ,s\}\), such that
and \(({\tilde{x}}',{\tilde{y}}')\ne ({\tilde{x}},{\tilde{y}})\). Then, there exist \(i_0\in \{1,\dots ,m\}\) or \(r_0\in \{1,\dots ,s\}\), such that  and \({\tilde{x}}'_{i_0}\ne {\tilde{x}}_{i_0}\), or
and \({\tilde{x}}'_{i_0}\ne {\tilde{x}}_{i_0}\), or  and \({\tilde{y}}'_{r_0}\ne {\tilde{y}}_{r_0}\). For the sake of simplicity, we continue the proof for the case
and \({\tilde{y}}'_{r_0}\ne {\tilde{y}}_{r_0}\). For the sake of simplicity, we continue the proof for the case  and \({\tilde{x}}'_{i_0}\ne {\tilde{x}}_{i_0}\); the proof for the other case is similar. It follows that there exists \(l_0\in \{0,\dots , k\}\), such that
and \({\tilde{x}}'_{i_0}\ne {\tilde{x}}_{i_0}\); the proof for the other case is similar. It follows that there exists \(l_0\in \{0,\dots , k\}\), such that  , \([{\tilde{x}}^{'-}_{i_0l_0}, {\tilde{x}}^{'+}_{i_0l_0}]\ne [{\tilde{x}}^{-}_{i_0l_0}, {\tilde{x}}^{+}_{i_0l_0}]\), and then \({\tilde{x}}^{'-}_{i_0l_0}< {\tilde{x}}^{-}_{i_0l_0}\) or \({\tilde{x}}^{'+}_{i_0l_0}< {\tilde{x}}^{+}_{i_0l_0}\). Suppose that \({\tilde{x}}^{'-}_{i_0l_0}< {\tilde{x}}^{-}_{i_0l_0}\). Then, there exists \(\delta <1\), \(\delta \ge 0\), such that \({\tilde{x}}^{'-}_{i_0l_0}\le \delta {\tilde{x}}^{-}_{i_0l_0}\). Since \(({\tilde{x}}',{\tilde{y}}')\in T_\mathrm{FDEA}\), then there exists \(\lambda \in {\mathbb {R}}^n_+\), with
, \([{\tilde{x}}^{'-}_{i_0l_0}, {\tilde{x}}^{'+}_{i_0l_0}]\ne [{\tilde{x}}^{-}_{i_0l_0}, {\tilde{x}}^{+}_{i_0l_0}]\), and then \({\tilde{x}}^{'-}_{i_0l_0}< {\tilde{x}}^{-}_{i_0l_0}\) or \({\tilde{x}}^{'+}_{i_0l_0}< {\tilde{x}}^{+}_{i_0l_0}\). Suppose that \({\tilde{x}}^{'-}_{i_0l_0}< {\tilde{x}}^{-}_{i_0l_0}\). Then, there exists \(\delta <1\), \(\delta \ge 0\), such that \({\tilde{x}}^{'-}_{i_0l_0}\le \delta {\tilde{x}}^{-}_{i_0l_0}\). Since \(({\tilde{x}}',{\tilde{y}}')\in T_\mathrm{FDEA}\), then there exists \(\lambda \in {\mathbb {R}}^n_+\), with  ,
, 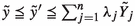 , that is, \(\sum _{j=1}^{n} \lambda _j {x}^{-}_{i_0 j l_0} \le {\tilde{x}}^{'-}_{i_0l_0}\le \delta {\tilde{x}}^{-}_{i_0l_0} ,\quad i=1,\dots , m, \ \ l=0,\ldots ,k\). Define \(\theta _{i_0l_0}^{'L}=\delta <1\), \(\lambda '=\lambda \), and the remaining variables equal to one in (LMFERM). Then, such \((\theta ',\gamma ',\beta ,\lambda ')\) is feasible for (LMFERM), with \(\frac{1}{2m(k+1)}\sum _{i=1}^{m} \sum _{l=0}^{k} (\theta _{il}^{'L}+\theta _{il}^{'R})<1\), contradicting the assumption that \(R^F({\tilde{x}},{\tilde{y}})=1\).
, that is, \(\sum _{j=1}^{n} \lambda _j {x}^{-}_{i_0 j l_0} \le {\tilde{x}}^{'-}_{i_0l_0}\le \delta {\tilde{x}}^{-}_{i_0l_0} ,\quad i=1,\dots , m, \ \ l=0,\ldots ,k\). Define \(\theta _{i_0l_0}^{'L}=\delta <1\), \(\lambda '=\lambda \), and the remaining variables equal to one in (LMFERM). Then, such \((\theta ',\gamma ',\beta ,\lambda ')\) is feasible for (LMFERM), with \(\frac{1}{2m(k+1)}\sum _{i=1}^{m} \sum _{l=0}^{k} (\theta _{il}^{'L}+\theta _{il}^{'R})<1\), contradicting the assumption that \(R^F({\tilde{x}},{\tilde{y}})=1\).
Appendix D: Proof of Theorem 3
To prove the result, suppose the contrary, i.e., \(R^F_M({\tilde{X}}_p^\mathrm{target},{\tilde{Y}}_p^\mathrm{target})<1\). Due to the way \(({\tilde{X}}_p^\mathrm{target},{\tilde{Y}}_p^\mathrm{target})\) is computed, there must exist an optimal solution \((\theta ^{*'},\gamma ^{*'},\beta ^{*'},\lambda ^{*'})\) for (LMFERM), which derives an optimal solution \((\theta ^*,\gamma ^*,\lambda ^*)\) of model (MFERM) and an optimal target of \(\mathrm{DMU}_p\) given by \({\tilde{X}}_p^\mathrm{target}={\sum _{j=1}^{n}} \lambda ^*_j {\tilde{X}}_{j}\) and \({\tilde{Y}}_p^{target}={\sum _{j=1}^{n}} \lambda ^*_j {\tilde{Y}}_{j}\). Analogously, let \((\theta ^{**},\gamma ^{**},\lambda ^{**})\) be the optimal solution of the (MFERM) model that projects \(({\tilde{X}}_p^\mathrm{target},{\tilde{Y}}_p^\mathrm{target})\). It follows that:
Since \(\theta _{il}^{**L},\theta _{il}^{**R}\le 1\), and \(\gamma _{rl}^{**L},\gamma _{rl}^{**R}\ge 1\) for all i, r, l, it is clear that \(R^F_M({\tilde{X}}_p^\mathrm{target},{\tilde{Y}}_p^\mathrm{target})<1\) implies that there must exist \(l_0\in \{0,\dots , k\}\), \(i_0\in \{1,\dots ,m\}\) and \(r_0\in \{1,\dots ,s\}\), such that \(\theta _{i_0l_0}^{**L}<1\) or \(\theta _{i_0l_0}^{**R}<1\) or \(\gamma _{r_0l_0}^{**L}>1\) or \(\gamma _{r_0l_0}^{**R}>1\). For the sake of simplicity of this proof, we only consider the first case \(\theta ^{**L}_{i_0l_0}<1\); the proof for the other cases is similar. Define \({\overline{\theta }}^{L}_{il}=\theta ^{*L}_{il}\theta ^{**L}_{il}\), \({\overline{\theta }}^{R}_i=\theta ^{*R}_{il}\theta ^{**R}_{il}\), \({\overline{\gamma }}^{L}_{rl}=\gamma ^{*L}_{rl}\gamma ^{**L}_{rl}\) and \({\overline{\gamma }}^{R}_{rl}=\gamma ^{*R}_{rl}\gamma ^{**R}_{rl}\) for all \(i\in \{1,\dots , m\}\), \(r\in \{1,\dots , s\}\) and \(l\in \{1,\dots , k\}\). It is clear that
Therefore, from definition of the target (11) and (12), and since \((\theta ^{**},\gamma ^{**},\lambda ^{**})\) is an optimal solution of (MFERM) for \(({\tilde{X}}_p^\mathrm{target},{\tilde{Y}}_p^\mathrm{target})\), and for all i, r, l
This implies that \(({\overline{\theta }},{\overline{\gamma }},\lambda ^{**})\) is a feasible solution of model (MFERM) for \(\mathrm{DMU}_{p}\), which combined with (D.2) and (D.3) implies that
contradicting the assumption that \((\theta ^*,\gamma ^*,\lambda ^*)\) is an optimal solution of (MFERM). This completes the proof.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arana-Jiménez, M., Sánchez-Gil, M.C., Lozano, S. et al. Efficiency assessment using fuzzy production possibility set and enhanced Russell Graph measure. Comp. Appl. Math. 41, 79 (2022). https://doi.org/10.1007/s40314-022-01780-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-022-01780-y
Keywords
- Efficiency
- Fuzzy data
- Fuzzy production possibility set
- Fuzzy enhanced Russell graph measure
- Fuzzy efficient targets





 if and only if
if and only if  if and only if
if and only if  ,
,  ,
, 

 ,
,  ,
, 
 ,
,  , it follows that:
, it follows that: 
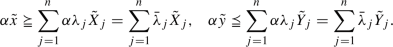


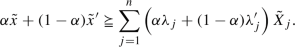


 ,
,  ,
,  ,
,  and
and  and
and  and
and  and
and  ,
,  ,
, 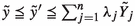 , that is,
, that is,