Multi-resonant Controller Design for a PV-Fed Multifunctional Grid-Connected Inverter in Presence of Unbalanced and Nonlinear Load

Abstract

The use of Active Power Filters (APFs) in future power grids with high penetration of nonlinear loads is unavoidable. Voltage Source Inverters (VSIs) interfacing Photovoltaic (PV) generator could play the APF role in addition to power supply. In this paper, the control of a PV-fed multifunctional grid-connected three-phase VSI is addressed with nonlinear and unbalanced load. The control objective is threefold. The first one is to deliver the maximum available power from the PV source to the grid satisfying power quality standards. The second one is the Voltage Balancing Control for DC-link capacitors to guarantee correct operation of the VSI. The last one is shunt APF control to compensate for nonlinear and unbalanced load harmonics, reactive power, and unbalanced sequences. A quasi-Proportional-Resonant (PR) controller with harmonic compensators is proposed for the current control loop. The quasi-PR controller parameters are determined through optimization algorithms such as Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and a combination of both PSO and GA. The aim of the objective function is to improve static and dynamic behavior. The different gains at the fundamental resonant frequency and the selected odd harmonics are obtained for the proposed quasi-PR controller. The dynamic characteristics of the optimized quasi-PR controllers show superiority against conventional ones in terms of gain margin, phase margin, overshoot, and robustness. With the proposed control scheme, the harmonics, reactive power, and unbalanced sequences are appropriately compensated. The performance of the PV-fed VSI shunt APF under irradiance change, load change, and distorted grid voltage conditions is validated through numerical simulations performed on $\hbox {PSIM}^{\copyright }$ software. The results show that the grid currents Total Harmonic Distortion for irradiance change case study are $4.57\%$, $4.57\%$, and $3.22\%$ in phase a, b, and c with the proposed control method, while they are $9.25\%$, $5.65\%$, and $10.12\%$ with conventional instantaneous $p-q$ theory.

1 Introduction

Table 1 A comparative analysis of different shunt APF compensation methods

Conventional power systems are experiencing serious challenges such as fossil fuel depletion, low energy efficiency, and environmental pollution. These problems are the main driving factors toward using renewable energy resources (Guerrero et al., 2011). These sources of energy are intermittent in nature; hence, interfacing power electronics converters are necessary to regulate voltage, current, and power. These converters are the sources of harmonic pollution in the power system. Nonlinear loads, such as diode-rectifiers, arc furnaces, electrified railways, and frequency control devices, could be considered as other sources of harmonic pollution which may jeopardize the power system’s safe and stable operation and may create serious power quality problems for both customers and suppliers. The harmonic power losses can lead to a rise in operational costs and create additional heating issues in power system components (Li et al., 2021). This can give rise to a reduction in their life span. As an example, the harmonic losses in facility transformers at the point of common coupling (PCC) can lead to an increase in the aging costs (Dao & Phung, 2018; Valedsaravi et al., 2022c). Other problems are overheating of capacitors, voltage waveform distortion, voltage flicker, and interference with the communication system. Moreover, the IEEE standard limit is 5% total harmonic distortion (THD) at PCC (IEEE, 2014). To cope with the power quality problems, active power filters (APF) and passive power filters (Wang et al., 2021) have been extensively used in industrial applications. They can be utilized for harmonic current compensation and harmonic voltage suppression in both shunt and series modes of operation.

In a grid-connected voltage source inverter (VSI) with photovoltaic-fed (PV-fed) system, the connection to the three-phase power grid is realized through a DC-link and an inverter. This inverter could work with multifunctional capability, including APF and power supply (Valedsaravi et al., 2022b). As a consequence, the control of a grid-connected PV-fed VSI can realize different aims such as delivering maximum power to the main grid, guaranteeing grid current high power quality, satisfying IEEE standards, and compensating for the nonlinear local load harmonics, reactive power, and unbalanced sequences.

Fig. 1

The schematic circuit diagram of the studied PV-fed system interfacing TLB converter and grid-connected three-phase inverter with shunt APF capability

The most popular control strategies for shunt APF compensation are the instantaneous $p-q$ power theory, based on abc to $\alpha \beta 0$ Clarke transformation, and the abc power theory (Akagi et al., 2017). The performance from the $p-q$ theory is poor under three-phase unbalanced load current and distorted grid voltage. The algorithm may produce some harmonics in the grid current, namely hidden currents, which are not present in the local load currents (Czarnecki, 2006). In addition, the algorithm suffers from extra calculation effort in case of multiple harmonic eliminations. In the abc power theory, the active and nonactive components of the currents are obtained through a minimization technique such as the Lagrange Multiplier method and the generalized Fryze currents (Aredes et al., 2003). In the first method, the constraint of the minimization problem is the three-phase instantaneous active power. This method results in poor performance for inconstant three-phase active power and in presence of zero-sequence components. Therefore, the compensation technique will draw undesirable zero-sequence current from the network (Czarnecki, 2004). In the second minimization method, the average value of three-phase instantaneous active power is used to obtain the active components of the currents. As a result, the algorithm is not an instantaneous theory and could have some malfunctions during transient periods (Bitoleanu & Popescu, 2013). To deal with these barriers, a control strategy is proposed in this paper for the shunt APF compensation. The proposed control strategy could have desirable performance in both three-phase three-wire and three-phase four-wire systems. Table 1 shows a comparative analysis of the different shunt APF compensation methods.

The proposed shunt APF control strategy is implemented in the abc reference frame. Therefore, the current control loop reference signal is a sinusoidal waveform with harmonic contents. The proportional-resonant (PR) controller with harmonic compensators is the most usable one in the current control loop. The PR controller design of a grid-connected VSI with an LCL output filter is a challenging task due to the LCL inherent resonance characteristic (Liserre et al., 2006). The control design is more challenging when harmonic compensators are added. The PR controller with harmonic compensators is usually limited to several low-order current harmonics since high-order harmonics can be out of control system bandwidth which can lead to instability problems. The stability analysis of PR-controlled grid-connected inverters with LCL filter is carried out in Liserre et al. (2006) which shows direct dependence on the controller parameters (Schiesser et al., 2018). To tune controller gains, the values of harmonic resonant coefficients are selected equally to the fundamental harmonic coefficient in Castilla et al. (2009) and in Chittora et al. (2017) and are selected inversely proportional to the value of the fundamental harmonic coefficient in Schiesser et al. (2018). However, these ways of coefficient selection are not optimum way as they don’t consider the performance of the controller in terms of steady-state and stability criteria. Moreover, the selection of the same coefficients for the higher-order compensators may lead to system instability. Therefore, in this paper, the multi-resonant PR controller coefficients are determined through optimization algorithms which considerably reduces controller design complexity. Moreover, the system’s static and dynamic behaviors are improved.

The rest of this paper is organized as follows. In Sect. 2, the system description and parameters are presented. In Sect. 3, the proposed control method with optimized multi-resonant controller are thoroughly presented. The theoretical results are validated through numerical simulations performed on ${\hbox {PSIM}}^{\copyright }$ software in Sect. 4. Finally, the concluding remarks are stated in the last section.

Fig. 2

The control diagram of the PV-fed VSI shunt APF

2 System Description

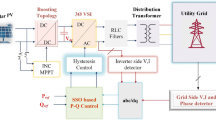
Figure 1 shows the scheme of the studied system in this paper. It consists of a PV source, a three-level boost (TLB) converter, and a three-phase four-wire grid-connected VSI with an LCL filter. It is worth mentioning that a three-phase network with more than one point grounded can also be classified as a three-phase four-wire system. In this system, the TLB converter performs maximum power point tracking (MPPT) control and DC-link voltage balancing control (VBC). The TLB is used to deliver maximum available power from the PV source to the main grid. A three-phase inverter is interfacing with the main grid and local load through an LCL filter to decrease switching harmonics injection. The nonlinear and unbalanced load involving full-wave bridge rectifiers, series resistor and inductor is located in parallel at PCC. The whole system is connected to the main grid through the PCC. Different components of load current such as harmonics, reactive power, and unbalanced sequences are separated through mathematical equations. Using these components, the reference of grid-side inverter current $i_{2}^{*}$ is obtained and then used in the current control loop. The three-phase grid voltages $v_{\text {g}a}$, $v_{\text {g}b}$, and $v_{\text {g}c}$ are considered sinusoidal as follows:

$$\begin{aligned} v_{\text {g}a}= & {} V_{\text {g}a}\sqrt{2} \sin (\omega _{\text {g}} t)\nonumber \\ v_{\text {g}b}= & {} V_{\text {g}b}\sqrt{2} \sin \left( \omega _{\text {g}} t-\frac{2\pi }{3}\right) \nonumber \\ v_{\text {g}c}= & {} V_{\text {g}c}\sqrt{2} \sin \left( \omega _{\text {g}} t+\frac{2\pi }{3}\right) \end{aligned}$$

(1)

where $V_{\text {g}a}$, $V_{\text {g}b}$, and $V_{\text {g}c}$ are the RMS values of grid voltages and $\omega _{\text {g}}$ is the grid angular frequency. Table 2 shows the system parameters.

Table 2 The circuit parameters

The DC-link consists of two identical capacitors each with a voltage $V_{\textrm{DC}}/2$ grounded at the midpoint. The LCL filter is used to limit current harmonic pollution at the PCC which should be below 5% according to the IEEE (2014) standard. The resistive and inductive value of the main grid at the PCC can be neglected (Wu et al., 2017). Furthermore, the filter resistances representing parasitic losses slightly change the dynamics of the ideal LCL filter and can also be neglected.

3 System Control

The whole control diagram of the PV-fed VSI shunt APF is shown in Fig. 2. The grid-side inverter current reference $i_{2}^{*}$ generation is an important task of the control system. The proposed control method is based on extracting harmonics, negative, and zero sequences of the local load current. First, the harmonic content of the three-phase load current is separated from its fundamental value by subtraction from the measured load current. The load current fundamental components enter the inverse Fortescue transformation to realize the unbalanced sequences of the local load current. The negative and zero sequence of grid-side inverter current references $i_{2_\text {ref}}^{-}$ and $i_{2_\text {ref}}^{0}$ are set to the load current negative and zero sequences. Thereafter, the positive sequence of grid-side inverter current $i_{2_\text {ref}}^{+}$ is obtained according to the PV power, local load reactive power, RMS value of the grid voltage, and grid synchronization term. Then, Fortescue transformation is used to determine compensated currents $i_{2a_\text {com}}$, $i_{2b_\text {com}}$, and $i_{2c_\text {com}}$ for each phase. The load current harmonic contents $i_{La_\text {H}}$, $i_{Lb_\text {H}}$, and $i_{\text {L}c_\text {H}}$ are all added to the compensated currents to obtain the grid-side inverter current references $i_{2a}^{*}$, $i_{2b}^{*}$, and $i_{2c}^{*}$. A multi-resonant controller is used for the current control loop. It has 3rd, 5th, 7th, 9th, 11th and 13th harmonic compensators to accurately track the references.

3.1 MPPT Control of the PV Source with TLB Converter

The output power of a PV generator is dependent on solar irradiation and ambient temperature. The power-voltage curve of a PV source has a maximum power point (MPP) value. In order to make the system to operate at MPP, different techniques have been proposed such as perturbation and observation (P &O), incremental conductance, and ripple correlation (Liu et al., 2008). In this paper, the most popular algorithm, P &O, is used for MPPT control of the PV source through the TLB converter. The control diagram of the TLB converter is illustrated in Fig. 3. The output voltage $V_{PV}$ and output current $I_{PV}$ of the PV generator are sensed and then applied as inputs to the MPPT block. The current value of the PV power compares with the past value and a step change is applied to the desired voltage reference $V_\text {ref}$ in the control loop. Proportional integral (PI) controllers are employed to regulate the input voltage of the TLB converter to its reference value. As shown in Fig. 3, the VBC is another important task of the TLB converter control to guarantee stable operation of the VSI. It can be performed by a PI controller with the input of DC-link voltages subtraction. The PI controller of VBC is designed in such a way that it should be faster than the MPPT control. The switching patterns of the TLB converter are realized through the pulse-width modulation (PWM) method. The phase difference of sawtooth carrier waveforms in the TLB switches is set to ${180}^{\circ }$.

Fig. 3

The control scheme of the TLB converter

3.2 Grid Synchronization

In the grid-connected application of VSI, the generated output voltage should be synchronized with the grid voltage. The injected current to the grid should have high power quality. The phase-locked loop (PLL), zero-crossing detection, artificial neural network, and adaptive linear neuron are some of the synchronization techniques proposed in the literature (Hoon et al., 2019). In this paper, the PLL approach is used which has three basic functional blocks known as phase detector, loop filter, and voltage-controlled oscillator as shown in Fig. 4. The loop filter cutoff frequency $\omega _{cf}$ is selected as ${30}\hbox {Hz}$. In the proposed PLL technique, the synchronization terms of the three-phase grid voltage, $\sin (\omega _\text {g} t)$, $\sin (\omega _\text {g} t-\frac{2\pi }{3})$, and $\sin (\omega _\text {g} t+\frac{2\pi }{3})$ are obtained. Table 3 illustrates the selected PI controllers’ parameters for the MPPT, VBC, and PLL determined through Ziegler-Nichols tuning method.

Table 3 The PI controllers’ parameters

Fig. 4

The proposed PLL control scheme

Fig. 5

The fundamental harmonic detection block

3.3 Shunt APF Control of VSI

In order to add the shunt APF capability to the three-phase VSI, the harmonic current and positive sequence of grid-side inverter current reference must be determined. The fundamental harmonic detection block is used for the load current harmonic detection. In addition, the PV power, the load reactive power, and the grid voltage are considered for obtaining the positive sequence of the grid-side inverter current reference.

3.3.1 Load Current Harmonic Detection

In order to improve power quality in grid-connected VSIs with nonlinear loads, the detection of harmonic components is needed. These components are part of the compensation signal in the control of grid-connected VSI (Asiminoael et al., 2007). A wide range of harmonic detection methods have been used in both time and frequency domains (Asiminoael et al., 2007). The fast Fourier transform (FFT), discrete Fourier transform, and recursive discrete Fourier transform are the examples of frequency-domain algorithms. In addition, the synchronous reference frame theory, the stationary frame filters, and the notch filters are some examples of the time-domain algorithms. Here in this paper, the FFT is used to detect load current harmonic content.

Figure 5 illustrates the block diagram of the fundamental harmonic detection block in phase a. The Fourier transform is utilized in each phase to extract the fundamental harmonic magnitudes and phases. Then, the fundamental harmonic signals are built in each phase. They are subtracted from the load currents to create the load current harmonic reference for the current controller. In each phase, the synchronization terms $\sin (\omega _{g}t)$, $\cos (\omega _{g}t)$, $\sin (\omega _{g}t-\frac{2\pi }{3})$, $\cos (\omega _{g}t-\frac{2\pi }{3})$, $\sin (\omega _{g}t+\frac{2\pi }{3})$, and $\cos (\omega _{g}t+\frac{2\pi }{3})$ are applied to the fundamental harmonic detection block. Therefore, the harmonic currents references in phases a, b, and c are extracted independently and imported to the proposed control diagram. The three-phase load current consists of fundamental components $i_{\text {L}a_\text {F}}$, $i_{\text {L}b_\text {F}}$, $i_{\text {L}a_\text {F}}$ and their harmonic terms $i_{\text {L}a_\text {H}}$, $i_{\text {L}b_\text {H}}$, $i_{\text {L}c_\text {H}}$ which can be expressed as follows:

$$\begin{aligned} \begin{aligned} i_{\text {L}a}&=i_{\text {L}a_\text {F}}+i_{\text {L}a_\text {H}} \\ i_{\text {L}b}&=i_{\text {L}b_\text {F}}+i_{\text {L}b_\text {H}} \\ i_{\text {L}c}&=i_{\text {L}c_\text {F}}+i_{\text {L}c_\text {H}} \end{aligned} \end{aligned}$$

(2)

where $i_{\text {L}a}$, $i_{\text {L}b}$, and $i_{\text {L}c}$ are the three-phase load current. Therefore, the load current harmonic references are obtained as follows

$$\begin{aligned} \begin{aligned} i_{\text {L}a_\text {H}}&=i_{\text {L}a}-i_{\text {L}a_\text {F}} \\ i_{\text {L}b_\text {H}}&=i_{\text {L}b}-i_{\text {L}b_\text {F}} \\ i_{\text {L}c_\text {H}}&=i_{\text {L}c}-i_{\text {L}c_\text {F}} \end{aligned} \end{aligned}$$

(3)

Fig. 6

The determination of positive sequence of the grid-side inverter current reference involving reactive power compensation

3.3.2 Positive Sequence of Grid-Side Inverter Current Reference

In order to obtain the positive sequence of the grid-side inverter current reference, the fundamental components of load current are used. The positive $i_{L}^{+}$, negative $i_{L}^{-}$, and zero sequence $i_{L}^{0}$ of the fundamental load current can be obtained using the inverse Fortescue transform (Akagi et al., 2017)

$$\begin{aligned} \begin{aligned} i_{L}^{0}&=\frac{1}{3}(i_{La_\text {F}}+i_{Lb_\text {F}}+i_{Lc_\text {F}})\\ i_{L}^{+}&=\frac{1}{3}(i_{La_\text {F}}+ai_{Lb_\text {F}}+a^{2}i_{Lc_\text {F}})\\ i_{L}^{-}&=\frac{1}{3}(i_{La_\text {F}}+a^{2}i_{Lb_\text {F}}+ai_{Lc_\text {F}}) \end{aligned} \end{aligned}$$

(4)

where $a=e^{j\frac{2\pi }{3}}$ and $i_\text {L}^{+}$ can be rewritten as follows

$$\begin{aligned} \begin{aligned} i_\text {L}^{+}=I_\text {L}^{+}\sin (\omega _{g}t+\phi _{i_\text {L}^{+}}) \end{aligned} \end{aligned}$$

(5)

where $I_\text {L}^{+}$ and $\phi _{i_\text {L}^{+}}$ are the magnitude and phase of the fundamental load current positive sequence, respectively. The magnitude of the grid-side inverter current reference positive sequence $I_{2_\text {ref}}^{+}$ is dependent on the PV power $P_\text {PV}$ which can be obtained as follows:

$$\begin{aligned} \begin{aligned} I_{2_{ref}}^{+}=\sqrt{2}\frac{P_\text {PV}}{3V_{\text {g}a}} \end{aligned} \end{aligned}$$

(6)

The phase of the grid-side inverter current reference positive sequence $\phi _{I_{2_{ref}}^{+}}$ is obtained through the PV power and the load reactive power $Q_{L}$. By neglecting the TLB power losses, the inverter active power $P_{i}$ can be considered equal to $P_{PV}$. The load reactive power is defined as follows:

$$\begin{aligned} \begin{aligned} Q_{L}=3V_{\text {g}a}\frac{I_\text {L}^{+}}{\sqrt{2}}\sin \phi _{i_{L}^{+}} \end{aligned} \end{aligned}$$

(7)

Therefore, the phase of grid-side inverter current reference positive sequence can be found as follows:

$$\begin{aligned} \begin{aligned} \phi _{I_{2_\text {ref}}^{+}}=\frac{180}{\pi }\arctan \frac{Q_\text {L}}{P_\text {PV}} \end{aligned} \end{aligned}$$

(8)

As a result, the positive sequence of the grid-side inverter current reference $i_{2_\text {ref}}^{+}$ is given by

$$\begin{aligned} \begin{aligned} i_{2_\text {ref}}^{+}=I_{2_\text {ref}}^{+}\sin (\omega _\text {g} t+\phi _{I_{2_\text {ref}}^{+}}) \end{aligned} \end{aligned}$$

(9)

The block diagram of the grid-side inverter current reference positive sequence determination is illustrated in Fig. 6. It could be equivalently expressed in the extended form as follows:

$$\begin{aligned} \begin{aligned} i_{2_\text {ref}}^{+}=I_{2_\text {ref}}^{+}(\sin \omega _\text {g}t\cos \phi _{I_{2_\text {ref}}^{+}}+\cos \omega _{g}t\sin \phi _{I_{2_\text {ref}}^{+}}) \end{aligned} \end{aligned}$$

(10)

At last, the compensated currents $i_{2a_\text {com}}$, $i_{2b_\text {com}}$, and $i_{2c_\text {com}}$ in each phase can be found as follows

$$\begin{aligned} \begin{aligned} i_{2a_\text {com}}&=i_{2_\text {ref}}^{0}+i_{2_\text {ref}}^{+}+i_{2_\text {ref}}^{-}\\ i_{2b_\text {com}}&=i_{2_\text {ref}}^{0}+a^{2}i_{2_\text {ref}}^{+}+ai_{2_\text {ref}}^{-}\\ i_{2c_\text {com}}&=i_{2_\text {ref}}^{0}+ai_{2_\text {ref}}^{+}+a^{2}i_{2_\text {ref}}^{-} \end{aligned} \end{aligned}$$

(11)

where $i_{2_\text {ref}}^{-}=i_{L}^{-}$ and $i_{2_\text {ref}}^{0}=i_{L}^{0}$. By the summation of the compensated current reference and harmonic current reference, the references of the grid-side inverter currents $i_{2a}^{*}$, $i_{2b}^{*}$, and $i_{2c}^{*}$ for shunt APF control of the VSI are given by

$$\begin{aligned} \begin{aligned} i_{2a}^{*}&=i_{2a_\text {com}}+i_{La_\text {H}}\\ i_{2b}^{*}&=i_{2b_\text {com}}+i_{Lb_\text {H}}\\ i_{2c}^{*}&=i_{2c_\text {com}}+i_{Lc_\text {H}} \end{aligned} \end{aligned}$$

(12)

3.4 Current Control Loop with AD

Different types of controllers have been used for the current control of grid-connected VSIs such as PI, PR (Zmood & Holmes, 2003), predictive (Maccari et al., 2020), hysteresis, and sliding mode control (Hollweg et al., 2021). The PI control strategy in the dq reference frame is the widely used one (Twining & Holmes, 2003). It has a desirable performance in balanced systems. However, it has poor performance in unbalanced and nonlinear systems (Timbus et al., 2009). In this paper, since all the reference signals are sinusoidal, the PR controller is utilized. This controller has less steady-state error and selective harmonics compensation capability (Bojoi et al., 2005).

Furthermore, the high peaking at LCL filter resonant frequency may lead to instability issues. To solve this problem, different damping techniques such as passive damping (PD) and active damping (AD) have been proposed. The PD consists of adding a resistor to one of the filter elements. The use of a resistor as a damper leads to extra losses and less efficiency. Another damping method is the AD method which consists of adding a feedback path to the control system. The advantage of this technique is the removal of power loss. However, it needs an extra sensor and adds complexity to the control system  (Dannehl et al., 2010). The damping technique used in this paper is an AD based on the capacitor current feedback loop as illustrated in Fig. 2.

3.4.1 Quasi Multi-resonant Controller Design

The transfer function of the LCL output filter with the additional AD feedback from the inverter output voltage $v_{ia}^{*}$ to the grid-side inverter current $i_{2a}^{*}$ is

$$\begin{aligned} G_\text {sys}(s)=\frac{1}{L_{1}L_{2}Cs^{3}+L_{2}CK_\text {AD}s^{2}+(L_{1}+L_{2})s} \end{aligned}$$

(13)

In the current control loop, a multi-resonant PR controller is used. The transfer function of the proposed multi-resonant PR controller with odd harmonic compensators up to 13th can be expressed as follows:

$$\begin{aligned} G_\text {c}(s)=K_\text {P}+\sum _{h=1}^{7} \frac{2K_{i(2h-1)}\omega _\text {c}s}{s^{2}+2\omega _\text {c}s+\omega ^{2}_{2h-1}} \end{aligned}$$

(14)

where $K_\text {P}$ is the proportional gain, $K_{i(2h-1)}\mid _{h=1...7}$ are the resonant gains at the fundamental and selected odd harmonics, $\omega _\text {c}$ is the cutoff frequency, and $\omega _{2h-1}$ is the frequency of the $2h-1$-th odd harmonics. Therefore, the transfer function of open-loop system $G_\text {c}(s).G_\text {sys}(s)$ is

$$\begin{aligned} G_\text {op}(s)=\frac{a_{1}s^{14}+a_{1}s^{13}+\cdots +a_{15}}{b_{1}s^{17}+b_{2}s^{16}+\cdots +b_{18}} \end{aligned}$$

(15)

where $a_{1},\cdots ,a_{15}$ are the nominator and $b_{1},\cdots ,b_{18}$ are the dominator coefficients of open-loop system. As shown in (15), the system loop is $17{\text {th}}$ order. Therefore, tuning the multi-resonant PR controller parameters is a challenging task. To select the controller parameters, different contradictory constraints should be considered. The first one is the requirement of steady-state error for the grid current. It is related to the magnitude of the loop gain at the fundamental frequency $f_{g}$. The second and the last constraints are the gain margin and the phase margin, respectively. Hence, a satisfactory region detection for the controller parameters is complex (Henz Mossmann et al., 2021). It is worth mentioning that if the steady-state error, phase margin, and gain margin specifications are excessively strict, the parametric region may be very small or perhaps non-existent. Therefore, in the literature, a simple PR controller is designed for the fundamental component and then its gain is used for all harmonic compensators.

The nine parameters $\omega _\text {c}$, $K_{P}$, $K_{i1}$, $K_{i3}$, $K_{i5}$, $K_{i7}$, $K_{i9}$, $K_{i11}$, and $K_{i13}$ need to be selected for the proposed quasi-PR current controller. The first one is $\omega _\text {c}$ which is related to the grid frequency by $2\pi f_{g}\Delta f_{g}$ (Ye et al., 2016). To design $\omega _\text {c}$, the standard limit of grid frequency variation $\Delta f_{n}$ is considered ±1%, thereby leading to $\omega _\text {c} \approx 3$. This value can satisfy a desirable bandwidth around the resonant frequencies. The application of optimization theories is vastly adopted in modern power systems (Abazari et al., 2019a, b). Also in this paper, to determine the next eight quasi-PR controller parameters, particle swarm optimization (PSO), genetic algorithm (GA), and a combination of PSO and GA named PSO-GA are employed. The objectives of the optimization algorithm are to improve dynamic behavior, stability margins, and reduce the steady-state error at selected odd harmonics. In the rest of this subsection, firstly, the PSO, GA, and PSO-GA algorithms are briefly reviewed and then an optimum quasi-PR current controller is designed.

3.4.2 Optimization Algorithms Definition

The most popular optimization method is the PSO algorithm. The PSO evolutionary algorithm imitates the social interaction of flocks of birds. It makes sufficient use of probabilistic transition rules to do parallel searches of the huge solution space. The feasibility and simplicity of the PSO algorithm make it a popular method for many optimization problems. The PSO algorithm utilizes a swarm of particles, which seek out a multidimensional search space to find the best solution. Each particle has the potential to be the best solution and is affected by the neighbor’s experiences. In each iteration of PSO algorithm, $i-$th particle have a present position $x_{i}(t)$, previous position $x_{i}(t-1)$, and moving velocity $v_{i}(t)$ in the $t-$th iteration. The position and velocity of the particle are updated as follows:

$$\begin{aligned} \left\{ \begin{aligned} x_{i}(t)&=x_{i}(t-1)+v_{i}(t) \\ v_{i}(t)&=Wv_{i}(t-1)+c_{1} \rho (pbest-x_{i}(t-1))+ \cdots \\&+c_{2}\rho (gbest-x_{i}(t-1)) \end{aligned} \right. \nonumber \\ \end{aligned}$$

(16)

where W is the PSO inertia weight, $c_{1}$ and $c_{2}$ are acceleration factors, and $\rho$ is a uniformly distributed random number between 0 and 1. The variables pbest and gbest are the personal best experience and global best experience, respectively. From equation (16), it is obvious that each particle velocity contains three parts. The first one introduces the searching ability of the PSO. The second one is related to the personal experience of the particle, called private thinking, and the last one is related to the global experience of all particles, named collaboration thinking. The PSO coefficients $c_{1},c_{2}$ determine the movement speed of particles to pbest and gbest locations. Particles may become away from target zones with small values of $c_{1},c_{2}$. However, large values of these coefficients may result in fast movement in the searching zone. Many research works proved that the acceleration constants $c_{1}$ and $c_{2}$ should be selected between 1 and 2 (Shi & Eberhart, 1998). The inertia weight W is chosen to make a balance between global and local exploration which results in less number of iterations to find a relatively optimal solution (Bratton & Kennedy, 2007). Figure 7 shows the flowchart of the proposed PSO algorithm.

Fig. 7

The PSO algorithm flowchart

Another popular optimization algorithm is the GA method. This algorithm is based on a natural selection process mimicking biological evolution. First, a random population of individual solutions is considered. Then, crossover and mutation are applied to the current population in order to create new children. The best solutions for the current population and the created children are considered for the next generation. The algorithm will stop searching when a certain criterion is achieved. The flowchart of the proposed GA algorithm is shown in Fig. 8.

Fig. 8

The GA algorithm flowchart

The last optimization technique used in this paper is the combination of the two previous optimization algorithms, called as PSO-GA. In the PSO-GA, both abilities of PSO and GA coexist in one optimization algorithm (Valedsaravi et al., 2022a). In this method, both operators of PSO and GA, including personal experience, global experience, crossover, mutation, and selection, are applied in each iteration. Figure 9 shows the flowchart of the proposed PSO-GA algorithm.

Fig. 9

The PSO-GA algorithm flowchart

3.4.3 Designing Multi-resonant PR Parameters by Optimization Algorithms

In this section, the proposed design approach of multi-resonant controllers’ coefficients is presented. The design approach is formulated as an optimization problem. The optimum values for the control system coefficients $K_{P}$, $K_{i1}$, $K_{i3}$, $K_{i5}$, $K_{i7}$, $K_{i9}$, $K_{i11}$, and $K_{i13}$ are obtained through different optimization techniques including PSO, GA, and PSO-GA. The objective function is selected to improve the system dynamic behavior, stability region, and steady-state response, and it is expressed as follows

$$\begin{aligned} \text {Objective Function}=-(Gm+Pm+\alpha \sum _{h=1}^{7} Mag_{2h-1}) \end{aligned}$$

(17)

where Gm, Pm, and $Mag_{2h-1}$ are the gain margin, phase margin, and harmonic magnitudes in the open-loop system, respectively. It should be noticed that the more magnitude at the selected frequencies, the least steady-state error at that harmonics. The factor $\alpha$ is added to the objective function in order to make a trade-off between stability and steady-state error at selected frequencies. This factor is set to 0.3 based on the authors’ experience in the optimization running. The optimization techniques parameters are shown in Table 4.

Table 4 The optimization techniques parameters

The optimum values of the control system coefficients obtained through different optimization techniques are given in Table 5.

Fig. 10

The objective function convergence for different optimization algorithms

Table 5 The obtained quasi-PR controller parameters through PSO, GA, and PSO-GA algorithms

Figure 10 shows the evolution of the objective function in terms of the iteration number with the proposed PSO, GA, and PSO-GA algorithms. The figure shows that the objective function convergence is very close to its optimum value with less than 40 iterations.

Table 6 shows the comparative analysis among the PSO-tuned, GA-tuned, and PSO-GA-tuned quasi-PR controllers and conventional PR controller (Conv.) with fixed gains at harmonic compensators. It can be seen that the gain margin, phase margin, and overshoot of the control system designed with optimization algorithms are more desirable than the conventionally designed controller. The phase margin, gain margin, and minimum magnitude at selected frequencies for the proposed quasi-PR controller with optimized parameters are obtained as ${8.11}\hbox {dB}$, ${31.8}^{\circ }$, and ${29.8}{\hbox {dB}}$, respectively. These values are appropriate for the practical control systems (Bolton, 2004). With these values, the control system has satisfactory performance in terms of asymptotic stability and steady-state error at selected odd harmonics.

Table 6 The dynamic performance comparative analysis

The comparative bode plot of the open-loop system with optimized quasi-PR controllers and the conventional controller is shown in Fig. 11 where the previous values of gain margin and phase margin can be appreciated. It is noteworthy that such stable margins cannot be obtained without the necessary damping which had been applied to the system. In Fig. 12, the step response of the closed-loop system with optimized quasi-PR controllers has been compared with the conventional PR controller. Moreover, the robustness of the optimized controllers against system parameter changes is shown in Fig. 13. The filter inductances and capacitance increase 50% which leads to instability in the system with conventional controller. However, the systems with optimized controllers are still stable. From these figures, it can be seen that the stability and robustness of system has improved with optimized quasi-PR controllers.

Fig. 11

The bode-diagram of the open-loop system with different controllers

Fig. 12

The step response of the closed-loop system with different controllers

Fig. 13

The bode-diagram of the open-loop system when LCL filter parameters increase by $50\%$

3.5 Inverter Modulation Technique

The last step is to obtain switching patterns of the VSI. There are different modulation techniques for three-phase inverters. The sinusoidal PWM (SPWM) and space vector PWM (SVPWM) are the widely used ones. In this paper, the SPWM technique is used. In this method, the same amplitude triangular carriers between $-1$ and 1 are applied for each phase. The switching pattern of VSI is determined as previously shown in Fig. 2.

4 Simulation Results

In this section, the effectiveness of the proposed control approach using optimized controller is validated through numerical simulation performed on $\hbox {PSIM}^{\copyright }$ software. The performance of the system is thoroughly analyzed under PV irradiation step change, nonlinear and unbalanced load step change, and distorted grid voltage. Moreover, the performance of proposed control method is compared with the conventional instantaneous $p-q$ theory. The nonlinear and unbalanced load parameters are given by Table 7.

Table 7 The nonlinear and unbalanced load parameters

4.1 PV Irradiation Step Change

In the first case study, in order to analyze the PV-fed VSI shunt APF performance, an irradiation step change for the PV is applied at $t=0.2$ s from 1000 to ${700}\,{\hbox {W}/{\hbox {m}^2}}$. The three-phase grid current, load current, and grid-side inverter current are illustrated in Fig. 14. The grid currents THD are $4.57\%$, $4.57\%$, and $3.22\%$ in phase a, b, and c.

Fig. 14

The three-phase currents under PV irradiation step change at $t=0.2$ s: a grid; b load; c inverter

The harmonic content of nonlinear and unbalanced load three-phase currents $i_{\text {L}a_\text {H}}$, $i_{\text {L}b_\text {H}}$, and $i_{\text {L}c_\text {H}}$ are shown in Fig. 15. The performance of MPPT and VBC control is illustrated in Fig. 16. As shown in this figure, the PV output voltage is appropriately tracking the reference voltage provided by the MPPT. Moreover, the DC-link voltages in the TLB converter output are balanced.

Fig. 15

The harmonic content of nonlinear and unbalanced load three-phase current

Fig. 16

The TLB performance under PV irradiation step change at $t=0.2$ s: a MPPT power tracking; b MPPT voltage tracking; c DC-link voltages

The grid current and voltage are shown in Fig. 17a. It can be seen in this figure that the grid current and voltage are in phase. It means that the reactive power is effectively compensated. Figure 17b and c illustrates the active and reactive power of the inverter, grid, and load. It can be seen that the injected grid power decreases when the PV output power reduces.

The results from the instantaneous $p-q$ theory and from the proposed method are shown in Fig. 18. As shown in this figure, the THD and the current unbalance factor (CUF) of the three-phase grid current for the proposed shunt APF control method are better than instantaneous $p-q$ theory. Namely, the CUF of negative and zero sequences of the grid current are $5\%$ and $1.4\%$ for the proposed shunt APF control method. However, they are $15\%$ and $1.7\%$ for the conventional instantaneous $p-q$ theory.

Fig. 17

The grid current and voltage, active power, and reactive power under PV irradiation step change at $t=0.2$ s: a grid current and voltage; b active power; c reactive power

Fig. 18

The comparison of three-phase grid current between instantaneous $p-q$ theory and the proposed control method under PV irradiation step change

4.2 Nonlinear and Unbalanced Load Step Change

Fig. 19

The three-phase currents under load step change at $t=0.2$ s: a grid; b load; c inverter

Fig. 20

Nonlinear and unbalanced load three-phase current and its harmonic content

Fig. 21

The TLB performance under load step change at $t=0.2$ s: a MPPT power tracking; b MPPT voltage tracking; c DC-link voltages

Fig. 22

The grid current and voltage, active power, and reactive power under load step change at $t=0.2$ s: a grid current and voltage; b active power; c reactive power

In the second case study of analyzing the PV-fed shunt APF inverter, a load step change is applied at $t=0.2$ s. The resistances of $R_{\text {L}c}$, $R_{\text {L}_{1}}$, and $R_{\text {L}_{2}}$ reduce to their half values and $R_{\text {L}a}$ changes to ${8}{\Omega }$ at $t=0.2$ s. The three-phase grid current, load current, and grid-side inverter current are illustrated in Fig. 19. The nonlinear and unbalanced load three-phase current and its harmonic content are shown in Fig. 20. The performance of MPPT and VBC control under load step change is depicted in Fig. 21. As shown in this figure, the MPPT and VBC are properly tracking the references.

In Fig. 22a, the grid current and voltage are illustrated. As shown in this figure, the grid current and grid voltage are in phase. Therefore, the load reactive power is totally compensated through the VSI. The active and reactive power of the inverter, the grid, and the load are illustrated in Fig. 22b and c. The PV power is fixed at 10 kW. Therefore, when the load power undergoes a step change, the main grid’s active power decreases.

The three-phase grid current is shown in Fig. 23 for both when the instantaneous $p-q$ theory used and the proposed control method. From this figure, the THD of $i_{\text {g}a}$, the THD of $i_{\text {g}b}$, the THD of $i_{\text {g}c}$, negative-sequence CUF, and zero-sequence CUF are $5.34\%$, $5.79\%$, $3.8\%$, $8.2\%$, and $2.34\%$ for the proposed shunt APF control method, respectively. These values validate the more satisfactory performance of the proposed method in comparison with conventional instantaneous $p-q$ theory.

4.3 Distorted Grid Voltage

Fig. 23

The comparison of three-phase grid current between instantaneous $p-q$ theory and the proposed control method under load step change

Fig. 24

The distorted grid voltages

Fig. 25

The three-phase currents under distorted grid voltage: a grid; b load; c inverter

Table 8 The grid current THD and CUF in both instantaneous $p-q$ and proposed method for different case studies

The performance of the proposed PV-fed shunt APF inverter is also analyzed under distorted grid voltages. The third harmonic with a magnitude of 60V is added to the grid voltage $v_{\text {g}a}$. The three-phase distorted grid voltage is illustrated in Fig. 24. The three-phase grid current, load current, and grid-side inverter current are illustrated in Fig. 25. The grid currents THD with the proposed control method are $5.87\%$, $5.12\%$, and $3.73\%$, while they are $10.33\%$, $7.97\%$, and $8\%$ with instantaneous $p-q$ theory. In addition, the three-phase grid current negative and zero CUF with the proposed control method are $8.2\%$ and $2\%$, respectively. However, they are $24.2\%$ and $3\%$ with instantaneous $p-q$ theory.

The performance of MPPT and VBC control under distorted grid voltage is illustrated in Fig. 26. It can be seen from this figure that the MPPT control and VBC have the desirable performances.

The grid current and voltage are illustrated in Fig. 27a. As shown in this figure, there is no any reactive power consumption from the main grid. Figure 27b and c illustrates the active and reactive power of the inverter, the grid, and the load. The PV power is fixed at $P_{max}$, 10 kW.

The instantaneous $p-q$ theory and the proposed control method are compared in Fig. 28. It can be observed that the three-phase grid current with the proposed shunt APF control method is balanced and has less harmonic pollution than the conventional instantaneous $p-q$ theory. The comparative analysis of the proposed control method and the conventional instantaneous $p-q$ theory for different case studies are given by Table 8.

Fig. 26

The TLB performance under distorted grid voltage: a MPPT power tracking; b MPPT voltage tracking; c DC-link voltages

Fig. 27

The grid current and voltage, active power, and reactive power under distorted grid voltage: a grid current and voltage; b active power; c reactive power

Fig. 28

The comparison of three-phase grid current between instantaneous $p-q$ theory and the proposed control method under distorted grid voltage

5 Conclusions

In this paper, the control of a PV-fed multifunctional grid-connected inverter has been addressed. The studied system consists of a TLB, a three-phase VSI, an LCL output filter, and a nonlinear and unbalanced load. The shunt APF control strategy has been presented to control the grid-side three-phase inverter current. A quasi-PR controller was employed to track the sinusoidal references properly due to the presence of nonlinear local load, containing harmonic pollution. To determine controller parameters, optimization algorithms with novel objective function have been used. The parameters of the objective function have been chosen based on static and dynamic performances. Each harmonic compensator of the quasi-PR controller has its own resonant gain with zero steady-state error at that particular harmonic. By virtue of the proposed control method, the PV-fed VSI can act as a shunt APF, capable of compensating harmonic currents, reactive power, and load unbalanced sequences. The proposed method with an optimized controller shows superiority against the conventional control technique. Its effectiveness has been verified by detailed simulations performed on the switched model of the system implemented in $\hbox {PSIM}^{\copyright }$ software. Its advantages can be summarized as follows:

• Injecting the PV power adaptively in grid-connected application with low grid current THD;

• Desirable performance under irradiation step change, load step change, and distorted grid voltage;

• Operating of the VSI as a shunt APF and a reactive power compensator;

• Removing zero and negative sequences from the main grid current and desirable CUF;

• Optimized quasi-PR controller for grid-side inverter current control;

• Desirable dynamic stability and reference tracking for the control system.