Manipulation Task Planning and Motion Control Using Task Relaxations

Abstract

This paper proposes a robotic manipulation task relaxation method applied to a task and motion planning framework adapted from the literature. The task relaxation method consists of defining regions of interest instead of defining the end-effector pose, which can potentially increase the robot’s redundancy with respect to the manipulation task. Tasks are relaxed by controlling the end-effector distance to a target plane while respecting suitable constraints in the task-space. We formulate the problem as a constrained control problem that enforces both equality and inequality constraints while being reactive to changes in the workspace. We evaluate the adapted framework in a simulated pick-and-place task with similar complexity to the one evaluated in the original framework. The number of plan nodes that our framework generates is 54% smaller than the one in the original framework and our framework is faster both in planning and execution time. Also, the end-effector remains within the regions of interest and moves toward the target region while satisfying additional constraints.

1 Introduction

One of the major goals in robotics is to design manipulator robots that autonomously plan and execute highly complex manipulation tasks. To that aim, plans can be obtained by integrating task and motion planning (ITMP) and executed by a closed-loop motion controller to cope with changes in the workspace. Also, some tasks require the robot to work under constraints, such as limits of joints and geometrical constraints due to obstacles in the workspace. However, some tasks may not be accomplished when there are too many hard constraints. Nonetheless, some of those tasks can be relaxed and do not require all degrees of freedom (DOF) all the time, hence increasing the chance of a successful execution. In this sense, this work proposes a methodology for solving the ITMP problem for manipulation tasks that can be relaxed in a computationally efficient manner by combining state-of-the-art task planners with constrained motion controllers.

In ITMP, the task planner generates a sequence of actions that the robot must execute, whereas the motion planner generates a trajectory for each action (Kaelbling and Lozano-Perez 2011). If a trajectory cannot be found, a new task plan is required (He et al. 2015; Bhatia et al. 2011; Dantam et al. 2018). As a result, ITMP frameworks spend a lot of time planning and replanning. After obtaining a feasible task and motion plan, a motion controller executes it. In this sense, in our previous work (Pereira and Adorno 2020), we have adapted the ITMP framework of He et al. (2015) to solve the ITMP challenge by using a new approach to replace the motion planning layer by a single constrained motion controller that executes the task plan without the need for replanning. The ITMP framework of He et al. (2015) uses linear temporal logic (LTL) to define task specifications. LTL allows to specify boolean and temporal constraints and has correctness and completeness guarantees (Baier and Katoen 2008, ch. 5), but the number of states of the specified task has combinatorial growth, which is also known as the state-explosion problem (Wongpiromsarn et al. 2010). Therefore, frameworks based on LTL usually build a discrete abstraction of the robotic system (Kress-Gazit et al. 2007; He et al. 2015; Kloetzer and Belta 2008; Bhatia et al. 2011), but such construction is usually non-trivial and may still suffer from the curse of dimensionality.

In contrast to LTL, Fikes and Nilsson (1971) propose a problem solver called STRIPS (Stanford Research Institute Problem Solver) that searches for a model in a space of world models to reach a desired goal. However, STRIPS does not regard temporal specifications, only uses linear sequences of operators, and requires lower layers to translate its very high-level plans to robot actions. Ferrer-Mestres et al. (2017) propose a constrained task and motion planning framework that encodes the ITMP problem into classical AI problems using Functional STRIPS as the planning language. The framework scales up to 30 or 40 objects, but it has a long preprocessing phase and is suitable only for static environments.

From the application point of view, LTL can be used to specify a wide range of robotic tasks such as coverage, sequencing, conditions, avoidance, and counting (Kress-Gazit et al. 2007; McMahon and Plaku 2014). For manipulation tasks, it is often desirable to specify tasks with temporal constraints that enable enforcing execution order. Hence, LTL is a suitable formalism.

From the task point of view, the framework proposed by He et al. (2015) only allows placing the object in exact locations of interest in the workspace. Nonetheless, some tasks may be relaxed, and thus benefit from using a region of interest instead of an exact location. A common solution is to discretize the workspace in multiple locations to define different possibilities for placing the manipulated objects. Garrett et al. (2018) propose the FFRob algorithm for solving the ITMP problem that uses workspace discretization by defining a relaxed state. In the FFRob, a state is represented by a set of values that indicate the robot configuration, the object being held, and the pose of each object. In this sense, the relaxed state is a set of states formed by all combinations of possible values for a state. In other words, it contains all the possible robot configurations, objects and their poses for the state. However, if a similar approach is used in the work of He et al. (2015), the number of possibilities that the planner must consider quickly grows and the state-explosion problem appears. Another possibility for task relaxation is to explore the kinematic redundancy in a low-level motion controller.

Classic techniques that tackle kinematic redundancy are based on a hierarchical architecture that allows controlling secondary tasks besides the main task. This is done by projecting the control input from lower-priority tasks into the nullspace of the Jacobian matrices associated with higher-priority tasks. Hence, a secondary task that does not disturb the main task and considers constraints can be added (Mansard and Chaumette 2007). In this context, Figueredo et al. (2014) propose the relaxation of task constraints and a switching strategy to automatically choose control objectives that demand fewer degrees of freedom, whenever possible, and hence perform secondary tasks. The switching strategy is based on relaxing the control requirements according to previously defined geometric task objectives. They define which task primitive (i.e. distance, position, orientation, or pose) should be controlled to achieve a geometric task.

To enhance the task relaxation capabilities, additional optimization criteria might be considered. To do this, a possible solution is to use hierarchical least-square optimization (Escande et al. 2014). Least-square optimization can be used to fulfill as best as possible a set of constraints that may not be feasible (Escande et al. 2014). Furthermore, when the constraints are linear in the control inputs, the least-square problem is written as a quadratic program. Thus, Escande et al. (2014) propose a method to solve a hierarchical quadratic program in a computationally efficient manner that allows solving problems with many variables fast enough to be used in real-time control.

In contrast to the aforementioned task relaxation methods, Marinho et al. (2019) propose a constrained motion controller based on optimization that allows keeping the robot outside a restricted region or inside a safe region by using constraints. This way, it is possible to define regions of interest and do a coarse discretization of the workspace, which greatly reduces the computational burden of the overall method. The idea is to specify geometrical constraints, based on the regions of interest, to accomplish the desired task generated by the high-level task-planner without resorting to low-level motion planning. Moreover, it is possible to add joints limits and obstacle avoidance constraints while satisfying the task relaxation constraints. After defining all the constraints, the controller can be described by minimization problems (Laumond et al. 2015) that make use of extra available DOFs of the robot to accomplish the task while respecting the constraints. This enables the generation of collision-free motions by using mathematical programming. Nonetheless, in the general case, there is no analytical solution and numeric solvers must be used (Goncalves et al. 2016; Escande et al. 2014).

We propose a robotic manipulation task relaxation method that adapts the ITMP framework of He et al. (2015) to use a motion controller that directly executes the task plan, without resorting to motion planning, reducing the total planning time. The task relaxation method consists of defining regions of interest instead of defining the end-effector pose, which can potentially increase the robot’s redundancy with respect to the manipulation task. Tasks are relaxed by controlling the end-effector distance to a target plane while respecting suitable constraints in the task-space. We formulate the problem as a constrained control problem that enforces both equality and inequality constraints while being reactive to changes in the workspace.

1.1 Statement of Contributions

This work builds upon our preliminary work (Pereira and Adorno 2020). The main contribution to the state of the art is a task relaxation methodology that reduces the number of DOFs required for a task while imposing joints limits and obstacle avoidance constraints without resulting in high computational complexity for the high-level planner. We also propose a new point-cone constraint that allows defining a circular target region in a simple way using only one constraint, in contrast to rectangular target regions that require four constraints (Pereira and Adorno 2020).

1.2 Organization of the Paper

Section 2 gives a brief introduction to LTL and presents the constrained motion controller. Section 3 describes our architecture for integration of task planning with constrained motion control using task relaxations. Section 4 presents a thorough evaluation of the framework through simulations. Finally, Sect. 5 concludes the paper and presents some suggestions for future works.

2 Preliminaries and Problem Definition

The framework for ITMP used in this paper relies on LTL for defining high-level tasks and a constrained motion controller to execute the manipulation tasks while respecting all geometrical constraints. This section briefly reviews those two techniques.

2.1 Linear Temporal Logic

In LTL, a proposition is a statement that can be true or false, but not both, and atomic propositions are the ones that do not depend on the truth or falsity of any other proposition. Let ${\mathbb {A}}=\{a_{0},a_{1},...,a_{N}\}$ be a set of atomic propositions. LTL semantics is defined over words on the alphabet $2^{{\mathbb {A}}}$, where $2^{{\mathbb {A}}}$ is the power set of ${\mathbb {A}}$. Given letters $A_{i}\in 2^{{\mathbb {A}}}$, with $i=0,1,2,\ldots$, words are finite or infinite sequences such as $\sigma =A_{0}A_{1}A_{2}\cdots A_{n}$ and $\sigma =A_{0}A_{1}A_{2}\cdots$.

An LTL formula $\varphi$ is composed of atomic propositions, Boolean operators, and basic temporal operators. More specifically, a formula $\varphi$ over ${\mathbb {A}}$, using a subset of LTL operators, results in¹

$$\begin{aligned} \varphi =a\,|\,\lnot a\,|\,\varphi _{1}\wedge \varphi _{2}\,|\,\varphi _{1}\vee \varphi _{2}\,|\,\varphi _{1}{\mathcal {U}}\varphi _{2}\,|\,{\mathcal {X}}\varphi _{1}\,|\,{\mathcal {E}}\varphi _{1}, \end{aligned}$$

(1)

where $a\in {\mathbb {A}}$, $\varphi _{1}$ and $\varphi _{2}$ are formulas. The Boolean operators are “negation” ($\lnot$), “and” ($\wedge$), and “or” ($\vee$). The temporal operator “until” (${\mathcal {U}}$) is such that $\varphi _{1}$ is true until $\varphi _{2}$ becomes true. The temporal operator “next” (${\mathcal {X}}$) means that $\varphi$ will definitely be true at the next step, and “eventually” (${\mathcal {E}}$) means that $\varphi$ will become true at some point in the future.²

Since the focus of this work is not on model checking, we give here an informal explanation to clarify what a formula $\varphi$ is, and what the operators mentioned above are. Let us define a simple set of atomic propositions containing two elements: ${\mathbb {A}}=\{a_{0},a_{1}\}$. Therefore,

• 1. $\varphi ={\mathsf {T}}$ is always true;³

• 2. $\varphi =a_{0}$ is true if and only if $a_{0}$ is true;

• 3. $\varphi =\lnot a_{0}$ is true if and only if $a_{0}$ is false;

• 4. if $\varphi _{0}=a_{0}$, $\varphi _{1}=a_{1}$, then $\varphi =\varphi _{0}\wedge \varphi _{1}$ is true if and only if both $a_{0}$ and $a_{1}$ are true;

• 5. if $\varphi _{0}=a_{0}$, $\varphi _{1}=a_{1}$, then $\varphi =\varphi _{0}\vee \varphi _{1}$ is true if and only if $a_{0}$ is true or $a_{1}$ is true or both are true;

• 6. if $\varphi _{0}=a_{0}$, $\varphi _{1}=a_{1}$, then $\varphi =\varphi _{0}{\mathcal {U}}\varphi _{1}$ is true if and only if $a_{1}$ becomes true after $a_{0}$ was already true;

• 7. if $\varphi _{1}=a_{1}$, then $\varphi ={\mathcal {X}}\varphi _{1}$ will be definitely true if and only if $a_{1}$ becomes true in the next time step;

• 8. if $\varphi _{1}=a_{1}$, then $\varphi ={\mathcal {E}}\varphi _{1}$ will be eventually true as $a_{1}$ will become true at some point in the future.

The formulas for $\varphi$, $\varphi _{1}$, and $\varphi _{2}$ could be any formula containing the operators in (1) with an arbitrary number of propositions. Although in the previous example we used simple formulas for the sake of clarity, they can be arbitrarily more complex.

In our current work, manipulation tasks must be achieved over a finite time horizon. Hence, we use only co-safe LTL formulas, which are the ones that can be interpreted by considering finite words (Kupferman and Y. Vardi 2001). Syntactically, co-safe LTL formulas contain only the temporal operators ${\mathcal {X}}$, ${\mathcal {E}}$, ${\mathcal {U}}$, and the negation operator is only allowed over atomic propositions, but not over temporal formulas.

Examples of LTL specifications for manipulation tasks are given in Sect. 3.1 and can also be found in our previous work (Pereira and Adorno 2020).

2.2 Constrained Kinematic Controller

The constrained controller (Marinho et al. 2019) is based on an optimization problem that minimizes the joint velocities, $\dot{\varvec{q}}\in {\mathbb {R}}^{n}$, in the $\ell _{2}$-norm sense while respecting hard constraints, such as obstacles in the workspace, joints limits, etc. The controller is derived from the desired closed-loop task-error dynamics. The differential kinematics, given by $\dot{\varvec{x}}=\varvec{J}\dot{\varvec{q}}$, provides the relation between the velocity of the joints and the task-space velocity. The vector $\varvec{q}\triangleq \varvec{q}(t)\in {\mathbb {R}}^{n}$ is the robot configuration, $\varvec{x}\triangleq \varvec{x}(\varvec{q})\in {\mathbb {R}}^{m}$ is the task vector, and $\varvec{J}\triangleq \varvec{J}(\varvec{q})\in {\mathbb {R}}^{m\times n}$ is the task Jacobian. Given a desired task vector $\varvec{x}_{d}\in {\mathbb {R}}^{m}$, we define the task error $\tilde{\varvec{x}}\triangleq \varvec{x}-\varvec{x}_{d}$. Considering $\dot{\varvec{x}}_{d}=\varvec{0}$ for all t, the error dynamics is given by $\dot{\tilde{\varvec{x}}}=\dot{\varvec{x}}$. To drive $\tilde{\varvec{x}}$ to zero with an exponential convergence rate, the desired closed-loop dynamics is given by $\dot{\tilde{\varvec{x}}}+\eta \tilde{\varvec{x}}=\varvec{0}$ where $\eta \in (0,\infty )$ is the gain that determines the convergence rate. Thus, $\varvec{J}\dot{\varvec{q}}+\eta \tilde{\varvec{x}}=\varvec{0}$ and the control input $\varvec{u}$ that minimizes the joint velocities $\dot{\varvec{q}}\in {\mathbb {R}}^{n}$ is obtained as:

$$\begin{aligned} \begin{aligned}\varvec{u}\in \,&\underset{\dot{\varvec{q}}}{\arg \!\min }&\left\| \varvec{J}\dot{\varvec{q}}+\eta \tilde{\varvec{x}}\right\| _{2}^{2}+\lambda \left\| \dot{\varvec{q}}\right\| _{2}^{2} \\&\text {subject to}&\varvec{W}\dot{\varvec{q}}\le \varvec{w}\\&&\end{aligned} \end{aligned}$$

(2)

where $\lambda \in [0,\infty )$ is a damping factor and $\varvec{W}\in {\mathbb {R}}^{l\times n}$ and $\varvec{w}\in {\mathbb {R}}^{l}$ are used to impose linear constraints in the control inputs. The constrained motion controller (2) allows choosing between different control objectives ${\mathfrak {O}}\in \left\{ {\mathfrak {O}}_{\mathrm {pose}},{\mathfrak {O}}_{\mathrm {orientation}},{\mathfrak {O}}_{\mathrm {position}},{\mathfrak {O}}_{\mathrm {line}},{\mathfrak {O}}_{\mathrm {plane}},{\mathfrak {O}}_{\mathrm {distance}}\right\}$ such as the control of end-effector pose (${\mathfrak {O}}_{\mathrm {pose}}$), orientation (${\mathfrak {O}}_{\mathrm {orientation}}$), or position (${\mathfrak {O}}_{\mathrm {position}}$), as well as primitives attached to the end-effector, such as lines (${\mathfrak {O}}_{\mathrm {line}}$) and planes (${\mathfrak {O}}_{\mathrm {plane}}$), in addition to distance control from target regions (${\mathfrak {O}}_{\mathrm {distance}}$) such as planes and cylinders (Adorno and Marques Marinho 2021). In this sense, the end effector will be driven, as best as possible, to the specified desired task vector $\varvec{x}_{d}$.

To prevent collisions with the workspace, we use the Vector Field Inequalities (VFI) framework (Marinho et al. 2019), which requires distance functions between two collidable entities and the corresponding Jacobian matrices, as better described in Sect. 3.3.

2.3 Problem Definition and Assumptions

Consider a robot in the workspace that can pick-and-place objects between regions. Given a finite set of objects $O=\{o_{1},...,o_{n}\}$, a finite set of regions $\Gamma \triangleq \{r_{1},...,r_{k},r_{\text {inter}}\}$, and a finite set of actions $\mathcal {M\triangleq }\{\mathrm {GRASP},\mathrm {PLACE},\mathrm {HOLD},\mathrm {MOVE}\}$, the first step is to find a finite sequence of actions $\alpha _{0},\alpha _{1},\dots ,\alpha _{m}\in {\mathcal {M}}$ that manipulate the objects $o_{0},o_{1},\dots ,o_{n}\in O$ between regions $r_{0},r_{1},\dots ,r_{k}\in \Gamma$ to satisfy a linear temporal logic (LTL) specification $\varphi$. The next step is to execute the sequence of actions. The actions of GRASP and PLACE are executed by closing and opening the end-effector, respectively, and HOLD and MOVE are executed by the constrained motion controller (2) with control objective ${\mathfrak {O}}$ and suitable constraints ${\mathfrak {W}}$. The following assumptions are considered:

• The planner is deterministic. Therefore, it will always generate the same sequence of actions.

• The environment is fully observable: the objects’ poses and the robot configuration are known at all times.

• The objects’ affordances are known.

3 Architecture for Integration of Task Planning and Motion Control

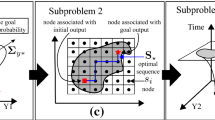
The framework for integration of task planning and motion control that we adapt from the literature is composed of a high-level planning framework and a low-level constrained motion controller. We use the high-level planner proposed by He et al. (2015) and the constrained motion controller proposed by Marinho et al. (2019). Figure 1 shows both layers.

Fig. 1

Adapted manipulation framework

3.1 Task Planning Framework

The task planning framework is divided into three steps: (1) LTL task specification and the creation of a deterministic finite automaton (DFA); (2) creation of a manipulation abstraction; (3) creation of a product graph.

In the first step, a manipulation task $\varphi$ is specified using co-safe LTL that depends only on the objects and the regions where the objects are located. For instance, in a pick-and-place task, we can specify where each object must be at the end without mentioning anything about the robot. Therefore, the propositions of the LTL formulas are defined as $(o_{i},r_{j})$, which means that “object $o_{i}$ is in region $r_{j}$” (He et al. 2015). Given a workspace with a finite set of objects O, a finite set of regions $\Gamma$, the atomic propositions of this scene are elements of $O\times \Gamma$. For instance, suppose a robot has to place an object $o_{1}\in O$ at a region $r_{1}\in \Gamma$. The specification for this task can be given by $\varphi _{1}={\mathcal {E}}(o_{1},r_{1})$, which means that “eventually object 1 will be in region 1.” To specify all the manipulation sequence possibilities the robot can do to execute the task, the specification $\varphi$ in LTL is then converted into a DFA.

In the next step of the planning framework, we use a manipulation abstraction that captures how the robot can manipulate the objects in the workspace. Each node in the abstraction is composed of an action $\alpha \in {\mathcal {M}}$, a region $r\in \Gamma$, a grasped object $o\in O$, and the region of each object in the world ${\mathfrak {o}}_{\Gamma }\in O_{\Gamma }$, with $O_{\Gamma }$ being the set of all the possibilities for objects regions.

The third step combines the manipulation abstraction with the DFA into a product graph that represents all the ways the robot can execute the task. Afterward, a graph search algorithm such as Dijkstra’s or a Breadth First Search (BFS) is used to search for a path on the product graph that represents a complete task plan.⁴

See our previous work (Pereira and Adorno 2020) for a formal definition of the planning framework.

3.2 Constrained Motion Control Using Task Relaxations

In the original framework of He et al. (2015), the task plan is sent to a low-level motion planner that generates a motion plan and sends the result back to a coordinating layer, which then sends the plan to the motion controller. If the motion planner does not find a solution, the coordinating layer increases the weight for that plan on the product graph and requires a new task plan on the product graph. This generates a synergy between layers resulting in the generation of feasible continuous trajectories for the manipulator.

Here we adopt a different strategy. Instead of using a motion planner to generate low-level trajectories and then sending those trajectories to a motion controller, the task plan is sent directly to the constrained motion controller that executes it. Hence, there is no need for a motion planner, and, hence, there is no replanning phase, thus saving computational time. Although we lose the probabilistic completeness of the original framework, the system is reactive to changes in the environment because of the closed-loop constrained control.

The constrained motion controller executes the actions of HOLD and MOVE, as mentioned in Sect. 2.3. The HOLD and MOVE actions are independent of each other. In the HOLD action, the robot holds an object towards a region of interest, whereas in the MOVE action, the robot moves the empty end-effector towards the object (HOLD means “moving while holding” whereas MOVE means “ moving without holding” ).

In our work, the robot moves the end-effector to pick objects with specific poses; hence, the control objective is set to ${\mathfrak {O}}_{\mathrm {pose}}$ during the MOVE action. Although there is some margin for relaxation when grasping an object, in the current work we are not exploiting such relaxations because they are highly dependent on the object type. However, we propose the relaxation of the HOLD action. Instead of moving the object to a specific pose, the robot holds the object to a target region on a target plane while satisfying appropriate constraints. This is done by controlling the end-effector distance to the target plane, as shown in Fig. 2, by setting the control objective ${\mathfrak {O}}_{\mathrm {distance}}$. This way, instead of using six DOFs to control the end-effector pose, only one DOF is used to control the distance of the object to the target plane. The target region is obtained by using the point-cone constraint presented in Sect. 3.3.1 to obtain a circular target region.

Fig. 2

Control of distance to target plane. The distance $d_{\mathrm {eff},n_{\underline{\varvec{\pi }}_{i}}}$ is the distance between the end-effector and the red target plane

3.3 Definition of Constraints

A relaxed task requires fewer DOFs than the original task, but the robot end-effector might perform undesired motions because the relaxed task is underspecified. Therefore, we must define appropriate inequality constraints to prevent those undesired motions. As a consequence, the end-effector is free to move only within the relaxed region. Now, we define such constraints.

3.3.1 Point-cone Constraint: A New Approach to Define Conic Constraints

Consider a manipulation task in which the end-effector must converge to a circular target region on a plane. To accomplish that, we define a cone cut by a plane such that the centerline of the cone is perpendicular to the plane, as shown in Fig. 3.⁵

Fig. 3

Point-cone constraint: the target circular region of interest is indicated in red, the green inverted cone trunk is the conical region of interest that constrains the end-effector

First, we define the desired radius r of the target circular region. Then, we calculate the cone base radius R as the distance between the end-effector and the centerline $\underline{\varvec{l}}$. Considering the height H of the cone, we use the triangle relationship given by

$$\begin{aligned} \frac{R(0)}{r}=\frac{H(0)}{h}=\frac{h_{c}(0)+h}{h} \end{aligned}$$

(3)

to obtain the distance h between the plane $\underline{\varvec{\pi }}$ and the cone apex $P_{A}$ as:

$$\begin{aligned} h=\frac{rh_{c}(0)}{R(0)-r}, \end{aligned}$$

(4)

where $h_{c}(0)$ is the initial distance between the end-effector and the plane $\underline{\varvec{\pi }}$. Now, we can calculate the tangent of the angle $\phi$ between the cone centerline $\underline{\varvec{l}}$ and the line $\underline{\varvec{l}}_{1}(0)$ that connects the cone apex $\varvec{p}_{A}$ to the initial end-effector position $\varvec{p}_{E}(0)$ as:

$$\begin{aligned} \text {tan}\phi =\frac{R(0)}{h_{c}(0)+h}. \end{aligned}$$

(5)

Since h and $\phi$ are defined using the initial conditions R(0) and $h_{c}(0)$, they are calculated only once, at the beginning of a particular HOLD action. However, as the manipulator moves, both $h_{c}(t)$ and R(t) may change for $t>0$. Therefore, the distance H(t) from the end-effector to the cone apex changes accordingly: $H(t)=h+h_{c}(t)$. Now, the maximum admissible squared distance ${\bar{R}}(t)$ between the end-effector and the centerline is obtained as:

$$\begin{aligned} {\bar{R}}(t)=\left( H\left( t\right) \text {tan}\phi \right) {}^{2}. \end{aligned}$$

(6)

At a given time t,  if the squared distance D(t) between the end-effector and the centerline $\underline{\varvec{l}}$ is smaller than ${\bar{R}}(t)$, then the end-effector is within the cone given by the appex $\varvec{p}_{A}$ and centerline $\underline{\varvec{l}}$.

To enforce that, we design the following differential inequality. We first calculate the squared-distance error

$$\begin{aligned} {\tilde{D}}_{l}(t)={\bar{R}}(t)-D(t), \end{aligned}$$

(7)

which is used to define the point-cone constraint given by

$$\begin{aligned} \dot{\tilde{D_{l}}}(t)\ge -\eta _{l}{\tilde{D}}_{l}(t), \end{aligned}$$

(8)

where

$$\begin{aligned} \dot{{\tilde{D}}}_{l}(t)=\dot{{\bar{R}}}(t)-\dot{D}(t). \end{aligned}$$

(9)

The derivative $\dot{D}(t)$ with respect to time is given by $\dot{D}(t)=\varvec{J}_{p,l}\dot{\varvec{q}}$ (Marinho et al. 2019). To calculate $\dot{{\bar{R}}}(t)$, recall that ${\bar{R}}(t)=(H(t)\tan \phi )^{2}=\left( h+h_{c}(t)\right) ^{2}\tan ^{2}\phi$. Hence,

$$\begin{aligned} \dot{{\bar{R}}}(t)=2(h+h_{c}(t))\tan ^{2}(\phi )\dot{h}_{c}. \end{aligned}$$

(10)

Since $\dot{h}_{c}=\varvec{J}_{\varvec{p},\pi }\dot{\varvec{q}}$ (Marinho et al. 2019), then $\dot{{\bar{R}}}(t)=2(h+h_{c}(t))\tan ^{2}(\phi )\varvec{J}_{\varvec{p},\pi }\dot{\varvec{q}}$. Therefore, by substituting $\dot{{\bar{R}}}(t)$ and $\dot{D}(t)$ in (9) and applying the result in (8), we obtain the point-cone constraint

$$\begin{aligned} {\mathfrak {W}}(l_{\mathrm {cone}}^{\mathrm {point}}):\underset{\varvec{J}_{\mathrm {cone},\varvec{p}}}{\underbrace{\big [\varvec{J}_{p,l}-2(h+h_{c}(t))\tan ^{2}(\phi )\varvec{J}_{\varvec{p},\pi }\big ]}}\dot{\varvec{q}}\le \eta _{l}{\tilde{D}}_{l}.\nonumber \\ \end{aligned}$$

(11)

Fig. 4

The red cuboid with the blue centerline is the object to be manipulated. The semi-infinite cylinders to prevent collisions with the non-manipulated objects are represented by the light shaded purple cylinder. The light shaded yellow planes are used to prevent collisions with the environment. The coordinate systems indicate locations in the scene, which are used to define the centers of the regions of interest. The light shaded green cylinder is used to prevent twisted configurations caused by the end-effector passing over the robot

3.3.2 Additional Constraints

We use three planes in the environment to prevent end-effector collisions with two walls and the table in the workspace as shown in Fig. 4. Similarly to the work of Quiroz-Omana and Adorno (2019), these three constraints are written as:

$$\begin{aligned} {\mathfrak {W}}(\pi _{i}):-\varvec{J}_{p,n_{\underline{\varvec{\pi }}_{i}}}\dot{\varvec{q}}\le \eta {\tilde{d}}_{p,n_{\underline{\varvec{\pi }}_{i}}}, \end{aligned}$$

(12)

where $i\in \{1,2,3\}$ and ${\tilde{d}}_{p,n_{\underline{\varvec{\pi }}_{i}}}=d_{p,n_{\underline{\varvec{\pi }}_{i}}}-d_{\pi ,\text {safe}}$, with $d_{\pi ,\text {safe}}$ being the safe distance to each plane and $d_{p,n_{\underline{\varvec{\pi }}_{i}}}$ and $\varvec{J}_{p,n_{\underline{\varvec{\pi }}_{i}}}$ are the point-static-plane distance and its Jacobian, respectively (Marinho et al. 2019).

In addition to the plane and point-cone constraints, we use joints velocities constraints to prevent saturation of actuators (Quiroz-Omaña and Adorno 2018). To write the joints velocities constraints ${{{\mathfrak {W}}}({\dot{\varvec{q}})}}$, let $\varvec{q}_{\min }$ and $\varvec{q}_{\max }$ represent the lower and upper limits of the joints, respectively. Given the limits of the joints $\varvec{q}_{\min }\le \varvec{q}(t)\le \varvec{q}_{\max }$, we convert them to constraints in the velocity of the joints as:

$$\begin{aligned} k(\beta \varvec{q}_{\min }-\varvec{q}(t))\le \dot{\varvec{q}}\le k(\beta \varvec{q}_{\max }-\varvec{q}(t)), \end{aligned}$$

(13)

where $0\ll \beta \le 1$ is selected to define a safety margin for the joints limits and $k>0$ is used to scale the feasible region of $\dot{\varvec{q}}$ (Quiroz-Omaña and Adorno 2018). To impose joints velocities constraints, (13) is rewritten as $\varvec{\eta }_{\min }\le \dot{\varvec{q}}\le \varvec{\eta }_{\max },$ where $\varvec{\eta }_{\min }=\max \{\varvec{v}_{\min },k(\beta \varvec{q}_{\text {min}}-\varvec{q})\}$ and $\varvec{\eta }_{\max }=\min \{\varvec{v}_{\max },k(\beta \varvec{q}_{\text {max}}-\varvec{q})\}$, in which $\varvec{v}_{\min }$ and $\varvec{v}_{\max }$ are the lower and upper limits for the joints velocities, respectively. Hence,

$$\begin{aligned} {\mathfrak {W}}(\dot{\varvec{q}}):\left[ \begin{array}{c} -\varvec{I}_{n}\\ \varvec{I}_{n} \end{array}\right] \dot{\varvec{q}}\le \left[ \begin{array}{c} -\varvec{\eta }_{\min }\\ \varvec{\eta }_{\max } \end{array}\right] , \end{aligned}$$

(14)

where $\varvec{I}_{n}\in {\mathbb {R}}^{n\times n}$ is the identity matrix.

To prevent end-effector collisions with static objects while an object is manipulated, we add semi-infinite cylindrical constraints to each non-manipulated object, as shown in Fig. 4. Therefore, each static object is constrained by an infinite cylinder cut by a plane. Given k objects, we associate a cylindrical and a plane constraint to each one of them, which yields the following inequality:

$$\begin{aligned} {\mathfrak {W}}(c_{j}):-\left[ \begin{array}{c} \varvec{J}_{\mathrm {semi},j}\\ \varvec{J}_{\mathrm {plane},j} \end{array}\right] \dot{\varvec{q}}\le \left[ \begin{array}{c} D_{\mathrm {semi},j}\\ d_{\mathrm {plane},j} \end{array}\right] , \end{aligned}$$

(15)

where $j\in \{1,\dots ,k\}$. The row vector $\varvec{J}_{\mathrm {semi},j}\in {\mathbb {R}}^{1\times n}$ is given by

$$\begin{aligned} \varvec{J}_{\mathrm {semi},j}={\left\{ \begin{array}{ll} \varvec{J}_{p,l_{j}} &{} \text {if }d_{p,n_{\underline{\varvec{\pi }}_{j}}}<0\\ \varvec{0}^{1\times n} &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(16)

in which $\varvec{J}_{p,l_{j}}$ satisfies $\dot{D}_{p,\text {l}_{j}}=\varvec{J}_{p,l_{j}}\dot{\varvec{q}}$. Also,

$$\begin{aligned} D_{\mathrm {semi},j}={\left\{ \begin{array}{ll} \eta _{l}{\tilde{D}}_{p,\text {object}_{j}} &{} \text {if }d_{p,n_{\underline{\varvec{\pi }}_{j}}}<0\\ 0 &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(17)

where ${\tilde{D}}_{p,\text {object}_{j}}=D_{p,\text {l}_{j}}-R_{j}^{2}$, with $R_{j}$ being the radius of the cylinder around the j-th object; $D_{p,l_{j}}$ is the squared-distance from the end-effector to the centerline of the cylinder enclosing the jth object. Analogously, $\varvec{J}_{\mathrm {plane},j}\in {\mathbb {R}}^{1\times n}$ is given by

$$\begin{aligned} \varvec{J}_{\mathrm {plane},j}={\left\{ \begin{array}{ll} \varvec{J}_{p,n_{\underline{\varvec{\pi }}_{j}}} &{} \text {if }{\tilde{D}}_{p,\text {object}_{j}}<0\\ \varvec{0}^{1\times n} &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(18)

and

$$\begin{aligned} d_{\mathrm {plane},j}={\left\{ \begin{array}{ll} \eta _{\pi }d_{p,n_{\underline{\varvec{\pi }}_{j}}} &{} \text {if }{\tilde{D}}_{p,\text {object}_{j}}<0\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(19)

The conditional values for the constraint parameters (16)–(19) mean that when $d_{p,n_{\underline{\varvec{\pi }}_{j}}}<0$, the end-effector is below the plane $\underline{\varvec{\pi }}_{j}$ that cuts the infinite cylinder enclosing the jth object. Therefore, the end-effector must stay outside the cylinder to prevent a collision with the object. Analogously, when ${\tilde{D}}_{p,\text {object}_{j}}<0$, the end-effector is within the infinite cylinder enclosing the jth object, but above it, and thus must stay above the plane $\underline{\varvec{\pi }}_{j}$ to prevent a collision with the object. Furthermore, the conditional values for (17) and (19) are defined to prevent the solution from becoming unfeasible. For example, if the end-effector is over the plane $\underline{\varvec{\pi }}_{j}$ (i.e., $d_{p,n_{\underline{\varvec{\pi }}_{j}}}>0$) and within the semi-infinite cylinder (i.e. ${\tilde{D}}_{p,\text {object}_{j}}<0$), then it is not colliding with the object. Therefore, $\varvec{J}_{\mathrm {semi},j}=\varvec{0}^{1\times n}$. As ${\tilde{D}}_{p,\text {object}_{j}}<0$, if $D_{\mathrm {semi},j}$ was not zeroed (i.e., if $D_{\mathrm {semi},j}=\eta _{l}{\tilde{D}}_{p,\text {object}_{j}}$), the constraint $-\varvec{J}_{\mathrm {semi},j}\dot{\varvec{q}}\le D_{\mathrm {semi},j}$ would be $0\le \eta _{l}{\tilde{D}}_{p,\text {object}_{j}}<0$, which is infeasible. Equation (17) ensures that $D_{\mathrm {semi},j}=0$ when the end-effector is above the object, and thus $-\varvec{J}_{\mathrm {semi},j}\dot{\varvec{q}}\le D_{\mathrm {semi},j}$ becomes $0\le 0$, which is always feasible. The same reasoning applies for (19).

To prevent twisted configurations caused by the end-effector passing over the robot, we also add an infinite cylindrical constraint collinear to the z-axis of the coordinate system of the robot base (see Fig. 4). The constraint is given by

$$\begin{aligned} {\mathfrak {W}}(l_{z}):-\varvec{J}_{p,l_{z}}\dot{\varvec{q}}\le \eta _{l}{\tilde{D}}_{p,l_{z}}, \end{aligned}$$

(20)

where ${\tilde{D}}_{p,l_{z}}=D_{p,l_{z}}-R_{z}^{2}$, with $R_{z}$ being the radius of the cylinder enclosing the manipulator’s base; $D_{p,l_{z}}$ is the squared-distance between the end-effector and the centerline of that cylinder, and $\varvec{J}_{p,l_{z}}$ is the Jacobian matrix that satisfies $\dot{D}_{p,l_{z}}=\varvec{J}_{p,l_{z}}\dot{\varvec{q}}$ (Marinho et al. 2019).

Lastly, the robot should not tilt the objects too much to prevent, for instance, dropping the contents from inside a bowl or cup. Hence, to keep a bounded inclination of the end-effector with respect to a vertical line passing through the origin of the end-effector coordinate system, we add line-cone constraints ${\mathfrak {W}}(l_{z,\mathrm {cone}})$ to constrain the end-effector z-axis within a cone (Quiroz-Omana and Adorno 2019).

4 Simulation & Discussion

We implemented our adapted task planning and motion control framework and the original ITMP framework proposed by He et al. (2015) in C++ with the Boost Graph Library⁶ and the automata utilities from the Open Motion Planning Library (OMPL) (Sucan et al. 2012). The LTL task is processed using Spot (Duret-Lutz and Poitrenaud 2004), and we performed simulations on CoppeliaSim⁷ using ROS.⁸ Motion planning was done with the CoppeliaSim OMPL tools with RRTconnect. Furthermore, we used the DQ Robotics library (Adorno and Marques Marinho 2021) for robot modeling and control and to define the geometrical constraints. We used the constrained convex optimization utilities from the DQ Robotics library that were implemented using IBM ILOG CPLEX Optimization Studio.⁹ All the experiments were done on a single computer running Ubuntu 20.04 x64 with an Intel Core i7-8550U CPU with 16GiB of memory and a video card GeForce MX150.

4.1 Evaluation of Our Planning Framework and comparison with the ITMP framework proposed by He et al. (2015)

To evaluate our framework and compare it with the original ITMP framework proposed by He et al. (2015), we created a simulation scene on CoppeliaSim in which a Kinova JACO robot must execute assistive tasks for a seated person, with limited or no lower limbs mobility, who cannot reach farther objects in the workspace. The robot is placed on a table and the person is seated on a chair in front of it. There are four colored cuboid objects $o_{\text {meat}}$, $o_{\text {salad }}$, $o_{\text {book}}$, $o_{\text {pen}}$ representing, meat (red), salad (green), book (blue) and a pen (orange), respectively. In addition, eight colored regions of interest are depicted representing preparation area $r_{\text {prep}}$ (dark gray), heating area $r_{\text {heat}}$ (red), cooling area $r_{\text {cool}}$ (green), waiting area $r_{\text {wait}}$ (cyan), book area $r_{\text {book}}$ (blue), two person-areas $r_{\text {pers}}$ (yellow), and pen area $r_{\text {pen}}$ (orange). Initially, the meat is in the preparation area, the salad is in the waiting area, the pen is in the pen area, and the book is in one of the person areas, as shown in Fig. 5.¹⁰

Fig. 5

Scene for an LTL specification. The red, green, blue and orange cuboids represent the meat, salad, book, and pen, respectively. The regions of interest are indicated in the figure

To compare both frameworks, we first analyze the number of nodes explored in the product graph and the total planning and execution time. We propose a task $\varphi$ that exploits the LTL temporal operators to plan for a task with a certain degree of spontaneity. In other words, we give the planner more possibilities to accomplish a task. Consider the subtasks $T_{A}$ to $T_{D}$ and the whole task T:

($T_{A}$):

Move both the pen and the book to the person.

($T_{B}$):

Heat the meat.

($T_{C}$):

Serve both the meat and the salad to the person.

($T_{D}$):

Move the book to the book place and the pen to the pen place.

(T):

Eventually do $T_{A}$, $T_{B}$, $T_{C}$ and $T_{D}$, but $T_{C}$ must be done only after $T_{B}$.

We define $p_{p,\mathrm {pers}}=(o_{\mathrm {pen}},r_{\mathrm {person}})$, $p_{b,\mathrm {pers}}=(o_{\mathrm {book}},r_{\mathrm {person}})$, $p_{m,h}=(o_{\mathrm {meat}},r_{\mathrm {heat}})$, $p_{m,\mathrm {pers}}=(o_{\mathrm {meat}},r_{\mathrm {person}})$, $p_{s,\mathrm {pers}}=(o_{\mathrm {salad}},r_{\mathrm {person}})$, $p_{b,b}=(o_{\mathrm {book}},r_{\mathrm {book}})$, and $p_{p,p}=(o_{\mathrm {pen}},r_{\mathrm {pen}})$. As a result, $\varphi$ is given by

$$\begin{aligned} \varphi ={\mathcal {E}}(\varphi _{A})\wedge {\mathcal {E}}\big (\varphi _{B}\wedge \mathcal {XE}(\varphi _{C})\big )\wedge {\mathcal {E}}(\varphi _{D}), \end{aligned}$$

(21)

in which $\varphi _{A}=p_{p,\mathrm {pers}}\wedge p_{b,\mathrm {pers}}$, $\varphi _{B}=p_{m,h}$, $\varphi _{C}=p_{m,\mathrm {pers}}\wedge p_{s,\mathrm {pers}}$, and $\varphi _{D}=p_{b,b}\wedge p_{p,p}$ enforces $T_{A}$ to $T_{D}$, respectively. The motivation of this task is that the person will eventually eat the food and eventually use the pen to make annotations in the book, but the order is not specified. Last, we add an arbitrary waiting time $T_{\mathrm {wait}}$ that the robot must wait every time after it places an object in front of the person. This is done to give some time for the person to accomplish her task and prevent the robot from moving the object away from the person too early.

The automaton generated from $\varphi$ has twelve states. Our adapted framework explores 244556 nodes in the product graph whereas the original framework explores 531748 nodes, as summarized in Table 1. To evaluate the computational burden of each method, we executed both methods successively until the time variance of the variables of interest stabilized at an approximately constant value. Therefore, we executed both our method and He et al. (2015)’s method 117 times. This is necessary because the motion planner used by He et al. (2015) is probabilistic. Hence, it generates different motion plans at each execution. Also, there is some intrinsic time variability during simulation because CoppeliaSim is subject to the operating system’s scheduler. Therefore, even deterministic formalisms, such as ours, have variability in the execution time when running in a simulated environment.

Figure 6 shows that our method has a faster execution time and a faster task-planning time than the method of He et al. (2015), not only in average but also considering the standard deviation, and it does not require motion planning. As a result, our method is considerably faster.

Table 1 Planning data for $\varphi$

Fig. 6

Average total planning and execution times, in logarithmic scale, of both planning frameworks. The variability whiskers represent the one standard deviation. The standard deviations are also in logarithmic scale. Therefore, although the task planning time variance of our method (0.4822 s) appears to be larger than in He et al. (2015)’s method (0.6618 s), it is not

With regard to the high-level plan, in our adapted framework there is no need to generate more than one high-level plan due to changes in the scene, in terms of the modeled geometric primitives, as long as there are mechanisms to track their changes. As a consequence, there is no increase in the number of generated planning nodes during the task planning phase, and Dijkstra’s algorithm searches for a task plan on a static graph. For the same task in the original framework, our approach has greatly reduced the number of generated task plan nodes. Nonetheless, some high-level plans might not be realizable, not only because of obstacles that prevent the robot from executing the plan, but because the closed-loop controller can get stuck in a local minimum. (The closed-loop system is stable, but not asymptotically stable.) This, of course, can be mitigated by searching for alternative plans in the product graph, in case the robot fails, but this is out of scope of the current work.

The smaller planning time in our framework is a result of task relaxations. More specifically, the number of valid nodes in the manipulation abstraction is given by $2(|\Gamma |+1)P_{|O|}^{(|\Gamma |+1)}$ (He et al. 2015), where $|\Gamma |$ is the number of regions, |O| is the number of objects and $P_{n}^{k}$ is the k-permutation from n elements. Differently from He et al. (2015), who partition the search space into a set of discrete poses and consequently need large values for $|\Gamma |$, partitioning the search space into regions provides a much coarser discretization, considerably reducing the computational time. Also, because those regions have fewer dimensions than the six-dimensional space of poses, the task requires fewer degrees of freedom and, consequently, the controller can potentially accommodate more constraints.

Fig. 7

Simulated scene with main constraints

From the point of view of real-world implementations, sensor resolutions determine the minimum size for a given region, which means that if we wanted to determine regions smaller than the sensor resolution, it would not be possible. Fortunately, we want the opposite, that is, we define large regions to give the controller more “ freedom” to place objects, which also has the side-effect of reducing the overall complexity. On the other hand, real-world implementations of He et al. (2015)’s framework rely on very accurate sensors to build the workspace. This is because their method is not robust even to small changes in the scene environment as it lacks reactivity. Indeed, after a motion plan is found, it is executed in open-loop, whereas our method accounts for those changes because the constraints are continuously updated during execution.

4.2 Evaluation of Relaxed Task Constraints

4.2.1 Description of the Constraints Used in the Simulation and Constraints Corresponding Parameters

The constraints used in the simulation are: three plane constraints to prevent collision with the two walls and the table, semi-infinite cylindrical constraints to prevent collisions with non-manipulated objects, an infinite cylindrical constraint around the robot z-axis to prevent twisted configurations, and a line-cone constraint to prevent the grasped objects from tilting too much, and the point-cone constraint to drive the object to the target region. Figure 7 shows the simulation scene with the constraints. The point-cone constraint is shown in Fig. 3 and also in Fig. 7. Table 2 presents the parameters used for each constraint.

Table 2 Simulation constraints and constraints parameters

4.2.2 Constrained Motion Controller Parameters

The parameters of the constrained motion controller were also constant during all simulations, in which $\eta =100$ and $\lambda =0.001$ (see (2)). For the sampling time, we used $T_{\mathrm {sampling}}=5$ ms.

4.2.3 Evaluation of Constraints

Fig. 8

Lateral views of the end-effector trajectory using the point-cone constraint: holding the meat from the intermediate location (the location that connects all regions) to the heating region during sub-task $T_{B}$ in $\varphi$

To illustrate the satisfaction of the constraints enforced by the constrained controller, we selected different parts during the execution of task $\varphi$. For instance, to evaluate the point-cone constraint, we selected the action HOLD that is used to move the meat to the heating region. Figure 8 shows the trajectory of the end-effector towards the target region while being constrained by a conical surface.

In comparison with the plane constraints used to define a squared region of interest in our previous work (Pereira and Adorno 2020), this point-cone constraint requires less complex calculations during running time and requires only one inequality. On the other hand, when using four planes to define a squared region of interest, it is necessary to calculate four Jacobian matrices, four point-static-plane distances, and they require four inequalities in the control law.

We also present the results for all other constraints during the whole execution of task $\varphi$. To verify if any collision happened, we analyze the signed distances between the respective collidable entities. Figure 9 shows the signed distance between the end-effector and the walls and the table. The signed distance remains positive during the whole task execution, meaning that there is no collision between the end-effector and those obstacles.

Fig. 9

Top: signed distance between the end-effector and the planes in the environment (table top, right wall, and front wall). Middle: signed distance between the end-effector and the vertical cylinder enclosing the robot base. In both cases, a positive distance means that the constraint has never been violated. Bottom: line-cone constraint angle between end effector z-axis and static line parallel to the z-axis of the reference frame located at the base of the manipulator. The dotted-black vertical lines indicate when an object is grasped or placed

Fig. 10

Signed distance between the end-effector and the objects. The dotted-black vertical lines indicate when an object is grasped or placed

Fig. 11

Constraints to enforce joints limits. The dotted-black vertical lines indicate when an object is grasped or placed

Figure 10 shows the signed distance between the end-effector and the cylinders enclosing the objects. The task planner decides to begin the task by heating the meat. Hence, it approaches the meat and the signed distance to it becomes slightly negative because we remove the constraints for a manipulated object. However, the signed distance to other non-manipulated objects remains positive, indicating that no collision occurred with those objects. Likewise, the signed distance remains slightly negative while the end-effector moves the meat because the robot is grasping it. Next, the end-effector places the meat on the heating region and moves away from it (i.e. the signed distance becomes positive and the constraints for the meat are inserted again as the meat is not manipulated). In the sequence, the end-effector approaches the pen (i.e. the signed distance decreases and becomes slightly negative because we remove the constraints for the pen). This procedure repeats until all the objects are manipulated and placed in the regions specified by the task. Also, a similar analysis can be done for the signed distance to the planes of the objects, which decreases when the end-effector is approaching an object to grasp it or placing an object on the table.

Figure 9 also shows the signed distance between the end-effector and the cylinder enclosing the robot base. It remains positive during the whole task execution indicating that the constraint was always satisfied. There is also the line-cone constraint that limits the tilting of the end-effector, and Fig. 9 shows that the angle between the end-effector z-axis and the static line remains within the safety angle $\phi _{\text {safe}}$. Last, Figure 11 shows that all joints angles are kept within the joints limits, indicating that the constraint is satisfied, as expected.

It is important to emphasize that, although the objects in our simulation are static, our framework is in principle suitable for dynamically changing environments, as opposed to the framework of Ferrer-Mestres et al. (2017). This is because the constrained motion controller that we employ can prevent collisions with moving obstacles, as shown by (Marinho et al. 2019, Sec. III.A). The only requirement is that the information about obstacles velocities must be available either by direct measurements or estimation. Finally, the task will always be completed correctly as long as the changes in the environment do not affect the sequencing order of the task and the constraints do not make the closed-loop system be stuck in local minima.

5 Conclusion

This work adapts the LTL-based manipulation framework of He et al. (2015), which uses sampling-based motion planners as the low-level planner, to use instead a constrained motion controller that allows the definition of regions of interest while making the system reactive. Furthermore, we exploit the use of regions of interest from our previous work (Pereira and Adorno 2020) to relax tasks in a computationally efficient way. This is achieved by doing a coarse discretization of the workspace instead of discretization in the robot’s and objects’ configuration spaces as in the work of He et al. (2015). As a result, the number of states in the planner is reduced. With respect to total execution and planning time, our framework is faster and more robust to changes in the environment due to the reactivity. Our other contribution is the definition of a novel point-cone constraint that ensures that the end-effector will move towards the target region by using only one simple inequality constraint. Hence, fewer complex calculations are needed during runtime.

Regarding the regions of interest, an interesting investigation would be a formalization of how to determine regions from a broad geometrical description. With regard to the controller, although in our framework we have a closed-loop system at the motion-control level, there is no feedback to the task planner in the case of failure. In this sense, a possible extension of the work would be to close the loop between the task planner and the motion controller. That way, the planner would try to find another solution whenever the closed-loop system gets stuck in a local minimum. (The closed-loop system is stable but not asymptotically stable.) Lastly, future works will explore combining the high-level LTL task specification in the constrained motion controller to obtain an abstraction-free planning framework that does not suffer from the curse of dimensionality.