Fixed-Time Adaptive Robust Synchronization with a State Observer of Chaotic Support Structures for Offshore Wind Turbines

Abstract

The chaotic support structures for offshore wind turbines are often subjected to a severe environment. A robust control scheme needs to be considered to maintain them in a safe operational limit. Robust sliding mode control (SMC) scheme can provide an excellent robust controller against this severe and challenging environment for these chaotic structures. This paper proposes a novel fixed-time adaptive sliding mode control scheme with a state observer to synchronize chaotic support structures for offshore wind turbines in the presence of matched parametric uncertainties. The proposed controller is a new integration of adaptive control concept, SMC method, fixed-time stability concept and a state observer. A fixed-time stability concept is used to provide stability for the system within a presented time regardless of initial conditions. The adaptive concept is utilized to provide an online estimator of the uncertain upper bound. Also, a nonlinear observer is employed to provide an online estimator of an unmeasured state in the controller. Lyapunov stability theorem is used to analyze fixed-time stability of the system based on SMC methodology. The simulation results demonstrate that the proposed controller is able to ensure fixed-time synchronization along with providing precise means to estimate the unmeasured state as well as uncertainty upper bound.

1 Introduction

In recent decades, synchronization of different systems has been investigated for a variety of control goals. This concept has been frequently used to control the renewable energy systems, particularly wind power systems. It has been also remarkably used for chaos control. A support structure system for an offshore wind turbine is one of the chaotic renewable energy systems. The offshore wind turbines are subjected to environmental loads including wave, wind, current and seismic excitations. These loads might cause some platform vibrations that would lead to the ruin of foundations and chaotic behavior. Therefore, it is necessary to use these kinds of systems (like support structure systems) to maintain the offshore platform in the safe operating limit (Manikandan & Saha, 2013; Prieto-Araujo & Gomis-Bellmunt, 2016).

Furthermore, the issue of applying robust control methods to foresee the aforementioned vibration of offshore structures has attracted great attention from researchers. A delayed robust nonfragile H∞ control approach has been proposed to diminish the amplitude of the vibrations for the offshore platform (Zhang et al. 2015). In (Aggarwal et al. 2014; Luo, 2012), a comprehensive study has been done on dynamic analysis and different control methods for the support structures of offshore wind turbines. In (Hall et al. 2013), a genetic algorithm has been used to provide optimal control for these support structures. In (Yan et al. 2009), an effective scheme has been proposed to protect the support structure of offshore wind farms against corrosion.

The SMC approach is a robust and popular control method (Eaton et al. 2009). It is known because of its low sensitivity toward disturbances, and parametric uncertainties or variations in the system. In (Zribi et al. 2004), the robust SMC scheme has been employed for an offshore structure to diminish the internal oscillations. In (Abadi et al. 2018), two finite-time and robust control schemes based on SMC technique have been proposed for synchronization of smart grid chaotic system. In (Chen et al. 2018), a new sliding mode synchronization (SMS) has been employed to address chaos control in the presence of uncertain parameters and disturbances. In (Teimoori et al. 2012), an optimal SMC method has been presented to provide an attitude control in finite time for a miniature helicopter.

In practical applications, it is often necessary to ensure system stability in a finite time (Hosseinabadi et al. 2018). In (Mohammadpour & Binazadeh, 2018), a finite-time stability concept has been considered to synchronize two chaotic systems. In (Hosseinabadi et al. 2018), the finite-time stability has been ensured in a presented stability time by using a terminal sliding mode control methodology for a hyperchaotic system. However, the presented stability time utilizing the finite-time stability concept is not independent of the initial conditions which can prohibit its practical application due to probable unknown system initial conditions. To solve this drawback, fixed-time stability has been introduced in 2012 by Polyakov (2011) which can provide a bounded stability time independent of initial conditions and speed up the convergence rate. In (Sergey Parsegov et al. 2012), a novel fixed-time stability protocol has been presented to ensure equidistant allocation on a segment where the stability time is estimated in advance. In (SE Parsegov et al. 2013), a novel fixed-time algorithm has been proposed to guarantee stability in a prespecified time independently of the initial conditions for multi-agent systems. In (Polyakov et al. 2015), the fixed-time and finite-time stability concepts have been studied for nonlinear systems. In (Ni et al. 2016), a robust SMC scheme has been integrated with a fixed-time stability concept for chaos control in the power system. Motivated by the aforementioned researches, a fixed-time stability concept is used in this study.

On the other hand, the knowledge of parametric uncertainty bound for sliding mode controller design is required, which might be unknown in practice. The adaptive control concept provides an effective scheme to deal with these unknown parametric uncertainties (Ma et al. 2015; Mahdavi et al. 2015). It utilizes online estimators to provide information on the uncertainty upper bounds (Krstic et al. 1995). Accordingly, the SMC scheme has been incorporated with an adaptive control concept to solve this issue by approximating the unknown parametric uncertainty bounds. In (Pai & Yau, 2011), an adaptive SMC (ASMC) scheme has been used for chaos control in horizontal platform systems where only asymptotic stability was ensured. In (Nourisola et al. 2015), adaptive control concept has been combined with SMC scheme to control the offshore platforms. In (Vaseghi et al. 2017), a finite-time ASMC approach has been used for chaos synchronization of communication systems.

Furthermore, the knowledge of the state measurements for the controller design is often required, which might be unmeasurable physically by utilizing sensors in practice. State observers can be designed to approximate the value of these unmeasured states instead of measuring them physically. It should be noted that it can reduce the size, weight, cost and even noise of measuring them by physical sensors. In (Xu et al. 2017), a comprehensive study has been done on parameter and state estimation for state delay systems where stability analysis was not discussed. In (Yang & Zhu, 2013), a sliding mode observer has been designed for synchronization of chaotic systems and the asymptotic stability of the observer error dynamic system has been obtained. In (Daly & Wang, 2009), a sliding mode controller with a state observer has been designed for the control of a nonlinear plant in the presence of unknown disturbances. However, the controller and state observer have been designed individually. Therefore, the system stability needs to be guaranteed by considering the controller and state observer simultaneously, because the separation principle does not hold for the nonlinear systems (Abadi et al. 2020).

The above literature survey demonstrates that a notable fixed-time stability concept, SMC scheme, adaptive control approach, and state observer have been successfully designed and presented individually for different systems. To the best of our knowledge, the FASMC scheme with a state observer is yet to be developed where a stability proof is obtained by considering adaptive law and observer law and control law in one candidate Lyapunov function.

Motivated by abovementioned discussion, a novel FASMC scheme with a state observer is introduced for chaotic synchronization of two support structures for offshore wind turbines with matched parametric uncertainties. Indeed, the incorporation of some control methods is considered in this study to utilize their advantages and to overcome the deficiencies of using them individually. More importantly, the fixed-time stability proof is obtained by utilizing only one candidate Lyapunov function by using designed control law, observer law, and adaptive law, simultaneously. Also, the upper bound of stability time is presented using a fixed-time stability concept which is regardless of initial conditions. The adaptive control concept is used to deal with unknown matched parametric uncertainties by estimating their upper bounds. It is assumed that the first state is measurable and available, while the second state is unmeasured and needs to be estimated by the state observer. It is proven that the nonlinear observer and adaptive scheme can provide precise estimated data in the designed controller to control the system. Additionally, the proposed method is shown to be very robust against system parametric uncertainties.

The paper is structured as follows. Section 2 is dedicated to mathematical preliminaries including some lemmas and standard definitions. Section 3 is devoted to the system description of the chaotic support structure for an offshore wind turbine. In Sect. 4, the problem formulation is given. Section 5 is devoted to methodology and controller design using the FASMC scheme with a state observer. In Sect. 6, the numerical simulation results and discussion are provided. Finally, Sect. 7 comes with the conclusions.

2 Mathematical Preliminaries

Some lemmas and standard definitions are given here that are utilized throughout this paper. Note that throughout the paper the dot displays differential with respect to time and sign function denotes the signum function.

Definition 1

The definition of sign function (which denotes the signum function) is given as Eq. (1)

$${\text{sign}}\left(a\right)=\left\{\begin{array}{ll}1;&a>0\\ 0;&a=0\\ -1;&a<0\end{array}\right.$$

(1)

Also, the following relations are always true

$$\left\{\begin{array}{l}{\text{sign}}\left(a\right)\times {\text{sign}}\left(a\right)=1; a\ne 0 \\ a\times {\text{sign}}\left(a\right)=\left|a\right| \\ \begin{array}{l}{\left|a\right|}^{b}{\text{sign}}\left(a\right)={\text{sig}}^{b}\left(a\right) \\ a\times {\text{sig}}^{b}\left(a\right)={\left|a\right|}^{b+1} \\ \begin{array}{l}\frac{d\left|u\right|}{{\text{d}}t}=\dot{u}\times {\text{sign}}\left(u\right); u\ne 0; \dot{u}=\frac{{\text{d}}u}{{\text{d}}t} \\ \left|a\times {\text{sign}}\left(b\right)\right|\le \left|a\right|\end{array}\end{array}\end{array}\right.$$

(2)

where $a, b\in {\mathbb{R}}$ and $u$ is a differentiable function. Note that the ${\text{sig}}(x)$ function has been defined in (Alinaghi Hosseinabadi et al. 2020; Wu & Li, 2018) as ${\text{sig}}^{a}\left(x\right)={\left|x\right|}^{a}{\text{sign}}(x)$, where $a\in {\mathbb{R}}$.

Definition 2

Consider a nonlinear system as Eq. (3)

$$\dot{x}=f\left(t,x\right); \quad x\left(0\right)={x}_{0}$$

(3)

where $x\in {\mathbb{R}}^{n}$ is the vector of the system states and $f(t,x)$ is a nonlinear function. The origin of system (3) is globally finite-time stable if it is globally asymptotically stable and any solution $x({x}_{0})$ of (3) reaches the equilibria at some finite-time moment, i.e., $\underset{t\to T}{{\mathrm{lim}}}x=0\, {\text{and}}\, x=0\,{\text{for}}\,t\ge T$, where $T$ is called settling time function (Bhat & Bernstein, 2000; Orlov, 2004).

Definition 3

The origin of system (3) is globally fixed-time stable if it is globally finite-time stable and the settling time function $T$ is bounded, i.e., $\exists T>0 :T\le {T}_{{\mathrm{max}}}, \forall {x}_{0}\in {\mathbb{R}}^{n}$. Therefore, the settling time is always bounded regardless of system initial conditions in fixed-time control methods (Polyakov, 2011; Zuo, 2015).

Lemma 1

Consider ${a}_{1}, {a}_{2}, \dots , {a}_{n}\in {\mathbb{R}}$ and $0<\gamma <2$, then we have (Yu et al. 2005).

$${\left|{a}_{1}\right|}^{\gamma }+{\left|{a}_{2}\right|}^{\gamma }+\dots + {\left|{a}_{n}\right|}^{\gamma }\ge {\left({a}_{1}^{2}+{a}_{2}^{2}+\dots +{a}_{n}^{2}\right)}^{\frac{\gamma }{2}}$$

(4)

Lemma 2

Consider ${a}_{1}, {a}_{2}, \dots , {a}_{n}\ge 0$, $0<b\le 1$ and $c>1$, then we have (Zuo & Tie, 2016).

$$\sum_{i=1}^{n}{a}_{i}^{b}\ge {\left(\sum_{i=1}^{n}{a}_{i}\right)}^{b}, \sum_{i=1}^{n}{a}_{i}^{c}\ge {n}^{1-c}{\left(\sum_{i=1}^{n}{a}_{i}\right)}^{c} $$

(5)

Lemma 3

Assume there exist four real numbers as ${\rho }_{1}, {\rho }_{3}>0, 0<{\rho }_{2}<1,$ and ${\rho }_{4}>1$ and a continuously differentiable positive function $V(x):{\mathbb{R}}^{n}\to {\mathbb{R}}_{\ge 0}$ such that; $V\left(x\right)=0$ for $x(t)=0$. If any solution $x(t)$ of Eq. (3) satisfies the inequality $\dot{V}\left(x\right)\le -{\rho }_{1}{V}^{{\rho }_{2}}-{\rho }_{3}{V}^{{\rho }_{4}}$, then the origin is globally fixed-time stable for the system of Eq. (3) and the settling time function is as $T\left({x}_{0}\right)\le \frac{1}{{\rho }_{1}\left(1-{\rho }_{2}\right)}+\frac{1}{{\rho }_{3}\left({\rho }_{4}-1\right)}$ (SE Parsegov et al. 2013; Zuo & Tie, 2016).

Lemma 4

Consider a scalar system as Eq. (6)

$$\dot{y}=-{\alpha }_{1}{y}^{{\alpha }_{2}}-{\alpha }_{3}{y}^{{\alpha }_{4}}, y\left(0\right)=0$$

(6)

It can be proved that the origin of Eq. (6) is fixed-time stable for ${\alpha }_{1},{\alpha }_{3}>0, {\alpha }_{4}>1,$ and $0<{\alpha }_{4}<1$. Also, the settling time $T$ satisfies inequality $T\le \frac{1}{{\rho }_{1}\left(1-{\rho }_{2}\right)}+\frac{1}{{\rho }_{3}\left({\rho }_{4}-1\right)}$ where ${\rho }_{1}={\alpha }_{1}{\left(2\right)}^{{(\alpha }_{2}+1)/2}, {\rho }_{3}={\alpha }_{3}{\left(2\right)}^{{(\alpha }_{4}+1)/2}, {\rho }_{2}=\frac{{\alpha }_{2}+1}{2},$ and ${\rho }_{4}= \frac{{\alpha }_{4}+1}{2}$.

Proof

Consider a candidate Lyapunov function as Eq. (7), which satisfies the conditions of Lemma 3

$$V=\frac{1}{2}{y}^{2}$$

(7)

By differentiating of Eq. (7) with respect to time, there comes

$$\dot{V}=y\dot{y}$$

(8)

By substituting Eq. (6) into Eq. (8), one can obtain

$$ \begin{aligned} \dot{V} & = y\left( { - \alpha_{1} y^{{\alpha_{2} }} - \alpha_{3} y^{{\alpha_{4} }} } \right) \\ & \Rightarrow \dot{V} = - \alpha_{1} \left| y \right|^{{\alpha_{2} + 1}} - \alpha_{3} \left| y \right|^{{\alpha_{4} + 1}} \\ \end{aligned} $$

(9)

From Eq. (7), we obtain

$$\left|y\right|={\left(2V\right)}^{1/2}$$

(10)

By substituting Eq. (10) into Eq. (9), there is

$$\dot{V}=-{\alpha }_{1}{\left(2\right)}^{{(\alpha }_{2}+1)/2 }{V}^{{(\alpha }_{2}+1)/2}-{\alpha }_{3}{\left(2\right)}^{{(\alpha }_{4}+1)/2 }{V}^{{(\alpha }_{4}+1)/2}$$

(11)

By considering ${\rho }_{1}={\alpha }_{1}{\left(2\right)}^{{(\alpha }_{2}+1)/2},{\rho }_{3}={\alpha }_{3}{\left(2\right)}^{{(\alpha }_{4}+1)/2}, {\rho }_{2}=\frac{{\alpha }_{2}+1}{2},$ and ${\rho }_{4}= \frac{{\alpha }_{4}+1}{2}$, we have

$$\dot{V}\left(x\right)\le -{\rho }_{1}{V}^{{\rho }_{2}}-{\rho }_{3}{V}^{{\rho }_{4}}$$

(12)

According to Lemma 3, the origin of Eq. (6) is fixed-time stable if ${\rho }_{1}, {\rho }_{3}>0$, $0<{\rho }_{2}<1$, and ${\rho }_{4}>1$. Thus, by choosing ${\alpha }_{1},{\alpha }_{3}>0, {\alpha }_{4}>1,$ and $0<{\alpha }_{4}<1$ the conditions of Lemma 3 are fulfilled and the origin of Eq. (6) is fixed-time stable. Also, with accordance to Lemma 3, the fixed-time stability can be presented as $T\le \frac{1}{{\rho }_{1}\left(1-{\rho }_{2}\right)}+\frac{1}{{\rho }_{3}\left({\rho }_{4}-1\right)}$. Therefore, the proof of Lemma 4 is completed.□

3 System Description

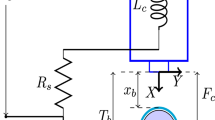
The mathematical model of the nonlinear support structure system for offshore wind turbines has been presented in (Aggarwal et al. 2014; Li et al. 2006; Manikandan & Saha, 2013) as Eq. (13)

$$\ddot{x} + 2\mu \dot{x} + {\omega }_{0}^{2}x+ \alpha {x}^{3}=F\cos\left(\varOmega t\right)$$

(13)

where the dot denotes differential with respect to time; $\mu$ and $\alpha$ are positive constants; $\mu$ is damping coefficient; $\alpha$ is nonlinear coefficient; ${\omega }_{0}$ is the natural frequency; and $F$ and Ω are the amplitude and frequency of the external excitation, respectively. By considering ${x}_{1}=x$ and ${x}_{2}=\dot{x}$ in Eq. (13), the state-space form is as Eq. (14)

$$\left\{\begin{array}{l}{\dot{x}}_{1}={x}_{2} \\ {\dot{x}}_{2}=-2\mu {x}_{2}-{\omega }_{0}^{2}{x}_{1}-\alpha {x}_{1}^{3}+F\cos\left(\varOmega t\right)\end{array}\right.$$

(14)

First, system (14) is investigated where the control signal is not yet applied to the system. Indeed, the uncontrolled response of system Eq. (14) is investigated. This system shows chaotic behavior without control signal for $\alpha =5, \mu =1, F=40,\varOmega =2, {\omega }_{0}=1$ and the initial conditions ${\left[{x}_{1}\left(0\right), {x}_{2}\left(0\right)\right]}^{{\mathrm{T}}}={\left[2, 1\right]}^{{\mathrm{T}}}$ (see Fig. 1). It is obvious that this response is not desirable in offshore platforms. Hence, applying the controller is necessary. Figure 1 represents the uncontrolled simulation of system Eq. (14).

Fig. 1

Uncontrolled response of system Eq. (14)

4 Problem Formulation

It is observed that the system has chaotic behavior without a controller (see Fig. 1). In this section, a control input $u$ is added to the second subsystem of Eq. (14). Also, a model of matched parametric uncertainties $d$ is added to the second subsystem of Eq. (14); therefore, Eq. (15) would be obtained. Indeed, a control input $u$ is added to Eq. (13) to provide a controller for this chaotic system. A model of parametric uncertainties, $d$, is added to Eq. (13) (due to existing $d$ in practical applications); hence, we have $\ddot{x} + 2\mu \dot{x} + {\omega }_{0}^{2}x+ \alpha {x}^{3}=F\cos\left(\varOmega t\right)+u+d$. Then, by considering ${x}_{1}=\dot{x}$ and ${x}_{2}=\ddot{x}$ in this equation, the state-space model would be as Eq. (15) as follows

$$\left\{\begin{array}{l}\begin{array}{l}{\dot{x}}_{1}={x}_{2} \\ {\dot{x}}_{2}=-2\mu {x}_{2}-{\omega }_{0}^{2}{x}_{1}-\alpha {x}_{1}^{3} \end{array}\\ \qquad+\,F\cos\left(\varOmega t\right)+u+d=f(x)+u+d\end{array}\right.$$

(15)

where $f(x)$ is a nonlinear and smooth function (which means "sufficient differentiable function"). It is assumed that the first system state ${x}_{1}$ is measured and the second system state ${x}_{2}$ is unmeasured and needs to be estimated. Hence, the vector of the states and their estimations for the slave system are as $x={\left[{x}_{1}, {x}_{2}\right]}^{{\mathrm{T}}}, \widehat{x}={\left[{x}_{1}, {\widehat{x}}_{2}\right]}^{{\mathrm{T}}}, n=(1, 2)$.

In order to design the combined controller/observer, the following assumptions are used:

Assumption 1

${x}_{1}$ as output feedback is measurable.

Assumption 2

The model of matched parametric uncertainties $d$ is bounded, but its upper bound is unavailable and needs to be estimated,

$$\left|d\right|\le h$$

(16)

where h is the parametric uncertainty upper bound which is positive constant.

Assumption 3

$f\left(x\right)$ and $f\left(\widehat{x}\right)$ fulfill $\left|f\left(x\right)-f\left(\widehat{x}\right)\right|\le \eta$, where $\eta$ is positive constant.

Assumption 4

${x}_{2}$ fulfills $\left|{x}_{2}\right|\le \delta$, where $\delta$ is positive constant.

Remark 1

It should be noted that Assumptions 3 and 4 might be restrictive in some applications. However, $\eta$ and $\delta$ are arbitrary positive constants (i.e., bounded) that are adjustable based on the application. In this application, as shown in Fig. 1, this system is chaotic and the system states are bounded (i.e., we have $\left|{x}_{2}\right|\le \delta$ given in Assumption 4). Moreover, a required condition for designing a state observer is to be stable which is obviously considered in the observer design in this study (i.e., $f\left(\widehat{x}\right)$ is bounded). Therefore, we have $\left|f\left(x\right)-f\left(\widehat{x}\right)\right|\le \eta$ given in Assumption 3. Also, the same assumptions and numerical values for $\eta$ and $\delta$ have been considered in (Abadi et al. 2020).

Remark 2

From practical point of view, the model of matched parametric uncertainties is bounded, but might be unavailable (which is given in Assumption 2). Also, the abovementioned assumptions can be found in some successful applications in (Abadi et al. 2020; Daly & Wang, 2009; Liu et al. 2016; Mohammadi et al. 2013; Nekoukar & Erfanian, 2011; Zhao et al. 2013).

Since the control goal of this study is to synchronize two chaotic support structures for offshore wind turbines, the master system and slave system should be defined. Therefore, Eq. (14) is used to define the master system as follows

$$\left\{\begin{array}{l}\begin{array}{l}{\dot{x}}_{1m}={x}_{2m} \\ {\dot{x}}_{2m}=-2\mu {x}_{2m}-{\omega }_{0}^{2}{x}_{1m}-\alpha {x}_{1m}^{3} \end{array}\\ \qquad+F\cos\left(\varOmega t\right)+{d}_{m}={f}_{m}(x)+{d}_{m}\end{array}\right.$$

(17)

The slave system is defined as Eq. (17) which is the same as the system (15),

$$\left\{\begin{array}{l}\begin{array}{l}{\dot{x}}_{1}={x}_{2} \\ {\dot{x}}_{2}=-2\mu {x}_{2}-{\omega }_{0}^{2}{x}_{1}-\alpha {x}_{1}^{3} \end{array}\\ \qquad+F\cos\left(\varOmega t\right)+u+d=f(x)+u+{d}_{s}\end{array}\right.$$

(18)

where ${d}_{m}$ and ${d}_{s}$ are the model of parametric uncertainties in Eqs. (17) and (18). To fulfill the synchronization goal for abovementioned master and slave systems, the synchronization error is defined as ${e}_{1}={x}_{1}-{x}_{1m}$ and ${e}_{2}={x}_{2}-{x}_{2m}$. As a result, the synchronization error dynamics is given as follows

$$\left\{\begin{array}{l}\begin{array}{l}{\dot{e}}_{1}={\dot{x}}_{1}-{\dot{x}}_{1m}={x}_{2}-{x}_{2m}={e}_{2} \\ {\dot{e}}_{2}=f\left(x\right)-{f}_{m}\left(x\right)+u+{d}_{s}-{d}_{m} \end{array}\\ \qquad = f\left(x\right)-{f}_{m}\left(x\right)+u+d\end{array}\right.$$

(19)

Let $d={d}_{s}-{d}_{m}$ be the model of matched parametric uncertainties in Eq. (19), where we have $\left|d\right|\le h$ [see Eq. (16)].

Remark 3

In most practical applications, measuring the states directly by using physical sensors might not be possible, and even if it is possible, the obtained data are easy to contaminate by noise. Also, utilizing lots of physical sensors makes the real system implementation more complex and more expensive (Benallegue et al. 2008). Hence, reducing the number of required physical sensors is preferable in practice which can decrease the size, weight, cost, and even noise of their direct measurements. That is why a state observer is designed and combined with a controller to estimate the unmeasured second state 2 and provide the estimated data in the designed controller.

5 Controller Design by Using FASMC Scheme with a State Observer

In this section, a robust fixed-time controller is designed based on the SMC technique to synchronize the master system (17) and the slave system (18); i.e., synchronization error reaches zero in a fixed time. The estimation of the uncertainty upper bound is done by using an adaptive concept and providing online data in the designed controller. A state observer is designed to estimate the unmeasured state (the second state) and provide online data in the controller. Before proceeding with designing the controller, let us have a short overview of SMC strategy.

Overview of SMC Methodology: SMC scheme is a robust nonlinear control approach. The SMC scheme provides a robust controller that can confirm maintaining stability and reliable performance against modeling inaccuracy and uncertainties. To design a controller using SMC methodology, a sliding surface and a control law should be designed. That is why, the following two steps are required for stability analysis: (1) a control law should be designed such that it guides the system to a sliding surface once it applied to the system (i.e., it should be proved by applying the designed control law to the system, the system will reach the sliding surface), (2) a sliding surface should be defined such that a desired behavior of the system should be ensured once the system reaches the sliding surface (i.e., the stability of the sliding surface $s=0$ should be proved) (Alinaghi Hosseinabadi et al. 2020; Utkin, 1977).

The sliding surface is chosen as Eq. (20)

$$s=\dot{{e}_{1}}+{{\alpha }}_{1}{\mathrm{e}}_{1}^{{{\alpha }}_{2}}+{{\alpha }}_{3}{\mathrm{e}}_{1}^{{{\alpha }}_{4}}$$

(20)

where we have ${\alpha }_{1},{\alpha }_{3}>0, {\alpha }_{4}>1, 0<{\alpha }_{2}<1$. Let $A={{\alpha }}_{1}{\mathrm{e}}_{1}^{{{\alpha }}_{2}}$, and $B={{\alpha }}_{3}{\mathrm{e}}_{1}^{{{\alpha }}_{4}}$ for simplification. The adaptive law is given as Eq. (21)

$$\dot{\widehat{h}}=\frac{r}{K}\left|s\right|$$

(21)

where $0<r<1$ and $K>1$. Also, the estimation error of the matched parametric uncertainties (using adaptive concept) is obtained as Eq. (22)

$$\stackrel{\sim }{h}= \widehat{h}-h$$

(22)

where h is the parametric uncertainty upper bound and $\widehat{h}$ is its estimate. As it is mentioned for Eq. (16), it is assumed there exists a positive constant $h>0$ which is the upper bound of parametric uncertainties $d$ (see Eq. 16; $\left|d\right|\le h$). It is proved in Theorem 1 that there is a positive value $\widehat{h}$ which is the estimation of h; i.e., $\stackrel{\sim }{h}=0$ is proved by using $\left|d\right|\le h\le \widehat{h}$ [which can be proved based on (Abadi et al. 2020)]. The proposed state observer is obtained as Eq. (23):

$$\left\{\begin{array}{l}{\dot{\widehat{x}}}_{1}=-{c}_{1}{\widehat{x}}_{1}+{\widehat{x}}_{2}+Qsign({\stackrel{\sim }{x}}_{1}) \\ \begin{array}{l}\begin{array}{l}{\dot{\widehat{x}}}_{2}=-{c}_{2}{\widehat{x}}_{2}+u+f\left(\widehat{x}\right) \\ Q=-\left|{c}_{1}{\widehat{x}}_{1}\right|-\left|{\widehat{x}}_{2}\right|-\eta -\left|{c}_{2}{\widehat{x}}_{2}\right|-\delta -\widehat{h}-2\left|s\right|\eta \end{array}\\ +\frac{2}{K}\left(\begin{array}{l}-{c}_{3}{\left|{\stackrel{\sim }{x}}_{1}\right|}^\frac{1}{2}-{c}_{4}{\left|\left|{\widehat{x}}_{2}\right|+\delta \right|}^\frac{1}{2}\\ -{c}_{5}{\left|{\stackrel{\sim }{x}}_{1}\right|}^{\frac{\beta +1}{2}}-{c}_{6}{\left|\left|{\widehat{x}}_{2}\right|+\delta \right|}^{\frac{\beta +1}{2}}\end{array}\right)\end{array}\end{array}\right.$$

(23)

where $\beta >1$, ${c}_{j}>0, j=(1, 2, 3, 4, 5, 6)$, $\eta >0,$ and $\delta >0$. Also, the estimation error of the fixed-time state observer is defined as Eq. (24)

$$\left\{\begin{array}{l}{\stackrel{\sim }{x}}_{1}={\widehat{x}}_{1}-{x}_{1} \\ {\stackrel{\sim }{x}}_{2}={\widehat{x}}_{2}-{x}_{2}\end{array}\right.$$

(24)

By using the FASMC scheme, the control law $u$ (25) is designed to provide a fixed-time stability for system (19). It should be noted that in the proposed control law $u$ (25), the adaptive term $\widehat{h}$ and observer term $f\left(\widehat{x}\right)$ are utilized. Furthermore, it will be proven that the estimation errors in Eqs. (22) and (24) reach zero in a fixed time once the proposed control law (25) is applied to the system (15). The designed control law is obtained as Eq. (25)

$$ \begin{aligned} u & = - f\left( {\hat{x}} \right) + f_{m} \left( x \right) - \dot{A} - \dot{B} \\ & \quad - \hat{h}{\text{sign}}\left( s \right) - 2\hat{h}^{\beta + 1} sig^{\beta } \left( s \right) \\ \end{aligned} $$

(25)

In the following, it is first proved the convergence of the error system (19) onto the sliding surface Eq. (20) (i.e., $s=0$) by applying the designed control law Eq. (25) to system Eq. (15) within a presented fixed time ${T}_{1}$. Simultaneously, it is proved that $\stackrel{\sim }{h}=0$ and ${\stackrel{\sim }{x}}_{1}=0$ and ${\stackrel{\sim }{x}}_{2}=0$ is achieved for $t>{T}_{1}$ by using one Lyapunov function (see Theorem 1). In Theorem 2, it is proved that the proposed sliding surface $s=0$ is fixed-time stable. In other words, the synchronization error (that its convergence to the sliding surface Eq. (20) was proved in Theorem 1; i.e., $s=0$) converges to zero in a fixed time ${T}_{2}$. Therefore, the total settling time to fulfill synchronization goal in this study will be as ${T=T}_{1}+{T}_{2}$ (which is presented in Remark 4).

Theorem 1

Consider the synchronization error dynamics Eq. (19) with Assumptions 1 to 4, the sliding surface Eq. (20), the adaptive law Eq. (21), the state observer Eq. (23), and the control law Eq. (25). If the designed control law Eq. (25) is applied to system Eq. (15), then the synchronization errors, described by system Eq. (19), will converge to the sliding surface Eq. (20) (i.e., $s=0$) in a presented fixed time ${T}_{1}$. Moreover, the estimation errors given in Eqs. (22) and (24) will reach zero. In other words, $\stackrel{\sim }{h}=0$, ${\stackrel{\sim }{x}}_{1}=0$, ${\stackrel{\sim }{x}}_{2}=0$, and $s=0$ will be satisfied for $t>{T}_{1}$, simultaneously. The upper bound of ${T}_{1}$ is obtained as Eq. (26)

$${T}_{1}\le \frac{1}{{\rho }_{1}\left(1-{\rho }_{2}\right)}+\frac{1}{{\rho }_{3}\left({\rho }_{4}-1\right)}$$

(26)

where the values of ${\rho }_{1}$, ${\rho }_{2}$, ${\rho }_{3}$, and ${\rho }_{4}$ have been presented in the following proof.

Proof

The candidate Lyapunov function Eq. (27) is chosen based on our control goal in this part (i.e., ensuring $\stackrel{\sim }{h}=0$, ${\stackrel{\sim }{x}}_{1}=0$, ${\stackrel{\sim }{x}}_{2}=0$, and $s=0$, simultaneously in a fixed time) and the conditions given in Lemma 4, there comes.

$$V=\frac{K}{2}({s}^{2}+{\stackrel{\sim }{h}}^{2}+\left|{\stackrel{\sim }{x}}_{1}\right|+|{\stackrel{\sim }{x}}_{2}|)$$

(27)

By differentiating of this function with respect to time, there is

$$\dot{V}=K\left(s\dot{s}+\stackrel{\sim }{h}\dot{\widehat{h}}+\frac{1}{2}({\dot{\widehat{x}}}_{1}-{\dot{x}}_{1}){\text{sign}}\left({\stackrel{\sim }{x}}_{1}\right)+\frac{1}{2}({\dot{\widehat{x}}}_{2}-{\dot{x}}_{2}){\text{sign}}\left({\stackrel{\sim }{x}}_{2}\right)\right)$$

(28)

where $\dot{\stackrel{\sim }{h}}=\dot{\widehat{h}}$ and ${\dot{\stackrel{\sim }{x}}}_{i}={\dot{\widehat{x}}}_{i}-{\dot{x}}_{i}, i=\mathrm{1,2}$ [considering Eqs. (22) and (24), respectively]. Before proceeding further, let us rewrite Eq. (20) as $s={e}_{2}+A+B$, where ${e}_{2}=\dot{{e}_{1}}$ [according to Eq. (19)], $A={\alpha }_{1}{e}_{1}^{{\alpha }_{2}}$, and $B={\alpha }_{3}{e}_{1}^{{\alpha }_{4}}$. Subsequently, its time derivative is $\dot{s}={\dot{e}}_{2}+\dot{A}+\dot{B}$. Then, by substituting the designed control law Eq. (25) into the synchronization error dynamics Eq. (19), and by placing ${\dot{e}}_{2}$ from Eq. (19) into $\dot{\mathrm{s}}$, there comes

$$\dot{s}=f(x)-{f}_{m}(x)-f\left(\widehat{x}\right)+{f}_{m}\left(x\right)-\dot{A}-\dot{B}-\widehat{h}{\text{sign}}\left(s\right)-2{\widehat{h}}^{\beta +1}{\text{sig}}^{\beta }\left(s\right) +d +\dot{A}+\dot{B}$$

(29)

By simplifying Eq. (29), we have

$$\dot{s}=f(x)-f\left(\widehat{x}\right)-\widehat{h}{\text{sign}}\left(s\right)-2{\widehat{h}}^{\beta +1}{\text{sig}}^{\beta }\left(s\right) +d$$

(30)

By placing Eqs. (21), (23) and (30) into Eq. (28), one can obtain

$$\dot{V}\le K\left(s(f(x)-f\left(\widehat{x}\right)-\widehat{h}{\text{sign}}\left(s\right)-2{\widehat{h}}^{\beta +1}{\text{sig}}^{\beta }\left(s\right) +d)+\frac{r}{K}\left|s\right|\stackrel{\sim }{h}+\frac{1}{2}(-{c}_{1}{\widehat{x}}_{1}+{\widehat{x}}_{2}+Qsign({\stackrel{\sim }{x}}_{1})-{\dot{x}}_{1}){\text{sign}}\left({\stackrel{\sim }{x}}_{1}\right)+\frac{1}{2}(-{c}_{2}{\widehat{x}}_{2}+u+f\left(\widehat{x}\right)-{\dot{x}}_{2}){\text{sign}}\left({\stackrel{\sim }{x}}_{2}\right)\right)$$

(31)

By placing ${\dot{x}}_{1}$ and ${\dot{x}}_{2}$ from Eq. (18) into Eq. (31). Also, by placing h instead of $d$ [considering Eq. (16) in Assumption 2, as $d\le \left|d\right|\le h$], as well as placing $\eta$ instead of $f\left(x\right)-f\left(\widehat{x}\right)$ (considering Assumption 2 as $f\left(x\right)-f\left(\widehat{x}\right)\le \left|f\left(x\right)-f\left(\widehat{x}\right)\right|\le \eta$), we have

$$\dot{V}\le K\left(s(\eta -\widehat{h}{\text{sign}}\left(s\right)-2{\widehat{h}}^{\beta +1}{\text{sig}}^{\beta }\left(s\right) +h)+\frac{r}{K}\left|s\right|\stackrel{\sim }{h}+\frac{1}{2}(-{c}_{1}{\widehat{x}}_{1}+{\widehat{x}}_{2}+Qsign({\stackrel{\sim }{x}}_{1})-{x}_{2}){\text{sign}}\left({\stackrel{\sim }{x}}_{1}\right)+\frac{1}{2}(-{c}_{2}{\widehat{x}}_{2}+u+f\left(\widehat{x}\right)-f\left(x\right)-u-d){\text{sign}}\left({\stackrel{\sim }{x}}_{2}\right)\right)$$

(32)

By using $s\le \left|s\right|$ and considering the mathematical rules of Definition 1 given in Eqs. (1) and (2); Eq. (32) can be rewritten as below

$$\dot{V}\le K\left(+\eta \left|s\right|-\widehat{h}\left|s\right|-2{\widehat{h}}^{\beta +1}{\left|s\right|}^{\beta +1}+h\left|s\right|+\frac{r}{K}\left|s\right|\stackrel{\sim }{h}+\frac{1}{2}(\left|{c}_{1}{\widehat{x}}_{1}\right|+\left|{\widehat{x}}_{2}\right|+Q)+\frac{1}{2}\left(\left|{c}_{2}{\widehat{x}}_{2}\right|+\left|{x}_{2}\right|+\left|f\left(x\right)-f\left(\widehat{x}\right)\right|+\left|d\right|\right)\right)$$

(33)

By using $\left|d\right|\le h$ placing $Q$ from Eq. (23) into Eq. (33), there comes

$$\dot{V}\le K\left(+\eta \left|s\right|-\widehat{h}\left|s\right|-2{{\widehat{h}}^{\beta +1}\left|s\right|}^{\beta +1}+h\left|s\right|+\frac{r}{K}\left|s\right|\stackrel{\sim }{h}+\frac{1}{2}(\left|{c}_{1}{\widehat{x}}_{1}\right|+\left|{\widehat{x}}_{2}\right|-\left|{c}_{1}{\widehat{x}}_{1}\right|-\left|{\widehat{x}}_{2}\right|-\eta -\left|{c}_{2}{\widehat{x}}_{2}\right|-\delta -\widehat{h}-2\left|s\right|\eta )+\frac{1}{2}\left(\left|{c}_{2}{\widehat{x}}_{2}\right|+\left|{x}_{2}\right|+\left|f\left(x\right)-f\left(\widehat{x}\right)\right|+h\right) \right)-{c}_{3}{\left|{\stackrel{\sim }{x}}_{1}\right|}^\frac{1}{2}-{c}_{4}{\left|\left|{\widehat{x}}_{2}\right|+\delta \right|}^\frac{1}{2}-{c}_{5}{\left|{\stackrel{\sim }{x}}_{1}\right|}^{\frac{\beta +1}{2}}-{c}_{6}{\left|\left|{\widehat{x}}_{2}\right|+\delta \right|}^{\frac{\beta +1}{2}}$$

(34)

By using $\left|d\right|\le h\le \widehat{h}$ we have $h-\widehat{h}\le 0$ (which clearly can be neglected in the above inequality). Also, we have $\left|f\left(x\right)-f\left(\widehat{x}\right)\right|-\eta \le 0$, $\left|{x}_{2}\right|\le \delta$ (given in Assumptions 3 and 4) and $\stackrel{\sim }{h}=\widehat{h}-h$ [given in Eq. (22)] and simplifying Eq. (34), there is

$$ \begin{aligned} \dot{V} & \le K\left( { + \eta \left| s \right| - \hat{h}\left| s \right| - 2\hat{h}^{\beta + 1} \left| s \right|^{\beta + 1} + h\left| s \right| + \frac{r}{K}\left| s \right|\tilde{h} + \frac{1}{2}\left( { - \eta - \delta - 2\left| s \right|\eta } \right) + \frac{1}{2}\left( {\delta + \eta } \right){ }} \right) - c_{3} \left| {\tilde{x}_{1} } \right|^{\frac{1}{2}} - c_{4} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{\frac{1}{2}} - c_{5} \left| {\tilde{x}_{1} } \right|^{{\frac{\beta + 1}{2}}} - c_{6} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{{\frac{\beta + 1}{2}}} { } \\ & \Rightarrow \dot{V} \le K\left( {\begin{array}{*{20}c} { + \eta \left| s \right| - \hat{h}\left| s \right| - 2\hat{h}^{\beta + 1} \left| s \right|^{\beta + 1} } \\ { + h\left| s \right| + \frac{r}{K}\left| s \right|\tilde{h} - \left| s \right|\eta } \\ \end{array} } \right) - c_{3} \left| {\tilde{x}_{1} } \right|^{\frac{1}{2}} - c_{4} \left| {\left| {\hat{h}_{2} } \right| + \delta } \right|^{\frac{1}{2}} - c_{5} \left| {\tilde{x}_{1} } \right|^{{\frac{\beta + 1}{2}}} - c_{6} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{{\frac{\beta + 1}{2}}} \\ \end{aligned} $$

(35)

By using $\stackrel{\sim }{h}= \widehat{h}-h$ [given in Eq. (22)] and adding $\pm \left|s\right|\stackrel{\sim }{h}$ to Eq. (35), one can obtain

$$ \begin{aligned} \dot{V} & \le - K\hat{h}\left| s \right| - 2K\hat{h}^{\beta + 1} \left| s \right|^{\beta + 1} + Kh\left| s \right| + r\left| s \right|\tilde{h}{ } \pm \left| s \right|\tilde{h} - c_{3} \left| {\tilde{x}_{1} } \right|^{\frac{1}{2}} - c_{4} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{\frac{1}{2}} \\ & \quad - c_{5} \left| {\tilde{x}_{1} } \right|^{{\frac{\beta + 1}{2}}} - c_{6} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{{\frac{\beta + 1}{2}}} { } \Rightarrow { }\dot{V} \\ & \le - K\left| s \right|\left( {\hat{h} - h} \right) - 2K\hat{h}^{\beta + 1} \left| s \right|^{\beta + 1} + r\left| s \right|\tilde{h}{ } \pm \left| s \right|\tilde{h} - c_{3} \left| {\tilde{x}_{1} } \right|^{\frac{1}{2}} - c_{4} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{\frac{1}{2}} \\ & \quad - c_{5} \left| {\tilde{x}_{1} } \right|^{{\frac{\beta + 1}{2}}} - c_{6} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{{\frac{\beta + 1}{2}}} { } \Rightarrow \dot{V} \\ & \le - \left( {K - 1} \right)\left| s \right|\tilde{h} - \tilde{h}\left( {\left| s \right| - r\left| s \right|} \right) - 2K\hat{h}^{\beta + 1} \left| s \right|^{\beta + 1} - c_{3} \left| {\tilde{x}_{1} } \right|^{\frac{1}{2}} - c_{4} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{\frac{1}{2}} \\ & \quad - c_{5} \left| {\tilde{x}_{1} } \right|^{{\frac{\beta + 1}{2}}} - c_{6} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{{\frac{\beta + 1}{2}}} \\ \end{aligned} $$

(36)

Since we have $\stackrel{\sim }{h}= \widehat{h}-h$ [given in Eq. (22)], where $h>0, \widehat{h}>0$, and $\left|d\right|\le h\le \widehat{h}$. Then, we have, $\stackrel{\sim }{h}= \widehat{h}-h\le \widehat{h}+h\Rightarrow \stackrel{\sim }{h}\le \widehat{h}+h\Rightarrow -\stackrel{\sim }{h}\ge -(\widehat{h}+h)$. Subsequently, we have ${\stackrel{\sim }{h}}^{\beta +1}\le {\left(\widehat{h}+h\right)}^{\beta +1}$. According to Lemma 2 because $\beta +1>1$, [note that we have $\beta >1$ given in Eq. (23)], there comes ${({2)}^{-\beta }\stackrel{\sim }{h}}^{\beta +1}\le {\widehat{h}}^{\beta +1}+{h}^{\beta +1}\Rightarrow {-({2)}^{-\beta }\stackrel{\sim }{h}}^{\beta +1}\ge -\left({\widehat{h}}^{\beta +1}+{h}^{\beta +1}\right)$. Then, by adding $\pm K{h}^{\beta +1}{\left|s\right|}^{\beta +1}$ to Eq. (36), one yields

$$ \begin{aligned} \dot{V} & \le - \left( {K - 1} \right)\left| s \right|\tilde{h} - \tilde{h}\left( {\left| s \right| - r\left| s \right|} \right) - K\hat{h}^{\beta + 1} \left| s \right|^{\beta + 1} - K\hat{h}^{\beta + 1} \left| s \right|^{\beta + 1} \pm Kh^{\beta + 1} \left| s \right|^{\beta + 1} \\ & \quad - c_{3} \left| {\tilde{x}_{1} } \right|^{\frac{1}{2}} - c_{4} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{\frac{1}{2}} - c_{5} \left| {\tilde{x}_{1} } \right|^{{\frac{\beta + 1}{2}}} - c_{6} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{{\frac{\beta + 1}{2}}} \Rightarrow { }\dot{V} \\ & \le - \left( {K - 1} \right)\left| s \right|\tilde{h} - \tilde{h}\left( {\left| s \right| - r\left| s \right|} \right) - K\left| s \right|^{\beta + 1} \left( {\hat{h}^{\beta + 1} + h^{\beta + 1} } \right) + K\left| s \right|^{\beta + 1} \left( {h^{\beta + 1} - \hat{h}^{\beta + 1} } \right) \\ & \quad - c_{3} \left| {\tilde{x}_{1} } \right|^{\frac{1}{2}} - c_{4} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{\frac{1}{2}} - c_{5} \left| {\tilde{x}_{1} } \right|^{{\frac{\beta + 1}{2}}} - c_{6} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{{\frac{\beta + 1}{2}}} \Rightarrow \dot{V} \\ & \le - \left( {K - 1} \right)\left| s \right|\tilde{h} - \tilde{h}\left( {\left| s \right| - r\left| s \right|} \right) - K\left| s \right|^{\beta + 1} \left( {(2)^{ - \beta } \tilde{h}^{\beta + 1} } \right) + K\left| s \right|^{\beta + 1} \left( {h^{\beta + 1} - \hat{h}^{\beta + 1} } \right) \\ & \quad - c_{3} \left| {\tilde{x}_{1} } \right|^{\frac{1}{2}} - c_{4} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{\frac{1}{2}} - c_{5} \left| {\tilde{x}_{1} } \right|^{{\frac{\beta + 1}{2}}} - c_{6} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{{\frac{\beta + 1}{2}}} \\ \end{aligned} $$

(37)

Note that $+K{\left|s\right|}^{\beta +1}({h}^{\beta +1}-{\widehat{h}}^{\beta +1})$ can be neglected where $+K{\left|s\right|}^{\beta +1}({h}^{\beta +1}-{\widehat{h}}^{\beta +1})\le 0$ because $h\le \widehat{h}\Rightarrow {h}^{\beta +1}\le {\widehat{h}}^{\beta +1}$. Then, by adding $\pm {\left|s\right|}^{\beta +1}{\stackrel{\sim }{h}}^{\beta +1}$ to Eq. (37), we have

$$ \begin{aligned} \dot{V} & \le - \left( {K - 1} \right)\left| s \right|\tilde{h} - \tilde{h}\left( {\left| s \right| - r\left| s \right|} \right) - K(2)^{ - \beta } \left| s \right|^{\beta + 1} \tilde{h}^{\beta + 1} \pm \left| s \right|^{\beta + 1} \tilde{h}^{\beta + 1} \\ & \quad - c_{3} \left| {\tilde{x}_{1} } \right|^{\frac{1}{2}} - c_{4} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{\frac{1}{2}} - c_{5} \left| {\tilde{x}_{1} } \right|^{{\frac{\beta + 1}{2}}} - c_{6} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{{\frac{\beta + 1}{2}}} \Rightarrow \dot{V} \\ & \le - \left( {K - 1} \right)\left| s \right|\tilde{h} - \tilde{h}\left( {\left| s \right| - r\left| s \right|} \right) - \left( {K2^{ - \beta } - 1} \right)\left| s \right|^{\beta + 1} \tilde{h}^{\beta + 1} - \left| s \right|^{\beta + 1} \tilde{h}^{\beta + 1} \\ & \quad - c_{3} \left| {\tilde{x}_{1} } \right|^{\frac{1}{2}} - c_{4} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{\frac{1}{2}} - c_{5} \left| {\tilde{x}_{1} } \right|^{{\frac{\beta + 1}{2}}} - c_{6} \left| {\left| {\hat{x}_{2} } \right| + \delta } \right|^{{\frac{\beta + 1}{2}}} \\ \end{aligned} $$

(38)

By considering Lemma 1 and utilizing ${|\widehat{x}}_{2}-{x}_{2}\left|\le {|\widehat{x}}_{2}\right|+|{x}_{2}|$, and our assumption $\left|{\widehat{x}}_{2}\right|\le \delta$ (given in Sect. 4), then, we have ${\stackrel{\sim }{x}}_{2}={\widehat{x}}_{2}-{x}_{2}\le {|\widehat{x}}_{2}-{x}_{2}\left|\le {|\widehat{x}}_{2}\right|+|{x}_{2}|\le \left|{\widehat{x}}_{2}\right|+\delta \Rightarrow \left|{\stackrel{\sim }{x}}_{2}\right|\le \left|{\widehat{x}}_{2}\right|+\delta$, yields

$$\dot{V}\le -\left(K-1\right)\stackrel{\sim }{h}\left|s\right|-(K\left({2)}^{-\beta }-1\right){\stackrel{\sim }{h}}^{\beta +1}{\left|s\right|}^{\beta +1}-\left(\left|s\right|-r\left|s\right|\right)\stackrel{\sim }{h}-{\left|s\right|}^{\beta +1}{\stackrel{\sim }{h}}^{\beta +1}-{c}_{3}{\left|{\stackrel{\sim }{x}}_{1}\right|}^\frac{1}{2}-{c}_{4}{\left|{\stackrel{\sim }{x}}_{2}\right|}^\frac{1}{2}-{c}_{5}{\left|{\stackrel{\sim }{x}}_{1}\right|}^{\frac{\beta +1}{2}}-{c}_{6}{\left|{\stackrel{\sim }{x}}_{2}\right|}^{\frac{\beta +1}{2}}$$

(39)

Let us consider ${\varDelta }_{1}=\left(K-1\right)\stackrel{\sim }{h}, {\varDelta }_{2}=(K\left({2)}^{-\beta }-1\right){\stackrel{\sim }{h}}^{\beta +1}$, ${\varDelta }_{3}=\left(\left|s\right|-r\left|s\right|\right),$ and ${\varDelta }_{4}={\left|s\right|}^{\beta +1}$. Then, we have

$$\dot{V}\le -{\varDelta }_{1}\left|s\right|-{\varDelta }_{2}{\left|s\right|}^{\beta +1}-{\varDelta }_{3}\stackrel{\sim }{h}-{\varDelta }_{4}{\stackrel{\sim }{h}}^{\beta +1}-{c}_{3}{\left|{\stackrel{\sim }{x}}_{1}\right|}^\frac{1}{2}-{c}_{4}{\left|{\stackrel{\sim }{x}}_{2}\right|}^\frac{1}{2}-{c}_{5}{\left|{\stackrel{\sim }{x}}_{1}\right|}^{\frac{\beta +1}{2}}-{c}_{6}{\left|{\stackrel{\sim }{x}}_{2}\right|}^{\frac{\beta +1}{2}}$$

(40)

Let us consider ${\varDelta }_{{m}_{1}}={\mathrm{min}}\left({\varDelta }_{1}, {\varDelta }_{3}, {\varDelta }_{4}, {c}_{3},{c}_{4}\right)$ and ${\varDelta }_{{m}_{2}}={\mathrm{min}}\left({\varDelta }_{2}, {\varDelta }_{5}, {\varDelta }_{6}, {c}_{5},{c}_{6}\right)$, (where ${\varDelta }_{1}, {\varDelta }_{2}, {\varDelta }_{3}, {\varDelta }_{4}, {\varDelta }_{5}, {\varDelta }_{6},{c}_{3},{c}_{4},{c}_{5}$, and ${c}_{6}>0$), yielding

$$\dot{V}\le -{\varDelta }_{{m}_{1}}\left( \left|s\right|+\stackrel{\sim }{h}+{\left|{\stackrel{\sim }{x}}_{1}\right|}^\frac{1}{2}+{\left|{\stackrel{\sim }{x}}_{2}\right|}^\frac{1}{2}\right)-{\varDelta }_{{m}_{2}}\left({\left|s\right|}^{\beta +1}+{\stackrel{\sim }{h}}^{\beta +1}+{\left|{\stackrel{\sim }{x}}_{1}\right|}^{\frac{\beta +1}{2}}+{\left|{\stackrel{\sim }{x}}_{2}\right|}^{\frac{\beta +1}{2}}\right)$$

(41)

By considering Lemma 1, there comes

$$\dot{V}\le -{\varDelta }_{{m}_{1}}{\left( {\left|s\right|}^{2}+{\stackrel{\sim }{h}}^{2}+\left|{\stackrel{\sim }{x}}_{1}\right|+\left|{\stackrel{\sim }{x}}_{2}\right|\right)}^\frac{1}{2}-{\varDelta }_{{m}_{2}}{\left({\left|s\right|}^{2\left(\beta +1\right)}+{\stackrel{\sim }{h}}^{2\left(\beta +1\right)}+{\left|{\stackrel{\sim }{x}}_{1}\right|}^{\beta +1}+{\left|{\stackrel{\sim }{x}}_{2}\right|}^{\beta +1}\right)}^\frac{1}{2}$$

(42)

According to our defined candidate Lyapunov function (27), $V=\frac{K}{2}({s}^{2}+{\stackrel{\sim }{h}}^{2}+\left|{\stackrel{\sim }{x}}_{1}\right|+|{\stackrel{\sim }{x}}_{2}|)$, we have $\frac{2}{K}V={s}^{2}+{\stackrel{\sim }{h}}^{2}+\left|{\stackrel{\sim }{x}}_{1}\right|+|{\stackrel{\sim }{x}}_{2}|$. Note that according to Lemma 2, we have ${\left(\frac{2}{K}V\right)}^{\beta +1}={\left({s}^{2}+{\stackrel{\sim }{h}}^{2}+\left|{\stackrel{\sim }{x}}_{1}\right|+\left|{\stackrel{\sim }{x}}_{2}\right|\right)}^{\beta +1}\Rightarrow {\left(4\right)}^{-\beta }{\left(\frac{2}{K}V\right)}^{\beta +1}\le {\left|s\right|}^{2\left(\beta +1\right)}+{\stackrel{\sim }{h}}^{2\left(\beta +1\right)}+{\left|{\stackrel{\sim }{x}}_{1}\right|}^{\beta +1}+{\left|{\stackrel{\sim }{x}}_{2}\right|}^{\beta +1}$, where $\beta +1\ge 1$. Accordingly, we have

$$\dot{V}\le -{\varDelta }_{{m}_{1}}{\left(\frac{2}{K}V\right)}^\frac{1}{2}-{\varDelta }_{{m}_{2}}{\left({\left(4\right)}^{-\beta }{\left(\frac{2}{K}V\right)}^{\beta +1}\right)}^\frac{1}{2}$$

(43)

Let us consider ${\rho }_{1}={\varDelta }_{{m}_{1}}\sqrt{\frac{2}{K}}, {\rho }_{2}=\frac{1}{2}, {\rho }_{3}={\varDelta }_{{m}_{2}}\sqrt{{\left(4\right)}^{-\beta }}{\left(\frac{2}{K}\right)}^{\frac{\beta +1}{2}},$ and ${\rho }_{4}=\frac{\beta +1}{2}$, then we have

$$\dot{V}\left(x\right)\le -{\rho }_{1}{V}^{{\rho }_{2}}-{\rho }_{3}{V}^{{\rho }_{4}}$$

(44)

In accordance with Lemma 3, ${\rho }_{1},{\rho }_{3}$ must be greater than zero, where we have ${\varDelta }_{{m}_{1}}\sqrt{\frac{2}{K}}>0$ and ${\varDelta }_{{m}_{2}}\sqrt{{\left(4\right)}^{-\beta }}{\left(\frac{2}{K}\right)}^{\frac{\beta +1}{2}}>0$. Also, ${\rho }_{2}$ must be $0<{\rho }_{2}<1$, which is true here. Moreover, ${\rho }_{4}$ must be ${\rho }_{4}>1$, where $\frac{\beta +1}{2}>1$. That is why $\beta >1$ is considered in our design. By considering Lemma 3, the stability time satisfies the following inequality as Eq. (45)

$${T}_{1}\le \frac{1}{{\rho }_{1}\left(1-{\rho }_{2}\right)}+\frac{1}{{\rho }_{3}\left({\rho }_{4}-1\right)}$$

(45)

where ${\rho }_{1}={\varDelta }_{{m}_{1}}\sqrt{\frac{2}{K}}, {\rho }_{2}=\frac{1}{2}, {\rho }_{3}={\varDelta }_{{m}_{2}}\sqrt{{\left(4\right)}^{-\beta }}{\left(\frac{2}{K}\right)}^{\frac{\beta +1}{2}},$ and ${\rho }_{4}=\frac{\beta +1}{2}.$ Therefore, by setting abovementioned values and utilizing Lemma 3, it is proved that our control goal (i.e., ensuring $\stackrel{\sim }{h}=0$ and ${\stackrel{\sim }{x}}_{1}=0$ and ${\stackrel{\sim }{x}}_{2}=0$ and $s=0$) is satisfied within a fixed time $t>{T}_{1}$ given in Eqs. (26) and (45). Consequently, the proof of Theorem 1 is completed.

Theorem 2

Consider the defined sliding surface (20). The synchronization errors ${e}_{1}$ and ${e}_{2}$ [described in Eq. (19)] reach zero within a fixed time ${T}_{2}$, once the system (19) reaches sliding surface $s=0$. In other words, the sliding surface $s=0$ is fixed-time stable. ${T}_{2}$ satisfies the given inequality as follows.

$$T\left({x}_{0}\right)\le \frac{1}{{\rho }_{1}\left(1-{\rho }_{2}\right)}+\frac{1}{{\rho }_{3}\left({\rho }_{4}-1\right)}$$

(46)

where ${\rho }_{1}={\alpha }_{1}{\left(2\right)}^{{(\alpha }_{2}+1)/2 },{\rho }_{3}={\alpha }_{3}{\left(2\right)}^{{(\alpha }_{4}+1)/2 }, {\rho }_{2}=\frac{{\alpha }_{2}+1}{2},$ and${\rho }_{4}= \frac{{\alpha }_{4}+1}{2}$. Also, we have${\rho }_{1}, {\rho }_{3}>0$, $0<{\rho }_{2}<1,$ and${\rho }_{4}>1$. Accordingly, we have ${\alpha }_{1},{\alpha }_{3}>0, {\alpha }_{4}>1,$ and$0<{\alpha }_{4}<1$.

Proof

It should be first noted that the sliding surface (20) is defined in this paper according to Lemma 4. Hence, the proof of Theorem 2 is similar to the proof of Lemma 4. Now let us proceed with the proof of Theorem 2 here.

By considering $s=0$, $\stackrel{\sim }{h}=0$, ${\stackrel{\sim }{x}}_{1}=0$, and ${\stackrel{\sim }{x}}_{2}=0$ (which is proved in Theorem 1), and sliding surface given in Eq. (20), for $t>{T}_{1}$ we have

$$\dot{{e}_{1}}=-{\alpha }_{1}{e}_{1}^{{\alpha }_{2}}-{\alpha }_{3}{e}_{1}^{{\alpha }_{4}}$$

(47)

where we have ${\alpha }_{1},{\alpha }_{3}>0, {\alpha }_{4}>1, 0<{\alpha }_{2}<1$. Let us consider ${e}_{2}=\dot{{e}_{1}}$ from Eq. (19), then we obtain

$${e}_{2}=-{\alpha }_{1}{e}_{1}^{{\alpha }_{2}}-{\alpha }_{3}{e}_{1}^{{\alpha }_{4}}$$

(48)

For $t>{T}_{1}$ we have $s=0$. Therefore, we have $\dot{s}=0$. Then, by differentiating Eq. (48) with respect to time, one yields

$${\dot{e}}_{2}=-\dot{A}-\dot{B}$$

(49)

where we have $A={\alpha }_{1}{e}_{1}^{{\alpha }_{2}}$, and $B={\alpha }_{3}{e}_{1}^{{\alpha }_{4}}$. Subsequently, the error dynamics (19), for $t>{T}_{1}$ will be as follows

$$\left\{\begin{array}{l}{\dot{e}}_{1}={e}_{2} \\ {\dot{e}}_{2}=-\dot{A}-\dot{B}\end{array}\right.$$

(50)

Indeed, the fixed-time stability proof of Eq. (50) (i.e., the fixed-time stability proof of $s=0$) is required to be obtained. According to our control goal in this part (which is to satisfy ${e}_{1}=0\,{\mathrm{and}}\,{e}_{2}=0$) and considering Lemma 3 and 4, a candidate Lyapunov function given in Eq. (51) is chosen as follows

$$V=\frac{1}{2}{e}_{1}^{2}$$

(51)

By differentiating of Eq. (51) with respect to time, we have

$$\dot{V}={e}_{1}\dot{{e}_{1}}$$

(52)

By substituting Eq. (47) into Eq. (52), one yields

$$ \begin{aligned} \dot{V} & = e_{1} \left( { - \alpha_{1} e_{1}^{{\alpha_{2} }} - \alpha_{3} e_{1}^{{\alpha_{4} }} } \right) \Rightarrow \dot{V} \\ & = - \alpha_{1} \left| {e_{1} } \right|^{{\alpha_{2} + 1}} - \alpha_{3} \left| {e_{1} } \right|^{{\alpha_{4} + 1}} \\ \end{aligned} $$

(53)

From Eq. (51), one can obtain

$$\left|{e}_{1}\right|={\left(2V\right)}^{1/2}$$

(54)

By substituting Eq. (54) into Eq. (53), there comes

$$\dot{V}=-{\alpha }_{1}{\left(2\right)}^{{(\alpha }_{2}+1)/2 }{V}^{{(\alpha }_{2}+1)/2}-{\alpha }_{3}{\left(2\right)}^{{(\alpha }_{4}+1)/2 }{V}^{{(\alpha }_{4}+1)/2}$$

(55)

Let us consider${\rho }_{1}={\alpha }_{1}{\left(2\right)}^{{(\alpha }_{2}+1)/2 },{\rho }_{3}={\alpha }_{3}{\left(2\right)}^{{(\alpha }_{4}+1)/2 }, {\rho }_{2}=\frac{{\alpha }_{2}+1}{2}, {\rho }_{4}= \frac{{\alpha }_{4}+1}{2}$, we have

$$\dot{V}\left(x\right)\le -{\rho }_{1}{V}^{{\rho }_{2}}-{\rho }_{3}{V}^{{\rho }_{4}}$$

(56)

where according to Lemmas 3 and 4, ${\alpha }_{1},{\alpha }_{2}, {\alpha }_{3},$ and ${\alpha }_{4}$ should be selected such that they fulfill the following given conditions as follows, ${\rho }_{1}, {\rho }_{3}>0$, $0<{\rho }_{2}<1,$ and ${\rho }_{4}>1$. That is why, ${\alpha }_{1},{\alpha }_{3}>0, {\alpha }_{4}>1,$ and $0<{\alpha }_{2}<1$ are considered and given for Eq. (20).

Note that by choosing candidate Lyapunov function in Eq. (51), the convergence of ${e}_{1}$ to zero is proved (i.e., ${e}_{1}=0$) in a fixed time presented in Eqs. (46) and (57)$.$ Considering Eq. (50), we have $\dot{{e}_{1}}={e}_{2}=0$. Consequently, we have ${e}_{1}=0\Rightarrow {\dot{e}}_{1}=0 \Rightarrow {\dot{e}}_{1}={e}_{2}=0\Rightarrow {\dot{e}}_{2}=0$. Hence, synchronization errors, ${e}_{1}$ and ${e}_{2},$ given in Eq. (50) reach zero in a fixed time ${T}_{2}$ which is presented as the following inequality

$${T}_{2}\le \frac{1}{{\rho }_{1}\left(1-{\rho }_{2}\right)}+\frac{1}{{\rho }_{3}\left({\rho }_{4}-1\right)}$$

(57)

It is obvious that for the system given in Eq. (50), the fixed-time stability is ensured at ${T}_{2}$ [given in Eqs. (46) and (57)]. Hence, the sliding surface $s=0$ ensures a desired behavior of the system (i.e., the fixed-time stability of the sliding surface $s=0$ is ensured). Also, all synchronization errors, observer errors, adaptive error, and sliding surface converge to zero for $t>{T}_{1} +{T}_{2}$. Therefore, the proof of Theorem 2 is completed.

Remark 4

By considering Theorems 1 and 2, the fixed-time synchronization for system (15) is fulfilled at $T$. Indeed, the synchronization goal [i.e., ${e}_{1}=0$ and ${e}_{2}=0$ presented in Eq. (19)] simultaneously with other control goals in this study (i.e., $\stackrel{\sim }{h}=0$, ${\stackrel{\sim }{x}}_{1}=0$, ${\stackrel{\sim }{x}}_{2}=0$, and $s=0$) by using the FASMC scheme for the chaotic system given in Eq. (15) is achieved in a fixed time regardless of initial conditions as ${T=T}_{1}+{T}_{2}$, where ${T}_{1}$ and ${T}_{2}$ are presented in Eqs. (26) and (46), respectively.

Remark 5

According to (26) and (46), it can be seen that the upper bound of convergence time is only dependent on the design parameters. Hence, the proposed combined controller/observer allows one to arbitrarily select the convergence rate, which makes it feasible for us to meet strict settling time requirements in practical applications. Also, the designed fixed-time method guarantees a fixed convergence time regardless of the initial conditions.

Remark 6

Sliding surface, control law, state observer, and adaptive law contain some optional design parameters including ${\alpha }_{1},{\alpha }_{3}>0, {\alpha }_{4}=\frac{p}{q}>1, 0<{\alpha }_{2}=\frac{m}{n}<1$, $0<r<1$, $K>1$, $\beta >1$, $\eta >0$, $\delta >0$, and ${c}_{j}>0;$ where $j=\left(1, 2, 3, 4, 5, 6\right)$. Note that $p$, $q$, $n$, and $m$ must be odd numbers to avoid the singularity problem. Additionally, a proper adjustment of these design parameters (considering their required conditions) of the proposed controller/observer is provided in this study for decreasing energy consumption, reducing total fixed settling time, and improving tracking performance.

Note that the proposed control law (25) is designed based on measurability of the first state ${x}_{1}$ (which is assumed to be available) and the unavailability of the second state, ${\widehat{x}}_{2}$, [which is estimated by the designed observer (23)] as well as the unavailability of the upper bound of parametric uncertainties, $\widehat{h}$ [which is estimated by using the adaptive law (21)]. A schematic block diagram of the designed FASMC scheme with a state observer for synchronization of the chaotic support structures for offshore wind turbines in the presence of parametric uncertainties is illustrated in Fig. 2.

Fig. 2

Schematic block diagram of the proposed FASMC scheme with a state observer for synchronization of the chaotic support structures for offshore wind turbines

6 Simulation Results and Discussion

In this section, the designed controller by using the FASMC scheme with a state observer for the chaotic support structure for the offshore wind system [given in Eq. (15)] is simulated. Two systems, master system (17) and slave system (18), are considered, and the numerical simulation is performed to show the validity of the proposed control scheme to fulfill the chaotic synchronization in this study. The numerical simulation is done in Simulink/MATLAB. The design parameters in this simulation are considered as

$$ \begin{aligned} \alpha_{1} & = \alpha_{3} = 1,\quad \alpha_{2} = \frac{99}{{101}},\quad \alpha_{4} = \frac{103}{{101}},\quad c_{1} = c_{2} = 0.0001, \\ c_{3} & = c_{4} = c_{5} = c_{6} = 0.001, \\ \delta & = \eta = 0.001,\quad \beta = \frac{103}{{101}},\quad r = 0.5,\quad K = 2 \\ \end{aligned} $$

(58)

The model of matched parametric uncertainty is considered as $d=0.001\mathrm{cos}\left(0.1t\right)$. The initial conditions for the slave system are considered as ${\left[{x}_{1}\left(0\right), {x}_{2}\left(0\right)\right]}^{{\mathrm{T}}}={\left[-2,-3\right]}^{{\mathrm{T}}}.$ and the initial conditions for the master system are considered as ${\left[{x}_{1m}\left(0\right), {x}_{2m}\left(0\right)\right]}^{{\mathrm{T}}}={\left[\mathrm{2,1}\right]}^{{\mathrm{T}}}$. The initial conditions for the state observer (23) are considered as ${\left[{\widehat{x}}_{1}\left(0\right), {\widehat{x}}_{2}\left(0\right)\right]}^{{\mathrm{T}}}={\left[\mathrm{0,0}\right]}^{{\mathrm{T}}}$. Also, $\alpha =5, \mu =1, F=40,\varOmega =2,$ and ${\omega }_{0}=1$ are considered for the master system (17) and the slave system (18) (where they show chaotic behavior without control input, see Sect. 3).

Figures 3 and 4 represent the response of the controlled system, where the slave system (18) is synchronized to the master system (17); and meanwhile, the estimated states converge to actual states of the slave system. Figure 5 shows the response of the controlled system by using the FASMC scheme with a state observer.

Fig. 3

Response of the controlled system for state ${x}_{1}$ using FASMC scheme with a state observer

Fig. 4

Response of the controlled system for state ${x}_{2}$ using FASMC scheme with a state observer

Fig. 5

Controlled response of the system using FASMC scheme with a state observer

From Figs. 3 and 4, it can be observed that the estimated states ${\widehat{x}}_{1}$ and ${\widehat{x}}_{2}$ reach the actual states ${x}_{1}$ and ${x}_{2}$ of the slave system (18) within $t\approx 1\left(s\right)\, {\mathrm{and}}\,3(s)$, respectively. Afterward, the states of the slave system ${x}_{1}$ and ${x}_{2}$ converge to the states of the master system ${x}_{1}$ and ${x}_{2}$ within $t\approx 4.5\left(s\right)\, \mathrm{and}\, 5(s)$, respectively. Therefore, the synchronization goal is fulfilled. It should be noted that the state observer provides the estimated data before controlling the system which is necessary for the system control. The preciseness of the responses is also obvious in Figs. 3 and 4. It should be noted that in spite of considering the matched parametric uncertainties for the slave system in Eq. (18), the response is very accurate. Consequently, the robustness of the proposed FASMC method is demonstrated in Figs. 3 and 4. From Fig. 5, it can be seen that the precise estimated data by state observer reach the actual data of the system (slave system) and then, the slave system is accurately synchronized to the master system.

Figures 6 and 7 display the synchronization errors ${e}_{1}$ and ${e}_{2}$ [described in Eq. (19)] after applying the proposed controller. Indeed, the errors of synchronization control are shown for the slave system (18) and the master system (17) using FASMC scheme with a state observer.

Fig. 6

Synchronization errors ${e}_{1}$ using FASMC scheme with a state observer

Fig. 7

Synchronization errors ${e}_{2}$ using FASMC scheme with a state observer

From Figs. 6 and 7, it can be observed that the synchronization errors ${e}_{1}$ and ${e}_{2}$ reach zero precisely within $t\approx 4.5$ and $5\left(s\right)$, respectively, after applying the proposed controller. Indeed, Figs. 6 and 7 demonstrate that the proposed FASMC scheme with a state observer fulfills the synchronization goal (i.e., ${e}_{1}=0$ and ${e}_{2}=0$) for the system (19) within a fixed time of $t\approx 4.5$ and $5(s)$.

Figures 8 and 9 show the state observer errors ${\stackrel{\sim }{x}}_{1}$ and ${\stackrel{\sim }{x}}_{2}$ [described in Eq. (24)] after applying the proposed observer (23). Indeed, the estimation errors of the fixed-time state observer, ${\stackrel{\sim }{x}}_{1}$ and ${\stackrel{\sim }{x}}_{2}$, are shown for the slave system (18) using the designed FASMC scheme with a state observer.

Fig. 8

State observer error ${\stackrel{\sim }{x}}_{1}$ after applying the proposed state observer

Fig. 9

State observer error ${\stackrel{\sim }{x}}_{2}$ after applying the proposed state observer

From Figs. 8 and 9, it can be seen that the state observer errors ${\stackrel{\sim }{x}}_{1}$ and ${\stackrel{\sim }{x}}_{2}$ accurately converge to zero within $t\approx 1\left(s\right)$ and $3\left(s\right)$, respectively, after applying the proposed observer (23). Indeed, Figs. 8 and 9 demonstrate that the proposed FASMC scheme with a state observer fulfill the state observer goal [i.e., ${\stackrel{\sim }{x}}_{1}=0$ and ${\stackrel{\sim }{x}}_{2}=0$ given in Eq. (24)] for the slave system (18) within a fixed time of $t\approx 1\left(s\right)$ and $3(s)$.

Figure 10 represents the control action due to the designed controller given in Eq. (25) using the FASMC scheme with a state observer. Figure 11 shows the estimation of the upper bound of the matched parametric uncertainties $\widehat{h}$ described in Eq. (21) using FASMC scheme with a state observer. Figure 12 displays the sliding surface $s$ given in Eq. (20) after applying the proposed controller.

Fig. 10

Control action due to the designed control law $u$ using the FASMC scheme with a state observer

Fig. 11

Estimation of the parametric uncertainty upper bound $\widehat{h}$ using FASMC scheme with a state observer

Fig. 12

Defined sliding surface $s$ (20) after applying the proposed controller

From Fig. 10, it can be observed that the undesirable chattering phenomenon is reduced by choosing proper design parameters in this study [see Eq. (58)]. However, it is recommended to work on eliminating this unwanted phenomenon for future works. From Fig. 11, it can be seen that the estimation of the upper bound of the matched parametric uncertainties $\widehat{h}$ reaches a logical and expected positive constant. Indeed, the adaptive control concept is used to estimate the upper bound of parametric uncertainties h (where $\left|d\right|\le h$). Also, it is obvious from Fig. 11 that $\widehat{h}$ is greater than $\left|d\right|$ (i.e., $\left|d\right|\le h\le \widehat{h}$, where $d$ is considered as $d=0.001\cos(0.1t)$). From Fig. 12, it can be observed that the fixed-time sliding surface $s$, defined in Eq. (20), reaches zero within $t\approx 2(s)$ and remains zero afterward (which is necessary for defining a sliding surface and using SMC scheme).

7 Conclusion

In this paper, the synchronization of two chaotic support structures for offshore wind turbines with considering matched parametric uncertainties is investigated where the only first state of the system is measured directly. A novel integration of fixed-time stability concept, adaptive concept, SMC scheme, and fixed-time state observer is used to introduce a new FASMC scheme with a state observer. Fixed-time control law, sliding surface, state observer, and adaptive law are designed and combined such that the convergence of the system to the sliding surface is ensured which is capable of ensuring a desired behavior of the system. Note that the estimated data of the states and the parametric uncertainties are used in the designed control law. It is proved that the estimated data using the adaptive concept and state observer accurately reach their actual values in a fixed time. The simulation results demonstrate the validity and effectiveness of the proposed FASMC method with a state observer to fulfill the synchronization control in this study. For future works, using a predefined stability concept and optimizing the design parameters are recommended.