Abstract
The proposal of this work is the study of the design of a three-phase distribution transformer and its optimization using techniques from natural differential evolution along with particle swarm optimization algorithms in order to minimize total losses and look at the inrush current. Transformer parameters were calculated analytically using the OCTAVE software, and the results obtained were used to define the geometry of the project and to carry out the following simulations: the first through the finite element method Finite Element Method Magnetics software, which analyzed the magnetic flux densities of the transformer core, and the second through Alternative Transient Program software for analyzing transformer inrush current. The analysis of the highest peak value of the energizing current of the three-phase transformer for the reference design and of the new optimized project is carried out by means of an approximate estimative analytical method applied to single-phase transformers and adapted in this research for use in three-phase transformers via analytical calculation and transient simulation. The verifications made through field results and measurements show that the methodology used for three-phase transformers is very efficient, minimizing losses with a consequent decrease in the energizing current.




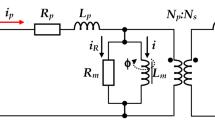
(Reproduced with permission from Malagoli et al. 2016)










Similar content being viewed by others
Abbreviations
- \( A_{\text{c}} \) :
-
Effective limb area (m2)
- \( A_{\text{bc}} \) :
-
Gross limb area (m2)
- \( A_{\text{j}} \) :
-
Yoke area (m2)
- \( {\text{ATT}} \) :
-
Total magnetomotive force (mmf) per meter of core length (Ae/m)
- \( A_{\text{w}} \) :
-
Window area (m2)
- \( B_{\text{j}} \) :
-
Maximum magnetic flux density in the yoke (T)
- \( B_{\text{m}} \) :
-
Maximum magnetic flux density in the limb (T)
- B s :
-
Saturation magnetic flux in the core (T)
- \( C_{1} \) :
-
Acceleration coefficients cognitive component to control the particle distance of the PSO algorithm
- \( C_{2} \) :
-
Acceleration coefficients social component to control the particle distance of the PSO algorithm
- \( d \) :
-
Low voltage coil internal diameter (mm)
- \( D \) :
-
Distance between the centers of two adjacent the limb cores (m)
- \( D_{\text{lc}} \) :
-
Diameter of the circumscribed section of the limb core (m)
- \( E_{\text{t}} \) :
-
Phase voltage per turn of the coil (V/e)
- \( f \) :
-
Frequency (Hz)
- \( F_{1} \) :
-
Magnetomotive force (mmf) in the unsaturated region of magnetization curve (Ae)
- \( F_{2} \) :
-
Magnetomotive force (mmf) in the saturated region of magnetization curve (Ae)
- \( {\text{gbest}} \) :
-
Position of PSO algorithm, or, best vector of all particles
- \( H \) :
-
The total core height (m)
- \( H_{\text{ns}} \) :
-
Magnetic field intensity in the unsaturated region (A/m)
- \( H_{\text{s}} \) :
-
Magnetic field intensity in the saturated region (A/m)
- \( h_{\text{j}} \) :
-
Yoke core height (m)
- \( h_{\text{b}} \) :
-
Coil height (m)
- \( h_{\text{w}} \) :
-
Window height (m)
- \( I_{\text{bt}} \) :
-
Current at the saturation point (A)
- \( {\text{Iph}}_{\text{LV}} \) :
-
Phase nominal current at low voltage winding (A)
- \( I_{0} \) :
-
No-load current (A)
- \( I_{\text{P}} \) :
-
The peak of the transient energization current (A)
- \( I_{p0} \) :
-
Component of active iron losses from the no-load current (A)
- \( I_{q0} \) :
-
Component of magnetization losses from the no-load current (A)
- \( {\text{It}} \) :
-
Number of iterations
- \( J \) :
-
Current density at the coil windings (A/mm2)
- \( J_{\text{LV}} \) :
-
Current density at the low voltage windings (A/mm2)
- \( J_{\text{HV}} \) :
-
Current density at the high voltage windings (A/mm2)
- \( k \) :
-
Factor which depends upon the number of steps in the limb core
- \( k_{\text{e}} \) :
-
Stacking factor
- \( K_{\text{t}} \) :
-
Constant for a transformer
- \( K_{\text{u}} \) :
-
Utilization factor
- \( Ksw \) :
-
Spacing factor of the transformer
- \( Ksw2 \) :
-
Spacing factor of the dry transformer
- \( L_{1} \) :
-
Width of the largest steps in limb core
- \( L_{\text{a}} \) :
-
Inductance in the unsaturated region of magnetization curve (H)
- \( L_{\text{b}} \) :
-
Inductance in the saturated region of magnetization curve (H)
- \( L_{n} \) :
-
Width of index n limb core step (m)
- \( L_{\text{ss}} \) :
-
Saturation reactance (H)
- \( M_{\text{c}} \) :
-
Mass of limb core (kg)
- \( M_{\text{j}} \) :
-
Mass of core yoke (kg)
- \( N_{\text{LV}} \) :
-
Number of turns in low voltage side
- \( {\text{OF}} \) :
-
Objective function
- \( {\text{Pbest}} \) :
-
Best vector of individual particle in the PSO algorithm
- \( P_{\text{ic}} \) :
-
Specific loss in the limb core (W/kg)
- \( P_{\text{ij}} \) :
-
Specific loss in the core yoke (W/kg)
- \( P_{03} \) :
-
No-load loss or core loss (W)
- \( P_{j3} \) :
-
Losses in the windings by Joule effect (W)
- \( P_{\text{t}} \) :
-
Total losses in the transformer (W)
- \( R_{\text{LV}} \) :
-
Resistance of the conductor at the low voltage side (Ω)
- \( R_{\text{HV}} \) :
-
Resistance of the conductor at the high voltage side (Ω)
- \( r_{1} \) :
-
Random value (with uniform probability) between 0 and 1
- \( r_{2} \) :
-
Random value (with uniform probability) between 0 and 1
- \( rel \) :
-
Ratio between the area of the yoke core and the area of effective limb
- \( Rjan \) :
-
Ratio between the height and width of the transformer core window
- \( S \) :
-
Apparent power (kVA)
- \( s_{0} \) :
-
Circumscribed circular section (m2)
- \( t_{1} \) :
-
Time interval for current to reach the saturation point of the magnetization curve (s)
- \( t_{\text{pk}} \) :
-
Maximum peak time of Inrush current (s)
- \( V_{\text{LV}} \) :
-
Line low voltage (V)
- \( V_{\text{a}} \) :
-
Instantaneous voltage of phase a (V)
- \( V_{\text{b}} \) :
-
Instantaneous voltage of phase b (V)
- \( V_{\text{c}} \) :
-
Instantaneous voltage of phase c (V)
- \( {\text{Vph}}_{\text{LV}} \) :
-
Low voltage per phase (V)
- \( V_{\text{ferc}} \) :
-
Iron volume in the limb core (m3)
- \( V_{\text{ferj}} \) :
-
Iron volume in the yoke (m3)
- \( v_{\text{it}} \) :
-
Particle speed it
- \( V_{\text{m}} \) :
-
Maximum supplying voltage (V)
- \( w \) :
-
Inertia coefficient (which is important to define the search space)
- \( W \) :
-
The total core width (m)
- \( w_{\text{a}} \) :
-
Angular speed (rad/s)
- \( W_{\text{c}} \) :
-
Width of limb core (m)
- \( W_{\text{ic}} \) :
-
Limb core-specific no-load loss (W)
- \( W_{\text{ij}} \) :
-
Yoke core-specific no-load loss (W)
- \( W_{\text{w}} \) :
-
Core window width (m)
- \( Y_{\text{r}} \) :
-
Residual flux (Wb)
- \( Y_{\text{s}} \) :
-
Saturation flux (Wb)
- \( \mu_{0} \) :
-
Permeability of air (\( \mu_{0} = 4 \times \pi \times 10^{ - 7} \))
- \( \emptyset_{1} \) :
-
Flux in the unsaturated region (Wb)
- \( \emptyset_{2} \) :
-
Flux in the saturated region (Wb)
References
Amoiralis, E. I., Tsili, M. A., Georgilakis, P. S., Kladas, A. G., & Souflaris, A. T. (2008). A parallel mixed integer programming-finite element method technique for global design optimization of power transformers. IEEE Transactions on Magnetics, 44(6), 1022–1025. https://doi.org/10.1109/TMAG.2007.915119.
Faiz, J., Ebrahimi, B. M., & Noori, T. (2008). Three-and two-dimensional finite-element computation of inrush current and short-circuit electromagnetic forces on windings of a three-phase core-type power transformer. IEEE Transactions on Magnetics, 44(5), 590–597. https://doi.org/10.1109/tmag.2008.917819.
Fitzgerald, A. E., Kingsley, C., Jr, C., & Umans, S. D. (2013). Electric machinery. New York: McGraw-Hill Higher Education.
IEC 60076-11. (2004). Power transformers—Part 11: Dry-type transformers.
Jazebi, S., León, F., & Wu, N. (2015). Enhanced analytical method for the calculation of the maximum inrush currents of single-phase power transformers. IEEE Transactions on Power Delivery, 30(6), 2590–2599. https://doi.org/10.1109/TPWRD.2015.2443560.
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. In Proceedings of the IEEE international conference on neural networks, Vol. 4, pp. 1942–1948. https://doi.org/10.1109/icnn.1995.488968.
León, F., Purushothaman, S., & Qaseer, L. (2014). Leakage inductance design of toroidal transformers by sector winding. IEEE Transactions on Power Electronics, 29(1), 473–480. https://doi.org/10.1109/tpel.2013.2251429.
Malagoli, J. A., Camacho, J. R., & da Luz, M. V. F. (2016). Optimal design variables to minimize the cost of materials the stator of asynchronous machine. Journal of Control, Automation and Electrical Systems, 27(2), 157–168. https://doi.org/10.1007/s40313-016-0227-5.
Malagoli, J. A., Camacho, J. R., da Luz, M. V. F., Ferreira, J. H. I., & Sobrinho, A. M. (2015). Design of three-phase induction machine using differential evolution algorithm. IEEE Latin America Transactions, 13(7), 2202–2208.
Malagoni, J. A., & Os Elementos Finitos no Estudo de Eletromagnetismo Utilizando os Softwares Gmsh/GetDP. (2012). Dissertação de Mestrado. Uberlândia, MG: Universidade Federal de Uberlândia. (in Portuguese).
Rocha, N. C., & Saramago, S. F. P. (2011). Estudo de Algumas Estratégias de Evolução Diferencial, Congresso de Matemática Aplicada e Computacional, I CMAC Sudeste (in Portuguese)
Salustiano, R. (2012). Análise Técnica de Transformadores para Redes de Média Tensão. Dissertação (Mestrado,) Universidade Federal de Itajubá, Itajubá-MG (in Portuguese).
Storn, R., & Price, K. (1995). Differential Evolution: a simple and efficient adaptive scheme for global optimization over continuous spaces”. Berkeley: International Computer Science Institute International.
Ülker, E. D., & Ülker, S. (2017). Enhanced leader particle swarm optimization for microwave matching networks. In IEEE conferences, international conference on computational intelligence and communication networks, pp 20–23.
Upadhyay, K. G. (2008). Design of electrical machines. New Delhi: New Age International Publishers.
Zhang, G., Gao, Q., Wang, M., Liu, Q., Zhong, D., Li, H., et al. (2015). Design of integrated supervisory control system for 110 kV dry-type transformer. In IEEE international conference on electrical utility deregulation and restructuring and power technologies (DRPT), pp. 1517–1521.
Zhang, Z., Pan, Z., Xu, Q., Pan, X., & Wang, Z. (2013). Optimal design of power transformer tank based on an accurate tank mechanical property analysis method. In IEEE international conference on electrical machines and systems (ICEMS), pp. 2229–2232.
Ziestsman, N. L., & Gule, N. (2015). Optimal design methodology of a three-phase rotary transformer for doubly fed induction generator application. In IEEE international electric machines & drives conference (IEMDC), pp. 763–768. https://doi.org/10.1109/iemdc.2015.7409145.
Zirka, S. E., Moroz, Y. I., Arturi, C. M., Chiesa, N., & Hoidalen, H. K. (2012). Topology-correct reversible transformer model. IEEE Transactions on Power Delivery, 27(4), 2037–2045. https://doi.org/10.1109/TPWRD.2012.2205275.
Acknowledgements
Adelício Maximiano Sobrinho thanks Universidade Federal do Tocantins (UFT) for the support and time to do this research, and to CNPq (National Council for Scientific and Technological Development) for the financial support to develop this work. The other authors wish to thank Universidade Federal de Uberlândia (UFU) for the infrastructure and resources to develop this research.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sobrinho, A.M., Camacho, J.R., Malagoli, J.A. et al. Optimization of Losses in a Three-Phase Transformer Design with Inrush Current Analysis. J Control Autom Electr Syst 29, 778–795 (2018). https://doi.org/10.1007/s40313-018-0413-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40313-018-0413-8