1 Introduction

The sparse optimization problem arises naturally from a wide range of practical scenarios such as compressed sensing [1,2,3,4], signal and image processing [5,6,7], pattern recognition [8], and wireless communications [9]. The typical problem of signal recovery via compressed sensing can be formulated as the following sparse optimization problem:

$$\begin{aligned} \min _{x}\left\{ \Vert y-A x\Vert _{2}^{2}: ~ \Vert x\Vert _{0} \leqslant k\right\} , \end{aligned}$$
(1)

where k is a given integer number reflecting the sparsity level of the target signal \(x^*\), \(A \in \mathbb {R}^{m\times n}\) is a measurement matrix with \(m \ll n\), \(\Vert x\Vert _0\) is the so-called \(\ell _0\)-norm counting the nonzeros of the vector x,  and y is the acquired measurements of the signal \(x^*\) to recover. The vector y is usually represented as \( y= Ax^*+\eta , \) where \(\eta \) denotes a noise vector.

Developing effective algorithms for the model (1) is fundamentally important in signal recovery. At the current stage of development, the main algorithms for solving sparse optimization problems can be categorized into several classes: convex optimization, heuristic algorithms, thresholding algorithms, and Bayes methods. The typical convex optimization methods include \(\ell _1\)-minimization [10, 11], reweighted \(\ell _1\)-minimization [12, 13], and dual-density-based reweighted \(\ell _1\)-minimization [4, 14, 15]. The widely used heuristic algorithms include orthogonal matching pursuit (OMP) [16, 17], subspace pursuit (SP) [18], and compressive sampling matching pursuit (CoSaMP) [19, 20]. Depending on thresholding strategies, the thresholding methods can be roughly classified as soft thresholding [21, 22], hard thresholding (e.g., [23,24,25,26,27]), and the so-called optimal thresholding methods [28, 29].

The hard thresholding is the simplest thresholding approach used to generate iterates satisfying the constraint of the problem (1). Throughout the paper, we use \(\mathcal{H}_k (\cdot )\) to denote the hard thresholding operator which retains the largest k magnitudes of a vector and zeroes out the others. The following iterative hard thresholding (IHT) scheme

$$\begin{aligned} x^{p+1}=\mathcal{H}_k \left( x^p +\lambda A^{\top }\left( y-A x^p \right) \right) , \end{aligned}$$

where \(\lambda > 0\) is a stepsize, was first studied in [23, 30]. Incorporating a pursuit step (least-squares step) into IHT yields the hard thresholding pursuit (HTP) [26, 31], and when \( \lambda \) is replaced by an adaptive stepsize similar to the one used in traditional conjugate methods, it leads to the so-called normalized iterative hard thresholding (NIHT) algorithms in [24, 32]. The theoretical performance of these algorithms can be analyzed in terms of the restricted isometry property (RIP) (see, e.g., [3, 23, 30]).

On the other hand, the search direction \( A^{\top } (y-Ax^p) \) of the above-mentioned algorithm is the negative gradient of the objective function of the problem (1). Such a search direction can be replaced by another direction provided that it is a descent direction of the objective function. Thus, an Newton-type direction was studied in [27, 33, 34]. The following iterative method is proposed and referred to as Newton-step-based iterative hard thresholding (NSIHT) in [27]:

$$\begin{aligned} x^{p+1}=\mathcal{H}_k \left( x^p +\lambda \left( A^{\top } A+\epsilon I\right) ^{-1} A^{\top }\left( y-A x^p \right) \right) , \end{aligned}$$
(2)

where \(\epsilon > 0\) is a parameter and \(\lambda > 0\) is the stepsize.

However, as pointed out in [28, 29], the weakness of the hard thresholding operator \(\mathcal{H}_k (\cdot )\) is that when applied to a non-sparse iterate generated by the classic gradient method, it may cause an ascending value of the objective of (1) at the thresholded vector, compared to the objective value at its unthresholded counterpart. As a result, direct use of the hard thresholding operator to a non-sparse or non-compressible vector in the course of an algorithm may lead to significant numerical oscillation and divergence of the algorithm. To overcome such a drawback of hard thresholding operator, Zhao [28] proposed an optimal k-thresholding technique which makes it possible to perform thresholding and objective-value reduction simultaneously. The optimal k-thresholding iterative scheme in [28] can be simply stated as

$$\begin{aligned} x^{p+1}=\mathcal{Z}^{\#}_k \left( x^p +\lambda A^{\top }\left( y-A x^p \right) \right) , \end{aligned}$$

where \(\lambda \) remains a stepsize, and \(\mathcal{Z}^{\#}_k (\cdot )\) is the so-called optimal k-thresholding operator. Given a vector u, the thresholded vector \(\mathcal{Z}^{\#}_k (u) = u\otimes w^*\) (the Hadamard product of two vectors) where the vector \( w^*\) is the optimal solution to the following quadratic 0-1 optimization problem:

$$\begin{aligned} w^* :=\text {arg}\min _{w}\left\{ \Vert y-A(u \otimes w)\Vert _{2}^{2}: ~ {\varvec{e}}^{\top } w=k, ~ w \in \{0,1\}^{n}\right\} , \end{aligned}$$

where \({\varvec{e}} = (1, \cdots , 1)^{\top } \in \mathbb {R}^n \) is the vector of ones, and \(\{0,1\}^{n} \) denotes the set of n-dimensional 0-1 vectors. To avoid solving such a binary optimization problem, an alternative approach is to solve its convex relaxation which, as pointed out in [28, 29], is the tightest convex relaxation of the above problem:

$$\begin{aligned} {\widehat{w}} :=\text {arg}\min _{w}\left\{ \Vert y-A(u \otimes w)\Vert _{2}^{2}: ~ {\varvec{e}}^{\top } w=k, ~ 0 \leqslant w \leqslant {\varvec{e}} \right\} . \end{aligned}$$
(3)

Based on the convex relaxation of the operator \(\mathcal{Z}^{\#}_k (\cdot ) ,\) efficient algorithms called relaxed optimal k-thresholding algorithms (ROT) and its variants have been proposed and investigated in [28, 29]. Simulations demonstrate that this new framework of thresholding methods works efficiently, and it overcomes the drawback of the traditional hard thresholding operator.

Due to the aforementioned weakness of \(\mathcal{H}_k\) which appears in the Newton-type iterative method (2), it makes sense to consider a further improvement of the performance of such a method. The purpose of this paper is to combine the optimal k-thresholding and Newton-type search direction in order to develop an algorithm that may alleviate or eliminate the drawback of hard thresholding operator and hence enhance the numerical performance of the Newton-type method (2). The proposed algorithms are called the Newton-type optimal k-thresholding (NTOT). The convex relaxation versions of this algorithm are also studied in this paper, which are referred to as Newton-type relaxed optimal thresholding (NTROT) algorithms, and its enhanced version with a pursuit step (NTROTP for short). The guaranteed performance and convergence of these algorithms are shown under the RIP assumption as well as suitable conditions imposed on the algorithmic parameters.

The paper is organized as follows. The algorithms are described in Sect. 2. The theoretical performances of the proposed algorithms in noisy settings are shown in Sect. 3. The empirical results are demonstrated in Sect. 4, which indicate that under appropriate choices of the parameter and stepsize the proposed algorithms are efficient for signal reconstruction and their performances are comparable to a few existing methods.

2 Algorithms

Some notations will be used throughout the paper. Let \(\mathbb {R}^{n}\) denote the n-dimensional Euclidean space and \(\mathbb {R}^{m \times n}\) denote the set of \(m \times n\) matrices. For a vector \(x \in \mathbb {R}^{n}\), the \(\ell _2\)-norm is defined as \(\Vert x\Vert _{2}:=\sqrt{\sum _{i}^{n} x_{i}^{2}}.\) We use [N] to denote the set \(\{1, \cdots , n\}\). Given a set \(\varOmega \subseteq [N]\), \(\overline{\varOmega }:=[N] \backslash \varOmega \) denotes the complement set of \(\varOmega \). \(x_{\varOmega }\) denotes the vector obtained from x by retaining the entries of x indexed by \(\varOmega \) and zeroing out the ones indexed by \(\overline{\varOmega }\). \(A^{\top }\) denotes the transpose of the matrix A. Give a vector u, \(\mathcal{L}_k(u)\) denotes the index set of the largest k magnitudes of u. Throughout the paper, a vector x is said to be k-sparse if \(\Vert x\Vert _0 \leqslant k\).

Note that the gradient and Hessian of the function \(f(x) = \frac{1}{2} \Vert y-A x\Vert _{2}^{2}\) are given as

$$\begin{aligned} \nabla f(x)=-A^{\top }(y-A x), \quad \nabla ^{2} f(x)=A^{\top } A . \end{aligned}$$

For the problem (1), the Hessian \(A^{\top } A \) is singular, and thus, the classic Newton’s method cannot be applied to the function f(x) directly. Modifying the matrix by adding \(\epsilon I\) leads to the non-singular matrix \(A^{\top }A+\epsilon I ,\) where \(\epsilon \) is a positive parameter and \(I \in \mathbb {R}^{n \times n}\) is the identity matrix. Then, we immediately obtain the following Newton-type iterative method for the minimization of f(x) : 

$$\begin{aligned} x^{p+1}=x^p+\lambda \left( A^{\top } A+\epsilon I\right) ^{-1} A^{\top }(y-A x^p), \end{aligned}$$

where \( \lambda \) is a stepsize. Different from the approach (2), we utilize the optimal k-thresholding operator instead of the hard thresholding operator to develop a Newton-type iterative algorithm, which is described as Algorithm 1.

figure a

Solving the 0-1 problem (\(\hbox {P}_1\)) is generally expensive, and Zhao [28] suggested solving its tightest convex relaxation, i.e., the problem (3). This results in the Newton-type relaxed optimal k-thresholding algorithm, which is described as Algorithm 2.

figure b

If the step (\(\hbox {P}_2\)) generates a 0-1 solution \(w^p\), i.e., \( w^p\) is exactly a k-sparse vector, then \( u^p \otimes w^p\) is exactly k-sparse, in which case the operator \(\mathcal{H}_k\) in (\(\hbox {P}_3\)) is superfluous. However, as the vector \( w^p\) may not necessarily be k-sparse, \( \mathcal{H} _k\) is used in (\(\hbox {P}_3\)) to truncate the iterate so that it satisfies the constraint of the problem (1). This is quite different from \( \mathcal{H}_k(u^p)\) that directly performs hard thresholding on \(u^p\) which may not be sparse at all. The vector \(w^p\) is either k-sparse or admits a compressible feature in which case performing hard thresholding on the resulting vector \( u^p\otimes w^p\) can avoid significant oscillation of the objective value of (1).

To further stabilize the NTROT, a pursuit step can be performed after solving the optimization problem (\(\hbox {P}_2\)). This leads to the algorithm called NTROTP, which is the main algorithm concerned in this paper.

figure c

The step (\(\hbox {P}_5\)) is a pursuit step at which a least-squares problem is solved on the support of the largest k magnitudes of the vector \( u^p \otimes w^p. \) In the next section, we establish sufficient conditions for the guaranteed performance and convergence of the algorithms NTOT, NTROT, and NTROTP.

3 Theoretical Analysis

Before going ahead, let us first recall the definition of restricted isometry constant (RIC).

Definition 1

[11] The q-th order RIC \(\delta _q\) of a matrix \(A \in \mathbb {R}^{m \times n}\) is the smallest number \(\delta _q \geqslant 0 \) such that

$$\begin{aligned} \left( 1-\delta _{q}\right) \Vert x\Vert _{2}^{2} \leqslant \Vert A x\Vert _{2}^{2} \leqslant \left( 1+\delta _{q}\right) \Vert x\Vert _{2}^{2} \end{aligned}$$

for all q-sparse vectors x, where q is an integer number.

If \( \delta _q<1\), we say that the matrix A satisfies the q-th order restricted isometry property (RIP). It is well known that the random matrices including Bernoulli, Gaussian and more general sub-Gaussian matrices may satisfy the RIP of a certain order with an overwhelming probability [1, 3, 11].

3.1 Analysis of NTOT in Noisy Scenarios

The following two lemmas are very helpful to show the main result in this section. The first one was taken from [27], and the second one can be found in [28].

Lemma 1

[27] Let \( A\in \mathbb {R}^{m\times n}\) with \( m\ll n\) be a measurement matrix. Given a vector \(u \in \mathbb {R}^{n}\) and an index set \(\varOmega \subset {[N]}\), if \((\epsilon , \lambda )\) is chosen such that \(\epsilon > \sigma _1^2\) and \(\lambda \leqslant \epsilon + \sigma _m^2\), where \(\sigma _1,\sigma _m\) are the largest and smallest singular values of the matrix A,  respectively, then one has

$$\begin{aligned} \begin{aligned}&\left\| \left[ (I - \lambda (A^{\top }A+\epsilon I)^{-1} A^{\top }A ) u \right] _\varOmega \right\| _2 \leqslant ( \delta _t + \sigma _1^2-\frac{\lambda \sigma _1^2}{\epsilon +\sigma _1^2} ) \Vert u\Vert _2 \end{aligned} \end{aligned}$$

provided that \(|\varOmega \cup {\text {supp}}(u)| \leqslant t\), where t is a certain integer number.

Lemma 2

[28] Let \(y=A \hat{x} + \eta \) be the measurements of the k-sparse vector \(\hat{x} \in \mathbb {R}^n\), and let \(u \in \mathbb {R}^n\) be an arbitrary vector. Let \(\mathcal{Z}_k^{\#}(u) \) be the optimal k-thresholding vector of u. Then, for any k-sparse binary vector \(\hat{w} \in \{0,1\}^n\) satisfying \({\text {supp}}(\hat{x}) \subseteq {\text {supp}}(\hat{w})\), one has

$$\begin{aligned} {\Vert }\mathcal{Z}_k^{\#}(u) - \hat{x}{\Vert }_2 \leqslant \sqrt{\frac{1+\delta _k}{1-\delta _{2k}}} {\Vert }(\hat{x} - u) \otimes \hat{w}{\Vert }_2 + \frac{2}{\sqrt{1-\delta _{2k}}} \Vert \eta \Vert _2. \end{aligned}$$
(4)

The bound (4) follows directly from the proof of Theorem 4.3 in [28]. In fact, the inequality (4) is obtained by combining the inequality (4.5) and the first inequality of (4.7) in [28].

We now state and show the sufficient condition for the guaranteed performance of NTOT in noisy settings.

Theorem 1

Let \(y=Ax+\eta \) be the measurements of the signal \(x \in \mathbb {R}^n\) with measurement error \( \eta .\) Let \(S=\mathcal{L}_k(x)\) and \(\sigma _1\) and \(\sigma _m\) be, respectively, the largest and smallest singular values of the matrix \(A \in \mathbb {R}^{m \times n}\). Suppose that the restricted isometry constant of A satisfies

$$\begin{aligned} \delta _{2k} < 0.534~9, \end{aligned}$$

and that \(\epsilon \) is a given parameter satisfying

$$\begin{aligned} \epsilon > \max \left\{ \sigma _1^2, \left( \frac{\sigma _1^2 - \sigma _m^2}{\sqrt{\frac{1-\delta _{2k}}{1+\delta _k}} - \delta _{2k}} - 1 \right) \sigma _1^2 \right\} . \end{aligned}$$
(5)

If the parameter \(\lambda \) in NTOT is chosen such that

$$\begin{aligned} \epsilon + \sigma _1^2 + \left( \delta _{2k} - \sqrt{\frac{1-\delta _{2k}}{1+\delta _k}} \right) \frac{\epsilon + \sigma _1^2}{\sigma _1^2} ~ < ~ \lambda ~ \leqslant ~ \epsilon + \sigma _m^2, \end{aligned}$$
(6)

then the sequence \(\{x^p\} \) generated by the NTOT satisfies that

$$\begin{aligned} \left\| x^{p+1}-x_S\right\| _{2} \leqslant \rho \left\| x^{p}-x_{S}\right\| _{2}+\tau \left\| Ax_{\overline{S}} + \eta \right\| _{2}, \end{aligned}$$
(7)

where

$$\begin{aligned} \rho = \sqrt{\frac{1+\delta _{k}}{1-\delta _{2 k}}}\left( \delta _{2 k}+\sigma _{1}^{2}-\frac{\lambda \sigma _{1}^{2}}{\epsilon +\sigma _{1}^{2}}\right) \end{aligned}$$

and

$$\begin{aligned} \tau = \frac{1}{\sqrt{1-\delta _{2 k}}} \left( \frac{\lambda \sigma _{1}^{2} \sqrt{1+\delta _k}}{\epsilon +\sigma _{1}^{2}} + 2 \right) . \end{aligned}$$

In particular, when x is k-sparse and \(\eta =0\), then the sequence \(\{x^{p}\}\) converges to x.

Proof

Let \(\hat{w}\) be a k-sparse binary vector such that \(S \subseteq {\text {supp}}(\hat{w})\), which implies \(x_S = x_S \otimes \hat{w}\). From the structure of NTOT, \(\mathcal{Z}_k^{\#}(u^p) = u^p\otimes \overline{w}^p \) where \(\overline{w}^p\) is the optimal solution to the problem (\(\hbox {P}_1\)). Note that \(y= Ax + \eta = Ax_S + \eta '\) where \(\eta ' = Ax_{\overline{S}} + \eta \). By Lemma 2, we immediately have

$$\begin{aligned} {\Vert }u^p \otimes \overline{w}^p - x_S{\Vert }_2&\leqslant \sqrt{\frac{1+\delta _k}{1-\delta _{2k}}} {\Vert }(u^p-x_S) \otimes \hat{w}{\Vert }_2 + \frac{2}{\sqrt{1-\delta _{2 k}}} \Vert \eta ' \Vert _2. \end{aligned}$$
(8)

By the definition of \( u^p\) in NTOT, we see that

$$\begin{aligned} u^{p}-x_{S}&=x^{p}-x_{S}+\lambda \left( A^{\top } A+\epsilon I\right) ^{-1} A^{\top }\left( y-A x^{p}\right) \nonumber \\&=\left( I-\lambda \left( A^{\top } A+\epsilon I\right) ^{-1} A^{\top } A\right) \left( x^{p}-x_{S}\right) +\lambda \left( A^{\top } A+\epsilon I\right) ^{-1} A^{\top } \eta ' . \end{aligned}$$
(9)

By the singular value decomposition of A, for any vector \(u \in \mathbb {R}^n\), it is very easy to verify that

$$\begin{aligned} \left\| \left( A^{\top } A+\epsilon I\right) ^{-1} A^{\top } u\right\| _{2} \leqslant \frac{\sigma _{1}}{\epsilon +\sigma _{1}^{2}}\Vert u\Vert _{2} . \end{aligned}$$
(10)

From the choices of \((\epsilon , \lambda )\), we see that \(\lambda \leqslant \epsilon +\sigma _m^2\) and \( \epsilon > \sigma _1^2\). Thus, it follows from (9) and (10) that

$$\begin{aligned} {\Vert }(u^p - x_S) \otimes \hat{w}{\Vert }_2 =&{\Vert }(u^p - x_S)_{{\text {supp}}(\hat{w})}{\Vert }_2 \nonumber \\ \leqslant&{\Vert } \left[ (I-\lambda (A^{\top }A + \epsilon I)^{-1}A^{\top }A) (x^p - x_S) \right] _{{\text {supp}} (\hat{w})} {\Vert }_2 \nonumber \\&+ \left\| \left( \lambda \left( A^{\top } A+\epsilon I\right) ^{-1} A^{\top } \eta ' \right) _{{\text {supp}}(\hat{w})}\right\| _{2} \nonumber \\ \leqslant&\left( \delta _{2k} + \sigma _1^2-\frac{\lambda \sigma _1^2}{\epsilon +\sigma _1^2} \right) {\Vert }x_S - x^p{\Vert }_2 + \frac{\lambda \sigma _{1}}{\epsilon +\sigma _{1}^{2}} \left\| \eta '\right\| _{2} , \end{aligned}$$
(11)

where the first term of the right-hand side follows from Lemma 1 with the fact \(|{\text {supp}}(\hat{w}) \cup {\text {supp}}(x^p-x_S)| \leqslant |{\text {supp}}(\hat{w}) \cup S \cup S^p| \leqslant 2k\) since \(S \subseteq {\text {supp}}(\hat{w})\). Combining (8) and (11) leads to

$$\begin{aligned} \left\| x^{p+1}-x_S\right\| _{2}={\Vert }u^p \otimes \overline{w}^p - x_S{\Vert }_2 \leqslant \rho \left\| x^{p}-x_S\right\| _{2} + \tau \left\| \eta '\right\| _{2} , \end{aligned}$$
(12)

where

$$\begin{aligned} \rho = \sqrt{\frac{1+\delta _{k}}{1-\delta _{2k}}} (\delta _{2k} + \sigma _1^2-\frac{\lambda \sigma _1^2}{\epsilon + \sigma _1^2}) , ~~ \tau = \frac{1}{\sqrt{1-\delta _{2 k}}}\left( \frac{\lambda \sigma _{1} \sqrt{1+\delta _{k}}}{\epsilon +\sigma _{1}^{2}}+2\right) . \end{aligned}$$

From (12), to guarantee the recovery of \(x_S\) by the NTOT, it is sufficient to ensure that \( \rho <1,\) which is equivalent to

$$\begin{aligned} \lambda > \epsilon + \sigma _1^2 + \left( \delta _{2k} - \sqrt{\frac{1-\delta _{2k}}{1+\delta _{k}}} \right) \frac{\epsilon + \sigma _1^2}{\sigma _1^2}. \end{aligned}$$

This is guaranteed under the choice of \(\lambda \) given in (6). The remaining proof is to show that the range in (6) exists. In fact, if the following two conditions are satisfied, the existence of such a range is guaranteed:

$$\begin{aligned} \delta _{2k} - \sqrt{\frac{1-\delta _{2k}}{1+\delta _{k}}} < 0 \end{aligned}$$
(13)

and

$$\begin{aligned} \epsilon + \sigma _1^2 + \left( \delta _{2k} - \sqrt{\frac{1-\delta _{2k}}{1+\delta _k}} \right) \frac{\epsilon + \sigma _1^2}{\sigma _1^2} < \epsilon + \sigma _m^2. \end{aligned}$$
(14)

By noting that \(\delta _k \leqslant \delta _{2k}\), it is straightforward to verify that the inequality (13) is guaranteed under the condition \(\delta _{2k} < 0.534\,9\). The inequality (14) can be written as

$$\begin{aligned} \epsilon > \left( \frac{\sigma _1^2 - \sigma _m^2}{\sqrt{\frac{1-\delta _{2k}}{1+\delta _k}} - \delta _{2k}} - 1 \right) \sigma _1^2 , \end{aligned}$$

which is also guaranteed under the choice of \( \epsilon \) given in (5). Thus, the desired result follows. In particular, if \(\eta =0\) and x is k-sparse, the relation (7) is reduced to

$$\begin{aligned} \left\| x^{p+1}-x\right\| _{2} \leqslant \rho \left\| x^{p}-x\right\| _{2} \leqslant \rho ^p \left\| x^0-x\right\| _{2}, \end{aligned}$$

which implies that \(\{x^{p}\}\) converges to x as \(p \rightarrow \infty \).

3.2 Analysis of NTROT in Noisy Scenarios

Still we denote by \(S=\mathcal{L}_k(x)\) the index set of the largest k magnitudes of x. The measurements are given as \( y= Ax+ \eta \), where \( \eta \in \mathbb {R}^m \) is a noise vector. We first recall some useful technical results which have been shown in [28, 29]. Lemma 3 is a property of the hard thresholding operator \( \mathcal{H}_k,\) whereas the second one is property of the solution of the optimization problem (\(\hbox {P}_2\)) in NTROT and (\(\hbox {P}_4\)) in NTROTP.

Lemma 3

[28] Let \(z \in \mathbb {R}^{n}\) be a given vector and \(v \in \mathbb {R}^{n}\) be a k-sparse vector with \(\varPhi = {\text {supp}}(v)\). Denote \(\varOmega = \mathcal{L}_{k} (z)\). Then, one has

$$\begin{aligned} {\Vert }v-\mathcal{H}_{k} (z){\Vert }_{2} \leqslant {\Vert }(v-z)_{\varOmega \cup \varPhi }{\Vert }_{2} + {\Vert }(v-z)_{\varOmega \backslash \varPhi }{\Vert }_{2}. \end{aligned}$$

Lemma 4

[29] Let \(\varLambda \subseteq \{ 1,\cdots ,n \}\) be any given index set, and let \(w \in \mathbb {R}^n\) be any given vector satisfying \({\varvec{e}}^{\top } w=k\) and \(0 \leqslant w \leqslant {\varvec{e}}\). Decompose the vector \( w_{\varLambda }\) as

$$\begin{aligned} w_{\varLambda } = w_{\varLambda _1} + \cdots + w_{\varLambda _{{q}-1}} + w_{\varLambda _{{q}}}, \end{aligned}$$

where q is a nonnegative integer number such that \(|\varLambda |=({q}-1) k+\alpha \) where \(0 \leqslant \alpha <k\), \(w_{\varLambda _1}\) is the first k largest magnitudes in \(\{w_i : i \in \varLambda \}\), \(w_{\varLambda _2}\) is the second k largest magnitudes in \(\{w_i : i \in \varLambda \}\), and so on. Then one has

$$\begin{aligned} \left\| w_{\varLambda _{1}}\right\| _{\infty }+\cdots +\left\| w_{\varLambda _{q-1}}\right\| _{\infty }+\left\| w_{\varLambda _{q}}\right\| _{\infty } \leqslant 2 . \end{aligned}$$

The next result is actually implied from the proof of Theorem 4.8 in [28]. Item (i) in the lemma below is immediately obtained by combining two inequalities in the proof of Theorem 4.8 in [28]. So we only outline a simple proof of the Item (ii) for this lemma.

Lemma 5

Let \(y=A x+\eta \) be the measurements of x and \(\hat{w} \in \{0,1\}^n\) be a k-sparse binary vector such that \(S = \mathcal{L}_k (x) \subseteq {\text {supp}}(\hat{w})\). Let \(S^{p+1} = {\text {supp}}(x^{p+1})\), \(u^p\) and \(w^p\) be defined in NTROT. One has

$$\begin{aligned} \begin{aligned}&\begin{aligned} \mathrm{(i)} ~ \left\| \left( x_S-u^{p} \otimes w^{p}\right) _{S \cup S^{p+1}}\right\| _{2} \leqslant&\sqrt{\frac{1+\delta _{k}}{1-\delta _{2 k}}}\left\| \left( x_S-u^{p}\right) \otimes \hat{w}\right\| _{2} +\frac{2}{\sqrt{1-\delta _{2 k}}}\left\| \eta '\right\| _{2} \\&+ \frac{1}{\sqrt{1-\delta _{2 k}}} \left\| A\left[ \left( x_S-u^{p} \otimes w^{p}\right) _{\overline{S \cup S^{p+1}}}\right] \right\| _{2} , \end{aligned} \\&\begin{aligned} \mathrm{(ii)} ~\left\| A\left[ \left( x_S-u^{p} \otimes w^{p}\right) _{\overline{S \cup S^{p+1}}}\right] \right\| _{2} \leqslant 2 \sqrt{1+\delta _k} \Vert \mathcal{H}_k (u^p-x_S) \Vert _2. \end{aligned} \end{aligned} \end{aligned}$$

Proof

By setting \(\varLambda := \overline{S \cup S^{p+1}}\) and \(w := w^p\) in Lemma 4, decompose the vector \((w^p)_{\overline{S \cup S^{p+1}}}\) into

$$\begin{aligned} (w^p)_{\overline{S \cup S^{p+1}}} = (w^p)_{\varLambda _1} + \cdots +(w^p)_{\varLambda _{q-1}} + (w^p)_{\varLambda _{q}} \end{aligned}$$

in the way described in Lemma 4. Since \((x_S)_{\overline{S\cup S^{p+1}}} = 0\), we have

$$\begin{aligned} \left( x_{S}-u^{p} \otimes w^{p}\right) _{\overline{S \cup S^{p+1}}}&= \left( (x_{S}-u^{p}) \otimes w^{p}\right) _{\overline{S \cup S^{p+1}}} \\&= \left( (x_{S}-u^{p}) \otimes w^{p}\right) _{\varLambda _1} + \cdots + \left( (x_{S}-u^{p}) \otimes w^{p}\right) _{\varLambda _{q}} \\&= v^{(1)}+v^{(2)}+\cdots +v^{(q)}, \end{aligned}$$

where \(v^{(i)} = \left( (x_{S}-u^{p}) \otimes w^{p}\right) _{\varLambda _i}\), \(i = 1, \cdots , q\). Thus,

$$\begin{aligned} \left\| A\left[ \left( x_{S}-u^{p} \otimes w^{p}\right) _{\overline{S \cup S^{p+1}}}\right] \right\| _{2} \leqslant \sum _{i=1}^{q}\left\| A v^{(i)}\right\| _{2} \leqslant \sqrt{1+\delta _{k}} \sum _{i=1}^{q}\left\| v^{(i)}\right\| _{2}, \end{aligned}$$

where the last inequality follows from the definition of \(\delta _k\) and the fact \(|{\text {supp}}(v^{(i)})| \leqslant k\). We also have that

$$\begin{aligned} \sum _{i=1}^{q} \left\| v^{(i)}\right\| _{2} =&\sum _{i=1}^{q} \left\| \left[ \left( u^{p}-x_S\right) \otimes w^{p}\right] _{\varLambda _{i}}\right\| _{2} \\ \leqslant&\sum _{i=1}^{q} \left\| (w^p)_{\varLambda _i}\right\| _{\infty } {\Vert }(u^p-x_S)_{\varLambda _i}{\Vert }_2 \\ \leqslant&2 \left\| \mathcal {H}_{k}\left( u^{p}-x_{S}\right) \right\| _{2}, \end{aligned}$$

where the last inequality follows from the fact \({\Vert }(u^p-x_S)_{\varLambda _i}{\Vert }_2 \leqslant \left\| \mathcal {H}_{k} \left( u^{p}-x_{S}\right) \right\| _{2}\) and Lemma 4 which claims that \(\sum _{i=1}^{q} \left\| (w^p)_{\varLambda _i}\right\| _{\infty } < 2\). Combining the above two inequalities yields

$$\begin{aligned} \left\| A\left[ \left( x_{S}-u^{p} \otimes w^{p}\right) _{\overline{S \cup S^{p+1}}}\right] \right\| _{2} \leqslant 2 \sqrt{1+\delta _{k}}\left\| \mathcal {H}_{k}\left( u^{p}-x_{S}\right) \right\| _{2} , \end{aligned}$$

which is exactly the relation given in Item (ii) of the lemma.

The main result in this section is stated as follows.

Theorem 2

Let \(y=Ax+\eta \) be the measurements of \(x \in \mathbb {R}^n\) with measurement error \( \eta .\) Let \(S=\mathcal{L}_k(x)\), and let \(\sigma _1\) and \(\sigma _m\) denote, respectively, the largest and smallest singular values of the matrix \(A \in \mathbb {R}^{m \times n}\). Suppose that the restricted isometry constant of A satisfies that

$$\begin{aligned} \delta _{3k} < 0.211~9 . \end{aligned}$$

Let \(\epsilon \) be a given parameter satisfying

$$\begin{aligned} \epsilon > \max \left\{ \sigma _1^2 , \left( \frac{\sigma _{1}^{2}-\sigma _{m}^{2}}{\frac{1}{3 \sqrt{\frac{1+\delta _{3 k}}{1-\delta _{3 k}}}+1}-\delta _{3 k}}-1\right) \sigma _{1}^{2} \right\} . \end{aligned}$$
(15)

If the parameter \(\lambda \) in NTROT satisfies

$$\begin{aligned} \epsilon +\sigma _{1}^{2}+\left( \delta _{3 k}-\frac{1}{3 \sqrt{\frac{1+\delta _{3 k}}{1-\delta _{3 k}}+1}}\right) \frac{\epsilon +\sigma _{1}^{2}}{\sigma _{1}^{2}} ~ < ~ \lambda ~ \leqslant ~ \epsilon +\sigma _{m}^{2}, \end{aligned}$$
(16)

then the sequence \(\{x^p\} \) generated by the NTROT satisfies that

$$\begin{aligned} {\Vert }x^{p+1} - x_{S}{\Vert }_{2} \leqslant \rho \left\| x^{p}-x_{S}\right\| _{2}+\tau \left\| A x_{\overline{S}}+\eta \right\| _{2}, \end{aligned}$$
(17)

where

$$\begin{aligned} \rho = \sqrt{\frac{1+\delta _{k}}{1-\delta _{2 k}}}\left( \delta _{2 k}+2 \delta _{3 k}+3 \sigma _{1}^{2}-3 \frac{\lambda \sigma _{1}^{2}}{\epsilon +\sigma _{1}^{2}}\right) +\delta _{3 k}+\sigma _{1}^{2}-\frac{\lambda \sigma _{1}^{2}}{\epsilon +\sigma _{1}^{2}} \end{aligned}$$
(18)

and

$$\begin{aligned} \tau = \frac{1}{\sqrt{1-\delta _{2 k}}}\left( \frac{3 \lambda \sigma _{1} \sqrt{1+\delta _{k}}}{\epsilon +\sigma _{1}^{2}}+2\right) +\frac{\lambda \sigma _{1}}{\epsilon +\sigma _{1}^{2}}. \end{aligned}$$
(19)

In particular, when x is k-sparse and \(\eta =0\), then the sequence \(\{x^{p}\}\) converges to x.

Proof

Let \( S, \sigma _1 , \sigma _m \) be defined as in the theorem. Note that \(y: = Ax+\eta = Ax_{S} + \eta '\) where \(\eta ' = Ax_{\overline{S}} + \eta . \) Denote by \(S^{p+1} = {\text {supp}}(x^{p+1})\). Applying Lemma 3, we immediately have

$$\begin{aligned} {\Vert }x_{S}-x^{p+1}{\Vert }_2&={\Vert }x_{S}- \mathcal{H}_k (u^p \otimes w^p) {\Vert }_2 \nonumber \\&\leqslant {\Vert }(u^p \otimes w^p - x_{S})_{S^{p+1} \cup S}{\Vert }_2 + {\Vert }(u^p \otimes w^p - x_{S})_{S^{p+1} \backslash S}{\Vert }_2 . \end{aligned}$$
(20)

In what follows, we bound each of the terms on the right-hand side of the above inequality. By the definition of \( u^p\) in NTROT, we have

$$\begin{aligned} u^p-x_{S} = \left( I-\lambda \left( A^{\top } A+\epsilon I\right) ^{-1} A^{\top } A\right) \left( x^{p}-x_S\right) + \lambda (A^{\top }A + \epsilon I)^{-1} A^{\top } \eta '. \end{aligned}$$

Noting that \((x_{S})_{{S^{p+1} \backslash S}} = (x_{S} \otimes w^{p})_{{S^{p+1} \backslash S}} = 0\), we have

$$\begin{aligned}&\qquad \quad {\Vert }(u^p \otimes w^p - x_{S})_{S^{p+1} \backslash S}{\Vert }_2 \nonumber \\&\quad = {\Vert }((u^p-x_{S}) \otimes w^p)_{S^{p+1} \backslash S}{\Vert }_2 \nonumber \\&\quad \leqslant {\Vert }(u^p-x_{S})_{S^{p+1} \backslash S}{\Vert }_2 ~~~~~~~~~~ (\text {since} ~ 0 \leqslant w^p \leqslant {\varvec{e}}) \nonumber \\&\quad = \left\| \left[ \left( I-\lambda \left( A^{\top } A+\epsilon I\right) ^{-1} A^{\top } A\right) \left( x^{p}-x_S\right) + \lambda (A^{\top }A + \epsilon I)^{-1} A^{\top } \eta ' \right] _{S^{p+1} \backslash S} \right\| _{2} \nonumber \\&\quad \leqslant \left\| \left[ \left( I-\lambda \left( A^{\top } A+\epsilon I\right) ^{-1} A^{\top } A\right) \left( x^{p}-x_S\right) \right] _{S^{p+1} \backslash S} \right\| _{2} \nonumber \\&\qquad + \lambda \left\| \left[ (A^{\top }A + \epsilon I)^{-1} A^{\top } \eta ' \right] _{S^{p+1} \backslash S} \right\| _{2} \nonumber \\&\quad \leqslant \left( \delta _{3k} + \sigma _{1}^{2} - \frac{\lambda \sigma _1^2}{\epsilon +\sigma _1^2} \right) {\Vert }x^{p} - x_{S} {\Vert }_{2}+ \frac{\lambda \sigma _1}{\epsilon + \sigma _1^2} {\Vert }\eta '{\Vert }_{2}, \end{aligned}$$
(21)

where the last inequality follows from Lemma 1 (with the fact \( |{\text {supp}}(x^p-x_S) \cup (S^{p+1}\backslash S)| \leqslant 3k\)) and (10). We now provide an upper bound for the first term of the right-hand side of (20). Let \(\hat{w}\) be a k-sparse binary vector satisfying \(S \subseteq {\text {supp}}(\hat{w})\). By Lemma 5, we have

$$\begin{aligned} \left\| \left( x_{S}-u^{p} \otimes w^{p}\right) _{S \cup S^{p+1}}\right\| _{2} \leqslant&\sqrt{\frac{1+\delta _{k}}{1-\delta _{2 k}}}\left\| \left( x_{S}-u^{p}\right) \otimes \hat{w}\right\| _{2} +\frac{2}{\sqrt{1-\delta _{2 k}}}\left\| \eta '\right\| _{2} \nonumber \\&+ \frac{1}{\sqrt{1-\delta _{2 k}}} \left\| A\left[ \left( x_{S}-u^{p} \otimes w^{p}\right) _{\overline{S \cup S^{p+1}}}\right] \right\| _{2} \end{aligned}$$
(22)

and

$$\begin{aligned} \left\| A\left[ \left( x_{S}-u^{p} \otimes w^{p}\right) _{\overline{S \cup S^{p+1}}}\right] \right\| _{2} \leqslant 2 \sqrt{1+\delta _k} \Vert \mathcal{H}_k (u^p-x_S) \Vert _2 . \end{aligned}$$
(23)

Applying Lemma 1 (with \(\epsilon > \sigma _1^2\), \(\lambda \leqslant \epsilon +\sigma _m^2\) and \(|{\text {supp}}(x^p - x_S) \cup {\text {supp}}(\hat{w})| \leqslant 2k\)) and (10), we have

$$\begin{aligned}&\qquad {\Vert }(x_S - u^p) \otimes \hat{w}{\Vert }_2 \nonumber \\&\quad \leqslant {\Vert } \left[ (I-\lambda (A^{\top }A + \epsilon I)^{-1}A^{\top }A) (x^p - x_S) \right] \otimes \hat{w} {\Vert }_2 + {\Vert }(\lambda (A^{\top }A + \epsilon I)^{-1} A^{\top } \eta ') \otimes \hat{w}{\Vert }_2 \nonumber \\&\quad \leqslant \left( \delta _{2k} + \sigma _1^2-\frac{\lambda \sigma _1^2}{\epsilon +\sigma _1^2} \right) {\Vert }x_S - x^p{\Vert }_2 + \frac{\lambda \sigma _1}{\epsilon +\sigma _1^2} {\Vert }\eta '{\Vert }_2. \end{aligned}$$
(24)

Denote by \(\varPhi = \mathcal{L}_k (x_{S} - u^{p})\). As \(|{\text {supp}}(x^p-x_S) \cup \varPhi | \leqslant 3k\), by a proof similar to (24), we also have

$$\begin{aligned} {\Vert }\mathcal{H}_k (x_{S} - u^{p}){\Vert }_2 =&{\Vert }(x_{S} - u^{p})_{\varPhi }{\Vert }_2 \nonumber \\ \leqslant&\left( \delta _{3 k}+\sigma _{1}^{2}-\frac{\lambda \sigma _{1}^{2}}{\epsilon +\sigma _{1}^{2}}\right) \left\| x^{p}-x_{S}\right\| _{2} + \frac{\lambda \sigma _{1}}{\epsilon +\sigma _{1}^{2}} {\Vert }\eta '{\Vert }_2 . \end{aligned}$$
(25)

Combining (22)–(25), we have

$$\begin{aligned} \left\| \left( x_{S}-u^{p} \otimes w^{p}\right) _{S \cup S^{p+1}}\right\| _{2} \leqslant \rho ' \left\| x_{S}-x^{p}\right\| _{2} + \tau ' \left\| \eta ^{\prime }\right\| _{2}, \end{aligned}$$
(26)

where

$$\begin{aligned} \rho ' {:}{=}\sqrt{\frac{1+\delta _{k}}{1-\delta _{2 k}}}\left( \delta _{2 k}+2 \delta _{3 k}+3 \sigma _{1}^{2}-\frac{3\lambda \sigma _{1}^{2}}{\epsilon +\sigma _{1}^{2}}\right) \end{aligned}$$

and

$$\begin{aligned} \tau ' = \frac{1}{\sqrt{1-\delta _{2 k}}}\left( \frac{3 \lambda \sigma _{1} \sqrt{1+\delta _{k}}}{\epsilon +\sigma _{1}^{2}}+2\right) . \end{aligned}$$

Substituting (26) and (21) into (20) yields (17) with constants \(\rho \) and \(\tau \) given in (18) and (19), respectively. Due to the fact \(\delta _k \leqslant \delta _{2k} \leqslant \delta _{3k}\), we see from (18) that

$$\begin{aligned} \rho \leqslant \left( 3\sqrt{\frac{1+\delta _{3k}}{1-\delta _{3k}}} + 1 \right) \left( \delta _{3 k}+\sigma _{1}^{2}-\frac{\lambda \sigma _{1}^{2}}{\epsilon +\sigma _{1}^{2}} \right) . \end{aligned}$$

Thus, to ensure \(\rho < 1\), it is sufficient to require that

$$\begin{aligned} \left( 3\sqrt{\frac{1+\delta _{3k}}{1-\delta _{3k}}} + 1 \right) \left( \delta _{3 k}+\sigma _{1}^{2}-\frac{\lambda \sigma _{1}^{2}}{\epsilon +\sigma _{1}^{2}} \right) < 1, \end{aligned}$$

which can be written as

$$\begin{aligned} \lambda > \epsilon + \sigma _{1}^{2} + \left( \delta _{3k} - \frac{1}{3\sqrt{\frac{1+\delta _{3k}}{1-\delta _{3k}}}+1} \right) \frac{\epsilon + \sigma _{1}^{2}}{\sigma _{1}^{2}} . \end{aligned}$$

This together with \(\lambda \leqslant \epsilon + \sigma _m^2\) implies that if the range of \(\lambda \) is given as (16), then it guarantees that \(\rho <1\). To ensure the existence of the interval in (16), it is sufficient to choose \(\epsilon \) such that

$$\begin{aligned} \epsilon +\sigma _{1}^{2}+\left( \delta _{3 k}-\frac{1}{3 \sqrt{\frac{1+\delta _{3 k}}{1-\delta _{3 k}}}+1}\right) \frac{\epsilon +\sigma _{1}^{2}}{\sigma _{1}^{2}} < \epsilon + \sigma _m^2, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \delta _{3k} - \frac{1}{3\sqrt{\frac{1+\delta _{3k}}{1-\delta _{3k}}}+1} < 0, ~~ \epsilon > \left( \frac{\sigma _{1}^{2} - \sigma _{m}^{2}}{\frac{1}{3\sqrt{\frac{1+\delta _{3k}}{1-\delta _{3k}}}+1} - \delta _{3k}} - 1 \right) \sigma _{1}^{2} . \end{aligned}$$

The first condition is ensured by \(\delta _{3k} < 0.211\,9\), and the second condition is ensured by the choice of \(\epsilon \) given in (15). The proof of the theorem is complete. In particular, if \(\eta =0\) and x is k-sparse, the relation (17) is reduced to

$$\begin{aligned} \left\| x^{p+1}-x\right\| _{2} \leqslant \rho \left\| x^{p}-x\right\| _{2} \leqslant \rho ^p \left\| x^0-x\right\| _{2}, \end{aligned}$$

which implies that \(\{x^{p}\}\) converges to x as \(p \rightarrow \infty \).

3.3 Analysis of NTROTP in Noisy Scenarios

Before showing the main result, we introduce a lemma concerning a property of the pursuit step.

Lemma 6

[28] Let \(y = A \hat{x} + \nu \) be the noisy measurements of the k-sparse signal \(\hat{x} \in \mathbb {R}^n\), and let \(u \in \mathbb {R}^n\) be an arbitrary k-sparse vector. Then, the optimal solution of the pursuit step

$$\begin{aligned} z^{*}=\arg \min _{z}\left\{ \Vert y-A z\Vert _{2}^{2}: ~ {\text {supp}}(z) \subseteq {\text {supp}}(u)\right\} \end{aligned}$$

satisfies that

$$\begin{aligned} \left\| z^{*}-\hat{x}\right\| _{2} \leqslant \frac{1}{\sqrt{1-\left( \delta _{2 k}\right) ^{2}}}\Vert \hat{x}-u\Vert _{2}+\frac{\sqrt{1+\delta _{k}}}{1-\delta _{2 k}}\Vert \nu \Vert _{2} . \end{aligned}$$

Theorem 3

Let \(y=Ax+\eta \) be the measurements of the signal \(x \in \mathbb {R}^n\) with measurement error \( \eta .\) Let \(S=\mathcal{L}_k(x)\) and \(\sigma _1\) and \(\sigma _m\) denote, respectively, the largest and smallest singular values of the matrix \(A \in \mathbb {R}^{m \times n}\). Suppose that the restricted isometry constant of A satisfies that

$$\begin{aligned} \delta _{3k} < 0.2 , \end{aligned}$$

and \(\epsilon \) is a given parameter satisfying

$$\begin{aligned} \epsilon > \max \left\{ \sigma _1^2 , \left( \frac{\sigma _{1}^{2} - \sigma _{m}^{2}}{\frac{1}{\frac{3}{1-\delta _{3k}} + \frac{1}{\sqrt{1-\left( \delta _{3 k}\right) ^{2}}}} - \delta _{3 k}} - 1 \right) \sigma _1^2 \right\} . \end{aligned}$$
(27)

If the parameter \(\lambda \) in NTROTP satisfies

$$\begin{aligned} \epsilon +\sigma _{1}^{2} + \left( \delta _{3 k} - \frac{1}{\frac{3}{1-\delta _{3k}} + \frac{1}{\sqrt{1-\left( \delta _{3 k}\right) ^{2}}}} \right) \frac{\epsilon + \sigma _1^2}{\sigma _1^2} ~ < ~ \lambda ~ \leqslant ~ \epsilon + \sigma _m^2 , \end{aligned}$$
(28)

then the sequence \(\{x^p\}\) generated by the NTROTP satisfies that

$$\begin{aligned} \left\| x^{p+1}-x_{S}\right\| _{2} \leqslant \tilde{\rho } \left\| x^{p}-x_{S}\right\| _{2}+\tilde{\tau } \left\| A x_{\overline{S}}+\eta \right\| _{2}, \end{aligned}$$
(29)

where

$$\begin{aligned} \tilde{\rho } = \left( \frac{3}{1-\delta _{3k}} + \frac{1}{\sqrt{1-\left( \delta _{3 k}\right) ^{2}}} \right) \left( \delta _{3 k}+\sigma _{1}^{2}-\frac{\lambda \sigma _{1}^{2}}{\epsilon +\sigma _{1}^{2}} \right) , \end{aligned}$$
(30)

and

$$\begin{aligned} \tilde{\tau } = \frac{\sqrt{1+\delta _{k}}}{1-\delta _{2 k}} + \frac{1}{(1-\delta _{2k}) \sqrt{1+\delta _{2k}}} \left( \frac{3 \lambda \sigma _{1} \sqrt{1+\delta _{k}}}{\epsilon +\sigma _{1}^{2}}+2\right) + \frac{\lambda \sigma _{1}}{(\epsilon +\sigma _{1}^{2}) \sqrt{1-\left( \delta _{2 k}\right) ^{2}}} . \nonumber \\ \end{aligned}$$
(31)

In particular, when x is k-sparse and \(\eta =0\), then the sequence \(\{x^{p}\}\) converges to x.

Proof

NTROTP comprises of NTROT and a pursuit step. From the proof of Theorem 2, we see that

$$\begin{aligned} \left\| x_{S}-\mathcal{H}_k (u^p \otimes w^p)\right\| _{2} \leqslant \rho \left\| x^{p}-x_{S}\right\| _{2}+\tau \left\| \eta ^{\prime }\right\| _{2}, \end{aligned}$$
(32)

where the constants \(\rho \) and \(\tau \) are given by (18) and (19), respectively. From the step (\(\hbox {P}_5\)), \(x^{p+1}\) is the solution to the pursuit step. By Lemma 6, we have

$$\begin{aligned} \left\| x_{S}-x^{p+1}\right\| _{2} \leqslant \frac{1}{\sqrt{1-\left( \delta _{2 k}\right) ^{2}}} \left\| x_{S}-\mathcal{H}_k (u^p \otimes w^p)\right\| _{2} + \frac{\sqrt{1+\delta _{k}}}{1-\delta _{2 k}}\Vert \eta '\Vert _{2} , \end{aligned}$$
(33)

where \(\eta ' = Ax_{\overline{S}}+\eta \). Using \(\delta _{k} \leqslant \delta _{2k} \leqslant \delta _{3k}\) and combining (32) and (33) lead to

$$\begin{aligned} \left\| x_{S}-x^{p+1}\right\| _{2} \leqslant \tilde{\rho } \left\| x^{p}-x_{S}\right\| _{2}+\tilde{\tau } \left\| \eta '\right\| _{2}, \end{aligned}$$

where \(\tilde{\rho }\) and \(\tilde{\tau }\) are defined as (30) and (31), respectively. Note that \(\tilde{\rho } < 1\) is equivalent to

$$\begin{aligned} \lambda > \epsilon +\sigma _{1}^{2} + \left( \delta _{3 k} - \frac{1}{\frac{3}{1-\delta _{3k}} + \frac{1}{\sqrt{1-\left( \delta _{3 k}\right) ^{2}}}} \right) \frac{\epsilon + \sigma _1^2}{\sigma _1^2}. \end{aligned}$$

This is ensured by the choice of \(\lambda \) given in (28). This means the choice of \(\lambda \) in (28) ensures that \(\tilde{\rho }<1\). To guarantee the existence of the range (28), it is sufficient to require that

$$\begin{aligned} \epsilon +\sigma _{1}^{2} + \left( \delta _{3 k} - \frac{1}{\frac{3}{1-\delta _{3k}} + \frac{1}{\sqrt{1-\left( \delta _{3 k}\right) ^{2}}}} \right) \frac{\epsilon + \sigma _1^2}{\sigma _1^2} < \epsilon + \sigma _m^2 , \end{aligned}$$
(34)

which is equivalent to

$$\begin{aligned} \delta _{3 k} - \frac{1}{\frac{3}{1-\delta _{3k}} + \frac{1}{\sqrt{1-\left( \delta _{3 k}\right) ^{2}}}} < 0, ~~ \epsilon > \left( \frac{\sigma _{1}^{2} - \sigma _{m}^{2}}{\frac{1}{\frac{3}{1-\delta _{3k}} + \frac{1}{\sqrt{1-\left( \delta _{3 k}\right) ^{2}}}} - \delta _{3 k}} - 1 \right) \sigma _1^2 . \end{aligned}$$
(35)

Note that \(\frac{1}{\sqrt{1-\left( \delta _{3 k}\right) ^{2}}}< \frac{1}{1-\delta _{3k}}\). The first condition in (35) is satisfied when \(\delta _{3k}<0.2\). The second condition (35) is also satisfied provided \(\epsilon \) is chosen large enough, i.e., satisfying (27). In particular, if \(\eta =0\) and x is k-sparse, the relation (29) is reduced to

$$\begin{aligned} \left\| x^{p+1}-x\right\| _{2} \leqslant \tilde{\rho }\left\| x^{p}-x\right\| _{2} \leqslant \tilde{\rho }^p \left\| x^0-x\right\| _{2}, \end{aligned}$$

which implies that \(\{x^{p}\}\) converges to x as \(p \rightarrow \infty \).

Remark 1

The bound for \(\delta _{3k}\) in Theorems 2 and 3 can be replaced by the one for \(\delta _{2k}\) either through a more subtle analysis (we believe), or through the relation \(\delta _{3k} < 3 \delta _{2k}\) which is shown in Proposition 6.6 in [3]. In fact, from \(\delta _{3k} < 3 \delta _{2k},\) it is evident that \(\delta _{2k} < 0.070~6 \) implies \(\delta _{3k} < 0.211~9\), and that \(\delta _{2k}<0.066~6\) implies \(\delta _{3k} < 0.2.\) Therefore, we may use the bound \(\delta _{2k} < 0.070~6\) in Theorem 2 and \(\delta _{2k}<0.066~6\) in Theorem 3 without any damage of the results in these theorems.

Remark 2

By the structure of the proposed algorithm, we only need to compute the matrix \((A^{\top }A+\epsilon I)^{-1}\) once. This inverse can be obtained by using singular value decomposition (SVD) of the matrix A, since it also provides information for the choice of the parameters \((\epsilon , \lambda )\) in the algorithms.

4 Numerical Experiments

Simulations were performed to test the performance of the proposed algorithms with respect to residual reduction, average number of iterations needed for convergence and success frequency for signal recovery. Without specified statement, the measurement matrices generated for experiments are Gaussian random matrices, whose entries are independent and identically distributed and follow the standard normal distribution \(\mathcal{N}(0,1)\). Nonzero entries of realized sparse signals also follow the \(\mathcal{N}(0,1)\), and their position follows a uniform distribution. We will compare the performances of the proposed PGROTP algorithm and several existing methods including \(\ell _1\)-minimization [10, 11], orthogonal matching pursuit (OMP) [16, 17], subspace pursuit (SP) [18], Newton-step-based hard thresholding pursuit (NSHTP) [27], quasi-Newton iterative projection (QNIP) [35], and quasi-Newton projection pursuit (QNPP) [36]. All involved optimization problems in algorithms were solved by the CVX which is developed by Grant and Boyd [37] with solver ‘Mosek’.

4.1 Residual Reduction

The experiment was carried out to compare the residual-reduction performance of the algorithms with given \((\epsilon , \lambda )\). In this experiment, we set \(A \in \mathbb {R}^{256 \times 512}\), \(y = Ax^*\), \(\Vert x^*\Vert _0 = 70\) and \(x^0=0\). The stepsize \(\lambda \) and parameter \(\epsilon \) are set, respectively, as

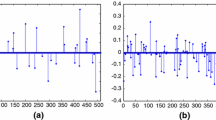
$$\begin{aligned} \lambda = 5, ~\epsilon = \max \{ \sigma _1^2+1, \lambda -\sigma _m^2 \}, \end{aligned}$$
(36)

which guarantees that \(\epsilon > \sigma _1^2\) and \(\lambda \leqslant \epsilon + \sigma _m^2\), where \(\sigma _1\) and \(\sigma _m\) denote the largest and the smallest singular value of the matrix. Figure 1 demonstrates the change of the residual value, i.e., \({\Vert }y-Ax{\Vert }_2\), in the course of iterations of the algorithms. From Fig. 1(a), it can be seen that the NTROTP is more powerful than other algorithms in residual reduction. In the same experiment environment, we also compare the residual change in the course of NSIHT and NTROT which use different thresholding operators. Figure 1(b) shows that the algorithm with optimal thresholding operator can reduce the residual more efficiently than the one with hard thresholding operator.

Fig. 1
figure 1

(a) Comparison of residual-reduction performances of several algorithms; (b) residual change in the course of iterations using different thresholding operators

Full size image

The performance of NTROT and NTROTP is clearly related to the choice of \((\epsilon , \lambda )\). Thus, we test the residual-reduction performance of the proposed algorithms in terms of different values of parameter \(\epsilon \) and stepsize \(\lambda \). The results are shown in Figs. 2 and 3, respectively. In Fig. 2, the stepsize \(\lambda \) is fixed as \(\lambda =10\), and \(\epsilon = \epsilon ^*, 1.1\epsilon ^*, 1.5 \epsilon ^*\) and \(2\epsilon ^*\), where \(\epsilon ^* = \sigma _1^2+1\). In Fig. 3, the parameter \(\epsilon \) is fixed as \(\epsilon = \sigma _1^2+1\), and stepsize \(\lambda \) is taken as \(\lambda = 1,2,5,10\), respectively. Such choices of \((\epsilon , \lambda )\) satisfy that \(\epsilon >\sigma _{1}^{2}\) and \(\lambda \leqslant \epsilon +\sigma _{m}^{2}\). It can be seen that the NTROT is more sensitive to the change of \(\epsilon \) and \(\lambda \) than the NTROTP which is generally insensitive to the change of \((\epsilon , \lambda )\). This indicates that NTROTP is a stable algorithm.

Fig. 2
figure 2

Residual reduction by NTROT and NTROTP with \(\lambda =10\) and different parameters \(\epsilon \): \(\epsilon _1=\epsilon ^*\), \(\epsilon _2 = 1.1 \epsilon ^*\), \(\epsilon _3 = 1.5 \epsilon ^*\), \(\epsilon _4 = 2 \epsilon ^*\)

Full size image
Fig. 3
figure 3

Residual reduction by NTROT and NTROTP with \(\epsilon = \sigma _1^2+1\) and different stepsizes \(\lambda = 1, 2, 5, 10\)

Full size image
Fig. 4
figure 4

Comparison of the average number of iterations required by different algorithms

Full size image

4.2 Number of Iterations

The simulations were also performed to examine the impact of sparsity levels and measurement levels on the average number of iterations needed for signal reconstruction via Newton-type iterative algorithms. In this experiment, all algorithms start from \(x^0=0\) and terminate either when \(r := \left\| x^{p}-x^{*}\right\| _{2} /\left\| x^{*}\right\| _{2} \leqslant 10^{-3}\) is met or when the maximum number of iterations (i.e., 50 iterations) is reached.

Figure 4(a) demonstrates the influence of sparsity levels on the number of iterations needed by NSIHT, NSHTP, NTROT, and NTROTP to reconstruct a signal. In this experiment, the size of measurement matrices is still \(256 \times 512\), and the ratio k/n varies from 0.01 to 0.35. The average number of iterations is calculated based on 50 random examples for each sparsity level k/n. A common feature of these algorithms is that with increase in the sparsity levels, the required iterations for the algorithms to reconstruct signals also increase. We also observe that both the optimal thresholding and pursuit step help reduce the required number of iterations of algorithms to reconstruct a signal.

Figure 4(b) compares the average number of iterations required by several algorithms applying to different measurement levels. The target signal is fixed as \(x^* \in \mathbb {R}^{500}\) with \({\Vert }x^*{\Vert }_0 = 50\), and the length of observed vector \(y = Ax^*\), i.e., the number of measurements, varies from 50 to 300. When \(m/n < 0.25\), we see that no algorithm could recover the target 50-sparse signal within 50 iterations, due to the fact that the measurement levels are too low for signal reconstruction. The more measurements obtained for the target signal \(x^*\), the less number of iterations needed for reconstruction, as shown in Fig. 4(b). Both NSHTP and NTROTP could recover the signal by using relatively a small number of iterations when the ratio \(m/n\geqslant 0.35\), and the NTROTP needs less iterations than NSIHT, NSHTP, and NTROT.

4.3 Performance of Signal Recovery

Simulations were carried out to compare the signal reconstruction performance of the NTROTP algorithm and several existing ones with both exact and inexact measurements. In this experiment, the size of matrices is still \(256 \times 512\). All iterative algorithms start at \(x^0=0\). The ratio k/n increases from 0.01 to 0.35. We first compare our algorithm with several heuristic algorithms including \(\ell _1\)-minimization, OMP, SP, NSHTP, and NTROTP. The results are given in Fig. 5. Then, we compare our algorithm with two existing Newton-Type methods for which the results are summarized in Fig. 6. The vertical axes in Figs. 5 and 6 represent the reconstruction success rates which is calculated based on 50 random examples.

In the experiments producing the results in Fig. 5, the measurements of \(x^*\) are set as \(y=Ax^*+0.001\theta \), where \(\theta \in \mathbb {R}^{256}\) is a standard Gaussian random vector. The iterative algorithms terminate after 20 iterations except for the OMP which stops after k iterations owing to the its structure, where \(k = {\Vert }x^*{\Vert }_0\). The choice of \((\epsilon , \lambda )\) is the same as (36). The condition \({\Vert }x^p-x^*{\Vert }_2/{\Vert }x^*{\Vert }_2 \leqslant 10^{-3}\) is set as the recovery criterion. Figure 5 indicates that the NTROTP is stable and robust for sparse signal recovery compared with other algorithms used in this experiments.

Fig. 5
figure 5

Comparison of success frequencies of signal recovery via different algorithms

Full size image

The entries of Gaussian random matrices used in the experiment that generates Fig. 6 follow the normal distribution \(\mathcal{N} (0, 1/m)\), where m denotes the number of measurements, i.e., \(m=256\). In such an experiment, the noisy measurements of \(x^*\) are set as \(y=Ax^*+10^{-5}\theta \), where \(\theta \in \mathbb {R}^{256}\) is a standard Gaussian random vector; all algorithms terminate when either the criterion \(\left\| x^{p}-x^{*}\right\| _{2} /\left\| x^{*}\right\| _{2} \leqslant 10^{-3}\) is met or a total of 50 iterations are performed for QNIP and NTROTP and 300 iterations are performed for QNIP (which works slowly and thus we allow this algorithm to perform much more iterations than the other two). For NTROTP algorithm, we set \(\epsilon = 10^{-5}\) to slightly perturb the singular Hessian \(A^{\top }A\) such that \(A^{\top }A+\epsilon I\) is positive definite. The parameter \(\lambda \) is set as \(\lambda = 1, 2\), and 5, respectively. As indicated in Fig. 6, QNPP and NTROTP algorithms are comparable, and they outperform QNIP even if we allow the QNIP to perform much more iterations than the other two algorithms. Figure 6 also indicates that the NTROTP with a small value of \(\epsilon \) is also efficient and robust for signal recovery, although this has not been shown rigorously from a theoretical viewpoint.

Fig. 6
figure 6

Comparison between QNIP, QNPP, and NTROTP with \(\epsilon = 10^{-5}\) and different parameters \(\lambda =1,2,5\)

Full size image

5 Conclusion

A class of Newton-type optimal k-thresholding algorithms is proposed in this paper. Under the restricted isometry property (RIP), we have proved that the NTOT, NTROT, and NTROTP algorithms are guaranteed to reconstruct sparse signals with proper choices of the algorithmic parameters. Simulations indicate that the NTROTP algorithm proposed in this paper is a very stable and robust algorithm for signal reconstruction.