Skip to main content
SpringerLink
Log in

Neural Network-Based Variational Methods for Solving Quadratic Porous Medium Equations in High Dimensions

  • Published:
Communications in Mathematics and Statistics Aims and scope Submit manuscript

Abstract

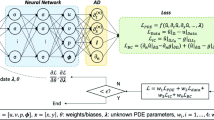
In this paper, we propose and study neural network-based methods for solutions of high-dimensional quadratic porous medium equation (QPME). Three variational formulations of this nonlinear PDE are presented: a strong formulation and two weak formulations. For the strong formulation, the solution is directly parameterized with a neural network and optimized by minimizing the PDE residual. It can be proved that the convergence of the optimization problem guarantees the convergence of the approximate solution in the \(L^1\) sense. The weak formulations are derived following (Brenier in Examples of hidden convexity in nonlinear PDEs, 2020) which characterizes the very weak solutions of QPME. Specifically speaking, the solutions are represented with intermediate functions who are parameterized with neural networks and are trained to optimize the weak formulations. Extensive numerical tests are further carried out to investigate the pros and cons of each formulation in low and high dimensions. This is an initial exploration made along the line of solving high-dimensional nonlinear PDEs with neural network-based methods, which we hope can provide some useful experience for future investigations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

References

  1. Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., Devin, M., Ghemawat, S., Irving, G., Isard, M., et al.: \(\{\)TensorFlow\(\}\): a system for \(\{\)Large-Scale\(\}\) machine learning. In: 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), pp. 265–283 (2016)

  2. Barron, A.R.: Universal approximation bounds for superpositions of a sigmoidal function. IEEE Trans. Inf. Theory 39(3), 930–945 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bing, Yu., et al.: The deep ritz method: a deep learning-based numerical algorithm for solving variational problems. Commun. Math. Stat. 6(1), 1–12 (2018)

  4. Boelens, A.M., Venturi, D., Tartakovsky, D.M.: Parallel tensor methods for high-dimensional linear PDEs. J. Comput. Phys. 375, 519–539 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  5. Brenier, Y.: Examples of hidden convexity in nonlinear PDEs (2020)

  6. Dektor, A., Venturi, D.: Dynamically orthogonal tensor methods for high-dimensional nonlinear PDEs. J. Comput. Phys. 404, 109125 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  7. Dektor, A., Rodgers, A., Venturi, D.: Rank-adaptive tensor methods for high-dimensional nonlinear PDEs. J. Sci. Comput. 88(2), 1–27 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  8. Dolgov, S., Kalise, D., Kunisch, K.K.: Tensor decomposition methods for high-dimensional Hamilton-Jacobi-Bellman equations. SIAM J. Sci. Comput. 43(3), A1625–A1650 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  9. Eigel, M., Neumann, J., Schneider, R., Wolf, S.: Non-intrusive tensor reconstruction for high-dimensional random PDEs. Comput. Methods Appl. Math. 19(1), 39–53 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  10. Han, J., Jentzen, A., et al.: Deep learning-based numerical methods for high-dimensional parabolic partial differential equations and backward stochastic differential equations. Commun. Math. Stat. 5(4), 349–380 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  11. Han, J., Jentzen, A., Weinan, E.: Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. 115(34), 8505–8510 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  12. Henry-Labordere, P.: Counterparty risk valuation: a marked branching diffusion approach. Available at SSRN 1995503 (2012)

  13. Henry-Labordere, P., Oudjane, N., Tan, X., Touzi, N., Warin, X.: Branching diffusion representation of semilinear PDEs and Monte Carlo approximation. In: Annales de l’Institut Henri Poincaré, Probabilités et Statistiques, vol. 55, pp. 184–210. Institut Henri Poincaré (2019)

  14. Jentzen, A., Salimova, D., Welti, T.: A proof that deep artificial neural networks overcome the curse of dimensionality in the numerical approximation of Kolmogorov partial differential equations with constant diffusion and nonlinear drift coefficients. arXiv preprint arXiv:1809.07321 (2018)

  15. Kingma, D.P., Ba, J.: Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014)

  16. Lagaris, I.E., Likas, A., Fotiadis, D.I.: Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 9(5), 987–1000 (1998)

    Article  Google Scholar 

  17. Leibenzon, L.S.: The motion of a gas in a porous medium. Complete Works, Vol. 2, Acad. Sci. URSS Moscow (Russian) 63, 8–9 (1930)

  18. Lu, J., Lu, Y., Wang, M.: A priori generalization analysis of the deep ritz method for solving high dimensional elliptic partial differential equations. In: Conference on Learning Theory, pp. 3196–3241. PMLR (2021)

  19. Marsaglia, G.: Choosing a point from the surface of a sphere. Ann. Math. Stat. 43(2), 645–646 (1972)

    Article  MATH  Google Scholar 

  20. Muskat, M.: The flow of homogeneous fluids through porous media. Soil Sci. 46(2), 169 (1938)

    Article  Google Scholar 

  21. Ngo, C., Huang, W.: A study on moving mesh finite element solution of the porous medium equation. J. Comput. Phys. 331, 357–380 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  22. Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. phys. 378, 686–707 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  23. Richter, L., Sallandt, L., Nüsken, N.: Solving high-dimensional parabolic PDEs using the tensor train format. In: International Conference on Machine Learning, pp. 8998–9009. PMLR (2021)

  24. Shmarev, S.: Interfaces in solutions of diffusion-absorption equations in arbitrary space dimension, pp. 257–273. Trends in Partial Differential Equations of Mathematical Physics (2005)

  25. Shukla, M.B., Kok, R., Prasher, S.O., Clark, G., Lacroix, R.: Use of artificial neural networks in transient drainage design. Trans. ASAE 39(1), 119–124 (1996)

    Article  Google Scholar 

  26. Vázquez, J.L.: The Porous Medium Equation: Mathematical Theory. Oxford University Press, Oxford (2007)

    MATH  Google Scholar 

  27. Warin, X.: Variations on branching methods for non linear PDEs. arXiv preprint arXiv:1701.07660 (2017)

  28. Warin, X.: Nesting Monte Carlo for high-dimensional non-linear PDEs. Monte Carlo Methods Appl. 24(4), 225–247 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  29. Wells, B.V.: A moving mesh finite element method for the numerical solution of partial differential equations and systems. PhD thesis, Citeseer (2004)

  30. Zang, Y., Bao, G., Ye, X., Zhou, H.: Weak adversarial networks for high-dimensional partial differential equations. J. Comput. Phys. 411, 109409 (2020)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work is supported in part by National Science Foundation via grant DMS- 2012286 and by Department of Energy via grant DE-SC0019449.

Author information

Authors and Affiliations

  1. Duke University, Durham, NC, USA

    Min Wang & Jianfeng Lu

Authors
  1. Min Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianfeng Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Min Wang.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, M., Lu, J. Neural Network-Based Variational Methods for Solving Quadratic Porous Medium Equations in High Dimensions. Commun. Math. Stat. 11, 21–57 (2023). https://doi.org/10.1007/s40304-023-00339-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40304-023-00339-5

Keywords

Mathematics Subject Classification

Search

Navigation