Parameter estimation for a bivariate beta distribution with arbitrary beta marginals and positive correlation

Abstract

We discuss a bivariate beta distribution that can model arbitrary beta-distributed marginals with a positive correlation. The distribution is constructed from six independent gamma-distributed random variates. While previous work used an approximate and sometimes inaccurate method to compute the distribution’s covariance and estimate its parameters, here, we derive all product moments and the exact covariance, which can be computed numerically. Based on this analysis we present an algorithm for estimating the parameters of the distribution using moment matching. We evaluate this inference method in a simulation study and demonstrate its practical use on a data set consisting of predictions from two correlated forecasters. Furthermore, we generalize the bivariate beta distribution to a correlated Dirichlet distribution, for which the proposed parameter estimation method can be used analogously.

1 Introduction

Probabilistic forecasts are important in many domains, among them finance and economics, business and marketing, politics, public health, engineering, and meteorological, ecological, and environmental science. For binary events these forecasts take the form of probability estimates that are either provided by humans or machine learning algorithms. In order to model these probability estimates one can use an arbitrary distribution on the interval [0, 1], such as the beta distribution, beta-generated distributions, the Kumaraswamy distribution, or any distribution on the real numbers transformed through the logistic function. In many cases the probabilities will be correlated, e.g. if different experts forecast the outcome of an election or the probability of rain. In order to be able to model such correlated probabilities, therefore, a bivariate distribution is needed. For example, one can use bivariate generalizations of the Kumaraswamy distribution [1], bivariate beta-generated distributions [2], or a multivariate Gaussian with logistic transformations [3]. However, the most common choice for modeling such probabilities is the beta distribution, since it is the standard distribution for probabilities in Bayesian statistics and is simply more familiar to practitioners than the other distributions [4, 5]. Therefore, in this paper we focus on bivariate beta distributions.

While a multitude of constructions for bivariate beta distributions have been proposed, they have different constraints and properties, which limit their applicability. We will first review previous constructions of bivariate beta distributions together with their respective properties and then examine the most promising construction that can model arbitrary beta marginals with a positive correlation [5]. For this construction of modeling arbitrary beta marginals with positive correlation, so far, there has not been an exact method for parameter inference and it has thus rarely been used. Here, we therefore introduce a new estimation method for this bivariate beta distribution with arbitrary beta marginals and positive correlation.

Many bivariate beta distributions have been proposed in the literature [1, 2, 5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. Among them, some approaches have been derived from general families of bivariate distributions, such as the Farlie-Gumbel-Morgenstern family of distributions [e.g. 7] and the Sarmanov family of distributions [e.g. 8]. Others derived a bivariate beta distribution from a bivariate extension of the F distribution [9, 13], whereas Nadarajah and Kotz [11] proposed different bivariate beta distributions constructed from products of univariate beta-distributed random variables. In general, using different copulas one can construct different bivariate distributions with the same beta marginals [2, 20]. However, as beta-distributed random variables can easily be constructed from normalized gamma-distributed random variables, it is natural to try and generalize this construction to the bivariate case. In this vein, several authors have introduced correlations through shared gamma-distributed random variables [1, 5, 10, 14, 18]. The most straightforward case of this construction has been studied by Olkin and Liu [10], building on the work of Libby and Novick [6]. They use three independent gamma-distributed random variables $U_1, U_2, U_3$ with respective shape parameters $\upsilon _1, \upsilon _2, \upsilon _3$ and same scale parameter to construct

$$\begin{aligned} X' = \frac{U_1}{U_1+U_3} \quad \textrm{and}\quad Y' = \frac{U_2}{U_2+U_3}. \end{aligned}$$

(1)

Using the standard construction of beta variates from gamma variates, the joint distribution of the random variables $X'$ and $Y'$ is a bivariate beta distribution with marginal distributions Beta($\upsilon _1$, $\upsilon _3$) for $X'$ and Beta($\upsilon _2$, $\upsilon _3$) for $Y'$. The correlation between $X'$ and $Y'$, which is obtained through the shared latent variable $U_3$ and its parameter $\upsilon _3$, is in the range [0,1]. For high values of $\upsilon _3$, the correlation tends to 0 whereas for low values of $\upsilon _3$, it tends to 1. However, if $\upsilon _3$ is high, the values of $X'$ and $Y'$ also tend to 0 and if $\upsilon _3$ is low they tend to 1 accordingly. This behavior severely limits the usefulness of the distribution for most applications. A further limitation is the constraint that the marginal distributions share the same second parameter $\upsilon _3$. Thus, the bivariate beta distribution proposed by Olkin and Liu does not allow for arbitrary beta marginals, which limits its flexibility in modeling probability forecasts.

Arnold and Ng [14] proposed a more flexible construction for a bivariate beta distribution. They use five independent gamma-distributed random variables $U_1, \dots , U_5$ with shape parameters $\upsilon _1, \dots , \upsilon _5$ and scale parameter 1 to define two correlated random variables

$$\begin{aligned} X = \frac{U_1 + U_3}{U_1 + U_3 + U_4 + U_5} \quad \textrm{and}\quad Y = \frac{U_2 + U_4}{U_2 + U_3 + U_4 + U_5} \end{aligned}$$

(2)

with marginal distributions Beta($\upsilon _1 + \upsilon _3, \upsilon _4 + \upsilon _5$) for X and Beta($\upsilon _2 + \upsilon _4, \upsilon _3 + \upsilon _5$) for Y. Compared to Olkin and Liu [10], this construction of a bivariate beta distribution can generate all correlations in the range [-1,1] and marginal distributions with differing second parameters. Nevertheless, because of how the two marginals share parameters, not all combinations of parameters of the marginal beta distributions are possible. For example, the marginals Beta(10, 4) for X and Beta(1, 1) for Y cannot be obtained.

Olkin and Trikalinos [18] base their construction of a bivariate beta distribution on the Dirichlet distribution. $U = (U_{00}, U_{01}, U_{10}, U_{11})$ is drawn from a 4-dimensional Dirichlet distribution with parameters $\upsilon _1, \dots , \upsilon _4$. By just using three of its components, $U_{00}, U_{01}, U_{10}$, new random variables

$$\begin{aligned} X = U_{00} + U_{10} \quad \textrm{and}\quad Y = U_{01} + U_{10} \end{aligned}$$

(3)

are constructed, with marginal distributions Beta($\upsilon _1 + \upsilon _3, \upsilon _2 + \upsilon _4$) for X and Beta($\upsilon _2 + \upsilon _3, \upsilon _1 + \upsilon _4$) for Y. As Dirichlet-distributed random variables can also be constructed from gamma random variables, we can equivalently construct X and Y in Eq. (3) from four independent gamma-distributed random variables $U_1, \dots , U_4$ with shape parameters $\upsilon _1, \dots , \upsilon _4$ and equal scale parameter 1, with

$$\begin{aligned} X = \frac{U_1 + U_3}{U_1 + U_2 + U_3 + U_4} \quad \textrm{and}\quad Y = \frac{U_2 + U_3}{U_1 + U_2 + U_3 + U_4}. \end{aligned}$$

(4)

As can easily be seen from this construction, all correlations in the range [-1,1] can be generated. In particular, the correlation tends to -1 if $\upsilon _3$ and $\upsilon _4$ tend to 0 and $U_3$ and $U_4$ will be negligible compared to $U_1$ and $U_2$. In this case $X \approx \frac{U_1}{U_1 + U_2} \approx 1 - Y$. Similarly, the higher the values of $\upsilon _3$ and $\upsilon _4$ relative to $\upsilon _1$ and $\upsilon _2$, the more negligible $U_1$ and $U_2$ will be and the correlation increases to 1 until $X \approx \frac{U_3}{U_3 + U_4} \approx Y$. Less obviously, a correlation of 0 is obtained in case $\upsilon _1 \cdot \upsilon _2 = \upsilon _3 \cdot \upsilon _4$ [18]. Still, this construction of a bivariate beta distribution does not allow arbitrary beta marginal distributions. Since all $\upsilon _i$ are constrained to be positive, for some combinations of marginal distributions the resulting system of linear equations for the parameters $\upsilon _i$ has no solution. For example, the two marginals Beta(2, 2) for X and Beta(1, 1) for Y cannot be generated, regardless of their correlation.

Magnussen [5] introduced yet another construction based on six gamma variates. While all the constructions thus far constrain the parameters of the marginal beta distributions, this construction does allow for arbitrary beta marginals with positive correlation, thus providing the necessary flexibility to model probability forecasts. Magnussen’s distribution is a special case of a more general 8-parameter bivariate beta distribution introduced by Arnold and Ng [14] and reviewed in Arnold and Ghosh [1], which even allows for positive and negative correlations. However, in many applications, it is enough to model positive correlations, for which the less complex 6-parameter distribution is sufficient. For example, if X and Y are probability estimates elicited from two skilled forecasters, we do not expect negative correlations. But we do want to allow for the possibility that their marginal forecasts have different distributions that should not be tied together by parameter constraints on the marginals. Hence, the bivariate beta distribution proposed by Magnussen [5], which can model arbitrary beta-distributed marginals with a positive correlation, is an appropriate distribution for modeling correlated probability forecasts.

However, just like any other distribution, the bivariate beta distribution can only be used if its parameters can be estimated correctly. While Magnussen [5] proposes a moment matching approach for fitting the distribution’s parameters, this approach relies on a rough and sometimes inaccurate approximation for the covariance. Also, Magnussen [5] did not discuss the fact that very similar data can be generated with different parameter values, which makes it hard to statistically infer the parameters of the bivariate beta distribution from data without constraining the distribution.

Therefore, in this work we introduce an alternative approach for estimating this bivariate beta distribution’s parameters. First, we will derive the full joint distribution, which is missing in the work of Magnussen [5], probably because it is intractable. We will then clarify the relationship between Magnussen’s distribution and the Olkin-Liu distribution [10]. Using this relationship with the Olkin-Liu distribution we derive all product moments and in particular the exact covariance function (and in passing we correct a small mistake in the product moments from Olkin and Liu [10]). For parameter inference, we propose to match moments numerically using the exact covariance we derived. While other estimation methods such as Bayesian inference could be used [22], here we focus on moment matching due to its simplicity and efficiency. In order to make parameter inference unambiguous, we additionally show how to reasonably constrain the distribution’s parameters. We evaluate the proposed parameter estimation method in a simulation study and demonstrate its practical use on a real data set consisting of predictions from two correlated forecasters. We discuss the relationship between the distribution’s parameters and the correlation and then extend the bivariate beta distribution to a correlated Dirichlet distribution, for which the proposed parameter estimation method can be used analogously.

The remainder of the paper is structured as follows. In Sect. 2 we discuss the bivariate beta distribution with arbitrary beta marginals, including its joint distribution in Sect. 2.1, its moments in Sect. 2.2, correlation and covariance in Sect. 2.3, and parameter inference in Sect. 2.4. Section 3 shows how to generalize the bivariate beta distribution to a correlated Dirichlet distribution.

2 A bivariate beta distribution with arbitrary beta marginals

Magnussen [5] uses six independent gamma-distributed random variables $A_1$, $A_2$, $B_1$, $B_2$, $D_1$, $D_2$ that are distributed according to

$$\begin{aligned} \begin{aligned} A_i&\sim \text {Gamma}(\alpha _i, 1)\quad i = 1,2 \\ B_i&\sim \text {Gamma}(\beta _i, 1)\hspace{0.02cm}\quad i = 1,2 \\ D_i&\sim \text {Gamma}(\delta _i, 1)\hspace{0.06cm}\quad i = 1,2, \end{aligned} \end{aligned}$$

(5)

to construct two bivariate-beta-distributed random variables

$$\begin{aligned} X&= \frac{A_1 + D_1}{A_1 + A_2 + D_1 + D_2} \quad \textrm{and}\quad Y = \frac{B_1 + D_1}{B_1 + B_2 + D_1 + D_2}. \end{aligned}$$

(6)

The resulting marginal distributions of X and Y are Beta($a_1$, $a_2$) and Beta($b_1$, $b_2$) with

$$\begin{aligned} a_1&= \alpha _1 + \delta _1&a_2&= \alpha _2 + \delta _2&b_1&= \beta _1 + \delta _1&b_2&= \beta _2 + \delta _2. \end{aligned}$$

(7)

The marginals follow immediately from the definition because the sum of gamma random variables of the same scale is gamma-distributed with the same scale but with the original shape parameters summed. In contrast to other constructions that were discussed above [10, 14, 18], this construction allows for arbitrary marginal distributions. In particular, when $\delta _1$ and $\delta _2$ tend to zero, we can model arbitrary independent marginal distributions Beta($\alpha _1$, $\alpha _2$) and Beta($\beta _1$, $\beta _2$).

Since all parameters $\alpha _1, \alpha _2, \beta _1, \beta _2, \delta _1, \delta _2$ need to be positive by definition, for fixed marginal distributions Beta($a_1, a_2$) for X and Beta($b_1, b_2$) for Y it must hold that $\delta _1 < \delta _1^{\text {max}} = \text {min}(a_1, b_1)$ and $\delta _2 < \delta _2^{\text {max}} = \text {min}(a_2, b_2)$. Therefore, for most marginal distributions the maximum correlation that can be generated is below 1. The higher the difference between two marginal distributions, the lower the possible maximum correlation. A perfect correlation approaching 1 can, of course, only be generated for equal marginal distributions, i.e. if $a_1 = b_1$ and $a_2 = b_2$ and $\alpha _1$, $\alpha _2$, $\beta _1$, and $\beta _2$ tend to 0, as also noted by Magnussen [5]. Note that this limitation applies to other bivariate distributions that do not allow for arbitrary marginal beta distributions as well [e.g. 18].

The construction of this bivariate beta distribution can also be seen as a pairwise combination of three beta distributions. First transform the six independent gamma-distributed random variables (5) into three independent gamma- and three independent beta-distributed random variables,

$$\begin{aligned} \begin{aligned} U_{1}&=A_{1}+A_{2},&U_{1}&\sim \text {Gamma}(\upsilon _{1},1)\\ U_{2}&=B_{1}+B_{2},&U_{2}&\sim \text {Gamma}(\upsilon _{2},1)\\ U_{3}&=D_{1}+D_{2},&U_{3}&\sim \text {Gamma}(\upsilon _{3},1)\\ W_{1}&=\frac{A_{1}}{A_{1}+A_{2}},&W_{1}&\sim \text {Beta}(\alpha _{1},\alpha _{2})\\ W_{2}&=\frac{B_{1}}{B_{1}+B_{2}},&W_{2}&\sim \text {Beta}(\beta _{1},\beta _{2})\\ W_{3}&=\frac{D_{1}}{D_{1}+D_{2}},&W_{3}&\sim \text {Beta}(\delta _{1},\delta _{2}) \end{aligned} \end{aligned}$$

(8)

with

$$\begin{aligned} \upsilon _{1}&=\alpha _{1}+\alpha _{2}&\upsilon _{2}&=\beta _{1}+\beta _{2}&\upsilon _{3}&=\delta _{1}+\delta _{2}. \end{aligned}$$

(9)

With these definitions we can then rewrite construction (6) as

$$\begin{aligned} \begin{aligned} X&=\frac{U_{1}}{U_{1}+U_{3}}\cdot W_{1}+\frac{U_{3}}{U_{1}+U_{3}}\cdot W_{3}=X'W_{1}+(1-X')W_{3}\\ Y&=\frac{U_{2}}{U_{2}+U_{3}}\cdot W_{2}+\frac{U_{3}}{U_{2}+U_{3}}\cdot W_{3}=Y'W_{2}+(1-Y')W_{3}, \end{aligned} \end{aligned}$$

(10)

where $X'$ and $Y'$ are defined as in (1) but with $\upsilon _1$, $\upsilon _2$, and $\upsilon _3$ as in (9). Furthermore, $X'$ and $Y'$ are independent of $W_1, W_2, W_3$. If parameters $\delta _1$ and $\delta _2$ and with them $U_3$ tend to 0, $X \approx W_1$ and $Y \approx W_2$ are independent with marginal distributions Beta($\alpha _1, \alpha _2$) for X and Beta($\beta _1, \beta _2$) for Y. Mixing in the shared component $W_3$ by increasing the values of parameters $\delta _1$ and $\delta _2$ increases the correlation between X and Y. If $U_1$ and $U_2$ are negligible compared to $U_3$ because $\delta _1$ and $\delta _2$ dominate the parameters, the correlation will be close to 1 with $X \approx W_3 \approx Y$ and hence X and Y have the same marginal distribution Beta($\delta _1$, $\delta _2$), as mentioned before.

2.1 Joint distribution

X and Y in (10) are linear transformations of $X'$ and $Y'$. Given $W_1,W_2,W_3$ it is easy to recover $X'$ and $Y'$ from observed X and Y,

$$\begin{aligned} \begin{aligned} X'&=\frac{X-W_{3}}{W_{1}-W_{3}}=\frac{|X-W_{3}|}{|W_{1}-W_{3}|}=f_1(X)\\ Y'&=\frac{Y-W_{3}}{W_{2}-W_{3}}=\frac{|Y-W_{3}|}{|W_{2}-W_{3}|}=f_2(Y). \end{aligned} \end{aligned}$$

(11)

Note that we can ignore the sign because according to (10) X is always between $W_1$ and $W_3$ and Y between $W_2$ and $W_3$, so that the numerator and denominator always have the same sign.

As $X'$ and $Y'$ jointly follow the Olkin-Liu distribution [10],

$$\begin{aligned} p'(x',y') = \frac{\left( x'\right) ^{\upsilon _{1}-1}\left( 1-x'\right) ^{\upsilon _{2}+\upsilon _{3}-1}\left( y'\right) ^{\upsilon _{2}-1}\left( 1-y'\right) ^{\upsilon _{1}+\upsilon _{3}-1}}{B(\upsilon _{1},\upsilon _{2},\upsilon _{3})\left( 1-x'y'\right) ^{\upsilon _{1}+\upsilon _{2}+\upsilon _{3}}}, \end{aligned}$$

(12)

where $B(\upsilon _{1},\upsilon _{2},\upsilon _{3})=\frac{\Gamma (\upsilon _1)\Gamma (\upsilon _2)\Gamma (\upsilon _3)}{\Gamma (\upsilon _1+\upsilon _2+\upsilon _3)}$, the joint distribution of X and Y given $W_1,W_2,W_3$ is

$$\begin{aligned} \begin{aligned}&p(x,y\mid w_1,w_2,w_3) =\left|\frac{df_1(x)}{dx}\frac{df_2(y)}{dy}\right|p'\left( f_1(x),f_2(y)\right) \\&= {\frac{1}{|w_{1}-w_{3} ||w_{2}-w_{3} |}} \\&{\hspace{0.3cm} \frac{\left( \frac{|x-w_{3}|}{|w_{1}-w_{3}|}\right) ^{\upsilon _{1}-1}\left( 1-\frac{|x-w_{3}|}{|w_{1}-w_{3}|}\right) ^{\upsilon _{2}+\upsilon _{3}-1}\left( \frac{|y-w_{3}|}{|w_{2}-w_{3}|}\right) ^{\upsilon _{2}-1}\left( 1-\frac{|y-w_{3}|}{|w_{2}-w_{3}|}\right) ^{\upsilon _{1}+\upsilon _{3}-1}}{B(\upsilon _{1},\upsilon _{2},\upsilon _{3})\left( 1-\frac{|x-w_{3}|}{|w_{1}-w_{3}|}\frac{|y-w_{3}|}{|w_{2}-w_{3}|}\right) ^{\upsilon _{1}+\upsilon _{2}+\upsilon _{3}}}} \\&= \frac{|w_{1}-w_{3}||w_{2}-w_{3}|}{B(\upsilon _{1},\upsilon _{2},\upsilon _{3})}\\&\hspace{0.3cm}\cdot \frac{|x-w_{3}|^{\upsilon _{1}-1}|x-w_{1}|^{\upsilon _{2}+\upsilon _{3}-1}|y-w_{3}|^{\upsilon _{2}-1}|y-w_{2}|^{\upsilon _{1}+\upsilon _{3}-1}}{\left( |w_{1}-w_{3}||w_{2}-w_{3}|-|x-w_{3}||y-w_{3}|\right) ^{\upsilon _{1}+\upsilon _{2}+\upsilon _{3}}} \end{aligned} \end{aligned}$$

(13)

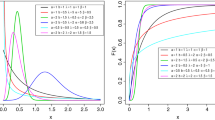
with x between $w_1$ and $w_3$ and y between $w_2$ and $w_3$ according to (10). We have not been able to integrate out $w_1,w_2,w_3$ from their joint distribution with x and y. However, we suspect that even if the joint density for X and Y could be expressed in terms of special functions, computing those might not be efficient enough for parameter inference for which we will resort to moment matching. Example plots with smoothed samples for the joint density are shown in Fig. 1 for several parameter settings showing different marginal distributions for X and Y and different correlations between X and Y. Sampling from the bivariate beta distribution is realized with JAGS [23].

Fig. 1

Joint densities of bivariate beta distributions with selected parameter values. The plots were created with kernel density estimation based on 10 million samples of the respective distributions. Note that the smoothing is inaccurate at the borders and produces artifacts close to zero and one as a consequence of smoothing with a symmetric kernel

2.2 Moments

As the marginal distributions for X and Y are beta-distributed, their moments are readily available, even in closed form. Computation of the product moments $\text {E}(X^kY^l)$ is more challenging but can be realized with help of the work of Olkin and Liu [10]. Looking at construction (10), X and Y are a linear combination of independent beta-distributed random variables $W_1,W_2,W_3$ with weights $X'$ and $Y'$. Thus, we can express the product moments as

$$\begin{aligned} \text {E}\left( X^k Y^l\right) = \text {E}\left( \left( X'W_{1}+(1-X')W_{3}\right) ^k \left( Y'W_{2}+(1-Y')W_{3}\right) ^l \right) . \end{aligned}$$

(14)

Since $X'$ and $Y'$ are independent of $W_1,W_2,W_3$, it is possible to compute the expectation if the moments of $W_1, W_2, W_3, X', Y'$ and the product moments of $X'$ and $Y'$ are known. $W_1, W_2, W_3$ as well as the marginals of $X'$ and $Y'$ are beta-distributed, so their moments can be computed straightforwardly in closed form. Furthermore, $X'$ and $Y'$ are jointly Olkin-Liu distributed according to (12), and Olkin and Liu [10] have shown how to compute their product moments. However, note that the derivation of $\text {E}((X')^k (Y')^l)$ in equation (2.2) in the work of Olkin and Liu [10] is incorrect and should read

$$\begin{aligned} \text {E}\left( (X')^k (Y')^l\right)&=\sum _{j=0}^{\infty }dA(j)\frac{B(\upsilon _1+k+j,\upsilon _2+\upsilon _3)}{B(\upsilon _1+j,\upsilon _2+\upsilon _3)}\frac{B(\upsilon _2+l+j,\upsilon _1+\upsilon _3)}{B(\upsilon _2+j,\upsilon _1+\upsilon _3)} \end{aligned}$$

(15)

$$\begin{aligned}&=\frac{\Gamma (\upsilon _1+\upsilon _3)\Gamma (\upsilon _2+\upsilon _3)\Gamma (\upsilon _1+k)\Gamma (\upsilon _2+l)\Gamma (\Upsilon )}{\Gamma (\upsilon _1)\Gamma (\upsilon _2)\Gamma (\upsilon _3)\Gamma (\Upsilon +k)\Gamma (\Upsilon +l)} \nonumber \\&\hspace{0.5cm}\sum _{j=0}^{\infty }\frac{(\upsilon _1+k)_{j}(\upsilon _2+l)_{j}(\Upsilon )_{j}}{(\Upsilon +k)_{j}(\Upsilon +l)_{j}}\frac{1}{j!} \end{aligned}$$

(16)

$$\begin{aligned}&= h \cdot {}_3F_2(\upsilon _1+k,\upsilon _2+l,\Upsilon ;\Upsilon +k,\Upsilon +l;1) , \end{aligned}$$

(17)

with

$$\begin{aligned} d&=\frac{\Gamma (\upsilon _1+\upsilon _3)\Gamma (\upsilon _2+\upsilon _3)}{\Gamma (\upsilon _3)\Gamma (\Upsilon )} \end{aligned}$$

(18)

$$\begin{aligned} A(j)&=\frac{\Gamma (\upsilon _1+j)}{\Gamma (\upsilon _1)}\frac{\Gamma (\upsilon _2+j)}{\Gamma (\upsilon _2)}\frac{\Gamma (\Upsilon )}{\Gamma (\Upsilon +j)}\frac{1}{j!} \end{aligned}$$

(19)

$$\begin{aligned} h&=\frac{\Gamma (\upsilon _1+\upsilon _3)\Gamma (\upsilon _2+\upsilon _3)\Gamma (\upsilon _1+k)\Gamma (\upsilon _2+l)\Gamma (\Upsilon )}{\Gamma (\upsilon _1)\Gamma (\upsilon _2)\Gamma (\upsilon _3)\Gamma (\Upsilon +k)\Gamma (\Upsilon +l)}, \end{aligned}$$

(20)

where $\Upsilon =\upsilon _1+\upsilon _2+\upsilon _3$ and ${}_pF_q$ is the generalized hypergeometric function. Equations  (15), (18), and (19) are taken directly from Olkin and Liu [10] with $a=\upsilon _1, b=\upsilon _2, c=\upsilon _3$. Equations (16), (17), and (20) are our corrections of their equations.

2.3 Correlation and covariance

The correlation r between X and Y is

$$\begin{aligned} r&=\frac{\text {Cov}(X,Y)}{\sqrt{\text {Var}(X)\text {Var}(Y)}} \end{aligned}$$

(21)

with the known variances of the beta marginals

$$\begin{aligned} \begin{aligned} \text {Var}(X)&=\frac{a_1a_2}{(a_1+a_2)^{2}(a_1+a_2+1)} \\&=\frac{(\alpha _{1}+\delta _{1})(\alpha _{2}+\delta _{2})}{(\alpha _{1}+\delta _{1}+\alpha _{2}+\delta _{2})^{2}(\alpha _{1}+\delta _{1}+\alpha _{2}+\delta _{2}+1)}\\ \text {Var}(Y)&=\frac{b_1b_2}{(b_1+b_2)^{2}(b_1+b_2+1)}\\&=\frac{(\beta _{1}+\delta _{1})(\beta _{2}+\delta _{2})}{(\beta _{1}+\delta _{1}+\beta _{2}+\delta _{2})^{2}(\beta _{1}+\delta _{1}+\beta _{2}+\delta _{2}+1)}. \end{aligned} \end{aligned}$$

(22)

For the covariance of X and Y Magnussen [5] gives an approximate solution, namely

$$\begin{aligned} \text {Cov}(X,Y)&\approx \frac{a_1 a_2 \delta _2 + (1+b_1)(1+b_2)\delta _1}{(a_1+b_1)(a_2+b_2)(1+a_1+b_1)(1+a_2+b_2)}, \end{aligned}$$

(23)

where $a_1$, $a_2$, $b_1$, and $b_2$ are defined based on $\alpha _1, \alpha _2, \beta _1, \beta _2, \delta _1, \delta _2$ as in (7). This approximation is inaccurate for small values of these parameters, e.g. for $a_1 = a_2 = b_1 = b_2 = 4, \delta _1 = \delta _2 = 3$, the approximated covariance is Cov$(X,Y) = 0.024$, while the true covariance computed from $10^6$ samples of the bivariate beta distribution is Cov$(X,Y) = 0.020$. This might seem like a small difference but it results in an overestimated correlation of $r = 0.854$ as opposed to the true correlation of $r = 0.730$. Even more worryingly, for $a_1 = a_2 = b_1 = b_2 = 1, \delta _1 = \delta _2 = \frac{4}{5}$, the approximated covariance is Cov$(X,Y) = \frac{1}{9}$, which results in an estimated correlation of $r=\frac{4}{3}$, which is greater than 1 and therefore wrong by definition.

Given the connection to the Olkin–Liu distribution [10], which we derived in Sect. 2.2, we therefore proceed to compute the exact covariance between X and Y:

$$\begin{aligned} \text {Cov}(X,Y)&= \text {E}(XY) - \text {E}(X)\text {E}(Y) \end{aligned}$$

(24)

where

$$\begin{aligned} \begin{aligned} \text {E}(X)&=\frac{a_1}{a_1+a_2} =\frac{\alpha _{1}+\delta _{1}}{\alpha _{1}+\delta _{1}+\alpha _{2}+\delta _{2}} \\ \text {E}(Y)&=\frac{b_1}{b_1+b_2} =\frac{\beta _{1}+\delta _{1}}{\beta _{1}+\delta _{1}+\beta _{2}+\delta _{2}} \end{aligned} \end{aligned}$$

(25)

are readily available as the means of the beta marginals. We can compute $\text {E}(XY)$ from (14) with $k=l=1$, which results in

$$\begin{aligned} \begin{aligned} \text {E}(XY)&=\text {E}\left( (X'W_{1}+(1-X')W_{3})(Y'W_{2}+(1-Y')W_{3})\right) \\&=\text {E}(X'Y')\text {E}(W_{1})\text {E}(W_{2}) + \left( \text {E}(X')-\text {E}(X'Y')\right) \text {E}(W_{1})\text {E}(W_{3}) \\&\hspace{0.4cm}+\left( \text {E}(Y')-\text {E}(X'Y')\right) \text {E}(W_{2})\text {E}(W_{3}) \\&\hspace{0.4cm}+\left( 1-\text {E}(Y')-\text {E}(X') +\text {E}(X'Y')\right) \text {E}(W_{3}^{2})\\ \end{aligned} \end{aligned}$$

(26)

with the moments of the beta marginals from (8)

$$\begin{aligned} \begin{aligned} \text {E}(W_{1})&=\frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}}\\ \text {E}(W_{2})&=\frac{\beta _{1}}{\beta _{1}+\beta _{2}}\\ \text {E}(W_{3})&=\frac{\delta _{1}}{\delta _{1}+\delta _{2}}\\ \text {E}(W_{3}^{2})&=\frac{\delta _{1}(\delta _{1}+1)}{(\delta _{1}+\delta _{2}+1)(\delta _{1}+\delta _{2})}\\ \end{aligned} \end{aligned}$$

(27)

and (10)

$$\begin{aligned} \begin{aligned} \text {E}(X')&=\frac{\upsilon _1}{\upsilon _1+\upsilon _3}\\ \text {E}(Y')&=\frac{\upsilon _2}{\upsilon _2+\upsilon _3} \end{aligned} \end{aligned}$$

(28)

with $\upsilon _1$, $\upsilon _2$, and $\upsilon _3$ as defined in (9). $\text {E}(X'Y')$ can be specialized from the moments (17) above with $k=l=1$:

$$\begin{aligned} \begin{aligned} \text {E}(X'Y')&=h\hspace{0.1cm}_{3}F_{2}(\upsilon _1+1,\upsilon _2+1,\Upsilon ;\Upsilon +1,\Upsilon +1;1)\qquad \text {with} \\ h&=\frac{\Gamma (\upsilon _1+\upsilon _3)\Gamma (\upsilon _2+\upsilon _3)}{\Gamma (\upsilon _3)\Gamma (\Upsilon +1)}\cdot \frac{\upsilon _1 \upsilon _2}{\Upsilon } \end{aligned} \end{aligned}$$

(29)

and $\Upsilon =\upsilon _1+\upsilon _2+\upsilon _3$ as before. According to Olkin and Liu [10] there is no closed-form solution for (17) and (29). However, using the generalized hypergeometric function the product moments and thus the covariance between X and Y can be computed numerically (e.g. by using the hyper function in sympy or the HypergeometricPFQ function in Mathematica). Note that with Raabe’s test one can show that the generalized hypergeometric function ${}_3F_2$ in (29) converges. According to Raabe’s test the series converges if

$$\begin{aligned} \lim _{j \rightarrow \infty } \rho _j > 1 \, \text {with} \, \rho _j = j\left( \frac{c_j}{c_{j+1}}-1\right) , \end{aligned}$$

(30)

where $c_j$ is the j-th element of the series described by the generalized hypergeometric function ${}_3F_2$ in (29), which is

$$\begin{aligned} c_j = \frac{(\upsilon _1+1)_{j}(\upsilon _2+1)_{j}(\Upsilon )_{j}}{(\Upsilon +1)_{j}(\Upsilon +1)_{j}}\frac{1}{j!}. \end{aligned}$$

(31)

Since $\lim _{j \rightarrow \infty } \rho _j = 1+\upsilon _3 > 1$, the generalized hypergeometric function ${}_3F_2$ in (29) converges. However, this analysis also suggests that convergence of the series might be very slow for small $\upsilon _3=\delta _1+\delta _2$.

2.4 Parameter inference

Magnussen [5] used the method of moments to infer the parameters $a_1$, $a_2$, $b_1$, $b_2$ for the marginal distributions. Given these parameters he then matched the empirical correlation to the correlation for the parameters $\delta _1, \delta _2$ (given marginal parameters $a_1$, $a_2$, $b_1$, $b_2$) using the approximate solution for the covariance given in (23). However, as shown in Sect. 2.3 this approximation can lead to very inaccurate correlation estimates. An additional problem with the distribution is that very similar data can be generated with different parameter values, as one can see in Fig. 2(a) and (b). Increasing $\delta _1$ and simultaneously decreasing $\delta _2$ or vice versa while keeping the marginal parameters $a_1, a_2$ and $b_1, b_2$ fixed, can result in very similar correlations, which is shown in Fig. 2(c). Since two distributions with very different parameters can lead to extremely similar data, it is hard to statistically infer the parameters $\delta _1$ and $\delta _2$ from data: The empirical correlation alone does not provide enough constraints and differences in higher moments can be subtle.

Fig. 2

Different parameters can generate similar data. (a) and (b) show samples generated from two bivariate beta distributions with the same marginal parameters $a=(8,6)$, $b=(6,5)$ and correlation parameters $\delta = (3.28, 2.73)$ for (a) and $\delta = (5,1.6)$ for (b). Both, the data in (a) and (b) show a correlation of $r = 0.47$. Correspondingly, (c) shows the correlations generated by different combinations of $\delta _1$ and $\delta _2$ given marginal parameters $a=(8,6)$ and $b=(6,5)$. Different combinations of $\delta _1$ and $\delta _2$ can lead to very similar correlations

Therefore, in order to make parameter inference unambiguous, we decided to constrain the 6-parameter bivariate beta distribution to five parameters: two for each marginal and one parameter to control the correlation. A reasonable way to constrain $\delta _1$ and $\delta _2$ is to set

$$\begin{aligned} \delta _2&= \frac{\delta ^{\text {max}}_2}{\delta ^{\text {max}}_1} \delta _1 \end{aligned}$$

(32)

with $\delta ^{\text {max}}_1 = \text {min}(a_1, b_1), \delta ^{\text {max}}_2 = \text {min}(a_2, b_2)$, because this enables the maximum possible correlation between X and Y when the maximum values for $\delta _1$ and $\delta _2$ are attained and the shared component between X and Y is as big as it can be without violating the marginal constraints.

2.4.1 Moment matching

Using this constraint (32), the model-inherent constraints $\delta _1< \delta ^{\text {max}}_1, \delta _2 < \delta ^{\text {max}}_2$, and the formula for the correlation derived in Sect. 2.3, we can now optimize the parameters numerically to match the empirical moments. First, the marginal parameters $a_1, a_2, b_1, b_2$ are obtained using the standard procedure of moment matching for the beta distribution. Given the estimated marginal parameters, an estimate of $\delta _1$ (and with it $\delta _2$) can be obtained numerically by minimizing the quadratic deviation between the theoretical correlation and the empirical correlation. To avoid the undefined cases $\delta _1 \le 0$ and $\delta _1 \ge \delta ^{\text {max}}_1$ we bound the optimization between $\varepsilon$ and $\delta ^{\text {max}}_1 - \varepsilon$ with $\varepsilon = 0.001$. Unless the empirical correlation is bigger than the maximum correlation that can be attained with the matched marginals or smaller than 0, it can be matched exactly for some $\delta _1$. Otherwise $\delta _1$ will take on its maximum value $\delta ^{\text {max}}_1 - \varepsilon$ or its minimal value $\varepsilon$. We implement inference in Python using the package mpmath [24] for the numerical computation of the generalized hypergeometric function and the package scipy [25] for optimization.

As an example we used this numerical moment matching approach on 5000 data points generated with parameters $a_1 = 8$, $a_2 = 6$, $b_1 = 6$, $b_2 = 5$, $\delta _1 = 3.28$, $\delta _2 = 2.73$, equivalent to the data shown in Fig. 2(a). We inferred the parameter values $\hat{a}_1 = 8.143, \hat{a}_2 = 6.193, \hat{b}_1 = 5.882, \hat{b}_2 = 4.931, {\hat{\delta }}_1 = 3.286, {\hat{\delta }}_2 = 2.754$. Figure 3(a) shows the correlations implied by different values for parameter $\delta _1$ compared to the desired correlation of $\hat{r}=0.47$. As one can see, the difference between r and $\hat{r}$ is zero for the inferred ${\hat{\delta }}_1 = 3.286$. Due to our constraint (32), ${\hat{\delta }}_2 = 2.754$ can be computed from $\delta _1$. In this case there is an almost linear relationship between $\delta _1$ and r but this is not true in general, especially for smaller parameter values.

This can be seen in a second example where we applied our moment matching approach on 5000 data points generated with parameters $a_1 = 0.2$, $a_2 = 0.9$, $b_1 = 0.4$, $b_2 = 1$, $\delta _1 = 0.1$, $\delta _2 = 0.45$ and received the inferred parameter values $\hat{a}_1 = 0.197, \hat{a}_2 = 0.903, \hat{b}_1 = 0.403, \hat{b}_2 = 1.017, {\hat{\delta }}_1 = 0.101, {\hat{\delta }}_2 = 0.462$. As seen in Fig. 3(b), for this second example the relationship between $\delta _1$ and the correlation is not well approximated by a linear function, in contrast to the first example in Fig. 3(a). Still, inference works as for the first example shown above.

Fig. 3

The correlations r implied by different values of correlation parameter $\delta _1$ compared to the desired correlation $\hat{r}$ given estimates of the marginal parameters $a_1, a_2, b_1, b_2$. $\delta _2$ is not displayed since it can be computed from $\delta _1$ using constraint (32). $r_{\text {max}}$ is the maximum correlation that can be reached for the given marginal parameters. (a) shows the first inference example with $a_1 = 8.143, a_2 = 6.193, b_1 = 5.882, b_2 = 4.931$, $\hat{r} = 0.47$, and $r_{\text {max}} = 0.864$. The difference between r and $\hat{r}$ is zero for $\delta _1 = 3.286$. In (b) we show the second inference example with $a_1 = 0.197, a_2 = 0.903, b_1 = 0.403, b_2 = 1.017$, $\hat{r} = 0.314$, and $r_{\text {max}} = 0.707$. The difference between r and $\hat{r}$ is zero for $\delta _1 = 0.101$. The dotted linear reference line additionally shows that the relationship between the correlation and $\delta _1$ is non-linear

2.4.2 Simulation study

The performance of the proposed approach for parameter inference was evaluated in a simulation study. We generated data from a bivariate beta distribution using different marginal parameters, correlation parameters, and different numbers of generated samples N and inferred $\delta _1$ from these data using the proposed moment matching approach. For half of all considered simulations, X and Y were chosen to have the same marginal parameters to be able to generate the full range of correlations from 0 to 1, hence $a_1=b_1, a_2=b_2$. All possible combinations of the values in [0.5, 1, 2, 3, 4, 5] for $a_1$ and $a_2$ were tested while omitting symmetric cases with $a_1 \le a_2$, resulting in 21 different marginal distributions. For the remaining simulations we considered differing marginal distributions. We chose a subset of 7 marginal distributions from the set of marginals above as [[0.5, 0.5], [1, 1], [1, 4], [2, 2], [2, 4], [3, 3], [4, 5]] and tested inference for all $\left( {\begin{array}{c}7\\ 2\end{array}}\right) = 21$ combinations of different marginals in this set. Thus, in total we inferred parameters for 42 combinations of marginals. The correlation parameters $\delta _1$ were chosen as $p \cdot \delta _1^{max}$ with $p = 0.01, 0.05, 0.25, 0.5, 0.75, 0.95, 0.99$ respectively, in order to show how inference works for data with different correlations between 0 and the maximum possible correlation for the respective marginals. $\delta _2$ was obtained using the constraint in (32). To test the effect of the number of samples N on the accuracy of parameter inference we evaluated with $N=100,500,1000$. For each of the $42 \cdot 7 \cdot 3 = 882$ parameter settings, we repeated the data simulation and inference process 50 times, resulting in 44100 inference results. These results are displayed in Fig. 4, for $N=100, 500, 1000$ in (a), (b), (c) respectively. We can see that the inferred ${\hat{\delta }}_1$ match the true value of $\delta _1$, the better the higher the number of available data samples N. The average standard deviations of all inferred ${\hat{\delta }}_1$ are 0.171 for $N=100$, 0.078 for $N=500$, and 0.055 for $N=1000$. Note that although the generalized hypergeometric function ${}_3F_2$ in (29) is guaranteed to converge, as we showed in Sect. 2.3, it can happen that its numerical computation fails due to very slow convergence. In our simulation study, this error occurred for 2.5% of all inference computations, only for low values of $\delta _1$.

Fig. 4

Results of a simulation study for evaluating the proposed moment matching approach for parameter inference. We generated data from a bivariate beta distribution using different marginal distributions with different correlations and different numbers of generated samples N and inferred $\delta _1$ from these data. We show inferred ${\hat{\delta }}_1$ against true $\delta _1$ for $N=100$ samples (a), $N=500$ samples (b), and $N=1000$ samples (c). ${\hat{\delta }}_1$ matches $\delta _1$, the better the higher the number of available data samples N

2.4.3 Application on a real data set of correlated forecasts

Fig. 5

The predicted winning probabilities from the chess classifier data set. (a) and (b) show the marginal distributions of X representing classifier 1 (Bayes Net), and Y representing classifier 2 (Random Forest). For both marginal distributions we show the relative frequencies of the predictions as well as the beta densities inferred with moment matching. (c) jointly shows X and Y, which are correlated with approximately $\hat{r}=0.483$. (d) shows a simulated data set consisting of 1527 samples of a bivariate beta distribution with the parameters inferred for the chess classifier data set

The bivariate beta distribution has broad applicability in many fields as diverse as Bayesian analysis, where it can model the correlation among priors for Binomial distributions [14], the modeling of proportions of hardwood forests over time, where it serves to estimate decadal changes in the relative land use of a region [5], the modeling of proportions of electorate voting in a two candidate election, proportions of substances in mixtures, or brand shares [16], and utility assessment [6]. Furthermore, the bivariate beta distribution can be used for modeling probabilities produced by two correlated forecasters. Correlations between forecasters are quite common, e.g. two bookmakers who base their odds on common information will produce correlated odds. For the same reason experts in risk assessment will often produce correlated forecasts. Similarly, different machine classifiers produce correlated predictions when trained on the same data [26]. These correlations should be taken into account when their predictions are combined, e.g. in different techniques for classifier fusion [27], since combining correlated classifiers can otherwise lead to overconfidence and high generalization error [28]. Here, we use such a data set consisting of the predictions of two classifiers as an illustrative example for the application of the proposed inference method. Two classifiers, a Bayes Net and a Random Forest, were trained on Alen Shapiro’s chess (King-Rook vs. King-Pawn) data set [29, 30].¹ The task is to predict if King+Pawn will win a chess match against King+Rook based on 36 categorical features of a chess position. For training both classifiers, we used 10-fold cross-validation. The two classifiers’ predictions on the respective 10 test sets form the data set we evaluate on. We only considered the predicted probabilities of winning King+Pawn for all 1527 match instances actually won by King+Pawn. The predicted probabilities of winning King+Rook for the matches actually won by King+Rook might follow a different distribution and are therefore excluded in our example. With the bivariate beta distribution we now model the winning probabilities the two classifiers predicted for King+Pawn.

Figure 5 shows the data and the inferred distribution. X is the predicted probability for King+Pawn winning of classifier 1, a Bayes Net, and Y the predicted probability of classifier 2, a Random Forest. In Fig. 5(a) and (b) we show histograms of the predictions of X and Y together with marginal beta densities that were inferred with moment matching: the parameters are $\hat{a}_1 = 2.094, \hat{a}_2 = 0.64$ for (a) and $\hat{b}_1 = 4.44, \hat{b}_2 = 0.288$ for (b). Figure 5(c) jointly shows X and Y with a correlation of approximately $\hat{r}=0.483$. Matching this correlation, too, as described in Sect. 2.4.1, we obtain ${\hat{\delta }}_1 = 1.723$ and ${\hat{\delta }}_2 = 0.237$. The corresponding correlation is $r = 0.483$, which matches the data’s empirical correlation up to numerical precision. Figure 5(d) shows a simulated data set consisting of 1527 samples drawn from a bivariate beta distribution with the inferred parameters, $\hat{a}_1 = 2.094, \hat{a}_2 = 0.64, \hat{b}_1 = 4.44, \hat{b}_2 = 0.288, {\hat{\delta }}_1 = 1.723$ and ${\hat{\delta }}_2 = 0.237$. As can be seen, the generated data set is similar to the real data set in Fig. 5(c) and the classifiers’ predictions can thus be modeled reasonably well with this bivariate beta distribution.

2.4.4 Relationship between $\delta _1$ and the correlation

We found empirically that over a large range of parameters the following approximate relationship holds:

$$\begin{aligned} r&\approx \frac{\delta _1}{\delta _1^{\text {max}}} r_{\text {max}}, \end{aligned}$$

(33)

while $\delta _1^{\text {max}} = \text {min}(a_1, b_1)$ and $r_{\text {max}}$ is the maximum possible correlation for the given marginals. While this relationship could be used for approximate inference of $\delta _1$, we still recommend the moment matching approach proposed in Sect. 2.4.1 that gives exact results. However, the shown relationship allows interpreting the correlation parameter $\delta _1$. Particularly for equal marginal distribution with $a_1 = b_1$ and $a_2 = b_2$, for which $r_{\text {max}} = 1$, this interpretation of $\delta _1$ is very simple: The fraction of $\frac{\delta _1}{\delta _1^{\text {max}}}$ approximately matches the generated correlation. For example, if $a_1 = b_1 = 2$ and $a_2 = b_2 = 4$, for $\delta _1 = 1$ we generate a correlation of $r = 0.468 \approx \frac{1}{2} r_{\text {max}} = 0.5$ with $r_{\text {max}} = 1$. For differing marginal distributions, interpreting $\delta _1$ is more difficult because $r_{\text {max}}$ must be computed numerically using the formulas given above. If, e.g., $a_1 = a_2 = 2$ and $b_1 = 1, b_2 = 4$, with $\delta _1 = 0.5$, we generate a correlation of $0.3 \approx \frac{0.5}{1} r_{\text {max}} = 0.313$ with $r_{\text {max}} = 0.627$. In Fig. 6, we plot the exact correlation and the approximated correlation computed with (33) for all parameter configurations used in the simulation study in Sect. 2.4.2. As can be seen, the relationship in (33) holds for all parameter values. The plateaus seen for approximate correlations of 0.25, 0.5, and 0.75 are a consequence of choosing $\delta _1 = p \cdot \delta _1^{\text {max}}$ with $p=0.25,0.5,0.75$ in the simulation study (Sect. 2.4.2) leading to approximate correlations of 0.25, 0.5, 0.75 for all simulations with equal marginals. We leave it as an open problem to show when approximation (33) holds to what accuracy.

Fig. 6

The exact correlation computed as in Sect. 2.3 compared to the approximate correlation computed with Eq. (33) for all parameter configurations used in the simulation study in Sect. 2.4.2

3 Generalization to the correlated Dirichlet distribution

The bivariate beta distribution can be generalized to a correlated Dirichlet distribution [27] in order to model two positively correlated random vectors $\varvec{X}=(X_1, \dots , X_k)$ and $\varvec{Y}=(Y_1, \dots , Y_k)$ with the two marginal vectors being Dirichlet-distributed. A k-dimensional correlated Dirichlet distribution can be constructed from 3k gamma-distributed random variables $A_1, \dots , A_k$, $B_1, \dots , B_k$, $D_1, \dots , D_k$ with 3k parameters $\alpha _1, \dots , \alpha _k$, $\beta _1, \dots \beta _k$, $\delta _1, \dots \delta _k$ distributed according to

$$\begin{aligned} \begin{aligned} A_i&\sim \text {Gamma}(\alpha _i, 1)\quad i = 1,\dots ,k \\ B_i&\sim \text {Gamma}(\beta _i, 1)\hspace{0.02cm}\quad i = 1,\dots ,k \\ D_i&\sim \text {Gamma}(\delta _i, 1)\quad \hspace{0.06cm} i = 1,\dots ,k. \end{aligned} \end{aligned}$$

(34)

These random variables are used to construct the correlated Dirichlet-distributed random variables $\varvec{X}=(X_1,\dots ,X_k)$ and $\varvec{Y}=(Y_1,\dots ,Y_k)$ with

$$\begin{aligned} X_i&= \frac{A_i + D_i}{\sum _{i=1}^{k}{A_i} + \sum _{i=1}^{k}{D_i}} \quad \qquad \textrm{and}\quad \qquad Y_i = \frac{B_i + D_i}{\sum _{i=1}^{k}{B_i} + \sum _{i=1}^{k}{D_i}}. \end{aligned}$$

(35)

The two resulting marginal distributions are Dirichlet($\varvec{X}; \alpha _1 + \delta _1, \dots , \alpha _k + \delta _k$) and Dirichlet($\varvec{Y}; \beta _1 + \delta _1, \dots , \beta _k + \delta _k$).

Analogous to the example for the bivariate beta distribution in Sect. 2.4.3, this correlated Dirichlet distribution can be used for modeling non-binary probabilistic predictions of experts, sensors, or classifiers. This is particularly useful for Bayesian approaches to classifier or expert fusion, which are the reason why we started working on this distribution in the first place. For example, in a companion paper we apply it to classifier fusion, but instead of using moment matching—as developed here—we use rather inefficient Markov-chain methods to sample from the posterior distribution over the parameters [27]. Being able to explicitly model the correlation between probabilistic classifiers or probability estimates given by human experts with the correlated Dirichlet distribution allows Bayes optimal fusion of classifiers or experts, avoids overconfidence of the ensemble and thereby improves its performance. Applications of classifier fusion are widespread. Popular examples are intrusion detection, fake news detection, detection of diseases in medicine, or recognition of human states such as emotions [31]. Another application of the correlated Dirichlet distribution is the generation of stochastic matrices with individual rows or columns being Dirichlet-distributed and correlated, which can be beneficial for Markov processes, in optimal control, or reinforcement learning.

The derivations of the product moments and the exact covariance of the correlated Dirichlet distribution are analogous to the derivations for the bivariate beta distribution shown in this work. Thus, the parameters of the correlated Dirichlet distribution can also be estimated using the proposed moment matching approach, extended to the higher dimensionality of the Dirichlet distribution.