Abstract
Teachers’ performances also depend on whether and how they are satisfied with their job. Therefore, Teacher Job Satisfaction must be considered as the driver of teachers’ accomplishments. To plan future policies and improve the overall teaching process, it is crucial to understand which factors mostly contribute to Teacher Job Satisfaction. A Common Assessment Framework and Education questionnaire was administered to 163 Italian public secondary school teachers to collect data, and a second-order factor analysis was used to detect which factors impact on Teacher Job Satisfaction, and to what extent. This model-based approach guarantees to detect factors which respect important properties: unidimensionality and reliability. All the coefficients are estimated according to the maximum likelihood estimation method in order to make inference on the parameters and on the validity of the model. Moreover, a new multi-group test for higher-order factor analysis was proposed and implemented. Finally, we analyzed in detail whether the factors impacting Teacher Job Satisfaction are characterized by gender.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Improving the quality of education and training is a key point in the political debate on education at European level. The need for policies and systems to guarantee and improve the quality of education has been widely recognized. Linked to the school system quality is its evaluation framework. If the main aim of evaluation process is the analysis of the student’s learning processes, the self-analysis or self-evaluation of the school, extended to all stakeholders, denote the strength of a school that aims at the effectiveness and efficiency of the training service. It happens because there is a close and direct relationship between student learning and quality organization in which learning processes are carried out. Self-evaluation by school staff has become increasingly important for the quality assurance of educational systems. Far-reaching collected researches on Job Satisfaction (JS) has revealed: teachers who are satisfied with their jobs perform better. Moreover, Teacher Job Satisfaction (TJS) has many important effects. First, it contributes to teacher well-being reducing stress and the risk of burnout. Second, satisfied teachers offer higher instructional quality and better learning support for their students. Finally, content teachers demonstrate stronger job commitment and are less prone to leave the profession, which is especially crucial in times when teacher turnover is high.
JS is a multidimensional phenomenon and measuring TJS has become a significant interdisciplinary focus of discussion for researchers. The aim of this paper is to measure the TJS through a model-based Composite Indicator by deeply understanding how policymakers and institutions can intervene to improve teacher performances increasing their JS. TJS is certainly a driver of performances by the teachers, thus validating which factors measure this multidimensional concept and how they contribute is a crucial aspect for future actions. Moreover, understanding whether the factors (i.e., Specific Indicators) that contribute to TJS definition are the same for males and females is useful to plan policies.
In Sect. 2, starting from a brief review of the literature regarding factors that may affect TJS, a conceptual model to analyse TJS is introduced. Section 3 deals with the collected data and statistical methodologies used. In detail, we propose a multi-group higher-order factor analysis based on a new test of the factor coefficients. In Sect. 4, the empirical findings examining the effects of the factors regarding public teacher performance are discussed. Finally, a conclusion is reached based on a discussion of the research findings.
2 Background and theoretical framework
In 2013, Italy started to define an evaluation program both for educational system and for schools. The National Evaluation System has different goals: helping each school to keep under control its own provided education; supporting the Ministry of Education to device actions for the schools’ improvement plans; evaluating headteachers and, finally, showing the results of educational action outside school. The school evaluation process contains four stages: school self-evaluation, external evaluation, implementation of improvement actions and social reporting which consists of sharing, publishing and disseminating the achieved results. School self-evaluation is based on data collected from several sources through periodical monitoring: Ministry of Education, INVALSI (National Institute of Evaluation of Educational System) and schools themselves. The evaluation ends with a Self-evaluation Report (RAV) and with the elaboration of an improvement plan. RAV consists of three sections: Context, Results and Processes. The session “Context” discusses the social structure in which an educational intervention is placed and comprises the following aspects: the school population; the territory and the social capital; economic and material resources; professional resources. The section “Results” is considered the most important part of the evaluation, and refers to the educational success of each student, overall as a person. The section “Processes” represents the fulcrum of the actions by the school and is divided in “Didactic and educational practices”, that considers the processes related to teaching and learning, and “Managing and organization practices”, which involves the processes realized in connection with the territory and families, that is, the actions related to the strategic orientation and the organization of the school, the development and enhancement of human resources, and, integration with the territory and relations with families. To achieve the requested goals, each section includes the definition of the area and the related indicators, the guide questions, the strong and weak points and the general criterion of quality.
TJS represents a crucial aspect of “Managing and organization practices”. In general, JS is defined as the affective orientation that an employee has towards his or her work [2, 24, 28, 29]. Others indicate JS as the feelings, attitudes or preferences of individuals regarding work [5, 28]. In literature, there are many theories which try to understand the nature of JS. Porter and Lawler [23] fixated the influences on JS in two groups of internal and external satisfactory dimensions. According to them, internal satisfactory dimensions are linked to the work itself (such as feeling of independence, feeling of achievement and other similar feelings obtained from work), whereas external satisfactory dimensions are not directly related to the work itself, and include dimensions such as good relationships with colleagues and leadership, good welfare, good school climate, good workplace conditions and strong involvement [1]. Dinham and Scott [11, 12] recognized in their studies a third dimension of variables that has an impact on TJS, the so-called school-based dimensions. The status of teachers and increased administrative workloads are school-based dimensions, such as school leadership, climate, decision making, school reputation (external school image), and school infrastructure. Self-evaluation by school staff has become increasingly important for the quality assurance of educational systems. Throughout the last few years, a variety of self-evaluation practices have emerged, and several goals ascribed to school self-evaluation: on the one hand, accountability to central authorities or local stakeholders, and on the other, stressing the potential for school improvement. Recent Organization for Economic Cooperation and Development (OECD) recommendations, made effective by the Italian School reform law number 107/15, indicate the need to align external evaluation with school self-evaluation order to improve school quality. With the law 107/15, self-evaluation became a procedure initiated and carried out by a school in order to describe and evaluate its operation [3]. Self-evaluation, however, can only work if team members are positively disposed towards it [19].
TJS, and the drivers that affect it, could be considered as latent constructs [25, 26, 30], each measured by several manifest variables. Such latent constructs represent the phenomenon to measure, TJS, and its specific factors. As a result, using a reflective hierarchical model, we arranged latent and manifest variables and their relationships within a framework. Research questions are:
-
RQ1)
What are the Factors Impacting Teacher Job Satisfaction?
-
RQ2)
To what extent do the Factors impact on Teacher Job Satisfaction?
-
RQ3)
Are the Factors Impacting Teacher Job Satisfaction characterized by gender?
Through a Self-Administered survey Questionnaire, the study provides an answer to the research questions.
3 Materials and methods
3.1 Questionnaire and data collection
In order to study the TJS, we consider a questionnaire (see Appendix) consisting of 25 four Likert Scale questions (1 = Disagree, 2 = Slightly Disagree, 3 = Agree, 4 = Strongly Agree) divided in six specific aspects/dimensions: Communication, External school image, Leadership, School Climate, Involvement and Infrastructure. The questionnaire is anonymous and includes demographic and personal aspects (e.g., gender). Our study considers 163 Italian public secondary school teachers, 48 (\(29.45\%\)) males and 115 (\(70.55\%\)) females (the respondents whom avoid filling in the variable gender are removed from the study).
The first dimension, Communication, is measured through five survey items including information access procedures, secretarial staff, school staff, website, and leadership communication. External school image evaluates the school’s initiatives to promote the latter aspect, and community recognition by two questionnaire items. Five items compose the third dimension (Involvement) which measures how personnel and families are involved in decisions and encouraged in many ways to make their contribution. The fourth dimension, Leadership, is measured through four questions regarding commitment to promote continuous improvement and to effectively organize the school’s work. School climate consists of six items intended to measure the relationship between colleagues, leadership, school staff, parents and students. And, finally, the sixth dimension, Infrastructure, is measured by two items that comprise technological equipment and work infrastructure.
3.2 Second-order Disjoint Exploratory Factor Analysis Model
The Second-order Disjoint Exploratory Factor Analysis (2O-DFA) model considers two typologies of latent unknown constructs (quantified as factors): H specific constructs and the general construct obtained by the two simultaneous models. The general construct has obtained by aggregating the specific ones. Formally, let \({\mathbf {x}}\) be the (\(J \times 1\)) multivariate random variable with mean vector \({\varvec{\mu }}_{\mathbf {x}} = [{\varvec{\mu }}_1,\dots ,{\varvec{\mu }}_J]'\), and J-dimensional variance-covariance matrix \({\varvec{\varSigma }}_{\mathbf {x}}\).
where \({\mathbf {A}}\) is the (\(J \times H\)) matrix of unknown specific factors loadings, \({\mathbf {y}}\) is the non-observable (\(H \times 1\)) random vector denoting the specific factor scores and \({\mathbf {e}}_{\mathbf {x}}\) is a (\(J \times 1\)) random vector of errors for the model (1). Whereas g is a realization of the general factor score \({\mathbf {g}}\) which is normally distributed with mean 0 and variance \(\sigma _{{\mathbf {g}}}^2=1\), \({\mathbf {c}}\) is a (\(H \times 1\)) vector of unknown general factor loadings and \({\mathbf {e}}_{\mathbf {y}}\) is a (\(H \times 1\)) random vector of errors for the model (2).
The complete model might be written including equation (2) into equation (1) and considering the loading matrix \({\mathbf {A}}\) equal to the product \({\mathbf {BV}}\), where \({\mathbf {B}}\) is a diagonal matrix and \({\mathbf {V}}\) a row stochastic and binary matrix. Thus, 2O-DFA for n multivariate observation, is defined
Under assumption of normality for \({\mathbf {y}}\), \({\mathbf {e}}_{\mathbf {x}}\) and \({\mathbf {e}}_{\mathbf {x}}\), it can be derived that \({\mathbf {x}} \sim N_J ({\varvec{\mu }}_{\mathbf {x}},{\varvec{\varSigma }}_{\mathbf {x}})\) with
where the correlation matrix of the specific factors \({\varvec{\varSigma }}_{\mathbf {y}}\) is equal to \({\mathbf {cc}}'+{\varvec{\varPsi }}_{\mathbf {y}}\), \({\varvec{\varPsi }}_{\mathbf {x}}\) is the J-dimensional diagonal positive definite variance-covariance matrix of the error of model (1) and \({\varvec{\varPsi }}_{\mathbf {y}}\) is the H-dimensional diagonal positive definite variance-covariance matrix of the error of model (2).
The aim of 2O-DFA is reconstructing \({\varvec{\varSigma }}_{\mathbf {x}}\) and \({\varvec{\varSigma }}_{\mathbf {y}}\) in terms of \(2J+H-1\) unknown free parameters in \({\mathbf {A}}={\mathbf {BV}}\), \({\varvec{\varPsi }}_{\mathbf {x}}\), \({\mathbf {c}}\) and \({\varvec{\varPsi }}_{\mathbf {y}}\). The discrepancy function to minimize with respect to \({\mathbf {B}}\), \({\mathbf {V}}\), \({\mathbf {c}}\), \({\varvec{\varPsi }}_{\mathbf {x}}\) and \({\varvec{\varPsi }}_{\mathbf {y}}\) is
where \({\mathbf {S}}_{{\mathbf {x}}}= \frac{1}{n} \sum _{i=1}^n ({\mathbf {x}}_i-\bar{{\mathbf {x}}})({\mathbf {x}}_i-\bar{{\mathbf {x}}})'\) is the J-dimensional sample variance-covariance matrix and \(\bar{{\mathbf {x}}}\) is the sample mean. In order to minimize the discrepancy function, a descent coordinates algorithm has been developed requesting that all the items on the diagonal of \({\mathbf {B}}\) and the elements of \({\mathbf {c}}\) must be nonnegative. 2O-DFA was used by Cavicchia, Sarnacchiaro and Vichi [4] in order to build a consistent Composite Indicator for Waste Management in EU.
3.3 2O-DFA multi-group analysis: test on coefficients
The model detected by 2O-DFA and the magnitude of its relationships could change because of the population’s heterogeneity, therefore researchers could be interested to test the presence of a group-effect in the definition of the general construct. As already explained in Sect. 3.2, 2O-DFA implies a two-order analysis where the relationships between the two typologies of latent constructs (i.e., specific and general constructs) are given by factorial coefficients (i.e., loadings). We propose to implement a multi-group procedure to test 2O-DFA second-order coefficients (i.e., the loading between the specific and general constructs). Therefore, our analysis wants to verify if the chosen model (i.e., the dimensions considered) is respected by the groups taken into account. The procedure proposed by Chin [6], successively explained and developed by Dibbern and Chin [10] and Chin and Dibbern [7], and the Henseler’s PLS Multi-Group Analysis (Henseler’s PLS-MGA, [16]) were developed to conduct a multi-group analysis within a Partial Least Square path modelling framework without imposing distributional assumptions. The latter is also well described by Sarstedt et al. [27]. For further details on observations’ random assignment to groups see Hair et al. [15], and Edgington and Onghena [13] for more details on randomization tests.
In our analysis, we consider an extension of Henseler’s PLS-MGA called PLS-MGA procedure (implemented also in SmartPLS) and proposed by Henseler et al. [18]. An adjustment of the latter procedure, called 2O-DFA Multi-group analysis (2O-DFA-MGA), has resulted feasible to test potential group differences in the definition of the general construct into 2O-DFA.
The 2O-DFA-MGA procedure is as follows:
- Step 1:
-
Select a coefficient in the definition of the general construct for the multi-group analysis (i.e., c: an element of vector \({\mathbf {c}}\));
- Step 2:
-
Run bootstrapping for each group (i.e., group of males, M, and group of females, F);
- Step 3:
-
Compare and evaluate the observed distribution of the bootstrap results. Hence, given two groups with the coefficient estimates, \(c_s^M\) and \(c_s^F\), it is possible to determine the conditional probability \(P(c_s^M > c_s^F | c^M \le c^F)\) where \(c^M\) and \(c^F\) represent the true population parameters of groups M and F, respectively;
- Step 4:
-
Similarly to a Mann-Whitney-Wilcoxon test [20, 31], compute the conditional probability:
$$\begin{aligned} P(c_s^M > c_s^F \big | c^M \le c^F) = 1 - \sum \nolimits _{\forall i, j} \frac{I(2\bar{c}_s^M - c_{sj}^M - 2\bar{c}_s^F + c_{si}^F)}{N^2} \end{aligned}$$(6)where N is equal to the number of bootstrap samples, I is the unit function which assumes value equal to 1 if its argument is larger than 0, otherwise 0, and, \(\bar{c}_s^M\) and \(\bar{c}_s^F\) denote the means of the coefficient over the bootstrap samples;
- Step 5:
-
Evaluate the results: if the probability computed at Step 4 is bigger than 0.95 or smaller than 0.05, it means that there is a significant difference of the group-specific coefficients.
We conduct the analysis for each second-order loading, that is, for each element of vector \({\mathbf {c}}\), in order to test the group-specific component for all dimensions.
Multi-group analyses imply the testing of measurement model invariance [17, 22] but in our case it is not necessary, as the definition of the latent constructs (both specific and general) is determined by the structure of the questionnaire and 2O-DFA estimates only the magnitude of loadings into matrix \({\mathbf {B}}\) and vector \({\mathbf {c}}\). This means that assuming the membership matrix \({\mathbf {V}}\) equal across groups guarantees to comply equal form measurement model invariance. In order to guarantee the consistency of the results and conclusions, the minimum number of bootstrapping permutation runs is advised to be equal to 5, 000; in our analysis we run the model 10, 000 times.
4 Results
4.1 Sample data analysis
In order to analyze our sample, 2O-DFA has been applied in a confirmatory framework. It allows us to propose a hierarchically aggregated index that best represents the TJS, via the statistical evaluation of reliable dimensions. Each dimension measures a specific aspect contributing to the definition of TJS. Our analysis is characterized by the study of the complete dataset and of both male and female ones separately. Our idea is to test if the conceptual hypothesized model is verified both in general, and per individual sub-sample. A few missing data are present in the studied sample, which are MCAR (Missing Completely at Random) and are imputed by the K-Nearest Neighbors method by setting \(K = 4\), and by using the Euclidean distance separately with respect to the gender. The descriptive analysis for the 25 variables (Table 1) shows that all of them had acceptable kurtosis and skewness values, always lying within \([-1; 1]\), both considering the entire sample and the two sub-samples separately.
The descriptive results highlight how males are generally more satisfied than females, the average of responses of males is smaller only for 3 of the 25 items (i.e., “The procedures to access to the information are simple” and “The website offers the possibility to access useful information and documentation in the dimension” in the dimension Communication, and “The initiatives of the school are known on the territory” in the dimension External school image) compared with the responses provided by females.
4.2 Teacher Job Satisfaction 2O-DFA
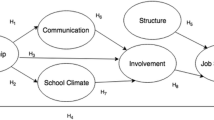
2O-DFA identifies a system of loadings able to define a second-order hierarchy with the general construct at the top of it. Hence, in our study, we hypothesize a hierarchical model in order to represent the multidimensionality of TJS and to define a Composite Indicator. The first order defines such six dimensions (Specific Indicators) through six disjoint sets of variables, whereas the second one is represented by the TJB index. Thus, it is worthy of remark that the model embroils the definition of six dimensions (as already explained in Sect. 3.1), and each dimension is characterized by some specific questionnaire items (i.e., questions). Furthermore, our approach takes into account the relations among the different manifest variables, while, at the same time, considers the correlations among the specific latent constructs. 2O-DFA allows the reconstruction of the observed covariance matrix via a hierarchical structure following Eq. (4).
The first scope of our analysis is to test whether the proposed model could properly measure TJB and whether the dimensions represented into the questionnaire reflected this multidimensional phenomenon. In order to do this, we first investigate whether all variables are concordant with the related dimensions and, consequently, with the general latent construct. All relationships result positive and statistically significant (Table 2); it means that all variables reflect the associated latent dimension. Moreover, the model is well constructed because all dimensions result unidimensional and strongly reliable (Table 3), thus, the general construct TJS results well identified by the six dimensions: Communication (Comm), External school image (Imag), Involvement (Invo), Leadership (Lead), School climate (Clim) and Infrastructure (Infr). Each dimension reliably measures a specific and unidimensional aspect of the TJS.
In order to asses the variable section and the goodness of the estimations, the standard errors and the p-values for the estimation of first-order factor loadings (\(\widehat{b}_j\)) for each model proposed in this paper (Tables 2, 4, and 5). In detail, we tested whether each loading is equal to zero (null hypothesis: \(b_j=0\)) according to the Student’s T statistic [8]. Thus, standard errors were equal to \(\sqrt{\frac{1-\widehat{b}_j^2}{n-2}}\) and \(P(T>|t_{\text {obs}}|)\) were calculated as the corresponding two-sided p-values for the t-distribution with \(n-2\) degrees of freedom. For assessing the reliability of the dimensions, we consider the widely used index Cronbach’s Alpha [9]. A credited rule of thumb for describing reliability was given by George and Mallery [14] as follows: if the index is larger than 0.9 the level of reliability is excellent, when it lies within [0.8, 0.9] the level is good, when the index is within [0.7, 0.8[ we can consider the level of reliability acceptable, and, finally, indices under 0.7 are unacceptable. For assessing unidimensionality, we used the second largest eigenvalue of the variance-covariance sub-matrices related to the two subsets of manifest variables, which must be smaller than 1.
The dimensions Involvement, Leadership and School climate are the most important in the definition of TJS (Fig. 1) with loadings equal to 0.86, 0.91 and 0.85, respectively. Therefore, the model underlines the high importance of items like “DSGA (Head of Administration) is able to handle its role with efficiency and effectiveness” and “The staff of the school receive appropriate tasks according to their specific skills”. All dimensions are positively correlated, thereby reflecting the same latent concept (i.e., the TJS). However, it is worth underscoring that Communication and Infrastructure are less correlated with all the other dimensions.
The obtained results show how the proposed questionnaire, as thought, can measure consistently a multidimensional concept as TJS. Therefore, the proposed model provides a hierarchically aggregated index for TJS by including six dimensions which represent the main aspects of it. This model presents good properties (i.e., it is statistically estimated and not normative, reliable, unidimensional) which make the model itself very useful to provide indications to policymakers and institutions to intervene if needed.
4.3 2O-DFA Multi-group analysis
2O-DFA-MGA consists of a separate study of the two considered subsamples and a comparison the obtained results testing the difference between the coefficients estimates. Therefore, after considering and analyzing the general case, we now apply 2O-DFA to the subsamples of Males and Females, separately.
The underlying hierarchical model is the same and considers the six dimensions. All manifest variables result statistically significant into the model both for males and for females (Tables 4 and 5, for males and females, respectively), thus, all posed questions are relevant in both analyses. As for Males, the dimensions are reliable and all of them result unidimensional, with the sole exception of Communication (Unidimensionality equal to 1.02). For Females, all dimensions are both unidimensional and reliable, except for Infrastructure that is slightly reliable (Cronbach’s \(\alpha \) equal to 0.69). It can therefore be asserted that the results confirm the chosen model and the findings of the complete sample. The complete results about reliability and unidimensionality are presented in Table 6.
The Specific Indicators Involvement, Leadership and School climate are the most important in the definition of TJS for both models (Fig. 2), however the coefficients of the model for males are always larger than those corresponding with females’. The models seem very similar, but it is important to underline some differences: for instance, the dimensions Communication and Infrastructure have roughly the same loading (i.e., coefficient) within the model for males, whereas they contribute very differently in the definition of TJS within the model for females.
It is possible to make the same consideration about the dimensions Leadership and School climate which have similar importance for males. However, there is a stark difference between what males and females consider the most important aspect of TJS: for the first, School climate is the most important dimension with coefficient equal to 0.94, whereas for the latter Leadership is the most contributing dimension with coefficient equal to 0.88. Notwithstanding that all manifest variables are statistically significant in both models, three items (“The secretarial staff provides all the necessary information”, “The school staff transmits the information effectively” and “The Management communicates effectively the strategic objectives that the institution set” in dimension Communication) result less important in the definition of the related specific latent factors both for males and for females.
Therefore, the models considered in our analysis have shown different results in terms of importance concerning the definition of TJS between males and females. Males define TJS attributing more importance at dimensions as Leadership and School climate and male teachers are, generally, more satisfied. Females, differently, consider more important Involvement and Leadership. Such differences must be statistically tested in order to deduce some policy conclusions. In order to test the gender-effect in the definition of TJS, we implement the 2O-DFA-MGA procedure, in detail we implement the procedure to test group differences in the definition of the TJS starting from the specific dimensions. 10, 000 bootstrapping runs guarantee the consistency of our results.
Two coefficients result to be statistically different, the ones regarding School climate and Infrastructure estimated for males are bigger than the corresponding for females (see Table 7). Therefore, the models considered for males and females, respectively, must be considered different and TJS must be measured differently by gender.
5 Discussion and conclusion
In the first part of the paper, the factors that influence TJS were analyzed (conceptual model). We verified that all the considered factors were statistically significant. In particular, it emerged that the most influential factors on TJS were Leadership, Involvement and School Climate. Through 2O-DFA, it was then verified whether this conceptual model presented any differences between males and females. Particularly, it was highlighted that both genders have the same factors in the conceptual model, yet the weight that each of them has on TJS is not always the same. Specifically, it arose that males perceive a greater importance of all factors than females. These results, obtained thanks to the 2O-DFA and the statistical test introduced, allow school management to have useful information about the levers on which to act in order to improve TJS and, consequently, the effectiveness of training.
In order to identify the primary areas of intervention, we used an importance vs satisfaction matrix [21], that yields insights into which aspects the school should focus on to achieve greater levels of teacher satisfaction (see Table 8). This analysis was based on the joint use of satisfaction and importance data for each item. The use of this matrix aimed at supporting two of the most important criteria for decision-making: the targeting of resources toward goods/services that are of the highest importance for customers (teachers in this case), and to target resources towards those goods/services where teachers are less satisfied. From this analysis, the items were distributed in four quadrants (Quadrant I, II, III and IV).
This matrix allows us to say that the items situated in Quadrant I are the most important aspects for further strategies, in as much as the school has to focus its efforts on Imag2 and Invo2 for males, Invo1 for females and Invo3, Invo4, Invo6 and Lead4 for both genders. In Quadrant II (high importance and satisfaction), we find the items that represent opportunities to gain or maintain competitiveness. These items, very different between males and females, are extremely important as they indicate good performance, hence leading the school to continue with the good work. Quadrant IV, characterized by low importance and satisfaction for both teachers’ genders, includes Infrastructure, indicating that this is of low priority and there is no need to concentrate efforts in these areas.
Observing Table 8, an important conclusion can be made: the relationship between importance and satisfaction expressed by males and females is substantially different. In fact, for 12 out of 25 items, males and females express a different opinion on the relationship between importance and satisfaction. This circumstance allows us to affirm that although males and females have the same factors that impact on TJS, the contribution that each of these items gives to the construction of TJS is profoundly different between males and females.
Change history
21 April 2021
A Correction to this paper has been published: https://doi.org/10.1007/s40300-021-00209-6
References
Aldridge, J.M., Fraser, B.J.: Teachers’ views of their school climate and its relationship with teacher self-efficacy and job satisfaction. Learn. Environ. Res. 19(2), 291–307 (2016)
Bishay, A.: Teacher motivation and job satisfaction: a study employing the experience sampling method. J. Undergrad. Sci. 3(3), 147–155 (1996)
Blok, H., Sleegers, P., Karsten, S.: Looking for a balance between internal and external evaluation of school quality: evaluation of the svi model. J. Educ. Policy 23(4), 379–395 (2008)
Cavicchia, C., Sarnacchiaro, P., Vichi, M.: A composite indicator for the waste management in the eu via hierarchical disjoint non-negative factor analysis. Soc. Econ. Plan. Sci. 73, 100832 (2021)
Chen, J., Silverthorne, C.: The impact of locus of control on job stress, job performance and job satisfaction in taiwan. Leadersh. Org. Dev. J. 29(7), 572–582 (2008)
Chin, W.W.: A permutation procedure for multi-group comparison of pls models. In: Vilares, M., Tenenhaus, M., Coelho, P., Esposito Vinzi, V., Morineau A. (eds.) PLS and related methods: proceedings of the international symposium PLS’03, pp. 33–43 (2003)
Chin, W.W., Dibbern, J.: An introduction to a permutation based procedure for multi-group PLS analysis: results of tests of differences on simulated data and a cross cultural analysis of the sourcing of information system services between Germany and the USA, pp. 171–193. Springer, Berlin, Heidelberg (2010)
Cramer, H.: Mathematical methods of statistics. Princeton University Press, Princeton (1946)
Cronbach, L.J.: Coefficient alpha and the internal structure of tests. Psychometrika 16(3), 297–334 (1951)
Dibbern, J., Chin, W.W.: Multi-group comparison: testing a PLS model on the sourcing of application software services across Germany and the USA using a permutation-based algorithm, pp. 135–160. Schaffer-Poeschel, Stuttgart (2005)
Dinham, S., Scott, C.: Modelling teacher satisfaction: Findings from 892 teaching staff at 71 schools. Tech. rep. (1997). Report presented at the Annual Meeting of the American Educational Research Association (Chicago, IL, March 24-28, 1997)
Dinham, S., Scott, C.: Teachers’ work and the growing influence of societal expectations and pressures. Tech. rep. (2000). Report presented at the Annual Meeting of the American Educational Research Association (New Orleans, LA, April 24–28, 2000)
Edgington, E., Onghena, P.: Randomization tests, 4th edn. Chapman and Hall Boca Raton, Chapman Hall/CRC, London (2007)
George, D., Mallery, P.: SPSS for Windows step by step: a simple guide and reference. 11.0 update, 4th edn. Allyn Bacon, Boston (2003)
Hair, J.F., Sarstedt, M., Ringle, C.M., Gudergan, S.P.: Advanced issues in partial least squares structural equation modeling (PLS-SEM). Sage, Thousand Oaks, CA (2007)
Henseler, J.: A new and simple approach to multi-group analysis in partial least squares path modeling. casualities explored by indirect observation. In: Martens, H. (ed.) Proceedings of the 50th international symposium on PLS and related methods (PLS07), pp. 104–107 (2007)
Henseler, J., Ringle, C., Sarstedt, M.: Testing measurement invariance of composites using partial least squares. Int. Mark. Rev. 33(3), 405–431 (2016)
Henseler, J., Ringle, C., Sinkovics, R.: The use of partial least squares path modeling in international marketing, pp. 277–319. Emerald Group Publishing Limited, Bingley (2009)
MacBeath, J.: Schools must speak for themselves: the case for school self- evaluation. Routledge, London (2005)
Mann, H., Whitney, D.: On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 18(1), 50–60 (1996)
Martilla, J.A., James, J.C.: Importance-performance analysis. J. Mark. 41(1), 77–79 (1996)
Millsap, R.: Statistical approaches to measurement invariance. Routledge, New York (2011)
Porter, L.W., Lawler, E.E.: Managerial attitudes and performance. Ill. R.D. Irwin, Homewood (1968)
Price, J.L.: Reflections on the determinants of voluntary turnover. Int. J. Manpow. 22(7), 600–624 (2001)
Sarnacchiaro, P., Boccia, F.: Some remarks on measurement models in the structural equation model: an application for socially responsible food consumption. J. Appl. Stat. 45(7), 1193–1208 (2018)
Sarnacchiaro, P., Scippacercola, S., Malafronte, P.: A statistical model for the self-evaluation of teacher satisfaction in school management: a study in the Italian Secondary School. Electron. J. Appl. Stat. Anal. 12(3), 637–656 (2019)
Sarstedt, M., Henseler, J., Ringle, C.: Multi-group analysis in partial least squares (pls) path modeling: alternative methods and empirical results. Adv. Int. Mark. 22, 195–218 (2011)
Skaalvik, E.M., Skaalvik, S.: Teacher self-efficacy and teacher burnout: a study of relations. Teach. Teach. Educ. 26(4), 1059–1069 (2010)
Skaalvik, E.M., Skaalvik, S.: Teacher job satisfaction and motivation to leave the teaching profession: relations with school context, feeling of belonging, and emotional exhaustion. Teach. Teach. Educ. 27(6), 1029–1038 (2011)
Spector, P.E.: Job satisfaction: application, assessment, causes, and consequences. Sage publications, Thousand Oaks (1997)
Wilcoxon, F.: Probability tables for individual comparisons by ranking methods. Biometrics 3(3), 119–122 (1947)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A The Questionnaire
Appendix A The Questionnaire
-
Section: Communication (Comm)
-
The procedures to access to the information are simple (Comm1)
-
The website offers the possibility to access useful information and documentation (Comm2)
-
The secretarial staff provides all the necessary information (Comm3)
-
The school staff transmits the information effectively (Comm4)
-
The Management communicates effectively the strategic objectives that the institution set (Comm5)
-
Section: External School Image (Imag)
-
The school is committed to spread its initiatives abroad (Imag1)
-
The initiatives of the school are known on the territory (Imag2)
-
Section: Involvement (Invo)
-
The personnel are involved in decisions and encouraged to make their contribution (Invo1)
-
The families actively cooperate in the educational activities of the school (Invo2)
-
The educational and organizational decisions are debated in advance (Invo3)
-
The planning of the Institution can guide each teacher (Invo4)
-
The Management is available to discuss with the personnel the Institution’s issues (Invo5)
-
The school personnel are satisfied of the PTOF (Invo6)
-
Section: Leadership (Lead)
-
The school Executive is assiduously committed to promote the continuous improvement (Lead1)
-
The Executive staff members are able to organize work effectively (Lead2)
-
DSGA (Head of Administration) is able to handle its role with efficiency and effectiveness (Lead3)
-
The staff of the school receive appropriate tasks according to their specific skills (Lead4)
-
Section: School Climate (Clim)
-
The Management is available to embrace the concerns of the employees (Clim1)
-
The relationship between colleagues are based on collaboration in making decisions together (Clim2)
-
The Relationship between colleagues are based on mutual respect on human relations (Clim3)
-
The school takes into account the training needs of each student (Clim4)
-
The school staff and the students respect each other and collaborate (Clim5)
-
The teachers and ATA collaborate together (Clim6)
-
Section: Infrastructure (Infr) The school rooms are comfortable and clean (Infr1)
-
The technological equipment is appropriate to the educational needs (Infr2)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cavicchia, C., Sarnacchiaro, P. A multi-group higher-order factor analysis for studying the gender-effect in Teacher Job Satisfaction. METRON 80, 23–38 (2022). https://doi.org/10.1007/s40300-021-00204-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40300-021-00204-x