Modelling consumer perceptions of service quality for urban public transport systems using statistical models for ordinal data

Abstract

The paper deals with ordinal response models to evaluate urban public transport systems with the purpose of interpreting consumers’ responses with reference to their profiles. New methodological developments provide opportunities for a more thorough and accurate analysis of perceived service quality. The evaluation of the uncertainty component accounts for accuracy in the assessments. Diagnostic procedures allow to evaluate model specification, with respect to the proportional odds assumption, the adequacy of the mean structure and the occurrence of heterogeneity. The impact of the covariates on the discrete distribution of the observed response is appraised through their marginal effects. The selection of the appropriate covariates leads to the identification of clusters of users, which are compared through ordinal superiority measures. Consequently critical situations are detected.

1 Introduction

This contribution concerns statistical models for rating data aimed to interpret consumers’ responses collected through a questionnaire on service evaluation of urban public transport systems.

The analysis of customer satisfaction related to service quality of transport companies is dealt with in several works for enhancing planning, quality management, schedule reliability and dispatching (see [7, 8, 26], among others). Studies concerning different means of transport elucidate that the concept of loyalty depends on users’ intentions to continue using the service, their willingness to recommend it to others, and their overall satisfaction [31]. Understanding consumers’ perceptions represents a fundamental step in developing policies for customer satisfaction and retention and in implementing strategies for a competitive advantage in service delivery [9, 21]. This understanding requires quantitative measurements based on data collected by means of surveys in which the assessments are expressed on ordinal scales.

The model extensively applied to analyse ratings is the cumulative model [17]. Recently an extension of this model in a two-component mixture model—the cup—has been introduced by [29] to account for uncertainty in the response process. In this paper we consider both models to interpret data from a “transport service quality and customer satisfaction survey” carried out in 2012 in the urban area of Naples.

Aim of the contribution is investigating the most relevant features which drive the response and analysing marginal effects of the explanatory variables. Clusters of users are identified. Consequently ordinal superiority measures are applied for comparing the clusters’ rating distributions. The income, the means of transport and the availability of alternative systems of connection are the covariates that affect the evaluation of public transport.

The paper is organized as follows. The next section briefly reviews the statistical models useful for the analysis of ratings, while Sect. 3 introduces the data. The models, along with all the necessary diagnostics, are illustrated in Sect. 4. Section 5 analyses the marginal effects of the covariates, Sect. 6 derives ordinal superiority measures among clusters of commuters, whereas Sect. 7 outlines the probability distribution of the response for selected users’ profiles. Some final remarks conclude the paper.

2 Statistical models for consumers perception

Let $\varvec{Y}=(Y_1, Y_2,\ldots , Y_n)'$ be a random sample generated by an ordinal variable $Y \sim G(y)$ on the support $\{1,\ldots ,m\}$, where m is a known integer. We interpret $Y_i$ as the rating expressed by the i-th subject on a definite item.

The two frameworks used for analysing rating data are derived by specifying G(y). They are the cumulative model and the cup model, respectively. The first is nested in the second one with the main difference given by the inclusion of the uncertainty in the response process.

2.1 The cumulative model

The cumulative model assumes that the ordinal response Y derives from the categorization of an underlying (continuous) latent variable $Y^*$. For any i-th statistical unit $Y_i=j$ when $\alpha _{j-1} < Y^*_i \le \alpha _{j}$, where $-\infty =\alpha _0< \alpha _1<\cdots< \alpha _{m-1}< \alpha _m=+\infty$ are the thresholds of the scale of $Y^*$. Let $\varvec{X}_i = \left( X_{i1}, \ldots , X_{ip}\right)$ be the vector of covariates for the i-th subject. The dependence of the response on the covariates is established through the latent regression model

$$\begin{aligned} Y_i^*= \varvec{X}_i {\varvec{\beta }} + \epsilon _i,\quad i=1, 2, \ldots , n, \end{aligned}$$

where ${\varvec{\beta }}=(\beta _1, \ldots , \beta _p)$ is the vector of regression coefficients, and $\epsilon _i \sim F_{\epsilon }(.)$.

The probability mass function of $Y_i$, conditionally on $\varvec{X}_i=\varvec{x}_i=\left( x_{i1}, \ldots , x_{ip}\right)$, for $j=1,\ldots ,m,$ is

$$\begin{aligned} Pr\displaystyle \left( {Y_i=j\mid \varvec{x}_i}\right) =Pr\displaystyle \left( {\alpha _{j-1} < Y_i^*\le \alpha _{j}} |\varvec{x}_i\right) =F_{\epsilon }(\alpha _{j}-\varvec{x}_i{\varvec{\beta }})-F_{\epsilon }(\alpha _{j-1}-\varvec{x}_i{\varvec{\beta }}), \end{aligned}$$

(1)

where $Pr\displaystyle \left( Y_i \le j| \varvec{x}_i\right) = F_{\epsilon }(\alpha _{j}-\varvec{x}_i {\varvec{\beta }})$ for $i=1,\ldots ,n$ and $j=1,2,\ldots ,m$.

Common choices for $F_{\epsilon }(.)$ are the Gaussian, the logistic, the (complementary) log-log and the Cauchy distribution, whose related models are named probit, logit, extreme value and cumulative cauchit model, respectively. Here we focus on the logit link function with $F_\epsilon (u)=1/\left\{ 1+ \exp (-u)\right\}$.

A usual assumption in ordinal regression implies that the explanatory variables have the same effect on the cumulative logit regardless of the category of the response, i.e.

$$\begin{aligned} logit\left\{ Pr\displaystyle \left( {Y_i \le j|\varvec{X}_i}\right) \right\} = \log \left\{ \frac{Pr\displaystyle \left( {Y_i \le j|\varvec{X}_i}\right) }{Pr\displaystyle \left( {Y_i > j| \varvec{X}_i}\right) }\right\} = \alpha _{j}-\varvec{X}_i {\varvec{\beta }}. \end{aligned}$$

(2)

For given $\varvec{X}_i$, the logit is altered only by the intercepts $\alpha _j$. Consequently, log-odds ratios for values of a single covariate $X_{ik}$—which differ by 1-unit—are constant. This is the proportional odds assumption, hence the related model is named Proportional Odds Model (POM). A test for this assumption is introduced in Sect. 4 (see also [4]).

Syntheses aimed to emphasise the effects of categorical and continuous covariates on ordinal responses have been proposed and summarized by many Authors, as in [2]. In this context, marginal effects (i.e., the change in the probability of the response due to a 1-unit change in one of the regressors) appear especially interesting (see [3] and reference therein).

Inference for this model is based on the likelihood function, whose expression can be found in [17]. Its maximization is carried out through iterative least squares estimation methods for Generalized Linear Models GLM (see [27]). The global validation of the fitted model is performed according to both likelihood-based methods and descriptive measures [33].

Further diagnostics can be based on various type of residuals, such as those recently introduced by [14].

2.2 The CUP model

The alternative modelling framework has been recently proposed by [29] who extend the class of cumulative models by introducing a further component to account for uncertainty in the response process. It mimics the idea of the cub  model [6, 25] assuming that the response of each individual is the combination of a feeling attitude towards the item (preference part) and an intrinsic uncertainty component surrounding the discrete choice. The feeling attitude accounts for the subjective perception towards the object being evaluated and considers any reasoned assessment, as well as the set of emotions, awareness and sensitivity logically connected with the object. The uncertainty component accounts for indecision in the process of selecting the ordinal response and considers elements not logically connected with the item being evaluated, such as the unconscious willingness to delight the interviewer, the difficulty in evaluation using limited information, lack of self-confidence, laziness, boredom, etc. Notice that the uncertainty component is different from randomness which is inherent to sampling variability of surveys. The mixture has been denoted as cup  model, that is a Combination of a discrete Uniform random variable U and a Preference random variable $Y^P$. Formally, let $Y_i$ be the response of an individual related to the explanatory variables $\varvec{X}_i$, the distribution of the cup  model for $j=1,2,\ldots ,m$ is

$$\begin{aligned} Pr\displaystyle ({Y_i=j \mid \varvec{X}_i})=\pi \,Pr_M{(Y^P_i=j \mid \varvec{X}_i)}+(1-\pi )\,Pr{(U_i=j)}, \end{aligned}$$

(3)

where $Y_i^P$ and $U_i$ are latent variables taking values from ${1, \ldots , m}$. The distribution of $Y_i^P$ is determined by $Pr_M(Y_i^P = j | \varvec{X}_i)$, which can be any ordinal model M, whereas $Pr(U_i = j) = 1/m$ represents the Uniform distribution. Here we consider model (1) for the probability of $Y^P$.

Equation (3) saves the traditional role of the predictors (as in the cumulative model) but considers the additional parameter $\pi$ (as in the family of the cub  model) to assess the uncertainty component.

An extension of this model allows the uncertainty parameter to depend on a vector of subjects’ covariates $\varvec{Z}_i$, through a logit function, i.e. $\pi _i=1 / \left\{ 1+ \exp (-\varvec{Z}_i {\varvec{\eta }})\right\}$. A further development replaces the Uniform distribution by a more flexible one to take into account different response styles [30].

Inference for this model is based on the likelihood function (see [29], for details).

3 Service quality and customer satisfaction in public transport of the urban area of Naples

The survey is an observational study on the service quality and customer satisfaction in public transport of people living in the urban area of Naples, Italy. It has been conceived and carried out by the Department of Political Sciences, University of Naples Federico II in December 2012. A large number of students has been randomly selected and each of them has been invited to recruit further subjects from their acquaintances by means of a chain sampling. The final sample is composed by 311 individuals, who were asked to rate their global perception of public transport, answering the question “Overall the transport system in the urban area of Naples is satisfactory?”, with responses on a 1–5 scale (1 = very unsatisfied; 5 = very satisfied). Further information on the individual characteristics of the subjects were collected along with the ratings. Table 1 reports their main features.

Table 1 Summary statistics concerning the characteristics of the 311 respondents of the survey

The frequency distribution of the global perception is illustrated in the left panel of Fig. 1, while the distribution of the mean of transport selected by respondents as the usual one is in the central panel. The dependence between the ratings and the means of transport is clearly evident in the mosaic plot displayed in the right panel of Fig. 1.

4 The model for the evaluation of the transport system

Initially a cup model is fitted to the data. Here we assume that $Y_i^p=j$ when $\alpha _{j-1} < Y_i^* \le \alpha _j$, with latent regression for the preference part given by

$$\begin{aligned} Y^*_i= & {} \beta _1 \, Income_i + \beta _2 \, Alternative_i + \gamma _1 \, City \,bus_i\\&+\gamma _2 \,Ferry\,boat_i +\gamma _3 \, Train_i +\gamma _4 \, Tube_i \\&+\gamma _5 \, Suburban\,bus_i + \epsilon _i, \qquad i=1,\ldots , n. \end{aligned}$$

Fig. 1

Left: frequency distribution of the overall satisfaction. Center: frequency distribution of the means of transport. Right: mosaic plot for overall satisfaction and means of transport. In labels: sbus stands for Suburban bus, tube for Tube, boat for Ferry boat, train for Train, cbus for Citybus, and ltrain for Local Train

Income is a variable collected on a 10 points scale ranging from 1 (end of month very difficult to reach) to 10 (end of month very easy to reach), which we handle as numeric by referring to [1, 5, 10]. It represents a proxy of the household income. Alternative is a binary variable which takes value 1 if alternative means of transport are available for the interviewed person and zero otherwise. The local train ($Local\,Train$), known as “circumvesuviana”, is the baseline mean of transport. Consequently CityBus, FerryBoat, Train, Tube and SuburbanBus are binary variables which identify the usual mean of transport (when different from the local train). The parameters related to the means of transport are denoted by $\gamma _r$, for $r=1,\ldots ,5$, to emphasize that the covariates correspond to different categories of a single polytomous variable. They measure the impact on the preference component of the different means of transport with respect to the baseline mean ($Local\,Train$).

The fitted model is

$$\begin{aligned} Y^*_i= & {} \underset{(0.097)}{0.254} \, Income_i +\underset{(0.327)}{0.991} \, Alternative_i +\underset{(0.412)}{1.130} \, City \,bus_i \\&+\underset{(0.702)}{1.915} \, Ferry\,boat_i +\underset{(0.480)}{1.675} \, Train_i +\underset{(0.396)}{1.618} \, Tube_i\\&+\underset{(0.559)}{1.711} \, Suburban\,bus_i+{\hat{\epsilon }}_i, \qquad i=1,\ldots , n, \end{aligned}$$

with estimated thresholds ${\hat{\alpha }}_1=1.551$, ${\hat{\alpha }}_2=2.836$, ${\hat{\alpha }}_3=4.432$, ${\hat{\alpha }}_4=5.777$. The estimate of the uncertainty parameter ${\hat{\pi }}=0.99$ is a boundary value, and indicates that there is no uncertainty in the response process. The ratings are entirely reasoned assessments.

Consequently subsequent analyses are based on the pom. It yields

$$\begin{aligned} Y^*_i= & {} \underset{(0.055)}{0.259} \, Income_i +\underset{(0.218)}{1.035} \, Alternative_i + \underset{(0.347)}{1.120} \, City \,bus_i \\&+\underset{(0.705)}{1.904} \, Ferry\,boat_i +\underset{(0.327)}{1.672} \, Train_i +\underset{(0.313)}{1.606} \, Tube_i \\&+\underset{(0.434)}{1.714} \, Suburan\,bus_i+{\hat{\epsilon }}_i, \qquad i=1,\ldots , n, \end{aligned}$$

with estimated thresholds ${\hat{\alpha }}_1=1.561$, ${\hat{\alpha }}_2=2.869$, ${\hat{\alpha }}_3=4.519$, ${\hat{\alpha }}_4=5.898$. The log-likelihood takes value $-426.0395$.

Table 2 $95\%$ confidence intervals for the regression coefficients related to the means of transport

Table 2 reports the $95\%$ confidence intervals for the regression coefficients related to the means of transport. They largely overlap suggesting that the value of the parameter may be unique. Hence the null hypothesis $\gamma _1=\ldots =\gamma _5$ has been tested. The likelihood ratio statistic is 3.778 and the p-value of the test is 0.437, so that the null hypothesis is not rejected. There is no significant difference in the satisfaction of the commuters by the various means of transport. The only exception is given by the users of local train, whose ratings tend to be lower, as made evident by the positive $\hat{\gamma }$’s.

Consequently the attention focuses on the model

$$\begin{aligned} Y_i^* = \beta _1 Income_i + \beta _2 Alternative_i +\ \beta _3 Local\,Train_i + {\epsilon _i} \end{aligned}$$

where $Local\,Train$ is a binary variable which takes value 1 if the mean of transport is the local train and zero otherwise (any other mean of transport). The final model is

$$\begin{aligned} Y_i^* = \underset{(0.054)}{0.261}Income_i + \underset{(0.216)}{1.020}Alternative_i - \underset{(0.269)}{1.535}Local\,Train_i + \hat{\epsilon _i} \end{aligned}$$

(4)

with estimated thresholds ${\hat{\alpha }}_1=0.034$, ${\hat{\alpha }}_2=1.335$, ${\hat{\alpha }}_3=2.966$ and ${\hat{\alpha }}_4=4.335$. The log-likelihood takes value $-427.9287$.

When Income increases higher responses become more likely. Also the availability of alternative means of transport induces a more positive evaluation of the service. The commuters are more generous in rating the service when they are not frustrated by the absence of choice. Finally users of the local train are less satisfied than other commuters.

Although the logit link is often chosen for the straightforward interpretation of the results, in the present case this link is also the one which provides the best fit. Table 3 reports the value of the AIC for various link functions. The minimum is attained by the logit link.

Table 3 Estimated model with different link function

When the proportional odds assumption fails to hold, for at least one covariate, the regression coefficients vary with the category j assumed by Y, and the parameter ${\varvec{\beta }}$ in (1) and (2) is replaced by the parameter ${\varvec{\beta }}_j$ corresponding to the response.

The proportional odds assumption may be formally tested via the Brant test [4]. The test can be carried out separately for each covariate or simultaneously for all the explanatory variables. The values of the test statistics and the corresponding p-values for each hypothesis are shown in Table 4: they confirm the validity of the POM.

Table 4 Brant test for assessing parallel assumption

The occurrence of heterogeneity effects can be tested by means of the cumulative-logit location-scale model of [17], which allows the scale $\sigma$ of the latent variable distribution to depend on the explanatory variables ($\sigma =\exp (\varvec{X}_i {\varvec{\delta }})$). Equation (2) is modified as follows

$$\begin{aligned} logit\left( Pr\displaystyle \left( {Y_i \le j| \varvec{X}_i}\right) \right) = \frac{\alpha _{j}- \varvec{X}_i {\varvec{\beta }}}{\exp (\varvec{X}_i {\varvec{\delta }})} \end{aligned}$$

for $i=1, 2, \ldots , n$ and $j=1, 2, \ldots , m-1$. Absence of heterogeneity effects implies ${\varvec{\delta }}=0$. The p-value of the test on this hypothesis is 0.366, so that no evidence of heterogeneity effects arises.

For checking misspecification of the latent mean structure we consider the surrogate residuals [14]. A continuous variable S with the same conditional distribution of the latent variable $Y^*$ truncated on the interval $(\alpha _{j-1}, \alpha _j)$ is generated when $Y=j$. The variable S acts as a surrogate for the ordinal response Y. The surrogate residual is defined as

$$\begin{aligned} R^s=S-E(S|\varvec{X})\,=\,S-E(Y^*|\varvec{X})= S - \varvec{X} {\varvec{\beta }} - \int _{-\infty }^{+\infty } \epsilon \,dF(\epsilon ). \end{aligned}$$

In practice, the residuals are computed by replacing the unknown parameters by their estimates. This yields the value of the i-th residual $r^S_i = s_i - \varvec{X}_i \hat{{\varvec{\beta }}} - \int _{-\infty }^{+\infty } \epsilon \,dF(\epsilon )$. Conditional sampling allows to consider the continuous space of the simulated data, rather than the discrete space of the original data. The plots of the surrogate residuals versus the covariates allow to check whether there is a misspecification in the latent mean structure. They are displayed in Fig. 2. The medians of the residuals are very close to zero confirming an adequate mean structure.

Fig. 2

Surrogate residual diagnostic plots for Income (left panel), Alternative (central panel) and $Local\, Train$ (right panel)

For model (4) the concordance index [12], that is a measure of predictive power that strictly uses ordinality, is 0.715 and $R^2$ of [19] is 0.245 whereas the pseudo $R^2$ of [18] is 0.089 indicating that the deviance for the model is 8.9% smaller than for the null model. Finally the percentage of Correctly Classified Responses (CCR) is 0.383. It does not appreciably differ from that of more complex models.

5 Marginal effects

In the cumulative model the regression coefficients express the influence of the explanatory variables on the latent variable $Y^*$, rather than on the observable (discrete) response [15]. Marginal effects instead allow to evaluate how a change in the explanatory variables affects the probability of the response categories. Mood [20] and Landerman et al. [13] argue that marginal effects can be substantially more informative than odds ratios, especially for comparing groups that arise within the statistical units of the sample.

In case of a continuous explanatory variable $X_k$, for each category j of Y, the marginal effect is defined as

$$\begin{aligned} \dfrac{\partial P(Y=j|\varvec{X}=\varvec{x}^*)}{\partial X_k}. \end{aligned}$$

(5)

It measures the change in $P(Y=j|\varvec{X}=\varvec{x}^*)$ for a 1-unit change in $X_k$ evaluated at $\varvec{X}=\varvec{x}^*$.

It is especially interesting to compute the marginal effects for the probability of the extreme responses, corresponding to an entirely unsatisfied ($Y=1$) or a thoroughly satisfied subject ($Y=m$). In case of the logit link, [3] show that

$$\begin{aligned}&\dfrac{\partial P(Y=1|\varvec{X}=\varvec{x}^*)}{\partial X_k}=-\beta _k P(Y=1|\varvec{X}=\varvec{x}^*)\left\{ 1-P(Y=1|\varvec{X}=\varvec{x}^*)\right\} , \\&\dfrac{\partial P(Y=m|\varvec{X}=\varvec{x}^*)}{\partial X_k}=\beta _k P(Y=m|\varvec{X}=\varvec{x}^*)\left\{ 1-P(Y=m|\varvec{X}=\varvec{x}^*)\right\} . \end{aligned}$$

Their highest absolute value is $|\beta _k|/4$ which occurs when the probability of the category is 1/2.

It is clear from (5) that the evaluation of the marginal effect varies with $\varvec{x}^*$. Its magnitude depends on the value of the regressor $X_k$, whose effect is computed, as well as on the values of all the other explanatory variables in the model [15]. Various approaches have been suggested in literature to circumvent this problem (see [3] and [16, pag. 242–246]). The first considers the average marginal effect (AME) of $X_k$ obtained as the mean of the marginal effects evaluated on the n sample values $\varvec{x}_1, \ldots , \varvec{x}_n$. Alternatively, after computing the mean $\bar{\varvec{x}}$ of $\varvec{x}_1, \ldots , \varvec{x}_n$, the marginal effect at the mean (MEM) can be obtained by setting $\varvec{x}^*=\bar{\varvec{x}}$. Finally the marginal effect can be computed for representative values of the explanatory variables (MER). This last approach is recommended when some explanatory variables can be regarded as group variables which identify clusters of statistical units, as in the case of the binary variables Alternative and $Local \, Train$. In this circumstance it is of interest to compare the marginal effects separately for the different groups. Hence, the analysis applies the MER approach to compare the marginal effects between commuters who travel by the local train and those who use different means of transport, and between commuters who have alternative means of transport and those who have no choice. Representative values are considered also for Income, they are the minimum $Income=1$, the mode $Income=4$ and the maximum $Income=10$.

The marginal effects of Income on the probability of $Y=1$ and $Y=5$ are shown in Table 5 for the four groups of commuters which arise from the binary variables. In parenthesis, below the estimated marginal effects, there are their standard errors computed by delta method. All the estimated marginal effects are significantly different from zero. Their maximum absolute value is ${\hat{\beta }}_1/4=0.065$, and several marginal effects for the probability of $Y=1$ are pretty close to this threshold especially for local train commuters and low incomes.

Increasing income reduces the probability of the extreme negative response ($Y=1$) and consequently increases the probability of the extreme positive response ($Y=5$). The impact of an increase of income is generally higher when the initial value is low and tapers off for higher incomes.

Table 5 Marginal effects for income

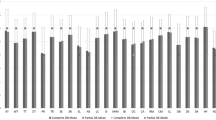
Figure 3 shows the marginal effects of Income on the probability of $Y=1$ for the various combination of the binary variables. For each bar, the asymptotic $95\%$ confidence interval is illustrated. It is computed as $ME \pm 1.96 SE(ME)$ where ME is the marginal effect and SE(ME) is its standard error.

Fig. 3

Marginal effects of income on $P(Y=1)$

When $X_k$ is a binary variable, its marginal effect is computed as

$$\begin{aligned} P(Y=j|\varvec{X}_{(k)}=\varvec{x}_{(k)}^*, X_k=1)-P(Y=j|\varvec{X}_{(k)}=\varvec{x}_{(k)}^*, X_k=0) \end{aligned}$$

where $\varvec{X}_{(k)}$ is the vector of the explanatory variables after removing $X_k$.

The marginal effects of the availability of alternative means of transport with respect to the usual one are displayed in Table 6. The estimates of all the marginal effects are significantly different from zero. Their maximum absolute value is $\hat{\beta _2}/4=0.255$.

The availability of alternative means of transport makes the passengers less critical, and reduces their propensity towards the extreme negative response ($Y=1$). This beneficial effect increases when they travel by the local train or have a low income. When the choice of the mean of transport is not a compulsory one, the commuters tend to be more satisfied.

Table 6 Marginal effects for alternative means of transport

The marginal effects of Alternative along with the asymptotic confidence intervals are displayed in the left panel of Fig. 4.

Table 7 shows the marginal effects for the local train. Also in this case all the estimates of the marginal effects are significantly different from zero. Their maximum absolute value if $\hat{\beta }_3/4=0.384$.

Traveling by the local train makes the commuters more critical and increases the probability of the lowest response ($Y=1$). This effect becomes sharper when no alternatives are available and the income decreases (the marginal effect for the probability of $Y=1$ is very close to their maximum).

Table 7 Marginal effects for Local Train

The marginal effects of Local Train are illustrated in the right panel of Fig. 4.

Fig. 4

Marginal effects of Alternative means of transport (left panel) and Local Train (right panel) on $P(Y=1)$

6 Ordinal superiority measures among clusters of users

The two binary variables of model (4) identify groups of subjects according to whether they travel or not by the local train and whether they have or not an alternative mean of transport. An approach to compare groups analyses the probability that an observation from one group falls above an independent observation from an alternative group. To this purpose it is useful to consider the ordinal superiority measures.

Let $Y_{g_1}$ and $Y_{g_2}$ be independent ordinal responses from two groups of statistical units, denoted by $g_1$ and $g_2$. Agresti and Kateri [2] define the ordinal superiority measures

$$\begin{aligned} \gamma =P(Y_{g_1}>Y_{g_2})+\dfrac{1}{2}P(Y_{g_1}=Y_{g_2}), \end{aligned}$$

and

$$\begin{aligned} \varDelta =P(Y_{g_1}>Y_{g_2})-{P(Y_{g_2}>Y_{g_1})}, \end{aligned}$$

where

$$\begin{aligned} \gamma \in [0,1], \quad \varDelta \in [-1,1], \end{aligned}$$

(6)

and

$$\begin{aligned} \gamma =(\varDelta +1)/2, \quad \varDelta =2 \gamma -1. \end{aligned}$$

(7)

When $\gamma > 1/2$ or $\varDelta >0$, the ratings from $g_1$ tend to be larger than the ratings from $g_2$ assessing an ordinal superiority of $g_1$ over $g_2$.

Agresti and Kateri [2] prove that for the logit link $\gamma$ can be approximated as follows

$$\begin{aligned} \gamma \approx \dfrac{exp({\hat{\beta }} /\sqrt{2})}{1+exp({\hat{\beta }} /\sqrt{2})}, \end{aligned}$$

(8)

where ${\hat{\beta }}$ in (8) is the maximum likelihood estimate of the group effect.

By considering the binary variables Alternative and $Local\,Train$ as group variables, the estimates of $\gamma$ and $\varDelta$ are displayed in Table 8 along with the $95\%$ confidence intervals. Consistently with the results of the previous sections, the value of $\hat{\gamma }_{Alternative}=0.673$ is significantly greater than 1/2. It indicates that the ratings of commuters who have an alternative mean of transport are higher than the ratings of people without choice with probability 0.673. On the contrary, the estimate ${\hat{\gamma }}_{Local\,Train}=0.252$ is significantly smaller than 1/2 and markedly low. This result points out that the ratings of the commuters by the local train are lower than the ratings by other commuters with probability 0.748, providing further evidence of the poor level of satisfaction associated to this mean of transport.

Table 8 Ordinal superiority measures between groups of commuters

Alternative ordinal superiority measures for comparing groups are the following [2]

$$\begin{aligned} \gamma ^\tau (g_1,g_2,\tilde{\varvec{x}}_0) = \sum _{j>k}{\hat{\tau }}_{{g_1},j}(\tilde{\varvec{x}}_0){\hat{\tau }}_{{g_2},k}(\tilde{\varvec{x}}_0) + \frac{1}{2} \sum _{j}{\hat{\tau }}_{{g_1},j}(\tilde{\varvec{x}}_0){\hat{\tau }}_{{g_2},j}(\tilde{\varvec{x}}_0). \end{aligned}$$

and

$$\begin{aligned} \varDelta ^\tau (g_1,g_2,\tilde{\varvec{x}}_0) = \sum _{j>k}{\hat{\tau }}_{{g_1},j}(\tilde{\varvec{x}}_0){\hat{\tau }}_{{g_2},k}(\tilde{\varvec{x}}_0) - \sum _{k>j}{\hat{\tau }}_{{g_1},j}(\tilde{\varvec{x}}_0){\hat{\tau }}_{{g_2},k}(\tilde{\varvec{x}}_0) \end{aligned}$$

where

$$\begin{aligned} {\hat{\tau }}_{{g_\ell }, j}(\tilde{\varvec{x}}_0) = {\hat{P}}(Y = j; g = g_\ell , \tilde{\varvec{x}}_0), \ \ \ \ell =1,2, \ \ j=1, \ldots , m \end{aligned}$$

is the estimated probability of $Y=j$ for the group identified by $g_\ell$ while the other covariates are fixed at the selected value $\tilde{\varvec{x}}_0$. Also in this case (6) and (7) hold.

The binary covariates (Alternative and $Local\,Train$) identify the following four groups of users

• 1. commuters by local train without alternative,

• 2. commuters by local train with alternative,

• 3. commuters by other means of transport without alternative,

• 4. commuters by other means of transport with alternative.

The probability distribution of Y for these groups has been estimated from model (4), with selected value for income fixed at the mode ($Income=4$). It yields the ordinal superiority measures reported in Table 9.

Table 9 Ordinal superiority measures between groups of commuters identified by the binary covariates (Alternative and $Local\,Train$) at the modal income

With the exception of the comparison between users of other means of transport without alternatives and local train commuters with alternatives, ${\hat{\gamma }}$ (${\hat{\varDelta }}$) is significantly different from 1/2 (zero), pointing out that the users from $Group \,1$ (in the table) tend to express larger ratings than users from $Group \, 2$. The results confirm the ordinal superiority of the ratings of people who have alternatives with respect to those without choice, and of the ratings of commuters by other means of transport with respect to local train users. Furthermore, it has to be noticed that the ratings of commuters who do not travel by the local train and have alternatives enjoy ordinal superiority with respect to all the other three groups. These outcomes are displayed in Fig. 5.

Fig. 5

Ordinal superiority measures among groups of commuters

7 Probability distribution of the responses for selected users’ profiles

By selecting the values of the covariates appearing in model (4), users’ profiles depending on income, the usual mean of transport and the availability of other services can be identified.

Fig. 6

Estimated probability distribution of the response for selected profiles. Gray lines are referred to users who usually use the Local Train whereas black dashed lines are referred to consumers who traditionally use Other Transports

Figure 6 shows the estimated probability distribution of the response for selected profiles. The distribution of local train users is systematically shifted leftward, concentrating larger probability on lower ratings. The availability of alternative means of transport instead moves the probability from the lower categories to the higher ones. Finally, when income increases the probability of lower ratings decreases.

8 Concluding remarks

Aim of the paper has been to show, through real-life data on service quality of urban transport systems, how models for ordinal responses can be used in the study and interpretation of human judgments, whenever opinions are measured by ratings.

The main points are: an appropriate treatment of the ordinal nature of the data; the possibility to measure both the level of the latent variable and the uncertainty surrounding the selection of the rating; the assessment of the impact of the individual characteristics on the variable of interest, the identification of clusters of users and the detection of critical opinions. Furthermore marginal effects measure the impact of a change in the explanatory variables on the discrete probability distribution of the response, while ordinal superiority measures allow to investigate differences among clusters of consumers and identify critical situations. These methodological tools are useful any time ratings need to be analysed in the field of service quality evaluation as for instance when one of the most famous tool ‘SERVQUAL’ is provided [22,23,24].

With reference to transport data, results show that there is no uncertainty in the response process, i.e. the ratings are entirely reasoned assessments. No difference arises among different means of transport, with the exception of the local train. Travelling by the local train makes the commuters more critical, while the availability of alternative means of transport increases their propensity towards positive responses. Also an increase in income makes the interviewee more generous in evaluation. The two binary variables Alternative and $Local\,Train$ identify four clusters of users. The ratings of commuters who do not travel by the local train and have alternative enjoy ordinal superiority (a comparatively higher evaluation of service) with respect to all the other groups of respondents. The cluster of the local train commuters with no alternative is the most critical one, identifying the mean of transport where corrective actions should be primarily focussed.

The present analysis provides a first insight; which can be extended by using more comprehensive questionnaire data including additional information such as the point of origin/destination route, the reason of travel, the frequency of use of the mean of transport, the time spent for travelling and so forth. Finally, an alternative approach to investigate commuters’ satisfaction is the analysis of multiple item questionnaires through the Item Response Theory, finalized to asses the ‘ability’ of users to be satisfied (see [11, 28, 32] for details). Useful models to this purpose are the partial credit model and the graded response model, among others.