Abstract
A novel approach for outlier detection is proposed, called local projections, which is based on concepts of the Local Outlier Factor (LOF) (Breunig et al. in Lof: identifying density-based local outliers. In: ACM sigmod record, ACM, volume 29, pp. 93–104, 2000) and ROBPCA (Hubert et al. in Technometrics 47(1):64–79, 2005). By using aspects of both methods, this algorithm is robust towards noise variables and is capable of performing outlier detection in multi-group situations. The idea is to focus on local descriptions of the observations and their neighbors using linear projections. The outlyingness of an observation is determined by a weighted distance of the observation to all identified projection spaces, with weights depending on the appropriateness of the local description. Experiments with simulated and real data demonstrate the usefulness of this method when compared to existing outlier detection algorithms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Classical outlier detection approaches in the field of statistics are experiencing multiple problems in the course of the latest developments in data analysis. The increasing number of variables, especially non-informative noise variables, combined with complex multivariate variable distributions makes it difficult to compute classical critical values for flagging outliers. This is mainly due to singular covariance matrices, distorted distribution functions and therefore skewed critical values (e.g. Aggarwal and Yu [2]). At the same time, outlier detection methods from the field of computer science, which do not necessarily rely on classical assumptions such as normal distribution, enjoy an increase in popularity even though their application is commonly limited due to large numbers of variables, possibly combined with only few observations (Zimek and Filzmoser [26]). This motivated the proposed approach for outlier detection incorporating aspects from two popular methods: the Local Outlier Factor (LOF) (Breunig et al. [4]), originating from computer science, and ROBPCA, a robust principal component analysis-based (PCA) approach for outlier detection coming from the field of robust statistics (Hubert et al. [13]). The core aim of the proposed approach is to measure the outlyingness of observations avoiding any assumptions on the underlying data distribution and being able to cope with high-dimensional datasets with fewer observations than variables (flat data structures).
LOF avoids any assumptions on the data distribution by incorporating a k-nearest neighbor algorithm. Within groups of neighbors, it evaluates whether or not an observation is located in a similar density as its neighbors. Therefore, multi-group structures, skewed distributions, and other obstacles have minor impact on the method as long as there are enough observations for modeling the local behavior. On the contrary, ROBPCA uses a robust approach for modeling the majority of observations, which are assumed to be normally distributed. It uses a projection on a subspace based on this majority. In contrast to most other approaches, ROBPCA does not only investigate this subspace but also the orthogonal complement, which reduces the risk of missing outliers due to the projection procedure.
The proposed approach aims at combining these two aspects by defining projections based on the local neighborhood of an observation where no reliable assumption about the data structure can be made and by considering the concept of the orthogonal complement similar to ROBPCA. The approach of local projections is an extension of Guided projections for analyzing the structure of high-dimensional data (Ortner et al. [19]). We identify a subset of observations locally, describing the structure of a dataset in order to evaluate the outlyingness of other nearby observations. While guided projections create a sequence of projections by exchanging one observation by another and re-project the data onto the new selection of observations, in this work, we re-initiate the subset selection in order to cover the full data structure as good as possible with n local descriptions, where n represents the total number of observations. We discuss how outlyingness can be interpreted with regard to local projections, why the local projections are suitable for describing the outlyingness of an observation, and how to combine those projections in order to receive an overall outlyingness estimation for each observation of a dataset.
The procedure of utilizing projections linked to specific locations in the data space has the crucial advantage of avoiding any assumptions about the distribution of the analyzed data as utilized by other knn-based outlier detection methods as well (e.g. Kriegel et al. [16]). Furthermore, multi-group structures do not pose a problem due to the local investigation.
We compare our approach to related and well-established methods for measuring outlyingness. Besides ROBPCA and LOF, we consider PCOut (Filzmoser et al. [10]), an outlier detection method focusing on high-dimensional data, KNN (Campos et al. [6]), since our algorithm incorporates knn-selection similar to LOF, subspace-based outlier detection (SOD) (Kriegel et al. [16]), a popular subspace selection method from computer science, and Outlier Detection in Arbitrary Subspaces (COP) (Kriegel et al. [17]), which follows a similar approach but has difficulties when dealing with flat data structures. Our main focus in this comparison is exploring the robustness towards an increasing number of noise variables.
The paper is structured as follows: Sect. 2 provides the background for a single local projection including a demonstration example. We then provide an interpretation of outlyingness with respect to a single local projection and a solution for aggregating the information based on series of local projections in Sect. 3. Section 4 describes all methods used in the comparison, which are then applied in two simulated settings in Sect. 5. Finally, in Sect. 6, we show the impact on three real-world data problems of varying dimensionality and group structure before we provide a brief discussion on the computation time in Sect. 7. We conclude with a discussion in Sect. 8.
2 Local projections
Let \(\varvec{X}\) denote a data matrix with n rows (observations) and p columns (variables). The observation are denoted by \(\varvec{x}_i=(x_{i1} \dots x_{ip})'\), for \(i=1,\ldots ,n\), and thus \(\varvec{X} = (\varvec{x}_1, \dots , \varvec{x}_n)'\). We assume that the observations are drawn from a p-dimensional random variable X, following a non-specified distribution function \(F_X\). We explicitly consider the possibility of \(p>n\) to emphasize the situation of high-dimensional low sample size data referred to as flat data, which commonly emerges in modern data analysis problems. We assume that \(F_X\) represents a mixture of multiple distributions \(F_{X_1}, \dots , F_{X_q}\), where the number of sub-distributions q is unknown. The distributions are unspecified and can differ from each other. However, we assume that the distributions are continuous. Therefore, no ties are present in the data, which is a reasonable assumption especially for a high number of variables. In the case of ties, a preprocessing step, excluding ties can be applied in order to meet this assumption. An outlier in this context is any observation, which deviates from each of the groups of observations associated with the q sub-distributions.
Our approach for evaluating the outlyingness of observations is based on the concept of using robust approximations of \(F_X\), which do not necessarily need to provide a good overall estimation of \(F_X\) on the whole support but only of the local neighborhood of each observation. Therefore, we aim at estimating the local distribution around each observation by a limited number of nearby observations in order to avoid the influence of inhomogenity in the distribution (e.g. multimodal distributions or outliers being present in the local neighborhood) of the underlying random variable.
For complex problems, especially high-dimensional problems, such approximations are difficult to find. We use projections onto groups of observations locally describing the distribution. Therefore, we start by introducing the concept of a local projection, which will then be used as one such approximation before describing a possibility of combining those local approximations. In order to provide a more practical incentive, we demonstrate the technical idea in a simulated example throughout the section.
2.1 Definition of local projections
Let \(\varvec{y}\) denote one particular observation of the data matrix \(\varvec{X}\). For any such \(\varvec{y}\), we can identify its k nearest neighbors using the Euclidean distance between \(\varvec{y}\) and \(\varvec{x}_i\), denoted by \(d(\varvec{y}, \varvec{x}_i)\) for all \(i=1, \dots ,n\):
where \(d_k\) is the k-smallest distance from \(\varvec{y}\) to any other observation in the dataset.
Using the strategy of robust estimation, we consider a subset of \({\lceil }{\alpha \cdot k}{\rceil }\) observations from \(knn(\varvec{y})\) for the description of the local distribution, where \(\alpha \) represents a trimming parameter describing the proportion of observations which are assumed to be non-outlying in any local neighborhood. Here, \({\lceil }{c}{\rceil }\) denotes the smallest integer \(\ge c\). The parameter \(\alpha \) is usually set to 0.5 in order to avoid neighbors that are heterogeneous (e.g. due to outliers) but it can be adjusted if additional information about the specific dataset is available. By doing so, we reduce the influence of outlying observations, which would distort our estimation. The idea is to get the most dense group of \({\lceil }{\alpha \cdot k}{\rceil }\) observations, which we call the core of the projection, initiated by \(\varvec{y}\), not including \(\varvec{y}\) itself. As a guidance, k should be selected typically as half of the number of observations of the smallest group that would be expected in the data set. If no prior knowledge is available, it should be taken as a small number, e.g. between 5 and 10. The center of this core is defined by
where \(d_{({\lceil }{\alpha \cdot k}{\rceil })}(\varvec{x}_i)\) represents the \({\lceil }{\alpha \cdot k}{\rceil }\)-largest distance between \(\varvec{x}_i\) and any other observation from \(knn(\varvec{y})\). The observation \(\varvec{x}_0\) can be used to define the core of a local projection initiated by \(\varvec{y}\):
A lower bound for the number of observations in the core may be 5.
In order to provide an intuitive access to the proposed approach, we explain the concept of local projections for a set of simulated observations. In this example, we use 200 observations drawn from a two-dimensional normal distribution. The original observations and the procedure of selecting the \(core(\varvec{y})\) are visualized in Fig. 1: The red observation was manually selected to initiate our local projection process and refers to \(\varvec{y}\). It can be exchanged by any other observation. However, in order to emphasize the necessity of the second step of our procedure, we selected an observation off the center. The blue observations are the \(k=20\) nearest neighbors of \(\varvec{y}\) and the filled blue circles represent the core of \(\varvec{y}\) using \(\alpha =0.5\). We note that the observations of \(core(\varvec{y})\) tend to be closer to the center of the distribution than \(\varvec{y}\) itself, since we can expect an increasing density towards the center of the distribution, which likely leads to more dense groups of observations.
Visualization of the core-selection process. The red observation represents the initiating observation \(\varvec{y}\). The blue observations represent \(knn(\varvec{y})\) and the filled blue observations represent \(core(\varvec{y})\). \(\varvec{x}_0\) itself is not visualized but it is known to be an element of \(core(\varvec{y})\) (color figure online)
Let us collect the observations of \(core(\varvec{y} )\) as rows in the matrix \({\varvec{X}_{\varvec{y}}}\), with \({\lceil }{\alpha \cdot k}{\rceil }\) rows and p columns. A projection onto the space spanned by these observations provides a description of the similarity between any observation and the core, which is especially of interest for \(\varvec{y}\) itself. Such a projection can efficiently be computed using the singular value decomposition (SVD) of the matrix \(\varvec{X}_{\varvec{y} }\), centered and scaled with respect to the core itself. Note that this component-wise normalization implies that the method is not invariant to orthogonal tranformations. Denote this matrix by \(\tilde{\varvec{X}}_{\varvec{y}}\), where centering and scaling is applied component-wise with the arithmetic mean and empirical standard deviation. The classical estimators still preserve robustness properties, since the observations have been included into the core in a robust way.
The SVD of \(\tilde{\varvec{X}}_{\varvec{y}}\) is
and thus \(\tilde{ \varvec{X} }_{\varvec{y}} \varvec{V}_{\varvec{y}}\) is a representation of the core observations of \(\varvec{y}\) in the core space of \(\varvec{y}\). In fact, any observation \({\varvec{x}}\) can be represented in this space: The observation first needs to be centered and scaled in the same way as \(\tilde{\varvec{X}}_{\varvec{y}}\), resulting in \(\tilde{\varvec{x}}\), and then
is the projection of \({\varvec{x}}\) into the core space of \(\varvec{y}\). Since the dimension of the core space is limited by \({\lceil }{\alpha \cdot k}{\rceil } - 1\), in any case where \(p\ge {\lceil }{\alpha \cdot k}{\rceil }\) holds and \(\varvec{X}_{core(\varvec{y})}\) is of full rank, a non-empty orthogonal complement of this core space exists. Therefore, any observation \(\varvec{x}\) consists of two representations, the core representation \(\varvec{x}_{core(\varvec{y})}\) given the core space, and the orthogonal representation \(\varvec{x}_{orth(\varvec{y})}\) given the orthogonal complement of the core space,
Figure 2a shows the representation of our 200 simulated observations from Fig. 1 in the core space. Note that in this special case, the orthogonal representation is constantly \(\varvec{0}\) due to the non-flat data structure of the core observations (\(p<k\)). We further see that the center of the core is now located in the center of the coordinate system.
Given a large enough number of observations and a small enough dimension of the sample space, we can approximate \(F_X\) with arbitrary accuracy given any desired neighborhood. However, in practice, the quality of this approximation is limited by a finite number of observations. Therefore, it depends on various aspects like the size of \(d_{(k)}\) and \(d_{({\lceil }{\alpha \cdot k}{\rceil })}\) and, thus, the approximation is always limited by the restrictions imposed by the properties of the dataset. Especially the behavior of the core observations will, in practice, significantly deviate from the expected distribution with increasing \(d_{({\lceil }{\alpha \cdot k}{\rceil })}\).
In order to take this local distribution into account, it is useful to include the properties of the core observations in the core space into the distance definition within the core space. A more advantageous way to measure the deviation of core distances from the center of the core than using Euclidean distances is the usage of Mahalanobis distances (e.g. De Maesschalck et al. [7]). For the projection space, an orthogonal basis is defined by the left eigenvectors of the SVD from Eq. (4), while the singular values given by the diagonal of the matrix \(\varvec{D}_{\varvec{y}}\) provide the standard deviation for each direction of the projection basis. Therefore, weighting the directions of the Euclidean distances with the inverse singular values directly leads to Mahalanobis distances in the core space,
which take the variation of each direction into account:
Plot (a) provides a visualization of the observations from Fig. 1 in the core space of \(\varvec{y}\). The red observation represents the initiating observation \(\varvec{y}\). The blue observations represent \(knn(\varvec{y})\) and the filled blue observations represent \(core(\varvec{y})\). The green ellipses represent the covariance structure estimated by the core observations representing the local distribution. Plot (b) uses the same representation as Fig. 1 but shows the concept of multiple local projections initiated by different observations marked as red dots. Each of the core distances represented by green ellipses refers to the same constant value taking the different covariance structures of the different cores into account
The computation of core distances can be derived from Fig. 2a. The green cross in the center of the coordinate system refers to the (projected) left singular vectors of the SVD. We note that the scale of the two axes in Fig. 2a differ appreciably. The green ellipses represent Mahalanobis distances based on the variation of the two orthogonal axes, which provide a more suitable measure for describing the distribution locally.
The distances of the representation in the orthogonal complement of the core cannot be rescaled as in the core space. All observations from the core, which are used to estimate the local structure, i.e. to span the core space, are fully located in the core space. Therefore, their orthogonal complement is equal to \(\varvec{0}\):
Since no variation in the orthogonal complement is available, we cannot estimate the rescaling parameters for the orthogonal components. Therefore, we directly use the Euclidean distances in order to describe the distance from any observation \(\varvec{x}\) to the core space of \(\varvec{y}\). We will refer to this distance as orthogonal distance (OD),
The concept of the two distances is visualized in Fig. 3. We visualize this approach in Fig. 3 in two plots. Plot (a) shows the first two principal components of the core space and plot (b) the first principal component of the core and the orthogonal space, respectively. In order to retrace our concept of interpreting core distances as the quality of the local description model and the core distances as a measure of outlyingness with respect to this description, we look at the two observations marked in red and blue. While the red observation is close to the center of our core as seen in plot (a), the blue one is located far off. Therefore, the blue observation is not as well described by the core as the red observation, which becomes evident when looking at the first principal component of the orthogonal complement in plot (b), where the blue observation is located far off the green line representing the projection space.
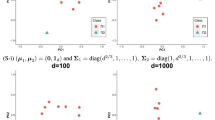
Visualization of orthogonal and core distances for a local projection of observations generated from a multivariate 100-dimensional normal distribution. Plot (a) describes the core space by its first two principal components. The measurement of the core distances is represented by the green ellipses. Plot (b) includes the orthogonal distance. The vertical green line represents the projection space
The two measures for similarity, CD and OD, are inspired by the score and the orthogonal distance of Hubert et al. [13]. In contrast to Hubert et al. [13], we do not try to elaborate critical values for CD and OD to directly decide if an observation is an outlier. Such critical values always depend on an underlying normal distribution and on the variation of the core and the orthogonal distances of the core observations. Instead, we aim at providing multiple local projections in order to be able to estimate the degree of outlyingness for observations in any location of a data set. A core and its core distances can be defined for every observation. Therefore, a total of n projections with core and orthogonal distances are available for analyzing the data structure. Figure 2b visualizes a small number (5) of such projections in order to demonstrate how the concept works in practice. The red observations are used as the initiating observations, the green ellipses represent core distances based on each of the 5 cores. Each core distance refers to the same constant value considering the different covariance estimations of each core. We see that observations closer to the boundary of the data are described less adequately by their respective core, while other observations, close to the center of the distribution, are well described by multiple cores.
3 Outlyingness through local projections
Most subspace-based outlier detection methods, including PCA-based methods such as PCOut (Filzmoser et al. [10]) and projection pursuit methods (e.g. Henrion et al. [11]), focus on the outlyingness of observations within a single subspace only. The risk of missing outliers due to the subspace selection by the applied method is evident as the critical information might remain outside the projection space. ROBPCA (Hubert et al. [13]) is one of the few methods considering also the distance to the projection space in order to monitor this risk as well.
We would like to use both aspects, distances within the projection space and to the projection space, to evaluate the outlyingness of observations as follows: The projection space itself is often used as a model, employed to measure the outlyingness of an observation. Since we are using a local knn-based description, we can not directly apply this concept as our projections are bound to a specific location defined by the cores. The core distance from the location of our projection rather describes whether an observation is close to the selected core. If this is the case, we can assume that the model of description (the projection represented by the projection space) fits the observation well. Therefore, if the observation is well-described, there should be little information remaining in the orthogonal complement leading to small orthogonal distances. On the other hand, if the orthogonal distance is big in this case, the observation is likely to be a local outlier. Thus, both aspects need to enter a measure of local outlyingness: the core distance, indicating how well the observation is described locally, and the orthogonal distance, indicating how far the observation is from the projection space. Note, however, that core observations have an orthogonal distance of zero, and thus they should not be used for an outlyingness measure.
So far we considered a single projection, based on an initializing observation \({\varvec{y}}\), where \({\varvec{y}}\) is a selected observation from the set \({\mathcal {X}}\) of all n observations \(\{ \varvec{x}_1,\dots , \varvec{x}_n \}\). Now consider any observation \(\varvec{x} \in {\mathcal {X}}\) for which an outlyingness measure needs to be computed. The basic idea for our local outlyingness measure is to consider the orthogonal distances from all projections, weighted by the inverse of the core distances. The weights, indicating the quality of the local description, are defined as
and the local outlyingness measure (LocOut) for an observation \({\varvec{x}}\) is defined as
The smaller the core distance of an observation for a specific projection is, the more relevant this projection is for the overall evaluation of the outlyingness of this observation. Therefore, we downweight the orthogonal distance based on the inverse core distances. In order to make the final outlyingness score comparable, we scale these weights by setting the sum of weights to 1. The scaled weights \(w_{\varvec{y}}\) make sure that the sum of contributions by all available projections remains the same.
Note that this concept of outlyingness is limited to high-dimensional data. Whenever we analyze data where the number of variables \(p < {\lceil }{\alpha \cdot k}{\rceil }\), the full information of all observations will be located in the core space of each local projection. Therefore, for varying core distances, the orthogonal distance will always remain zero. Thus, the weighted sum of orthogonal distances cannot provide any information on outlyingness.
4 Evaluation setup
In order to evaluate the performance of our proposed methodology, we compare it with related algorithms, namely LOF (Breunig et al. [4]), RobPCA (Hubert et al. [13]), PCOut (Filzmoser et al. [10]), COP (Kriegel et al. [17]), KNN (Ramaswamy et al. [21]), and SOD (Kriegel et al. [16]). Each of those algorithms tries to identify outliers in the presence of noise variables. Some methods use a configuration parameter describing the dimensionality of the resulting subspace or the number of neighbors in a knn-based algorithm. In our algorithm, we use \({\lceil }{\alpha \cdot k}{\rceil }\) observations, where \(\alpha \) is set to 0.5, to create a subspace, which we employ for assessing the outlyingness of observations. In order to provide a fair comparison, the configuration parameters of each method are adjusted individually for each dataset: We systematically test different configuration values and report the best achieved performance for each method. Instead of outlier classification, we rather use each of the computed measures of outlyingness since not all methods provide cutoff values. The performance itself is reported in terms of the commonly used area under the ROC Curve (AUC) (Fawcett [8]).
4.1 Compared methods
Local outlier factor (LOF) (Breunig et al. [4]) is one of the main inspirations for our approach. The similarity of observations is described using ratios of Euclidean distances to k-nearest observations. Whenever this ratio is close to 1, there is a consistent group of observations and, therefore, no outliers. As for most outlier detection methods, no explicit critical value can be provided for LOF (e.g. Campos et al. [6]; Zimek et al. [25]). In order to optimize the performance of LOF, we estimate the number of k-nearest neighbors for each evaluation. We used the R-package Rlof (Hu et al. [12]) for the computation of LOF.
The second main inspiration for our approach is the ROBPCA algorithm by Hubert et al. [13]. The approach employs distances (similar to the proposed core and orthogonal distances) for describing the outlyingness of observations with respect to the majority of the underlying data. This method should work fine with one consistent majority of observations. In the presence of a multigroup structure, we would expect it to fail since the majority of data cannot be properly described with a model of a single normal distribution. ROBPCA calculates two outlyingness scores, namely orthogonal and score distances.Footnote 1 ROBPCA usually flags observations as outliers if either the score distance or the orthogonal distance exceed a certain threshold. This threshold is based on transformations of quantiles of normal and \(\chi ^2\) distributions. We use the maximum quantile of each observation for the distributions of orthogonal and score distances as a measure for outlyingness in order to stay consistent with the original outlier detection concept of ROBPCA. The dimension of the subspace used for dimension reduction is selected in order to achieve good results. We used the R-package rrcov (Todorov and Filzmoser [24]) for the computation of ROBPCA.
In addition to LOF and ROBPCA, we compare the proposed local projections with PCOut by Filzmoser et al. [10]. PCOut is an outlier detection algorithm where location and scatter outliers are identified based on robust kurtosis and biweight measures of robustly estimated principal components. The dimension of the projection space is automatically selected based on the proportion of the explained overall variance. A combined outlyingness weight is calculated during the process, which we use as an outlyingness score. The method is implemented in the R-package mvoutlier (Filzmoser and Gschwandtner [9]).
Another method included in our comparison is the subspace-based outlier detection (SOD) by Kriegel et al. [16]. The method is looking for relevant dimensions parallel to the axis in which outliers can be identified. The identification of those subspaces is based on knn, where k is optimized in a way similar to LOF and local projections. We used the implementation of SOD in the ELKI framework (Achtert et al. [1]) for performance reasons.
All three methods, LocOut, LOF and SOD, implement knn-estimations in their respective procedures. Therefore, it is reasonable to monitor the performance of k-nearest neighbors (KNN), which can be directly used for outlier detection as suggested in Ramaswamy et al. [21]. The performance is optimized over all reasonable k between 1 and the minimal number of non-outlying observations of a group which we take from the ground truth in our evaluation. We used the R-package dbscan for the computation of KNN.
Similar to the proposed local projections, Outlier Detection in Arbitrary Subspaces (COP) by Kriegel et al. [17] locally evaluates the outlyingness of observations. The k-nearest neighbors of each observation are used to estimate the local covariance structure and robustly compute the representation of the evaluated observation in the principal component space. The last principal components are then used to measure the outlyingness, while the number of principal components to be cut off is selected in order to achieve good results. Although the initial concept looks similar to our proposed algorithm, it contains some disadvantages. The number of observations used for the knn estimation needs to be a lot larger than the number of variables. A proportion of observations to variables of three to one is suggested. Therefore, the method can not be employed for data with more variables than observations, which represent the focus of the proposed approach for outlier analysis. For this reason we did not include COP in the simulation evaluation, but only in the low-dimensional real data evaluation of Sect. 6.
5 Simulation results
We used two simulation setups to evaluate the performance of the methods in order to determine their usability for high-dimensional data: the first setup is based on data simulated from multivariate normal distributions, and for the second setup we consider multivariate log-normal distributions. For both setups we simulate three groups of data with 150, 150, and 100 observations, and each group will contain outliers. The number of informative variables is 50, and starting from 0 noise variables, this number is increased gradually, up to 5000.
In more detail, each of the three groups of observations is simulated based on a randomly rotated covariance matrix \(\varvec{\Sigma }^i\) as performed in Campello et al. [5],
for \(i=1,2,3\), where \(\varvec{I}_{noise}\) is an identity matrix describing the covariance of uncorrelated noise variables, and \(\varvec{\Sigma }^i_{inf}\) the covariance matrix of informative variables, which are variables containing information about the separation of present groups, where \(\rho ^i\) is randomly selected between 0.1 and 0.9, \(\rho ^i \sim U[0.1, 0.9]\). \(\varvec{\Omega }^i\) represents the randomly generated orthonormal rotation matrix. For our simulation setups we always consider the dimensionality of \(\varvec{\Sigma }^i_{inf}\) to be 50. While the mean values of the noise variables are fixed to zero for all groups, the mean values of the informative variables are set as follows for the three groups:
Therefore, for each informative variable, one group can be distinguished from the two other groups. The degree of separation, given by \(\mu \), is randomly selected from a uniform distribution \(U_{[ -6,-3 ] \cup [ 3,6 ]}\). The first simulation setup uses multivariate normally distributed groups of observations using the parameters \(\varvec{\mu }_i\) and \(\varvec{\Sigma }_{inf}^i\), for \(i \in \{ 1,2,3 \}\), and the second setup uses multivariate log-normally distributed groups of observations with the same parameters. Note that noise variables can be problematic for several of the outlier detection methods, and skewed distributions can create difficulties for methods relying on elliptical distributions.
After simulating the groups of observations, scatter outliers are generated by replacing 5% of the observations of each group with outlying observations. Therefore, we use the same location parameter \(\varvec{\mu }_i\), but their covariance matrix is a diagonal matrix with constant diagonal elements \(\sigma \) which are randomly generated between 3 and 9, \(\sigma \sim U[3,9],\) for informative variables. The reason for using scatter outliers instead of location outliers (changed \(\varvec{\mu }_i\)) is the advantage, that outliers will not form a separate group but will stick out of their respective group in random directions.
The outcome of the first simulation setup based on multivariate normal distribution is visualized in Fig. 4. Figure 4a shows the performance with 1000 noise variables measured by the AUC value, for 100 repetitions presented as boxplots. Note again that for all methods, the tuning parameters have been optimized in a sensible grid in order to show best performance. It can be seen that local projections (LocOut) outperform all other methods, while LOF, SOD, and KNN perform approximately at the same level. For smaller numbers of noise variables, SOD performs marginally better than local projections, as it can be seen in Fig. 4b, showing the median performance of all methods with a varying number of noise variables. We see that the performance of SOD drops quicker than other methods, while local projections are effected the least by an increasing number of noise variables. The horizontal grey line corresponds to a performance of 0.5, which refers to random outlier scores.
Evaluation of outliers in three multivariate normally distributed groups with a varying number of noise variables. 5% of the observations were replaced by outliers. Plot (a) shows boxplots for the setup with 1000 noise variables. Each setup was repeatedly simulated 100 times. Plot (b) shows the median performance of each method for various numbers of noise variables
Setup 2, visualized in Fig. 5, shows the effect of a skewed distribution on the outlier detection methods. The order of performance changes since the methods are affected differently. Also, the performance has generally increased since the outliers are more extreme when generated with log-normal distribution. SOD is stronger affected than LOF, since it is easier for SOD to identify useful spaces for symmetric distributions, while LOF does not benefit from such properties. LocOut still shows the best performance, at least for an increasing number of noise variables.
Evaluation of outliers in three multivariate log-normally distributed groups with a varying number of noise variables. 5% of the observations were replaced by outliers. Plot (a) shows boxplots for the setup with 1000 noise variables. Each setup was repeatedly simulated 100 times. Plot (b) shows the median performance of each method for various numbers of noise variables
6 Application on real-world datasets
In order to demonstrate the effectiveness of local projections in real-world applications, we analyze three different datasets, varying in the number of groups, the dimension of the data space, and the separability of the groups. We always use observations from multiple groups as non outlying observations and a small number of one additional group to simulate outliers in the dataset. As noted above, the tuning parameters for the different methods were selected in order to achieve good results. For our method we have selected k as 8 for the olive oil data, and as 5 for the melon and the glass vessels data.
6.1 Olive oil
The first real-world dataset consists of 120 samples of measurements of 25 chemical compositions (fatty acids, sterols, triterpenic alcohols) of olive oils from Tuscany, Italy (Armanino et al. [3]). The dataset is used as a reference dataset in the R-package rrcovHD (Todorov [23]). It consists of four groups with 50, 25, 34, and 11 observations, respectively. We use observations from the smallest group with 11 observations to sample 5 outliers, and repeat the procedure 50 times.
Since this is not yet a high-dimensional data set, it is possible to include COP in the evaluation. It is important to note that at least 26 observations must be used by COP in order to be able to locally estimate the covariance structure, while there will always be a smallest group of 25 observations at most present for each setup. Thus, we would assume, that COP has problems distinguishing between outliers and observations from this smallest group which does not yield enough observations for the covariance estimation.
We show the performance of the compared outlier detection methods based on the AUC values in Fig. 6. We note that all methods but PCOut and COP perform at a very high level. For KNN, SOD and LocOut, there is only a non-significant difference in the median performance.
6.2 Melon
The second dataset used for the evaluation is a fruit data set, which consists of 1095 observations in a 256 dimensional space corresponding to spectra of the different melon cultivars. The observations are documented as members of three groups of sizes 490, 106 and 499, but in addition, during the cultivation processes, different illumination systems have been used leading to subgroups. The dataset is often used to evaluate robust statistical methods (e.g. Hubert and Van Driessen [14]).
We sample 100 observations from two randomly selected main groups to simulate a highly inconsistent structure of main observations and add 7 outliers, randomly selected from the third remaining group. We repeatedly simulate such a setup 150 times in order to make up for the high degree of inconsistency. As Fig. 7 shows, the identification of outliers is extremely difficult for this dataset. The reason might be that when the main group containing the outliers is randomly selected, these outliers may create additional difficulties for all methods. A combination of properly reducing the dimensionality and modeling the existing sub-groups is required. LocOut outperforms the compared methods, followed by LOF and PCOut.
6.3 Archaeological glass vessels
The observations of the glass vessels dataset, described e.g. in Janssens et al. [15], refer to archaeological glass vessels which have been excavated in Antwerp (Belgium). In order to distinguish between different types of glass, which have either been imported or locally produced, 180 glass samples were chemically analyzed, resulting in the composition of some chemical elements of the glass samples. Figure 8a uses this chemical information to reveal the grouping structure of the data, visible by different colors. In addition to the chemical variables, the glass samples were analyzed using electron probe X-ray microanalysis (EPXMA), resulting in a spectrum at 1920 different energy levels. We use only this high-dimensional data set for outlier detection, but a few (11) of those variables/energy levels contain no variation and are therefore removed from our experiments in order to avoid problems during the computation of outlyingness. In previous studies (Lemberge et al. [18], Serneels et al. [22]) it was realized that during the EPXMA analysis, the detector efficiency has changed, which results in a different high-dimensional data structure of the bigger group. Therefore, the black group in Fig. 8a is displayed with two symbols referring to these differences.
In the following experiments we perform outlier detection in the space of the remaining 1909 spectra, by using the main groups (two black, blue, red) as regular data, and the green group as outliers. Within 50 replications, we randomly sample 100 observations from the main groups (regular data), and 5 observations from the green group (outliers). The performance of the methods is visualized in Fig. 8b. Again, LocOut outperforms all compared methods, while LOF and PCOut have problems to deal with this data setup.
7 Discussion of runtime
The algorithm for local projections was implemented in an R-package which is publicly available at https://github.com/tortnertuwien/lop. The package further includes the glass vessels data set used in Sect. 6. Based on this R-package, we performed simulations to test the required computational effort for the proposed algorithm and the impact of changes in the number of observations and the number of variables.
For each projection, the first step of our proposed algorithm is based on the k-nearest neighbors concept. Therefore, we need to compute the distance matrix for all n available p-dimensional observations leading to an effort of \(O(n(n-1)p/2)\) for the computation of each Euclidean distance, where \(n(n-1)/2\) represents the combinations of observations, and p the number of variables.
After the basic distance computation, we need to compare those distances (which scales with n but only contributes negligibly to the overall effort) and scale the data based on the location and scale estimation for the selected core (which also does not significantly affect the computation time).
For all of the n cores, we perform an SVD decomposition leading to an effort of \(O(p^2n^2+n^4)\). Therefore, a total effort of \(O(n^2p(1+p) + n^4)\) is expected for the computation of all local projections. In this calculation, reductions, such as the multiple computation of the projection onto the same core, are not taken into account. Such an effect is very common due to the presence of hubs in data sets (Zimek et al. [25]). Figure 9 provides an overview of the overall computation time decomposed into the different aspects of the computation algorithm. The computations were done on a standard PC with 8 cores.
Visualization of the computation time of the local projections. Plots (a) and (b) evaluate the development of the overall computation time for increasing n in plot (a) and increasing p in plot (b). Those evaluations are performed for varying k. Plot (c) and (d) focus on different components of the computation for a fixed \(k=40\) and increasing n and p
We observe that the computation time increases approximately linearly with p, while it increases faster than a linear term with increasing n. There is an interaction effect between k and n visible in plot (a) of Fig. 9 as well, due to the necessity of n knn computations. Plots (c) and (d) show that the key factors are the n SVDs. Especially the core estimation and the computation of the core distance are just marginally affected by increasing n and not affected at all by increasing p. The orthogonal distance computation is non-linearly affected by increasing n and p which however remains relatively small when being compared to the SVD estimations.
8 Conclusions
We proposed a novel approach for evaluating the outlyingness of observations based on their local behavior, named local projections. By combining techniques from the existing robust outlier detection ROBPCA (Hubert et al. [13]) and from Local Outlier Factor (LOF) (Breunig et al. [4]), we created a method for outlier detection, which is highly robust towards large numbers of non-informative noise variables and which is able to deal with multiple groups of observations, not necessarily following any specific standard distribution.
These properties are gained by creating a local description of a data structure by robustly selecting a number of observations based on the k-nearest neighbors of an initiating observation and projecting all observations onto the space spanned by those observations. Doing so repeatedly, where each available observation initiates a local description, we describe the full space in which the data set is located. In contrast to existing subspace-based methods, we create a new concept for interpreting the outlyingness of observations with respect to such a projection by introducing the concept of quality of local description of a model for outlier detection. By aggregating the measured outlyingness of each projection and by downweighting the outlyingness with this quality-measure of local description, we define the univariate local outlyingness score, LocOut. LocOut measures the outlyingness of each observation in comparison to other observations and results in a ranking of outlyingness for all observations. We do not provide cut off values for classifying observations as outliers and non-outliers. While at first consideration this poses a disadvantage, it allows for disregarding any assumptions about the data distribution. Such assumptions would be required in order to compute theoretical critical values.
We showed that this approach is more robust towards the presence of non-informative noise variables in the data set than other well-established methods we compared to (LOF, SOD, PCOut, KNN, COP, and ROBPCA). Additionally, skewed non-symmetric data structures have less impact than for the compared methods. These properties, in combination with the new interpretation of outlyingness allowed for a competitive analysis of high-dimensional data sets as demonstrated on three real-world application of varying dimensionality and group structure. Note, however, that the local projection method is not orthogonal invariant.
The overall concept of the proposed local projections utilized for outlier detection opens up possibilities for more general data analysis concepts. Any clustering method and discriminant analysis method is based on the idea of observations being an outlier for one group and therefore being part of another group. By combining the different local projections, a possibility for avoiding assumptions about the data distribution—which are in reality often violated—is provided. Thus, applying local projections on data analysis problems could not only provide a suitable method for analyzing high-dimensional problems but could also reveal additional information on method-influencing observations due to the quality of local description interpretation of local projections.
Notes
For a multivariate interpretation of outlyingness based on those two scores, we refer to Pomerantsev [20].
References
Achtert, E., Kriegel, H.-P., Zimek, A.: Elki: a software system for evaluation of subspace clustering algorithms. In: Scientific and statistical database management, Springer, New York, pp. 580–585 (2008)
Aggarwal, C.C., Yu, P.S.: Outlier detection for high dimensional data. In: ACM Sigmod Record, ACM, volume 30, pp. 37–46 (2001)
Armanino, C., Leardi, R., Lanteri, S., Modi, G.: Chemometric analysis of tuscan olive oils. Chemometr. Intell. Lab. Syst. 5(4), 343–354 (1989)
Breunig, M.M., Kriegel, H.-P., Ng, R.T., Sander, J.: Lof: identifying density-based local outliers. In: ACM sigmod record, ACM, volume 29, pp. 93–104 (2000)
Campello, R.J., Moulavi, D., Zimek, A., Sander, J.: Hierarchical density estimates for data clustering, visualization, and outlier detection. ACM Trans. Knowl. Discov. Data (TKDD) 10(1), 5 (2015)
Campos, G.O., Zimek, A., Sander, J., Campello, R.J., Micenková, B., Schubert, E., Assent, I., Houle, M.E.: On the evaluation of unsupervised outlier detection: measures, datasets, and an empirical study. Data Min. Knowl. Disc. 30(4), 891–927 (2016)
De Maesschalck, R., Jouan-Rimbaud, D., Massart, D.L.: The mahalanobis distance. Chemometr. Intell. Lab. Syst. 50(1), 1–18 (2000)
Fawcett, T.: An introduction to roc analysis. Pattern Recogn. Lett. 27(8), 861–874 (2006)
Filzmoser, P., Gschwandtner, M.: mvoutlier: Multivariate outlier detection based on robust methods. R package version 2, 6 (2015)
Filzmoser, P., Maronna, R., Werner, M.: Outlier identification in high dimensions. Comput. Stat. Data Anal. 52(3), 1694–1711 (2008)
Henrion, M., Hand, D.J., Gandy, A., Mortlock, D.J.: Casos: a subspace method for anomaly detection in high dimensional astronomical databases. Stat. Anal. Data Min. ASA Data Sci. J. 6(1), 53–72 (2013)
Hu, Y., Murray, W., Shan, Y.: Australia Rlof: R Parallel Implementation of Local Outlier Factor (LOF). R package version 1(1), 1 (2015)
Hubert, M., Rousseeuw, P.J., Vanden Branden, K.: Robpca: a new approach to robust principal component analysis. Technometrics 47(1), 64–79 (2005)
Hubert, M., Van Driessen, K.: Fast and robust discriminant analysis. Comput. Stat. Data Anal. 45(2), 301–320 (2004)
Janssens, K., Deraedt, I., Freddy, A., Veekman, J.: Composition of 15-17th century archeological glass vessels excavated in Antwerp, Belgium. Mikrochim. Acta. 15(iSuppl), 253–267 (1998)
Kriegel, H.-P., Kröger, P., Schubert, E., Zimek, A.: Outlier detection in axis-parallel subspaces of high dimensional data. Adv. Knowl. Discov. Data Min. pp. 831–838 (2009)
Kriegel, H.-P., Kroger, P., Schubert, E., Zimek, A.: Outlier detection in arbitrarily oriented subspaces. In: Data mining (ICDM), 2012 IEEE 12th international conference on, pp. 379–388. IEEE (2012)
Lemberge, P., De Raedt, I., Janssens, K.H., Wei, F., Van Espen, P.J.: Quantitative analysis of 16–17th century archaeological glass vessels using pls regression of epxma and \(\mu \)-xrf data. J. Chemom. 14(5–6), 751–763 (2000)
Ortner, T., Filzmoser, P., Rohm, M., Breiteneder, C., Brodinova, S.: Guided projections for analysing the structure of high-dimensional data. J. Comput. Graph. Stat. 27(4), 750–762 (2018)
Pomerantsev, A.L.: Acceptance areas for multivariate classification derived by projection methods. J. Chemom. 22(11–12), 601–609 (2008)
Ramaswamy, S., Rastogi, R., Shim, K.: Efficient algorithms for mining outliers from large data sets. In: ACM Sigmod Record, volume 29, pp. 427–438. ACM (2000)
Serneels, S., Croux, C., Filzmoser, P., Van Espen, P.J.: Partial robust m-regression. Chemometr. Intell. Lab. Syst. 79(1), 55–64 (2005)
Todorov, V.: rrcovHD: Robust Multivariate Methods for High Dimensional Data. R package version 0.2-5 (2016)
Todorov, V., Filzmoser, P.: An object-oriented framework for robust multivariate analysis. J. Stat. Softw. 32(3), 1–47 (2009)
Zimek, A., Schubert, E., Kriegel, H.-P.: A survey on unsupervised outlier detection in high-dimensional numerical data. Stat. Anal. Data Min. ASA Data Sci. J. 5(5), 363–387 (2012)
Zimek, A., Filzmoser, P.: There and back again: outlier detection between statistical reasoning and data mining algorithms. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 8(6), e1280 (2018)
Acknowledgements
Open access funding provided by TU Wien (TUW). The authors want to thank the editorial team as well as two reviewers for their helpful comments. This work has been partly funded by the Vienna Science and Technology Fund (WWTF) through project ICT12-010 and by the K-project DEXHELPP through COMET—Competence Centers for Excellent Technologies, supported by BMVIT, BMWFW and the province Vienna. The COMET program is administrated by FFG.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ortner, T., Filzmoser, P., Rohm, M. et al. Local projections for high-dimensional outlier detection. METRON 79, 189–206 (2021). https://doi.org/10.1007/s40300-020-00183-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40300-020-00183-5