Acceleration-Based Switching Surfaces for Impulsive Trajectory Design Between Cislunar Libration Point Orbits

Abstract

A method is proposed to generate an initial guess for impulsive trajectory design in the circular restricted three-body problem. The method uses acceleration-based switching surfaces to obtain near-impulsive solutions. A numerical continuation is performed on the maximum acceleration value to find near-impulsive solutions. A nonlinear programming problem is formulated by providing primer vector based analytical gradients. The solution space is narrowed down to aid the optimizer with the use of the near-impulsive solutions. The proposed method is used for the trajectory design of four different maneuvers between L1 and L2 Halo orbits in the Earth–Moon system. The results demonstrate the utility of the proposed method in generating extremal impulsive trajectories.

1 Introduction

The interest in cislunar space has increased with NASA’s Artemis mission. Artemis lunar-orbiting Gateway platform enables scientific missions on the lunar surface and crewed space missions [1]. The current baseline orbit for the Gateway is a Near Rectilinear Halo Orbit (NRHO) [2]. The mission design process can benefit greatly from enhanced computational tools for design of complex missions in multi-body regimes like the Gateway within multiple gravity fields. For crewed missions, chemical propulsion systems are used, which leads to short mission flight times. Thus, the generation of optimal (with respect to time of flight and fuel consumption) trajectories for spacecraft equipped with chemical propulsion systems has practical implications.

The necessary conditions for optimal impulsive trajectories are established by Lawden [3] through the introduction of the primer vector theory. The primer vector profile can be used to identify the requirements to be satisfied by one or many additional impulses when a cost improvement (in terms of total $\Delta v$) is considered [4]. The task of determining the number of impulses, N, and the locations and times of applying the impulses can be stated as an N-impulse optimization problem. The N-impulse optimization approach, along with the analytical gradients of the minimum-$\Delta v$ cost is derived for the two-body problem in Ref. [5]. The initial guess for the impulse location and time is determined by using the norm of the primer vector, such that the greatest decrease in the cost function is achieved. Furthermore, a Nonlinear Programming (NLP) problem can be formed to determine the locations and times of the impulses. Under the two-body dynamics, Lambert’s problem can also be used as part of the solution to the N-impulse optimization problem [6, 7]. The initial guess in primer-vector-based methods is usually a two-impulse Lambert solution, which is improved by using the primer vector time history [8]. Hughes et al. compared the direct and the primer vector based indirect approaches for solving minimum-fuel problems [9]. Shen et al. used a homotopic approach for impulsive trajectory optimization by formulating an indirect approach to obtain global optimal solutions [10]. Evolutionary algorithms have also been used for N-impulse trajectory optimization [11,12,13]. Even though the evolutionary algorithms do not require an initial guess, they may not provide optimal solutions since the number of impulses is not known in advance [14]. Recently, Saloglu et al. have shown that under two-body dynamics, it is possible to have infinitely many multiple-impulse minimum-$\Delta v$ solutions [15].

Hiday et al. derived the necessary conditions for the elliptic restricted three-body problem by extending the work of Lawden [8, 16]. When an impulsive trajectory violates the necessary conditions, the addition of one or multiple impulses or terminal coasts can improve the cost. However, when multiple impulses are to be added, the introduction of impulses is typically performed one impulse at a time until the necessary conditions are satisfied [8, 16,17,18,19,20]. Therefore, an iterative process is required to obtain an extremal solution starting with a two-impulse initial guess. Catalogs of orbits in the three-body dynamics have been used as an initial guess for trajectory generation for libration point transfers, by ensuring continuity using differential-correction schemes [21,22,23].

Invariant manifolds have also been used for generating libration point impulsive and low-thrust transfers in various three-body dynamical systems [24,25,26,27,28,29,30,31]. For instance, a greedy global search technique is utilized for placing impulsive maneuvers to connect points of invariant manifolds [32]. Poincaré maps are used to generate initial impulsive guesses along with the multiple-shooting targeting schemes to relate the dynamical structures [33, 34]. An approximate analytical solution to Lambert’s problem under three-body dynamics is used to generate the impulsive transfers between libration point orbits [35]. The initial guess generation can also be achieved using the notion of motion primitives obtained from the common features of dynamical structures in the circular restricted three-body problem (CR3BP) systems [36]. The “patch periodic orbit” method patches periodic orbits to design low-energy transfers and to leverage existing dynamical structures and periodic orbits [37]. The orbit-chaining method provides a dynamics-based initial guess by the construction of orbit chains to guide the optimizer in the solution space for a direct collocation method, where the impulsive solutions are obtained from using the low-thrust solution as an initial guess [38,39,40]. The orbit-chaining method also relies on patching periodic orbits, but its application is demonstrated with respect to the low-thrust trajectory design. Recently, Oshima has developed a regularized direct method for designing low-thrust and near-impulsive trajectories between cislunar periodic orbits [41].

As an alternative to existing methods to generate high-quality initial guesses, thrust-based continuation methods have also been used to determine the number, time instances, and locations of the impulses [42, 43]. In this context, a high-quality initial guess is one that is sufficiently close to an impulsive solution with respect to the total impulse value. The impulsive case is the limiting (high-thrust) solution of the finite-thrust problem formulation [42, 44]. The connection between high-thrust and impulsive solutions is successfully leveraged by introducing the idea of switching surfaces [45] to answer Edelbaum’s question [46] originally posed under an inverse-square two-body gravity model. The low-thrust and impulsive solutions are connected by applying a standard continuation on the maximum thrust value (for a low-thrust minimum-fuel formulation of the orbital maneuver [47]) to obtain an initial guess for the impulsive solution under two-body dynamics [45]. The acceleration-based formulation is introduced in [48] to simplify the problem by removing the mass, the specific impulse, and the thrust value, making the problem formulation directly connected to minimum-$\Delta v$ maneuvers. Numerical continuation on the maximum value of the propulsive acceleration is performed to obtain near-impulsive trajectories. Continuation-based methods are also used for multi-revolution, multi-impulse trajectory generation under inverse-square gravity models with various propulsive acceleration models [49].

The contributions of this work are as follows. Firstly, the idea of acceleration-based switching surfaces is used as an initial guess to generate near-impulsive trajectories under three-body dynamics. The initial guess characterizing the times and locations of the impulses is generated from a high-acceleration solution. The high-acceleration solution is obtained by solving multiple two-point boundary-value problems (TPBVPs) with a continuation performed on the maximum acceleration value. Then, an NLP problem is formulated with the analytical gradients to obtain extremal impulsive trajectories. Secondly, the proposed method avoids the steps of adding additional impulses or terminal coast arcs, since near-impulsive arcs separated by coast arcs are determined automatically through the continuation procedure. Therefore, this method provides the number of impulses, approximate impulse locations and times as well as the existence of terminal coast arcs. As a consequence, the number of NLP iterations used for solving the N-impulse optimization problem is decreased. Especially, when a hybrid/indirect method is used for impulsive trajectory optimization, one should evaluate the primer vector and add impulses or terminal coast arcs to obtain an extremal solution. If the pure direct method is considered, the problem has to be solved with a different number of impulses to obtain the extremal solution. However, the proposed method circumvents going through the aforementioned steps at the expense of solving many neighboring TPBVPs. The proposed method can be viewed as an alternative to existing initial guess generation methods. Thirdly, this work is an extension of the work in Ref. [50] by solving more complex problems in the cislunar space, including halo-to-halo orbit transfers, transfers from L2 to NRHO and transfers between L2 southern Halo orbits.

The remainder of the paper is organized as follows. Dynamical models and problem formulations are presented in Sect. 2. The equations of motion under the CR3BP model are given in Sect. 2.1. Then, key elements of the acceleration-based method are presented in Sect. 2.2. Furthermore, the multiple-shooting impulsive trajectory optimization framework is explained in Sect. 2.3. Numerical results for four halo-to-halo orbit rendezvous maneuvers in the Earth–Moon system are given in Sect. 3. Finally, the concluding remarks and the summary of the work are presented in Sect. 4.

2 Dynamical Models and Problem Formulation

2.1 Circular-Restricted Three-Body Problem

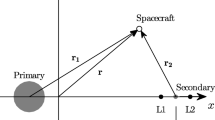
The motion of a spacecraft under the influence of two massive bodies can be expressed by the CR3BP equations, where the orbits of the primary and secondary bodies (i.e., Earth and Moon in this paper, respectively) are assumed to be circular. The spacecraft motion is expressed in the synodic rotating frame, where the origin is the barycenter, the x-direction points to the secondary body, and the z-axis is in the direction of the angular momentum of the system. The y-axis completes the right-handed coordinate system. The mass ratio of the system, $\mu$, is defined such that the mass of the Moon is divided by the summation of the Earth and the Moon’s masses. In the nondimensional system, the distance between the primary and secondary bodies is defined as the length unit (LU). The locations of the primary and secondary bodies are along the x-axis at $-\mu$ and $1-\mu$, respectively. The time unit (TU) is chosen such that the gravitational parameter, G, becomes 1.

Let $\varvec{r} = [x, y, z]^{\top }$ and $\varvec{v} = [\dot{x}, \dot{y}, \dot{z}]^{\top }$ denote the position and velocity vectors of the center of mass of the spacecraft, respectively. Let $\varvec{x} = [{\varvec{r}}^{\top }, {\varvec{v}}^{\top }]^{\top }$ denote the state vector and let $\varvec{a} = [a_x,a_y,a_z]^{\top }$ denote the propulsive acceleration vector. The spacecraft equations of motion can be written as

$$\begin{aligned} \begin{aligned} \ddot{x}&=2 {\dot{y}}+x-(1-\mu ) \frac{x+\mu }{r_{1}^{3}}-\mu \frac{x-1+\mu }{r_{2}^{3}}+a_x, \\ \ddot{y}&=-2 {\dot{x}}+y-(1-\mu ) \frac{y}{r_{1}^{3}}-\mu \frac{y}{r_{2}^{3}} +a_y, \\ \ddot{z}&=-(1-\mu ) \frac{z}{r_{1}^{3}}-\mu \frac{z}{r_{2}^{3}}+a_z, \end{aligned} \end{aligned}$$

(1)

where $r_1 =\sqrt{(x+\mu )^{2}+y^{2}+z^{2}}$ and $r_2=\sqrt{(x+\mu -1)^{2}+y^{2}+z^{2}}$ are distances between the spacecraft and the Earth and Moon, respectively. The state transition matrix (STM), $\Phi (t,t_0)$, of the system can be propagated using the state transition matrix differential equation, ${\dot{\Phi }}\left( t, t_{0}\right) =\frac{\partial {\dot{\varvec{x}}}}{\partial {\varvec{x}}}(t) \Phi \left( t, t_{0}\right)$ with $\Phi \left( t_0, t_{0}\right)$ being equal to the identity matrix, $I_{6 \times 6}$. The STM can be used to map the states from an initial time, $t_0$, to another time, $t\in [t_0,t_f]$. Thus, the STM can be propagated along with the states for the indirect single-shooting and direct differential correction algorithms that will be used as part of the solution procedure [47]. The energy-like integral of the motion, Jacobi constant, for the system can be defined as $JC = 2U - v^2$ where $v = \Vert \varvec{v}\Vert$ and the pseudo-potential is defined as $U = ({x^{2}+y^{2}})/{2}+({1-\mu })/{r_{1}}+{\mu }/{r_{2}}$.

2.2 Acceleration-Based Problem Formulation

Formulation of the low-thrust trajectory optimization problem is obtained by the acceleration-based method utilizing the indirect formalism of optimal control. The cost functional can be written in Lagrange form as [50]

$$ \begin{aligned} \underset{\Vert \hat{\varvec{\alpha }}\Vert =1~ \& ~ \delta \in [0,1]}{{\text {minimize}}} \quad J= \int _{t_{0}}^{t_{f}} ~a_{\max }\delta (t)~d t, \end{aligned}$$

(2)

where $a_{\text {max}}$ is the maximum acceleration value and $\delta \in [0,1]$ is the engine throttle input. The acceleration vector is expressed as $\varvec{a}=a_{\max } \delta \hat{\varvec{\alpha }}$, where $\hat{\varvec{\alpha }}$ is a unit steering vector. The costate dynamics can be derived using the Euler-Lagrange equations. The optimal steering vector is in the direction of the primer vector, $\varvec{p} = -\varvec{\lambda }_{v}$, and the throttle, $\delta$, is determined by the sign of the switching function, $S=\left\| \varvec{\lambda }_{v}\right\| -1$, where $\varvec{\lambda }_{v}$ is the velocity costate vector. Hyperbolic tangent smoothing is used to enforce bang-bang profiles for optimal throttle, $\delta ^{*}(S;\rho )= 0.5[1+\tanh ({S}/{\rho })]$, with the smoothing parameter $\rho$. The detailed steps of formulating the associated TPBVP are given in Ref. [49].

In this study, all the trajectory optimization problems considered are fixed-time, rendezvous-type maneuvers. Therefore, the initial and final states at the boundaries are fixed and known. Hence, the residual vector of the resulting TPBVPs can be expressed as a vector of equality conditions of a nonlinear shooting problem written as

$$\begin{aligned} \varvec{\psi }(\varvec{\lambda }(t_0);\rho , a_{\text {max}})=\left[ \begin{array}{l} \varvec{r}\left( t_{f}\right) -\varvec{r}_{T} \\ \varvec{v}\left( t_{f}\right) -\varvec{v}_{T} \end{array}\right] =\varvec{0}, \end{aligned}$$

(3)

where $\varvec{r}_{T}$ and $\varvec{v}_{T}$ are target position and velocity vectors, respectively. In Eq. (3), $\varvec{\lambda }(t_0)$ denotes the unknown initial costate vector. The nonlinear root-finding problem given in Eq. (3) corresponds to solving a two-parameter family of neighboring TPBVPs associated with the cost functional defined in Eq. (2).

The resulting two-parameter family of neighboring TPBVPs is typically solved by employing single- or multiple-shooting solution schemes. In this work, MATLAB’s fsolve is used by providing the gradients calculated by the STM of the system. For the single-shooting method, costates are initialized randomly. When a single-shooting method does not converge due to the nonlinearity of the shooting problem, we use a pseudospectral collocation-based direct method, TOPS (Tiger OPtimization Software) [51]. The initial guess for TOPS is obtained using the orbit-chaining method or patched periodic orbit by linking periodic orbits [37, 38, 40]. Numerical continuation is performed on the value of $\rho$ to generate near bang-bang throttle profiles. Also, numerical continuation on the $a_{\max }$ value is performed to obtain the high-acceleration solutions that are used as initial guesses to the N-impulse trajectory optimization algorithm that is explained in the next section. This method maps the low-acceleration solution to a high-acceleration solution [45, 48, 49], whereas the reverse approach is also investigated in the literature [42, 43].

For the considered examples, the continuation steps are as follows. We first solve a low-acceleration problem, starting typically from $a_{\text {max}}$ being equal to $1.0\times 10^{-4}$ or $1.0\times 10^{-3}$ m/$s^2$ level when $\rho = 1$. The exact values are provided in Sect. 3. Once a solution is obtained, the value of $\rho$ is decreased to $\rho = 1.0\times 10^{-3}$ in 100 logarithmic steps. Then, we increase the acceleration by 1% and continue until the change in the approximate $\Delta v$ is small enough compared to the previous step. Also, the primer vector norm vs. time plot can be useful to determine how close the solution is to an impulsive solution, namely, by checking how close the norm of the primer vector is to 1 at the candidate impulse times. In addition, during the continuation, solver tolerances can be relaxed (increased) for faster convergence. Then, once the highest $a_{\text{ max }}$ solution is obtained, the last TPBVP can be solved by taking smaller tolerances and decreasing $\rho$ to smaller values, e.g., $1.0\times 10^{-4}$. At every step of the continuation on $a_{\text {max}}$, the costate information is saved. When we solve the corresponding TPBVP, $\varvec{\lambda _v}$ information is available and we can evaluate the S(t) for each continuation step of $a_{\text {max}}$. Then, the S vs. time curve for each $a_{\text {max}}$ are concatenated to generate the switching surface plots in Sect. 3.

2.3 Multiple-Shooting Impulsive Trajectory Optimization

Once a high-acceleration solution is generated using the procedure outlined in Sect. 2.2, we can feed the trajectory as a near-impulsive guess (with respect to the minimum value of $\Delta v$) to a dedicated N-impulsive trajectory optimization tool. The optimization process is a combination of a multi-segment differential correction scheme and a gradient-descent optimization algorithm. The impulsive trajectory optimization task is formulated as a dual-level multiple-shooting optimization problem. The outer-level optimization process iterates over the position and time of the impulses, whereas the inner-level targeting algorithm performs a multi-segment differential correction to enforce position continuity and returns the cost value. The reason for using a multi-segment differential correction is attributed to the sensitivity of the optimization problems associated with the CR3BP dynamics.

For the outer-level optimization process, the cost can be written as

$$\begin{aligned} \underset{\varvec{Z}}{{\text {minimize}}} \ J = \sum _{k=1}^{N+1}\left\| \Delta \varvec{v}_{k}\right\| , \end{aligned}$$

(4)

where $N+1$ is the total number of impulses and $\varvec{Z}$ is the vector of design variables defined as $\varvec{Z}=\left[ \begin{array}{llllllll} t_{2},&t_{3},&\ldots&, t_{N},&\varvec{r}_{2+}^{\top },&\varvec{r}_{3+}^{\top },&\ldots&, \varvec{r}_{\text{N}+}^{\top } \end{array}\right] ^{\top }$ consisting of the times and locations of the impulses. The k-th impulse magnitude is denoted as $\left\| \Delta \varvec{v}_{k}\right\|$ (i.e., the discontinuity of velocity at the impulse locations is the required impulse at that location). The initial value for the design variables ($\varvec{Z}_{init}$) is retrieved from the high-acceleration solution similar to the procedure outlined in [45] (see Eq. (17) in [45]). The continuity of the position is enforced with the multiple-shooting algorithm.

Gradients of Eq. (4) with respect to the design variables can be expressed in terms of the primer vector and its derivative [52] as

$$\begin{aligned} \begin{aligned} \frac{d J}{d \varvec{r}_{m+}}&=\dot{\varvec{p}}_{m+}^{\top }-\dot{\varvec{p}}_{m-}^{\top },&\frac{d J}{d t_{m}}&=-(\dot{\varvec{p}}_{m+}^{\top } \varvec{v}_{m+}-\dot{\varvec{p}}_{m-}^{\top } \varvec{v}_{m-}), \end{aligned} \end{aligned}$$

(5)

where $m = 2, \ldots , N$, and $\dot{\varvec{p}}$ is the time derivative of the primer vector. The subscripts ‘−’ and ‘$+$’ represent the values of the corresponding state immediately before and after the impulse. An extremal trajectory satisfies the following conditions: $\Vert \varvec{p}(t)\Vert \le 1$, $\varvec{p}(t_k)=\Delta \varvec{v}_k/{\Delta v_k}$, and ${\dot{p}}(t_k)=\dot{\varvec{p}}^{\top }(t_k) \varvec{p}(t_k)=0$ with $t_k$ denoting the k-th impulse time. Note that $\varvec{p}$ and $\dot{\varvec{p}}$ can be evaluated using STM between two consecutive impulses to verify extremal solutions [52].

Depending on the sensitivity of the problem and the quality of the initial guess, single-segment differential corrections might not converge. Thus, inner segment nodes can be added depending on the sensitivity of the trajectory leg to obtain multi-segment differential corrections, similar to the procedure explained in Ref. [19], but for the fixed-time class of maneuvers. The trajectory legs are defined as coast arcs between two consecutive impulses and segments are the arcs between inner nodes in a leg. In Fig. 1, an example trajectory is shown with two nodes in the first leg. The segment nodes are determined by propagating the STM between the leg nodes. Whenever the infinity norm of the STM becomes greater than a predefined sensitivity limit, a segment node is placed at that point, which may lead to multiple nodes per segment with state continuity enforced at nodes.

Fig. 1

Schematic of a representative multi-segment multi-impulse trajectory

The adopted multiple-segment optimization algorithm results in an NLP problem, which can be solved using a variety of NLP solvers (e.g., MATLAB’s fmincon, which is a Quasi-Newton-based NLP solver). To summarize the multiple-shooting impulsive trajectory optimization algorithm, the flowchart of the algorithm is given in Fig. 2. Here, $\varvec{X}_{seg}$ represents a matrix, each row of which denotes the initial free variable vector for each leg of the inner-level multi-segment differential correction algorithm.

Fig. 2

Multiple-segment impulsive trajectory optimization algorithm

3 Numerical Results

Four examples are considered to showcase the capability of the tool in solving problems with different mission times and numbers of impulses. However, the method is general and applicable to other classes of orbit transfers. The main motivation for maneuvers between L2 Halo orbits is to consider possible trajectories for efficient transport of cargo, crew, and payloads to and from the Gateway platform for enabling deep-space missions. The trajectory from L1 to L2 might be a possible trajectory for spacecraft launching from Earth that first arrives at the L1 point and continues its trajectory towards the L2 point.

The following tolerances are used. In the single-shooting method, fsolve tolerances are $1.0\times 10^{-10}$ and $1.0\times 10^{-14}$ for “function” and “step-size”, respectively. During continuation, these tolerances are relaxed to $1.0\times 10^{-8}$ and $1.0\times 10^{-6}$. We also use bvp4c of MATLAB for solving low-thrust problems with tolerances $1.0\times 10^{-9}$ with relaxing it to $1.0\times 10^{-3}$ during continuation. For the multi-impulse trajectory optimization, fmincon’s “function” and “step-size” tolerances are set to $1.0\times 10^{-15}$ and $1.0\times 10^{-12}$, respectively. Multi-segment differential correction tolerance is $1.0\times 10^{-8}$. We use MATLAB’s ode45 function for the integration of the set of state-costate equations with $1.0\times 10^{-10}$ relative and absolute tolerances. The numerical simulations are performed on a workstation with Intel Xeon Silver 2.40 GHz Processor and 64 GB memory, on MATLAB R2021b. Note that the developed codes are not written in a way that is optimized for shorter runtimes. The numerical data for the considered examples are given in Appendix.

3.1 L1 Halo to L2 Halo Transfer

We first performed the numerical continuation on $a_{\text {max}}$ to construct the switching surface starting from a low-acceleration solution. The initial and final values of $a_{\text {max}}$ are $3.33\times 10^{-3}$ and $2.01\times 10^{-2}$ m/s$^2$, respectively. The $a_{\text {max}}$ value is increased with %1 in 182 steps. The computational time for the continuation is 10.26 seconds. Fig. 3 shows the switching surface. Acceleration arcs are apparent when the switching function is positive, shown in gray. In all the switching surface plots, the $a_{\text {max}}$ axis is plotted in a logarithmic scale. For low $a_{\text {max}}$ values, acceleration arcs have a longer time duration. At the high-acceleration value, there are two candidate impulses at the beginning and end of the trajectory in Fig. 3.

Fig. 3

The L1 Halo to L2 Halo problem: a switching surface plot; b Top view (contour plot) of the switching surface

The high-acceleration trajectory corresponding to $a_{\max } = 2.01 \times 10^{-2}$ m/$\text {s}^2$ and $\rho = 10^{-4}$ is plotted in Fig. 4a. The acceleration arcs are located at the initial and final phases of the trajectory. The total impulse required is $\Delta v = 541.40$ m/$\text {s}$. Figure 4b shows the time history of the primer vector magnitude, $\Vert \varvec{p}\Vert$, for the high-acceleration solution. The violations of the necessary conditions occur at the initial and final phases of flight.

Fig. 4

L1 Halo to L2 Halo problem: a trajectory with $\rho = 10^{-4}$ and $a_{\max } = 2.01 \times 10^{-2}$ m/$\text {s}^2$; b $\Vert \varvec{p}\Vert$ vs. time for the high-acceleration trajectory

Since the problem is a fixed-time problem, introducing a terminal coast is not considered. Thus, solving the differential correction is sufficient to obtain the two-impulse solution. The obtained impulsive trajectory is presented in Fig. 5, which is almost identical to the high-acceleration trajectory plotted in Fig. 4a. The red cross markers represent the locations of the impulses. The total impulse value is $\Delta v = 531.45$ m/$\text {s}$. Magnitudes of the individual impulses are 335.80 m/s and 195.65 m/s. Impulses occur at the beginning and end of the trajectory, 0 and 1.1 TU, which corresponds to the boundary positions. The reduction in the total impulse value is 9.95 m/$\text {s}$ compared to the high-acceleration solution. The primer vector magnitude history of the impulsive solution is plotted in Fig. 6 and it does not violate the unity constraint. Also, the derivative of the primer vector magnitude ($\dot{p} = \dot{\varvec{p}}^{\top }\varvec{p}$) is not necessarily equal to zero at the initial and final impulse times, since a fixed-time problem is considered. Thus, the solution satisfies Lawden’s necessary conditions and qualifies to be an extremal solution.

Fig. 5

L1 Halo to L2 Halo problem: two-impulse trajectory with $\Delta v = 531.45$ m/s

Fig. 6

L1 Halo to L2 Halo problem: a $\Vert \varvec{p} \Vert$ vs. time and b ${\dot{p}}$ vs. time for the impulsive trajectory

3.2 L2 Halo to L2 Halo Transfer

A maneuver between an L2 Halo to another L2 Halo orbit is considered. The continuation on $a_{\text {max}}$ is performed starting from $8.0\times 10^{-5}$ until $3.19\times 10^{-3}$ m/${\text{s}}^2$ in 372 steps with %1 increments. The runtime for performing all continuation steps is 175.33 seconds.

Fig. 7

L2 Halo to L2 Halo problem: a switching surface plot; b top view (contour plot) of the switching surface

The switching surface for this trajectory is plotted in Fig. 7. The final high-acceleration solution has four acceleration arcs. However, for lower values of $a_{\max }$, there exist five acceleration arcs. In Fig. 7, the first thrust arc is very short and it is at the very beginning of the trajectory. As the $a_{\max }$ value is increased, the time duration of the acceleration arcs gets smaller while the trajectory gets closer to an impulsive solution. In Fig. 8, the high-acceleration solution is presented. The value of $a_{\max }$ is $3.19 \times 10^{-3}$ m/$\text {s}^2$ and $\Delta v = 59.178$ m/s. The necessary conditions are violated in terms of the primer vector magnitude, but this solution qualifies as a “high-quality” initial guess for the multiple-shooting impulsive algorithm, since the duration of the acceleration arcs is short. The impulsive trajectory solution is given in Fig. 9. The total impulse value is $\Delta v = 58.74$ m/s. The number of segment nodes used for each leg is 1. In total, 3 segment nodes are used since the trajectory consists of three legs. In this example, the improvement in the total impulse value is 0.43 m/s compared to the high-acceleration solution. Figure 10 depicts time histories of the primer vector magnitude and its derivative, which shows that the solution is an extremal solution.

Fig. 8

L2 Halo to L2 Halo problem: a trajectory plot with $\rho = 1.0 \times 10^{-4}$ and $a_{\max } = 3.19 \times 10^{-3}$ m/s$^2$; b $\Vert \varvec{p}\Vert$ vs. time

Fig. 9

L2 Halo to L2 Halo problem: impulsive solution with $\Delta v = 58.74$ m/s

Fig. 10

L2 Halo to L2 Halo problem: a $\Vert \varvec{p} \Vert$ vs. time and b ${\dot{p}}$ vs. time for the impulsive trajectory

3.3 Transfer Between L2 Southern Halo Orbits

In this case, the initial and target orbits are chosen from the L2 Southern Halo orbit family. Due to the nonlinearity of the dynamics and the large mission time for this case, we use a direct transcription approach using the pseudo-spectral solver, TOPS [51]. TOPS supports multiple NLP solvers (with the ability to generate first- and second-order derivatives using algorithmic differentiation [53]), but for this application, IPOPT (Interior Point Optimizer) is used [54]. We resort to this method since a single-shooting method could not solve the resulting TPBVP associated with the rather sensitive boundary-value problem. However, TOPS was able to generate the low-acceleration solution.

Initial guess generation for TOPS is constructed using the orbit-chaining method [38, 40]. Two orbits are used as intermediate orbits in addition to the initial and the target orbits. On each orbit, one revolution is considered for the initial guess. Mission time is determined from the total time spent on all four orbits in the initial guess.

Once a low-acceleration solution is obtained using TOPS with $a_{\max } = 1 \times 10^{-4}$ m/s$^2$, continuation on the $a_{\max }$ parameter is performed until $a_{\max } = 5.48 \times 10^{-4}$ m/s$^2$ in 171 steps with %1 increments. MATLAB’s boundary-value solver bvp4c is used along with the acceleration-based indirect formulation for the continuation step. The solution obtained from TOPS is used as an initial guess to bvp4c with the states, control, and costate estimates. During the continuation, bvp4c tolerance is set to $1.0\times 10^{-3}$. When the final solution is obtained, we re-solve the problem with a higher tolerance set to $1.0\times 10^{-9}$. The elapsed time for the continuation process is 101.33 seconds. The switching surface for this problem is shown in Fig. 11. The first acceleration arc between 0 and 2 TU is divided into two acceleration arcs as the acceleration is increased. Also, two of the acceleration arcs vanish, around 5 TU and 10 TU, when $a_{\text {max}}$ value is increased. In total, 5 short acceleration arcs remain at the highest acceleration value. The locations and times of those short acceleration arcs are used as an initial guess for the impulsive trajectory design.

Fig. 11

L2 Southern Halo orbit transfer with four orbits: a switching surface plot; b top view (contour plot) of the switching surface

The high-acceleration solution is given in Fig. 12 with total $\Delta v = 248.45$ m/s and $a_{\max } = 5.48 \times 10^{-4}$ m/s$^2$. The time of flight of the trajectory is 56.87 days. Figure 12a depicts the three-dimensional trajectory. In Fig. 12b, acceleration arcs occur when the primer magnitude is above 1.

Fig. 12

L2 Southern Halo orbit transfer with four orbits: a trajectory with $\rho = 1.0 \times 10^{-3}$ and $a_{\max } = 5.48 \times 10^{-4}$ m/s$^2$; b $\Vert \varvec{p}\Vert$ vs. time

The impulsive solution is shown in Fig. 13. The trajectory has 5 impulses and an initial coast arc. The number of segment nodes used for this case is 7, 14, 15, and 3 for each leg. As the coast time increases between impulsive maneuvers, more nodes are required. As expected, the total $\Delta v = 246.38$ m/s of the pure impulsive solution is lower compared to the high-acceleration solution (with $\Delta v = 248.45$ m/s). The time histories of the primer vector norm and its derivative are shown in Fig. 14. The solution satisfies the necessary conditions for optimality and qualifies as an extremal solution.

Fig. 13

L2 Southern Halo orbit transfer problem: impulsive solution with $\Delta v = 246.38$ m/s. a three-dimensional and b x–z views of the trajectory

Fig. 14

L2 Southern Halo orbit transfer problem: a $\Vert \varvec{p} \Vert$ vs. time and b ${\dot{p}}$ vs. time for the impulsive trajectory

3.4 Low-Amplitude L2 Halo Orbit to NRHO Transfer

This case is from a low-amplitude L2 Southern Halo to the 9:2 NRHO. The low-acceleration solution is obtained with TOPS with an acceleration level of $a_{\max } = 1.0 \times 10^{-3}$ m/s$^2$, which is 10 times higher than the previous case. The high-acceleration solutions, in some cases, are easier to obtain. The acceleration continuation is performed for completeness, but the initial solution already has a relatively high acceleration value compared to other cases presented. The $a_{\text {max}}$ value is increased to $4.34\times 10^{-2}$ m/s$^2$ in 379 steps with $\%1$ increments. The computational time is 113.19 s. The switching surface plots are shown in Fig. 15. Notice that the x-axis of Fig. 15b has a jump since we removed the large coast arc part from the switching surface to focus on the first and last two acceleration arcs. Since the switching function values of the impulses are close to zero (on the order of $10^{-5}$), they are not visible on the switching surface.

Fig. 15

L2 Southern Halo orbit to NRHO transfer: a switching surface plot; b top view (contour plot) of the switching surface

The high-acceleration solution is presented in Fig. 16a. The total $\Delta v = 348.31$ m/s for this solution and the total time of flight is 61.48 days. Solution has four impulses. For each leg, 7, 47, and 3 segment nodes are added. The largest coast time corresponds to the leg where the most number of segment nodes are added. The primer vector magnitude for the high-acceleration solution is shown in Fig. 16b. The value of the primer magnitude is almost equal to 1 or slightly higher at four points, which are the potential impulse points for the impulsive trajectory.

Fig. 16

L2 Southern Halo orbit to NRHO transfer: a trajectory with $\rho = 1.0 \times 10^{-4}$ and $a_{\max } = 4.34 \times 10^{-2}$ m/s$^2$; b $\Vert \varvec{p}\Vert$ vs. time

The impulsive solution is shown in Fig. 17. The target point is the perilune of the NRHO orbit. Thus, spacecraft does not have a close approach to the Moon. The total impulsive $\Delta v$ is 347.84 m/s, which is lower than the one obtained in the high-acceleration solution. The primer vector magnitude and its derivative are shown in Fig. 18. The solution satisfies the necessary conditions for optimality.

Fig. 17

L2 Southern Halo orbit to NRHO transfer trajectory with $\Delta v = 347.84$ m/s. a three-dimensional view; b $x-z$ view

Fig. 18

L2 Southern low-amplitude Halo orbit to NRHO transfer: a $\Vert \varvec{p} \Vert$ vs. time and b ${\dot{p}}$ vs. time for the impulsive trajectory

3.5 Discussion

From the numerical results, the proposed method is able to generate impulsive maneuvers similar to the ones found in the literature. The method requires performing a continuation on the maximum acceleration parameter, $a_{\text {max}}$. Therefore, multiple TPBVPs have to be solved to obtain the high-acceleration solution, which is one of the limitations of the current method. The required computational time of the continuation process for the examples we solved is under 3 min. One of the limitations of this method is that it requires solving a low-thrust trajectory optimization problem first, which can be challenging depending on the problem. Single-shooting methods are usually not suitable for solving trajectory optimization problems in CR3BP models due to the nonlinearity of the dynamics. The indirect methods are sensitive to the costate initial guesses. A multi-shooting method or a direct collocation method can be an alternative to obtain the low-acceleration solution for the first step of the continuation, which is considered for one of the examples.

In general, the solution to practical trajectory optimization problems, using the indirect formalism of optimal control theory, is typically achieved through homotopy and/or numerical continuation methods [55]. Existing methods for initial guess generation require extensive knowledge from mission designers with respect to the solution structures that exist in the three-body dynamics. To the authors’ best knowledge, no general method exists for initial guess generation under three-body dynamics. The proposed acceleration-based method can be viewed as an alternative initial guess generation method. It provides a high-quality initial guess to warm-start the NLP solver for solving the N-impulse trajectory optimization problems within CR3BP models.

4 Conclusion

An initial-guess-generation method is presented to obtain impulsive trajectories under circular-restricted three-body dynamics via an impulsive multiple-shooting optimization tool. The initial guess to the NLP solver is obtained from the high-acceleration solution, which is generated by performing a parameter continuation on the maximum acceleration value. The example trajectories include L1 Halo to L2 Halo, L2 Halo to L2 Halo, between L2 Southern Halo orbits, and low-amplitude L2 to the Near Rectilinear Halo orbit designated for the lunar Gateway. The number of impulses varies from 2 to 5 in the considered trajectories, ranging from 4.8 days to approximately 62 days.

The results indicate that the high-acceleration solutions offer a high-quality initial guess for impulsive trajectory optimization. The location and the number of the impulses or the existence of coasting arcs information can be obtained from the high-acceleration solutions. Due to the sensitivity of the three-body dynamics, a single-shooting solution method might not be suitable for problems with a high number of impulses or a longer time of flight. For those cases, multiple-shooting methods have to be employed as well as direct method optimizers. Additionally, multi-segment differential corrections are instrumental in overcoming the sensitivity issues in the three-body dynamics for impulsive trajectory optimization. It is known that initial guesses can impact the convergence performance of the gradient-based methods. Our results indicate that the solutions obtained using the acceleration-based switching surfaces serve as a high-quality initial guess achieved in under 3 min for the considered transfer problems. However, high-quality initial guesses are achievable by solving a family of neighboring TPBVPs, and the trade-off between computational time and robustness has to be taken into consideration.

Appendix: Data for Test Cases

Position and velocity boundary conditions are given in Tables 1 and 2, respectively. Boundary orbit parameters are given in Table 3. Low-acceleration solution costates are given in Tables 4 and 5. High-acceleration solution costates are given in Tables 6 and 7. Impulsive trajectory $\Delta \varvec{v}$ vectors, positions, and times of the impulses are given in Tables 8, 9, and 10, respectively. Transfer maneuvers in the Earth–Moon system are considered with the following parameters [43, 48]: Length Unit $(\textrm{LU})$ is $3.84405000 \times 10^{5}~(\textrm{km})$, Time Unit $(\textrm{TU})$ is $3.75676967 \times 10^{5}~(\textrm{seconds})$, Velocity Unit $(\textrm{VU})$ is $1.02323281~(\textrm{km} / \textrm{s})$, and the normalized mass parameter is $\mu = 1.21506683 \times 10^{-2}$. Cases 1, 2, 3, and 4 correspond to the problems in Sects. 3.1, 3.2, 3.3 and 3.4, respectively. The maximum acceleration values of the high-acceleration solutions for the respective cases are 0.020165680783715 m/s$^2$, 0.003198183826998 m/s$^2$, $5.482200524324486\times 10^{-4}$ m/s$^2$, 0.043431083453211 m/s$^2$. The $a_{\text {max}}$ parameters for each low-acceleration solution are as follows: 0.00333 m/s$^2$, $8 \times 10^{-5}$ m/s$^2$, $1 \times 10^{-4}$ m/s$^2$, $1 \times 10^{-3}$ m/s$^2$. Initial $\rho = 1$ for Cases 1, 2, 3 and $\rho = 10^{-2}$ for Case 4. Final $\rho = 10^{-4}$ for Cases 1, 2, 4, and $\rho = 10^{-3}$ for Case 3. Mission times for the respective cases are 1.09999440024227, 3.44977231462796, 13.0789122308048, and 14.1402386607240 in nondimensional time (TU).

Table 1 Position values for boundary and intermediate (Int.) orbits

Table 2 Velocity values for boundary and intermediate orbits

Table 3 Jacobi constant and orbital period values for boundary and intermediate (Int.) orbits

Table 4 Initial position costate values for low-acceleration solutions

Table 5 Initial velocity costate values for low-acceleration solutions

Table 6 Initial position costate values for high-acceleration solutions

Table 7 Initial velocity costate values for high-acceleration solutions

Table 8 Impulse $\Delta \varvec{v}$ vector components

Table 9 Impulsive $\Delta \varvec{v}$ locations

Table 10 Impulsive $\Delta \varvec{v}$ times