Space-Based Sensor Tasking Using Deep Reinforcement Learning

Abstract

To maintain a robust catalog of resident space objects (RSOs), space situational awareness (SSA) mission operators depend on ground- and space-based sensors to repeatedly detect, characterize, and track objects in orbit. Although some space sensors are capable of monitoring large swaths of the sky with wide fields of view (FOVs), others—such as maneuverable optical telescopes, narrow-band imaging radars, or satellite laser-ranging systems—are restricted to relatively narrow FOVs and must slew at a finite rate from object to object during observation. Since there are many objects that a narrow FOV sensor could choose to observe within its field of regard (FOR), it must schedule its pointing direction and duration using some algorithm. This combinatorial optimization problem is known as the sensor-tasking problem. In this paper, we developed a deep reinforcement learning agent to task a space-based narrow-FOV sensor in low Earth orbit (LEO) using the proximal policy optimization algorithm. The sensor’s performance—both as a singular sensor acting alone, but also as a complement to a network of taskable, narrow-FOV ground-based sensors—is compared to the greedy scheduler across several figures of merit, including the cumulative number of RSOs observed and the mean trace of the covariance matrix of all of the observable objects in the scenario. The results of several simulations are presented and discussed. Additionally, the results from an LEO SSA sensor in different orbits are evaluated and discussed, as well as various combinations of space-based sensors.

1 Introduction

As more resident space objects (RSOs) are added to the United States Space Command’s (USSPACECOM) RSO catalog with the advent of proliferated satellite constellations and the deployment of more accurate sensors that can detect smaller objects, the need for exquisite space situational awareness (SSA)—the capabilities of detecting, cataloging, and tracking RSOs—grows more critical for sustaining long-term space operations. There are currently more than 4500 active satellites in low Earth orbit (LEO) [1] and it is estimated that by 2025 over 1000 satellites could be launched each year [2]. The number of satellites will likely greatly outpace any increased capacity of SSA sensors, making efficient tasking of existing and future sensors—including both ground- and space-based narrow field of view (FOV) sensors—extremely valuable.

The SSA sensor-tasking problem suffers from the curse of dimensionality, a challenging aspect of the problem wherein the complexity of the object-tracking problem grows exponentially as the number of targets and length of the observation window grows linearly. Scheduling agents trained using reinforcement learning methods have been shown in the literature [3,4,5]. More recently the authors have developed and trained a scheduler for ground-based narrow-FOV sensors to efficiently observe RSOs orbiting overhead using deep reinforcement learning with the proximal policy optimization (PPO) algorithm and population-based training (PBT) [6,7,8]. In this paper, the scheduler is adapted for a constantly moving space-based sensor situated in LEO. The adapted scheduler outperforms myopic policies—those in which only the benefits of a small number of estimated, future observations are considered—across several figures of merit, including RSO covariance and the number of unique RSOs observed during the study period.

The problem becomes much more untenable using traditional methods when we realize that owners of SSA sensors typically own multiple sensors across a geographical area, if not world-wide. Governmental organizations such as the US Space Surveillance Network, Russian Academy of Sciences’s International Scientific Optical Network (ISON) and ILRS [9], and commercial companies such as ExoAnalytic Solutions, LeoLabs, and Numerica all operate multiple sensors across a wide area. A mix of sensor modalities may be used as well within an organization with wildly varying performance and figures of merits. Optimally tasking all of these sensors as a networked system for a particular performance metric (e.g. minimizing covariance of all space objects or for a subset of objects, or keeping custody of particular objects) is an even more difficult problem.

In reinforcement learning, an agent is trained to complete a task. During the training phase, the agent receives observations from the environment (state) and submits an action at each time step according to its policy. The action results in some reward from the environment as a measure of the success from that state in completing a goal, and the policy is updated guided by the received rewards. The actor-critic network comprises of two function approximators, called Critics and Actors. A Critic returns the predicted discounted value of the long-term reward, whereas an actor returns as output the action that maximizes the predicted discounted long-term reward. Agents that use only critics to select their actions are also referred to as value-based, while agents that only use actors are referred to as policy-based, whereas agents that use both an actor and a critic are referred to as actor-critic agents. In these agents, the actor learns the best action to take using feedback from the critic instead of using the reward directly. At the same time, the critic learns the value function from the rewards so that it can properly criticize the actor. In general, these agents can handle both discrete and continuous action spaces. Some notable Actor-Critic methods include Advantage Actor-Critic (A2C) and Asynchronous Advantage Actor-Critic (A3C) [10], Proximal Policy Optimization (PPO) [11], Trust Region Policy Optimization [12], Deep Deterministic Policy Gradient (DDPG) [13], Twin-Delayed Deep Deterministic Policy Gradient (TD3) [14], and Soft Actor-Critic (SAC) [15].

For multiple-agent and ensemble problems, Multi Agent Reinforcement Learning (MARL) techniques have recently been researched. The multi-agent formulations can have agents that cooperate with one another, or be put in an adversarial role with one another, with varying levels of information being shared between them. Agents playing a game of teamed hide-and-seek in a 3D environment has been shown [16], as well as in adversarial multiplayer video game environments [17, 18].

2 Space-Based Sensors

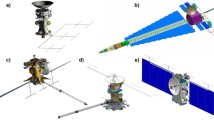
Although most of the sensors in the U.S. Space Surveillance Network (SSN)—including dedicated and contributing optical, radar, and radiofrequency sensors—are fixed to the Earth’s surface, a growing number of the Network’s space object observations are being collected by relatively new space-based sensors. Currently, the U.S. Space Force (USSF) publicly acknowledges four space-based sensor systems that contribute observations to the SSN: the U.S. military’s Space Based Space Surveillance (SBSS) and Geosynchronous Space Situational Awareness Program (GSSAP) systems, the Canadian military’s Sapphire system, and MIT Lincoln Laboratory’s SensorSat. A number of other space-based sensor systems have been demonstrated on orbit, but do not actively contribute observations to the SSN. See Table 1 for a summary of operational space-based sensors and Appendix A for a brief history of their development and use.

Regardless of whether they work in conjunction or independently of the SSN, space-based sensors offer unique advantages over their ground-based counterparts. Space-based sensors in any orbital regime offer clearer, more frequent, and more diverse space object observations than ground-based sensors.

Ground-based optical sensors, in particular—which are perhaps most akin to the narrow-FOV, taskable space-based sensors evaluated as part of this study—are limited to observing space objects at night, when the sky is dark and illuminated space objects can be more easily observed against the cosmic background. Additionally, ground-based sensors are limited in their field of regard (FOR)—the fraction of the sky observable from their location on the Earth’s surface. Ground-based optical sensors also must collect observations through the Earth’s atmosphere, which abberates optimal measurements, requiring adaptive methodologies and other data-cleaning efforts. This issue is exacerbated at low elevation angles, further constricting ground-based sensors’ FOR. Lastly, ground-based sensors are subject to local weather conditions, including cloud cover and precipitation, as well as other environmental effects, such as light and air pollution.

When a sensor is in orbit, its instantaneous FOR is larger than that of a ground-based sensor, as it can observe objects with negative elevation angles, as shown in Fig. 2. Due to its position above the densest portion of the Earth’s atmosphere, most portions of the sky can be observed such that the line of sight does not intersect the Earth or the lower reaches of its atmosphere. Due to its orbital velocity, a space-based sensor’s aggregate FOR over the course of one orbital period is the entire sky.

With these advantages at play, space-based sensors allow SSA operators to collect more observations of more space objects at shorter timescales.

2.1 Sensor Tasking

There is a spectrum of SSA data collection methodology spanning from tasked sensors tracking one object exquisitely, to fence-mode surveillance methods where the sensor is collecting data on all objects within its FOR or FOV. An imaging radar sensor, for example, will track one object for some duration, whereas an optical or radar “fence” will acquire data on objects that come into its wide FOR or FOV. SensorSat is a space-based optical sensor that “sweeps” the GEO belt from an equatorial orbit and is not tasked.

For event-based SSA and high-interest object tracking, narrow FOV sensors will need to be tasked to gather observation data. SSA sensors today are often tasked to gather data on specific objects, though the list of objects is not prohibitive and thus scheduling is often done manually. As the number of objects grows rapidly, gathering data with these narrow-FOV sensors will become more important.

Table 1 Operational space-based sensors for space situational awareness

3 Space Situational Awareness Environment

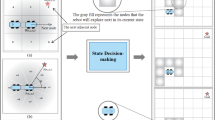
In this section, details about the space-based SSA environment are provided. The space-based SSA environment shares a similar architecture to the SSA environment used in past literature [6,7,8]. An example scenario of the SSA environment is shown in Fig. 1, where a single space-based sensor located in LEO is tasked to keep track of near-GEO-altitude RSOs.

Fig. 1

Example scenario with a single LEO space-sensor and 20 near-GEO-altitude RSOs over a 7-h observation period

3.1 Sensor Model

The space-based sensor is modeled to have a 4$^{\circ }$ $\times$ 4$^{\circ }$ FOV that can be accurately pointed to any arbitrary direction with a finite slew and settle time. The settle time consists of the exposure and data readout time. An action slew rate of 2$^{\circ }$/s and a settle time of 4 s are used. The space-based sensor is equipped with a position measuring payload such as a laser ranging device to provide a noisy position measurement for each RSO within the sensor’s current FOV. Note that while there are a number of ground-based laser ranging sensors: however, space-based laser ranging sensors are still in their infancy stage. For a simplified sensor measurement model, a 3-D position observation data is assumed in our environment. The assumptions of the sensor model are as follows:

• 1. The sensor has a Gaussian measurement noise;

• 2. The sensor can perfectly assign each measurement to the correct target; and

• 3. The RSOs’ detection probability is unity, i.e. RSOs within the FOV are always observed regardless of viewing conditions such as illumination condition or relative distance.

Range-based acquisition difficulties for sensor modalities such as SLR or radars (range ambiguity and range gate selection) are not modeled and all RSOs within the FOV is considered to be observable.

The orbit of the space-based sensor is modeled based on Sapphire’s orbit with the orbital elements (OEs) described in Table 2. The space-based sensor is propagated using the Simplified General Perturbation 4 (SGP4) propagation model [31] with the assumption that it can carry out daily station-keeping maneuvers to reject any external perturbations without compromising its mission capabilities.

Table 2 Orbital elements of the Sapphire space-based sensor on August 4, 2021

3.2 Field of Regard and Pointing Direction Discretization

Throughout the paper, we will be using the horizontal coordinate system, where the observer’s local horizon will be used as the fundamental plane to describe the azimuth and elevation angle. The local horizon is defined as the plane which is tangent to a reference spheroid centered at Earth’s origin and extending out to the current position of the observer.

We assume that the sensor payload is fully gimballed and omnidirectional in its pointing, i.e., continuous over the complete 4-$\pi$ steradian solid angle surrounding the spacecraft. However, we limit the elevation due to Earth limb exclusion, such that the FOR for the space-based sensor evaluated as part of this study spans the full range of possible azimuth angles (0$^{\circ }$ to 360$^{\circ }$), but only a fraction of all possible elevation angles (−14$^{\circ }$ to 90$^{\circ }$ as opposed to −90$^{\circ }$ to 90$^{\circ }$). The −14$^{\circ }$ elevation limit means a sensor in a circular orbit at 500 km altitude can point 14$^{\circ }$ away from its velocity vector in the radial direction, towards Earth. The FOR is discretized into non-overlapping FOVs, such that each FOV spans 4$^{\circ }$ in both azimuth and elevation. This discretization simplifies the continuous action space, by representing it as a discrete space, resulting in a finite number of pointing directions. This also results in a fixed observation space regardless of the number of RSOs in the SSA environment. Under this discretization, the FOR is fully covered by a spatial grid with 90 discrete azimuth angles and 26 discrete elevation angles for a total of 2340 possible pointing directions. The simplified illustration of the sensor’s FOR geometry is shown in Fig. 2.

Fig. 2

Simplified geometry of the nominal field of regard for the space-based sensor, which is used to generate the observational array for the trained agent

However, the effective FOV of the sensor changes with the elevation angle, whereas the effective azimuth viewing angle increases with elevation angle. That is, at high elevation angles, the effective FOV of the sensor starts to overlap one another as shown in Fig. 3. This variation in the effective FOV is taken into account when identifying RSOs that are within the agent’s current FOV.

Fig. 3

Field of view of the sensor at different pointing direction projected onto the observation array

3.3 SSA Environment Formulation

The SSA environment is developed using OpenAI’s Gym environment framework [32]. The SSA environment consists of 5 major modules as shown in Fig. 4: environment initialization, observations generation, Unscented Kalman Filter (UKF) propagation, measurement generation, and UKF update.

Fig. 4

Architecture of the space-based SSA environment

Here, a distinction is made between observation and measurement. Observation is used to represent the state of the environment that is accessible to the agent during the decision-making (sensor-tasking) process, whereas measurement corresponds to the Cartesian position measurement generated from a successful detection of a RSO.

3.3.1 Environment Initialization

The environment initialization module first initializes the sensor parameters as well as the RSOs’ OEs and covariance. During training, the environment initialization module randomly initializes the RSO population in the SSA environment from a uniform distribution to ensure diversity in the training scenario. This randomization prevents the solution from over-fitting to a particular subset of scenarios and improves the robustness of the solution. The RSOs are uniformly sampled to be within the near-GEO-altitude orbital regime (semi-major axis a of 37,000 to 45,000 km) with low to moderate eccentricities ($e<0.6$) and no restrictions to the RSOs’ right ascension of ascending node (RAAN) $\Omega$, inclination i, argument of perigee $\omega$, or mean anomaly M. The RSOs’ covariance is randomly initialized as a diagonal matrix based on the Two-Line Element (TLE) uncertainties observed in [33] and reproduced in Table 3. The first and third quartiles of the observed TLE covariance are used as the lower and upper bound of the uniform sampling range, respectively. The uncertainties in the mean motion are inflated by a factor of 100 to introduce additional uncertainties.

Table 3 Sampling bound for diagonal of RSO covariance

3.3.2 Observation Generation

In the observation generation module, a grid-based observation of the environment is generated using the predicted states and covariance of the RSOs. The observation is provided in a three-dimensional array with dimensions of $90\times 26\times X$. The first two dimensions correspond to the azimuth and elevation angles, whereas the third dimension, X, consists of the RSO data to describe the state of the environment for that grid. When there are multiple RSOs within the same grid, only the values corresponding to the RSO with the largest uncertainties are used. The various action policies will have to select an action based only on this observation array.

3.3.3 UKF Propagation

The UKF propagation module takes in the new pointing direction as an action input and computes the required action slew and settle time for the selected action. The RSOs states are then propagated forward in time based on the required slew and settle time using the Simplified General Perturbation 4 (SGP4) propagation model with no additional external perturbations [31]. Meanwhile, the RSOs covariance are propagated using a UKF formulation.

3.3.4 Measurement Generation

The measurement generation module then identifies all RSOs located within the sensor’s FOV and generates a noisy measurement for each of these RSOs based on the sensor model. The measurements are corrupted by white noise with a magnitude of 10 km on all axes to model imperfect measurements. The sensor is assumed to be able to perfectly associate each noisy measurement to the correct RSO.

3.3.5 UKF Update

The state and covariance of the observed RSOs are then updated in the UKF update module using a UKF formulation. The UKF uses the following parameters for the unscented transform: $\alpha = 0.001$, $\beta = 2$, and $\kappa = 0$. Due to the strong nonlinearity of the problem, a small $\alpha$ value of 0.001 is used. The $\beta$ value is set to 2 which is optimal for Gaussian distribution and the $\kappa$ value is set to 0 based on normal conventions.

The updated state and covariance data are then passed back to the observation generation module and a new observation grid is then generated. The whole process is repeated until a termination condition is reached. In this study, an observation window of 60 min is used, i.e. a termination condition is reached once 60 min has elapsed within the SSA environment.

4 Deep Reinforcement Learning

The objective of the SSA system is to reduce the mean covariance of the RSO population during each episode within a particular scenario. Two figures of merit are used to compare performance: (1) the number of RSOs observed and (2) the mean covariance of all of the RSOs at each time step during the episode. The sensor’s action is determined by evaluating the deep reinforcement learning (DRL) agent that has been trained. The flowchart of this process for each step is shown in Fig. 5 and the training process is described in Sect. 4.5. The space sensor DRL agent that is made up of an actor-critic neural network will receive the observation array generated by the SSA environment as an input and then select a new pointing direction. The observation array contains the current state of the environment. Once an action is chosen by the agent, the SSA environment uses that information to calculate the action slew, settle, and dwell times. The RSOs’ states and covariance are then propagated forward in time based on the action time. RSOs that are in the agent’s FOV are identified and the environment performs the covariance update for those RSOs. A new observation array is then generated based on the new current state of the environment and the process is repeated.

Fig. 5

Evaluation process for a single-sensor DRL agent

The DRL agents are optimized using proximal policy optimization (PPO) [11] and population-based training (PBT) [34]. The optimization algorithms were implemented using the open-source Ray and Tune libraries [35, 36]. The PPO algorithm is a model-free policy gradient method that uses the actor-critic neural network architecture. It improves the training stability and convergence of policy gradient methods by using a clipped surrogate objective function that discourages large policy change. The readers are referred to the PPO paper for more information [11]. The training of DRL agents is sensitive to the choices of training hyperparameters, such as learning rate, training batch size, and mini-batch size. Non-optimal training hyperparameters can lead to slow learning, and in the worst case, divergence of the DRL agent. The PBT algorithm is used to overcome this issue by concurrently optimizing the neural network and training hyperparameters. The PBT algorithm has previously been shown to improve convergence and achieve a higher final reward for a suite of challenging DRL problems [34]. The PBT algorithm trains a population of DRL agents in parallel with different training hyperparameters. It then uses information from all of the agents to refine the training hyperparameter and allocate resources to promising models. As the training of the population of DRL agents progresses, this refinement process is performed periodically to consistently explore new and promising hyperparameters.

4.1 Neural Network Formulations

Instead of designing a neural network architecture from scratch, we looked into past successful neural network architectures and adapted them for our application. To this end, several neural network architectures were explored as shown in Table 4. The actor model is responsible for generating the action policy $\pi$ that is used to select an action for the agent, whereas the critic model estimates the action’s reward and provides feedback to improve the action policy. Conv2d and FCL correspond to a 2D convolution layer and a fully connected layer, respectively. Architecture CNN_v1 was based on a neural network architecture that was previously successfully applied for the sensor tasking of ground-based optical telescope for SSA and this architecture has demonstrated great robustness and outperformed baseline policies [7]. In CNN_v2 and CNN_v3, we experimented with varying the “width" of the neural network. In CNN_v2, we used a narrower network, where the “width" of each layer is halved compared to CNN_v1. Having a narrower network forces greater compression onto the input data and can help to prevent over-fitting. On the other hand, in CNN_v3, we widen the neural network such that each layer contains more neurons compared to CNN_v1. Having a wider neural network increases the amount of information/features that can be extracted and retained at each layer at the expense of longer training time and the risk of over-fitting. In CNN_v4, we experimented with a shallower network to study the effects of network depth on the agent’s performance.

Table 4 Comparison of explored neural network architectures

The neural network architecture for CNN_v1 with the input and output of the various layers is shown in Fig. 6. For all neural network layers, zero padding is used to avoid losing information at the boundaries of the data. The rectified linear unit (ReLU) activation function is used for all layers except the last fully connected layer of the actor and critic models. The actor model takes in the observation and outputs an action probability distribution at the bottom-most layer. The actor model consists of two parallel dataflow paths. The primary dataflow path is located on the left where the observation data is passed through subsequent neural network layers as outlined in Table 4, whereas the secondary dataflow path corresponds to the action masking layers (action masking function). Here, the action-masking function penalizes actions that select an empty field of view to observe. Thus, it encourages the action policy to focus on actions that can lead to a successful RSO measurement and hence leads to a higher final reward. On the other hand, the critic model takes in the observation and outputs a value function for the current state. The value function is then used as feedback to improve the action policy.

Fig. 6

Neural network architecture for CNN_v1

4.2 Action Space

The pointing direction is the action chosen by the agent. In order to reduce the action space for the agent and simplify the model, the pointing direction can be discretized into a grid of potential FOVs. The FOV was chosen to be 4$^{\circ }$ $\times$ 4$^{\circ }$ based on the Zimmerwald SMall Aperture Robotic Telescope (ZimSMART) [37]. A minimum elevation limit of -14$^{\circ }$ is used, which yields an action space that is represented by a $90\times 26$ grid for azimuth and elevation positions respectively.

4.3 Observation Space

The choice of which data to be included in the observation space is flexible; however, less-meaningful and redundant data will simply act as noise to the RL agent and lead to slower training. The observable data used for the SSA environment developed as part of this study is shown in Table 5. When there are multiple RSOs within the same grid, only the values corresponding to the RSO with the largest uncertainties are used for Layers 2 through 7.

Table 5 Observation information for each grid in the observation

The observation array is oriented such that the current pointing direction of the sensor—regardless of the particular azimuth and elevation values of that pointing direction—is situated at the center row of the observation array, i.e. located in the $45{\text {th}}$ row.

Due to the large range of action slew time, the observation grid is partitioned into 23 regions as shown in Fig. 7, where each region uses a different propagation time based on the approximate action slew time required by the sensor. The observation grid is populated using RSO states with propagation times that offset by 3 s for the first interval and 4 s for the subsequent intervals (4 s, 7 s, 11 s, $\cdots$, 87 s, and 91 s), with increasing propagation time as we move farther away from the current pointing direction. This propagation time corresponds to the average slew time to reach that region. Different propagation times are used to better capture the true expected relative position of the RSOs and more accurately reflect what the agent is expected to observe.

Fig. 7

Field of regard demarcated with graduated propagation times

Note that the projection of the spherical pointing direction to a fixed-size Cartesian grid observation space means that the higher elevation FOVs will overlap one another. If an RSO is located within multiple FOVs—as they are prone to do in higher elevations—those observation grids are all marked as having a visible line of sight to the RSO.

4.4 Reward

DRL agent training is inherently sensitive to the reward function used. Reward shaping can be used to guide some desired behavior from the trained agent. In the sensor-tasking problem, there can be a multitude of objectives. For example, maximizing the number of RSOs observed may be preferable, or in other situations, the maximum uncertainty of any RSO may need to be below a certain threshold. For all of these performance metrics, the reward defined by the environment can be tweaked such that the trained agent performs well for the particular metric that the user emphasizes. In this paper, minimizing the total uncertainty over all RSOs is the principal goal, i.e., minimizing the mean trace covariance across all RSOs at the end of our observation window.

Two reward functions are explored in this paper and we did not utilize a different final reward at the end of the observation run or episode. The first reward function rew1 is based on the time-discounted maximum trace reduction as shown in [6, 7]. The second reward function rew2 is simply the first reward without the time-discount factor. These rewards R[t] at timestep k are shown in Eqs. 1 and 2, respectively.

$$\begin{aligned}&R_{\texttt {rew1}}[k] = \frac{\underset{a_k}{\mathrm {argmax}} \left[ tr \left( P_{k \vert k-1}^{(a_k)} \right) - tr \left( P_{k \vert k}^{(a_k)} \right) \right] }{T[k]-T[k-1]} \end{aligned}$$

(1)

$$\begin{aligned}&R_{\texttt {rew2}}[k] = \underset{a_k}{\mathrm {argmax}} \left[ tr\left( P_{k \vert k-1}^{(a_k)}\right) - tr\left( P_{k \vert k}^{(a_k)}\right) \right] \end{aligned}$$

(2)

where $tr\left( P_{k \vert k-1}^{(a_k)}\right)$ is the trace of the covariance for RSOs within the FOV selected by action $a_k$ and T[k] is the time at timestep k.

4.5 Training

Training and evaluation were done on the MIT Lincoln Laboratory Supercomputing Center (LLSC) [38]. At each timestep, the DRL agent collects the state, action, and reward pair which are then used to update the agent’s weights and biases in a mini-batch fashion.

The hyperparameter initialization and mutation sampling range used for the population-based training of the DRL agents are shown in Table 6.

Table 6 Initialization and mutation range of hyperparameters for hyperparameter optimization with PBT for the DRL agents

Seven DRL agents are trained concurrently using the PBT framework. After every 100 training iterations, the trained agents are ranked according to their mean episodic reward. The training hyperparameters and neural network parameters of the relatively poorly performing DRL agents (those with mean episodic rewards that rank in the bottom $30\%$) are replaced by those of the top-performing DRL agents (those with mean episodic rewards that rank in the top $30\%$). The training hyperparameters of these duplicated top-performing agents are then varied with a $25\%$ probability to be re-sampled from the mutation range provided in Table 6 or to be perturbed from their current values.

The evolution of the mean reward for agent CNN_v1 through training is shown in Fig. 8. The means reward 1, rew1_100 term, was the mean reward obtained from agent CNN_v1 with 100 RSOs in the training environment. Due to the nature of the PBT algorithm, where better-performing agents are copied over to replace the least performing agent, we can sometimes observe that the plots jump back in time. When a least performing agent is replaced, the training metadata (i.e training iterations) of the better performing agent is copied over together with the training hyperparameters and network weights. The real-time training duration was between 36 seconds per iteration for the environment with 100 satellites and 67 and 77 seconds per iteration for 400 satellites.

Fig. 8

Training statistics for the three different reward functions

Figure 9 shows the evolution of the hyperparameters for the CNN_v1 DRL agent trained on an SSA environment with 400 near-GEO-altitude RSOs using the (rew1) reward function over 3400 training iterations. The DRL agent started with a highly negative mean episodic reward and the value slowly increases with the number of training iterations before converging to a value of 20. The increase in the mean episodic reward indicates that the DRL agent was able to learn from its past experiences and slowly converge toward a more optimal action policy. The same trend was observed in the agent’s policy loss where the value gradually decreases with training iterations from a policy loss value of −0.07 to approximately −0.035. The decrease in policy loss followed by the oscillatory behavior with additional training iterations hinted at the DRL agent converging towards a local minimum. On the other hand, the DRL agent started with a high value function loss, which indicates that initially the critic network is doing a poor job in estimating the correct value function. After more training iterations, the value function loss converges to a small steady-state value. This indicates that there is still room for improvement on the critic network architecture. The total loss is simply the summation of the policy loss and value function loss. The total loss plot shows that the loss function is dominated by the value function loss, which can indicate that the architecture of the critic network can still be further improved. Figure 9e–h shows the mutation of the training hyperparameters. The training hyperparameters of this DRL agent were mutated twice; once at approximately 300 training iterations and the other at approximately 700 training iterations. Additional training statistics and evolution of the hyperparameters with training iterations for the other CNN architectures are included in Appendix B.

Fig. 9

Training statistics (a–d) and evolution of hyperparameters (e–h) for the Best Performing CNN_v1 DRL Agent trained using 400 near-GEO-altitude RSOs and rew1 over 3400 training iterations

4.6 Baseline Myopic Methods

Two baseline myopic algorithms are used to provide a baseline comparison to evaluate the performance of the trained agents. The myopic algorithms are computationally efficient and easy to implement; however, they only consider the instantaneous reward and are incapable of long-term action planning. The first myopic algorithm is a greedy algorithm which selects the RSO with the highest covariance within the sensor’s FOR regardless of action slew duration. The action policy for this agent is given by Eq. 3.

$$\begin{aligned} a^* = \underset{a}{\mathrm {argmax}} \left( tr[{P}_{i,k}^x] \right) \end{aligned}$$

(3)

where $tr[{P}_{i,k}^x]$ is the trace of the a posteriori state covariance for RSO i at time step k.

However, the time spent on slewing the sensor greatly affects the performance of the policy due to the limited observation window and the fast-moving RSOs. The second myopic algorithm (the advanced greedy algorithm) takes the required action slew duration into account when deciding which RSO to be observed. It first penalizes the covariance of each RSO within the FOR by the required action slew duration. The advanced greedy algorithm then uses a greedy policy to select which RSO to be observed based on the scaled covariance. The action policy for the advanced greedy algorithm is given by Eq. 4.

$$\begin{aligned} a^* = \underset{a}{\mathrm {argmax}} \left( tr[{P}_{i,k}^x] \, / \, \delta t_i^{1/D} \right) \end{aligned}$$

(4)

where $tr[{P}_{i,k}^x]$ is the trace of the a posteriori state covariance for RSO i at time step k, $\delta t_i$ is the action slew time to move from the current pointing direction to observe RSO i, and D is a time discount factor. The advanced greedy algorithm is evaluated with different values of D (ranging from 1 to 10) over 100 Monte Carlo runs to identify the best time discount factor. The performance statistics of the advanced greedy algorithm with different time discount factors are shown in Fig. 10. The best performance is obtained when a time discount factor of 3 is used, where the lowest average RSO uncertainties and the highest average number of unique RSOs observed are achieved.

Fig. 10

Performance of the advanced greedy algorithm with different time discount factors D over 100 Monte Carlo runs; a statistics of the final mean trace covariance over 100 Monte Carlo episodes, where lower y-axis values correspond to better performance; b statistics of final cumulative number of unique RSO observed over 100 Monte Carlo episodes, where higher y-axis values correspond to better performance

4.7 Multi-agent Formulation

There are many methods of implementing a multi-agent formulation, in which more than one sensor is collaboratively observing the RSOs in the environment and contributing to the same space object catalog with instantly updated covariance records. A scheduling agent could be created to oversee multiple sensors. The action and observation space for such a scheduler would grow rapidly with each sensor and the number of sensors as well as the placement of each sensor may require a distinct trained agent suited for that setup.

Another method of implementing a multi-agent formulation is to use multiple single-agents in parallel, with the environment tasked with querying the agents at the appropriate times. The environment will propagate all orbits until the next agent is available at which point the agent will be queried for its selected action.

This method of using multiple instances of the same trained agent in the same environment is explored in this paper. In this method, a number of instances of the same agent, each with their own identical copy of the trained neural network, inform the pointing direction for the same number of independent sensors, placed in different locations on the Earth’s surface or in Earth orbit. A scheduler is in charge of keeping track of which agent has completed which actions. The flowchart of the process is shown in Fig. 11. This method allows the user to evaluate the agents for various scenarios, including those in which the number of sensors and their locations varies. An environment with three distributed agents is used for performance evaluation.

Fig. 11

Evaluation process for a multi-sensor approach

5 Results and Discussion

The trained and myopic agents were evaluated in several different environments, including those in which the observer sensor was placed in a polar, inclined, and equatorial orbit—corresponding to the inclinations of the Sapphire, STSS, and SensorSat space-based sensors, as described in Table 1—for 100, 400, and 800 RSOs at near-GEO altitudes. For each of these environments, a statistical comparison is done via 100 Monte Carlo runs with randomized RSO locations and covariance within the specified bounds.

Figure 13, which shows a typical pointing history for an episode, reveals several interesting details of how the DRL agent instructs sensors to observe RSOs. The saw-tooth pattern visible in the pointing direction’s azimuth angle shows that the agent is rotating around the Earth-sensor axis—the axis connecting the sensor to the center of the Earth—to point in a systematic manner. Some runs show a clockwise rotation while others show a counterclockwise rotation; no preferential direction is shown for the trained agents. However, this pattern does show that the agents learn some efficient methods to search over the FOR, as jumping around in azimuth would require more slew time and therefore less observation time. Another interesting characteristic is the fact that most of the observation happens near 0$^{\circ }$ elevation, which corresponds to pointing directions in the space-based sensor’s local horizontal plane. This may be so such that the most number of RSOs may be gathered within the FOV, which would maximize the reward. For each of the observations, the agents chose a FOV that often contained RSOs, demarcated with dark gray squares in the example observation array in Fig. 12.

Fig. 12

An example of an instantaneous RSO distribution in an agent’s observation array; light gray squares correspond to azimuth-elevation coordinate pairs at which one RSO could be observed, whereas dark gray squares correspond to azimuth-elevation coordinate pairs at which two RSOs could be observed

Fig. 13

An example of pointing directions chosen by the DRL agent over a 60-min observation window

5.1 Training Results Using Different Reward Functions

Two different DRL agents were trained using the reward function rew1 and rew2, respectively, as described in Sect. 4.4. Both agents were trained on an SSA environment containing 400 near-GEO-altitude RSOs until convergence, i.e plateauing in the episodic mean reward. The performance of the trained DRL agents and myopic policies were then evaluated over 100 Monte Carlo runs. Results showing the final mean trace covariance of all RSOs as well as the cumulative number of unique RSOs observed over the observation window are shown in Fig.14.

Fig. 14

Comparison of results for agents trained with various reward functions; a statistics of final mean trace covariance over 100 Monte Carlo episodes; b statistics of final cumulative number of unique RSO observed over 100 Monte Carlo episodes; note: CNN_v1_rew1 3400 represents a CNN-based DRL agent (CNN_v1) that has undergone 3400 training iterations using the rew1 reward function

As expected, the performance of the trained DRL agents is strongly influenced by the reward function. The DRL agent trained using rew1 performed the best out of all policies with the lowest final uncertainties and highest number of unique RSOs observed. The time-discount factor in rew1 penalizes actions that require relatively long slew times and motivates the DRL agent to look for rewarding actions within the proximity instead of spending large time resources on slewing. The DRL agent trained using rew2 was able to outperform the greedy policy but not the advanced greedy policy. The rew2 reward function encourages the DRL agent to select actions that strongly minimize the mean trace covariance regardless of action slew time. Unsurprisingly, the DRL agent trained using rew2 ended up spending more time slewing compared to the agent trained using rew1, which resulted in a lower number of observations and consequently a lower cumulative number of unique RSOs observed.

5.2 Training Results Using Different Neural Network Architectures

The neural network architectures outlined in Sect. 4.1 were trained on an SSA environment with 400 near-GEO-altitude RSOs using reward function rew1. The trained DRL agents were then evaluated over 100 Monte Carlo simulations. Their performances are shown in Fig. 15. The DRL agent CNN_v1 outperformed all other DRL agents and both myopic policies across both figures of merit. The DRL agent CNN_v2 has a smaller, narrower network than that of CNN_v1 which limits its expressiveness. Thus it is not able to fully capture the physics behind the high-dimensional environment.

The DRL agent CNN_v3 has a larger, wider network than that of CNN_v1 but is more susceptible to over-fitting and convergence to local minima or saddle points and thus resulting in a sub-par performance. The performance of the DRL agent CNN_v3 could be further improved by introducing additional regularization into the neural network architecture and training using a larger population.

The DRL agent CNN_v4 has a shallower network than CNN_v3 in order to reduce the effects of data over-fitting; however, the issue was not fully eliminated and the agent would benefit from additional regularization.

Fig. 15

Comparison of results for agents trained with different neural network architectures; a statistics of final mean trace covariance over 100 Monte Carlo episodes; b statistics of the final cumulative number of unique RSO observed over 100 Monte Carlo episodes

5.3 Robustness Analysis of Trained DRL Agent

For any trained DRL agent, it is important to note its performance in an environment that is different from the one in which it was trained. These robustness studies will help analysts better identify possible modes of failure as well as shed light on the agent’s limitations.

With a good understanding of the limits of the DRL agent’s flexibility and robustness, a single trained agent can be used for multiple different scenarios. The knowledge gained from the robustness studies can also be used to better inform future training of DRL agents and the design of neural network architectures.

5.3.1 Robustness to Changes in the Number of RSOs in the SSA Environment

As part of this work, the robustness of the trained DRL agent to variation in the number of RSOs within the environment was studied. An additional CNN_v1 DRL agent was trained independently on an SSA environment with only 100 near-GEO-altitude RSOs using reward function rew1. The trained DRL agents and myopic policies were then evaluated on environments with 100, 400, and 800 RSOs. The aggregate results over 100 Monte Carlo runs are shown in Figs. 16, 17, and 18 for an SSA environment with 100, 400, and 800 RSOs, respectively.

Fig. 16

Performance of DRL agents trained with different numbers of RSOs on an environment with 100 RSOs; a statistics of final mean trace covariance over 100 Monte Carlo episodes; b statistics of the final cumulative number of unique RSO observed over 100 Monte Carlo episodes

Fig. 17

Performance of DRL agents trained with different numbers of RSOs on an environment with 400 RSOs; a statistics of final mean trace covariance over 100 Monte Carlo episodes; b statistics of the final cumulative number of unique RSO observed over 100 Monte Carlo episodes

Fig. 18

Performance of DRL agents trained with different numbers of RSOs on an environment with 800 RSOs; a statistics of final mean trace covariance over 100 Monte Carlo episodes; b statistics of the final cumulative number of unique RSO observed over 100 Monte Carlo episodes

Interestingly, the DRL agent trained in an SSA environment with 400 RSOs always performed better than the agent trained with 100 RSOs, despite the fact that the agents trained with 100 RSOs were trained with more episodes. This may be due to the fact that with fewer RSOs, the agent has such a sparse set of possible rewarding actions (RSOs) to choose from. This results in an environment with sparse rewards that poses a significant challenge to DRL algorithms.

In the SSA environment with 400 RSOs, there are a higher number of rewarding options to choose from; the DRL agent receives useful feedback information more frequently from the environment, leading to more efficient learning of an optimal policy.

5.3.2 Robustness to Changes in Action Slew and Sttle Times

The action slew and settle times for space-based sensors can vary depending on the platform’s actuator, size, and weight. Furthermore, the action slew and settle times of a space-based sensor can also vary throughout the sensor’s operational lifetime due to component degradation and changes in the sensor’s weight and moment of inertia. Hence, it is important to characterize the effects of changes in the sensor’s slew and settle times on the performance of the DRL agent.

To explore this problem, the DRL agent that was trained using an optical sensor with a slew rate of 2$^{\circ }$/s and a settle time of 4 s is applied to another optical sensor with a slower slew rate but a faster settle time. The slew rate of the space-based sensor is reduced by a factor of 10 to 0.2$^{\circ }$/s and the settle time is increased by a factor of 10 to 0.4 s. The propagation time used to generate the observation grid in Fig. 7 is varied to match the changes in slew and settle times. The advanced greedy algorithm is also adjusted to use the new slew and settle times when deciding which RSO to observe.

Like previous evaluations, 100 Monte Carlo runs were then simulated; their aggregate performance is shown in Fig. 19.

Fig. 19

Aggregate performance of trained DRL agent on an environment with slew and settle times reduced by a factor of 10 over 100 Monte Carlo runs; a statistics of final mean trace covariance over 100 Monte Carlo episodes; b statistics of the final cumulative number of unique RSO observed over 100 Monte Carlo episodes

Although the DRL agent was not specifically trained for this faster-moving space-based sensor scenario, it was still able to outperform both of the myopic policies. The DRL agent achieved an average final mean trace covariance of 0.01023 over 100 Monte Carlo runs, which represents a $6.4\%$ improvement over the advanced greedy algorithm—the stronger of the two myopic policies—which achieved an average final mean trace covariance of 0.01093 over its 100 Monte Carlos runs.

5.3.3 Robustness to Changes in the Orbital Plane

In order to offer continuous coverage for the entire GEO regime—that is, enclose all near-GEO-altitude RSOs in the network’s field of regard at every time step in the observations period—multiple space-based sensors with different OEs, such as different inclinations, are required. Thus, it is useful to benchmark how the trained DRL agent will respond to changes in the orbital plane. Although the DRL agent was trained on a particular orbit, it might be able to generalize to different orbits due to the observation formulation where the SSA environment converts the observations into the agent’s local frame, describing RSO positions using azimuth and elevation angles.

To explore this problem, the CNN_v1 DRL agent that was trained in a Sapphire-like orbit (786 km altitude, 98.6$^{\circ }$ inclination) with 400 near-GEO-altitude RSOs and placed in other LEO space-sensor orbits such as STSS (1350 km altitude, 58$^{\circ }$ inclination) and SensorSat (600 km altitude, 0$^{\circ }$ inclination). Figure 20 shows a comparison of several agents’ performance after 100 Monte Carlo runs.

Fig. 20

Mean trace covariance (a–c) and number of unique RSOs observed (d–f) at the end of the episode using a DRL agent trained in a Sapphire-like orbit and evaluated in different orbits

Though the DRL agent was trained in a sun-synchronous orbit and performed well compared to the myopic policies, it also performed well in two different inclined orbits. This shows the robustness of the agent to be used in different orbits. This flexibility allows one such agent to be extended for use in other orbits, eliminating the need to train an agent that is specific to each orbital regime. This may be due to the fact that the observation data provided by the environment to the agent during training is consistent and independent of the orbit in which the sensor resides. For example, the same coordinate space is used for the observation grid with the center column always corresponding to the current pointing direction. This shows that clever ways to formulate the problem may allow a more robust agent for varying use cases. In future work, the limits of this robustness can be explored, with the agent placed in eccentric or much higher altitudes. Extending the RSO population from near-GEO-altitude to LEO orbital regime could also be investigated.

5.4 Multi-agent Environments

Two different multi-agent formulations with three space-based sensors were explored in this work. For the first formulation, all three sensors are evenly spaced along the Sapphire orbit. Each of these sensors is controlled by a distributed action policy that only has information about RSOs within its FOR.

The second formulation consists of three sensors, each in a different orbit. The space-based sensors are each placed using OEs similar to those of Sapphire, STSS, and SensorSat as shown in Table 7. Again, each sensor is controlled by a distributed action policy.

Table 7 Orbital elements used for the multi-agent scenario

Fig. 21

Aggregate performance of trained DRL agents with multiple sensors on a single orbital plane; a statistics of final mean trace covariance over 100 Monte Carlo episodes; b statistics of the final cumulative number of unique RSO observed over 100 Monte Carlo episodes

Fig. 22

Aggregate performance of trained DRL agents with multiple sensors on different orbital planes; a statistics of final mean trace covariance over 100 Monte Carlo episodes; b statistics of the final cumulative number of unique RSO observed over 100 Monte Carlo episodes

As shown in Figs. 21 and 22, CNN_v1 outperforms the myopic policies in both scenarios, ending the episode with both a lower mean trace covariance and a higher number of unique RSOs observed. Further investigation into these multi-agent formulations and other formulations will be explored in future work, though it is clearly seen that this type of decentralized multi-agent method shows promise and is robust.

6 Conclusion

Previous work shows that terrestrial sensor tasking for SSA is possible using DRL. Space-based SSA sensors are being used today, and their relatively high performance and high cost mean that efficient tasking is likely an important area of interest for SSA network operators.

In this paper, we showed that a DRL-enabled solution to the sensor-tasking problem for a space-based SSA can be trained to perform well compared to baseline myopic policies. We also show that a set of space-based sensors can also perform well using the single-sensor agent in a parallel manner, allowing for flexibility in the multi-agent formulation. The agent can be also trained in one LEO orbit and then placed in another without loss of performance—this robustness allows for ease of use in varying scenarios for simulations as well as live sensor-tasking of multiple space-based sensors.

Future work may include exploration of recurrent neural networks (RNNs) such as long short-term memory (LSTM) for this problem as it is naturally highly time-series dependent. For the multi-agent scheduler, training a multi-agent scheduler as opposed to the parallel single-agent method that has been used in this paper may be of interest. Higher fidelity sensor modeling can be used to differentiate between optical, radar, and satellite laser-ranging sensors. A combination of space-based and ground-based sensors can also be used for a higher-fidelity simulation of the SSA architectures used today.

Appendices

A: History of Space Sensor Development and Operation

With only a handful of public-record space-based sensors launched to orbit thus far, the history of space-based sensor deployment and operation is short when compared to ground-based space object sensing. While most of the systems described in this appendix operate in low-Earth orbit (LEO), some of them can be used to detect and track objects in other orbital regimes, including the high-value geosynchronous orbital regime (GEO).

An early example of such a system was the Space-Based Visible (SBV) sensor developed by MIT Lincoln Laboratory and launched onboard the Midcourse Space Experiment (MSX) in 1996 to an 898 km altitude, nearly sun-synchronous orbit [19]. The sensor used an electro-optical camera to collect space object observations—with a focus on objects in GEO—in the visible and near-infrared spectrum and became the first space-based contributor to the SSN in 1997. After more than 12 years of operation, MSX was decommissioned in 2008 [39].

Space-based sensors are not always dedicated to orbital space object observation, and instead can be commissioned for a different primary purpose. In 2009, two satellites were launched as part of the U.S. Missile Defense Agency’s Space Tracking and Surveillance System (STSS) to a 1350 km altitude orbit with 58$^{\circ }$ inclination [40]. Although the satellites were designed to detect and track sub-orbital ballistic missiles during flight, their narrow-FOV sensors are capable of detecting small, high-velocity objects against the cold background of space—the same capabilities required to track Earth-orbiting space objects. The follow-on program to STSS, which was designed to replicate the first two demonstrator satellites’ capabilities across many more orbital planes, was canceled in 2013 [41]. Although the demonstrator satellites were designed for only four years of operation, their prime contractor stated in 2019 that they are both still operational [42].

Two years after MSX was decommissioned, the first satellite from its follow-on system SBSS was launched to a 630 km altitude, sun-synchronous orbit [22]. The satellite reached operational status in 2012. Like STSS, SBSS was intended to be the first of many similar satellites that work to track space objects in tandem. Although the U.S. Air Force (USAF) predicted that the next portion of the SBSS system would be launched in 2021, the first satellite remains the only portion of the system currently in orbit [43].

The U.S. government is not alone in its investment in space-based sensor development and operations. In 2013, two Canadian space-based sensors were simultaneously launched to approximately 785 km altitude, sun-synchronous orbits: the Canadian Department of National Defence’s (DND) Sapphire sensor system and Near-Earth Orbit Surveillance Satellite (NEOSSat). Unlike SBSS, Sapphire uses a body-fixed sensor, where the satellite body is slewed to point the telescope toward its targets [23]. Sapphire is the only non-U.S. satellite that contributes observations to the SSN. Unlike Sapphire, NEOSSat is also tasked with a second mission objective—to discover natural near-Earth objects (NEOs), such as comets and asteroids—in addition to its SSA mission, and spends only $50\%$ of its operations on observing artificial space objects [25]. NEOSSat is a joint project of Defence Research and Development Canada and the Canadian Space Agency [24].

One of the most recent examples of space-based sensor operations in LEO is the USSF’s Operationally Responsive Space 5, better known as SensorSat. Launched in 2017 to a 600 km altitude, equatorial orbit, SensorSat was developed by MIT Lincoln Laboratory to observe the GEO belt. Similar to Sapphire, SensorSat has no mechanical gimbal and plans to operate for a shorter time than previously launched space-based sensors. SensorSat reached operational capacity in 2018 and later became the largest contributor of space object observations to the SSN [44].

The only publicly acknowledged space-based sensor system with satellites in GEO is the USSF’s GSSAP system. The USSF currently operates two pairs of GSSAP satellites—the first launched in 2014 and the second in 2016—which observe GEO objects from both above and below GEO altitude [26]. Prior to public remarks made just months before the first GSSAP launch by Gen. William Shelton, the Commander of the USAF Space Command at the time, the program was classified [45].

Table 1 features a list of operational space-based sensors for SSA, including their operator, launch year, mass, orbit, and FOV, when available.

B: Training Statistics and Evolution of Hyperparameters for the Best Performing Agent

Figure 23 shows the evolution of the hyperparameters for the best performing CNN_v1 DRL agent trained on an SSA environment with 400 near-GEO-altitude RSOs using the rew2 reward function over 6200 training iterations.

Fig. 23

Training statistics (a–d) and evolution of hyperparameters (e–h) for the best-performing CNN_v1 DRL agent trained using 400 near-GEO-altitude RSOs and the rew2 reward function over 6200 training iterations

Figure 24 shows the evolution of the hyperparameters for the best-performing CNN_v1 DRL agent trained on an SSA environment with 100 near-GEO-altitude RSOs using the rew1 reward function over 4,800 training iterations.

Fig. 24

Training statistics (a–d) and evolution of hyperparameters (e–h) for the best-performing CNN_v1 DRL agent trained using 100 near-GEO-altitude RSOs and rew1 over 4,800 training iterations

Figure 25 shows the evolution of the hyperparameters for the best-performing CNN_v2 DRL agent trained on an SSA environment with 400 near-GEO-altitude RSOs using the rew1 reward function over 6600 training iterations.

Fig. 25

Training statistics (a–d) and the evolution of hyperparameters (e–h) for the best-performing CNN_v2 DRL agent trained using 400 near-GEO-altitude RSOs and rew1 over 6600 training iterations

Figure 26 shows the evolution of the hyperparameters for the best-performing CNN_v3 DRL agent trained on an SSA environment with 400 near-GEO-altitude RSOs using rew1 over 3000 training iterations.

Fig. 26

Training statistics (a–d) and the evolution of hyperparameters (e–h) for the best-performing CNN_v3 DRL agent trained using 400 near-GEO-altitude RSOs and rew1 over 3000 training iterations

Figure 27 shows the evolution of the hyperparameters for the best-performing CNN_v4 DRL agent trained on an SSA environment with 400 near-GEO-altitude RSOs using rew1 over 3200 training iterations.

Fig. 27

Training statistics (a–d) and evolution of hyperparameters (e–h) for the best-performing CNN_v4 DRL agent trained using 400 near-GEO-altitude RSOs and rew1 over 3200 training iterations