Angular Velocity and Covariance Estimates for Rigid Bodies in Near Pure-Spin Using Orientation Measurements

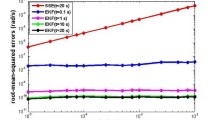
Abstract

The problem of estimating relative pose and angular velocity for uncooperative space objects has garnered great interest, especially within applications such as asteroid mapping and satellite servicing. This paper provides a batch estimator based on orientation measurements to estimate not only the angular velocity magnitude and spin-axis direction of a target body (either external or oneself) undergoing pure-spin, but also the associated uncertainty bounds for the resulting angular velocity magnitude and spin-axis direction estimates under reasonable assumptions. In addition, this paper derives statistics for the third eigenvalue of the stacked measurement matrix, which enable detection of whether the target body’s spin-axis direction is changing. The statistics of the third eigenvalue are shown to match those of a Monte-Carlo-based Gamma distribution fit. Instead of a recursive filtering methodology, the batch formulation pursued in this paper is well-suited to exploit the geometric properties associated with singular value decomposition techniques and Toeplitz recursion. This batch approach relinquishes the need for an iterative scheme to compute the error bounds upon the estimated spin-axis direction.

Appendix:

The derivation for the standard deviation of the third eigenvalue of the noisy spatiotemporal matrix is outlined as follows. As presented in Eq. 36, the noisy measurement matrix is linearized to:

$$ \begin{array}{@{}rcl@{}} Z_{n+1} &= \bar{Z}_{n+1} + {\Delta} Z_{n+1} \end{array} $$

(72)

which is a sum of the noise-free measurement matrix $\bar {Z}_{n+1}$ (in Eq. 6) and a noise-induced additive error matrix ΔZ_n+ 1. Recall that we assume ΔZ_n+ 1 is composed of zero-mean, uncorrelated elements with variance ε² (that is, for example: ${\Delta } Z_{n+1;(i,j)} \sim \mathcal {N}(0,\varepsilon ^{2}) \big )$. Here onward, the subscript (n + 1), indicating the total number of measurements, will be omitted for conciseness. The noisy spatiotemporal matrix Q := ZZ^T can thus be written as:

$$ \begin{array}{@{}rcl@{}} Q :&=& Z Z^{T} \\ &=& \bar{Z} \bar{Z}^{T} + \bar{Z} ({\Delta} Z)^{T} + ({\Delta} Z) \bar{Z}^{T} + ({\Delta} Z) ({\Delta} Z)^{T} \\ Q &=& \bar{Q} + \varepsilon \widehat{Q}^{(1)} + \varepsilon^{2} \widehat{Q}^{(2)} \end{array} $$

(73)

where $\widehat {Q}^{(1)} := \bar {Z} ({\Delta } \widehat Z)^{T} + ({\Delta } \widehat Z) \bar {Z}^{T}$, and $\widehat {Q}^{(2)} := ({\Delta } \widehat Z) ({\Delta } \widehat Z)^{T}$. Note that ${\Delta } \widehat Z := ({\Delta } Z) / \varepsilon$, so each element is a standard normal variable. Equation 73 is thus a second-order perturbation expansion of Q = ZZ^T. The corresponding perturbation expansion for the third eigenvalue λ₃ of Q has the form:

$$ \begin{array}{@{}rcl@{}} \lambda_{3} = \varepsilon \widehat \lambda_{3}^{(1)} + \varepsilon^{2} \widehat \lambda_{3}^{(2)} + \varepsilon^{3} \widehat \lambda_{3}^{(3)} + \dots \end{array} $$

(74)

Assuming the third eigenvalue is unique, the perturbation terms are given by [8, 15]:

$$ \begin{array}{@{}rcl@{}} \widehat\lambda_{3}^{(1)} &=& \operatorname{tr}\left[\widehat Q^{(1)} P_{3}\right] \end{array} $$

(75)

$$ \begin{array}{@{}rcl@{}} \widehat\lambda_{3}^{(2)} &=& \operatorname{tr}\left[\widehat Q^{(2)} P_{3} - \left( \widehat Q^{(1)}K_{3}\right) \left( \widehat Q^{(1)}P_{3}\right) \right] \end{array} $$

(76)

$$ \begin{array}{@{}rcl@{}} \widehat\lambda_{3}^{(3)} &=& \operatorname{tr}\left[-\widehat{Q}^{(1)} K_{j} \widehat{Q}^{(2)} P_{3} - \widehat{Q}^{(2)} K_{3} \widehat{Q}^{(1)} P_{3} + \widehat{Q}^{(1)} K_{3} \widehat{Q}^{(1)} K_{3} \widehat{Q}^{(1)} P_{3} \right. \end{array} $$

(77)

$$ \begin{array}{@{}rcl@{}} &&\left. - \widehat{Q}^{(1)} {K_{3}^{2}} \widehat{Q}^{(1)} P_{3} \widehat{Q}^{(1)} P_{3}\right] \end{array} $$

where:

$$ \begin{array}{@{}rcl@{}} P_{j} &=& \bar{\boldsymbol{u}}_{j} \bar{\boldsymbol{u}}_{j}^{T} \end{array} $$

(78)

$$ \begin{array}{@{}rcl@{}} \\ K_{3} &=& \frac{P_{1}}{\bar\lambda_{1} - \bar\lambda_{3}} + \frac{P_{2}}{\bar\lambda_{2} - \bar\lambda_{3}} = \frac{P_{1}}{\bar\lambda_{1}} + \frac{P_{2}}{\bar\lambda_{2}} \end{array} $$

(79)

As shown in Venturi [15], the standard deviation of the third eigenvalue is given by:

$$ \begin{array}{@{}rcl@{}} \sigma_{\lambda_{3}} = \left[\varepsilon^{2} \left\langle\left( \widehat{\lambda}_{3}^{(1)}\right)^{2}\right\rangle + \varepsilon^{4} \left( \left\langle\left( \widehat{\lambda}_{3}^{(2)}\right)^{2}\right\rangle - \left\langle\widehat{\lambda}_{3}^{(2)}\right\rangle^{2} + \left\langle\widehat{\lambda}_{3}^{(1)} \widehat{\lambda}_{3}^{(3)}\right\rangle\right) + \cdots\right]^{1 / 2} \end{array} $$

(80)

It remains to evaluate the various third eigenvalue perturbation terms. The process involves tedious, but straightforward algebra and matrix manipulation. For example, the derivation for the first-order perturbation term $\widehat {\lambda }_{3}^{(1)}$ is the following:

$$ \begin{array}{@{}rcl@{}} \widehat{\lambda}_{3}^{(1)} &=& \operatorname{tr}\left[\widehat Q^{(1)} P_{3}\right] \\ &=& \operatorname{tr}\left[ \left( \bar{Z} ({\Delta} \widehat Z)^{T} + ({\Delta} \widehat Z) \bar{Z}^{T}\right) \bar{\boldsymbol{u}}_{3} \bar{\boldsymbol{u}}_{3}^{T}\right] \\ &=& \bar{\boldsymbol{u}}_{3}^{T} \left( \bar{Z} ({\Delta} \widehat Z)^{T} + ({\Delta} \widehat Z) \bar{Z}^{T}\right) \bar{\boldsymbol{u}}_{3} \\ &=& 2 \bar{\boldsymbol{u}}_{3}^{T} \left( \bar{Z}({\Delta} \widehat Z)^{T} \right) \bar{\boldsymbol{u}}_{3} \\ &=& 2 \bar{\boldsymbol{u}}_{3}^{T} \left( {\sum}_{i=1}^{3} \left( \bar{\boldsymbol{u}}_{i}\right) \bar{s}_{i} \left( \bar{\boldsymbol{v}}_{i}\right)^{T} \right)({\Delta} \widehat Z)^{T} \bar{\boldsymbol{u}}_{3} \\ &=& 2 \underbrace{\bar{\boldsymbol{u}}_{3}^{T} \bar{\boldsymbol{u}}_{3}}_{=1} \bar{s}_{3} \bar{\boldsymbol{v}}_{3}^{T}({\Delta} \widehat Z)^{T} \bar{\boldsymbol{u}}_{3} \\ &=& 2 \bar{s}_{3} \bar{\boldsymbol{v}}_{3}^{T}({\Delta} \widehat Z)^{T} \bar{\boldsymbol{u}}_{3} \\ &=& 2 \bar{s}_{3} \bar{\boldsymbol{u}}_{3}^{T}({\Delta} \widehat Z) \bar{\boldsymbol{v}}_{3} \end{array} $$

(81)

(82)

Therefore, the mean is also zero:

(83)

Following a similar derivation process:

$$ \begin{array}{@{}rcl@{}} \widehat\lambda_{3}^{(2)} &=& \operatorname{tr}\left[\widehat Q^{(2)} P_{3} - \left( \widehat Q^{(1)}K_{3}\right) \left( \widehat Q^{(1)}P_{3}\right) \right] \\ &=& \bar{\boldsymbol{u}}_{3}^{T} ({\Delta} \widehat Z )({\Delta} \widehat Z)^{T} \bar{\boldsymbol{u}}_{3} - \left[ \left( \bar{\boldsymbol{u}}_{3}^{T} ({\Delta} \widehat Z ) \bar{\boldsymbol{v}}_{1}\right)^{2} + \left( \bar{\boldsymbol{u}}_{3}^{T} ({\Delta} \widehat Z ) \bar{\boldsymbol{v}}_{2}\right)^{2} \right] \end{array} $$

(84)

$$ \begin{array}{@{}rcl@{}} \\ \left( \widehat\lambda_{3}^{(2)}\right)^{2} &=& \left( \bar{\boldsymbol{u}}_{3}^{T} ({\Delta} \widehat Z) ({\Delta} \widehat Z)^{T} \bar{\boldsymbol{u}}_{3} \right)^{2} + \left( \bar{\boldsymbol{u}}_{3}^{T} ({\Delta} \widehat Z) \bar{\boldsymbol{v}}_{1} \right)^{4} + \left( \bar{\boldsymbol{u}}_{3}^{T} ({\Delta} \widehat Z) \bar{\boldsymbol{v}}_{2} \right)^{4} \end{array} $$

(85)

(86)

Taking the respective means:

(87)

$$ \begin{array}{@{}rcl@{}} \left\langle \left( \widehat\lambda_{3}^{(2)}\right)^{2} \right\rangle &=& (n+1)\Big((n+1) + 2 \Big) + 3 + 3 - 2\Big((n+1) + 2 \Big) - 2\Big((n+1) + 2 \Big) + 2 \\ &=& (n+1) \Big((n+1) - 2 \Big) \end{array} $$

(88)

$$ \begin{array}{@{}rcl@{}} \\ \left\langle \widehat\lambda_{3}^{(1)}\widehat\lambda_{3}^{(3)} \right\rangle &= 0 \end{array} $$

(89)

Thus, substituting the means into Eq. 80 results in the second-order approximation for the standard deviation of the third eigenvalue of the noisy measurement matrix:

(90)