Introduction

In South Korea, the national launch facility is a non-equatorial launch named the “Naro Space Center (NSC)”, located in the mid-latitudes (approximately 34°) of the northern hemisphere. It was built for two purposes: to test the main engine of the Korea Space Launch Vehicle-II (KSLV-II), and to launch sun synchronous orbit satellites in the future. Although NSC has a 34° northern latitude, the only available launch azimuth is approximately 172° due to range safety requirements. This results in inclinations after separation at a minimum of 80° [3].

Despite this high initial inclination, we show that it is still possible to launch a GEO satellite efficiently. Normally a high inclination insertion would require a large plane-change maneuver to insert into GEO at zero inclination. Several previous studies demonstrated that an LGA could be used to solve this problem.

For our purposes in this paper, “circumlunar” free-returns refer to those that pass on the far side of the Moon and “cislunar” free-returns pass on the near side of the Moon  [16]. Graziani provided a concept of a GEO transfer from mid latitude sites via the LGA. A circumlunar free-return trajectory was adopted, and it was shown that LGAs are an efficient method if the initial launch site latitude is greater than 25.9° [6]. Jah also verified that LGA transfers require less ∆V than either the Hohmann or Bi-elliptic transfers [7]. Circi studied cislunar free-return trajectories and discovered that they required slightly less ∆V than circumlunar free-return trajectories. [4]. Ocampo provided an example of a circumlunar free-return using the restricted three-body problem [12]. Ramanan applied a genetic algorithm with adaptive bounds to overcome the problem of high sensitivity to initial orbital parameters; a Geostationary transfer orbit (GTO) of 300 × 35,900 km was used as an initial orbit and the desired final inclination was less than 1° [15]. An LGA transfer was used operationally in May 1998 after a launch vehicle upper stage failure: AsiaSat-3/HGS-1 became the first satellite to transfer to GEO via a Moon flyby (actually using two flybys) and successfully returned to operations [13].

Previous studies only focused on achieving near equatorial inclinations after the LGA, which forces the Moon to be very near the Moon’s ascending or descending node with respect to the Earth’s equator. However, many GEO satellites have orbits with non-zero inclinations, which can be seen by examining NORAD two-line element (TLE) datasets (e.g., as retrieved from www.space-track.org). For this paper, we study transfers with final GEO inclinations less than 20° because approximately 98% of the GEO satellites is in this range.

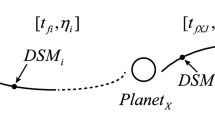
In addition, the previous studies only looked at few paths among all possible paths. Specifically, there are two possible Earth departures when transferring to the Moon; one is to leave Low Earth Orbit (LEO) when descending (from North to South) and the other is to leave LEO when ascending (from South to North). Overall geometries of these departures are depicted in Fig. 1. Furthermore, the flyby can occur on the far side and near side of the Moon. These different possibilities can be selected by targeting appropriate B-Plane parameters (“BdotT” and “BdotR”) at the time of the flyby. Finally, we consider the two nodes of the Moon’s orbit; one when the flyby occurs at the “ascending node” of the Moon’s orbit w.r.t Earth equator and the other when the flyby occurs at the “descending node” of the Moon’s orbit. The time interval between the nodes is around 2 weeks because the orbital period of the Moon is around 4 weeks. One node occurs near the perigee and the other node occurs near the apogee for a given month. We investigated eight possible paths described above, including two Earth departures, two free-returns, and two Moon’s nodes at lunar encounter, so that we could more fully understand the characteristics of the LGA transfer.

Fig. 1
figure 1

Four possible trajectories arriving at ascending node of Moon’s orbit [8, 16]

Full size image

As ascent trajectory of KSLV-II taking 870 s from NSC to LEO is used, and we assume that the launch vehicle places a satellite into a circular LEO at 300 km attitude. After a chosen coast duration, the launch vehicle upper stage places the satellite into a GTO. For comparison purposes, in this study we assume that the launch vehicle places the spacecraft into a 300 × 35,786 km GTO. After the GTO, our trajectories use 3.5 phasing loops prior to the lunar flyby (rather than a direct transfer) to lower the size of trajectory correction maneuvers and to reflect other actual operational spacecraft considerations. By investigating all possible paths, we found that circumlunar free-returns have a much shorter return time (around 3 days) than the cislunar free-returns (more than 10 days). The instantaneous 2-body apogee altitude after the flyby for the circumlunar free-returns tends to be higher than the cislunar free-returns, and consequently requires a larger GEO insertion ∆V. We compare these results with previous studies to assess the feasibility of transfer from highly-inclined Earth parking orbit.

This study is organized as follows: Section 2 describes the various possible GEO transfer paths that use an LGA. Section 3 describes the high-fidelity force model dynamics and orbit propagation models. In order to show how GEO transfer is designed sequentially, the numerical search method, independent variables and equality constraints are described in detail. Section 4 gives an overview of the ascending cislunar and ascending circumlunar at descending node, as well as of all possible paths. Section 5 compares our results with previous studies in terms of the dynamic models, possible paths, initial orbit elements, transfer time, and required ∆V.

Problem Description

Possible Paths for LGA

The four possible lunar flyby trajectories that arrive at the Moon’s ascending node are depicted in Fig. 1 [8, 16]. The other four paths occur at the Moon’s descending node. Thus, eight possible paths can be defined, with their abbreviations given in Table 1. Most of the previous studies focused on circumlunar free-returns [4, 6, 7, 12, 13, 15]. Only Circi studied the cislunar free-returns [4].

Table 1 Abbreviations for all possible paths
Full size table

As previously mentioned, an initial inclination of 80° is achieved when the GEO satellite is launched from NSC. In case of AsiaSat-3/HUG-1, 2420 m/s were required to nominally transfer from GTO to GEO with 51.6° inclination [13]. To solve this problem using the Moon, after the upper stage had failed, an LGA was used. Two necessary conditions were introduced to use the LGA for AsiaSat-3 [12].

The apogee radius vector needs to lie in the lunar orbit plane. This requires a unique combination of argument of perigee (AOP, ω) and right ascension ascending of node (RAAN, Ω). There are two Earth departure trajectories (and thus two AOP values) for every case. In case of the ascending departure trajectory (i.e. the TLI occurs near the equator while the spacecraft is traveling south-to-north), the AOP should be near zero, and in case of the descending departure trajectory (i.e. the TLI occurs near the equator while the spacecraft is traveling north-to-south), the AOP should be near 180°. Circi and Ramanan examined a descending departure but Ocampo used an ascending departure [4, 12, 15]. For the initial RAAN, it should be equal to the right ascension (αM) at the lunar flyby and it is also related to the direction of the departure trajectories (descending or ascending). Further explanations in this regard are detailed in Section 3.2.

The lunar flyby can occur either at the ascending or descending node of the Moon’s orbit [12]. Figure 2 shows the declination (or Latitude) of the Moon between November 2020 and February 2021. The JPL DE421 ephemeris was used for this study. The declination of the Moon is sinusoidal over a month because the Earth’s equator is tilted 23.5° with respect to the Ecliptic and Moon’s orbit is within 5.0° of the ecliptic plane. The Moon has six nodal crossings during this period. A Red inverted triangle (▼) shows the descending node and a green triangle (▲) the ascending node of the Moon’s orbit. The target flyby dates (red box) are the descending node on Dec 9, 2020 and the ascending node on Dec 22, 2020.

Fig. 2
figure 2

Declination of the Moon and target dates for Flyby

Full size image

Satellites in GEO

As of May 11, 2020, there are 955 satellites currently in GEO according to www.space-track.org. According to Fig. 3, most of the satellites in GEO have an inclination less than 20.0°. Only 9 satellites are between 20 and 35°, and 12 satellites are between 50° and 60° respectively. It can be also seen that 538 satellites are currently active, and most of them have an inclination less than 20.0°. For this reason, we deal with a low inclination as final target orbit in this study, although previous studies were only focused on near zero inclination GEO.

Fig. 3
figure 3

Number of satellites in GEO (955 GEO missions)

Full size image

Mission Scenario Overview

This mission scenario is designed to include a LEO parking orbit and GTO to reflect launch conditions in South Korea and to compare with previous studies (Table 6 in Section 5). The KSLV-II puts the satellite into a circular LEO with an altitude of 300 km (hp0, ha0). The upper stage then performs a maneuver (∆V0 ≈ 2427 m/s) to move the apogee altitude to 35,786 km (ha1) while leaving perigee at 300 km (hp1). Normally, a satellite in GTO needs approximately 1500 m/s to insert into a circular GEO without any plane change maneuvers. Operational considerations often require that this circularization maneuver be broken up into several maneuvers to minimize gravity losses. For example, four maneuvers were planned for GEO-KOMPSAT-2A launched in 2018 with a magnitude of each burn between 298.8 ~ 478.1 m/s [14].

Our baseline trajectory requires three perigee maneuvers to reach the lunar flyby targeting parameters as depicted in Fig. 4. The first maneuver (PM1) and the second maneuver (PM2) have ∆V1 = ∆V2 = 300 m/s to raise the apogee altitude from 35,786 km (ha1) to 65,000 km (ha2) and 197,500 km (ha3), respectively. The final maneuver (PM3) raises the apogee altitude to the lunar flyby targeting parameters. The PM3 (∆V3) varies amongst the cases because the flyby targeting parameters are different depending on the node of encounter and departure/arrival geometry depicted in Fig. 1. The first perigee (hp1) and the second perigee (hp2) remain at an altitude of 300 km but, in fact, the third perigee (hp3) can vary between 260 and 390 km due to the lunisolar perturbation at the third apogee ha3 (197,500 km) and the departure direction.

Fig. 4
figure 4

3.5 phasing loops trajectory of ascending departure (Earth Inertial Frame)

Full size image

The Lunar B-plane, which consists of BdotT and BdotR, is a mathematical construct that lies perpendicular to the incoming asymptote of hyperbola and provides a convenient set of linear targets for a spacecraft approaching the Moon as depicted in Fig. 5. Typical B-plane definitions involve a reference vector for the R direction. In our case we will use the Lunar pole vector as our reference. For our study, B-plane components are used as coarse pointing parameters to design the LGA. B-plane parameters are not only intuitively easy to understand but also easy to use as constraints in a search algorithm due to the linear behavior of these parameters for trajectories near a flyby body. Note that positive direction of the BdotT is ‘rightward’ and positive direction of the BdotR is ‘downward’ [5]. Targeted BdotT and BdotR values for a lunar flyby should be selected to position the trajectory on the correct “side” of the Moon and to easily distinguish between the two different free-return trajectories. For example, the targeted BdotT of circumlunar free-return should be negative to place perilune on the far side [16]. On the other hand, the BdotT of cislunar free-return should be positive to place perilune on the near-earth side of the Moon [16]. For the BdotR, a zero value is selected for both free-return trajectories to create the lowest possible inclination after the lunar flyby. All possible paths for GEO transfer are simulated based on this approach and methodology in Section 3.

Fig. 5
figure 5

B-plane definition and targeted B-plane for two free-return trajectories [5]

Full size image

The transfer time (∆t) is an important parameter in designing the GEO transfer. It is the sum of the flight time (∆t1) from the final perigee to the lunar flyby (green solid line in Fig. 4), which is independent of the initial inclination, and the return time (∆t2) from the lunar flyby to the geostationary perigee (blue solid line in Fig. 6). Miele concluded that an optimal flight time between the Earth and the Moon was 4.5 days for clockwise arrival and 4.37 days for counterclockwise arrival to the Moon [11]. Choi shown that optimal flight time was between 4.3 days and 5.2 days when considering the two Earth departure trajectories [3]. At the end of ∆t2, the final inclination (if) less than 20.0° and final perigee altitude (hpf = 35,786 km) conditions should be met. After the flyby, approximately 1100 m/s is required to enter a GEO, so three GEO insertion maneuvers (GEOIMs) are planned for circularization to minimize finite burn losses. The GEOIM1 maneuver (∆V4) is planned to insert the spacecraft into an elliptical orbit of 35,786 × 140,000 km. The remaining two GEOIMs (∆V5 and ∆V6) are performed to meet the final semi-major axis (af = 42,164.135 km) and eccentricity (ef ≈ 0) conditions.

Fig. 6
figure 6

Cislunar free-return with descending node at encounter (Earth Inertial Frame)

Full size image

Dynamic Model and Numerical Search Method

Dynamic and Propagation Model

The equations of motion for this problem can be written as follows [2]. The first term of Eq. (1) describes the Newton’s formulation of gravitation of two orbiting bodies and the second term describes third-body gravitational perturbation. Sun, Earth and the Moon are applied for the third-body gravitational perturbation because satellite in this problem passes near Earth several times and the Moon one time.

$$ \ddot{\mathbf{r}}=-\mu \frac{\mathbf{r}}{{\left\Vert \mathbf{r}\right\Vert}^3}+\sum \limits_{i>0}{\mu}_i\left(\frac{{\mathbf{r}}_{Bi}-\mathbf{r}}{{\left\Vert {\mathbf{r}}_{Bi}-\mathbf{r}\right\Vert}^3}-\frac{{\mathbf{r}}_{Bi}}{{\left\Vert {\mathbf{r}}_{\mathrm{B}i}\right\Vert}^3}\right)+\frac{1}{m}{\mathbf{F}}_s $$
(1)

where \( \ddot{\mathbf{r}} \) and r are the acceleration and position of the spacecraft relative to a coordinate system with origin B0. μ and μi are the gravitational parameter for B0 (reference gravitational body) and Bi (ith gravitational body). rBi is the position of the Bi relative to B0. m is the mass of the spacecraft [2]. Fs consists of atmospheric drag and solar radiation pressure force. Atmospheric drag is modeled because the satellite passes low perigee altitude more than 3 times and solar radiation pressure is also modeled to reflect the perturbation from the Sun during long transfer trajectory. Drag coefficient (CD) is assumed to be 2.2 and solar radiation pressure coefficient (CR) is assumed to be 1.0. Cross-sectional area and total mass are assumed to be as 20 m2 and 1000 kg respectively.

A GEO transfer using an LGA is a multi-body problem in Earth-Moon space. If the satellite is orbiting the Earth, the reference central body should be the Earth while the Sun and the Moon are modeled as point masses to integrate Eq. (1). If the satellite is orbiting within the Moon’s sphere of influence (SOI), the reference central body should be the Moon while the Sun and the Earth are modeled as point masses. Based on these assumptions, two propagator models are described in detailed in Table 2. Moon propagator is used when the distance between the satellite and the Moon is less than 60,000 km (SOI of the Moon) and Earth propagator is used if not. The propagation is performed with a 7th order Runge-Kutta-Fehlberg integrator with 8th order error control and variable step size control. The integrator uses an absolute error tolerance of 1e–10 and a relative error tolerance of 1e–13.

Table 2 Propagator model for Earth and Moon
Full size table

Numerical Search Method

We consider a launch from NSC (34.43°N, 127.54E) so that the satellite is put on the circular parking orbit with an altitude of 300 km and an inclination of 80°.When the satellite reaches circular parking orbit, the upper stage places the apogee altitude of 35,786 km. The orbital parameters after separation at GTO are given as below;

  • $$ {a}_1=\mathrm{24,421.135}\ \mathrm{km},{e}_1=0.7265,{i}_1=80.0{}^{\circ},{\upsilon}_1=0.0{}^{\circ} $$

In order to have geostationary perigee altitude after flyby, orbital parameters can be fixed as below; For the final inclination (if), less than 20.0° would be targeted to have a low inclination GEO although below target inclination shows only zero.

  • $$ {h}_{pf}=\mathrm{35,786}\ \mathrm{km},{i}_f=0.0{}^{\circ} $$

Remaining orbit parameters are AOP (ω1) and RAAN (Ω1). In this study, we calculate the launch trajectory using boundary condition data of the KSLV-II (initial and final position and velocity vector) with an ascent duration of 870 s. After the powered ascent, the spacecraft spends a duration of ∆tc1 in a circular parking orbit until reaching the ascending or descending departure near Earth’s equator. This approach changes these initial orbit parameters into launch time (t1) and coast duration (∆tc1) because launch time establishes the RAAN (Ω1) and coast duration establishes the direction of the line-of-apsides (ω1) [9]. Mission scenario contains three perigee maneuvers to go to the lunar flyby targeting parameters. Two perigee maneuvers in the phasing loops are fixed at 300 m/s for simplification and the final perigee maneuver (∆V3) will be found by an iterative differential corrector search algorithm. The independent variables of this iterative search method are launch time (t1), coast duration (∆tc1) and PM3 (∆V3). For the initial AOP (ω1), ascending departure at descending node occurs at near 0° but descending departure occurs at near 180°. For the initial RAAN (Ω1), launch time should be equal to the right ascension (αM) of the Moon at the lunar flyby in case of ascending departure at descending node and descending departure at ascending node. However, launch time for the descending departure at descending node and ascending departure at ascending node should be equal to the right ascension (αM) + 180° to reflect the changed departure direction and node of Moon’s orbit.

The numerical differential corrector search algorithm makes use of a Newton-Raphson formulation to solve this problem [1]. Equation (2) describes Newton-Raphson multi-variable problem. This algorithm finds the nearest local solution that meets constraints within tolerance. The f(x) involves propagation with independent variables x and the results of f(x) are performed comparison with equality constraints of yd in iteration process.

$$ {\mathbf{x}}_{\mathrm{k}+1}={\mathbf{x}}_{\mathrm{k}}-{\mathbf{J}}_{\mathbf{n}}^{-\mathbf{1}}\left(\mathbf{f}\left({\mathbf{x}}_{\mathrm{k}}\right)-{\mathbf{y}}_{\mathrm{d}}\right) $$
(2)

where J (Jacobian matrix) consists of the partial derivatives of f(x) with respect to x. If the J is not square, pseudo inverse is performed.

A series of separate Newton-Raphson solutions is used to achieve the final solution. First “coarse” targeting step is implemented to find a solution that has similar characteristics to our desired solution, and in this case to meet B-Plane parameters. Then more precise or “fine” targeting step is implemented to find a final solution that meets all the desired constraints.

The first “coarse” step is only focused on distinguishing cislunar or circumlunar free-return trajectory using BdotT and BdotR parameters that place the solution on the correct “side” of the Moon. In this step, the independent variables are x= [t1, ∆tc1, ∆V3] and equality constraints are yd= [BdotT, BdotR, ∆t1]. The chosen flyby targeting parameters for the first “coarse” step are important because these values change a high inclination (~80°) and low perigee altitude (~300 km) departure orbit into a low inclination (if) and geostationary perigee altitude (hpf) orbit after the flyby. The flyby distance found by Graziani was 5866 km and Ramanan found 7815 ~ 8845 km for a circumlunar free-return [6, 15]. Based on this information, we can use a BdotT of −10,000 km for a circumlunar solution because this trajectory should pass on the far side Moon in the opposite direction of the Moon’s motion. BdotR is selected 0.0 km to have near zero inclination after flyby. For ∆t1, a 5.0-day transfer time is used which is close to optimal [3, 11]. As a result, equality constraints are yd= [−10,000 km, 0.0 km, 5.0 days]. When a cislunar free-return solution is desired, a BdotT target should be selected of 10,000 km because the trajectory should pass on the near side of the Moon, also in the opposite direction of the Moon’s motion as depicted in Fig. 5. If we select ADCCL (ascending departure, descending node at encounter, circumlunar free-return), descending node occurs on 9 Dec 2020 19:20:00(UTC) as depicted in Fig. 2. Therefore, initial values for the independent variables are x0= [30 Nov 2020 00:00:00(UTC), 46 min, 80 m/s]. The initial launch time about 10 days ahead of the descending node occurrence is applied in consideration of the 3.5 phasing loops duration.

After we have chosen to pass on either the near or far side of the Moon (with our selection of B-plane parameters), we then use the “fine” step in our solution to reach the low inclination geostationary orbit using the converged independent variables of the first step. The independent variables are same with the first step x= [t1, ∆tc1, ∆V3] but the initial values for the independent variables (x0) are the converged values from the first step. Our first step has placed us on the desired side of the Moon, and the second step will achieve our desired constraints precisely from this point. Equality constraints for this step are yd= [hpf = 35,786 km, if = 0.0°]. Note that the BdotT and BdotR used in the first step will not be maintained once the second step solution has been found. These “coarse” parameters were merely intermediate placeholders that allowed us to choose which type of solution was desired.

Once the satellite reaches the low inclination earth orbit with geostationary perigee altitude, three consecutive GEOIMs would be performed to have GEO as depicted in Fig. 6. Independent variables are x= [∆V4, ∆V5, ∆V6] and equality constraints are yd= [ha4 = 140,000 km, ha5 = 70,000 km, ,ef = 0.0].

Simulation Results

Trajectory Overview (ADCSL and ADCCL)

Figure 7 shows ADCSL and ADCCL trajectories with respect to an Earth inertial frame and an Earth-Moon rotating frame launching on Nov 29, 2020. The Earth-Moon rotating frame used places the Moon at the top of the figure with the Earth at the center [10]. The target flyby date for these two trajectories is Dec 9, 2020(UTC) depicted in Fig. 2. The black solid lines are the trajectory from launch to final perigee maneuver, the green solid line is the departure trajectory for ∆t1. The blue solid line is the free-return trajectory for ∆t2 and the magenta solid lines are a sequence of three maneuvers for GEO insertion.

Fig. 7
figure 7

ADCSL and ADCCL w.r.t Earth inertial frame (a, b) and Earth-Moon rotating frame (c, d)

Full size image

A launch period of 5 days for each path is used in this study to reflect the inclination of current satellites in GEO as depicted in Fig. 3. Figure 8 shows only both the departure trajectory and the free-return trajectory (i.e. no phasing loops) because it is easy to see how those trajectories change across the launch period from Nov 27, 2020(UTC) to Dec 02, 2020(UTC).

Fig. 8
figure 8

Departure and free-return trajectories of ADCSL (a) and ADCCL (b)

Full size image

Table 3 shows the detailed time information with the Moon’s declination (at flyby) and the Earth inclination (after flyby) for both ADCSL and ADCCL. The launch time difference between them is less than 10 min. The duration from launch to flyby time is around 10 days with the launch time slipping earlier less than 1 h per day across the launch period. The major time difference between each day takes place after the flyby. It also shows that Earth inclination after the flyby is very close to the declination of the Moon at flyby. As the satellite flies the Moon’s near-zero declination, a resultant equatorial orbit is possible.

Table 3 Major time (UTC), declination and the Earth inclination of ADCSL and ADCCL
Full size table

Simulation Results of all Paths

Figure 9(a) shows the launch time from Nov 27 to Dec 02, 2020 for the descending node at encounter and from Dec 10 to Dec 14, 2020 for the ascending node at encounter. The difference of launch time between descending and ascending departure for the days within launch period is around 12 h due to the precession of the Earth’s orbit around the Sun. It also shows that launch time are similar if the departure and node at encounter are same. Figure 9(b) shows that zero Earth inclination after flyby is available. As the launch dates are gradually far away at interval of 1 day from the third launch day, the inclination gradually increases.

Fig. 9
figure 9

Launch time and Earth inclination after flyby. (a) Launch time. (b) Earth inclination after flyby

Full size image

The RAAN (Ω1) and AOP (ω1) that meet the final desired orbit elements are found using a numerical search method with results depicted in Fig. 10(a). The ω1 converged by Circi was 180.45° (descending departure), the ω1 converged by Ocampo was 0.6° (ascending departure) and the ω1 converged by Ramanan was between 182.8° ~ 184.6° (descending departure). Our results verify that the ω1 for descending departure are near 180° and the ω1 for ascending departure are near 0°. The Ω1 from Circi was 12.39° (DACCL) and the Ω1 from Ramanan was −0.75° ~ −2.25° (DACCL) but Ω1 from Ocampo was −173.9° (AACCL) [4, 12, 15]. This also verifies that Ω1 for descending departure at ascending node (▲) and ascending departure at descending node (⁎) is near zero. However, Ω1 for descending departure at descending node (●) and ascending departure at ascending node (♦) is near 180°.

Fig. 10
figure 10

Initial RAAN/AOP and PM ∆V. (a) Initial RAAN and AOP. (b) PM3 ∆V

Full size image

Three perigee maneuvers are performed to raise the apogee altitude from GTO to the lunar flyby. Since the PM1 (∆V1) and PM2 (∆V2) are fixed as 300 m/s, PM3(∆V3) is varied for each case to reach the lunar flyby. According to the ∆V3 as depicted in Fig. 10(b), the descending node (●, ⁎) case requires a few m/s less than the ascending node (▲, ♦) case because Moon is located in near perigee at the descending node and Moon is located in near apogee at the ascending node in these cases. For these cases, the ∆V3 for cislunar free-returns (dashed blue line) is a few m/s less than circumlunar free-returns (solid red line) because the perilune for circumlunar free-returns occurs at the far side of the Moon in this case but the perilune for the cislunar free-returns occurs near side of the Moon [16].

The BdotR and BdotT after the second step are depicted in Fig. 11(a). BdotR and BdotT for the circumlunar free-returns are concentrated around a mean of −9000 km and near zero km respectively. On the other hand, the BdotT for all cislunar free-returns has a positive value with large variations. The minimum distance defined from center of the Moon to the flyby targeting parameters is one of the DDCSLs and this value is 6356 km. The maximum distance is one of the DACSLs with a value of 16,861 km. The only difference between the two cases is the selected node for the lunar encounter. These results show it is difficult to predict in advance what exact lunar flyby targeting parameters will be required to reach the low inclination GEO.

Fig. 11
figure 11

BdotR/BdotT and Instantaneous apogee altitude after flyby. (a) BdotR and BdotT. (b) Instantaneous apogee altitude

Full size image

The instantaneous apogee altitudes after flyby are depicted in Fig. 11(b). This value is very important because GEOIM ∆V directly effects the instantaneous apogee altitude. Looking at the results, the circumlunar free-returns tend to have more elliptical orbits than cislunar free-returns. ADCSL has the minimum instantaneous apogee altitude which requires the least amount ∆V to insert into a GEO.

As GEOIM ∆V are directly related to the instantaneous altitude after flyby, Figs. 11(b) and 12(a) are very similar. The GEOIM ∆V value varies over several tens of m/s. To find the most efficient solution, it is important to find out which path provides the lowest instantaneous apogee altitude. As the ADCSL produces the lowest instantaneous apogee altitude, this is the best path to reduce GEOIM ∆V.

Fig. 12
figure 12

GEOIM ∆V and return time (∆t2). (a) GEOIM ∆V. (b) Return time (∆t2)

Full size image

The return times (∆t2) of circumlunar free-return are from 2.7 to 3.6 days but the return times of the cislunar free-returns are several times longer as depicted in Fig. 12(b). The shorter the calculated return time, the less GEOIM ∆V is derived. On the other hand, it is difficult to find the relation between return time of circumlunar free-returns and instantaneous apogee altitude.

Total ∆V of all possible paths from GTO to the final GEO is depicted in Fig. 13. According to these results, cislunar free-return trajectories tend to have less ∆V than circumlunar free-return trajectories. It also shows that the ADCSL solutions require the minimum ∆V. The magnitude is near 1762 m/s but ∆V of the DDCCL requires 80 m/s higher than the ADCSL. As previously mentioned, a satellite in GTO (for example, GEO-KOMPSAT-2A) requires approximately 1500 m/s to enter GEO without plane change maneuver. However, AsiaSat-3/HUG-1 in GTO with an inclination of 51.6° required 2420 m/s to enter GEO if LGA was not used. Simulation results shows that if only 262 m/s is added to the satellite in GTO, it can reach GEO despite the highly inclined initial orbit (80°) when path of the ADCSL is used. On the other hand, if the launch vehicle can put the satellite into an elliptical initial orbit of 300 × 65,000 km, PM1(∆V1=300 m/s) is not necessary, only 1462 m/s would be required to enter GEO. By designing all possible paths, we can understand overall pattern of these trajectories and select alternative ways to overcome highly inclined initial orbit.

Fig. 13
figure 13

Total ∆V (PM ∆V + GEOIM ∆V)

Full size image

Discussion

Comparisons with previous studies are performed to assess these results. Ocampo used the restricted three body problem for a GEO transfer using LGA [12]. Ramanan used non-spherical gravity models of the Earth (10 × 0) field and the Moon (9 × 0) field. The Sun was used as a third body and it was concluded that at least the second zonal harmonic of the Earth should be included for the orbit propagation model [15]. High-fidelity dynamic and propagation models are applied for this study. Non-spherical gravity of the Earth (21 × 21) field and the Moon (48 × 48) field are modeled and the Earth, the Moon and the Sun are modeled as third bodies. Atmospheric drag and solar radiation pressure models are also included.

There are eight possible paths to go to GEO using the LGA. Graziani used the ascending node at encounter case but it was not described whether the Earth departure was the ascending or descending. Circi and Ramanan used DACCL and Ocampo used AACCL [4, 12, 15]. ADCCL was used to rescue the AsiaSat-3 in 1998, and Circi was only author who studied a cislunar free-return using DACSL [4, 13].

The first part of Table 4 describes initial LEO while the second part describes the initial GTO. For the comparison with this study, “∆V compensation” is introduced. This approach makes it possible to compare these results with others by adding appropriate ∆V, although the initial orbits were different. For example, Ocampo used initial orbit of 200 × 200 km and Circi used 250 × 250 km but LEO parking orbit in this study was 300 × 300 km [4, 13]. ∆V from 200 × 200 km to 200 × 378,000 km (Moon’s mean altitude) requires 3131.4 m/s and ∆V from 300 × 300 km to 300 × 378,000 km requires 3106.5 m/s. The ∆V between them is around 25 m/s and the ∆V due to the initial orbit between 250 × 250 km and 300 × 300 km is around 12.5 m/s. Therefore, ∆V of −25 m/s and − 12.5 m/s should be compensated for the initial orbit of 200 × 200 km and 250 × 250 km to compare with this study.

Table 4 Initial orbits and ∆V compensation [4, 6, 12, 13, 15]
Full size table

The GEOIM ∆V depends on the initial inclination. If the initial inclination increases from 30 to 90°, ∆V increases up to 30 m/s [6]. It means if the initial inclination increases 10°, 5 m/s more ∆V is necessary. Previous studies focused on the initial inclination around 50° but this study focuses on the initial inclination of 80° due to the NSC latitude and constraints. Therefore, +15 m/s should be compensated for initial inclination. For example, based on this compensation approach, total + 2.5 m/s should be compensated for Circi due to the lower initial orbit (250 × 250 km, −12.5 m/s) and the lower initial inclination (50°, +15 m/s). In case of GTO, ∆V from 200 × 36,000 km to 200 × 378,000 km (Moon’s mean altitude) requires 673 m/s and ∆V from 300 × 35,786 km to 300 × 378,000 km requires 680 m/s. The ∆V between them is around 7 m/s so that ∆V of +7 m/s should be compensated for initial orbit of 200 × 36,000 (Ocampo). The ∆V difference between 300 × 35,900 km and 300 × 35,786 km to the Moon is around 2 m/s.

The flight times (∆t1), return times (∆t2) and transfer times (∆t) that meet the final geostationary orbit parameters are shown in Table 5. For the circumlunar free-returns, flight times have around 5 days and the free-return times have around 3 days so that total transfer times would be around 7 ~ 10 days. For the cislunar free-return, flight times are similar with the circumlunar free-returns but the return times are several times longer than the circumlunar free-returns. Total transfer times of the cislunar free-return are around 15 ~ 24 days.

Table 5 Transfer time ∆t (∆t1 + ∆t2) summary [6, 4, 12, 13,15]
Full size table

The total ∆V from initial orbit to GEO is summarized in Table 6 and “∆V compensation” described in Table 4 is applied. The first part of Table 6 shows the ∆V from LEO to GEO and the second part shows the ∆V from GTO to GEO. All ∆V from LEO to the lunar flyby have similar values but the GEOIM ∆V, which is mainly impacted by free-return type, has large variations. Specifically, Circi studied four different dates of both circumlunar and cislunar free-return to investigate the effects of the Sun. These results show that seasonal ∆V variation for circumlunar free-return is 25 m/s (1,152 – 1127) and cislunar free-return is 11 m/s (1,116–1104). On the other hand, this study shows that geometrical ∆V variation is higher than seasonal ∆V. For example, geometrical ∆V variation for circumlunar free-return is 48 m/s (1,165–1117) and cislunar free-return is 46 m/s (1,133–1087). This study also shows that the ADCSL requires the minimum GEOIM ∆V (around 1087 m/s) among all possible paths. This geometry not only decreases apogee altitude at flyby (near side of the Moon) but also helps decrease the instantaneous apogee altitude after flyby using LGA. All ∆V values from GTO to GEO show this similar pattern. The ADCSL example in Table 6 requires the minimum ∆V (1762 = 675 + 1087) and it is 23 m/s lower than Ramanan’s (1,785 = 680 + 1105).

Table 6 ∆V summary [4, 6, 12, 13, 15]
Full size table

Conclusion

Launching a GEO mission from non-equatorial launch site (NSC) required a large plane change maneuver due to the high inclination after separation. A GEO transfer with LGA was applied to solve this problem. There were many possible paths depending on departure direction, free-return type and node at encounter. A launch period for 5 days was simulated in consideration of current satellites in GEO. High-fidelity orbit propagation models and a numerical search method using Newton-Raphson differential corrector were applied to solve the problem. B-Plane parameters were used as constraints in the first step to distinguish between the free-return trajectory and the second step of this solution was designed to reach the low inclination GEO.

Simulation results shown that BdotT of cislunar and circumlunar had similar value with opposite sign, and BdotR of both free-return trajectories had values that could make the satellite have low inclination orbit. We demonstrated that the instantaneous apogee altitude after flyby was directly related to the GEOIM ∆V and cislunar free-return trajectories tended to have lower ∆V than circumlunar free-return trajectory. Most of all, we demonstrated that the ADCSL case required the minimum ∆V among all possible paths.

“∆V compensation” method was introduced to conduct direct comparison with previous studies. This method shown that geometrical ∆V variation was larger than seasonal ∆V variation and that the ADCSL case had the minimum ∆V among all possible paths in this study and among all previous studies. In the future, we will perform optimization and extend the flyby targets over an entire year to further analyze the effect of seasonal factors.