Abstract
A central problem in orbit transfer optimization is to determine the number, time, direction, and magnitude of velocity impulses that minimize the total impulse. This problem was posed in 1967 by T. N. Edelbaum, and while notable advances have been made, a rigorous means to answer Edelbaum’s question for multiple-revolution maneuvers has remained elusive for over five decades. We revisit Edelbaum’s question by taking a bottom-up approach to generate a minimum-fuel switching surface. Sweeping through time profiles of the minimum-fuel switching function for increasing admissible thrust magnitude, and in the high-thrust limit, we find that the continuous thrust switching surface reveals the N-impulse solution. It is also shown that a fundamental minimum-thrust solution plays a pivotal role in our process to determine the optimal minimum-fuel maneuver for all thrust levels. Remarkably, we find that the answer to Edelbaum’s question is not generally unique, but is frequently a set of equal-Δv extremals. We further find, when Edelbaum’s question is refined to seek the number of finite-duration thrust arcs for a specific rocket engine, that a unique extremal is usually found. Numerical results demonstrate the ideas and their utility for several interplanetary and Earth-bound optimal transfers that consist of up to eleven impulses or, for finite thrust, short thrust arcs. Another significant contribution of the paper can be viewed as a unification in astrodynamics where the connection between impulsive and continuous-thrust trajectories are demonstrated through the notion of optimal switching surfaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Most space trajectory design algorithms make use of low-fidelity dynamical models and idealized control input assumptions to make the search space tractable [1,2,3,4,5,6,7,8,9]. Specifically, traditional impulsive-based trajectory analysis tools, typically with inverse-square gravity models, hold a special place for preliminary mission design [10,11,12,13,14,15,16,17,18]. The output of preliminary mission design studies is the starting design for higher-fidelity optimization. Making these approximations in preliminary mission design is driven by practicality, which is natural, given the level of complexity of the overall mission design challenge. Edelbaum’s question [19] was posed in the setting of inverse-square gravity models, however, the generalized question for high-fidelity force models is straightforward to ask (but not to answer).
Impulsive solutions are important since they determine both the theoretical minimum-time and minimum-fuel extremals and also provide reachability insights. For the most part, preliminary mission design methods rely on low-fidelity dynamical models, which in turn, frequently lead to analytical propagation of the state dynamics through Keplerian orbit models [20] or by utilizing the solution of Lambert’s problem [21,22,23,24,25]. Impulsive maneuvers are also used extensively for solving formation flight optimal control problems [26,27,28,29,30,31,32,33,34,35,36] and orbit reachability analyses problems [37,38,39,40,41,42,43].
For the impulsive thrust idealization, a fundamental quest has been to determine the optimal number, times, magnitude, and direction of the impulses, to accomplish general three-dimensional (3D) multiple-revolution orbit transfers while minimizing the total Δv. This is Edelbaum’s heretofore not rigorously answered question [19]: How many impulses?
Optimal continuous and impulsive formulations were originally investigated by Lawden beginning in the early 1950’s. In his seminal and pioneering 1963 work on optimal trajectories, Lawden derived a set of criteria [44] that define the optimality of impulsive solutions by introducing the “primer vector”, p. The primer vector, for either continuous or impulsive thrusting, defines the instantaneous optimal direction for the thrust vector. Due to the importance of Lawden’s impulsive necessary conditions, they are repeated here: 1) the primer vector and its first derivative are continuous everywhere, 2) the magnitude of the primer vector remains less than unity, i.e., p ≡∥p∥ < 1 except for the impulse times where ∥p∥ = 1, 3) at the impulse times, the primer vector is a unit vector along the optimal direction of impulse, and 4) at any intermediate impulse time, \(dp/dt = \dot {p} = \dot {\textbf {p}}^{\top } \textbf {p} = 0\). Undoubtedly, Lawden’s introduction of the concept of primer vector is the most fundamental breakthrough in the field of space trajectory optimization.
Violation of the necessary conditions can be used as a measure of sub-optimality of approximate impulsive solutions and has been used to improve sub-optimal impulsive solutions [45]. Specifically, first-order variation of a 2-impulse cost functional is derived to establish necessary conditions for a small variation that result in an improved solution through: 1) the introduction of an additional mid-course impulse, and 2) introduction of terminal coasts (either initial or final). We briefly discuss the N-impulse literature wherein a number of algorithms have been devised to seek minimum-Δv impulsive solutions. The above ideas can be utilized to improve approximate impulsive solutions through classical gradient-based optimization algorithms [46]. The time history of the primer vector (and possible violation of the optimality conditions) is frequently used in numerical algorithms to place additional impulses near maxima of p. The time and location of the impulses have to be finalized by direct optimization. So, we have a four-dimensional augmentation of the search space for every additional impulse. In order to minimize the cost function, the point at which p takes its maximum value is usually taken as an initial iterate [45]. This approach leads to a direct method, a multivariate search problem, that has to be solved in a robust manner to result in a converged solution [47].
The search for N-impulse solutions has been most commonly initiated from a minimum-Δv 2-impulse (Lambert) solution for which the existence of 2Nrev,max + 1 solutions is demonstrated in [48, 49], where Nrev,max is the maximum number of revolutions that has to be determined and depends on the prescribed time of flight. Multiple-revolution Lambert algorithms are used to generate multiple reference trajectories, each of which are considered for multiple impulse optimization and further improvements. An initial policy is required to select those solutions that are hypothesized to lead to improvements, which in most cases is to select among the non-unique Lambert solutions those with cheaper 2-impulse Δv requirements. The improved solution (a 3-impulse solution) divides the problem into two new sub-arcs, each one of which can be treated similar to the original 2-impulse solution. However, this approach requires that a decision be made on which sub-arc to be optimized first. Therefore, there are N − 1 decisions to be made, which result in 2N− 1 different possibilities (analogous to branches of a tree-search problem) for values of the cost functional. Alternatives for decision making are given in [46]. While presenting important advancements, these heuristic bootstrapping approaches with associated gradient-based solvers may get stuck in local optima since there is no guarantee of a unimodal performance surface and these methods rely on classical parameter optimization methods [49,50,51]. A common aspect among most of these methods is that they rely solely on impulsive-based solutions. Application of semi-infinite convex optimization using a relaxation scheme and duality theory in normed linear spaces is demonstrated in [52] for fixed-time minimum-fuel rendezvous between close elliptic orbits without fixing a priori the number of impulses.
In order to avoid local sub-optimal convergence, a number of studies have focused on the application of evolutionary algorithms [53,54,55,56,57] that compromise between local and global search processes to identify multiple local minima. In addition, indirect-based methods are studied in [58] and a homotopic-based indirect scheme is presented in [59], which improves potential 2-impulse Lambert solutions out of the total 2Nrev,max + 1 solutions. Nevertheless, while all of the aforementioned methods have been able to find multi-impulse solutions that improve on the 2-impulse solutions with varying degrees of success, none can claim global optimality, nor can they answer Edelbaum’s question with certainty.
Under some conditions, i.e., a linear neighborhood of reference trajectories, the maximum number of impulses is shown not to exceed the number of state variables [19, 60]. For a linear system, Lawden’s necessary conditions are also sufficient for an optimal trajectory [61]. For both circular and elliptic orbits, the necessary and sufficient conditions for the optimal (fixed-terminal state and fixed-time) solution are derived in [62, 63]. For rendezvous and transfer problems assuming a linear dynamical model, the number of impulses is at most equal to the dimension of the state space [61]. The case of planar transfer between co-planar elliptical orbits is also studied in [64]. Rendezvous of two spacecraft in neighboring near-circular non-coplanar orbits is reported with up to six impulses [65]. It is shown that the representation of the primer vector in polar coordinates leads to the separation of the in-plane and out-of-plane components of the primer vector. A complete analytic solution for the out-of-plane component of the primer vector is shown to exist, which is independent of the semi-major axis of the transfer orbit [66]. The problem of time-fixed fuel-optimal out-of-plane elliptic rendezvous between spacecraft in a linear setting is studied with a complete analytical closed-form solution [67].
On the other hand, there is a direct theoretical connection between optimal finite-thrust continuous control and an optimal sequence of velocity impulses; this connection becomes apparent in the switching surfaces introduced and discussed herein. The fact that impulsive maneuvers constitute the limiting case of the more general finite-thrust trajectory optimization problems has been stated in [58, 68] not only when the thrust magnitude increases, but also when the transfer time increases [69]. In fact, the work of Zhu, et al. [70], has been motivated by the fact that “... the optimal bang-bang control and impulsive maneuvers can be obtained through continuously increasing the thrust magnitude from a minimum-thrust solution.” Implicitly, they used neighboring converged co-states to initiate the two-point boundary-value problem (TPBVP) solution for each new assigned thrust magnitude, T, along with appropriate changes that result in the switching function, S of the indirect formulation of optimal control trajectories.
The procedure Zhu, et al. followed in [70] is dependent upon beginning with a 2-impulse Lambert solution. As we discuss below, assuming a 2-impulse starting solution is generally not theoretically justified, nor does it offer any convergence guarantee because the optimal N-impulse solution we seek is obviously not generally near a Lambert 2-impulse trajectory. We show herein that optimality generally does not result in impulses at the prescribed initial and final times; and there are generally optimal initial and final coast arcs that need to be admitted. For sufficiently short time of flight, however, we can anticipate the 2-impulse solution will indeed be the optimal impulsive extremal and will be unique for orbit transfer maneuvers spanning a fraction of one revolution. However, for longer time intervals, as will be evident in the developments herein, one must consider fully the local behavior associated with the local extrema on each feasible specification of the number of en-route revolutions along the transfer orbit.
In this investigation, we use indirect optimization methods. The most fundamental feature of indirect methods is that any trajectory satisfying the necessary conditions and all boundary conditions (BCs) is guaranteed to yield a local extremal. In space applications the equations of motion (EOM) are of relatively low order, so indirect methods, when combined with reliable initialization and homotopy approaches, are attractive and lead to fast convergence to at least local extremals. These approaches are especially attractive when no state variable inequality path constraints are imposed [71]. Indirect methods utilizing convergence enhancement homotopy techniques and control smoothing methods, while artistic, have ameliorated many of the challenges of numerically solving the TPBVPs and have been applied successfully to a number of optimal control problems (OCPs) [70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97].
Indirect methods exploit first-order necessary conditions, which in principle and most frequently, converge to local extremals. Therefore, methods for establishing starting co-states within the domain of attraction of the desired global extremum are desirable. As is evident herein, we have established important insights on this difficult issue. Local extrema have been found, somewhat analogous to the multi-revolution Lambert problem, to be associated with the number (Nrev) of intermediate revolutions the extremal transfer makes en-route to satisfying the final BCs. So analogous to the Lambert’s problem, we specifyNrev and seek out all local extremals associated with each Nrev. The global extremum and the associated optimal Nrev is obtained by selecting the best (with respect to the cost) of the local minima. The “fundamental” minimum-thrust solution, i.e., the minimum of all local minima is critical in the analysis of a comprehensive approach that is devised to address global minimum-fuel solutions and its related optimal N-impulse solutions. Remarkably, this fundamental minimum-thrust solution belongs to the same continuous extremal field map of neighboring minimum fuel extrema that are the solutions we seek. This method is different from the previously mentioned approaches that are reviewed above. In general, the fundamental minimum-thrust solutions are obtained to establish the first profile on a switching surface for all thrusts \(T > T_{{\min \limits }}\). Since the minimum thrust, \(T_{{\min \limits }}\), to reach the final state is established by this process, obviously the minimum thrust is the boundary of the reachability domain. For each Nrev, the associated switching surface (for \(T > T_{{\min \limits }}\)) is an ensemble of all switching functions associated with the entire family of extremal solutions. These switching surfaces turn out to be very informative tools and provide an enhanced global understanding of the space of extremal solutions while revealing, for example, late-departure and early-arrival time boundaries. The fundamental minimum-thrust solution is critical in constructing the switching surface that, for the case of limiting thrust magnitude, \(T \rightarrow \infty \), reveals the associated impulsive solution.
We consider herein a number of test cases along with their switching surfaces and their associated impulsive solutions. An algorithm is outlined, which uses the high-thrust behavior to approximate accurately the N-impulse solutions for multiple-revolution trajectories. A final process is described that adjusts these impulses slightly to isolate infinite thrust limit: the optimal impulsive solution. It is possible to extend the proposed process to account for the high-fidelity force models and to converge to the final solution.
The paper is organized as follows. First, a concise review of the formulation of the minimum-fuel TPBVPs using the indirect method and Pontryagin’s Minimum Principle (PMP) is given. Then, we review the details of a continuation procedure when the magnitude of thrust is swept to generate the desired switching surfaces. The details of a robust algorithm that has been used to generate the N-impulse solutions are presented next. Then, the results are given for a number of test cases. Interpretation of the results is presented that provide insights to neighboring extremals for various thrust values, T, and the limiting high-thrust extremal, which are the corresponding impulsive maneuvers. In reviewing the results for these distinctly different family of optimal transfers, the versatility of the methodology to handle various unique circumstances becomes evident. Then, a discussion is given on the number of impulses, and interestingly, the (heretofore, unknown in the literature) non-uniqueness of the impulsive solutions. Application of the method for solving transfer problems from a Geostationary Transfer Orbit (GTO) to a Halo orbit around the L1 point of the Earth-Moon restricted three-body model is demonstrated. A section is given to the connection among features of the optimal switching surfaces and reachability in astrodynamics followed by a discussion on the computational effort of the method. Finally, concluding remarks are presented.
Indirect Formulation of Minimum-Fuel Problem and Continuation Procedure
In this section, EOMs and the minimum-fuel cost functionals are discussed. Optimal control theory is used to establish the necessary conditions for optimal trajectories and to define the TPBVPs to be solved numerically. In all example problems studied, it is assumed that there are no state variable path constraints other than the terminal BCs. Numerical schemes used for solving the resulting TPBVPs are discussed separately.
Equations of Motion
We consider the trajectory optimization for a spacecraft moving in an inverse-square gravitational field of a central body, where the spacecraft is affected also by the acceleration induced by an on-board propulsion system. Implicit in this problem, the spacecraft attitude must be controlled to steer the thrust vector, however, we ignore rotational dynamics. This usual approximation is justified because the controlled attitude error dynamics is typically several orders of magnitude faster than the orbital dynamics and attitude errors are usually a small fraction of a degree. This approximation is well-justified to design virtually all optimal interplanetary trajectories, and most near-Earth trajectories.
The EOMs are expressed in terms of the modified equinoctial orbital elements (MEEs) [98] and the variation of mass is included. MEEs are suitable for optimization of low-thrust trajectories because the most general MEE representation includes circular, elliptic, and hyperbolic orbits without singularities at zero eccentricity or zero inclinations. Unlike the inertial Cartesian coordinates that are changing quickly over a revolution, the MEEs are well-behaved and varying slowly except for the perturbed true longitude, l, which is a smoothly varying function of time that reduces to Kepler’s equation in the absence of perturbations [71, 94]. Furthermore, prescribing the osculating final orbit’s true longitude as a terminal BC permits convenient control of Nrev in accounting for the total angular displacement through intermediate revolutions and fractions thereof by simply adding 2πNrev to the final true longitude lf (in the osculating final orbit). Specifically, we replace lf by \(l^{*}_{f} = l_{f} + 2\pi N_{\text {rev}}\), and choose integer values for Nrev over a feasible set. This takes advantage of the evident fact that having the osculating true longitude as a coordinate permits Nrev to be specified in the final BC. This is a key element in formulating and solving TPVBPs where multiple extremals with different number of revolutions are possible to occur [71].
Why is it important to have control over Nrev? By removing the freedom to converge to any Nrev, we ensure that the resulting switching surfaces are unique for each specification of Nrev. This is a critical enabler since our goal is to perform a systematic study (over the number of feasible revolutions), which avoids converging quasi-randomly to solutions with different number of en-route revolutions.
Furthermore, the procedure we develop herein finds the optimal Nrev to minimize a standard minimum-fuel performance index (\( J = \frac {T}{c} {\int \limits }_{t_{0}}^{t_{f}} \delta ~dt \)) over all feasible Nrev specifications, where δ is engine throttling input. Let x = [p,f,g,h,k,l]⊤ and m denote the vector of MEEs, and the spacecraft mass, respectively, and let \(\textbf {u} = [u_{r}, u_{t}, u_{n}]^{\top } = \frac {T}{m} \delta \boldsymbol {\alpha } \) denote the thrust acceleration vector with its components expressed in the local-vertical/local-horizontal (LVLH) osculating orbital reference frame. α, T and δ ∈ [0,1] denote the thrust steering unit vector, thrust magnitude, and engine throttle input, respectively. The state/co-state dynamics become
where c = Ispg0 is the exhaust velocity, Isp and g0 are the engine’s specific impulse and the reference gravitational acceleration at sea level, respectively. The \(\textbf {f} = \textbf {f}(\textbf {x})\in \mathbb {R}^{6}\) is the unforced part of the state dynamics and \(\mathbb {B} = \mathbb {B}(\textbf {x}) \in \mathbb {R}^{6 \times 3}\) denotes the control influence matrix
In these equations, two intermediate positive variables are \(w=1+f\cos \limits (l)+g\sin \limits (l)\), s2 = 1 + h2 + k2, and μ is the gravitational mass parameter of the central body. The co-state vector associated with the equinoctial orbit state vector is denoted by λ = [λp,λf,λg,λh,λk,λl]⊤ and λm is the co-state associated with the mass. H is the Hamiltonian that corresponds to the minimum-fuel cost functional, \(J = \frac {T}{c}{\int \limits }_{t_{0}}^{t_{f}} ~\delta ~dt\), where t0 and tf are fixed. The Hamiltonian becomes
The optimal control direction and throttling input that minimize H are
where the primer vector, \(\textbf {p} \equiv -\mathbb {B}^{\top } \pmb {\lambda }\) and the switching function, S, is defined as
In addition, we recently introduced the hyperbolic tangent smoothing (HTS) method [96, 99] as a means for smoothing the otherwise jump-discontinuous engine throttle input as
where ρ > 0 is the smoothing level (and is used as the continuation parameter for the numerical continuation procedure). The HTS method accurately approximates the optimal throttle, δ∗(S), by a smooth, differentiable function, δ∗(S,ρ); this smoothed throttle is quite effective since it enlarges the domain of convergence such that, in most cases, even a moderate number of random sets of initial co-state guesses leads to convergence to the local extrema. For the rare cases that S = 0 for a finite time interval, we may have a singular control (0 < δ < 1). In the event a singular sub-arc is encountered, \(S = \dot {S} = \ddot {S} = 0\) can be investigated as functions of (t,x(t),λ(t)), along with the remaining necessary conditions (including Kelly condition [100])], to see if there exists a singular throttle function 0 < δ∗ < 1.
For a fixed-time rendezvous problem, the final BCs (seven equality constraints) can be written as
where xT denotes the final target state values associated with the target body. The final value of the mass co-state has to be zero since the final mass is free. For multi-revolution transfers, the number of en-route revolutions, Nrev, is an unknown and has to be determined. Computational experience indicates, for Nrev greater than some problem-dependent minimum integer, there is one local extremum for each Nrev choice.
While we have no theoretical proof that there is only one extremal for each Nrev choice (for fixed terminal BCs and time of flight), we believe this to be true for inverse-square force fields, based on extensive computations. This is an important point, because our method presently hypothesizes this to be true. If there is only one minimum-fuel local extrema per Nrev, then the minimum of all local minima will identify \(N^{*}_{\text {rev}}\) and the global minimum-fuel trajectory.
Let z = [x⊤,m,λ⊤,λm]⊤ denote the state-costate vector, then, we can write,
where α = α∗ and δ = δ∗(S,ρ) (Note \(\dot {\textbf {x}}\), \(\dot {m}\), \(\dot {\boldsymbol {\lambda }}\), \(\dot {\lambda }_{m}\) are shorthand for the RHS of Eqs. 1, 2, 3, and 4). Once these values are substituted into F, the EOMs can be integrated numerically, if initial BCs are fully specified. However, only the initial state x(t0) = x0 and m(t0) = m0 are specified. The final state x(tf) as well as the final co-states are a function of the initial co-state η(t0), where \(\boldsymbol {\eta }(t_{0}) = [\boldsymbol {\lambda }^{\top }(t_{0}),\lambda _{m}(t_{0})]^{\top }\) is the vector of unknowns to be determined such that Eq. 11 is satisfied. Thus, we have a TPBVP that requires a starting estimate η(t0) within the domain of convergence of the algorithm used to satisfy the prescribed BCs. There are seven constraints in Eq. 11 and seven unknown elements in η(t0).
Thrust Magnitude Sweeping for Construction of Switching Surfaces
The continuation procedure over the thrust magnitude is considered to generate a family of switching function profiles that constitute the switching surface. It is noteworthy that the application of extremal field maps for analysis of globally optimal coplanar time-free orbit transfers has been investigated in [101,102,103].
Figure 1 depicts the time histories of a typical switching function and its associated (constant) thrust profile for \(T_{{\min \limits }}\). Local extrema of the switching function are denoted by triangles. A slight increase in the thrust magnitude leads to a downward shift and distortion of the switching function and the appearance of a coast arc for a finite time interval, Δt, as is shown in Fig. 2. Ultimately, a procedure can be devised to sweep over increasing values of the thrust magnitude until the zeros of the switching function occur in pairs that are a small Δt < 𝜖 apart. If the thrust duration satisfies Δt = 𝜖 < (tf − t0)/1000, one can usually approximate the short thrust arcs as impulses.
We find for a sufficiently large thrust that the time duration of all thrust arcs becomes shorter than 𝜖 (a prescribed threshold based on the mission time). Then, we can approximate the thrust as impulsive with near-negligible error. Figure 3 shows representative profiles of the switching function and thrust magnitude versus time for very high thrust values, i.e., \(T \gg T_{{\min \limits }}\). As the thrust magnitude is assigned increasingly large values, we observe that the time duration of all the thrust arcs shrink while the thrusting time sequence remains approximately unchanged and the solution becomes closely approximated by isolated impulses. At this stage, we seek to replace the continuous thrust by a finite number of impulsive thrusts by formulating and solving an N −impulse trajectory optimization problem, with the number, times, magnitudes, and direction of the thrust impulses known approximately.
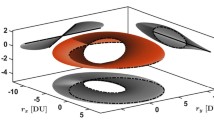
Our goal is to generate a surface that is formed by sweeping the variable of interest, in this case thrust magnitude, T, and concatenating the switching functions. Figure 4 depicts a representative switching surface where a solid blue curve denotes the switching function associated with the minimum-thrust extremal. In practice, we may require logarithmic scales on the (T,S) axes to reveal sufficient details of these surfaces. Using a topographic analogy, increasing T leads to the S < 0 coast “canyons” being wider while the S > 0 thrust “ridges” have lower peak S-values and become more narrow (in time). This switching surface has six thrust ridges and seven coast canyons when thrust magnitude is swept in its defined bound \(T \in [T_{{\min \limits }}, T_{{\max \limits }}]\), where \(T_{{\max \limits }} \gg T_{{\min \limits }}\). By increasing the thrust value, the time duration of all thrust arcs become smaller. Qualitatively, it is useful to consider the plane defined by S = 0 to represent the surface of an S = 0 “lake” defined by its shore lines (contour) intersection defining the boundary with the S > 0 topography. The thrust ridges at high thrust magnitudes approach six impulses of negligible time duration as the “coast lakes” become wider and the thrust ridges more narrow. The considered switching surface in Fig. 4 has a well-behaved topography, however, for many orbit transfers, the width of thrust ridges may not always decrease monotonically as the thrust magnitude is increased as in this illustration, and in some cases there are surprising and counter-intuitive features. Specifically, there are cases in which a thrust ridge will be created at some critical thrust value (either as an independent “island” in the middle of one of the coast “lakes” or as a “peninsula” that “breaks off” from a thrust ridge). These cases are associated with bifurcations that occasionally occur in the switching surface.
The individual switching surface topography for each orbit transfer is a function of the two sets of orbital BCs (including especially, relative phasing, inclination, size, shape, and orientation) and the force model assumptions. The high dimensionality of the space that underlies each switching surface makes it difficult to predict the fine structure meandering of these surfaces, especially at low thrust levels. The optimal control switching surface is a fundamental attribute of controls associated with the family of extremals and does not depend, for example, on the choice of coordinates, although nonlinearity and efficient convergence to the solution underlying TPBVP does indeed depend on coordinate choice [71, 94]. A discussion on this point is given later in a separate section.
Study of the topography of the particular generated switching surface associated with a family of extremals, as will be shown, is very useful for trajectory and mission design purposes because decisions on optimal thrust level, for example, need to be informed by the consequences of alternative designs. Note that every time slice (constant T profile) of the surface in Fig. 4 corresponds to the on-off switching function for a particular extremal trajectory, i.e., a minimum-fuel optimal transfer between the prescribed initial and final states over t ∈ [t0,tf].
Optimization Scheme For N-Impulse Solutions
Given our ability to use the switching surface high-thrust limiting behavior to approximate accurately the number, time, direction, and magnitude of all velocity impulses, only slight adjustments are required to achieve final convergence. Our experience is that for multiple-revolutions, the convergence of the final direct optimization problem can be made more efficient if the whole trajectory is divided into several segments with the boundary of each segment defined by each impulse time and a forward-backward numerical integration scheme is adopted.
Figure 5 shows the switching function of a representative multiple-revolution trajectory that consists of six impulses. The main reason for adopting such a scheme for impulsive optimization is the observation that impulse times (the position and velocity vectors at the associated impulse times) change negligibly due to the use of switching surface to estimate these times precisely. In the majority of the test cases, qualitatively, these impulses are found by the converged indirect solution to be applied near the peripasis/apoapsis (of the intermediate elliptical orbits) and/or the ascending/descending nodes of the initial and final orbits. Therefore, the time interval between consequent impulses (time duration of each segment), at most, corresponds to a complete revolution around the central body. This scheme allows us to utilize parallel computation, and improves the convergence. Also, we frequently invoke a high-fidelity force model at this stage, and the use of parallel computation is facilitated to improve wall-clock computational efficiency for final convergence.
The trajectory is, therefore, divided into M segments. In this example, seven segments M = 7 (colored differently in the upper part of the Fig. 5) are considered. The times of intermediate impulses are denoted by ti, i = 1,⋯ ,6. The discussion herein is for a solution in which the trajectory consists of intermediate impulses only (and no impulses occur at t0 or tf denoted by squares in Fig. 5). However, the methodology is general and can handle impulses that are applied at the initial and final times, as well, should the switching function (at \(T_{{\max \limits }}\)) indicate terminal impulses. Except for the first and last segments, the beginning and the end of each segment consists of an impulse denoted by green circles.
Let \(t^{-}_{i}\) and \(t^{+}_{i}\) denote the time instants immediately before and after the ith impulse, respectively, the velocity vectors are similarly denoted as \(\textbf {v}^{-}_{i}\) and \(\textbf {v}^{+}_{i}\). At the moment of impulse, the position vector remains the same, i.e., \(\textbf {r}^{-}_{i} = \textbf {r}_{i} = \textbf {r}^{+}_{i}\). Consider the fourth segment with time duration as Δts,4 = t4 − t3. States (position and velocity) are propagated forward (subscript ‘F’) from t = t3 to \(t = t_{3} + \frac {\Delta t_{s,4}}{2}\) to get rF and vF. Similarly, the states are propagated backward (subscript ‘B’) from t = t4 to \(t = t_{4} - \frac {\Delta t_{s,4}}{2}\) to get rB and vB.
The error between the states is used to from a residual vector (at the mid-point of the segment marked by a red star)
where \(\boldsymbol {\Delta }_{s,i} \in \mathbb {R}^{6}\), i = 1,⋯ ,N denotes the state residual vector at the mid-point of the ith segment and is defined as
The matrix of decision variables is denoted by X becomes
where each impulse consists of ten decision variables (i.e., position, velocity, velocity impulse vectors, and time of impulse). The initial and final variables can be fixed by setting their lower and upper bounds to be equal to the desired parameters. If impulses at the initial and final times have to be considered, the lower and upper bounds of the decision variables are modified accordingly. Ultimately, an optimization problem for the impulsive solution can be formulated as
Any Nonlinear Programming (NLP) solver (we have used MATLAB’s fmincon) chosen for minimizing the cost defined in Eq. 16 benefits from a good approximation of the time, direction, and magnitude of the impulsive thrusts, which accelerates the convergence performance. These are precisely the information that we extract from the extremal field map, i.e., from the extremal associated with the high thrust limit of the switching surface thrust ridges. Moreover, due to the ensured quality of our starting estimate of the optimal maneuver, we do not have to guess the number of impulses. For instance, in Fig. 5, we can readily see that there exist six thrust arcs where good estimates of the velocity impulses can be obtained by using simple formula as
where Δti denotes the thrust time interval, T denotes the thrust level and mi denotes the mass at the mid-point, ti, of the respective ith thrust interval. At each impulse time, ti, the direction of the thrust is also known from the direction of the primer vector, \(\textbf {p}(t_{i}) = - \mathbb {B}(\textbf {x}(t_{i}),t_{i})^{\top } \boldsymbol {\lambda }(t_{i})\). It is straightforward to calculate the impulse vector as Δvi = Δviαi, where αi = p(ti)/∥p(ti)∥. All of the required values are retrievable from the extremal, which is the solution of the TPBVP for \(T \gg T_{{\min \limits }}\). Note that it is possible to parameterize the impulsive optimization problem by position-formulation (also known as Feasible Iterate Approach (FIA) [51]). The FIA parameterization uses Lambert problem and satisfaction of the position boundary conditions are guaranteed when two-body dynamics govern the motion. It reduces the number of design variables considerably. However, the method proposed in this paper is a general method applicable to beyond two-body dynamics.
The analysis of these switching surfaces are best explained in the context of specific orbit transfers, while there are several generalized points of view that emerge, there are also specific features and behaviors that may or may not arise in the switching surface associated with a particular orbit transfer. So, we consider different cases to permit the diversity of behaviors to be explained and see the relevance of switching surface analysis in each case.
There are two key points that require explanation. First, the above construction is dependent on a reliable method to solve the underlying family of OCPs. For spacecraft trajectories, indirect methods are critical elements of the proposed procedure since, based on our experience, these methods can be significantly faster. However, the key point is that they provide more rigorous and accurate optimal trajectories than the corresponding direct methods. Therefore, a detailed discussion is devoted to an enhanced process to solve the TPBVPs that arise in the indirect formulation of OCPs. It is also possible, in principle, to approximate these surfaces using any type of direct optimization method. The second important point is related to the fact that the minimum-thrust trajectory (also, because a duality exists, this minimum-thrust trajectory is also a minimum-time trajectory if the corresponding thrust is judiciously specified) is the base solution from which the computation of the switching surface is initiated.
On the other hand, minimum-time and minimum-fuel trajectories typically have one local extrema for each of a number of Nrev en route revolutions in the orbit transfer (we emphasize that we are dealing with rendezvous-type, fixed-time maneuvers), and the number of revolutions (we will see) affects the structure of the switching surface. Therefore, a reliable strategy is required to find the fundamental minimum-thrust solution, which implicitly requires us to find the local extremals associated with multiple revolutions. Note, when the constant thrust is always ‘on’, the minimum-thrust extremal is also the minimum-fuel extremal. This process is somewhat analogous to finding all solutions in the multiple-revolution 2-impulse Lambert problems [22, 104, 105]. The details of an algorithm for finding fundamental minimum-thrust solutions are explained in the next section. The final observation is that the methods of this section are well suited for parallel computation, which will facilitate efficient computations when high-fidelity force models are used for final convergence.
Procedure for Finding Minimum-Thrust Solution
As discussed earlier, the minimum-thrust solution is, in fact, nothing but the minimum-time solution for the prescribed boundary conditions, and time of flight. However, the minimum-time solution is not unique. We seek the thrust \(T_{{\min \limits }}\) for which not only the minimum time (\(t^{*}_{f} - t_{0}\)) is equal to the desired maneuver time (tf − t0), but also requires the least amount of propellant. Therefore, a procedure is devised to find the solution to the minimum-thrust solution, which is based on the formulation of minimum-time trajectory optimization problem. For minimum-time problem the state/co-state dynamics is the same as those in Eqs. 1–4. The optimal control vector is known [87] and is characterized by
Note that the switching function of the minimum-time problem has a different mathematical expression and is known to remain non-negative along the entire trajectory, i.e., \(S=\frac {c ||\mathbb {B}^{\top } \pmb {\lambda }||}{m}+\lambda _{m} -1> 0\). In practice, mass and its associated co-state can be omitted from the numerical analysis; however, we kept this formulation since we can use the vector of converged solution to start the minimum-fuel continuation procedure. Since the terminal time, tf, is free, optimality conditions require the following condition on the final value of the Hamiltonian, H∗(tf) = 0. On the other hand, neither the state equations, cost functional, nor the terminal constraints depend on time explicitly, which means that the Hamiltonian is a constant along the optimal trajectory, i.e., H∗(t) = 0. Therefore, for a rendezvous-type maneuver and its associated boundary conditions (that we have considered in this paper), the vector of terminal constraints become
The TPBVP associated with the minimum-time problem consists of vector Θ = [λ⊤(t0),λm(t0),tf]⊤ with eight unknown values and the vector of terminal constraints is given in Eq. 20.
The first step is to determine the minimum-thrust solution. In order to find a solution, the above TPBVP is augmented with thrust magnitude as one additional unknown variable, T. We also augment the vector of final constraints with an additional equality constraint, i.e., \(t_{f}^{*} - t_{f} = 0\), where \(t_{f}^{*}\) is the minimum time of flight. The inclusion of this equality constraint is crucial to guide the solution toward the minimum-thrust magnitude, \(T_{{\min \limits }}\). Therefore, the augmented (subscript ‘a’) design vector of the optimization problem is \(\boldsymbol {\Theta }_{a} = [\boldsymbol {\Theta }^{\top },T]^{\top }\) and the augmented vector of final constraints becomes
In the above optimization problem, obviously a good estimate for the time of flight is known. In fact, the prescribed time of flight, \(t_{f}^{*}\), is the desired minimum time solution, corresponding to the \(T_{{\min \limits }}\) for which the sought extremal is also the minimum time maneuver. However, a good estimate of the thrust magnitude will enhance the convergence performance of any chosen solver.
A simple numerical procedure is outlined to provide an estimate for the thrust, which is based on work-energy principle. The work/energy principle states that for a particle, the work done by all forces equals the change in the kinetic energy, which in our problem can be written as
where vf = ∥vf∥ and v0 = ∥v0∥. In addition, the final mass, mf, is related to the initial mass, m0, through \(m_{f} = m_{0} - \frac {T}{c} (t_{f}-t_{0})\). The second integral on the right-hand side of Eq. 22 is not straightforward to evaluate because it depends on the unknown path and the associated optimal steering direction vector for thrust. However, it is known that the maximum change in the kinetic energy is achieved when the thrust is aligned with or against the velocity vector, i.e., α = ±v/∥v∥. This fact is frequently used to generate initial guesses for low-thrust trajectory optimization [2, 106]. Therefore, the second integral can be approximated as
where \(\bar {r} = \frac {r_{0}+r_{f}}{2}\) and \(\dot {\bar {\theta }} = \sqrt {\frac {\mu }{\bar {r}^{3}}}\) are mean radius and mean angular velocities, respectively. It is further assumed that \(\|\textbf {v}\| \approx r \dot {\theta }\), which neglects the non-planar, and radial components of velocity; these components are usually small but definitely not negligible. So this assumption will typically give a smaller than optimal variation in the orbit due to thrust, or to put in another way, would lead to a similar large thrust to accomplish the change in kinetic energy. Over-estimating the thrust is preferred, because larger than minimum thrust still leads to feasible solutions and thrust can be reduced until the switching function just touches zero at one point to identify the desired thrust \(T_{{\min \limits }}\). After all, the result of this simplifying approach will be used as an initial guess for the actual minimum-thrust optimization problem, which justifies “reasonable” simplifications to start the process with a thrust level near, but greater than \(T_{{\min \limits }}\).
Upon substitution of Eq. 23 into 22 and evaluating the first integral (that leads to \(\frac {\mu m_{f}}{r_{f}}-\frac {\mu m_{0}}{r_{i}}\) assuming crudely that m is evaluated at the terminal points), one can solve for an estimated value for the thrust using the following relation
The proper sign of ± is determined by the fact that for trajectories to more (less) energetic orbits, the energy has to increase (decrease). The thrust obtained through Eq. 24 can be used as a good initial guess for minimum-thrust optimization problem. Table 1 shows the results of the above optimization algorithms for finding the minimum-thrust magnitude for the Earth-to-1998ML and Earth-to-Venus cases under two-body dynamical model. MATLAB fsolve is used for solving the TPBVP associated with the minimum-thrust optimization problem.
We would like to add that we have also tried Edelbaum’s method [107] that establishes a relation between Δv, time of flight, and thrust level for circular to circular orbit transfers. Since the considered test cases are rendezvous maneuvers, the amount of required Δv in Edelbaum’s relation has to be increased to take into account the additional required energy. Our experience shows that 1.5 ×Δv leads to convergence for the considered problems under two-body dynamics, for a large but not exhaustive number of tests.
The number of revolutions is a factor that has to be considered during the procedure of solving minimum-thrust optimization problem. The projection of the initial and target position vectors onto the x − y plane of an inertial frame make angles, 𝜃0 ∈ [0,2π] and 𝜃T ∈ [0,2π], respectively, with respect to the x axis. Without loss of generality and assuming that 𝜃T > 𝜃0, the difference between the angles is denoted by Δ𝜃 = 𝜃T − 𝜃0. The number of revolutions is considered to update the final angles through 𝜃f = Δ𝜃 + 2π × Nrev. A more rigorous way to define Nrev is to count the number of successive piercings of the trajectory through the inertially fixed plane defined by the initial orbit radius and orbit normal. Our experience shows that the global “optimal” minimum-fuel (and also the minimum-thrust) solution corresponds to a unique number of revolutions required to achieve the maneuver. Therefore, the minimum-thrust problem has to be sought starting from a lower number of revolutions, Nrev,l.
For two-body problems, let τl and τu denote the smaller and larger values of the orbital periods of the involved bodies bounded from below and above according to the following relation
where Nrev,l and Nrev,u denote the lower and upper bounds for the number of revolutions, respectively, and ceil and floor operators return the next larger (next smaller) integer number from their arguments. This formula neglects the truth that thrusting, even low thrusting, alters the two-body period of the transfer vehicle from the starting orbital period. We specify this in the perturbed true anomaly desired for the optimal maneuver, but as we near convergence, the physical number of revolutions is defined more rigorously as the number of actual passages of the transfer orbit through the reference plane defined by the initial orbit normal and the initial position vector. Except where the starting and arrival position vectors are nearly co-linear, Eq. 25 holds. In other words, Nrev revolutions using the period of the starting orbit is not guaranteed to correspond to Nrev revolutions of the perturbed transfer orbit, but any discrepancy encountered is easily cleared up by counting revolutions.
Starting from Nrev,l, if convergence to satisfaction of the necessary conditions of optimality is achieved, the solution is the minimum-thrust value; otherwise, the value of the selected number of en route revolutions should be incremented by one. The process is repeated until convergence is achieved. Alternatively, all of these extremals, can be solved simultaneously, and the one with the smallest value of the propellant mass consumed will be the global extremal, i.e., the fundamental minimum-thrust solution. Note that numerical results in this case indicate that there exist more solutions with Nrev > Nrev,u, but they are typically not of practical interest since they lead to sub-optimal solutions with larger fuel consumption. On the other hand, there exist no solutions when Nrev < Nrev,l; reachability of the given target state requires a specific minimum number of revolutions which may be Nrev = 0,1,2,⋯ . Technically, of course, the solution is generally reached in Nrev plus a fraction of the Nrev + 1 revolution.
For instance, for the Earth-to-Venus problem (which is one of the test cases studied in this paper), Fig. 6 shows the changes in minimum-thrust and its associated final mass for different number of en route revolutions. Clearly, the fundamental minimum-thrust solution corresponds to Nrev = 10. For Nrev ≥ 11 the trajectories make unnecessary revolutions by getting closer to the Sun. Note that all of these solutions are local minimum-time solutions (δ∗(t) = 1), but with different thrust levels. Figure 6 is obviously useful for sizing and mission planning purposes.
Results
Five minimum-fuel trajectory optimization problems (under two-body dynamics) are considered where the strength and nonlinearity of the gravitational field vary significantly. As a consequence, distinct topological features in the respective switching surfaces appear, in particular, for multi-revolution trajectories. A sixth case is considered to show that the method can handle more than one gravitating body: a minimum-fuel rendezvous-type maneuver from GTO to a Halo orbit around L1 point in restricted three-body dynamics of the Earth-Moon systems is studied.
For the solar interplanetary cases, the canonical units are adopted to normalize the state and control inputs, where one distance unit (DU) is equal to the astronomical unit (AU), and 2π × Time Unit (TU) is 1 year. In the numerical simulations, the gravitational parameter of the Sun is set to μ⊙ = 132712440018 km3/s2, acceleration due to Earth’s gravity is set to g0 = 9.8065 m/s2, whereas the gravitational parameter of the Earth is set μ⊕ = 398600 km3/s2. For the near Earth orbit transfer problems, a distance unit (DU) is equal to the Earth radius at the equator, Re = 6378 km, and a Time Unit (TU) is 806.78557 seconds, \(\text {TU} = R_{e}^{3/2}/\sqrt {\mu _{\oplus }}\). In both cases, the TU is the time for a satellite in the circular reference orbit to move through one radian of true anomaly. For the GTO to Halo orbit transfer around the L1 point, the standard Canonical units of the Synodic coordinate system are used.
Interplanetary Rendezvous From Earth to Mars
The first test case is chosen similar to the first interplanetary Earth-to-Mars transfer case in [70] in order to validate the results and to present more insights into the ensemble of solutions as intended, in the light of the switching surface. The same BCs are taken along with the specified time of flight, tf − t0 = 793 days. The following values are considered for the parameters of the spacecraft and its low-thrust propulsion system: m0 = 2000 kg, and Isp = 3000 s. Some fraction of m0 is the propellant mass.
For a fixed dry mass, by maximizing the final spacecraft mass, we minimize the fuel required and maximize the useful payload we can deliver to the final state. The value of thrust is considered as the sweeping parameter, to generate an infinite family of optimal maneuvers, i.e., \(T \in [T_{{\min \limits }},T_{\text {u}}]\), where Tu is some upper value of thrust and is set to Tu = 10 N. Several slices of the switching surface will be studied in more details to introduce particular concepts that may re-appear in other switching surfaces.
The family of state and co-state variables that underlie the switching surface constitute an extremal field map. Obviously, this extremal field map, for an infinite family of maximum thrust values has immediate utility in sizing of propulsion systems for mission design purposes, which will be explained. The Earth position and velocity vectors at the departure time, t0, are
As is usual for preliminary design of solar missions, we assume we are just outside the Earth’s sphere of influence at departure and Mars sphere of influence at arrival, i.e., we ignore Earth and Mars gravity. The position and velocity vectors of Mars at the final time, tf, are
The minimum-Δv 2-impulsive solution can be obtained by solving the corresponding Lambert problem. The magnitude of the impulses at the initial and final time instants are Δv(t0) = 3.0157 km/s and Δv(tf) = 3.0318 km/s, respectively, which correspond to a solution with one revolution around the Sun, i.e., Nrev = 1.
Before generating the switching surface, we need to determine the optimal number of en-route revolutions (and its associated minimum-thrust solution) based on the algorithm outlined earlier. Figure 7 shows the changes in \(T_{{\min \limits }}\) and mf vs. the feasible values for Nrev. The critical value of thrust for the fundamental minimum-thrust (or minimum-time) for the given BCs is found to be \(T_{{\min \limits }} = 0.1996\) N. Thus, a relatively low thrust can send a significant payload to Mars, but the time of flight is significant. The fundamental minimum-thrust solution corresponds to \(N^{*}_{\text {rev}}=1\), which indicates that the maneuver completes one plus a fraction of the second revolution along the transfer trajectory. The initial phase angle between the position vectors is small, but Nrev = 0 does not lead to a solution. In other words, with the given parameters of the propulsion system and BCs, the amount of propellant required for Nrev = 0 is larger than the initial mass of the spacecraft.
We found the same minimum-thrust magnitude for the given BCs as in [70], i.e., \(T_{{\min \limits }} = 0.1996\) N. The thrust value is then swept in the given range T ∈ [0.1996,10] N. Figure 8 shows the top-view of the switching surface generated by sweeping the thrust magnitudes, where dark blue regions denote thrust ridges, whereas the light blue regions denote coast canyons (S < 0). At first glance, the contour plot seems to consists of three main thrust ridges (S > 0) with wide bases (for very low-thrust) that all ridges have a tapering trend up to the top of the curve as thrust magnitude increases.
This surface can be viewed in many ways, which reveals a number of interesting and illuminating facts. There is a significant number of changes in the topology of the switching surface that occur at the lower part of the plot, in the region of very low-thrust magnitudes. These changes are due to the local changes in the switching function and gradual passages of interesting local features through S = 0 as explained in the previous section.
The second region is associated with the medium thrust values with only four thrust ridges. Any given thrust value corresponds to a horizontal profile (slice) of this surface, which is the switch function for that particular maximum thrust level. As the thrust magnitude is increased, there is a slender dagger-like thrust ridge between the first two main thrust ridges that vanishes as the thrust is increased. Beyond this thrust magnitude, T > 2.2682 N, the whole family of optimal minimum-fuel trajectories are characterized by three thrust ridges and the time duration (width) of these thrust ridges keep shrinking as thrust magnitude increases. It is a trivial observation that these three thrust ridges are tending toward three impulsive thrusts for this case. Figure 10 shows an enlarged view of the lower thrust region so we can discuss the changes in the topology of the switching surface.
We mention without proof that the center-line location of the “persistent high thrust ridges” S = 0 contour is very insensitive to T/m and Isp as T becomes large. Figure 9 shows the 3D fundamental switching surface for the Earth-to-Mars problem. Note that an opposite-angle view is chosen so that the high (“mountainous”) region of the surface does not hide the interesting features. On the other hand, the difference of the values of the switching function at low- and high-thrust levels is sufficiently small that it is difficult to see the actual 3D features of the switching surface. Therefore, an enlarged view (S < 0.02) is shown in Fig. 9 for demonstration purposes so the low thrust details are more visible. The switching function of the fundamental minimum-thrust solution (with \(T_{{\min \limits }} = 0.1996\) N) is shown using solid blue line (only a portion of the fundamental minimum-thrust solution is visible in the enlarged view).
The switching surface S = 0 contour map is also shown in Fig. 8, where dark blue regions denote (S > 0) thrust ridges, whereas the light blue regions denote (S < 0) coast canyons. We draw your attention to a bifurcation that occurs at t = 12 TU and log(T) ≈− 0.587 N. This bifurcation phenomenon (“peninsula” form) results in the creation of a thrust ridge if the thrust is slightly increased. These thrust ridges are not due to a branching phenomenon of a core thrust ridge (see, for instance, the dagger-like thrust ridge near t = 4 TU, which appears near log(T) ≈− 0.39 N and vanishes around log(T) ≈ 0.39 N). We should mention logarithmic scales are used for the thrust axis to magnify the lower region of the switching surface where a number of significant changes occur. Another important point is the fact that beyond a critical thrust magnitude, all of the minimum-fuel trajectories consist of a final coast phase.
In other words, the right-most points of the last thrust ridge (see Fig. 10) define what we describe as an early-arrival boundary. Clearly, the early-arrival boundary has an interesting profile especially near the bifurcation point. Although this condition does not exist in the switching surface of the Earth-to-Mars problem, in general, we should anticipate the existence of late-departure boundaries that correspond to the existence of an initial coast phase.
We proceed by inspecting the solution and switching function of a number of particular slices of the switching surface. Figure 11 shows the switching function for minimum-thrust magnitude where the switching function is non-negative except for an individual point where it osculates (kisses) the S = 0 line.
Figure 12 shows the heliocentric trajectory of the minimum-thrust case. Vertical scale of Fig. 12 greatly exaggerates the out-of-plane motion to emphasize that the maneuver is fully three dimensional. It reveals the existence of a number of interesting phenomena. The first coast arc, obviously, is centered around the time instance of 10 TU. However, as the thrust magnitude increases a second coast appears close to 1.9 TU. Figures 13 and 14 show the switching function, thrust profile, and heliocentric trajectory for this critical thrust, T ≈ 0.203 N.
There are two interesting phenomena that occur as the thrust magnitude is increased. The first one is a bifurcation, i.e., creation of a new thrust arc. Note, that this is the third main thrust ridge among the total three thrust ridges that does not disappear as the thrust magnitude is increased. Unlike the other two main thrust ridges that have a wide root at the low thrust beginning, this thrust ridge is created at a higher thrust magnitude where a corner is easy to distinguish.
Figure 15 appears to show a relatively flat profile of S ≈ 0 over a finite time interval, which triggers an alarm for the possible presence of a singular arc. In fact, this bifurcation point can be characterized by confirming three identities: S = 0, \(\dot {S} = 0\), and \(\ddot {S} = 0\) over a small finite time interval. Figures 15 and 16 show the switching function, thrust profile and heliocentric trajectory for this unique critical thrust, T ≈ 0.2588 N.
Note that the thrust profile takes intermediate values over a finite but small time interval. This fact is directly related to the fact S = 0 over a finite time interval in the vicinity of 12 TU, i.e, we have detected the presence of a singular arc. This is the singu larity reported in [70], but not identified as a near-singular thrust arc. Insofar as is known, this is the first singular thrust arc found for an Earth-to-Mars low-thrust transfer. The singular control is characterized through an intermediate thrust level. We have verified that the optimal maneuver is, however, weakly sensitive to the intermediate thrust value, so this finding is mainly of academic interest in the current computations.
The second interesting phenomenon is that the terminal phase of flight becomes a pure ballistic coast arc. As the maximum thrust magnitude is increased above T ≈ 0.2588 N, the singular thrust arc takes on an off-bang-off optimal structure; however, beyond another critical thrust magnitude, T ≈ 0.3146 N, there is no final thrust arc at time tf. This is the thrust magnitude at which the switching function at the final time crosses S = 0 line and takes a negative value (thrust off). Figure 17 shows the corresponding switching function for this critical thrust value and Fig. 18 depicts the respective trajectory, where a small thrust vector exists at the end and it is about to vanish.
In other words, with a propulsion system that creates a higher thrust, it is possible to reduce the time of mission, and rendezvous with Mars at an earlier time than the chosen tf. This time coincides with the right-most point of the last thrust ridge created due to the bifurcation. The locus of these points is coined as “early-arrival” boundary. Had we formulated the optimal maneuver with free final time (but confined within a range), this early arrival time would have been found and along this free final time boundary, the Hamiltonian would vanish (since the Hamiltonian is not an explicit function of time in our formulation). Thus, the fixed initial and final time switching surface clearly reveals the boundaries for an infinite set of free initial and final time maneuvers.
A slight increment in the thrust magnitude permits a shift in the time of flight from tf to a point on the early-arrival boundary corresponding to that particular thrust magnitude. This point denotes the beginning of the early-arrival boundary (see Fig. 10). The physical interpretation of such a trajectory is that the spacecraft rendezvous with the Mars on its orbit at an earlier time and coasts with the Mars for the remainder of time until tf.
Note that, in this problem, the early-arrival boundary has its own profile. While the thrust magnitude is increased in a monotonic manner, the time of flight (governed by the profile of the early-arrival boundary) exhibits a decrease-increase-decrease profile. Therefore, the shortest time of flight in the lower part of the surface corresponds to the left-most point of this early-arrival boundary (see Fig. 10). A weak local minimum in the time of flight occurs in the vicinity of T ≈ 0.3758 N. This local minimum in the time of flight occurs in the lower-thrust region. For T > 0.44 N, the yellow line in Fig. 10 shows that the boundary monotonically shifts to the left of this local minimum. It is interesting that the analysis of the switching surface reveals transfer-type solutions while the original problem has been formulated as a rendezvous-type maneuver with a fixed time of flight.
By increasing the thrust magnitude a branching occurs in the middle thrust ridge and divides it into two thrust ridges, i.e., one small thrust ridge is created (branched out) to the left of the main middle thrust ridge. Figures 19 and 20 show the switching function, thrust profile, and heliocentric trajectory for this critical thrust, T ≈ 0.3775 N. At first glance, one might anticipate the possibility of another singular arc near t = 4.1 TU, however, a zoom on this region reveals distinct local zeros at the switch function. However, the width of the small (dagger-like) thrust ridge shrinks (to a double zero of S, \(\dot {S} = 0\) and \(\ddot {S} > 0\) at a point), where the thrust ridge eventually disappears at some specific value of thrust, T ≈ 2.2682 N. Figures 21 and 22 show the switching function, thrust profile, and heliocentric trajectory for this critical thrust, T ≈ 2.2682 N. Another important point worthy of mentioning is that this narrow thrust ridge lasts over a large range of thrust values, T ∈{0.3775,2.2682} N.
For thrust magnitudes beyond this critical magnitude, application of the traditional control smoothing methods (we tried both logarithmic [74] and hyperbolic tangent smoothing) encounter difficulties due to the fact that the length of the thrust ridges becomes so small that smoothing parameter, \(\rho _{{\min \limits }}\) has to take very small values to capture the optimal off-bang-off thrust profile; in fact, the typical continuation procedures become very sensitive to the changes in the continuation parameter. Therefore, the methodology outlined in [70] becomes extremely helpful for those very high-thrust regions of the switching surface. Beyond this critical thrust magnitude, T = 2.2682 N optimal trajectories consist of only three thrust ridges separated by coast canyons and the width of thrust ridges shrink as the thrust magnitude is increased.
On the other hand, the number of remaining thrust ridges can be viewed as an early indication of the number of impulses in a pure N-impulse solution, which corresponds to when the y axis goes to infinity in such a fashion that the thrust magnitude times delta time remains finite, i.e., T ×Δt ⇒Δv. For a finite thrust, the product of the thrust and the time duration is approximately the Δv of each impulse (see Eq. 17). Note that from the switching surface, the shortest transfer time coincides with the early arrival moment of the last impulse. Therefore, the impulsive solution, in general, is found to establish the lower limit of the time of flight.
The switching function at a high-trust magnitude (T ≈ 3 N) is used for generating the impulsive solution; we see S > 0 only in three small time intervals. On the other hand, the minimum-Δv 2-impulse solution can be obtained by solving the corresponding Lambert problem. The magnitude of the impulses at the initial and final time instants are Δv(t0) = 3.0157 km/s and Δv(tf) = 3.0318 km/s, respectively, which correspond to a solution with one revolution around the Sun, i.e., Nrev = 1. Table 2 summarizes the optimized solution and the minimum-Δv 2-impulse solution obtained by solving the Lambert problem.
Figure 23 shows the details of the minimum-Δv 3-impulse trajectory for the Earth-to-Mars problem. In all trajectory plots, initial and final locations correspond to the positions at the departure date, t0, and the arrival date, tf. The green arc denotes the last coast arc while on Mars orbit if the time of flight has been set to tf = 793 days. The optimal number of impulses for this problem is not large, but it serves as the prelude to study problems with a greater number of impulses.
The numbers indicate that the optimal minimum-Δv 3-impulse solution corresponds to a 7.2% reduction in the total Δv as compared to the minimum-Δv 2-impulse solution obtained by solving the Lambert problem. In addition, time of flight of the 3-impulse trajectory, tf = 711.72 days shows a 10.24% reduction compared to the time of flight of minimum-Δv 2-impulse solution, tf = 793 days. Note that the spacecraft rendezvous with Mars at the time instant of the third impulse (about 81.28 days earlier, i.e., nearly three months).
One may ask the following question: is it possible to recover the original 2-impulse solution by increasing thrust magnitude to infinity, \(T = \infty \)? The answer lies in the fact that optimality conditions have been guaranteed to establish that three thrust impulses are required to minimize propellant consumption. In other words, it is not possible to recover 2-impulse minimum-Δv solution (where the impulses are at prescribed initial and final times) since the 2-impulse solution is obviously not optimal. This is a known fact and is used for designing many-impulse solutions. In other words, the time history of the magnitude of the primer vector for the initial bi-impulsive solution violates the optimality conditions of Lawden; hence, it is possible, in principle, to improve the solution [45].
Interplanetary Rendezvous From Earth to Asteroid 1989ML
This problem is taken from [6] and Table. 3 gives the classical orbital elements of the asteroid 1989ML in which the epoch date is given as the Modified Julian Date (MJD).
The eccentricity and inclination of this asteroid make it a moderately difficult-to-reach target (see Table 3), due to ≈ 4.4∘ inclination. The following values are considered for the parameters of the spacecraft and its low-thrust propulsion system: m0 = 1000 kg, and Isp = 3000 s. The specified time of flight is tf − t0 = 560 days. The Earth position and velocity vectors at the departure time, t0 are r⊕ = [− 109310123.96,− 103935506.96,1736.32]⊤ km, v⊕ = [20.0414,− 21. 7003,0.000309]⊤ km/s, respectively. The position and velocity vectors of the asteroid 1989ML at the final time, tf are given as rT = [81709931.65,− 143042471.97, − 3344947.036]⊤ km, vT = [26.5207,14.3234,− 2.2390]⊤ km/s, respectively.
Figure 24 shows the fundamental switching surface for the Earth-to-1989ML problem and Fig. 25 shows an enlarged view of the surface for S < 0.2. The value of thrust is swept over \(T \in [T_{{\min \limits }},T_{{\max \limits }}]\), where \(T_{{\max \limits }} = 1.5\) N. Figure 26 shows the changes in \(T_{{\min \limits }}\) and final mass mf versus three different feasible values of Nrev; there is no feasible minimum-fuel solution for Nrev = 0 due to the adverse initial phasing, which requires more-than-available propellant. The fundamental minimum-thrust solution corresponds to \(N^{*}_{\text {rev}} = 1\). The fundamental minimum-thrust magnitude for the given BCs is \(T_{{\min \limits }} = 0.12659\) N. The thrust value is then swept in the given range, T ∈ [0.1266,1.5] N.
Figure 27 shows the switching surface S = 0 contour map, where it is easy to distinguish late-departure and early-arrival boundaries. In addition, the early-arrival boundary consists of two segments. The first part lies in the low thrust region. Then, the final coast phase is replaced by a final thrust ridge. Then, with a further increase in the thrust magnitude, the final phase of flight becomes a pure coast and the duration of the coast phase increases as the thrust magnitude is increased.
Clearly, to establish a rendezvous with the target body, a greater thrust value and a longer flight time are needed, which corresponds to the rightmost point on the last thrust ridge as it remains on the t = tf boundary. The peculiar profile of the early-arrival boundary is an indication of the difficulty encountered in reachability analysis in astrodynamics. Eventually, only three thrust ridges remain and become increasingly narrow for increasing thrust values. This indicates that the optimal number of impulses is three at the high-thrust limit. Table 4 summarizes the impulsive solutions and Fig. 28 shows the details of the minimum-Δv 3-impulse trajectory for the Earth-to-1989ML problem.
Interplanetary From Earth and Rendezvous With Asteroid Dionysus
Here, an interplanetary minimum-fuel mission from the Earth to asteroid Dionysus is studied, where the optimal solution is known from [71]. This asteroid is a fairly difficult and expensive target to reach due to the orbit’s high eccentricity and inclination values of 0.542 and 13.54 degrees, respectively. The BCs and parameters are chosen to match those reported in [71]. The solution to this problem consists of multiple revolutions around the Sun with intermediate thrust and coast arcs, so we can expect this family of orbit transfers to result in a very different switching surface than the one obtained in the Earth-to-Mars and Earth-to-1989ML transfer cases. The following values are considered for the parameters of the spacecraft and its low-thrust propulsion system: m0 = 4000 kg, and Isp = 3000 s.
Table 5 gives the classical orbital elements of the asteroid Dionysus in which the Epoch date is given as the Modified Julian Date (MJD).
The spacecraft departs from the Earth on December 23, 2012 and the mission time of flight is 3534 days. So we have a relatively large spacecraft and we wish to use moderate thrust values - it is not surprising that the time of flight will be thousands of days. Any low-thrust trajectory from the Earth to asteroid Dionysus must undergo large changes in eccentricity and inclination values and the optimal solutions with low thrust unsurprisingly requires several revolutions around the Sun. The position and velocity vectors of the Earth at the departure time are r⊕ = [− 3637871.081,147099798.784,− 2261.441]⊤ km, v⊕ = [− 30.265097,− 0.8486854,0.0000505]⊤ km/s, respectively.
Figure 29 shows the fundamental switching surface for the Earth-to-Dionysus problem over the given range of the thrust magnitudes. Unlike the previous two test cases, Figure 30 shows that the fundamental minimum-thrust solution, \(T_{{\min \limits }} = 0.1671\) N corresponds to an intermediate number of revolutions, \(N^{*}_{\text {rev}} = 5\) when \(T_{{\min \limits }} = 0.1673\) N. Figure 31 shows the switching surface S = 0 contour map for the Earth-to-Dionysus problem. The problem consists of six thrust ridges and the switching surface reveals the existence of late-departure and early-arrival boundaries. Figure 32 shows an envelope of the switching functions for the Earth-to-Dionysus problem.
Figure 33 shows the details of the minimum-Δv 6-impulse trajectory for the Earth-to-Dionysus problem. The first five impulses are applied at the perihelion of the intermediate osculating elliptical orbits, which coincides with the line of nodes of the orbits of the Earth and asteroid Dionysus. The final impulse is also applied at the osculating ascending node, which changes the inclination and energy of the spacecraft at the time of (early) rendezvous. The spacecraft arrives early and coasts with the asteroid on its orbit for nearly 501.808 days. Had we left tf in the optimal control formulation, we would have found that the free final time transversality condition (Hamiltonian = 0) would have converged to the free final time on the early-arrival boundary. A different color is used to denote the final coast phase. This shows that the time of flight can be reduced significantly, in this case, when impulsive maneuvers are performed.
Table 6 summaries the time and magnitude of the six impulses. Minimum-Δv Lambert solutions require significant amount of propellant and are not reported since they are 2-impulse solutions. This is a challenging problem for traditional methods used for generating impulsive trajectories since the number of impulses and the dimension of search space becomes large.
GTO-to-GEO Test Problem
The fourth test problem that we considered is an orbit raising problem from a geostationary transfer orbit (GTO) to a geostationary Earth orbit (GEO) with their parameters defined in Table 7. Sending a spacecraft to GEO is of practical use since its orbital period is identical to the Earth’s rotation period, which makes GEO an ideal orbit for placing communication satellites. It is assumed that the true anomaly of the spacecraft at the departure on the GTO is zero so that the initial position vector is aligned along the positive x-axis of the Earth-centered inertial equatorial frame. In addition, the target point lies along the negative x-axis, i.e., the x-y plane phase angle between the initial and final position vectors is 180 degrees. The initial and final position and velocity vectors are r0 = [6738.9,0.0,0.0]⊤ km, v0 = [0.0,10.0258,1.231]⊤ km/s, rT = [− 42165,0.0,0.0]⊤ km, vT = [0.0,− 3.0746,0.0]⊤ km/s.
In this problem, the initial mass of spacecraft is m0 = 100 kg, and the propulsion system is a low-thrust engine with a specific impulse of Isp = 3100 seconds. It is assumed that the constant time of flight is tf = 6 days. Figure 34 shows the changes in minimum-thrust and its associated final mass for different number of en route revolutions. The fundamental minimum-thrust solution corresponds to \(N^{*}_{\text {rev}} = 8\) with \(T_{{\min \limits }} = 0.4098\) N. Figure 35 shows the switching surface S = 0 contour map. The thrust is varied within a given range of \(T \in [T_{{\min \limits }},T_{{\max \limits }}]\) where \(T_{{\max \limits }} = 3.4\) N. Figure 36 shows the fundamental switching surface and its topology over the range of thrust magnitudes from an opposite view so that the details at the low-thrust region can be seen. The switching function associated with the fundamental minimum-thrust solution is shown by a solid blue line. This scenario is envisioned to provide a low-cost means of inserting multiple small spacecraft in GEO, by “dropping them off” on a GTO orbit and using electric propulsion in view of a much more expensive chemical propulsion to circularize them at apogee of the GTO transfer.
Similar to the Earth-to-Dionysus problem, there are a number of changes and topographic features that occur near the low-thrust region of the surface. There are eight thrust ridges that remain at high thrust magnitudes all of which correspond to apogee thrusting arcs. At the lower region of the switching surface, a very small needle-like thrust arc around t = 50 TU is a different feature.
Figures 37 and 38 show the switching function, thrust profile, and trajectory for the minimum-thrust solution \(T_{{\min \limits }} \approx 0.40985\) N. Although the overall topology of the switching function seems not to possess any significant difference from the previous switching function, the surface features in the right-most portion of Fig. 37 is indeed quite revealing after the explanation below is reviewed. Several of the distinct features of this switching function are due to the strength and nonlinearity of the gravitational field of the Earth compared to the previous interplanetary problems, especially due to the eccentricity of the GTO orbit.
One can quickly distinguish between two types of minima. Starting from left of the plot in Fig. 37, the first five minima are individual ones, whereas the rest of the switching function contains “tooth-like” double minima. The former indicate the existence of perigee thrusting that might be “believed” (incorrectly) to vanish by increasing the thrust value. These local minima correspond to the inner-most revolutions, where perigee thrusting becomes increasingly “inefficient” as the thrust value gets larger. The later tooth-like minima, however, represent a peculiar feature associated with them, i.e, there is a local maximum of S flanked by two local minima.
What do these tooth-like features point to? Actually, as we seek to answer this question, we see now there is more to this switching function than first meets the eyes in part because the unusual phenomena lie in the region below T ≈ 0.42 N, not shown in Fig. 35. The answer to what these features point to, lies in the types of the orbit and the regions where it is most efficient to apply thrust.
These features denote thrusting at the perigee of quasi-elliptical-shaped intermediate orbits and their characteristic symmetry (of the local minima around a local maximum) is associated with the fact that the thrusting occurs during perigee passages. These types of perigee thrusting arcs appear at higher perigee altitudes where perigee becomes less well-defined. We will show this through the numerical results, but, for now, it is possible to imagine that at some thrust magnitude, both local minima touch the S = 0 line at the same time. Then, a slight increase in the thrust magnitude implies that these local minima assume negative value, i.e., there is a short interval of thrusting surrounded by short coast arcs before and after the thrust arc. At some higher thrust magnitude, the local maximum will also cross S = 0 line and assumes a negative values, i.e., this perigee thrusting arc will vanish completely and there will be no local perigee thrust arc for large values of thrust.
Note, referring to Figs. 37 and 39, we see \(T_{{\min \limits }} = 0.4099\) N and we also see that there are four of these tooth-like features and each getting larger (in size) compared to the one on the left. Figure 40 shows the trajectory corresponding to the switching function shown in Fig. 39. This means that the perigee thrust arcs, at higher altitudes later in the spiral transfer, are those that will vanish last. This makes sense physically as the perigee thrust arcs that occur at higher altitudes are more efficient (lower-velocity, less intense gravity, and less gravity losses) compared to the low-altitude perigee thrust arcs (for a highly eccentric orbit). For instance, Figs. 41 and 42 show the switching function, thrust profile, and trajectory for the thrust magnitude, T ≈ 0.412 N at which the first tooth-like feature is about to touch S = 0 line. Note that two of the regular-formed perigee thrust arcs to its left have already disappeared (as thrust magnitude is increased). This fact can be seen clearly in the trajectory plot.
Figure 41 shows the enlarged view of the switching function and its associated thrust profile. Figure 42 shows the whole trajectory for the thrust magnitude, T ≈ 0.412 N at which there is a perigee thrust arc that is surrounded by two coast arcs. A blue rectangle on the trajectory plot shows this perigee thrust arc.
A very important aspect of these tooth-like local switch function features is that they may appear (created at other regular perigee thrust arcs) as the thrust magnitude is increased. For instance, the fact that at first, there are only four of these features (see Fig. 37) does not mean that their number will remain the same throughout the process of sweeping the thrust magnitudes. In other words, it is possible (for various BCs and system parameter variations) that even perigee thrust arcs at the inner-most revolutions also reveal such tooth-like features; it is due to the fact that thrust magnitude is increased to a level that the optimality conditions demand a short perigee thrusting structure.
The creation of these tooth-like thrust level features qualitatively denote of an impending (or a tendency towards) short perigee thrust and coast arcs. For instance, Fig. 43 shows the thrust magnitude, T = 0.42 N at which the previously believed-to-be regular perigee thrust arc is now modifying its shape to become a tooth-like feature! At this point, we have quantitative clues on why a small (needle-like) thrust ridge exists on the lower-left region of the switching surface (at t = 50 TU).
By inspecting Fig. 35, it is easy to confirm that the life of the osculating perigee thrust ridge, at t ≈ 500 TU, is shorter than this needle-like thrust at a lower osculating perigee altitude since the former vanishes at a lower magnitude of the thrust. Eventually, the needle-like perigee thrust ridge also vanishes. The next important phenomenon occurs at a thrust magnitude where the last thrust arc detaches from tf, i.e., the time of flight is dictated by the time of the last thrust ridge.
There is, however, another important distinction that is worthy of explanation. Unlike the previous optimal transfer example problems, the last presumably perigee thrust ridge remains, even for high thrust levels. In fact, the distinction between apogee and perigee thrust ridges is becoming mute at high altitudes because of the fact that the trajectory is becoming near-circular, i.e., e ≈ 0, to satisfy the final orbit BCs. This last very small thrust ridge acts as the final thrust kick to circularize the orbit. For the sake of brevity, the details of each of the above critical thrust magnitudes and their respective switching functions and trajectories are omitted. After all of the perigee thrust arcs vanish, the remaining thrust arcs denote pure apogee thrust arcs.
An interesting aspect of low-thrust fuel-optimal solutions for the GTO-to-GEO problem that include plane changes is that the apogee is initially raised to beyond that of the GEO orbit and a series of apogee and perigee thrust arcs are performed to achieve an optimal trajectory depending on the thrust magnitude. The results too confirm the fact that, significant portion of the thrust arcs at high thrust levels are performed near apogee to achieve simultaneous changes in the shape, and especially, the orientation of the orbit.
Figure 44 shows the time history of three osculating classical orbit elements along with the mass of the spacecraft for three different thrust values. Figure 45 shows the variation of the osculating apogee versus time for three thrust magnitudes. The non-monotonic increasing/decreasing nature of osculating apogee variations versus time is remarkable, especially for low thrust values. Note that the apogee is raised to above GEO altitude, where it is efficient to perform all plane-change maneuvers. It is also interesting to see that the apogee value undergoes relatively pronounced nonlinear oscillatory trend in the second half of the maneuver, where the apogee is not reduced monotonically, and this trend is amplified for lower thrust levels. In addition, the shortest transfer time belongs to a 8-impulse solution, where the impulses can be verified to occur centered around the first and last high-thrust ridges of Fig. 35.
All qualitative explanations are presented to shed some quantitative light as to why we see these results are based on the evident existence of these optimal solutions and our effort to interpret them through fundamental orbital mechanics principles. There is no direct way of guessing such subtle variations in the control structure; in fact, if this information was available and easy to predict, there was no need to solve an optimal control problem. However, the ultimate interpretation of the optimal maneuver results comes from the fact that they are based on the first principles. Nonetheless, it is useful to seek heuristic physical and geometrical understanding to appreciate the results. The main point we make here is that using the systematic analysis of the switching surface topography allows us to study the behavior of the family of optimal low-thrust maneuvers in more detail than has been heretofore feasible.
Table 8 summarizes the times and magnitudes of the corresponding minimum impulsive solution for the eight impulses. This problem is challenging where the conventional impulsive approaches encounter significant numerical difficulty in converging to the solution of such problems. Figure 46 shows the details of the minimum-Δv 8-impulse trajectory for the GTO-to-GEO problem, where all of the impulses are applied at the apogee of the intermediate elliptical orbits. These apogee Δv kicks, with judicious direction (primer vector) and magnitude are responsible for a simultaneous increase in the energy and change in the inclination. The impulses are applied very close to the descending node, which happens to be near apogee in this case.
Earth to Venus
This example orbit transfer is to an inner planet of the Solar system where minimum-fuel multiple-revolution trajectories from the Earth to planet Venus are investigated. The following values are considered for the parameters of the spacecraft and its low-thrust propulsion system: m0 = 3000 kg, and Isp = 3800 s. The time of flight is chosen as 3000 days. The position and velocity vectors of the Earth at the departure time are r⊕ = [145234429.88,35542120.342,− 249.986]⊤ km and v⊕ = [− 7.576,28.83077,0.00044765]⊤ km/s, respectively. The position and velocity vectors of Venus at the rendezvous time are r♀ = [− 49025885.0573, 95580637.6882,4137770.887]⊤ km and v♀ = [− 31.278,− 16.1786,1.5837]⊤ km/s, respectively.
Figure 47 shows the fundamental switching surface for the Earth-to-Venus problem along with the switching function of the fundamental minimum-thrust solution. Figure 48 shows that fundamental minimum-thrust solution, which consists of ten revolutions around the Sun, \(N^{*}_{\text {rev}} = 10\). Figure 49 shows the switching surface S = 0 contour map of the Earth-to-Venus problem where it is easy to recognize the existence of both late-departure and early-arrival boundaries. Once again, we notice some irregular features in the low-thrust region, but very regular behavior at high thrust values. There are eleven thrust ridges that remain for increasing thrust, approaching straight lines locating the times for impulsive thrusts.
Table 9 lists the times and magnitudes of the impulses for this many-revolution, many-impulse solution. The considered time of flight and number of revolutions is, of course, formidable. However, the outlined procedure and the proposed construct allows us to solve such challenging problems in a systematic manner.
Figure 50 shows the details of the minimum-Δv 11-impulse trajectory for the Earth-to-Venus problem where the impulses are split between the ascending and descending nodes of the line of nodes of the orbits of the Earth and Venus. The arc denoted by a different color denotes the separatix that acts as a boundary where the impulses switch from being applied only at aphelion to, remarkably, being applied only at perihelion passages.
Remarks On \(N^{*}_{\text {rev}}\) and Optimal Number of Impulses
In the above studied test cases, the fundamental switching surface is used for determining the number of impulses. The switching surface corresponding to the fundamental minimum-thrust solution is important since the extremal field map is guaranteed to be the minimum of minima for continuous-thrust minimum-fuel trajectories.
However, there is no guarantee that the impulsive solution obtained from the fundamental switching surface has the smallestΔv! For instance, for the Earth-to-Dionysus problem, we considered a high-thrust minimum-fuel solution for different number of revolutions, i.e., Nrev ∈{4,5,6,7} (case with Nrev = 5 is already considered) and used their associated switching function to generate local minimum Δv impulsive solutions. The results in Table 10 clearly indicate that there are multiple local minimum Δv solutions with (exact to seven digits) the same total required Δv, where it is also possible to have four, six and seven impulses. It is of vital interest to note that the solution with Nrev = 4 and only four impulses has the shortest time of flight, tf = 1840.314 days, which means that the spacecraft can reach the asteroid 4.637 years earlier with the same Δv. Obviously, this 4-impulse solution is the preferred solution due to the shorter time of flight.
Figures 51 and 52 show the trajectories associated with the impulsive solutions with four and seven impulses (the first and the third rows in Table 10). Figure 53 shows the impulsive solution with five impulses.
The results clearly indicate that there are multiple impulsive solutions with different number of impulses, whereas the total Δv is the same. In this problem, we conclude that four local extrema (quite distinct multi-impulse transfer orbits) give the identical minimizing total Δv, therefore we have answered Edelbaum’s question, but the answer is not unique! Note that each solution has a different number of impulses.
This curious result is approximately consistent with some planar cases we found in the literature [57, 59]. However, the results in our paper correspond to significantly more difficult multiple-revolution 3D cases and more precisely computed extremals, where it is shown that the exact same Δv (up to seven+ significant digits) exists with different number of impulses. Thus, we conclude Edelbaum’s question “How many impulses?” does not generally have a unique answer, if the total Δv is the only performance metric. However, there are generally secondary considerations, and it is obvious that the early arrival associated with Nrev = 4 would be appealing in many circumstances.
It must be noted, however, that minimum-Δvdoes not equate to minimum fuel for any specific rocket engine with a finite thrust level, a given initial mass, and a specified specific impulse. In fact, when the thrust level is specified, then the minimum fuel criterion, as will be shown herein, eliminates the lack of uniqueness associated with attempting to minimize Δv.
While the impulsive thrust is an idealized realization of maneuvers, it ignores mass variation associated with any actual rocket motor. Observe the earlier thrust arcs have to accelerate much larger mass than do the later thrust arcs, and this physical truth allows us to find the unique optimal solution from the point of view of maximizing the payload mass (or equivalently, minimizing the propellant consumption). While the impulsive idealization remains useful in early design studies, at some point, the mission design invariably must focus on optimality for a specific payload, propellant, and engine design (or a parametric range of designs).
Table 11 compares the final mass and rendezvous time of different minimum-fuel solutions for the Earth-to-Dionysus problem with different values of Nrev when two different thrust magnitudes are used, T = 1 N and T = 1.4 N. As we expect, at each particular thrust level, the largest final mass corresponds to a unique solution, in this case, the solution with Nrev = 5. Recall the Nrev = 5 is also the fundamental extremal, which also results in the smallest thrust level that can satisfy the final BCs. However, when Nrev = 4, an increase in the thrust magnitude by 0.4 Newtons reduces the rendezvous time significantly, whereas only 20 more kg of additional propellant is required (see Fig. 54 for the last thrust arc, which is a result of a bifurcation). This particular test case, shows the importance of the switching surfaces, to understand the infinite family of feasible optimal solutions. Figures 55 shows the switching surface for Nrev = 6. Figures 56, 57, 58 and 59 show the finite-thrust trajectories when T = 1 N for different values of Nrev. Figure 60 shows the switching surface for Nrev = 7.
A reasonable question to ask is: How does the number of revolutions change if the initial mass of the spacecraft is modified? In order to answer this question, the initial mass of the Earth-to-Dionysus problem is halved to m0 = 2000 kg. Then, the minimum-thrust algorithm is invoked to satisfy Eq. 20 for this problem. The results are plotted in Fig. 61 and show that the fundamental number of revolutions, \(N^{*}_{\text {rev}}\) does not change. In comparison with the results in Fig. 30, the minimum-thrust values have decreased in a near-linear manner.
To gain further confidence and perspective, we consider the corresponding extremals for other choices of Nrev. Figure 54 shows an enlarged view of the switching surface for the Earth-to-Dionysus problem with Nrev = 4. Note that there exists an unusual bifurcation at a frailly high thrust level that creates an “island” thrust ridge. The solid blue line in Fig. 54 corresponds to the switching function of the minimum-thrust for the particular number of revolutions and touches S = 0 at an individual point. Figure 55 shows the switching surface for the Earth-to-Dionysus problem with Nrev = 6. Figure 60 shows the switching surface for the Earth-to-Dionysus problem with Nrev = 7. Based on this result and other numerical simulations not reported in detail here, we are confident that the four extremals (Table 11) represent the non-unique answer to Edelbaum’s question (minimum total Δv), and the Nrev = 5 extremal (Table 11) represents the specific extremal that corresponds to the spacecraft design with an initial mass, m0 = 4000 kg, and Isp = 3000 s, and thrust of T = 1 N. The family of neighboring designs with variable thrust levels underly Figs. 29 and 32.
Table 12 also summarizes the impulsive solutions for the GTO-to-GEO problem for different values of Nrev. It shows that the solutions differ with negligible change in the total Δv. The case with Nrev = 9 consists of ten impulses: t1 = 0.220847, t2 = 0.72598, t3 = 1.16227, t4 = 1.704234, t5 = 2.26117, t6 = 2.80307, t7 = 3.53088, t8 = 4.247474, t9 = 5.02344, t10 = 5.53719. Δv1 = 0.18774, Δv2 = 0.00007, Δv3 = 0.40844, Δv4 = 0.04923, Δv5 = 0.058367, Δv6 = 0.203009, Δv7 = 0.175899, Δv8 = 0.12519, Δv9 = 0.29177, Δv10 = 0.005166. The total impulse is \({\sum }_{k=1}^{10} {\Delta } v_k = 1.50489\) km/s. In Table 12, once again, we have three extremals with negligible difference in required Δv, so we are free to invoke secondary criteria to choose a solution. Notice Nrev = 6 results in five impulses, but the fourth impulse is so small that we can consider it a 4-impulse maneuver. On the other hand, if we seek to minimize for a specific engine, we are led to select Nrev = 8 to be optimal because (Fig. 34) this maneuver belongs to the fundamental minimum-fuel surface of Fig. 36.
In the literature, it is hypothesized that for multiple-revolution non-coplanar cases, a large number of N impulses (with unknown times, impulse magnitudes, and directions) may become more convenient for optimal rendezvous [50, 59]. However, finding the optimal N impulses by NLP becomes a complex task, for large N, through traditional approaches as discussed in [46].
As documented in the examples above, the systematic approach of the current paper has been successful in solving problems in which the number of “optimal” impulses vary from N∗ = 3 up to N∗ = 11. The key point is that the high thrust limit of the family of extremals that underlie the switching surface approach with high precision the impulsive limit, so we have excellent velocity impulse starting iteratives and can know the time and number of impulses. We need only to refine the number of significant digits in the approximate starting solutions. The number of impulses is dictated by the high thrust asymptotic structure (number of surviving thrust ridges including those due to bifurcation) of the switching surface. According to the reported results and our experience, the optimal number of impulses depend strongly on the types of orbits, time of flight, angular phasing, and the orbits’ relative orientation. Furthermore, we find that the minimum Δv frequently can be achieved by more than one set of impulses. Thus, again, we emphasize the answer to Edelbaum’s question is not unique, but answering this question usually reveals attractive solutions when secondary criteria are considered.
Our studies indicate that location and number of solution bifurcations are important features of the switch surface at critical thrust values and lead to the creation of thrust ridges that alter the number of persistent optimal thrust ridges (in the switching function), which affects the number of optimal thrust arcs. These features are difficult to predict, but emerge from the creation of switching surface. In our numerical examples, a thrust arc, which is created due to a bifurcation at a critical value of the thrust is found to be persistent (i.e., does not vanish) with increasing maximum thrust specification. We digress briefly to make qualitative statements inferred from our analysis on the physics and numerics in the problems studied to date, using the switching surfaces as the focal point for analyzing families of extremals. We have found that the bifurcations of the switching surfaces are frequently associated with regions where either the accelerations due to the gravitational physical forces are nearly in balance (for example near L1 point in the restricted three-body problem), or in regions where the local “effectiveness” of the optimal controls is low, in that the local variations of the thrust have a small effect on the performance index and the BCs (see Earth-to-Mars problem).
Our hypothesis is that, with all BCs fixed and for a fixed takeoff and arrival time, the optimal number of impulses N∗, the optimal number of revolutions, \(N^{*}_{\text {rev}}\), associated with the fundamental minimum-thrust solution, and the number of bifurcations, Nbifur, are all properties of the optimal switching surface associated with the feasible values for Nrev; these features are discoverable by actually generating the switching surface by increasing the thrust value from \(T_{{\min \limits }}\) to find the high thrust value asymptotic behavior. Table 13 summarizes the results of the five test cases studied in this paper.
While we list a specific value for N∗ in Table 13, the minimum Δv is generally achieved by several values of N and the listed value is associated with one of several minimizing extremals. To choose a specific N and the associated extremal, we can invoke a secondary consideration such as minimum fuel (for any chosen finite thrust engine and propellant Isp), or time of arrival when the final thrust occurs and rendezvous is achieved at a time before the specified tf. In this table, we chose N∗ that corresponds to the fundamental minimum-fuel solution for a family of constant thrust engine designs, with \(T_{{\min \limits }} < T < T_{{\max \limits }}\).
Importantly, the possibility of terminal impulses is governed by the prescribed time of flight. As a result, the optimal number of impulses depends also on the departure and arrival times, which are in turn associated with the angular phase in the initial and target orbits. Note that the optimal number of revolutions itself depends on the time of flight, BCs, and the ratio of the acceleration due to the propulsion to that due to the central body. We conclude that a generally applicable, explicit, and unique algebraic answer to Edelbaum’s question does not exist. We have conclusively shown that the answer is generally not unique (frequently a set containing several local extremals with different number of impulses been shown to have the same total Δv). At some point in the mission design process we always have to consider specific propulsion systems and abandon the idealized notion that Δv should be minimized and instead recognize that the minimization of fuel consumed associated with the specific finite thrust engine (or a set of possible designs) is a more meaningful index, we are generally led to the true optimal trajectory of interest (or a specific family of trajectories when considering a family of spacecraft/engine designs).
As a consequence, we believe that Edelbaum’s question should be more specific and refined to read: “For a given spacecraft initial mass and engine with a specified Isp and maximum thrust, what is the optimal sequence of thrusts and coasts to minimize fuel consumed when transferring from orbit A to orbit B?” We have developed and demonstrated a method that answers this more specific question, and in the process, we can identify a set of extremals that minimize Δv.
On the other hand, the results clearly indicate that the high-thrust short arcs of thrusting, as well as limiting case of impulses, are predominantly applied near the peripasis/apoapsis and/or the ascending or descending nodes, as might be anticipated for orbit raising/lowering and changes in the inclination [108]. We also note that the number, time, direction, and magnitude of impulses are accurately approximated by the high thrust limits of the corresponding minimum-fuel switching surfaces. So in that sense, we have established a means to answer, even if not uniquely, the original minimum-impulsive velocity maneuver question raised by Edelbaum in 1967.
The impulsive idealization has always served as a first step in assessing mission feasibility and to establish candidate approximate trajectories. The methodology of this paper can be used to establish multiple minimum impulsive velocity extremals. More importantly, we provide the means to establish an associated family of minimum-fuel extremals, considering a specific spacecraft and a family of engine designs. For a maximum thrust specification, these extremal switching surfaces all approach the impulsive limit.
Based on the results, we have the following conjecture: for rendezvous-type, fixed-time, minimum-fuel trajectories in a Newtonian gravitational field, i.e., 1/r2, there is at most one local extremal for each integer specification of the number of en-route revolutionsNrev ∈{0,1,2,⋯ } made during the transfer orbit.
Choice of Coordinates/Elements And Its Impact On The Switching Surfaces
It is important to emphasize that switching surfaces are a concatenation (or an ensemble) of switching functions as the parameter of interest is swept over the defined range. Thus, switching functions are the building blocks that form the topology of the switching surfaces. The underlying optimal state and co-state trajectories that minimize fuel consumption constitute an extremal field map (actually a hyper-surface, in this case, of dimension 14).
On the other hand, these switching functions are associated with solutions that are guaranteed to be extremals since they are systematically generated to satisfy the Pontryagin’s necessary conditions. The optimal thrust is an independent identity and described as a physical vector function associated with each optimal trajectory in the extremal field map. Irrespective of the chosen set of coordinates or elements used for modeling the motion of spacecraft, the thrusting regions of space are invariant under coordinate transformation. This means that the switching surfaces are independent of the choice of coordinates. Furthermore, each extremal trajectory for any choice of coordinates can be mapped to another coordinate choice through a coordinate transformation applied at each time instant.
On the other hand, as explored in [71, 94], it is known that the choice of coordinates and/or elements is important when it comes to efficiently solving TPBVPs. Set of Cartesian coordinates is shown to produce sub-optimal solutions. For instance, for the same boundary conditions and with a fixed maximum thrust magnitude of T = 0.32 N, the problem of minimum-fuel trajectories from Earth to asteroid Dionysus is studied in [71] when the EOM are written in terms of Cartesian coordinates and MEEs. 50 TPBVPs are solved where the solution procedure involves a random initialization of the unknown initial elements of the co-state vector. A similar continuation procedure is used for solving each TPBVP (but HTS method is used for control smoothing); only 43 of the trials converged and revealed the existence of seven levels of extremal solutions that satisfy the optimality conditions, where six of these levels correspond to sub-optimal solutions. Figure 62 shows these solution levels (values of the final mass).
There are actually two main reasons for obtaining different local sub-optimal solutions. The first one is related to how TPBVPs are typically formulated when Cartesian coordinates are used. Unlike the other choices of coordinates or elements, Nrev does not appear explicitly as one of the parameters in the formulation of the TPBVP when Cartesian coordinates are used. The terminal constraints are on the position and velocity coordinates, and possibly the final value of the co-state associated with the mass, λm(tf). This can be interpreted as a positive aspect of using Cartesian coordinates as we usually do not know the correct value of the number of revolutions. At the same time, this freedom has a negative consequence because failure to fix Nrev is the main cause of getting sub-optimal solutions (the number of revolutions may be known from prior studies). Thus, this freedom can be interpreted to be positive and negative simultaneously. For any systematic study, the mentioned freedom has to be harnessed.
To sweep out a family of extremals for each Nrev, however, any approach that does not allow us to constrain Nrev is, at least, inconvenient. For minimum-fuel problems with a large time of flight, the optimal trajectories have a tendency to get close to the central body (Sun in our problem) to utilize its gravitational potential to early on gain kinetic energy. Efficient increase in the energy of orbits is achieved at perihelion passages of elliptical orbits, where the velocity takes its maximum value. In other words, for some optimal trajectories, the optimal solution initially dives toward the central body. This is a characteristic of multi-revolution trajectories and impacts the solution when the number of revolutions are significantly large. But, for problems with relatively small number of revolutions, this is frequently encountered. Figures 63 and 64 show the profile of the magnitude of the radius vector, r = ∥r∥, versus time of flight for representative solutions of all seven levels. Clearly, those solutions with a higher number of revolutions (compared to the optimal solution with the lowest number of revolutions) require more fuel. The optimal solution makes only five revolutions around the Sun in this case, whereas the worst sub-optimal solution makes eleven revolutions around the Sun. Figure 64 shows clearly what we stated earlier, where the majority of the time of flight is spent at lower radius, and closer to the Sun. Our intent is not to perform an extensive analysis on the number of levels of sub-optimal solutions, but these results indicate that formulation of minimum-fuel optimal control problems using Cartesian coordinates will, most of the time, result in convergence to sub-optimal solutions.
The existence of these sub-optimal solutions (associated with Nrev en route revolutions) is a direct consequence of large time of flight and thrust acceleration magnitude and the additional freedom to make as many revolutions as possible, within the given time. Figures 65, 66, 67 and 68 show trajectories and thrust profiles of the four sub-optimal solutions.
GTO To A Halo Orbit Around L1
This example illustrates how to design an optimal low-thrust transfer from a GTO to an L1 halo orbit in the restricted three-body problem associated with the Earth-Moon system. The EOM are given in [99]. The departure of the spacecraft is from the perigee of an elliptical orbit with perigee × apogee altitude ratio of 400 × 35,864 km (GTO). The spacecraft with an initial mass of m0 = 1500 kg uses an electric engine with a specific impulse of Isp = 3000 seconds.
The target orbit is a halo orbit with an out-of-plane amplitude of 8000 km [109]. Figure 69 shows the halo orbit and the point on orbit at which the spacecraft will enter the orbit. The parameters used in numerical simulations are : g0 = 9.80665 (m/s2), Length unit (LU) = 3.84405000 × 105 (km), Time unit (TU) = 3.75676967 × 105 (s), Velocity unit (VU) = 1.02323281 (km/s), μ = 1.21506683 × 10− 2 (LU3/TU2). LU is actually the reference semi-major axis of the Moon’s orbit relative to the Earth (the distance between Earth and Moon).
This problem is more difficult compared to the previous cases where the dynamics were simpler. For the three-body dynamical models, convergence is also found to be more difficult to achieve using a finite difference approach for calculating sensitivities. Therefore, the STM method (with HTS) is used for the sensitivities according to the procedure described in [71]. When integrating the state and co-state equations, we make use of HTS to enhance the convergence through a continuation procedure.
Finding the minimum-thrust solution is the first step for constructing the switching surface. Figure 70 shows the switching surface for Nrev = 6. However, the minimum-thrust solution is not unique, which is an important factor. For instance, Figs. 71 and 72 show the switching function, thrust profile, and trajectory for a minimum-thrust solution with \(T_{{\min \limits }} \approx 9.675\) N with Nrev = 6. Clearly, the switching function is positive along the whole trajectory. However, this is not the fundamental minimum-thrust solution since the number of revolutions are greater than the global optimal solution. If this local extremal solution is considered as the base solution and the thrust magnitude is swept, Fig. 70 shows the resulting switching surface for T ∈ [9.675,20] N with Nrev = 6. Note that when Cartesian elements are used for formulating the TPBVPs, the number of revolutions does not appear explicitly. There appears to be seven main thrust ridges that remain at high thrust levels. There is a late-departure boundary, whereas the last thrust ridge is attached to the final arrival time, which indicates that there is no early-arrival boundary.
However, the global minimum-thrust solution to this problem has been found to correspond to \(T_{{\min \limits }} \approx 8.141\) N with Nrev = 5. Figures 73 and 74 show the switching function, thrust profile, and trajectory for the fundamental minimum-thrust solution with \(T_{{\min \limits }} \approx 8.141\) N. It is interesting to note that in Fig. 71, the profile of the switching function has a different behavior during the time interval t ∈ [0.5,1] TU compared to the smoother one, with two fewer maxima, in Fig. 73.
Figure 75 shows the resulting optimal switching surface when T ∈ [8.141,15] N is considered. There appears to be only seven main thrust ridges that remain at “high” thrust levels. The boundary conditions result in a switching surface without early-arrival or later-departure boundaries. Note that the thrust is not necessarily high enough as the width of the thrust ridges are still large.
Figure 76 shows the optimal switching surface for T ∈ [8.141,40] N when \(\rho _{{\min \limits }} = 9.15 \times 10^{-6}\). Note that in practice, a relatively small value is chosen for the final smoothing parameter in order to facilitate the higher precision generation of the switching surface. For particular regions of interest, it is possible to use a smaller value for \(\rho _{{\min \limits }}\).
There is an interesting bifurcation phenomenon at T ≈ 19 N, see Fig. 76. The nature of this bifurcation point is completely different from the previously shown bifurcations in the two-body dynamics (where a corner point was the beginning point of the bifurcation and the beginning of the thrust arc was attached to a thrust ridge, see Fig. 10). In addition, in the two-body dynamics \(\ddot {S} >0\) in the vicinity of the bifurcation point, whereas here the sign of \(\ddot {S}\) changes near the higher order zero: \(S=\dot {S}=\ddot {S}=0\) at the bifurcation; hence, this bifurcation appears in the middle of a coast canyon. Clearly, the creation of this thrust ridge has also visibly correlated to sharp features on the two closest thrust ridges to its right and left, where two “corner points” are noticeable and their time duration (width) shrinking rate with increasing thrust is thereafter increased.
Figures 77 and 78 show the switching function and the trajectory for this bifurcation point. In order to be able to isolate these shorter thrust arcs more accurately, we set \(\rho _{{\min \limits }} = 1.0 \times 10^{-6}\), which shows a small increase in the thrust magnitude at which this bifurcation occurs. The enlarged part shows the time when the switching function (blue line) nearly touches the S = 0 line, whereas the red line shows the derivative of the switching function with respect to time, \(\dot {S}\). Figure 78 shows the trajectory where the point of the creation of the new thrust arc is shown. The final phase of the flight consists of a thrust arc, where the trajectory undergoes a relatively sharp turn and reaches the entry point to the L1 orbit with a final mass, mf = 1394.85 kg. The trajectory looks quite different when plotted in a non-rotating frame as is shown in Fig. 79, where the blue line denotes the path made by the entry point along the time of flight. It also shows a 3D view of the trajectory in which the out-of-plane motion is noticeable.
Remarks On Reachability Analysis
One of the fundamental challenges in astrodynamics is to determine the time-specific reachability of an object (e.g., planet, asteroid, spacecraft or debris) given the time of flight and specifications of the propulsion system. In almost all of the space targeting and space situational awareness problems, information regarding the reachability of an object is deemed invaluable since such information can be used to rule out unreachable targets immediately during the optimization process or for other purposes.
One key point in the above developments is that the optimal switching surface is just the “top layer” of an extremal field map with a wealth of additional information. Each profile on the surface corresponds to a particular minimum-fuel optimal transfer trajectory (states, co-states, and optimal thrust direction). These layers of extremal solution information can be plotted/stored/interpolated/analyzed for an infinity of uses, e.g., reachability analysis purposes.
In all of the considered cases, inspection of the switching surfaces shows that impulsive solutions set the lower theoretical limits on both time of flight, (ta − td) (where td and ta are departure and arrival times, respectively) and minimum-Δv. Note that the initial and final times, t0 and tf, are fixed, but the departure and arrival times could be different and is governed by the profile of late-departure and early-arrival curves. The minimum-Δv is related to the propellant ratio through Tsiolkovsky rocket equation, mf = m0 × e(−Δv/c). The theoretical shortest time of flight is the time difference between the last impulse and the first impulse. On the other hand, these two time instants belong to the late-departure and early-arrival boundaries we have found for the cases that these two impulses are not applied at the initial and final times, and when \(T \rightarrow \infty \). The fact that these late-departure and early-arrival boundaries are an attribute of the optimal switching surface is obviously important.
For sufficiently short specified time of flight and high thrust, we can expect the optimal \(N^{*}_{\text {rev}}\) will be found to be 0 (a fraction of the first orbit). For all finite thrust cases, sweeping through Nrev will lead to switching surfaces, which are analogous to Figs. 27 and 49. For each Nrev, the shape of these early arrival or late departure boundaries can be expressed as a function of the sweep parameter (thrust in this case) as tEA = tEA(T) and tLD = tLD(T), where tEA and tLD denote the early-arrival and the late-departure times, respectively. The shortest time associated with a minimum-fuel finite-thrust trajectory can be evaluated as tEA − tLD. Moreover, it is possible to use the final mass and define a parameter to represent the mass ratio on the early-arrival boundary as
where mEA is the final mass of the spacecraft at the instant of rendezvous with the target (i.e., on the early-arrival boundary).
The knowledge of optimal thrust magnitude during minimum-time solutions is obviously very useful information. It is known that for minimum-time low-thrust trajectories, thrust is always “On”, which translates directly into the required mass through the constant mass flow rate relation \(m_{f} = m_{0} - \frac {T}{c} (t_{f}-t_{0})\). This minimum-fuel reachability information can be used to rule out any target simply due to the lack of sufficient propellant. However, for higher thrust magnitudes, Γ has utility for reachability analysis. Recognition of the existence of local extrema proves to be crucial since the information on the minimum-fuel switching surface that corresponds to \(N_{\text {rev}}^{*}\) is needed for any analysis. Note that for finite-thrust analysis, there is always one unique number of en-route revolutions, \(N_{\text {rev}}^{*}\), that corresponds to the least consumption of fuel. Thus we specify the number (Nrev) of en route revolutions and solve the minimum-fuel problem for each and determine the minimum of the minima. Having this pivotal extremal, we can then construct the switching surface over the thrust range of interest and have visibility of all neighboring extremals when engaged in mission design analysis reachability. The other switching surfaces (with different values for Nrev) are associated with sub-optimal local extremal solutions and will definitely require more fuel and can usually be ignored.
In some settings, one or more of these local optimal trajectories may be considered if other, secondary optimality or feasibility constraints (not specifically included in trajectory optimization) are invoked. For example, if the global extremal that resulted from the above logic passed too close to the Earth (or the Sun in interplanetary trajectories) en route to the target orbit, then obviously such an un-specified constraint (in the original OCP formulation) would be obvious and a filtering can be invoked to rule out such physically inadmissible solutions. Such spurious solutions are regrettably encountered occasionally when optimal control theory is applied, because in our quest for simplicity of the formulation, not all conceivable physical inequality constraints are considered, until we see that a ridiculous extremal results. Sometimes such spurious solution indicates a need to re-formulate the OCP, other times, we can see why the inadmissible extremal simply be deleted in favor of the second best local extremal that satisfies all constraints. For constrained OCP, direct optimization methods will provide more flexibility.
A key point is that if we have enough propulsion capability, a 2-impulse maneuver could satisfy the BCs in a near zero time of flight. On the other hand, if the maximum velocity is bounded by the escape speed, then, an Nrev = 0 2-impulse Lambert solution would be the practical min-time maneuver. So, reachability is a function of t0, tf − t0, maximum thrust, T, and phasing. Optimal Nrev likely depends on most of these as well. All of these decisive factors can be explored one or two parameters at a time. We are providing an approach for such explorations of extremal solutions.
Computational Effort
In this section, the computational effort associated with solving the underlying TPBVPs is discussed. The proposed methodology relies on solving TPBVPs to generate switching functions, which, as thrust is swept, gives rise to neighboring extremals that underlie the optimal switching surface. The first step has to do with the determination of the minimum-thrust solution for each Nrev. The second step, deals with generating the corresponding switching surfaces. A third step, if one desires to determine the idealized impulsive trajectories, is to perform N-impulse optimization.
Solving TPBVPs efficiently and reliably in the presence of high nonlinearity, and high dimensionality is a challenging task [110, 111] and there are several approaches to enhance convergence when discontinuous inputs are forcing the differential equations [71]. Our experience is that for a majority of switching control type fuel-optimal trajectory cases, the HTS is quite helpful and alleviates a number of difficulties associated with solving the TPBVPs [96, 112]. On the other hand, if our goal is to determine a set of impulsive solutions, in order to generate the results similar to those reported in Table 10, it is not (usually) required to sweep over the thrust magnitudes, in a dense incremental fashion. Instead, it is possible to choose a relatively large thrust level and solve the corresponding minimum-fuel TPBVP directly. Even though, we use the HTS, only the final large-thrust trajectory needs to approach the very sharp control switches. As mentioned earlier, the impulsive solution reveals itself at high-thrust levels encountered in the family of optimal trajectory problems under consideration.
This strategy has been adopted to generate the results in Table 10. For the Earth-to-Dionysus problem, the computation wall-time to obtain an impulsive solution using MATLAB and running Windows operating system is usually only 30 to 60 seconds. This time takes into account the time it takes to solve the family of minimum-thrust problem according to the methodology outlined in in this paper while relying on HTS, converging with a large value of thrust that solves the corresponding minimum-fuel TPBVP, including the optimal switching function, and the time it takes to solve the N-impulse optimization problem. The N-impulse optimization is the least computationally demanding part of the overall scheme. Of course, harder problems with highly nonlinear trajectories and more impulses require more computation time. The GTO-to-GEO orbit transfer problem proved to be the most computationally demanding studied case when two-body dynamics was considered. Generating the results of this paper, including the GTO-to-GEO impulsive solutions, took several minutes. Generation of the switching surfaces associated with the trajectories in the restricted three-body dynamics was also computationally demanding.
All computations were performed on a Core i7 desktop machine with two 3.4-GHz processors and 16 GB of RAM and the propagation of the differential equations was achieved using a compiled version of MATLAB’s ode45 function to speed up the numerical simulations. The absolute and relative integration convergence tolerances were set to 1.0 × 10− 10 in all simulations. For MATLAB’s fmincon optimizer, the function and constraint tolerances were set to TolFun = 10 × 10− 6 and TolCon = 10 × 10− 7, respectively.
Conclusions
We used indirect methods of optimal control theory along with Lawden’s primer vector theory to introduce illuminating switching surfaces for large and low-thrust minimum-fuel trajectories. These surfaces establish the connection between impulsive and continuous-thrust trajectories. The impulsive limits tell us “how many impulses” are associated with each application of Nrev, the number of revolutions.
We have shown that there exists a fundamental minimum-thrust solution that plays a pivotal role in determining fundamental switching surface, and an associated \(N^{*}_{\text {rev}}\), which in turn reveals the “optimal” number of thrust arcs for any finite specification of maximum thrust. The fundamental switching surface is generated by a homotopic sweep of the maximum thrust away from the minimum-thrust extremal among all minimum-thrust solutions, considering all feasible multi-revolution solutions. This fundamental minimum-thrust solution is used to construct the switching surfaces that reveal the number and approximate time, direction, and magnitudes of the impulses associated with the optimal impulsive solution as a by-product. A number of optimal orbit transfers with different number of revolutions for the fundamental extremal are studied and the corresponding impulsive solution with as many as eleven impulses are found, which demonstrate the capability of the proposed construct. According to these results and our experience, the optimal number of thrusting arcs at high thrust levels depend strongly on the size and shape of the initial and final orbits, time of flight, angular phasing and the orbits’ relative orientation.
While the switching surface can be generated for very high thrust values to approach with arbitrary precision the impulsive limit, we find that after the elapsed thrust-on time of all short thrust arcs is less than some tolerance (e.g., < 0.001 × (time of flight)) then the impulsive approximation can be invoked with a good accuracy. A direct method can then be initiated accurately to converge to the impulsive solution and satisfy the force model and all boundary conditions to a high precision. It is vital to note that when the mass variation is accounted for, considering any real propulsion system, that minimizing Δv does not minimize fuel consumption (or maximize payload mass for a given engine). We showed two examples where minimizing Δv led to multiple distinct local extremals, with identical minimum Δv values; the local extremals Δv matched to 7 digits. Only one of these extremals belonged to the fundamental switching surface that minimizes fuel consumption. So, we conclude that Edelbaum’s question does not have a unique answer, in general. However, invoking the minimum propellant consumption for a specific engine model gives a unique extremal.
We showed that the other secondary criteria, such as the time of flight (for cases with early arrival) can also be invoked, for the same total Δv and modest fuel increases. The results clearly indicate the intuitively reasonable truth that the optimal short thrusting arcs, as well as, the limiting case of impulses are predominantly applied near the peripasis/apoapsis and/or the ascending or descending nodes, as might be anticipated for orbit raising/lowering and changes in inclination.
Finally, we note that the switching surfaces provide a unified means for optimizing low thrust, high thrust, and impulsive maneuvers, and enable important global insights into mission design. In principle, the methodology proposed in this paper can be pursued for many engineering systems if/when a systematic study of the resulting switching surfaces are performed by sweeping various important parameters of interest.
Abbreviations
- f :
-
vector function of unforced dynamics
- \(\mathbb {B}\) :
-
control influence matrix
- c = Ispg0 :
-
exhaust velocity, m/s
- g 0 :
-
Earth gravitational acceleration, m/s2
- h :
-
specific angular momentum vector, km2/s
- H :
-
Hamiltonian
- I sp :
-
specific impulse, s
- J :
-
cost functional
- m :
-
mass, kg
- N :
-
number of impulses
- N rev :
-
number of revolutions
- N bifr :
-
number of bifurcations
- p :
-
primer vector
- r :
-
position vector, km
- S :
-
switching function
- t :
-
time, s
- T :
-
thrust magnitude, N
- \(T_{{\min \limits }}\) :
-
critical minimum-thrust magnitude, N
- v :
-
velocity vector, km/s
- x :
-
state vector
- Δt :
-
time interval, s
- Δv :
-
impulse magnitude, km/s
- ρ :
-
smoothing parameter
- u :
-
control vector
- α :
-
unit direction vector of thrust
- δ :
-
engine throttle input
- ψ :
-
vector of terminal constraints
- λ :
-
co-state vector associated with states
- λ m :
-
co-state associated with mass
- μ :
-
gravitational parameter, km3/s2
- 0:
-
initial
- f:
-
final
- i :
-
impulse
- ⊕:
-
Earth
- ♂:
-
Mars
- T:
-
target body
- ♀:
-
Venus
- *:
-
optimal
References
Petropoulos, A.E., Longuski, J.M.: Shape-based algorithm for the automated design of low-thrust, gravity assist trajectories. J. Spacecr. Rocket. 41(5), 787–796 (2004). https://doi.org/10.2514/1.13095
Taheri, E., Abdelkhalik, O.: Shape based approximation of constrained low-thrust space trajectories using Fourier series. J. Spacecr. Rocket. 49(3), 535–546 (2012). https://doi.org/10.2514/1.58789
Zuiani, F., Vasile, M., Palmas, A., Avanzini, G.: Direct transcription of low-thrust trajectories with finite trajectory elements. Acta Astronaut. 72, 108–120 (2012). https://doi.org/10.1016/j.actaastro.2011.09.011
Avanzini, G., Palmas, A., Vellutini, E.: Solution of low-thrust lambert problem with perturbative expansions of equinoctial elements. J. Guid. Control Dynam. 38(9), 1585–1601 (2015). https://doi.org/10.2514/1.G001018
Kluever, C.A.: Designing transfers to geostationary orbit using combined Chemical–Electric propulsion. J. Spacecr. Rocket. 52(4), 1144–1151 (2015). https://doi.org/10.2514/1.A33259
Taheri, E., Abdelkhalik, O.: Initial three-dimensional low-thrust trajectory design. Adv. Space Res. 57(3), 889–903 (2016). https://doi.org/10.1016/j.asr.2015.11.034
Zeng, K., Geng, Y., Wu, B.: Shape-based analytic safe trajectory design for spacecraft equipped with low-thrust engines. Aerosp. Sci. Technol. 62, 87–97 (2017). https://doi.org/10.1016/j.ast.2016.12.006
Roa, J., Peláez, J., Senent, J.: New analytic solution with continuous thrust: generalized logarithmic spirals. J. Guid. Control Dynam. 39(10), 2336–2351 (2016). https://doi.org/10.2514/1.G000341
Taheri, E., Kolmanovsky, I., Atkins, E.: Shaping low-thrust trajectories with thrust-handling feature. Adv. Space Res. 61, 879–890 (2018). https://doi.org/10.1016/j.asr.2017.11.006
Longuski, J.M., Williams, S.N.: Automated design of gravity-assist trajectories to Mars and the outer planets. Celest. Mech. Dyn. Astron. 52(3), 207–220 (1991). https://doi.org/10.1007/BF00048484
Izzo, D., Becerra, V.M., Myatt, D.R., Nasuto, S.J., Bishop, J.M.: Search space pruning and global optimisation of multiple gravity assist spacecraft trajectories. J. Glob. Optim. 38(2), 283–296 (2007). https://doi.org/10.1007/s10898--006--9106--0
Olympio, J.T., Izzo, D.: Designing optimal multi-gravity-assist trajectories with free number of impulses. In: International Symposium on Space Flights Dynamics, Toulouse, France. ESA ESTEC (2009)
Vasile, M. , Ceriotti, M.: 8 incremental techniques for global space trajectory design. Spacecraft Trajectory Optimization, edited by B. Conway 29, 202–237 (2010). https://doi.org/10.1017/CBO9780511778025
Englander, J.A., Conway, B.A., Williams, T.: Automated mission planning via evolutionary algorithms. J. Guid. Control Dynam. 35(6), 1878–1887 (2012). https://doi.org/10.2514/1.54101
Abdelkhalik, O., Gad, A.: Dynamic-size multiple populations genetic algorithm for multigravity-assist trajectory optimization. J. Guid. Control Dynam. 35(2), 520–529 (2012). https://doi.org/10.2514/1.54330
Chilan, C.M., Conway, B.A.: Automated design of multiphase space missions using hybrid optimal control. J. Guid. Control Dynam. 36(5), 1410–1424 (2013)
Ellison, D.H., Conway, B.A., Englander, J.A., Ozimek, M.T.: Analytic gradient computation for Bounded-Impulse trajectory models using Two-Sided shooting. J. Guid. Control Dynam. 41(7), 1449–1462 (2018). https://doi.org/10.2514/1.G003077
Landau, D.: Efficient maneuver placement for automated trajectory design. J. Guid. Control Dynam. 41(7), 1531–1541 (2018). https://doi.org/10.2514/1.G003172
Edelbaum, T.N.: How many impulses?. Astronautics and Aeronautics 5(11), 64–69 (1967). https://doi.org/10.2514/6.1966--7
Sims, J.A., Flanagan, S.N.: Preliminary design of low-thrust interplanetary missions. In: AAS/AIAA Astrodynamics Specialist Conference AAS Paper 99–338, Girdwood, Alaska (1997)
Gooding, R.: A procedure for the solution of Lambert’s orbital boundary-value problem. Celest. Mech. Dyn. Astron. 48(2), 145–165 (1990)
Battin, R.H.: An introduction to the mathematics and methods of astrodynamics, AIAA, chp. 7 (1999)
Izzo, D.: Revisiting Lambert’s problem. Celest. Mech. Dyn. Astron. 121(1), 1–15 (2015). https://doi.org/10.1007/s10569--014--9587--y
Arora, N., Russell, R.P., Strange, N., Ottesen, D.: Partial derivatives of the solution to the Lambert boundary value problem. J. Guid. Control Dynam. 38 (9), 1563–1572 (2015). https://doi.org/10.2514/1.G001030
Bombardelli, C., Gonzalo, J.L., Roa, J.: Approximate analytical solution of the multiple revolution Lambert’s targeting problem. J. Guid. Control Dynam. 41(3), 792–801 (2018). https://doi.org/10.2514/1.G002887
Vaddi, S., Alfriend, K.T., Vadali, S., Sengupta, P.: Formation establishment and reconfiguration using impulsive control. J. Guid. Control Dynam. 28(2), 262–268 (2005). https://doi.org/10.2514/1.6687
Gurfil, P.: Relative motion between elliptic orbits: generalized boundedness conditions and optimal formation keeping. J. Guid. Control Dynam. 28(4), 761–767 (2005). https://doi.org/10.2514/1.9439
Woffinden, D.C., Geller, D.K.: Navigating the road to autonomous orbital rendezvous. J. Spacecr. Rocket. 44(4), 898–909 (2007). https://doi.org/10.2514/1.30734
Ichikawa, A., Ichimura, Y.: Optimal impulsive relative orbit transfer along a circular orbit. J. Guid. Control Dynam. 31(4), 1014–1027 (2008). https://doi.org/10.2514/1.32820
Kim, D.-Y., Woo, B., Park, S.-Y., Choi, K.-H.: Hybrid optimization for multiple-impulse reconfiguration trajectories of satellite formation flying. Adv. Space Res. 44(11), 1257–1269 (2009). https://doi.org/10.1016/j.asr.2009.07.029
Huang, W.: Optimal multi-impulse orbit transfer using nonlinear relative motion dynamics. J. Astronaut. Sci. 59(1-2), 237–258 (2012). https://doi.org/10.1007/s40295--013--0015--4
Spencer, D.A., Lovell, T.A.: Maneuver design using relative orbital elements. J. Astronaut. Sci. 62(4), 315–350 (2015). https://doi.org/10.1007/s40295--015--0072--y
Roscoe, C.W., Westphal, J.J., Griesbach, J.D., Schaub, H.: Formation establishment and reconfiguration using differential elements in J2-Perturbed orbits. J. Guid. Control Dynam. 38(9), 1725–1740 (2015). https://doi.org/10.2514/1.G000999
Sobiesiak, L.A., Damaren, C.J.: Impulsive spacecraft formation maneuvers with optimal firing times. J. Guid. Control Dynam. 38(10), 1994–2000 (2015). https://doi.org/10.2514/1.G001095
Starek, J.A., Schmerling, E., Maher, G.D., Barbee, B.W., Pavone, M.: Fast, safe, Propellant-Efficient spacecraft motion planning under Clohessy–Wiltshire–Hill dynamics. J. Guid. Control Dynam. 40(2), 418–438 (2016). https://doi.org/10.2514/1.G001913
Chernick, M., D’Amico, S.: New closed-form solutions for optimal impulsive control of spacecraft relative motion. J. Guid. Control Dynam. 41(2), 301–319 (2018). https://doi.org/10.2514/1.G002848
Vinh, N.X., Gilbert, E.G., Howe, R.M., Sheu, D., Lu, P.: Reachable domain for interception at hyperbolic speeds. Acta Astronaut. 35(1), 1–8 (1995). https://doi.org/10.1016/0094--5765(94)00132--6
Xue, D., Li, J., Baoyin, H., Jiang, F.: Reachable domain for spacecraft with a single impulse. J. Guid. Control Dynam. 33(3), 934–942 (2010). https://doi.org/10.2514/1.43963
Zhang, G., Cao, X., Ma, G.: Reachable domain of spacecraft with a single tangent impulse considering trajectory safety. Acta Astronaut. 91, 228–236 (2013). https://doi.org/10.1016/j.actaastro.2013.06.016
Wen, C., Zhao, Y., Shi, P., Hao, Z.: Orbital accessibility problem for spacecraft with a single impulse. J. Guid. Control Dynam. 37(4), 1260–1271 (2014). https://doi.org/10.2514/1.62629
Holzinger, M.J., Scheeres, D.J., Erwin, R.S.: On-Orbit Operational range computation using gauss’s variational equations with J2 perturbations. J. Guid. Control Dynam. 37(2), 608–622 (2014). https://doi.org/10.2514/1.53861
Wen, C., Zhao, Y., Shi, P.: Precise determination of reachable domain for spacecraft with single impulse. J. Guid. Control Dynam. 37(6), 1767–1779 (2014). https://doi.org/10.2514/1.G000583
Chen, Q., Qiao, D., Shang, H., Liu, X.: A new method for solving reachable domain of spacecraft with a single impulse. Acta Astronaut. 145, 153–164 (2018). https://doi.org/10.1016/j.actaastro.2018.01.040
Lawden, D.F.: Optimal trajectories for space navigation, Butterworths, Chp. 3 (1963)
Lion, P.M., Handelsman, M.: Primer vector on fixed-time impulsive trajectories. AIAA J 6(1), 127–132 (1968). https://doi.org/10.2514/3.4452
Jezewski, D.J., Rozendaal, H.L.: An efficient method for calculating optimal free-space n-impulse trajectories. AIAA J 6(11), 2160–2165 (1968). https://doi.org/10.2514/3.4949
Prussing, J.E.: 2 primer vector theory and applications. Spacecraft Trajectory Optimization, edited by B. Conway 29, 16–36 (2010). https://doi.org/10.1017/CBO9780511778025
Prussing, J.E., Conway, B.A.: Orbital Mechanics. Oxford University Press, USA (1993)
Prussing, J.E.: A class of optimal two-impulse rendezvous using multiple-revolution Lambert solutions. J. Astronaut. Sci. 48(2-3), 131–148 (2000)
Prussing, J.E., Chiu, J.-H.: Optimal multiple-impulse time-fixed rendezvous between circular orbits. J. Guid. Control Dynam. 9(1), 17–22 (1986). https://doi.org/10.2514/3.20060
Hughes, S.P., Mailhe, L.M., Guzman, J.J.: A comparison of trajectory optimization methods for the impulsive minimum fuel rendezvous problem (2003)
Arzelier, D., Bréhard, F., Deak, N., Joldes, M., Louembet, C., Rondepierre, A., Serra, R.: Linearized impulsive fixed-time fuel-optimal space rendezvous: a new numerical approach. IFAC-PapersOnLine 49(17), 373–378 (2016). https://doi.org/10.1016/j.ifacol.2016.09.064
Abdelkhalik, O., Mortari, D.: N-impulse orbit transfer using genetic algorithms. J. Spacecr. Rocket. 44(2), 456–460 (2007). https://doi.org/10.2514/1.24701
Pontani, M., Ghosh, P., Conway, B.A.: Particle swarm optimization of multiple-burn rendezvous trajectories. J. Guid. Control Dynam. 35(4), 1192–1207 (2012). https://doi.org/10.2514/1.55592
Luo, Y.-Z., Tang, G.-J., Li, Y.-J., Li, H.-Y.: Optimization of multiple-impulse, multiple-revolution, rendezvous-phasing maneuvers. J. Guid. Control Dynam. 30(4), 946–952 (2007). https://doi.org/10.2514/1.25620
Sentinella, M.R., Casalino, L.: Cooperative evolutionary algorithm for space trajectory optimization. Celest. Mech. Dyn. Astron. 105(1-3), 211 (2009)
Luo, Y.-Z., Zhang, J., Li, H.-y., Tang, G.-J.: Interactive optimization approach for optimal impulsive rendezvous using primer vector and evolutionary algorithms. Acta Astronaut. 67(3-4), 396–405 (2010). https://doi.org/10.1016/j.actaastro.2010.02.014
Colasurdo, G., Pastrone, D.: Indirect optimization method for impulsive transfers. Astrodynamics Conference, pp. 3762 (1994)
Shen, H.-X., Casalino, L., Luo, Y.-Z.: Global search capabilities of indirect methods for impulsive transfers. J. Astronaut. Sci. 62(3), 212–232 (2015). https://doi.org/10.1007/s40295--015--0073--x
Neustadt, L.W.: Optimization, a moment problem, and nonlinear programming. Journal of the Society for Industrial and Applied Mathematics, Series A:, Control 2 (1), 33–53 (1964). https://doi.org/10.1137/0302004
Prussing, J.E.: Optimal impulsive linear systems: Sufficient conditions and maximum number of impulses. The Journal of the Astronautical Sciences 43(2), 195–206 (1995)
Carter, T.: Optimal impulsive space trajectories based on linear equations. Journal of Optimization Theory and Applications 70(2), 277–297 (1991). https://doi.org/10.1007/BF00940627
Carter, T., Brient, J.: Fuel-optimal rendezvous for linearized equations of motion. J. Guid. Control Dynam. 15(6), 1411–1416 (1992)
Lawden, D.F.: Optimal transfers between coplanar elliptical orbits. J. Guid. Control Dynam. 15(3), 788–791 (1992). https://doi.org/10.2514/3.20909
Baranov, A., Roldugin, D.: Six-impulse maneuvers for rendezvous of spacecraft in near-circular noncoplanar orbits. Cosm. Res. 50(6), 441–448 (2012). https://doi.org/10.1134/S0010952512050012
Iorfida, E., Palmer, P., Roberts, M.: Geometric approach to the perpendicular thrust case for trajectory optimization. J. Guid. Control Dynam., pp. 1059–1068. https://doi.org/10.2514/1.G001525 (2016)
Serra, R., Arzelier, D., Rondepierre, A.: Analytical solutions for impulsive elliptic out-of-plane rendezvous problem via primer vector theory. IEEE Trans. Control Syst. Technol. 26(1), 207–221 (2018). https://doi.org/10.1109/TCST.2017.2656022
Neustadt, L.W.: A general theory of minimum-fuel space trajectories. Journal of the Society for Industrial and Applied Mathematics, Series A:, Control 3(2), 317–356 (1965). https://doi.org/10.1137/0303023
Gergaud, J., Haberkorn, T.: Orbital transfer: some links between the low-thrust and the impulse cases. Acta Astronaut. 60(8-9), 649–657 (2007). https://doi.org/10.1016/j.actaastro.2006.10.009
Zhu, Z., Gan, Q., Yang, X., Gao, Y.: Solving fuel-optimal low-thrust orbital transfers with bang-bang control using a novel continuation technique. Acta Astronaut. 137, 98–113 (2017). https://doi.org/10.1016/j.actaastro.2017.03.032
Taheri, E., Kolmanovsky, I., Atkins, E.: Enhanced smoothing technique for indirect optimization of minimum-fuel low-thrust trajectories. J. Guid. Control Dynam. 39(11), 2500–2511 (2016). https://doi.org/10.2514/1.G000379
Kluever, C.A., Pierson, B.L.: Optimal earth-moon trajectories using nuclear electric propulsion. J. Guid. Control Dynam. 20(2), 239–245 (1997). https://doi.org/10.2514/2.4058
Caillau, J.-B., Noailles, J.: Coplanar control of a satellite around the Earth. ESAIM: Control, Optimisation and Calculus of Variations 6, 239–258 (2001)
Bertrand, R., Epenoy, R.: New smoothing techniques for solving bang–bang optimal control problems—numerical results and statistical interpretation. Optimal Control Applications and Methods 23(4), 171–197 (2002). https://doi.org/10.1002/oca.709
Caillau, J.-B., Gergaud, J., Noailles, J.: 3D geosynchronous transfer of a satellite: Continuation on the thrust. Journal of Optimization Theory and Applications 118(3), 541–565 (2003). https://doi.org/10.1023/B:JOTA.0000004870.74778.ae
Haberkorn, T., Martinon, P., Gergaud, J., et al.: Low-thrust minimum-fuel orbital transfer: a homotopic approach. J. Guid. Control Dynam. 27, 1046–1060 (2004). https://doi.org/10.2514/1.4022
Bonnard, B., Caillau, J.-B., Trélat, E.: Geometric optimal control of elliptic Keplerian orbits. Discrete and Continuous Dynamical Systems-Series S, pp. 929–956 (2005)
La Mantia, M., Casalino, L.: Indirect optimization of low-thrust capture trajectories. J. Guid. Control Dynam. 29(4), 1011–1014 (2006). https://doi.org/10.2514/1.18986
Russell, R.P.: Primer vector theory applied to global low-thrust trade studies. J. Guid. Control Dynam. 30(2), 460–472 (2007). https://doi.org/10.2514/1.22984
Silva, C., Trélat, E.: Smooth regularization of bang-bang optimal control problems. IEEE Trans. Autom. Control 55(11), 2488–2499 (2010). https://doi.org/10.1109/TAC.2010.2047742
Jiang, F., Baoyin, H., Li, J.: Practical techniques for low-thrust trajectory optimization with homotopic approach. J. Guid. Control Dynam. 35(1), 245–258 (2012). https://doi.org/10.2514/1.52476
Dutta, A., Arora, N., Russell, R.P.: Peer-to-peer refueling strategy using low-thrust propulsion. J. Spacecr. Rocket. 49(5), 944–954 (2012). https://doi.org/10.2514/1.A32106
Pan, B., Lu, P., Pan, X., Ma, Y.: Double-homotopy method for solving optimal control problems. J. Guid. Control Dynam. 39(8), 1706–1720 (2016). https://doi.org/10.2514/1.G001553
Zhao, S., Zhang, J.: Minimum-fuel station-change for geostationary satellites using low-thrust considering perturbations. Acta Astronaut. 127, 296–307 (2016). https://doi.org/10.1016/j.actaastro.2016.05.028
Zhao, S., Gurfil, P., Zhang, J.: Initial costates for low-thrust minimum-time station change of geostationary satellites. J. Guid. Control Dynam. 39(12), 2746–2756 (2016). https://doi.org/10.2514/1.G000431
Chi, Z., Yang, H., Chen, S., Li, J.: Homotopy method for optimization of variable-specific-impulse low-thrust trajectories. Astrophysics and Space Science 362, 216 (2017). https://doi.org/10.1007/s10509-017-3196-7
Taheri, E., Li, N.I., Kolmanovsky, I.: Co-state initialization for the minimum-time low-thrust trajectory optimization. Adv. Space Res. 59(9), 2360–2373 (2017). https://doi.org/10.1016/j.asr.2017.02.010
Mall, K., Grant, M.J.: Epsilon-Trig Regularization method for Bang-Bang optimal control problems. J. Optim. Theory Appl. 174(2), 500–517 (2017). https://doi.org/10.1007/s10957--017--1129--9
Sullo, N., Peloni, A., Ceriotti, M.: Low-thrust to solar-sail trajectories: a homotopic approach. J. Guid. Control Dynam. 40(11), 2796–2806 (2017). https://doi.org/10.2514/1.G002552
Zhu, J., Trélat, E., Cerf, M.: Geometric optimal control and applications to aerospace. Pacific Journal of Mathematics for Industry 9(1), 8 (2017). https://doi.org/10.1186/s40736--017--0033--4
Saranathan, H., Grant, M.J.: Relaxed autonomously switched hybrid system approach to indirect multiphase aerospace trajectory optimization. J. Spacecr. Rocket. 55(3), 611–621 (2017). https://doi.org/10.2514/1.A34012
Saghamanesh, M., Baoyin, H.: A robust homotopic approach for continuous variable low-thrust trajectory optimization. Adv. Space Res. 62(11), 3095–3113 (2018). https://doi.org/10.1016/j.asr.2018.08.046
Pérez-Palau, D., Epenoy, R.: Fuel optimization for low-thrust Earth–Moon transfer via indirect optimal control. Celest. Mech. Dyn. Astron. 130(2), 21 (2018). https://doi.org/10.1007/s105
Junkins, J.L., Taheri, E.: Exploration of alternative state vector choices for Low-Thrust trajectory optimization. J. Guid. Control Dynam. 42(1), 47–64 (2018). https://doi.org/10.2514/1.G003686
Pan, B., Pan, X., Zhang, S.: A new probability-one homotopy method for solving minimum-time low-thrust orbital transfer problems. Astrophysics and Space Science 363(9), 198 (2018). https://doi.org/10.1007/s10509--018--3420--0
Taheri, E., Junkins, J.L.: Generic smoothing for optimal bang-off-bang spacecraft maneuvers. J. Guid. Control Dynam. 41(11), 2470–2475 (2018). https://doi.org/10.2514/1.G003604
Pan, B., Pan, X., Ma, Y.: A quadratic homotopy method for fuel-optimal low-thrust trajectory design. Proceedings of the Institution of Mechanical Engineers, Part G:, Journal of Aerospace Engineering 233(5), 1741–1757 (2019). https://doi.org/10.1177/0954410018761965
Walker, M.: A set of modified equinoctial orbit elements. Celest. Mech. Dyn. Astron. 38(4), 391–392 (1986). https://doi.org/10.1007/BF01227493
Taheri, E., Junkins, J.: A generic approach for optimal bang-off-bang spacecraft maneuvers. In: 41st Annual AAS Guidance & Control Conference, Breckenridge, Colorado, AAS 18-088 (2018)
Kelley, H.J.: A second variation test for singular extremals. AIAA J. 2(8), 1380–1382 (1964). https://doi.org/10.2514/3.2562
Breakwell, J.: Minimum impulse transfer. AIAA Astrodynamics Conference, August 19–21, pp. 416 (1963)
Small, H.W.: Minimum N-impulse time-free transfer between elliptic orbits. AIAA J. 9(4), 594–599 (1971)
Small, H.W.: Globally optimal parking orbit transfer. AIAA/AAS Astordynamics Conference, August 19–11, pp. 1478. https://arc.aiaa.org/doi/pdfplus/10.2514/6.1982-1478 (1982)
Prussing, J.: Optimal two-and three-impulse fixed-time rendezvous in the vicinity of a circular orbit. AIAA J. 8(7), 1221–1228 (1970). https://doi.org/10.2514/2.7041
Woollands, R.M., Read, J.L., Probe, A.B., Junkins, J.L.: Multiple revolution solutions for the perturbed lambert problem using the method of particular solutions and picard iteration. J. Astronaut. Sci. 64(4), 361–378 (2017). https://doi.org/10.1007/s40295--017--0116--6
Taheri, E., Abdelkhalik, O.: Fast initial trajectory design for low-thrust restricted-three-body problems. J. Guid. Control Dynam. 38(11), 2146–2160 (2015). https://doi.org/10.2514/1.G000878
Edelbaum, T.N.: Propulsion requirements for controllable satellites. ARS J 31(8), 1079–1089 (1961). https://doi.org/10.2514/8.5723
Vinh, N.X., Kuo, S.H., Marchal, C.: Optimal time-free nodal transfers between elliptical orbits. Acta Astronaut. 17(8), 875–880 (1988). https://doi.org/10.1016/0094--5765(88)90170--1
Martin, C., Conway, B.A.: Optimal low-thrust trajectories using stable manifolds. Spacecraft Trajectory Optimization, pp. 238–262 (2010)
Betts, J.T.: Survey of numerical methods for trajectory optimization. J. Guid. Control Dynam. 21(2), 193–207 (1998). https://doi.org/10.2514/2.4231
Woolley, R.C., Baker, J.D., Landau, D.F., Nicholas, A.K.: Cargo logistics for a notional mars base using solar electric propulsion. Acta Astronaut. 156, 51–57 (2019). https://doi.org/10.1016/j.actaastro.2018.08.026
Woollands, R.M., Taheri, E., Junkins, J.L.: Efficient computation of optimal low thrust gravity perturbed orbit transfers. The Journal of the Astronautical Sciences, pp 1–27. https://doi.org/10.1007/s40295--019--00152--9 (2019)
Acknowledgments
We are pleased to thank our sponsors: AFOSR (Dr. Stacie Williams), AFRL (Dr. Alok Das) and ADS (Dr. Matt Wilkins), for their support and collaborations under various contracts and grants. We are indebted to many colleagues; we especially appreciate the interactions we have had on the ideas in this paper with Prof. Manoranjan Majji. We also appreciate the constructive comments and suggestions made by the reviewers.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
On behalf of both authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Taheri, E., Junkins, J.L. How Many Impulses Redux. J Astronaut Sci 67, 257–334 (2020). https://doi.org/10.1007/s40295-019-00203-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40295-019-00203-1