Skip to main content
SpringerLink
Log in

Parallel Implicit Runge-Kutta Methods Applied to Coupled Orbit/Attitude Propagation

  • Published:
The Journal of the Astronautical Sciences Aims and scope Submit manuscript

Abstract

A variable-step Gauss-Legendre implicit Runge-Kutta (GLIRK) propagator is applied to coupled orbit/attitude propagation. Concepts previously shown to improve efficiency in 3DOF propagation are modified and extended to the 6DOF problem, including the use of variable-fidelity dynamics models. The impact of computing the stage dynamics of a single step in parallel is examined using up to 23 threads and 22 associated GLIRK stages; one thread is reserved for an extra dynamics function evaluation used in the estimation of the local truncation error. Efficiency is found to peak for typical examples when using approximately 8 to 12 stages for both serial and parallel implementations. Accuracy and efficiency compare favorably to explicit Runge-Kutta and linear-multistep solvers for representative scenarios. However, linear-multistep methods are found to be more efficient for some applications, particularly in a serial computing environment, or when parallelism can be applied across multiple trajectories.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. The quaternion is defined here such that \(\bar {\boldsymbol {q}}_{4 \times 1} = \left [ \boldsymbol {e}^{T} \sin \left (\phi / 2 \right ), \quad \cos \left (\phi / 2 \right ) \right ]^{T}\), where e 3×1 is the rotation axis and ϕ is the rotation angle.

  2. A cylindrical Earth shadowing function is assumed in this paper.

  3. The area and orientation of each individual panel i is taken into account in the calculation of C a,i .

  4. The defining arrays of the GLIRK method are calculable for arbitrary s, and may be obtained to high precision using, for example, the Mathematica function NDSolve‘ImplicitRungeKuttaGaussCoefficients [3].

  5. The embedded solution requires a single additional high-fidelity dynamics model evaluation at the initial time and state of the step.

  6. It is noted that, for any ODE solver, the propagation of state transition tensors may be parallelized within a single propagation step over the dimension of the state.

  7. All input options for LSODE are set to default values (with method flag = 10) except for the relative and absolute tolerance parameters: The absolute tolerance is set uniformly to machine epsilon, and the relative tolerance is varied.

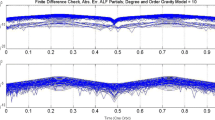
  8. Each subfigure displays results corresponding to a single identical value of relative LTE tolerance, rtol=10−15.

  9. Note that the spherical harmonics formulation of the geopotential is used because it is more efficient than the interpolation model for the low degree and order used for GEO propagation.

  10. Excepting possibly the effect of aerodynamic acceleration on an SO in an extremely low orbit.

  11. This value is problem- and integrator-dependent.

  12. It is noted that erratic behavior for an implicit method can also be caused by frequent divergence of the iterative procedure used to solve the RK update equations, but divergence does not occur over the range of tolerances displayed in the figures in this paper.

  13. Unless the SO is in the Earth’s shadow.

References

  1. Continuing kepler’s quest: assessing air force space command’s astrodynamics standards. Tech. rep., national research council of the national academies, Washington, D. C., pp. 19–43 (2012)

  2. OpenMP application program interface, version 4.0. OpenMP architecture review board (2013)

  3. Wolfram language & system documentation center: Implicitrungekutta method for NDSolve. https://reference.wolfram.com/language/tutorial/NDSolveImplicitRungeKutta.html. Accessed 18 Nov. 2015 (2015)

  4. Aristoff, J.: Method and system for propagating the state of an object and its uncertainty. US Patent 8,909, 588 (2014)

  5. Aristoff, J.M., Poore, A.B.: Implicit Runge-Kutta methods for orbit propagation. In: AAS/AIAA Astrodynamics Specialist Conference, Minneapolis, MN (2012)

  6. Aristoff, J.M., Horwood, J.T., Poore, A.B.: Orbit and uncertainty propagation: a comparison of Gauss-Legendre-, dormand-Prince-, and Chebyshev-Picard-based approaches. Celest. Mech. Dyn. Astr. 118(1), 13–28 (2014a)

  7. Aristoff, J.M., Horwood, J.T., Singh, N., Poore, A.B.: Error estimation and control for efficient and reliable orbit (and uncertainty) propagation. In: AAS/AIAA Space Flight Mechanics Meeting, Santa Fe, NM (2014b)

  8. Aristoff, J.M., Horwood, J.T., Poore, A.B.: Implicit-Runge-Kutta-based methods for fast, precise, and scalable uncertainty propagation. Celest. Mech. Dyn. Astr. 122(2), 169–182 (2015)

    Article  MathSciNet  Google Scholar 

  9. Arora, N., Russell, R.P.: A fast, accurate, and smooth planetary ephemeris retrieval system. Celest. Mech. Dyn. Astr. 108(2), 107–124 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  10. Arora, N., Vittaldev, V., Russell, R.P.: Parallel computation of trajectories using graphics processing units and interpolated gravity models. J. Guid. Control. Dynam. 38(8), 1345–1355 (2015)

    Article  Google Scholar 

  11. Bai, X., Junkins, J.L.: Modified chebyshev-Picard iteration methods for orbit propagation. J. Astronaut. Sci. 58(4), 583–613 (2011)

    Article  Google Scholar 

  12. Bate, R.R., Mueller, D.D., White, J.E.: Fundamentals of Astrodynamics, pp 177–212. Dover Publications, Inc, New York (1971)

    Google Scholar 

  13. Berry, M., Healy, L.: Implementation of gauss-Jackson integration for orbit propagation. J. Astronaut. Sci. 52(3), 331–357 (2004)

    MathSciNet  Google Scholar 

  14. Bradley, B.K., Jones, B.A., Beylkin, G., Sandberg, K., Axelrad, P.: Bandlimited implicit Runge-Kutta integration for astrodynamics. Celest. Mech. Dyn. Astr. 119(2), 143–168 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  15. Doornbos, E.: Thermospheric Density and Wind Determination from Satellite Dynamics. Ph.D Dissertation, TU Delft (2011)

  16. Früh, C, Jah, M.K.: Attitude and orbit propagation of high area-to-mass ratio (HAMR) objects using a semi-coupled approach. J. Astronaut. Sci. 60(1), 32–50 (2014)

    Article  Google Scholar 

  17. Fukushima, T.: Simple, regular, and efficient numerical integration of rotational motion. Astron. J 135(6), 2298–2322 (2008)

    Article  Google Scholar 

  18. Hairer, E., Wanner, G.: Stiff differential equations solved by Radau methods. J. Comput. Appl. Math. 111, 93–111 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  19. Hairer, E., Lubich, C., Wanner, G.: Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations, 2nd edn. No. 31 in Springer Series in Computational Mathematics, pp 30–35, 101, 147, 330–332. Springer, Berlin (2006)

    Google Scholar 

  20. Hairer, E., Norsett, S.P., Wanner, G.: Solving Ordinary Differential Equations 1: Nonstiff Problems, 3rd edn. No. 8 in Springer Series in Computational Mathematics, pp 196–200. Springer, Berlin (2008)

    Google Scholar 

  21. Hatten, N., Russell, R.P.: Parallel implicit Runge-Kutta methods applied to coupled orbit/attitude propagation. In: 26th AAS/AIAA Space Flight Mechanics Meeting, Napa, CA (2016a)

  22. Hatten, N., Russell, R.P.: A smooth and robust Harris-Priester atmospheric density model. In: 26th AAS/AIAA Space Flight Mechanics Meeting, Napa, CA (2016b)

  23. van der Houwen, P.J., Sommeijer, D.P.: Parallel iteration of high-order Runge-Kutta methods with stepsize control. J. Comput. Appl. Math. 29(1), 111–127 (1990)

  24. Jackson, J.: Note on the numerical integration of d 2 x/d t 2 = f(x,t). Mon. Not. R. Astron. Soc. 84, 602–606 (1924)

    Article  Google Scholar 

  25. Jay, L.O.: Structure preservation for constrained dynamics with super partitioned additive Runge-Kutta methods. SIAM J. Sci. Comput. 20(2), 416–446 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  26. Jones, B.A.: Orbit propagation using Gauss-Legendre collocation. In: AAS/AIAA Astrodynamics Specialist Conference, Minneapolis, MN (2012)

  27. Jones, B.A., Anderson, R.L.: A survey of symplectic and collocation integration methods for orbit propagation. In: 22nd Annual AIAA/AAS Space Flight Mechanics Meeting, Charleston, SC (2012)

  28. Kouya, T.: Practical implementation of high-order multiple precision fully implicit runge-Kutta methods with step size control using embedded formula. Int. J. Numer. Meth. Applic. 9(2), 85–108 (2013)

    MATH  MathSciNet  Google Scholar 

  29. Krogh, F.T.: On testing a subroutine for the numerical integration of ordinary differential equations. J. ACM 20(4), 545–562 (1973)

    Article  MATH  Google Scholar 

  30. Le Fevre, C., Morand, V., Delpech, M., Gazzino, C., Henriquel, Y.: Integration of coupled orbit and attitude dynamics and impact on orbital evolution of space debris. In: AAS/AIAA Space Flight Mechanics Meeting, Williamsburg, VA (2015)

  31. Long, A.C., Cappellari Jr., J.O., Velez, C.E., Fuchs, A.J.: Goddard Trajectory Determination System (GTDS) Mathematical Theory Revision 1. NASA, Goddard Space Flight Center, MD (1989)

  32. Macomber, B.D.: Enhancements to the Chebyshev-Picard Iteration Efficiency for Generally Perturbed Orbits and Constrained Dynamical Systems. Ph.D. Dissertation, Texas A&M University (2015)

  33. Markley, F.L.: Spacecraft Attitude Determination and Control, pp 510–522. Kluwer Academic Publishers, Dordrecht (1978)

    Google Scholar 

  34. van der Merwe, R.: Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models. Ph.D. Dissertation, Oregon Heath & Science University (2004)

  35. Montenbruck, O.: Numerical integration methods for orbital motion. Celest. Mech. Dyn. Astron. 53, 59–69 (1992)

    Article  Google Scholar 

  36. Ocampo, C.A.: An architecture for a generalized spacecraft trajectory design and optimization system. In: International Conference on Libration Point Missions and Applications, Girona, Spain (2002)

  37. Prince, P.J., Dormand, J.R.: High order embedded runge-Kutta formulae. J. Comput. Appl. Math. 7(1), 67–75 (1981)

    Article  MATH  MathSciNet  Google Scholar 

  38. Radhakrishnan, K., Hindmarsh, A.: Description and use of LSODE, the Livermore Solver for Ordinary Differential Equations. Tech. Rep. UCRL-ID-113855 Lawrence Livermore National Laboratory, Livermore, CA (1993)

  39. Shampine, L.F., Reichelt, M.W.: The MATLAB ODE suite. SIAM J. Sci. Comput. 18(1), 1–22 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  40. Urrutxua, H., Bombardelli, C., Roa, J.: Gonzalo JL. In: AAS/AIAA Space Flight Mechanics Conference, Napa, CA. Quantification of the performance of numerical orbit propagators (2016)

  41. Wetterer, C.J., Crassidis, J.L., Linares, R., Kelecy, T.M., Ziebart, M.K., Jah, M.K., Cefola, P.J.: Refining space object radiation pressure modeling with bidirectional reflectance distribution functions. J. Guid. Control. Dynam. 37(1), 185–196 (2014)

    Article  Google Scholar 

  42. Woodburn, J., Tanygin, S.: Efficient numerical integration of coupled orbit and attitude trajectories using an Encke type correction algorithm. In: AAS/AIAA Astrodynamics Specialist Conference, Quebec City (2001)

  43. van Zon, R., Schofield, J.: Numerical implementation of the exact dynamics of free rigid bodies. J. Comput. Phys. 225, 145–164 (2007)

Download references

Acknowledgments

This work was funded, in part, by a Phase II SBIR from the Air Force Research Laboratory, contract FA9453-14-C-0295, under a subcontract from Emergent Space Technologies, Inc.

Author information

Authors and Affiliations

  1. Department of Aerospace Engineering and Engineering Mechanics, University of Texas at Austin, Austin, TX, USA

    Noble Hatten & Ryan P. Russell

Authors
  1. Noble Hatten
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ryan P. Russell
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Noble Hatten.

Appendix: A: Local Truncation Error Estimation

Appendix: A: Local Truncation Error Estimation

Position accuracy as a function of high-fidelity dynamics function evaluations (a proxy for CPU time) for three methods of calculating the “comparison solution” for estimating the local trunction error (LTE) is shown in Fig. 13. The figure displays results for three-orbit propagations of the tumbling LEO scenario (Fig. 13a) and non-tumbling GEO scenario (Fig. 13b) introduced in this paper. The variable-fidelity dynamics strategy is used, and the GLIRK solution uses eight stages. The “Kouya” method, which is based on a nearly embedded solution of order s, is the strategy used to produce the results given in this paper [28]. The “Jay” method uses an internal tolerance parameter to generate a less conservative estimate of the LTE based on the order-s comparison solution [25]. The “Radau” method produces a comparison solution using a non-embedded s-stage Radau-IA propagation, which produces a solution of order (2s−1) [19]. For the results presented in Fig. 13, it is assumed that the initial guess for the Radau-IA solution is accurate enough that only one high-fidelity dynamics function evaluation per stage is required to achieve convergence.

Fig. 13
figure 13

Position accuracy as a function of high-fidelity dynamics function evaluations for three LTE calculation methods; relative LTE tolerance of propagators is varied from 10−5−10−15. The Kouya method is used to produce the results given in this paper

Full size image

The inexpensiveness of the nearly embedded Kouya method generally produces a more efficient propagation than the Radau method for a given accuracy when using variable-fidelity dynamics models, even though the Radau method generally uses larger step sizes. On the other hand, the Jay method uses very few function evaluations, but the internal tolerance tends to produce such large step sizes that global error control is poor compared to the other two methods.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hatten, N., Russell, R.P. Parallel Implicit Runge-Kutta Methods Applied to Coupled Orbit/Attitude Propagation. J of Astronaut Sci 64, 333–360 (2017). https://doi.org/10.1007/s40295-016-0103-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40295-016-0103-3

Keywords

Search

Navigation